A Multi-Stage Homotopy Perturbation Method for the Fractional Lotka-Volterra Model
Abstract
:1. Introduction
2. Preliminaries
3. Main Result
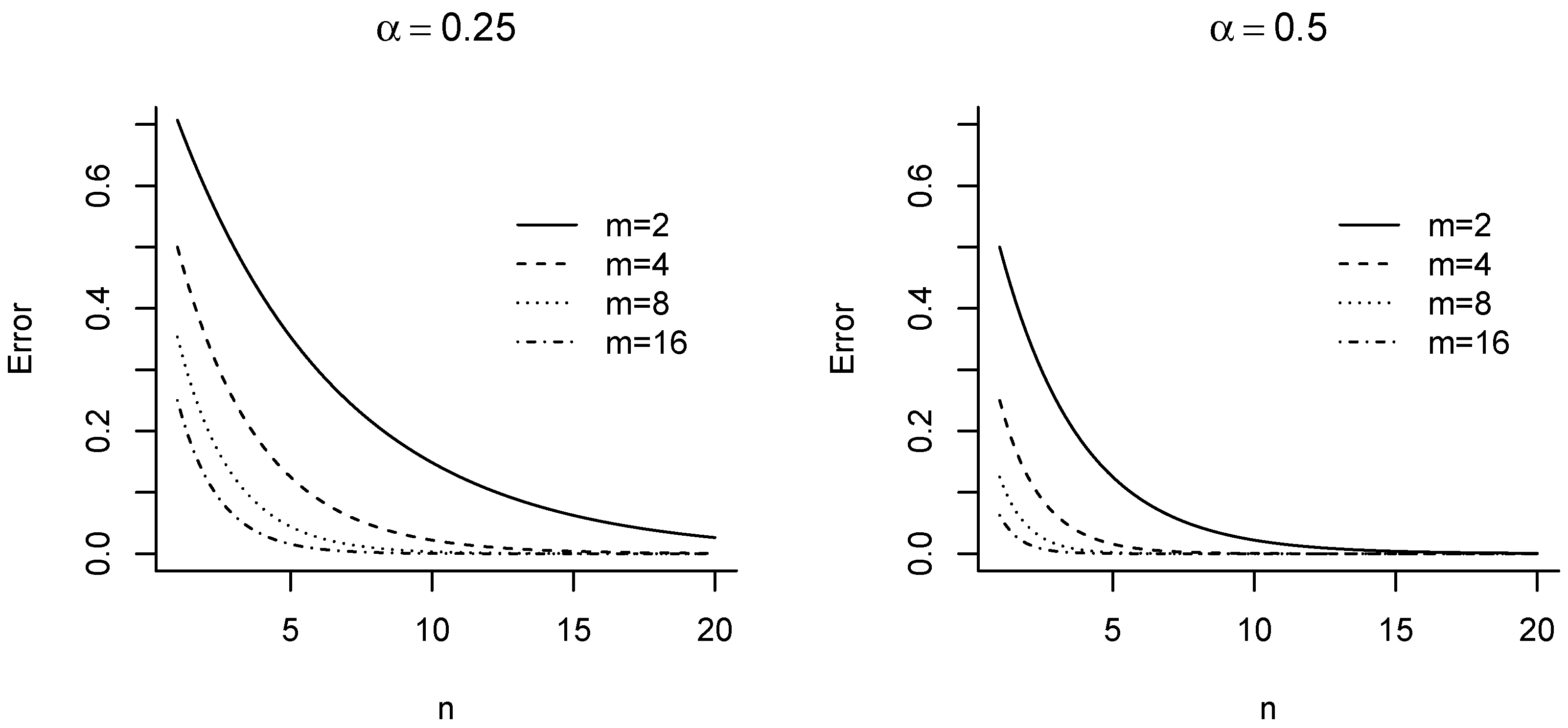
Convergence
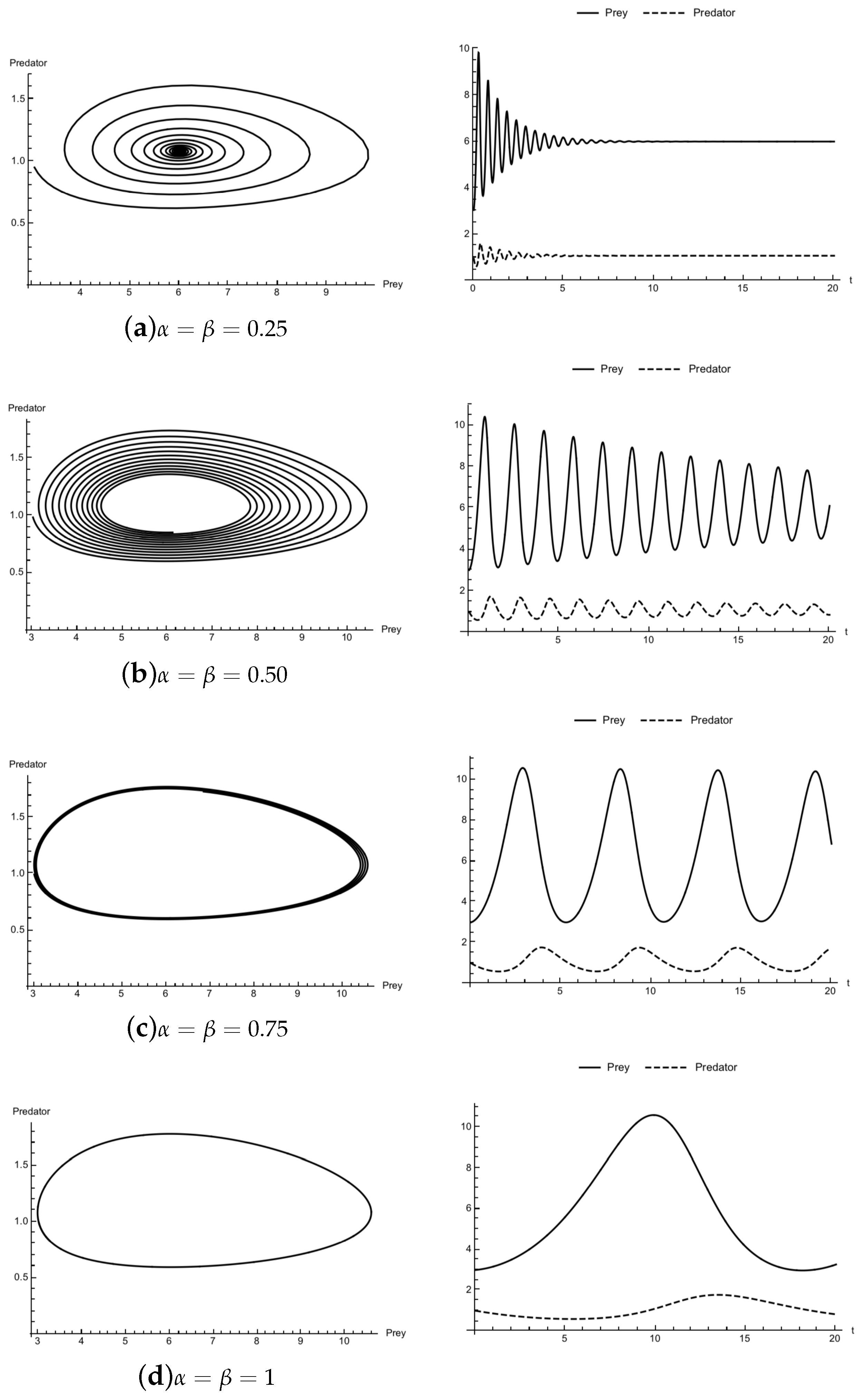
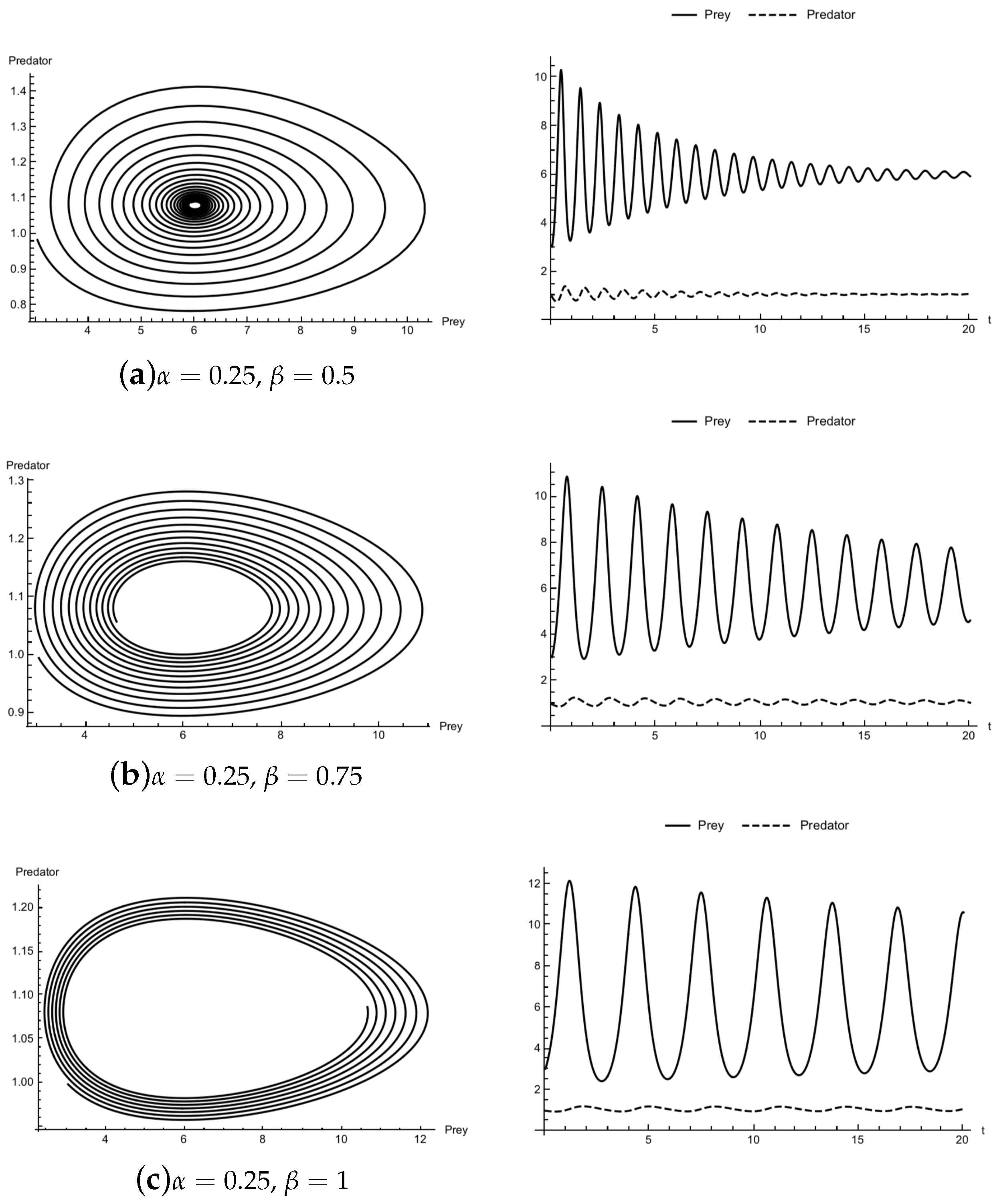
4. Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| HPM | Homotopy perturbation method |
| MHPM | Multistage homotopy perturbation method |
References
- Lotka, A.J. Elements of Physical Biology; Williams and Wilkins: Baltimore, MD, USA, 1925. [Google Scholar]
- Volterra, V. Variazioni e fluttuazioni del numero di individui in specie animali conviventi. Mem. Acad. Lincei 1926, 2, 31–113. [Google Scholar]
- Ahmad, S.; Lazer, A.C. Average conditions for global asymptotic stability in a nonautonomous Lotka-Volterra system. Nonlinear Anal. Theory Methods Appl. 2000, 40, 37–49. [Google Scholar] [CrossRef]
- van den Driessche, P.; Zeeman, D.L. Three-dimensional competitive Lotka-Volterra systems with no periodic orbits. SIAM J. Appl. Math. 1998, 58, 227–234. [Google Scholar]
- Teng, Z.; Chen, L. Global asymptotic stability of periodic Lotka-Volterra systems with delays. Nonlinear Anal. Theory Methods Appl. 2001, 45, 1081–1095. [Google Scholar] [CrossRef]
- Lu, G.; Lu, Z. Permanence for two-species Lotka-Volterra cooperative systems with delays. Math. Biosci. Eng. 2008, 5, 477–484. [Google Scholar] [CrossRef]
- Chen, S.; Shi, J.; Wei, J. A note on Hopf birfucations in a delayed diffusive Lotka-Volterra predator-prey system. Comput. Math. Appl. 2011, 62, 2240–2245. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.; El-Saka, A. Equilibrium points, stability and numerical solution of fractional-order predator-prey and rabies model. J. Math. Anal. Appl. 2007, 321, 542–545. [Google Scholar] [CrossRef]
- Elsadany, A.A.; Matouk, A.E. Dynamical behaviors of fractional-order Lotka-Volterra predator-prey model and its discretization. J. Appl. Math. Comput. 2015, 49, 269–283. [Google Scholar] [CrossRef]
- Bonilla, B.; Rivero, M.; Rodriguez, M.; Trujillo, J.J. Fractional differential equations as alternative models to nonlinear differential equations. Appl. Math. Comput. 2007, 187, 79–88. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A. (Ed.) Handbook of Fractional Calculus with Applications; De Gruyter: Berlin, Germany, 2019; Volumes 1–8. [Google Scholar]
- Napoles, J.E.; Rodriguez, J.M.; Sigarreta, J.M. New Hermite-Hadamard Type Inequalities Involving Non-Conformable Integral Operators. Symmetry 2019, 11, 1108. [Google Scholar] [CrossRef]
- Bisci, G.M.; Radulescu, V.D.; Servadei, R. Variational Methods for Nonlocal Fractional Problems; Encyclopedia of cs and its Applications; Cambridge University Press: Cambridge, UK, 2016; Volume 162. [Google Scholar]
- Javeed, S.; Baleanu, D.; Waheed, A.; Shaukat Khan, M.; Affan, H. Analysis of Homotopy Perturbation Method for Solving Fractional Order Differential Equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
- He, J.H. Homotophy Perturbation Technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Rafei, M.; Daniali, H.; Ganji, D.D.; Pashaei, H. Solution of the prey and predator problem by homotophy perturbation method. Appl. Math. Comput. 2007, 188, 1419–1425. [Google Scholar]
- Kadem, A.; Baleanu, D. Homotopy pertubation method for the coupled fractional Lotka-Volterra equations. Rom. J. Phys. 2011, 56, 332–338. [Google Scholar]
- Chowdhury, M.S.H.; Hashim, I.; Roslan, R. Simulation of the predator-prey problem by the homotopy-perturbation method revised. J. Juliusz Schauder Center 2008, 31, 263–270. [Google Scholar]
- Das, S.; Gupta, P.K. A mathematical model on fractional Lotka-Volterra equations. J. Theor. Biol. 2011, 277, 1–6. [Google Scholar] [CrossRef]
- Dhaigude, D.B.; Birajdar, G.A. Numerical solution of fractional partial differential equations by discrete Adomian decomposition method. Adv. Appl. Math. Mech. 2014, 6, 107–119. [Google Scholar] [CrossRef]
- Muhammed, I.S.; Mohammed, A.O. A Numerical Method for Solving a Class of Nonlinear Second Order Fractional Volterra Integro-Differntial Type of Singularly Perturbed Problems. Mathematics 2018, 6, 48. [Google Scholar] [CrossRef]
- Pitolli, F. A Fractional B-spline Collocation Method for the Numerical Solution of Fractional Predator-Prey Models. Fractal Fract. 2018, 2, 13. [Google Scholar] [CrossRef]
- Pilar, M.; Trujillo, J.J.; Luis, V.; Rivero, M. Fractional dynamics of populations. Appl. Math. Comput. 2011, 218, 1089–1095. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications Fractional Differential Equations; Elsevier: San Diego, CA, USA, 2006. [Google Scholar]
- Tavazoei, M.S.; Haeri, M. Chaotic attractors in incommensurate fractional order systems. Phys. D 2008, 237, 2628–2637. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arciga-Alejandre, M.P.; Sanchez-Ortiz, J.; Ariza-Hernandez, F.J.; Catalan-Angeles, G. A Multi-Stage Homotopy Perturbation Method for the Fractional Lotka-Volterra Model. Symmetry 2019, 11, 1330. https://doi.org/10.3390/sym11111330
Arciga-Alejandre MP, Sanchez-Ortiz J, Ariza-Hernandez FJ, Catalan-Angeles G. A Multi-Stage Homotopy Perturbation Method for the Fractional Lotka-Volterra Model. Symmetry. 2019; 11(11):1330. https://doi.org/10.3390/sym11111330
Chicago/Turabian StyleArciga-Alejandre, Martin P., Jorge Sanchez-Ortiz, Francisco J. Ariza-Hernandez, and Gabriel Catalan-Angeles. 2019. "A Multi-Stage Homotopy Perturbation Method for the Fractional Lotka-Volterra Model" Symmetry 11, no. 11: 1330. https://doi.org/10.3390/sym11111330
APA StyleArciga-Alejandre, M. P., Sanchez-Ortiz, J., Ariza-Hernandez, F. J., & Catalan-Angeles, G. (2019). A Multi-Stage Homotopy Perturbation Method for the Fractional Lotka-Volterra Model. Symmetry, 11(11), 1330. https://doi.org/10.3390/sym11111330




