A New Stability Theory for Grünwald–Letnikov Inverse Model Control in the Multivariable LTI Fractional-Order Framework
Abstract
1. Introduction
2. Fractional-Order State–Space System Representation
3. Fractional-Order Perfect Control
4. An Application of Parameter Matrix Right Inverses into Fractional-Order Perfect Control Law
4.1. Selection of Nonunique Right Inverse
4.2. Inverses of Nonsquare (Parameter) Matrices
4.3. Employment of Right Inverses into Fractional-Order Perfect Control Law
4.4. Necessary Conditions for Application of Right Inverses to the Product of
5. Stability of Fractional-Order Discrete-Time Perfect Control
5.1. Integer-Order Instance
5.2. Fractional-Order Instance
6. Control Zeros and Minimum-Phase Property
6.1. Control Zeros
6.2. Pole-Free Fractional-Order Perfect Control
6.3. Minimum-Phase Property of the Discrete-Time Fractional-Order Systems
7. Robustness of Fractional-Order Perfect Control
8. Simulation Examples
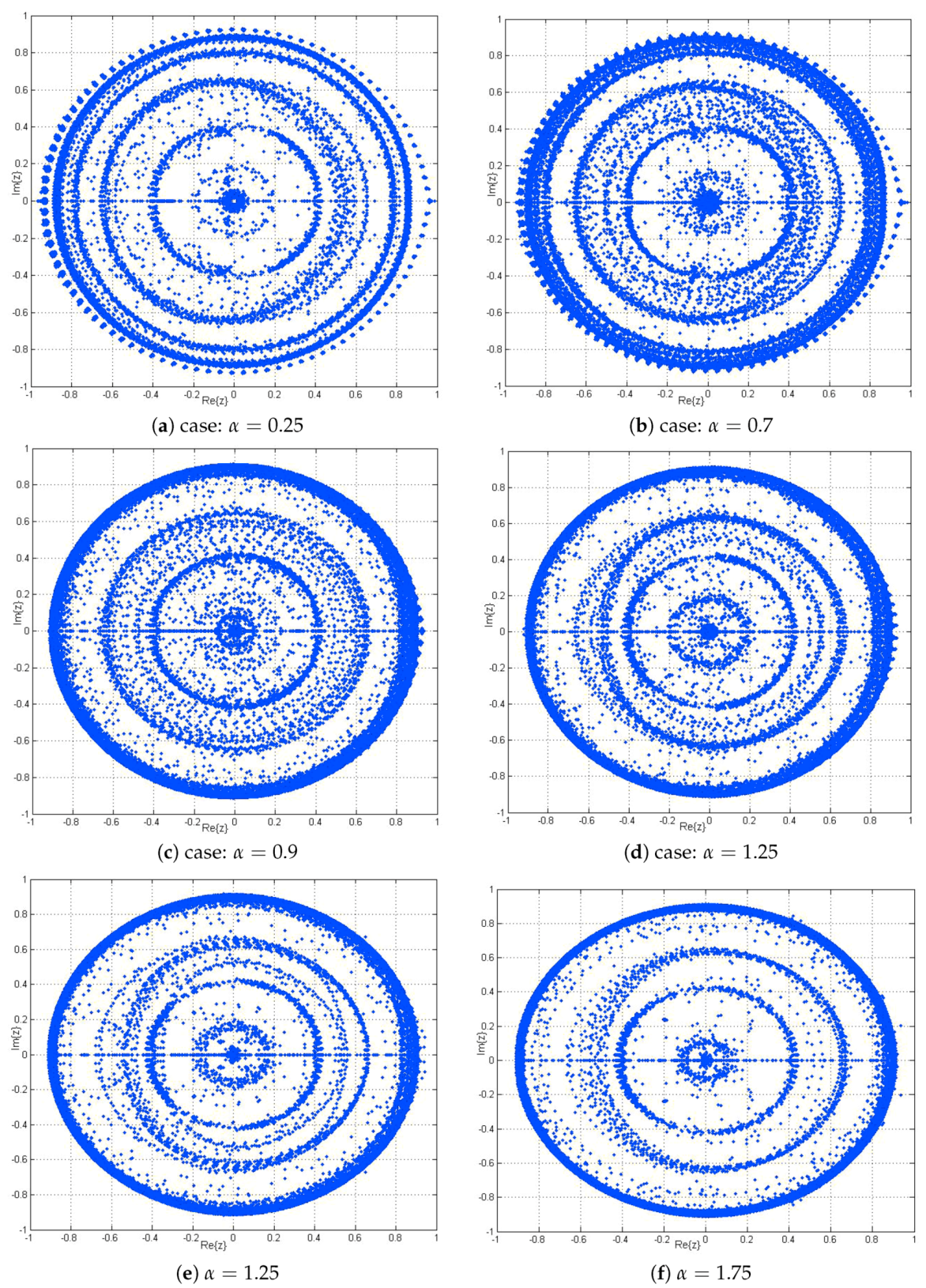
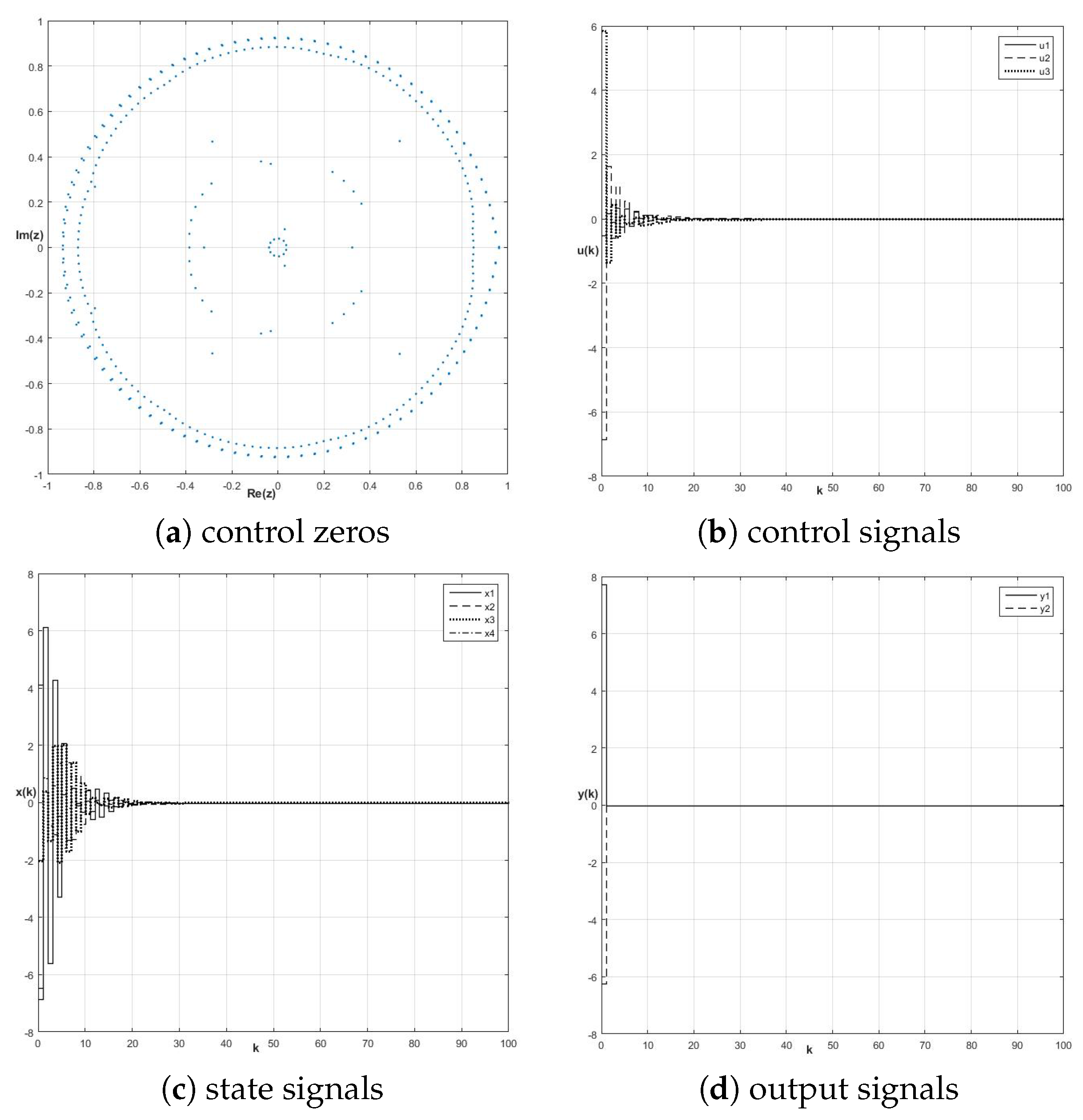
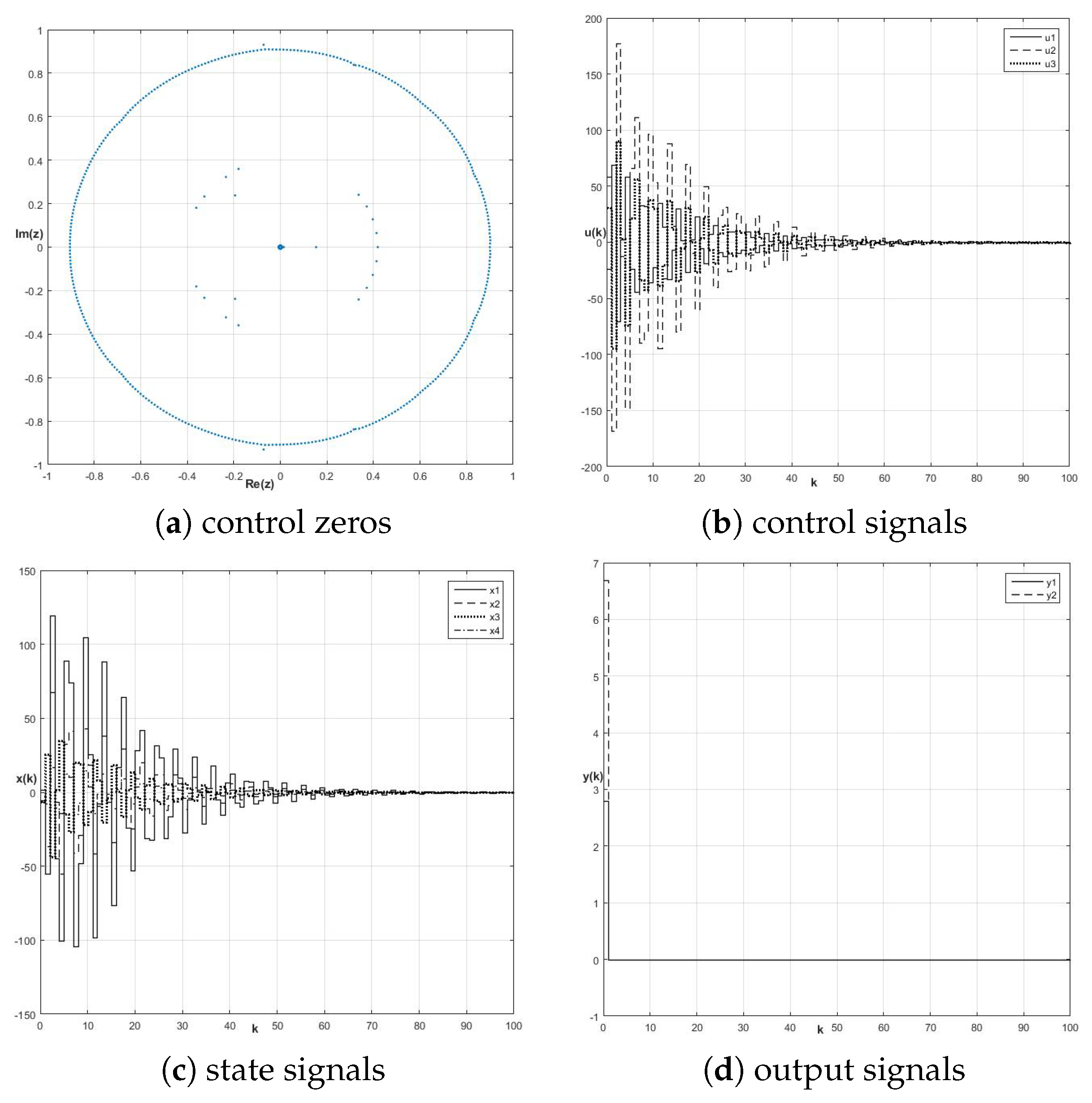
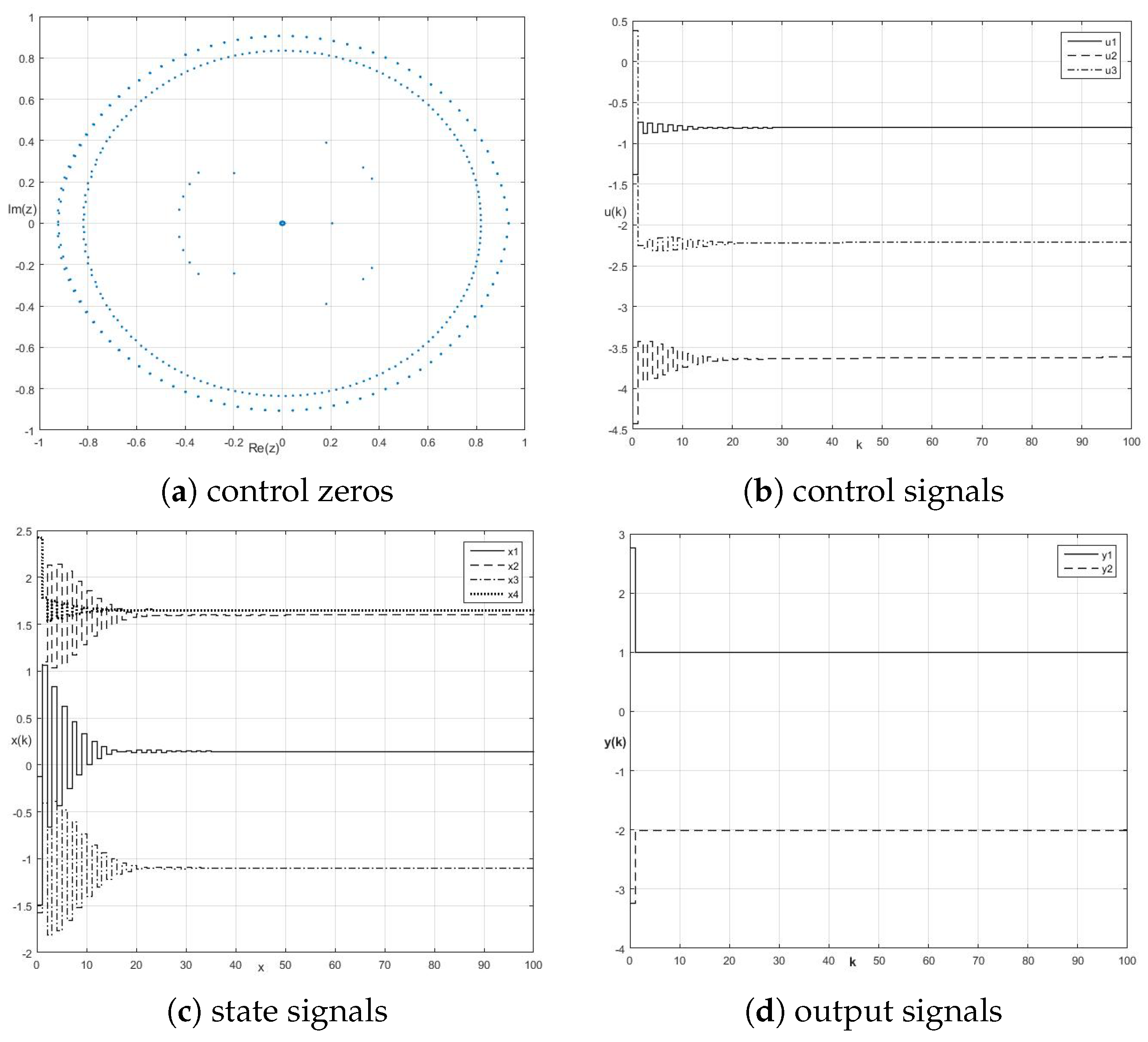
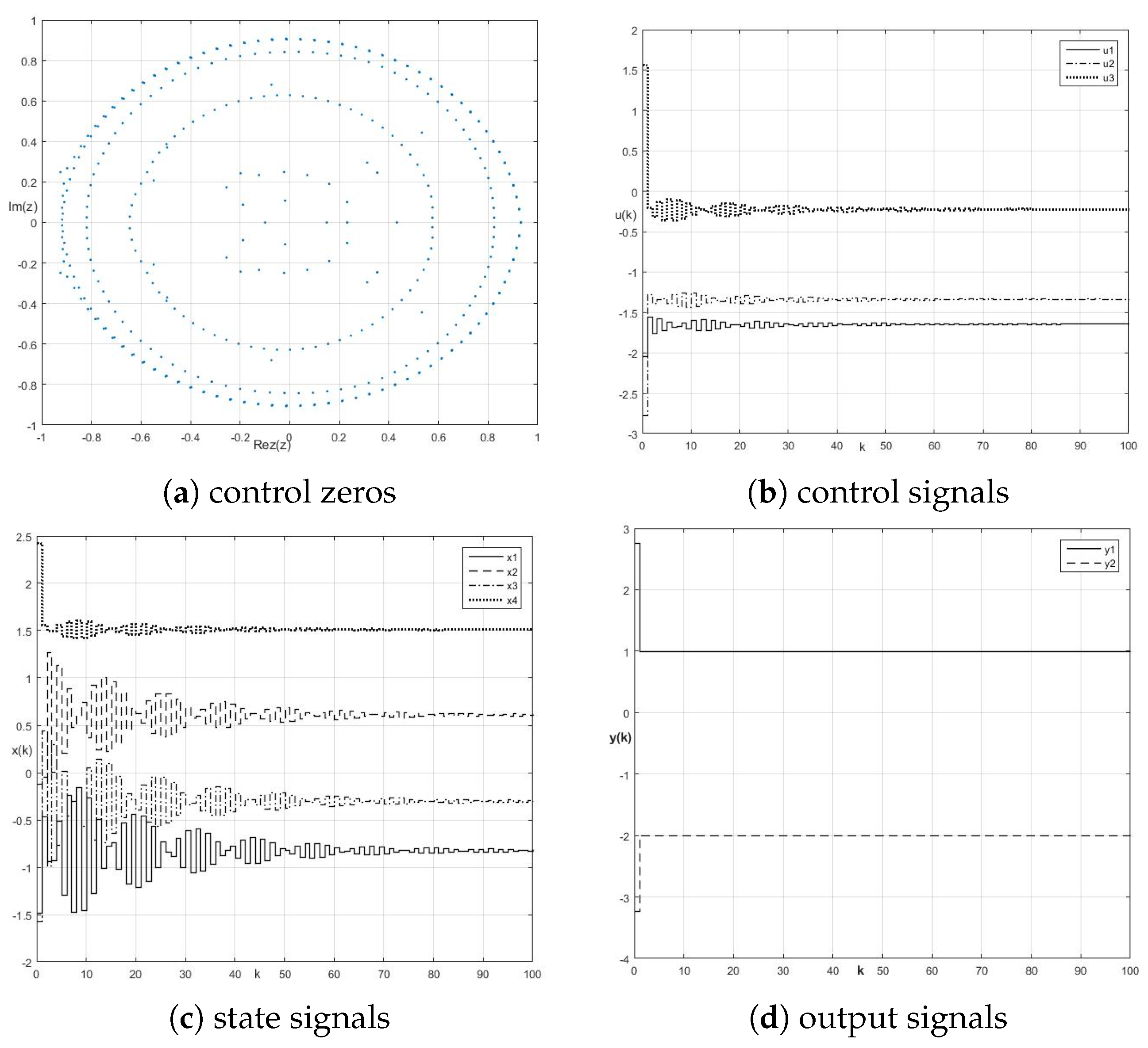
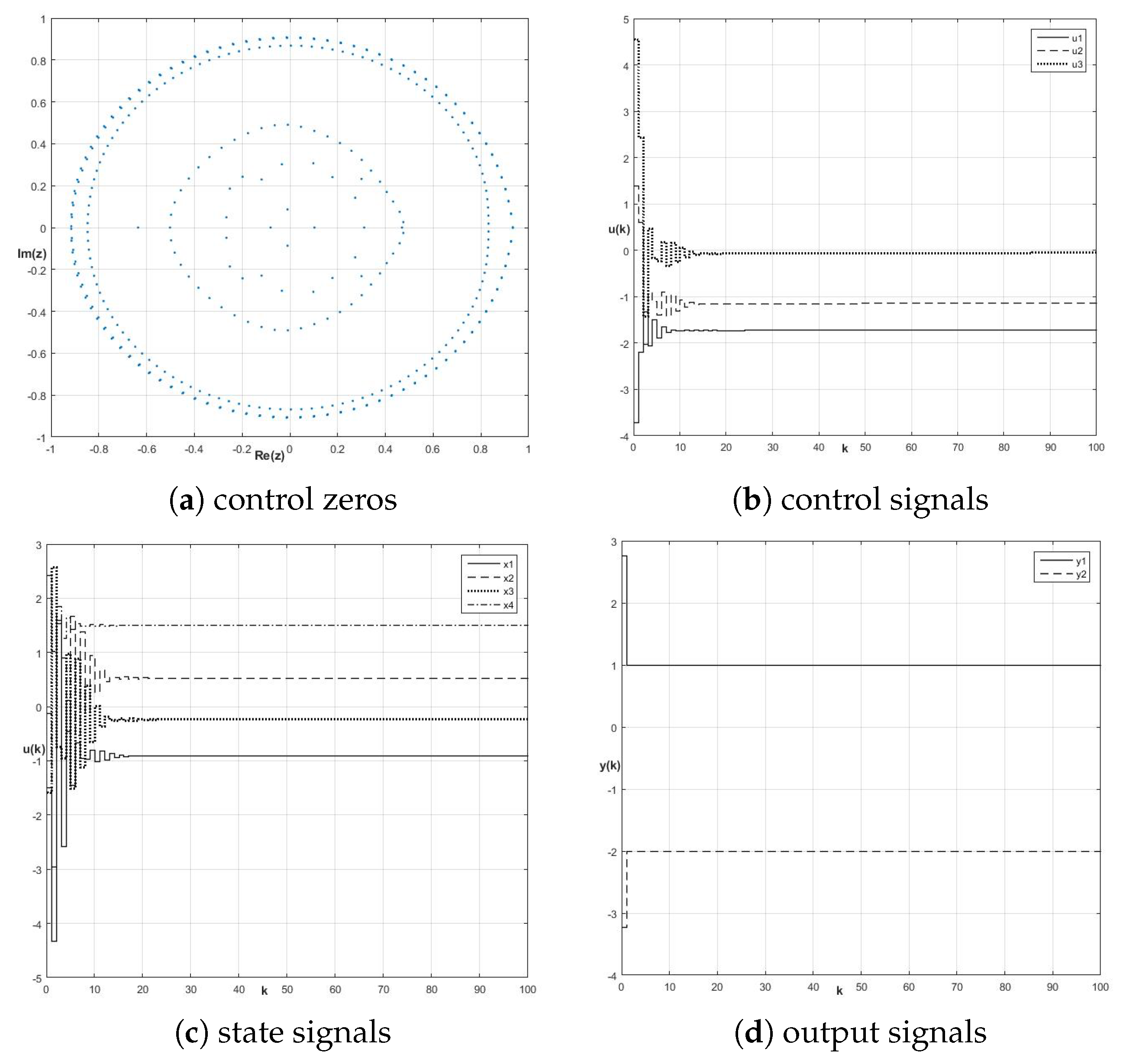
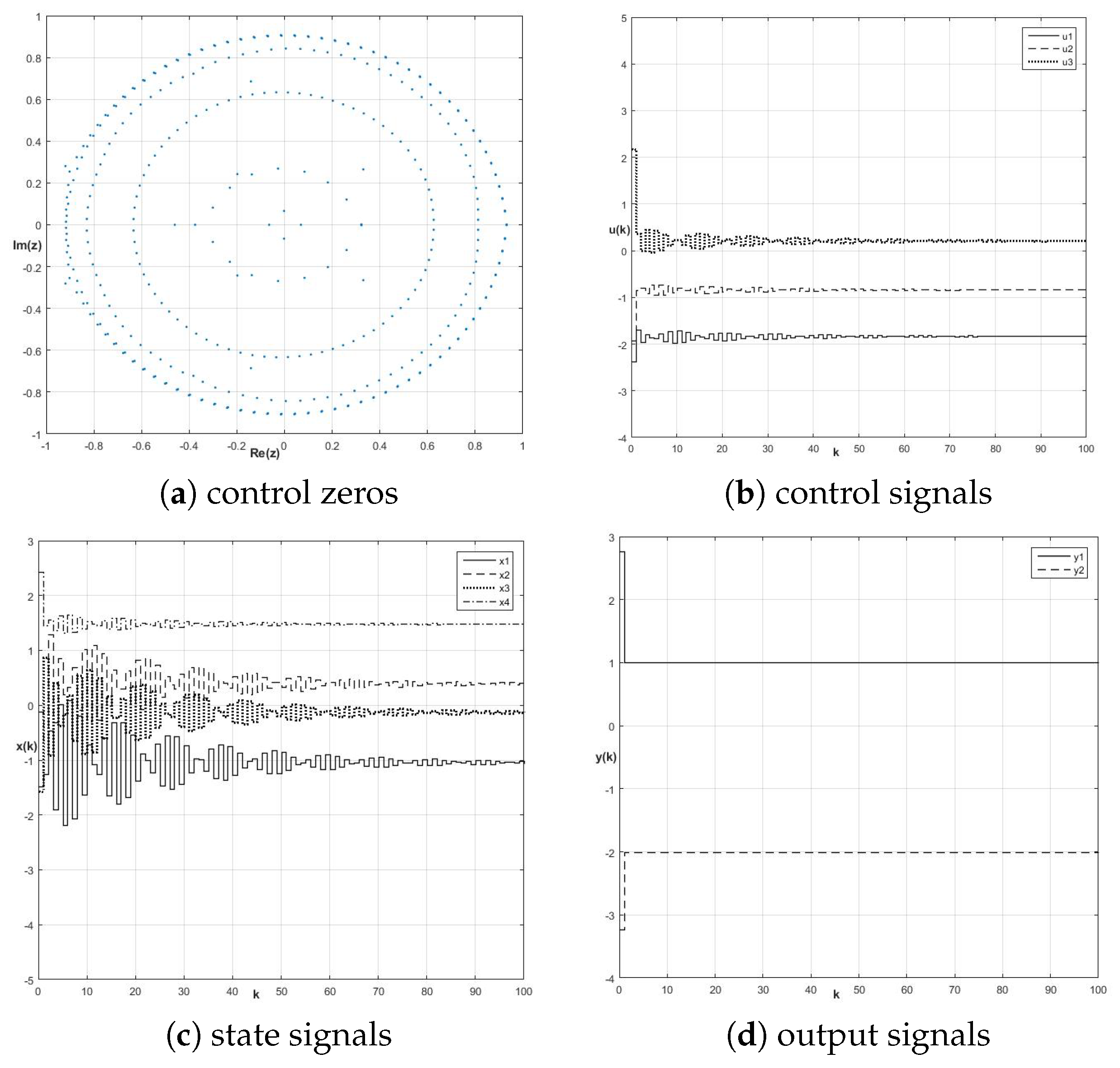
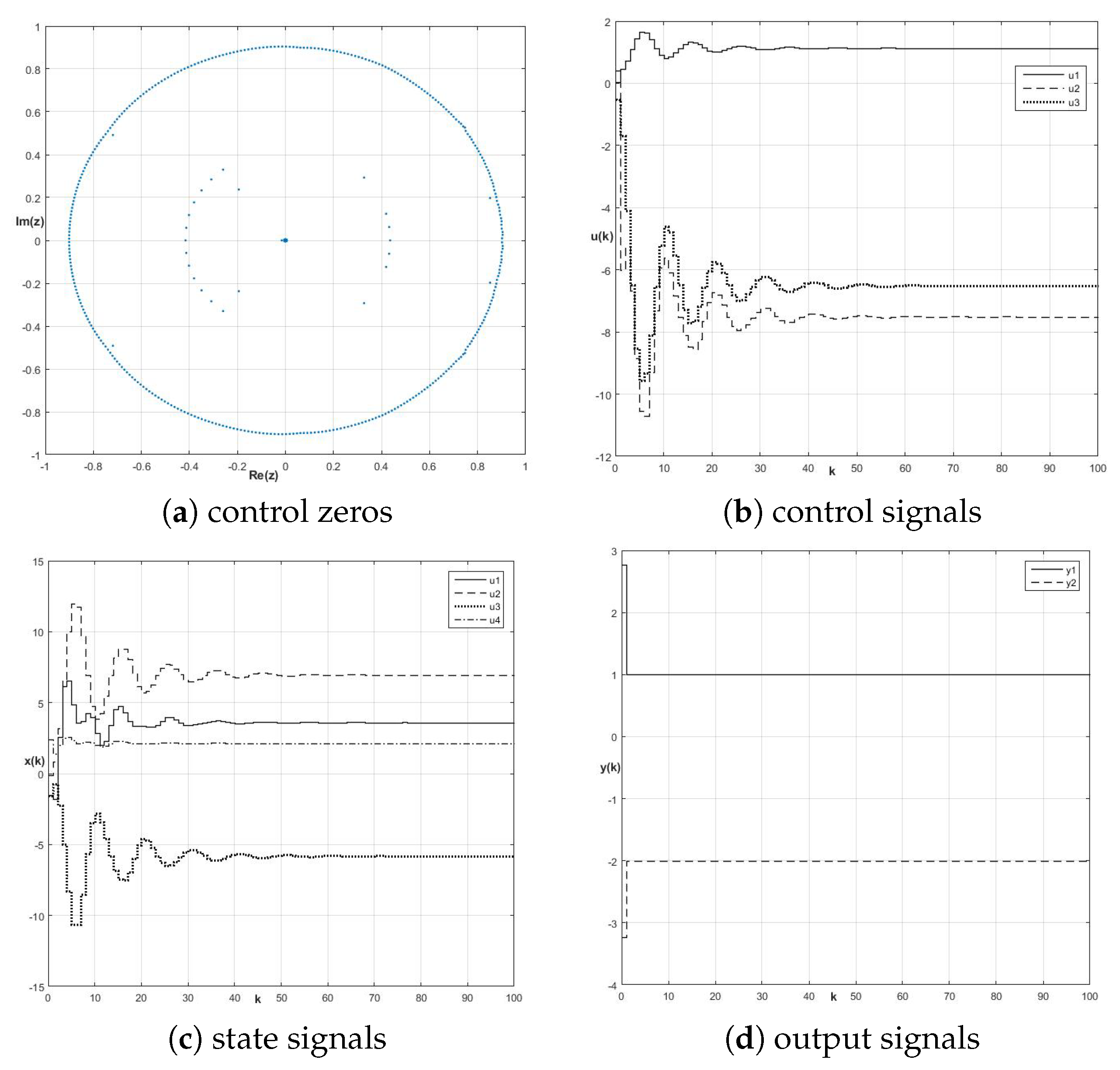
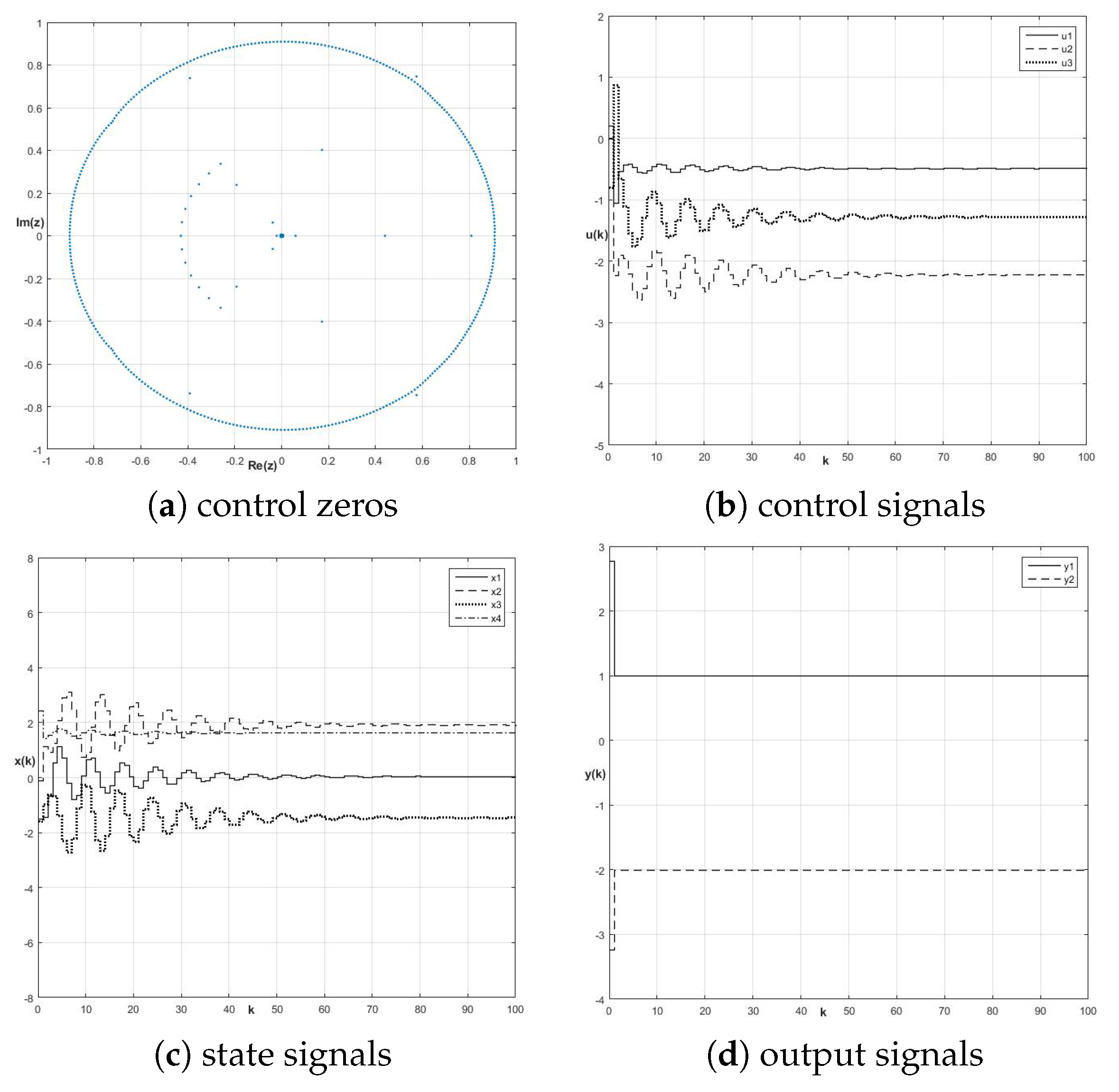
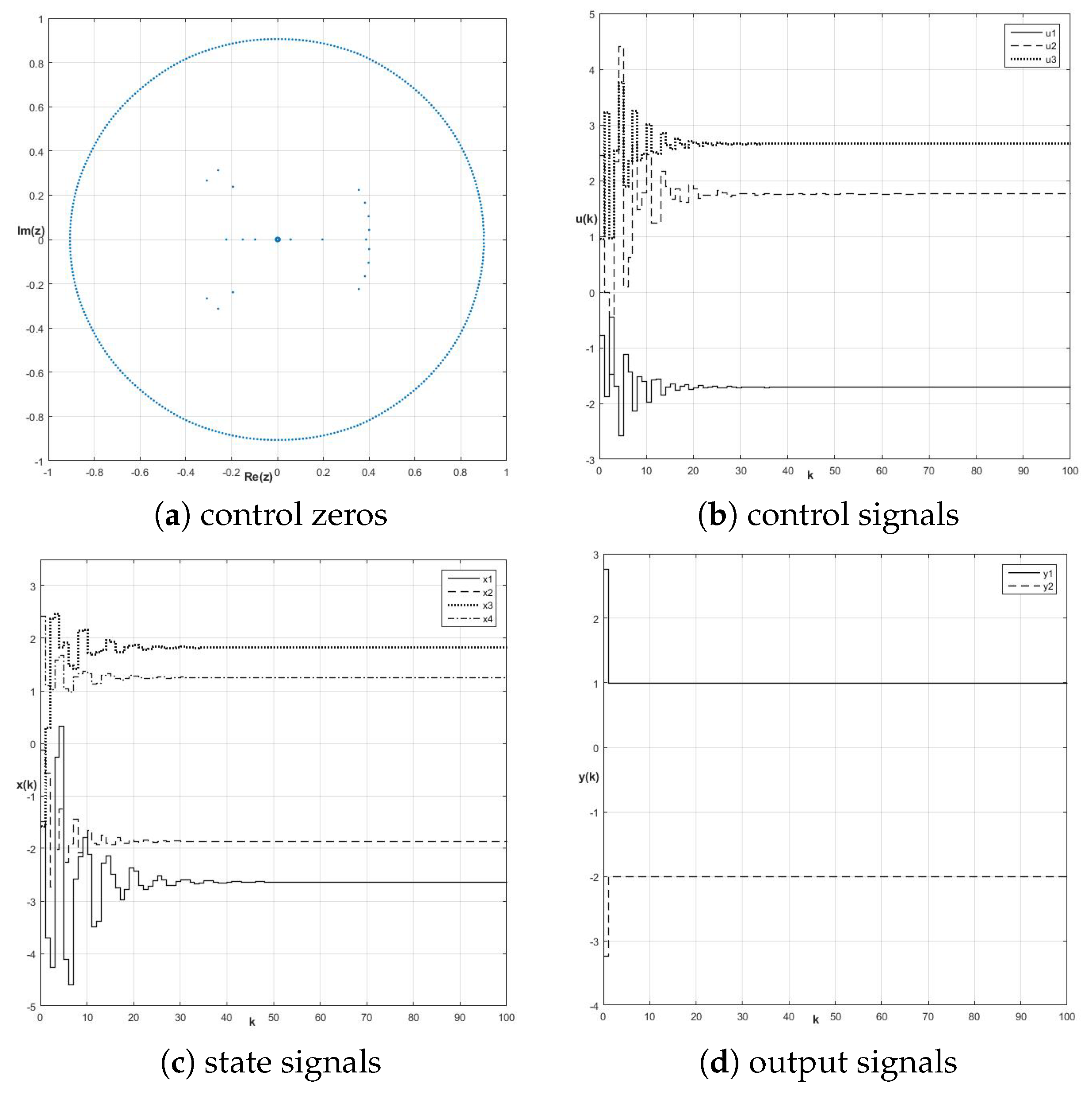
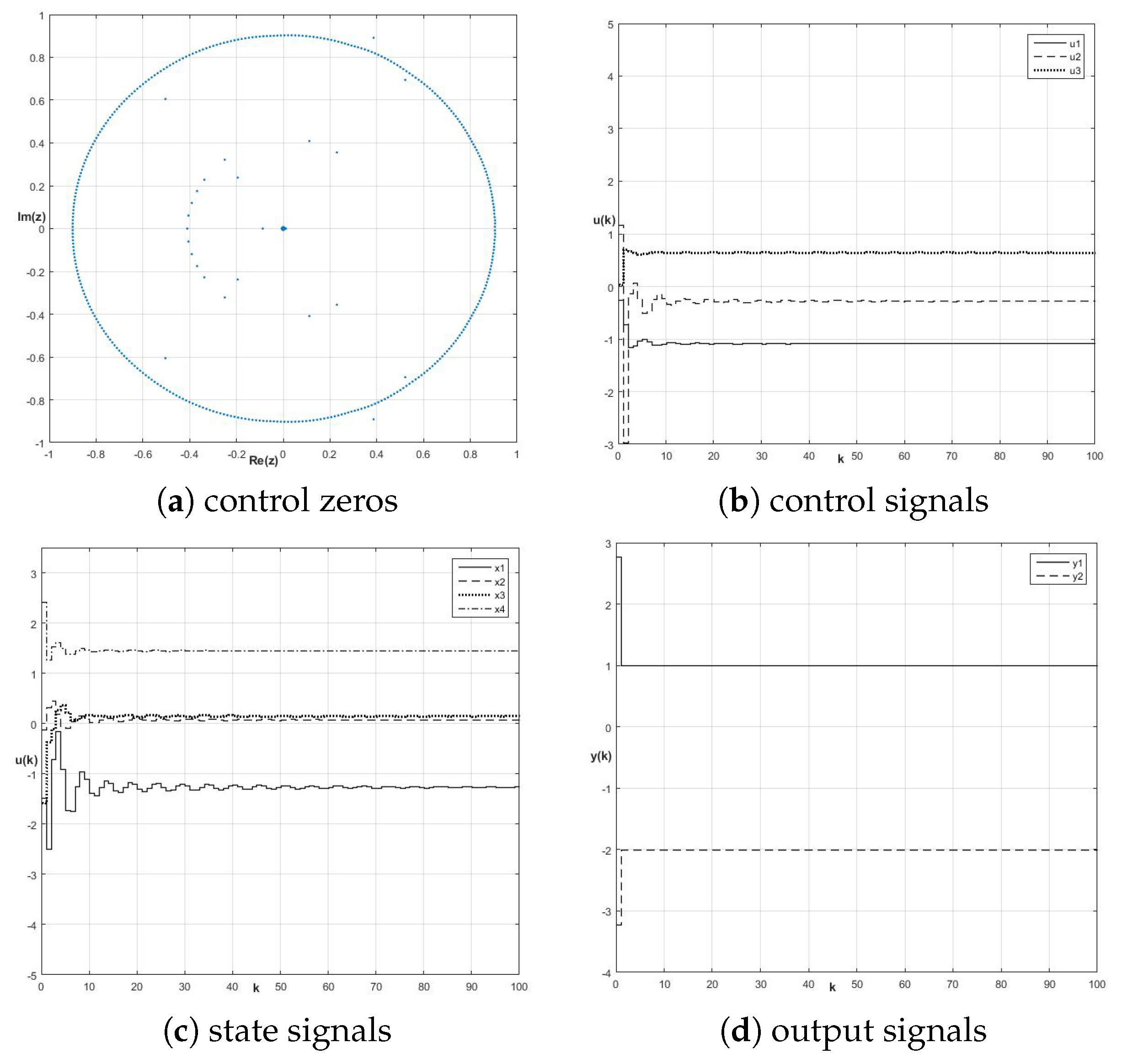
8.1. Control Zeros and Fractional-Order Perfect Control Stability
8.2. Energy-Based Approach to Robustness of Fractional-Order Perfect Control
9. Conclusions and Open Problems
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| G-L | Grünwald–Letnikov |
| IMC | Inverse Model Control |
| LTI | Linear Time-Invariant |
| MIMO | Multiple-Input/Multiple-Output |
| MVC | Minimum Variance Control |
| Fractional-Order Plant | |
| Integer-Order Plant |
References
- Latawiec, K.; Bańka, S.; Tokarzewski, J. Control zeros and nonminimum phase LTI MIMO systems. Annu. Rev. Control. 2000, 24, 105–112. [Google Scholar] [CrossRef]
- Borisson, U. Self-tuning regulators for a class of multivariable systems. Automatica 1979, 15, 209–215. [Google Scholar] [CrossRef]
- Åström, K.J. Introduction to Stochastic Control Theory; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Åström, K.J.; Wittenmark, B. On self-tuning regulators. Automatica 1973, 9, 185–199. [Google Scholar] [CrossRef]
- Ryan, E.P.; Sangwin, C.J.; Townsend, P. Controlled functional differential equations: Approximate and exact asymptotic tracking with prescribed transient performance. ESAIM COCV 2009, 15, 745–762. [Google Scholar] [CrossRef]
- Hunek, W.P. Control Zeros for Continuous-Time LTI MIMO Systems and Their Application in the Theory of Circuits and Systems. Ph.D. Thesis, Opole University of Technology Press, Opole, Poland, 2003. [Google Scholar]
- Dadhich, S.; Birk, W. Analysis and control of an extended Quadruple tank process. In Proceedings of the 13th IEEE European Control Conference (ECC’2014), Strasbourg, France, 24–27 June 2014; pp. 838–843. [Google Scholar] [CrossRef]
- Hunek, W.P.; Latawiec, K. A study on new right/left inverses of nonsquare polynomial matrices. Int. J. Appl. Math. Comput. Sci. 2011, 21, 331–348. [Google Scholar] [CrossRef]
- Lin, Z.; Saberi, A.; Sannuti, P.; Shamash, Y.A. Perfect regulation of linear discrete-time systems: A low-gain-based design approach. Automatica 1996, 32, 1085–1091. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.G.; Zhong, Z.Y.; Cai, G.P. Hysteresis model and adaptive vibration suppression for a smart beam with time delay. J. Sound Vib. 2015, 358, 35–47. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, B.T.; Li, H.G.; Meng, G. Dynamic modeling and adaptive vibration control study for giant magnetostrictive actuators. Sens. Actuators A Phys. 2013, 190, 96–105. [Google Scholar] [CrossRef]
- Tokarzewski, J. Zeros in Linear Systems: A Geometric Approach; Warsaw University of Technology Press: Warsaw, Poland, 2002. [Google Scholar]
- Tokarzewski, J. A note on some characterization of invariant zeros in singular systems and algebraic criteria of nondegeneracy. Int. J. Appl. Math. Comput. Sci. 2004, 14, 149–159. [Google Scholar]
- Tokarzewski, J. Finite Zeros in Discrete Time Control Systems; Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 2006; Volume 338. [Google Scholar] [CrossRef]
- Hunek, W.P.; Krok, M. Pole-free perfect control for nonsquare LTI discrete-time systems with two state variables. In Proceedings of the 2017 13th International Conference on Control & Automation (ICCA), Xi’an, China, 20–23 August 2017; pp. 329–334. [Google Scholar]
- Nastac, S.; Debeleac, C.; Vlase, S. Hysteretically Symmetrical Evolution of Elastomers-Based Vibration Isolators within α-Fractional Nonlinear Computational Dynamics. Symmetry 2019, 11, 924. [Google Scholar] [CrossRef]
- Jajarmi, A.; Hajipour, M.; Mohammadzadeh, E.; Baleanu, D. A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J. Frankl. Inst. 2018, 355, 3938–3967. [Google Scholar] [CrossRef]
- Wei, Y.Q.; Liu, D.Y.; Boutat, D. Innovative fractional derivative estimation of the pseudo-state for a class of fractional order linear systems. Automatica 2019, 99, 157–166. [Google Scholar] [CrossRef]
- Wach, Ł.; Hunek, W.P. Perfect control for fractional-order multivariable discrete-time systems. In Theoretical Developments and Applications of Non-Integer Order Systems; Springer: Cham, Switzerland, 2016; pp. 233–237. [Google Scholar]
- Hunek, W.P. An application of new polynomial matrix σ-inverse in minimum-energy design of robust minimum variance control for nonsquare LTI MIMO systems. IFAC-PapersOnLine 2015, 48, 150–154. [Google Scholar] [CrossRef]
- Hunek, W.P.; Krok, M. A study on a new criterion for minimum-energy perfect control in the state-space framework. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2019. [Google Scholar] [CrossRef]
- Wang, G.; Wei, Y.; Qia, S. Generalized Inverses: Theory and Computations; Science Press: Beijing, China, 2018. [Google Scholar]
- Wei, Y.; Stanimirović, P.S.; Petković, M.D. Numerical and Symbolic Computations of Generalized Inverses; World Scientific Publishing Co. Pte Ltd.: Singapore, 2018. [Google Scholar]
- Hunek, W.P. New SVD-based matrix H-inverse vs. minimum-energy perfect control design for state-space LTI MIMO systems. In Proceedings of the 2016 20th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 13–15 October 2016; pp. 14–19. [Google Scholar]
- Noueili, L.; Chagra, W.; Ksouri, M. New Iterative Learning Control Algorithm Using Learning Gain Based on σ Inversion for Nonsquare Multi-Input Multi-Output Systems. Model. Simul. Eng. 2018, 2018, 4195938. [Google Scholar] [CrossRef]
- Hunek, W.P.; Wach, Ł. Towards a New Stability Criterion for Fractional-Order Perfect Control of LTI MIMO Discrete-Time Systems in State Space. In Proceedings of the 2017 3rd IEEE International Conference on Cybernetics (CYBCONF), Exeter, UK, 21–23 June 2017; pp. 1–6. [Google Scholar]
- De la Sen, M. On Cauchy’s Interlacing Theorem and the Stability of a Class of Linear Discrete Aggregation Models Under Eventual Linear Output Feedback Controls. Symmetry 2019, 11, 712. [Google Scholar] [CrossRef]
- Ben-Israel, A.; Greville, T. Generalized Inverses, Theory and Applications, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Bronnikov, A.; Borovkov, A. Inverse control of discrete-time multivariable systems. J. Frankl. Inst. 2002, 339, 335–345. [Google Scholar] [CrossRef]
- Karampetakis, N.P.; Tzekis, P. On the computation of the generalized inverse of a polynomial matrix. IMA J. Math. Control Inf. 2001, 18, 83–97. [Google Scholar] [CrossRef]
- Penrose, R. A generalized inverse for matrices. Math. Proc. Camb. Philos. Soc. 1955, 51, 406–413. [Google Scholar] [CrossRef]
- Hunek, W.P.; Latawiec, K.; Stanisławski, R.; Łukaniszyn, M.; Dzierwa, P. A new form of a σ-inverse for nonsquare polynomial matrices. In Proceedings of the 2013 18th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2013; pp. 282–286. [Google Scholar]
- Hunek, W.P.; Latawiec, K.J.; Majewski, P.; Dzierwa, P. An application of a new matrix inverse in stabilizing state-space perfect control of nonsquare LTI MIMO systems. In Proceedings of the 2014 19th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 2–5 September 2013; pp. 451–455. [Google Scholar]
- Majewski, P. Research towards Increasing the Capacity of Wireless Data Communication Using Inverses of Nonsquare Polynomial Matrices. Ph.D. Thesis, Opole University of Technology Press, Opole, Poland, 2017. [Google Scholar]
- Dabiri, A.; Butcher, E.A.; Poursina, M.; Nazari, M. Optimal Periodic-Gain Fractional Delayed State Feedback Control for Linear Fractional Periodic Time-Delayed Systems. IEEE Trans. Autom. Control 2018, 63, 989–1002. [Google Scholar] [CrossRef]
- Kaczorek, T. Minimum energy control of fractional descriptor positive discrete-time linear systems. Int. J. Appl. Math. Comput. Sci. 2014, 24, 735–743. [Google Scholar] [CrossRef]
- Kaczorek, T. Minimum energy control of fractional positive continuous-time linear systems using Caputo-Fabrizio definition. Bull. Pol. Acad. Sci.-Tech. Sci. 2017, 65, 45–51. [Google Scholar] [CrossRef][Green Version]
- Klamka, J. Controllability and Minimum Energy Control Problem of Fractional Discrete-Time Systems. In New Trends in Nanotechology and Fractional Calculus Applications; Baleanu, D., Guvenc, Z.B., Machado, J.A.T., Eds.; Springer: Cham, The Netherlands, 2010; pp. 503–509. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F.; Karimi-Ghartemani, M. Method for designing PIλDμstabilisers for minimum-phase fractional-order systems. IET Control Theory Appl. 2010, 4, 61–70. [Google Scholar] [CrossRef]
- Yige, Z.; Meirong, X. Stability and stabilization for a class of fractional-order linear time-delay systems. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 11340–11344. [Google Scholar] [CrossRef]
- Yuan, T.; Zheng, M.; Zhang, K.; Huang, T. Fractional-order PID controllers for stabilization of fractional-order time delay systems based on region stability. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 6633–6638. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hunek, W.P.; Wach, Ł. A New Stability Theory for Grünwald–Letnikov Inverse Model Control in the Multivariable LTI Fractional-Order Framework. Symmetry 2019, 11, 1322. https://doi.org/10.3390/sym11101322
Hunek WP, Wach Ł. A New Stability Theory for Grünwald–Letnikov Inverse Model Control in the Multivariable LTI Fractional-Order Framework. Symmetry. 2019; 11(10):1322. https://doi.org/10.3390/sym11101322
Chicago/Turabian StyleHunek, Wojciech Przemysław, and Łukasz Wach. 2019. "A New Stability Theory for Grünwald–Letnikov Inverse Model Control in the Multivariable LTI Fractional-Order Framework" Symmetry 11, no. 10: 1322. https://doi.org/10.3390/sym11101322
APA StyleHunek, W. P., & Wach, Ł. (2019). A New Stability Theory for Grünwald–Letnikov Inverse Model Control in the Multivariable LTI Fractional-Order Framework. Symmetry, 11(10), 1322. https://doi.org/10.3390/sym11101322




