Effect of Voids Behind Lining on the Failure Behavior of Symmetrical Double-Arch Tunnels
Abstract
1. Introduction
2. Experimental Study
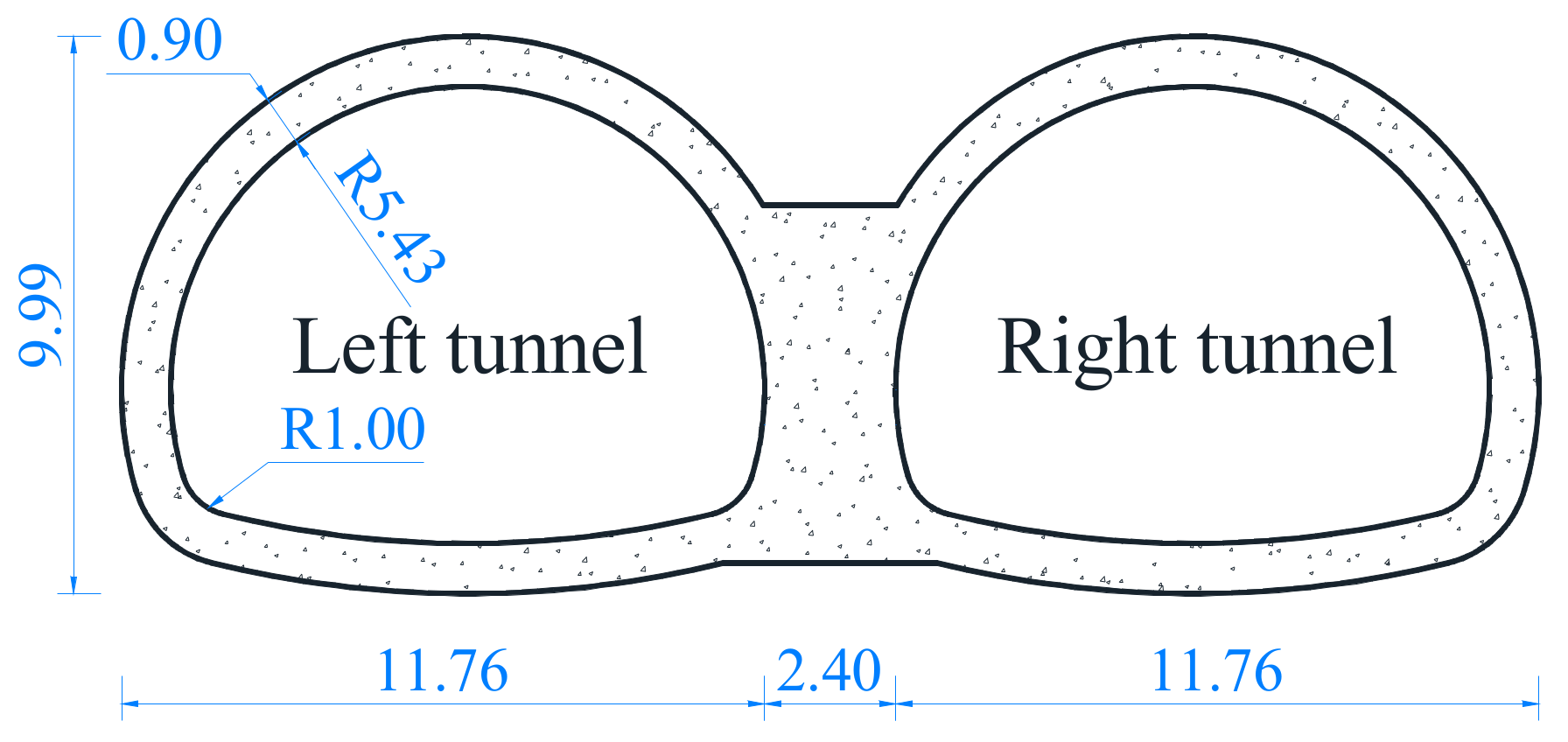
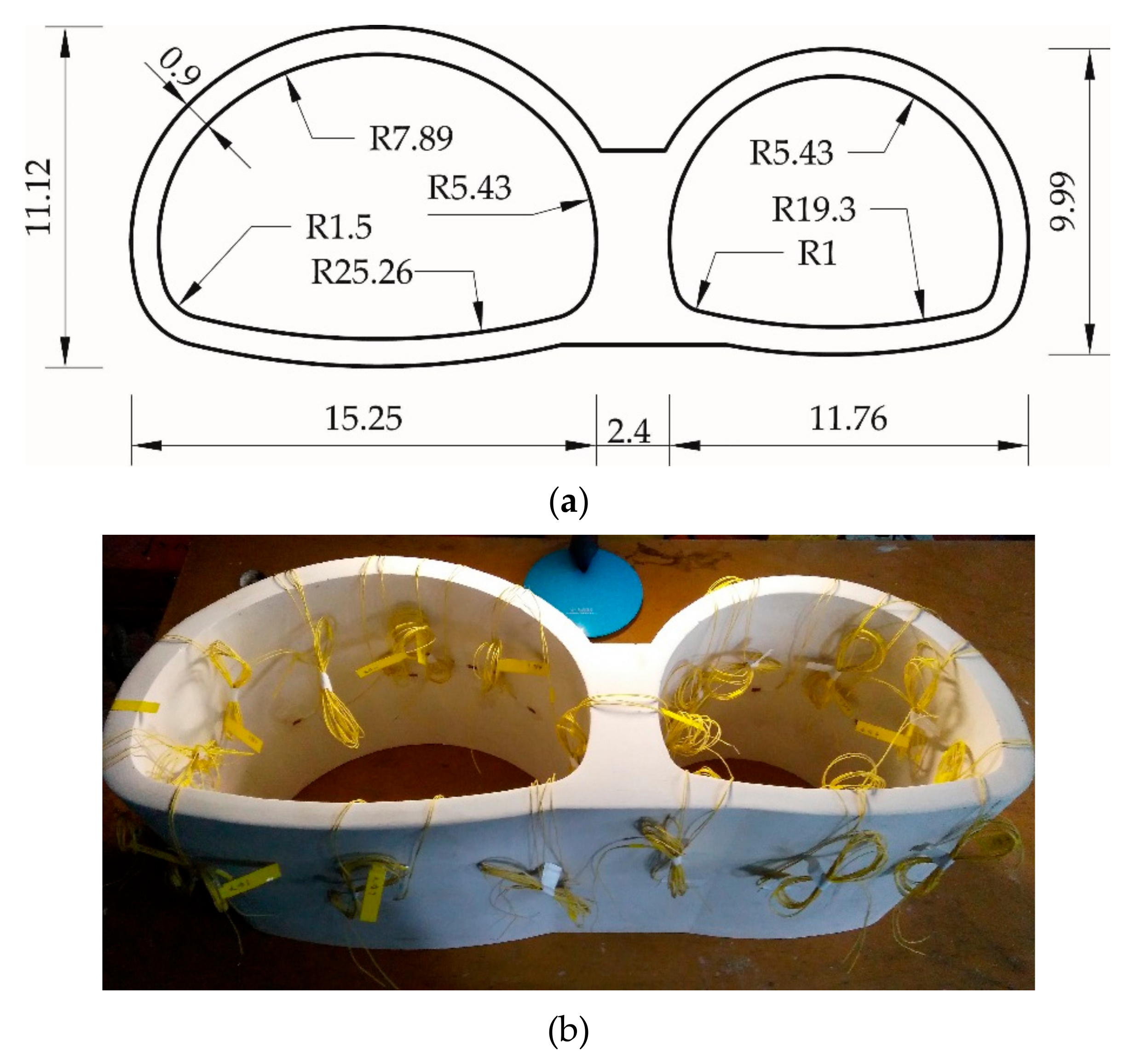
2.1. Experimental Schemes
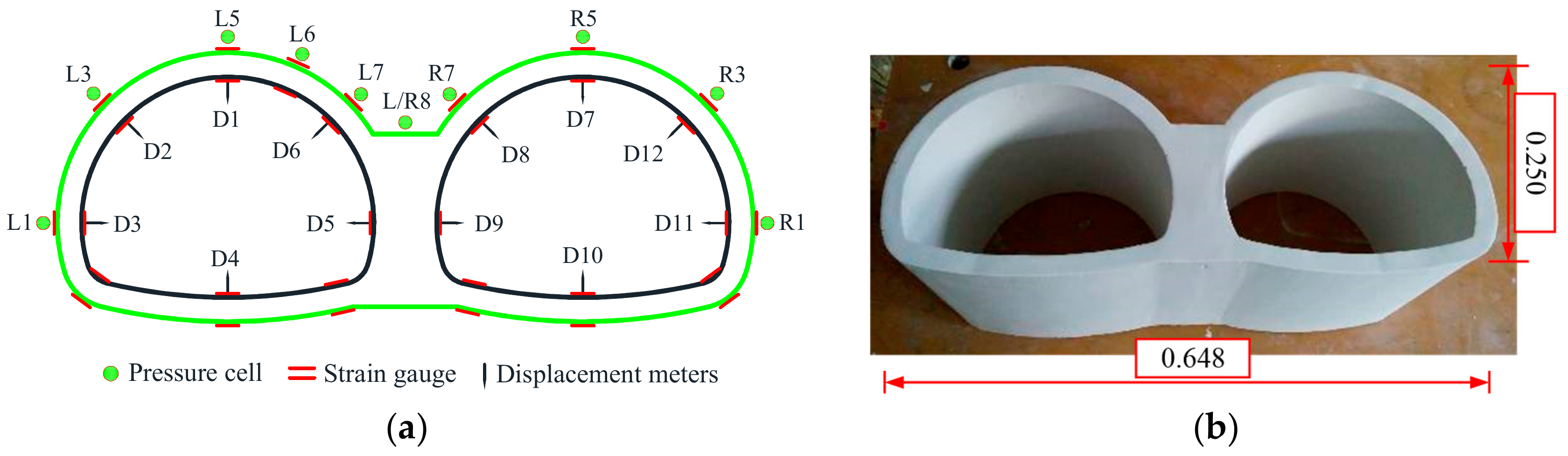
2.2. Experimental Process
2.3. Experimental Results
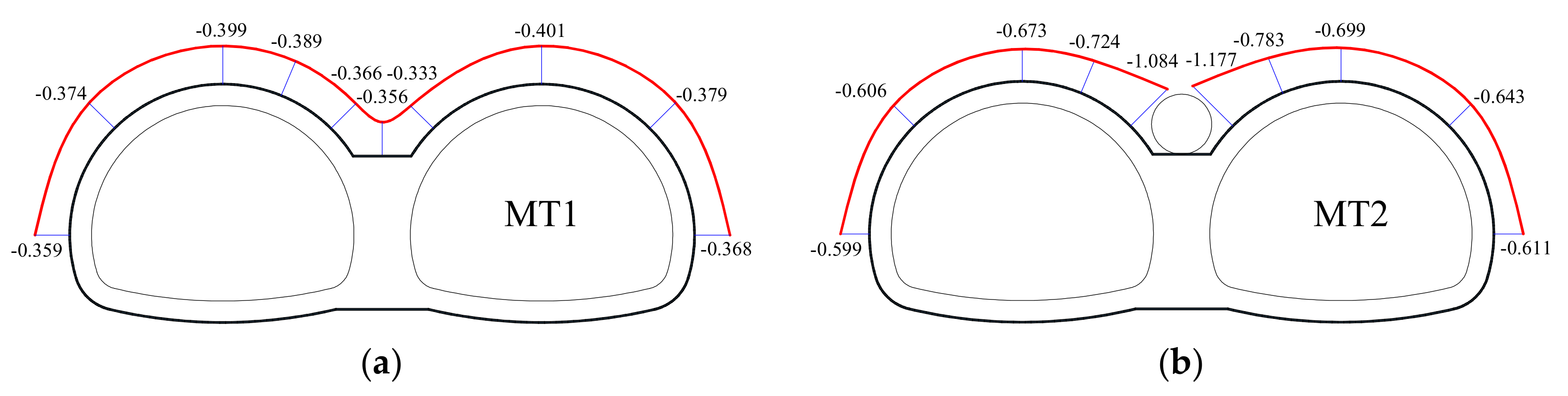
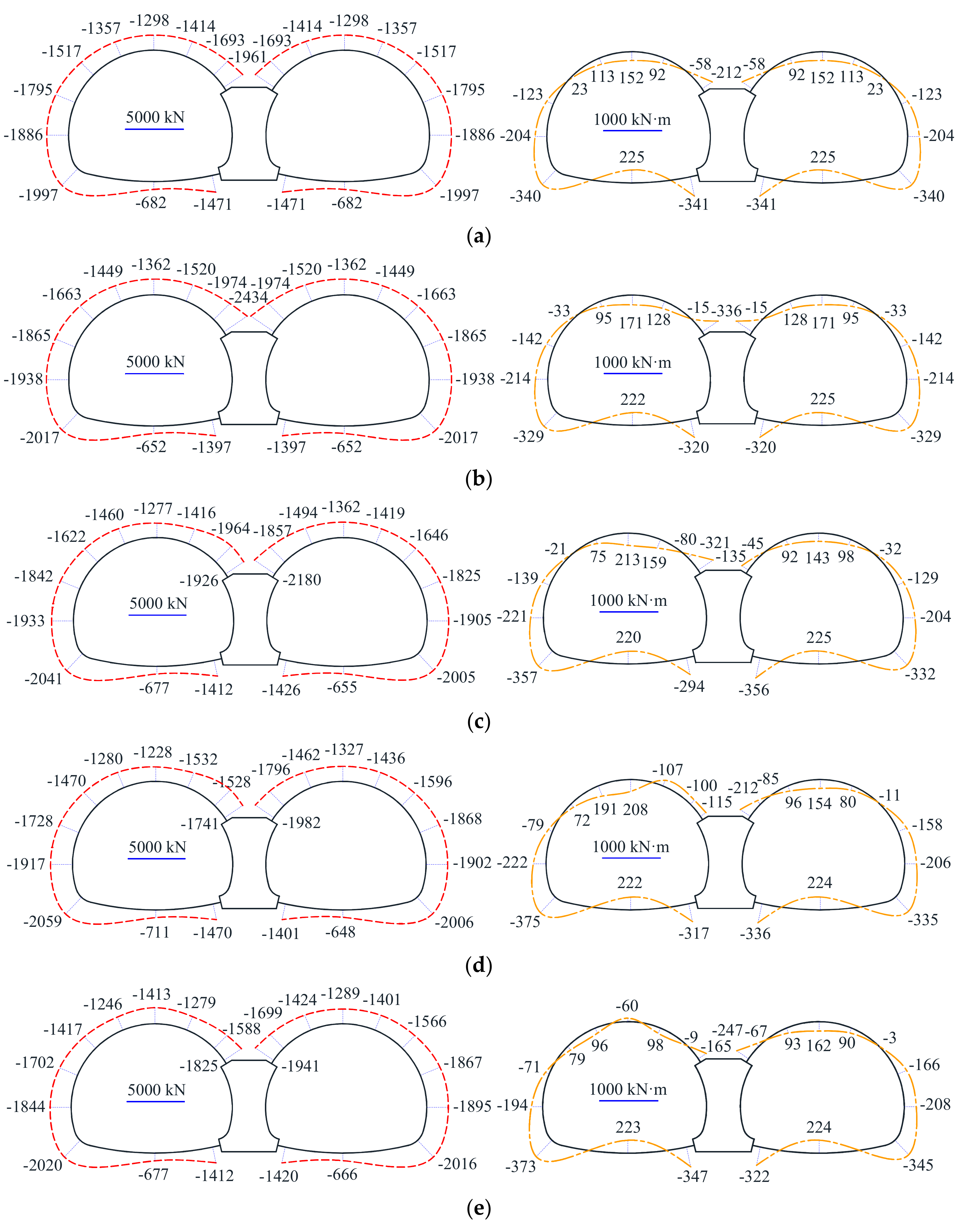
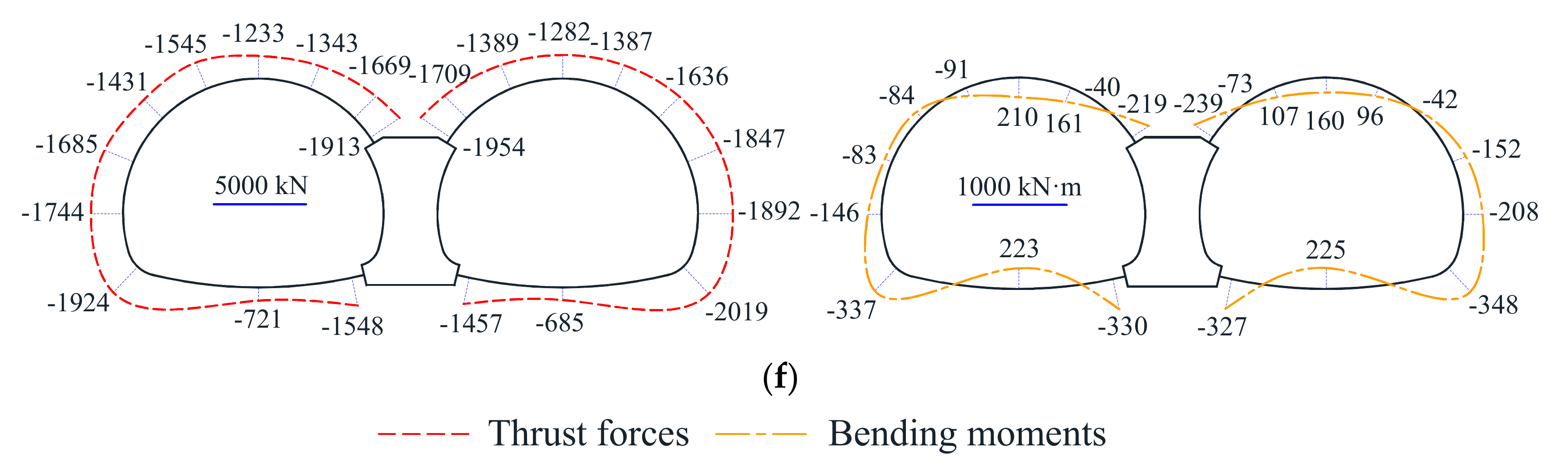
2.3.1. Earth Pressure Distribution
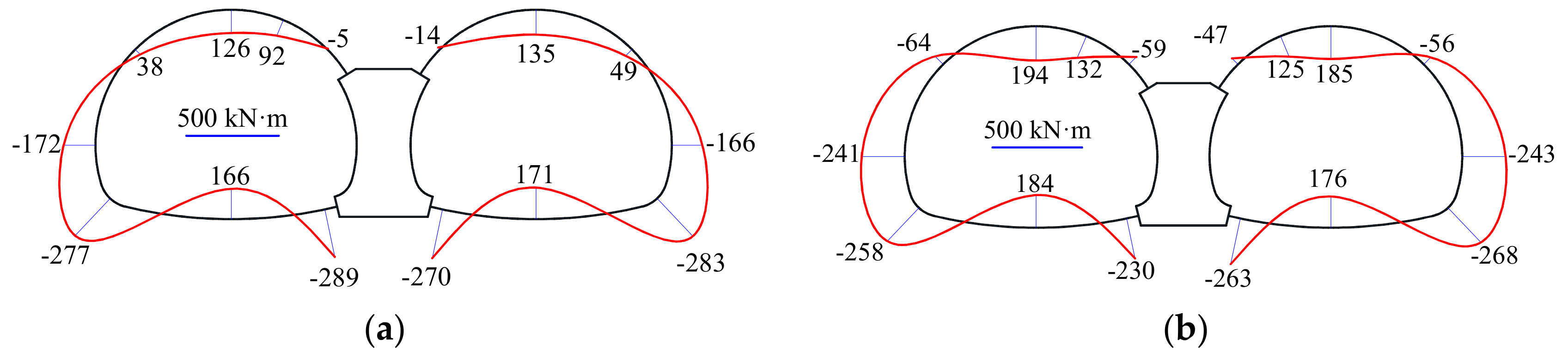
2.3.2. Distribution of Bending Moments
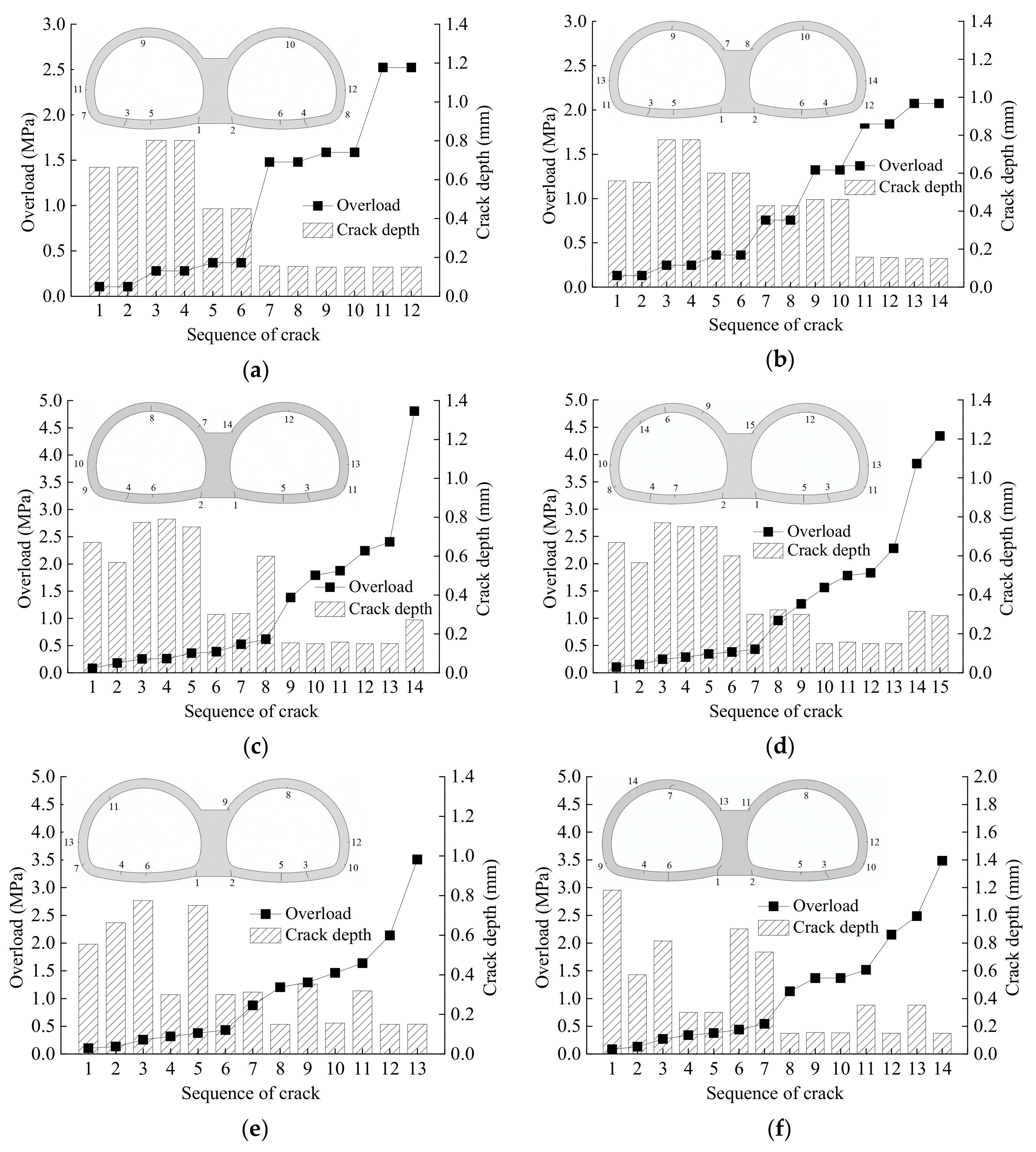
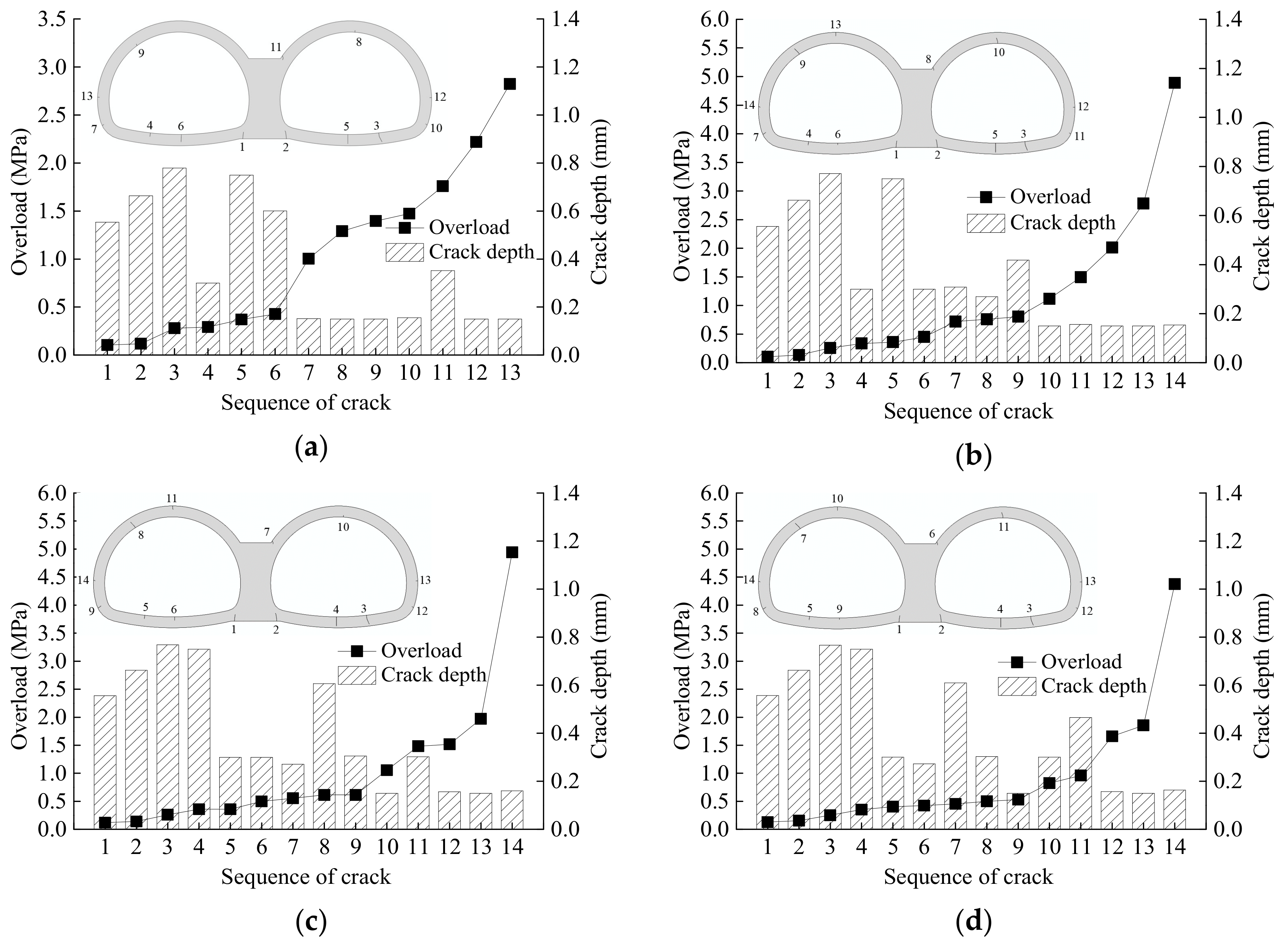
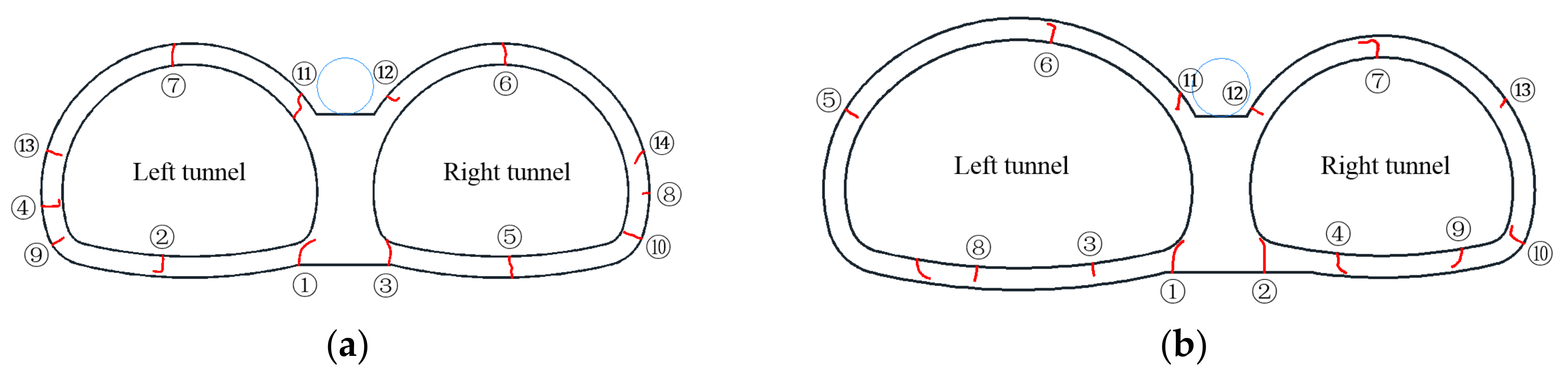
2.3.3. Lining Failure and Cracking
3. Numerical Study
3.1. Numerical Model
3.2. Numerical Schemes
3.3. Numerical Results
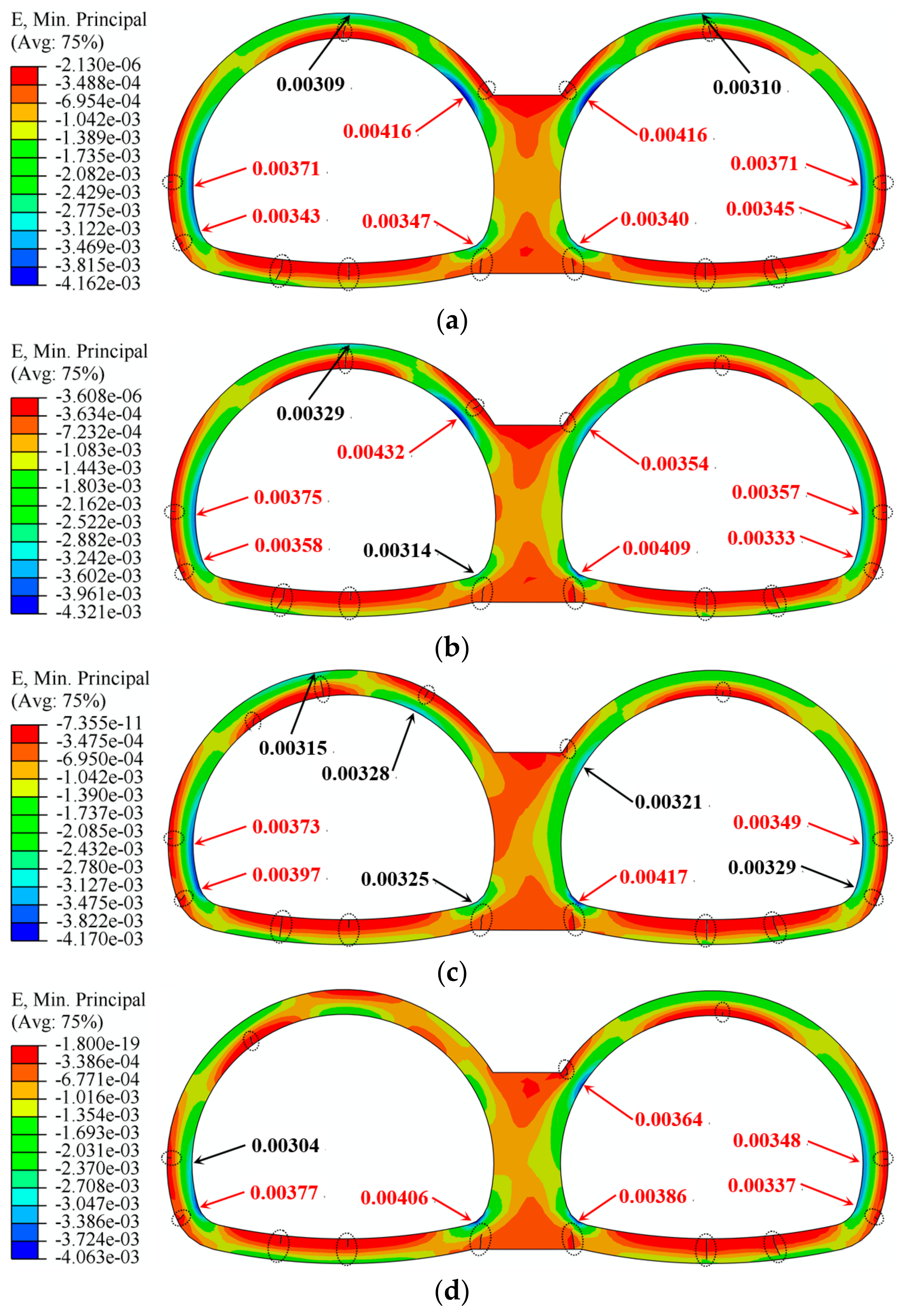
3.3.1. Effect of Void Location
3.3.2. Effect of Void Size
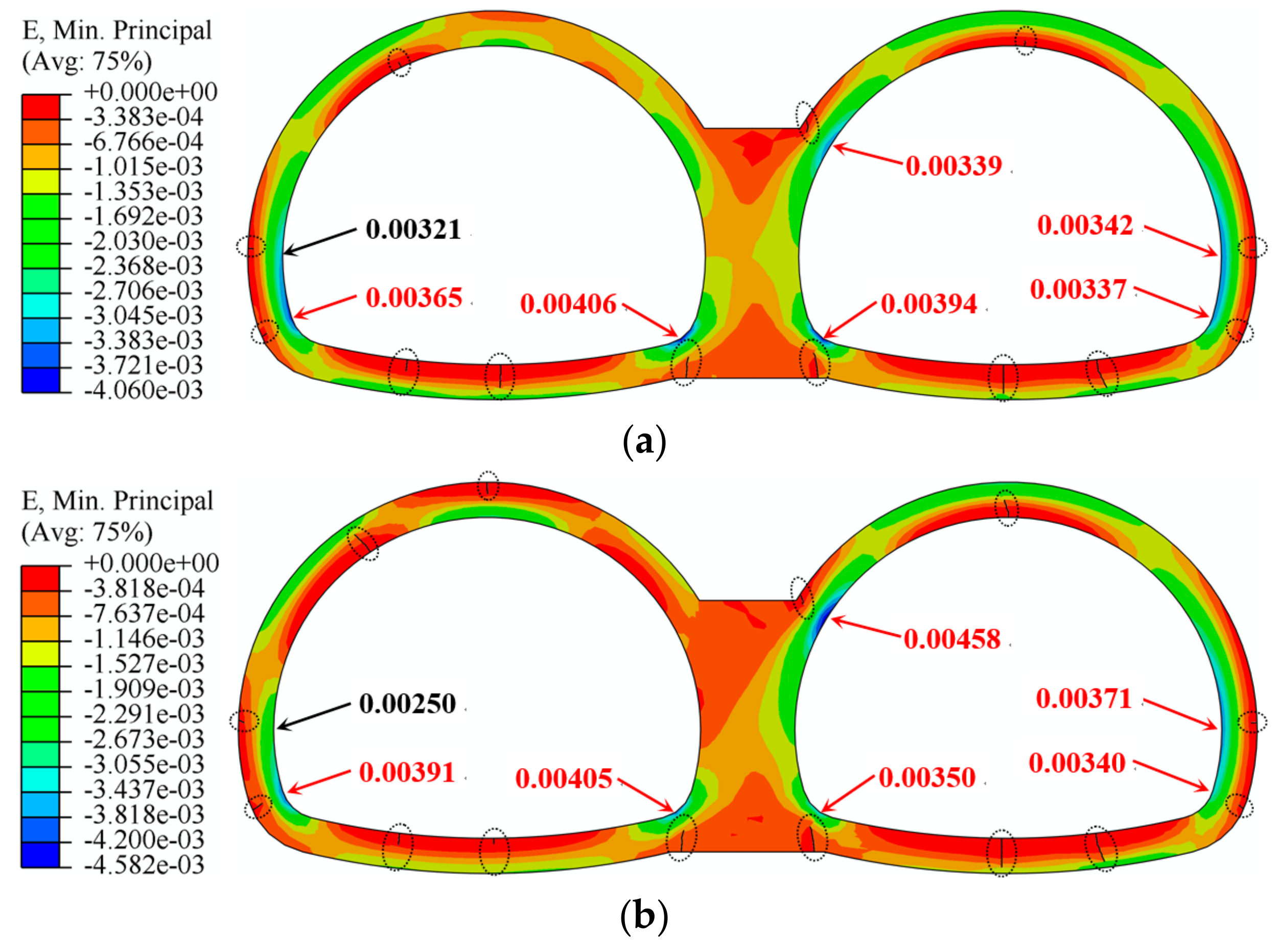
4. Comparisons with Asymmetrical Double-Arch Tunnels
4.1. Without Voids behind the Lining
4.2. Without a Void on the Top of the Central Wall
5. Summary and Conclusions
- (1)
- The existence of a void behind the central wall, affecting the re-distribution of the earth pressure compared with the case without voids, results in the concentration of stress on both sides of the void located on the top of the central wall, associated with it the emergence of cracks in the lining on the upper right and left corners of the central wall of symmetrical double-arch tunnels.
- (2)
- Due to the presence of voids behind the lining, significant changes in the internal forces in the lining were found at the areas in close vicinity of the void, whereas only a few changes were found at the invert and central wall. The lining at the bottom of the central wall of the symmetrical double-arch tunnel, which is regarded as the weak part, suffered the most severe damage.
- (3)
- Given that the presence of a void can generally preclude any symmetry, the cracks adjacent to the central wall of symmetrical double-arch tunnels are more sensitive to the location of the void. With the growth in the angle of voids, the positive bending moments in the lining on the inside of the void increased, and the cracks are likely to appear at the outer fiber of the lining.
- (4)
- Compared with asymmetrical double-arch tunnels, the introduction of a void behind the central wall leads to lighter damage and later emergence of cracks in the lining on the upper left corner of the central wall. The location of the initial cracking of the double-arch tunnels is basically the same, while the lining failure of the large-section tunnel seems to be more complicated.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, C.P.; Han, K.H.; Zhang, D.L. Face stability analysis of shallow circular tunnels in cohesive-frictional soils. Tunn. Undergr. Space Technol. 2015, 50, 345–357. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.P.; Zhu, W.J.; Zhang, D.L. Upper-bound solutions for the face stability of a non-circular NATM tunnel in clays with a linearly increasing undrained shear strength with depth. Comput. Geotech. 2019, 114, 103136. [Google Scholar] [CrossRef]
- Han, K.H.; Zhang, C.P.; Zhang, D.L. Upper-bound solutions for the face stability of a shield tunnel in multilayered cohesive–frictional soils. Comput. Geotech. 2016, 79, 1–9. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.P.; Zhang, X. Stability analysis of the tunnel face in the cohesive-frictional soils considering the arch effect and rotational mechanism. J. Chin. Inst. Eng. 2018, 41, 697–709. [Google Scholar] [CrossRef]
- Lai, J.X.; Qiu, J.L.; Fan, H.B.; Chen, J.X.; Hu, Z.N.; Zhang, Q.; Wang, J.B. Structural safety assessment of existing multiarch tunnel: A case study. Adv. Mater. Sci. Eng. 2017, 2017, 1697041. [Google Scholar] [CrossRef]
- Yan, Q.X.; Zhang, C.; Lin, G.; Wang, B. Field monitoring of deformations and internal forces of surrounding rocks and lining structures in the construction of the Gangkou double-arched tunnel-A case study. Appl. Sci. 2017, 7, 169. [Google Scholar] [CrossRef]
- Meguid, M.A.; Dang, H.K. The effect of erosion voids on existing tunnel linings. Tunn. Undergr. Space Technol. 2009, 24, 278–286. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, Y.J.; Li, B. Estimation of effect of voids on frequency response of mountain tunnel lining based on microtremor method. Tunn. Undergr. Space Technol. 2014, 42, 184–194. [Google Scholar] [CrossRef]
- Yasuda, N.; Tsukada, K.; Asakura, T. Elastic solutions for circular tunnel with void behind lining. Tunn. Undergr. Space Technol. 2017, 70, 274–285. [Google Scholar] [CrossRef]
- Leung, C.; Meguid, M.A. An experimental study of the effect of local contact loss on the earth pressure distribution on existing tunnel linings. Tunn. Undergr. Space Technol. 2011, 26, 139–145. [Google Scholar] [CrossRef]
- Wang, J.F.; Huang, H.W.; Xie, X.Y.; Bobet, A. Void-induced liner deformation and stress redistribution. Tunn. Undergr. Space Technol. 2014, 40, 263–276. [Google Scholar] [CrossRef]
- Li, S.C.; Yuan, C.; Feng, X.D.; Li, S.C. Mechanical behaviour of a large-span double-arch tunnel. KSCE J. Civ. Eng. 2016, 20, 2737–2745. [Google Scholar] [CrossRef]
- He, J.; Zhang, C.P.; Yang, G.B.; Wang, M.S. Experimental study on mechanical behavior of nonsymmetric multi-arch tunnel in sand-cobble ground. Chin. Civ. Eng. J. 2017, 50, 116–124. (In Chinese) [Google Scholar]
- Min, B.; Zhang, X.; Zhang, C.P.; Gong, Y.P.; Yuan, T.F. Mechanical behavior of double-arch tunnels under the effect of voids on the top of the middle wall. Symmetry 2018, 10, 703. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. JTG 3370.1-2018, Specifications for Design of Highway Tunnels: Section 1 Civil Engineering; China Communications Press Co., Ltd.: Beijing, China, 2019. (In Chinese) [Google Scholar]
- ABAQUS. Abaqus v6.14 Documentation; Dassault Systèmes: Providence, RI, USA, 2015. [Google Scholar]
- Yan, Q.X.; Xu, Y.J.; Zhang, W.L.; Geng, P.; Yang, W.B. Numerical analysis of the cracking and failure behaviors of segmental lining structure of an underwater shield tunnel subjected to a derailed high-speed train impact. Tunn. Undergr. Space Technol. 2018, 72, 41–54. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB 50010-2010, Code for Design of Concrete Structures; China Architecture & Building Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
- Li, Z.H.; Zhu, H.H.; Ding, W.Q. Key Technology of Design and Construction for Highway Twin-Tunnel; China Communications Press: Beijing, China, 2010; pp. 223–224. (In Chinese) [Google Scholar]
- Zhang, C.P.; Cai, Y.; Zhu, W.J. Numerical study and field monitoring of the ground deformation induced by large slurry shield tunnelling in sandy cobble ground. Adv. Civ. Eng. 2019, 2019, 4145721. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C.P.; Wang, J.C. Effect of closely spaced twin tunnel construction beneath an existing subway station: A case study. J. Test. Eval. 2018, 46, 1559–1573. [Google Scholar] [CrossRef]
- Zhang, C.P.; Zhang, X.; Fang, Q. Behaviors of existing twin subway tunnels due to new subway station excavation below in close vicinity. Tunn. Undergr. Space Technol. 2018, 81, 121–128. [Google Scholar] [CrossRef]



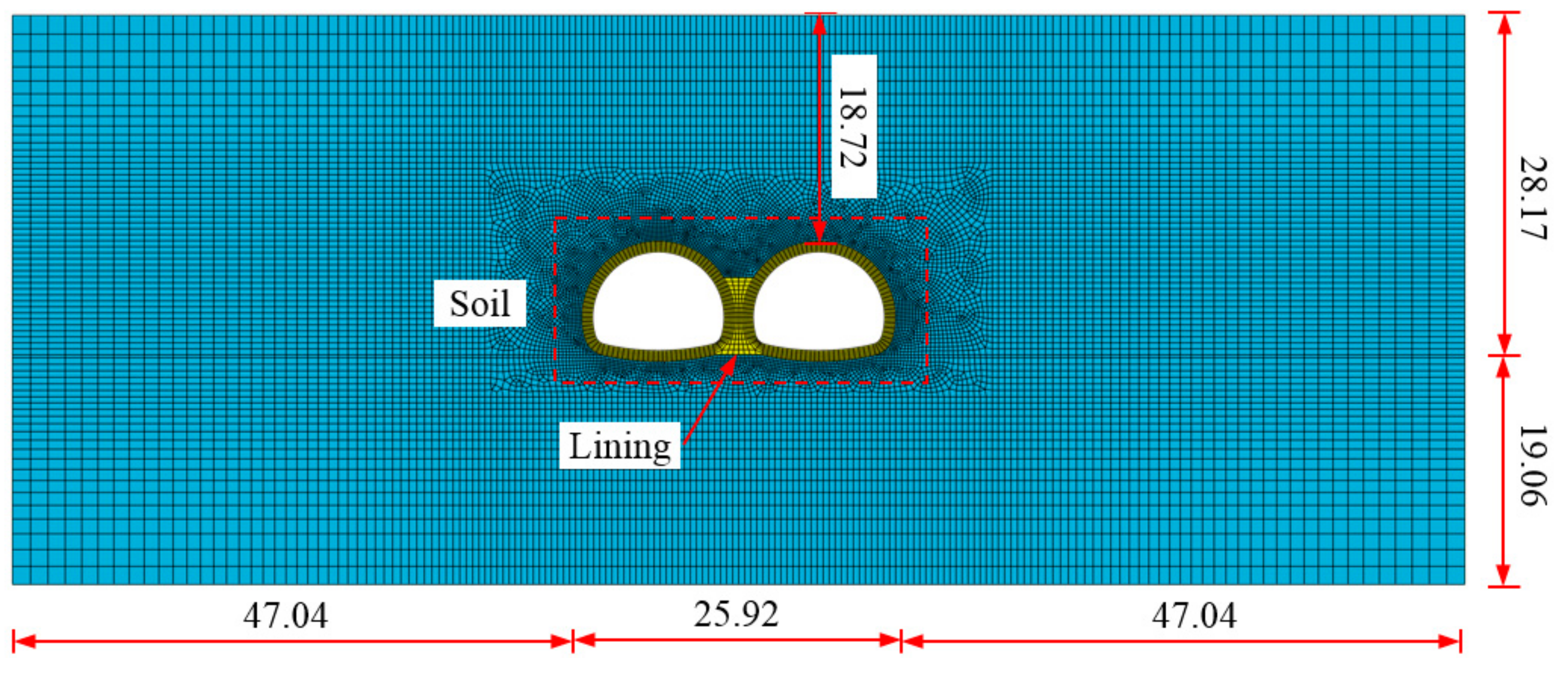


| Materials | Unit Weight (kN/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Soil | 18 | 0.0068 | 0.37 | 4.6 | 24 |
| Lining | 8.3 | 0.8350 | 0.20 | — | — |
| Materials | Unit Weight (kN/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Soil | 18 | 0.27 | 0.37 | 182 | 24 |
| Lining | 25 | 33.5 | 0.20 | — | — |
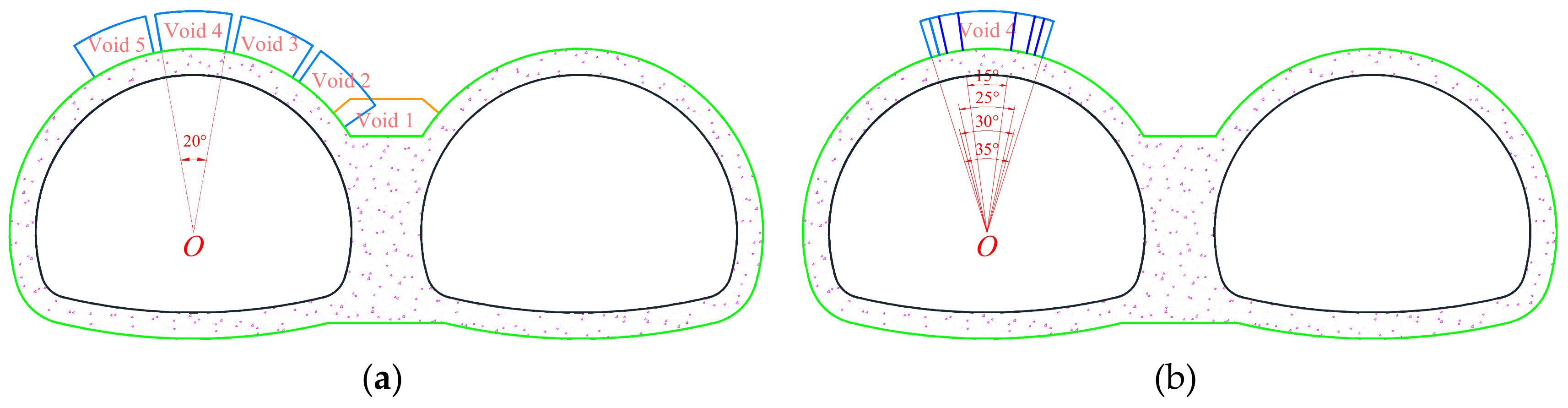
| Scheme | Void Location | Void Size θ (°) |
|---|---|---|
| Numerical Test 1 | None (base case) | — |
| Numerical Test 2 | Central wall (void 1) | — |
| Numerical Test 3 | Right haunch (void 2) | 20 |
| Numerical Test 4 | Right shoulder (void 3) | 20 |
| Numerical Test 5 | Vault (void 4) | 20 |
| Numerical Test 6 | Left shoulder (void 5) | 20 |
| Numerical Tests 7–10 | Vault (void 4) | 15, 25, 30, 35 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Ye, Z.; Min, B.; Xu, Y. Effect of Voids Behind Lining on the Failure Behavior of Symmetrical Double-Arch Tunnels. Symmetry 2019, 11, 1321. https://doi.org/10.3390/sym11101321
Zhang X, Ye Z, Min B, Xu Y. Effect of Voids Behind Lining on the Failure Behavior of Symmetrical Double-Arch Tunnels. Symmetry. 2019; 11(10):1321. https://doi.org/10.3390/sym11101321
Chicago/Turabian StyleZhang, Xu, Zijian Ye, Bo Min, and Youjun Xu. 2019. "Effect of Voids Behind Lining on the Failure Behavior of Symmetrical Double-Arch Tunnels" Symmetry 11, no. 10: 1321. https://doi.org/10.3390/sym11101321
APA StyleZhang, X., Ye, Z., Min, B., & Xu, Y. (2019). Effect of Voids Behind Lining on the Failure Behavior of Symmetrical Double-Arch Tunnels. Symmetry, 11(10), 1321. https://doi.org/10.3390/sym11101321





