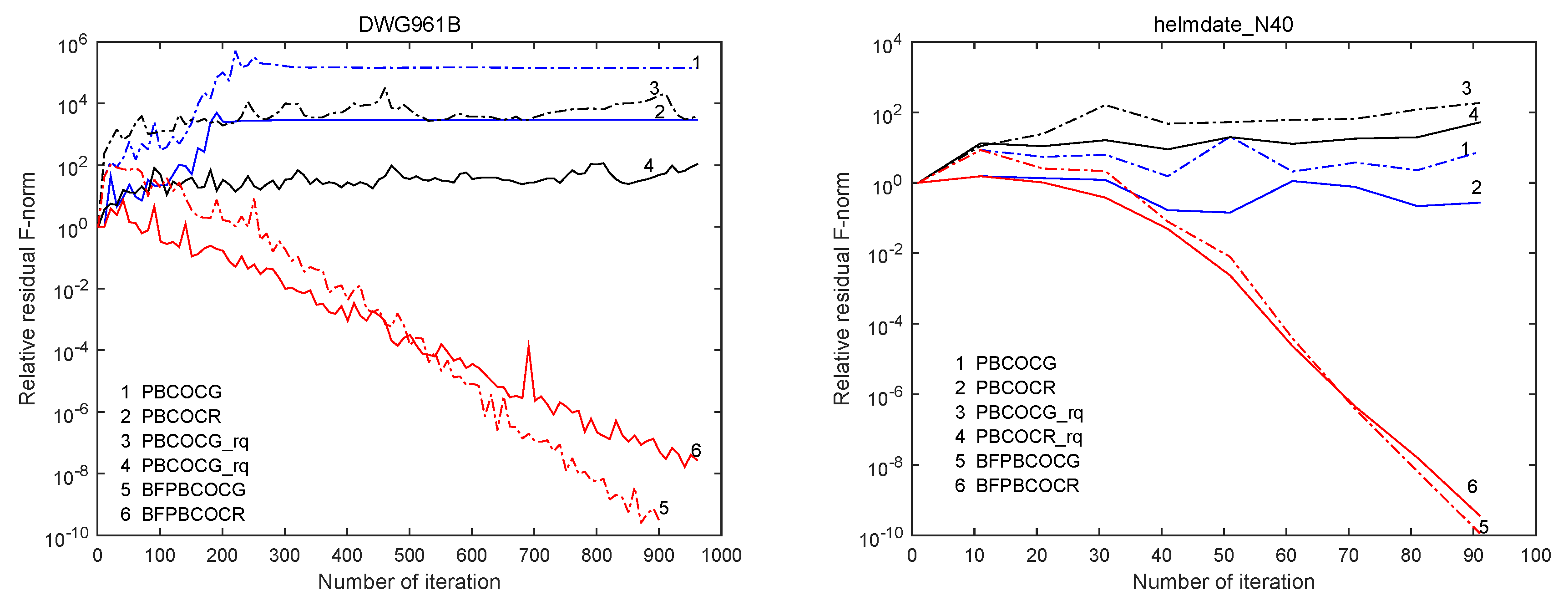
In this section, we present our main algorithms, i.e., the breakdown-free block COCG algorithm (BFBCOCG) and the breakdown-free block COCR algorithm (BFBCOCR) in detail. We first introduce the block COCG (BCOCG) and block COCR (BCOCR) methods briefly and then give the derivation of BFBCOCG and BFBCOCR with their orthogonality properties, respectively. In the end, the preconditioned variants of BFBCOCG and BFBCOCR are also proposed, denoted by BFPBCOCG and BFPBCOCR, respectively. We use an underscore “_” to distinguish the breakdown-free and the non-breakdown-free algorithms.
2.2. BFBCOCG and BFBCOCR
If the block size
p is large, then the vectors of the block search direction will inevitably be linearly dependent on the increasing of the iteration number for BCOCG, hence rank deficiency occurs. In the following, in order to overcome this problem, we consider applying the breakdown-free strategy to BCOCG and propose the breakdown-free block COCG algorithm (BFBCOCG). The rationale of BFBCOCG is extracting an orthogonal basis
from the current searching space by using the operation
. Thus, compared with (
2), the new recurrence relation becomes
Therefore, again using the orthogonality condition (
3), we can get the Lemma 1. Here, we denote
.
Lemma 1. For all , , , and .
Proof. Because
for all
, and
by (
3), thus
and
. Then
can be obtained by the second orthogonality condition in (
3). □
Similarly, the following Theorem 1 is obtained to update the parameters and .
Theorem 1. Under the orthogonality condition (3), the value of parameters and in the recurrence relation (4) can be obtained by solving the following equations: Proof. From Lemma 1 and (
4), we have the following two equations:
and
So, solving (
6), we can easily get the
.
Pre-multiplying
to (
7), then from the third equation of (
4), we have
From Lemma 1, we have
, and by the first equation of (
5), one has
. Thus the above equation can be rewritten as
which can be used to update matrix
. □
The following Algorithm 1 is the breakdown-free block COCG.
| Algorithm 1 Breakdown-free block COCG (BFBCOCG) |
- 1.
Given the initial guess and a tolerance ; Compute: , , ; - 2.
For until , do
Solve: ; Update: , , Solve: (; Update: , ;
End For
|
Similar to BFBCOCG, we can also easily get BFBCOCR by using
in the orthogonality condition (
3). The following Algorithm 2 is the breakdown-free block COCR.
| Algorithm 2 Breakdown-free block COCR (BFBCOCR) |
- 1.
Given the initial guess and a tolerance ; Compute: , , ; - 2.
For until , do
Solve: ; Update: , , Solve: ; Update: , ;
End For
|
2.3. BFPBCOCG and BFPBCOCR
As we all know, if the coefficient matrix has poor spectral properties, then the Krylov subspace methods may not robust, while a preconditioning strategy can make it better [
11]. The trick is preconditioning (
1) with a symmetric positive matrix
M, which approximates to the inverse of matrix
A; we get the following equivalent system:
Let
be the Cholesky decomposition of
M. Then system (
9) is equivalent to
We add a tilde “˜” on the variables derived from the new system. Then applying the BFBCOCG method and its recurrence relations (
4) to (
10), we have the orthogonality conditions
It is easy to see
,
. The approximate solution
is from
. Set
, then
. The new recurrence relation becomes
The orthogonality condition (
11) become
Under the recurrence relation (
12) and the orthogonality condition (
13), we can get the following Lemma 2 and Theorem 2 to update the matrices
and
. Here, we omit the proof because it is like the proof of Lemma 1 and Theorem 1. We denote
.
Lemma 2. For all , , , and .
Remark 1. Under the preconditioned strategy, the relations of the block residuals are changed from orthogonal for BFBCOCG to M-orthogonal for BFPBCOCG. Here, two vectors x and y are M-orthogonal, meaning , i.e., .
Theorem 2. Under the orthogonality condition (13), the value of parameters and in the recurrence relations (12) can be obtained by solving the following equations: The following Algorithm 3 is the breakdown-free preconditioned block COCG algorithm.
| Algorithm 3 Breakdown-free preconditioned block COCG (BFPBCOCG) |
- 1.
Given the initial guess and a tolerance ; Compute: , , , ; - 2.
For until , do
Solve: ; Update: , , ; Solve: ; Update: , ;
End For
|
Change the orthogonality conditions (
11) to the following conditions:
The breakdown-free preconditioned block COCR (BFPBCOCR) can be deduced with the similar derivation of BFPBCOCG. Algorithm 4 shows the code of BFPBCOCR.
| Algorithm 4 Breakdown-free preconditioned block COCR (BFPBCOCR) |
- 1.
Given the initial guess and a tolerance ; Compute: , , , ; - 2.
For until , do
Solve: ; Update: , , ; Solve: ; Update: , ;
End For
|
At the end of this section, we will give the complexity for six algorithms. They are the block COCG algorithm, block COCR algorithm, breakdown-free block COCG algorithm, breakdown-free block COCR algorithm, breakdown-free preconditioned block COCG algorithm, and breakdown-free preconditioned block COCR algorithm, which are denoted by BCOCG, BCOCR, BFBCOCG, BFBCOCR, BFPBCOCG, BFPBCOCR, respectively. The pseudocodes of BCOCG and BCOCR are from [
1].
Table 1 shows the main costs per cycle of the six algorithms. Here, we denote as “block vector” the matrix with size
, “bdp” the dot product number of two block vectors, “bmv” the product number of a matrix with
and a block vector, “bsaxpy” the number of two block vectors summed with one of the block vectors being from multiplying a block vector to a
matrix, “LE” the number of solving linear equations with a
coefficient matrix, and “bSC” the storage capacity of block vectors.
From
Table 1, we can see the last four algorithms need one more dot product of two block vectors than the original two algorithms, i.e., BCOCG and BCOCR. For the product number of a matrix with a block vector, BFBCOCR and BFPBCOCR are both twice BFBCOCG and BFPBCOCG, respectively. This may result in more time to spend in BFBCOCR and BFPBCOCR, especially for a problem with a dense matrix. We reflect on the phenomenon in Example 1.