Abstract
The paper focuses on the vibration analysis of a vehicle equipped with two identical engines. Such solutions are encountered in practice when less power is needed for a vehicle for a certain period of time and then greater power the rest of the time. An example of this would be a mobile drilling rig. During transport (a relatively short period of time) only one engine operates and then, in service (most of the operating time), both engines operate. A characteristic of such an aggregate is the existence, within the transmission, of two identical engines. The existence of identical parts in mechanical systems leads to properties that allow the computations to be simplified in order to obtain suggestive and rapid results, with reduced computation effort. These properties refer to the eigenvalues and eigenmodes of vibration for these types of systems and have been stated and demonstrated in the paper. It also allows for a qualitative analysis of the behavior of the system in case of vibrations. The existence of these properties allows for easier calculation and shortening of the design time. The mechanical consequences of the existence of symmetries or identical parts have begun to be studied in more detail in the last decade (see references), and the work is part of these trends. The vibration properties of a transmission of a truck with two identical engines have been stated and proven and a real example is analyzed. Two 215 hp engines were used in the application. In order to establish a useful solution in practice, two constructive variants with a different clutch position in the transmission are analyzed in parallel.
1. Introduction
The structural symmetries and the properties that they give to the structures have been observed by the researchers and used especially in the static case; they are presented in the classical courses of strength of materials or structural analysis. An analysis of the different types of symmetries in applied mechanics is made in [1]. Symmetries are encountered in all aspects of human life, and engineering applications are no exception in using the properties and benefits that these symmetries bring.
Symmetries in mechanics have been studied mainly from the point of view of mathematicians [2,3,4] as they have effects in writing equations of motion, but with fewer applications in practice. A presentation of the application of symmetries in continuous mechanics is made in [5,6]. In January 2018, a special issue of the Symmetry magazine dedicated to applications in structural mechanics was launched (Civil Engineering and Symmetry—2018, a special issue of Symmetry—ISSN 2073-8994, see ref. [7]). A European project was also funded to study this type of problem (mechanics and symmetry in Europe: The geometry and dynamics of deformable systems. Project. HPRN-CT-2000-00113, funded under: FP5-HUMAN POTENTIAL, see ref. [8]) and courses were held at the Center for Solid Mechanics—CISM from Udine (similarity, symmetry and group theoretical methods in mechanics, September 7, 2015–September 11, 2015. Lectures at the International Center for Mechanical Sciences, see ref. [9]).
Lately, numerous works have been published that aim to use symmetries in order to obtain properties that allow for a simplified analysis of the models used, in different fields [10,11,12,13]. Different mechanical systems with symmetries and properties induced by these symmetries are also analyzed [14,15]. In the vibrations research field, the effect of symmetries was less used but there are works that have begun to study this type of problem, sometimes with implications in other works, which focus on different other aspects [16,17,18,19,20,21,22,23].
However, there are many situations that can be studied and, therefore, the paper aims to complete some of the studied cases by offering some ideas for the application of these properties that could help a design engineer.
In the spirit of these works, some vibration properties of the considered symmetrical mechanical system (in our case the transmission of a truck) are stated in the paper, then they are proved and are applied in a real, concrete example of a truck equipped with two 215 HP identical engines. Numerical results are obtained, with real values of the parameters, which confirm the theoretical results obtained and, thus, shorten the time to calculate eigenfrequencies and eigenmodes of vibrations for these kinds of systems.
2. Materials and Methods
If we have already verified and found convenient engines, a solution used in practice in order to obtain greater power is to use two identical engines within a machine. It is possible that, for a period of time, only the power of one engine is required and, after a while, the power of both engines is needed. For example, in the case of the above mentioned mobile drilling plant, only the power of an engine is required for the movement of the vehicle, while for the actual drilling operations, the power of both engines to be required [1] (Figure 1).

Figure 1.
Mobile oil drilling plant type TW125 CAA6 mounted on a chassis ROMAN 75,540 MFEG (12 × 8) [24].
A mobile drilling plant is a special commercial vehicle, designed and manufactured so as to ensure the dynamics and durability/reliability imposed by the conditions under which the drilling is performed, conditions that involve both the operation and moving in harsh conditions (unpaved roads). Another practical application is the use of two engines in certain special vehicles just to obtain higher power. Such a vehicle can be equipped with a power outlet that could be connected to a machine and can only be operated by a single engine. Such a system has been studied in our work, but the results obtained are valid and can be applied to any vehicle equipped with two identical engines from which the power is collected and summed using a combiner transmission box. The demands of the active and passive components of these types of vehicles are large and complex, including high static demands and dynamic demands through vibrations and shocks. The dynamics that such vehicles must provide and the mechanical strength (stresses and deformations) that must exist make these vehicles interesting for research, especially considering the demands and environmental conditions of exploitation [1].
The main components of the powertrain are the drive system, consisting of two diesel engines supercharged with electronic injection and the add-on box/add-on and distribution box, with the role of summing the torques transmitted by the two engines. If there is no need for both engines to produce power, only the power transmitted by an engine can be used. The gearboxes in the add-on gearbox bring the advantages of high transmission efficiency, the possibility of transmitting extremely high-value torque, the stable operation and high durability/reliability indices.
The kinematic transmission diagram of the truck and the combiner transmission box connected to the two engines arepresented in Figure 1, Figure 2 and Figure 3.
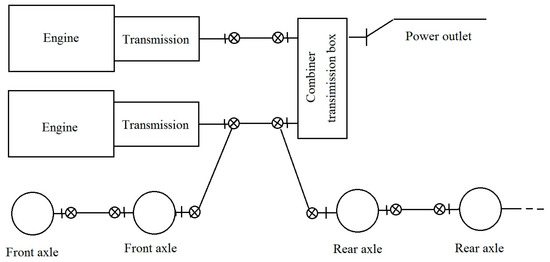
Figure 2.
The kinematic transmission diagram.
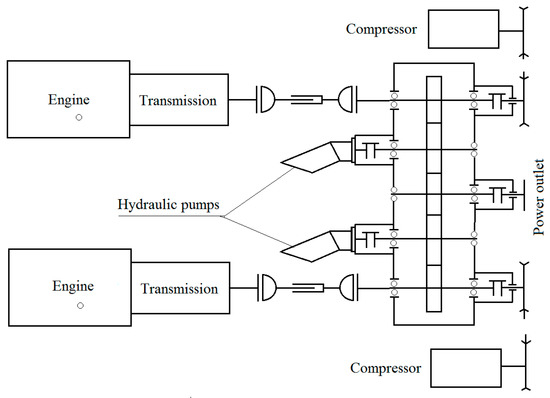
Figure 3.
The combiner transmission box.
Let us consider a vehicle equipped with two identical engines. Two constructive solutions have been proposed by the designer: one solution with the clutch located behind the engines and the other solution with the clutch located in front of the engines. The constructive schemes of the two solutions are presented in Figure 4 and Figure 5.
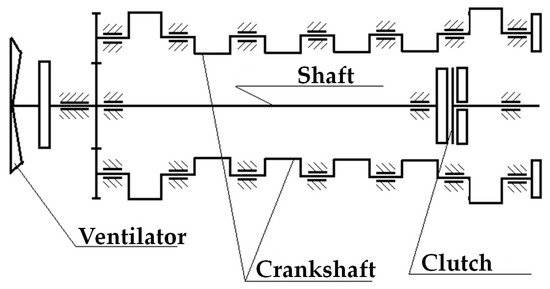
Figure 4.
The variant with the clutch located behind the engines.
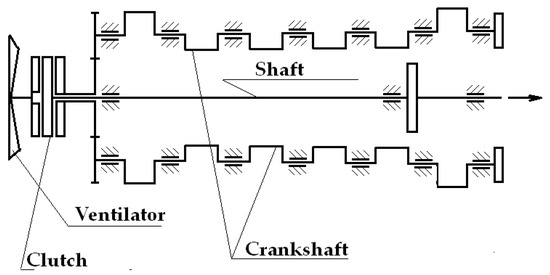
Figure 5.
The variant with the clutch located in front of the engines.
The model for the study of vibrations of the system in the two situations is shown in Figure 6. (the clutch is considered coupled). The model with wheels (for one single engine) is presented in Figure 7. The fact that the two engines are identical leads to the highlighting of some properties of the equations of motion that describe the free vibration of the system that can allow for the necessary calculations to be made easier and to obtain qualitative conclusions regarding the vibrating system.
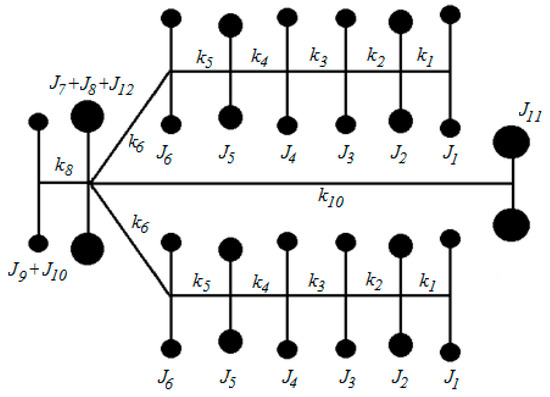
Figure 6.
The two-engined vehicle, the front clutch.
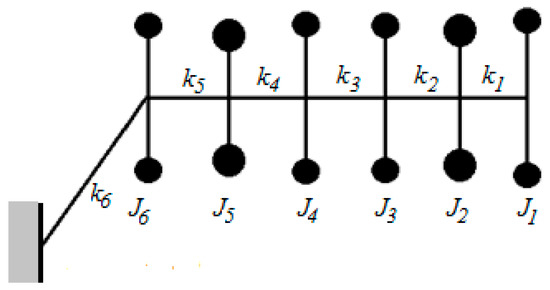
Figure 7.
The mechanical model of a single engine.

Table 1.
The moments of inertia.

Table 2.
The moment of inertia of the wheels in the two studied cases.

Table 3.
Stiffness of the shafts between two neighboring steering wheels.
3. Results
If we consider:
In (1) represents the vector of the rotations of the flywheels of the first engine, represents the vector of the rotations of the flywheels of the second engine and the vector of the other rotations of the system.
The motion equations for the free non-damped vibrations for the whole structure can be obtained:
For one single engine, the equations are:
Using the results presented in [9,10,11] the following property has been established:
3.1. Theorem T1. The Eigenvalues for the System (3) are Eigenvalues for the System (2) As Well
That means that the solutions of algebraic equations:
are also solutions of the algebraic equation:
or:
We could write:
which implies that the polynomial in from Equation (6) is divided by the polynomial in from Equation (4).
We consider:
For the vibrating system (as a whole) the free undamped torsional vibrations will be the system of equations (2), which can be written in compact form:
where represents the vector of the rotations of the flywheels, being the matrix of inertia and being the stiffness matrix. The characteristic equation for the presented system (7) can be written:
Theorem T1 will be now proven.
Proof.
The characteristic polynomial for the single-engine system is:
If we consider , we obtain the natural frequencies for a single engine, taken separately.
The characteristic polynomial for the whole system is:
By direct calculus, applying Laplace’s rule for determinants, we obtain in this case:
If , then we immediately have , so the natural frequencies for the system consisting of a single engine are also natural frequencies for the whole system. □
We will consider being the natural frequencies of a single engine and being the natural frequencies of the whole system. In our situation, , .
This property is valid in a more general context. This fact will be demonstrated as follows using [9].
Preliminary considerations:
Let us consider , a sub-matrix of M and For the chosen matrix U we consider the complementary matrix
. We call an algebraic complement of the minor (the cofactor of ) the determinant with the sign .
Considering the lines being fixed we have:
This formula generalizes the Laplace expansion formula according to a line of the matrix M determinant.
is a matrix (n – k) × (n – k) and considering V its square sub-matrix of indices , of determinant and correspondingly matrix we may write:
therefrom we have:
3.2. If We Consider the Square Polynomial Matrices with Complex Coefficients, of Size n, Noted A, B, C, L, Z = On and matrix , then det(M) is Dividable by det(A)
Proof.
Considering an expansion of type (13) with minors of the nth order having elements on the first n lines we have [25]:
We shall prove the sentence demonstrating that for this special type of matrix if a term of the previous sum is not dividable by det(A), then there is a term in the expansion so that .
We shall analyze the possible cases, one by one. We shall highlight for the start the columns of the blocks which intervene in matrix M namely A = (A1..An), B = (B1..Bn), C = (C1..Cn), L = (L1..Ln) and Z = (Z1..Zn) = (0..0).
- For j1 = 1, jn = n we have .
- For j1 = 2n + 1, jn = 3n we have and .
- For the rest, we notice that:
- if there is an index then the column k from is null thus .
- is non-null if and in this case where . For such a fixed we have three possibilities for namely:
- has a column 0 thus = 0;
- = det(A);
- = . In this case, we can determine in a unique way the matrix for each of the two possible versions:
- If there is then contains twice the column Lt thus ;
- If then we consider and will be a determinant having the same C type columns located in the same position as in and the L type columns will be the same but permutated as far as the position is concerned. A direct calculation of signs will lead to .
Thus the sentence has been proved. □
In our case we have:
that is a more particular case.
3.3. The Natural Modes of Vibration
To find the natural modes of vibration for this problem is the same with solving the linear homogenous system:
where the eigenvector was partitioned according to the subsystems composed of the two engines and the rest of the flywheels.
Theorem T2. The system (15) has, for , solutions such as (skew-symmetrical eigenmodes):
Proof.
From equations (17) and (18) we have:
whereas, by the statement:
then (20) can only take place if:
From (19) we have:
so that:
□
Theorem T3. The system (15) has, for () solutions such as (symmetrical eigenmodes):
Proof.
In this case , so (17) and (18) from Theorem T2 can be written as:
having the solution:
□
In Table 4, the eigenvalues for the two constructive solutions of a motor vehicle with two identical engines are presented and, for the sake of compassion, the eigenvalues of a single engine are also presented. We observed the six values of the natural frequencies of a single engine that coincide with six of the natural frequencies of the whole assembly.

Table 4.
Eigenvalues for the two models.
The representation of the vibration modes for the branched system is suggestive for presenting the results (Figure 8 and Figure 9). If the natural frequencies of the branched system coincide with the natural frequencies of the single engine, the vibration modes will be skew-symmetric, and for the other natural frequencies, the natural modes will be symmetrical.
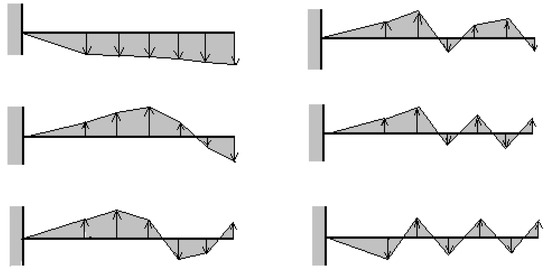
Figure 8.
The natural modes of vibration for one engine.
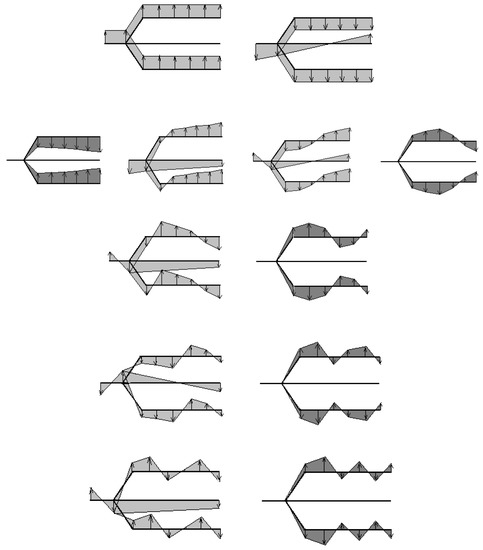
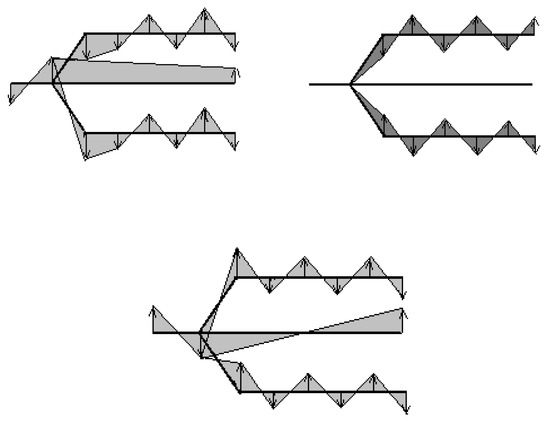
Figure 9.
The natural modes of vibration for the whole system.
4. Discussion
For a mechanical transmission presenting symmetry, some properties regarding eigenvalues and eigenmodes were stated and demonstrated. These properties suggest a method that would facilitate the calculation of eigenvalues. Thus, in Section 3 we have shown that eigenvalues for a single engine were among the eigenvalues of the whole mechanical system. From this, a method to simplify the calculus was presented: First, we calculated the eigenvalues for one single engine; then, these eigenvalues (which we already determined) were eliminated from the characteristic equation of the whole system. In this way, the size of the system was reduced and the calculation became easier. We have also shown that eigenmodes could be classified into symmetric and skew-symmetric modes of vibration and the skew-symmetric modes could be immediately built if one knows the eigenmodes for a single engine.
In the paper, two variants of mechanical systems that were equipped with two identical engines were analyzed, from the point of view of vibrations. The results show that the differences, from this point of view, were insignificant in terms of performance. Considering this, the choice of the optimum solution will be made according to criteria other than the vibrations of the transmission. In the paper, it was shown that the constructive symmetries that exist could help ease the calculation. Thus it was shown that the vibrations of the symmetrical parts could also be found among the natural frequencies of the whole system. The vibration modes were of two types: some were skew-symmetric, while others respected the symmetry of the system (symmetrical vibration modes). The problem studied allowed to highlight the properties of some symmetrical systems, applicable in any type of system with symmetrical parts, which allowed the calculation to be made in an easier way.
The method could also be applied for other mechanical systems presenting some symmetries. For small systems, with a reduced number of degrees of freedom, the method had no obvious advantages. For large systems, with a large number of degrees of freedom (as we could find in the Finite Element Method), the use of the presented properties for calculating eigenvalues and eigenmodes of vibration could significantly reduce the computation time by reducing the dimensions of the studied system. Thus, instead of calculating the eigenvalues and the eigenmodes for the whole system, we first calculated them for a symmetrical part and then we eliminated the determined values from the written equations for the whole system, in this way reducing the complexity of the problem, making it easier to be solved.
Author Contributions
Conceptualization, S.V., M.M. and M.P.; methodology, S.V. and M.P.; software, M.M.; validation, S.V. and M.P.; formal analysis, M.M. and M.P.; investigation, M.M. and S.V.; resources, S.V.; data curation, S.V.; writing—original draft preparation, S.V.; writing—review and editing, M.M.; visualization, M.M. and S.V.; supervision, S.V.; project administration, S.V. and M.M.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ambrus, C. Analiza Dinamică a Solicitărilor din Ansamblul Motor-Transmisie al Instalațiilor Mobile de Foraj de Mare Putere (Dynamic Analysis of Stresses in the Motor-Transmission Assembly of Mobile Power Drilling Installations). Ph.D. Thesis, Transylvania University of Brasov, Brasov, Romania, 2017. [Google Scholar]
- Holm, D.D.; Stoica, C.; Ellis, D.C.P. Geometric Mechanics and Symmetry; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 13 978-0387986432. [Google Scholar]
- Singer, S.F. Symmetry in Mechanics; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-1-4612-0189-2. [Google Scholar]
- Celep, Z. On the axially symmetric vibration of thick circular plates. Ingenieur-Archiv 1978, 47, 411–420. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Generalized Eigenvalue Analysis of Symmetric Prestressed Structures Using Group Theory. J. Comput. Civ. Eng. 2012, 26, 488–497. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Bausys, R.; Antucheviciene, J. Civil Engineering and Symmetry. Symmetry 2019, 14, 501. [Google Scholar] [CrossRef]
- Mechanics and symmetry in Europe: The geometry and dynamics of deformable systems. Project. HPRN-CT-2000-00113, Funded under: FP5-HUMAN POTENTIAL, University of Surrey, United Kingdom, Centre National de la Reserche Scientifique, France, Instituto Superior Tecnico, Portugal, Swiss Federal Institute of Technology of Nottingham, Switzerland, Universita degli studi di Padova, Italy, University of Nottingham, United Kingdom, Universite du Litoral, France, Utrecht University, Netherlands. Available online: https://cordis.europa.eu/project/rcn/53964/factsheet/en (accessed on 12 October 2019).
- Ganghoffer, J.F.; Mladenov, I. Similarity, Symmetry and Group Theoretical Methods in Mechanics; International Centre for Mechanical Sciences: Udine, Italy, 2015. [Google Scholar]
- Mangeron, D.; Goia, I.; Vlase, S. Symmetrical Branched Systems Vibrations. Sci. Mem. Rom. Acad. 1991, 12, 232–236. [Google Scholar]
- Weimann, S.; Kremer, M.; Plotnik, Y.; Lumer, Y.; Nolte, S.; Makris, K.G.; Segev, M.; Rechtsman, M.C.; Szameit, A. Topologically protected bound states in photonic parity-time-symmetric crystals. Nat. Mater. 2017, 16, 433–438. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Yang, H.L.; Meng, F.W. Sixth-order symplectic and symmetric explicit ERKN schemes for solving multi-frequency oscillatory nonlinear Hamiltonian equations. Calcolo 2017, 54, 117–140. [Google Scholar] [CrossRef]
- Niiranen, J.; Balobanov, V.; Kiendl, J.; Hosseini, S.B. Variational formulations, model comparisons and numerical methods for Euler-Bernoulli micro- and nano-beam models. Math. Mech. Solids 2019, 24, 312–335. [Google Scholar] [CrossRef]
- Bourada, F.; Amara, K.; Bousahla, A.A.; Tounsi, A.; Mahmoud, S.R. A novel refined plate theory for stability analysis of hybrid and symmetric S-FGM plates. Struct. Eng. Mech. 2018, 68, 661–675. [Google Scholar]
- Sun, X.J.; Zhang, H.; Meng, W.J.; Zhang, R.H.; Li, K.N.; Peng, T. Primary resonance analysis and vibration suppression for the harmonically excited nonlinear suspension system using a pair of symmetric viscoelastic buffers. Nonlinear Dyn. 2018, 94, 1243–1265. [Google Scholar] [CrossRef]
- Vlase, S.; Păun, M. Vibration analysis of a mechanical system consisting of two identical parts. Rom. J. Tech. Sci. Appl. Mech. 2015, 60, 216–230. [Google Scholar]
- Vlase, S.; Marin, M.; Scutaru, M.L.; Munteanu, R. Coupled transverse and torsional vibrations in a mechanical system with two identical beams. AIP Adv. 2017, 7, 065301. [Google Scholar] [CrossRef]
- Othman, M.I.A.; Marin, M. Effect of thermal loading due to laser pulse on thermoelastic porous medium under G-N theory. Results Phys. 2017, 7, 3863–3872. [Google Scholar] [CrossRef]
- Vlase, S.; Năstac, D.C.; Marin, M.; Mihălcică, M. A method for the study of the vibration of mechanical bars systems with symmetries. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2017, 60, 539. [Google Scholar]
- Hassan, M.; Marin, M.; Ellahi, R.; Alamri, S.Z. Exploration of convective heat transfer and flow characteristics synthesis by Cu–Ag/water hybrid-nanofluids. Heat Transf. Res. 2018, 49, 1837–1848. [Google Scholar] [CrossRef]
- Zingoni, A. Symmetry recognition in group-theoretic computational schemes for complex structural systems. Comput. Struct. 2012, 94–95, 34–44. [Google Scholar] [CrossRef]
- Zingoni, A. Group-theoretic exploitations of symmetry in computational solid and structural mechanics. Int. J. Numer. Methods Eng. 2009, 79, 253–289. [Google Scholar] [CrossRef]
- Zingoni, A. Group-theoretic insights on the vibration of symmetric structures in engineering. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef]
- Catalog. Roman Autocamioane S.A Brașov. Roman Trucks & Buses—Special vehicles. 2012. Available online: http://www.roman.ro/index.php?lang=ro&showlang=&cat=PRODUSE%20/%20AUTOVEHICULE%20CIVILE&subcat=Autovehicule%20pentru%20industria%20petroliera&subid=3112&main=produse&end=fnpr (accessed on 12 October 2019).
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).