Classical Limit for Dirac Fermions with Modified Action in the Presence of a Black Hole
Abstract
1. Introduction
2. Dirac Fermions in the Black Hole in the Painleve–Gullstrand Reference Frame
3. Covariant Formulation of the Theory and Its Classical Limit
4. The Stress–Energy Tensor of the Non-Interacting Classical Particles
4.1. General Expression for the Stress–Energy Tensor
4.2. The Stress–Energy Tensor in the Limit
4.3. Expression for the Stress–Energy Tensor for Finite in the Case When the Substance Is Co-Moving with the Space Flow
5. Description of the Gravitational Collapse in the Generalized Painlevé-Gullstrand Coordinates
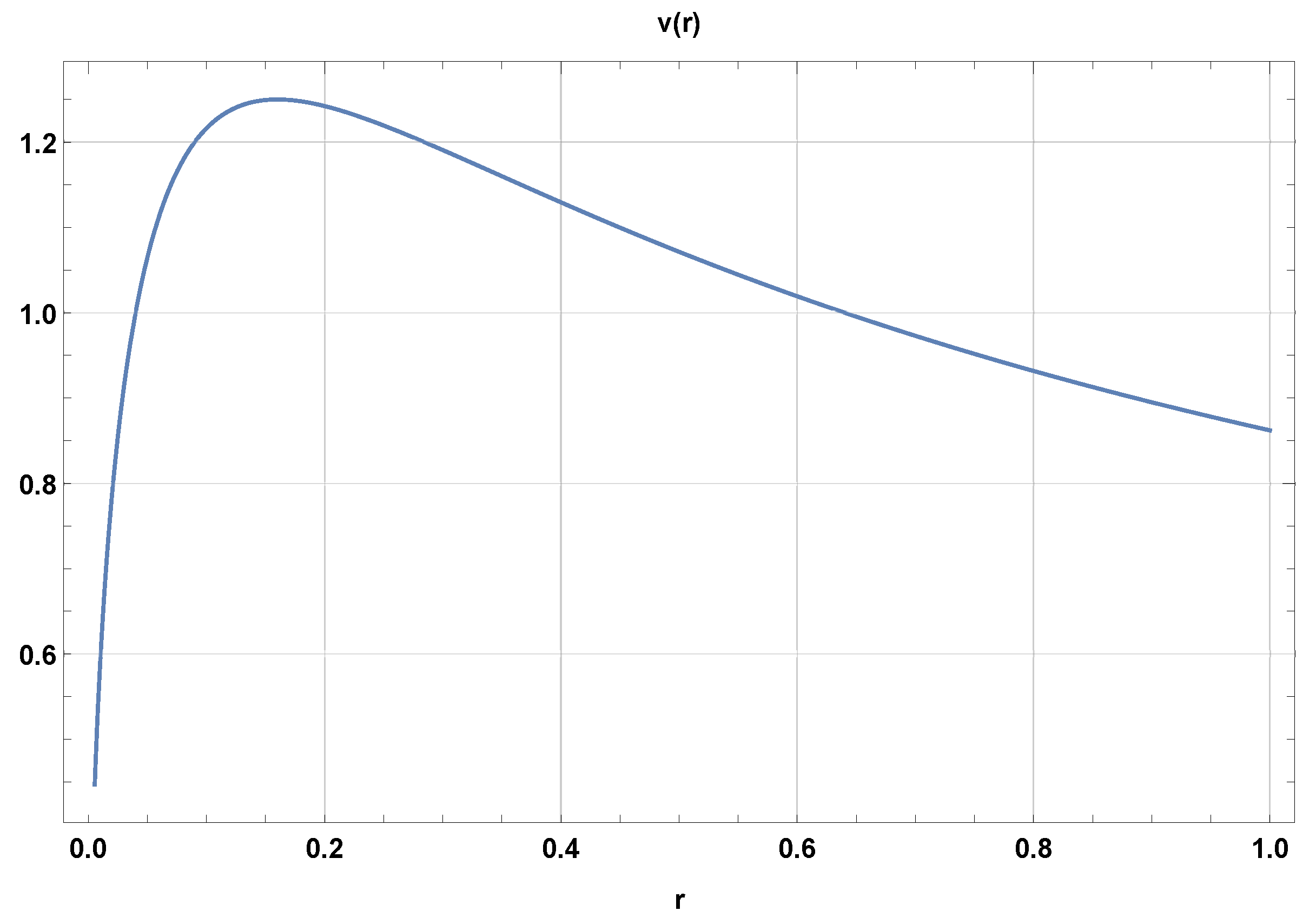
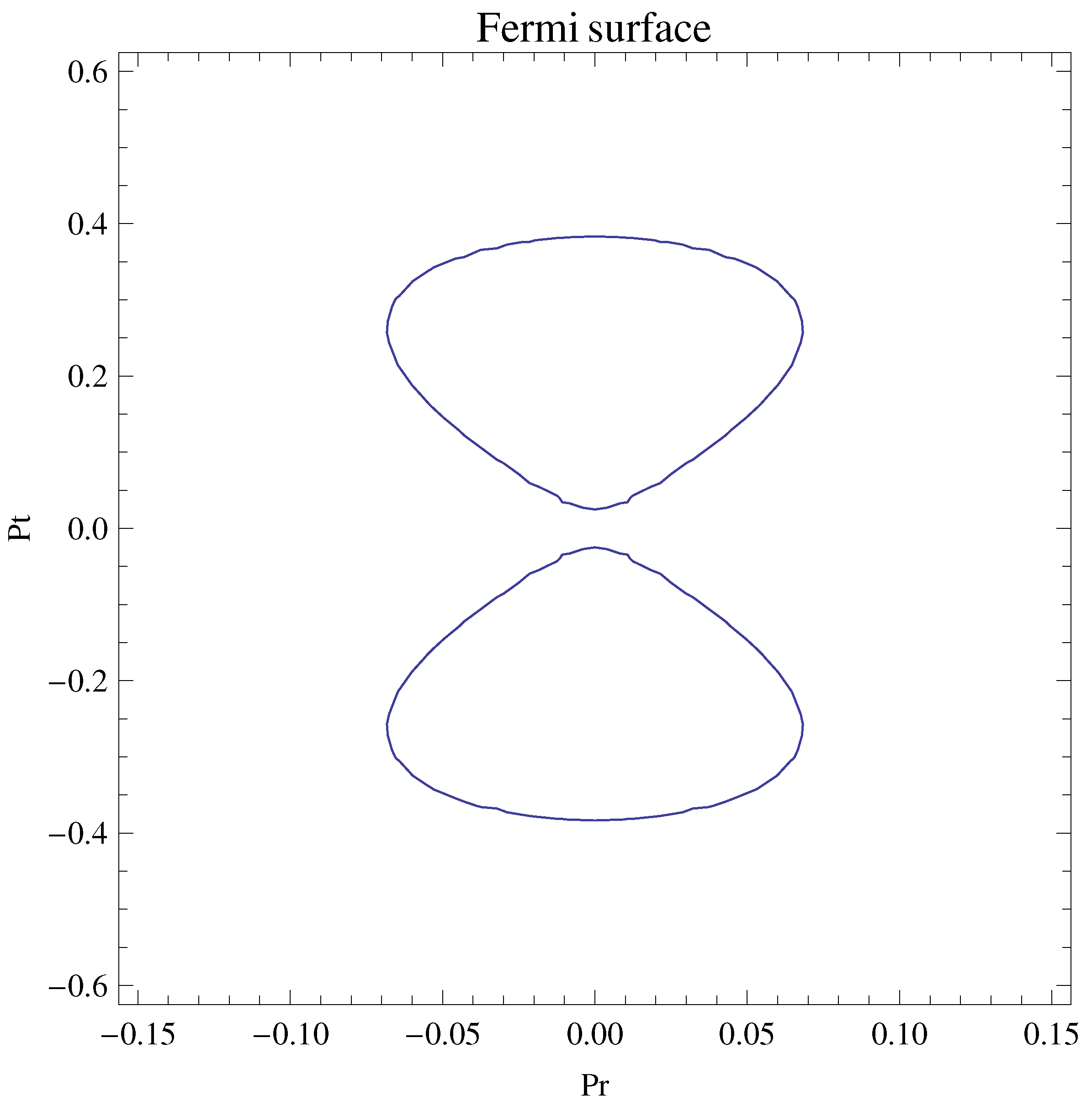
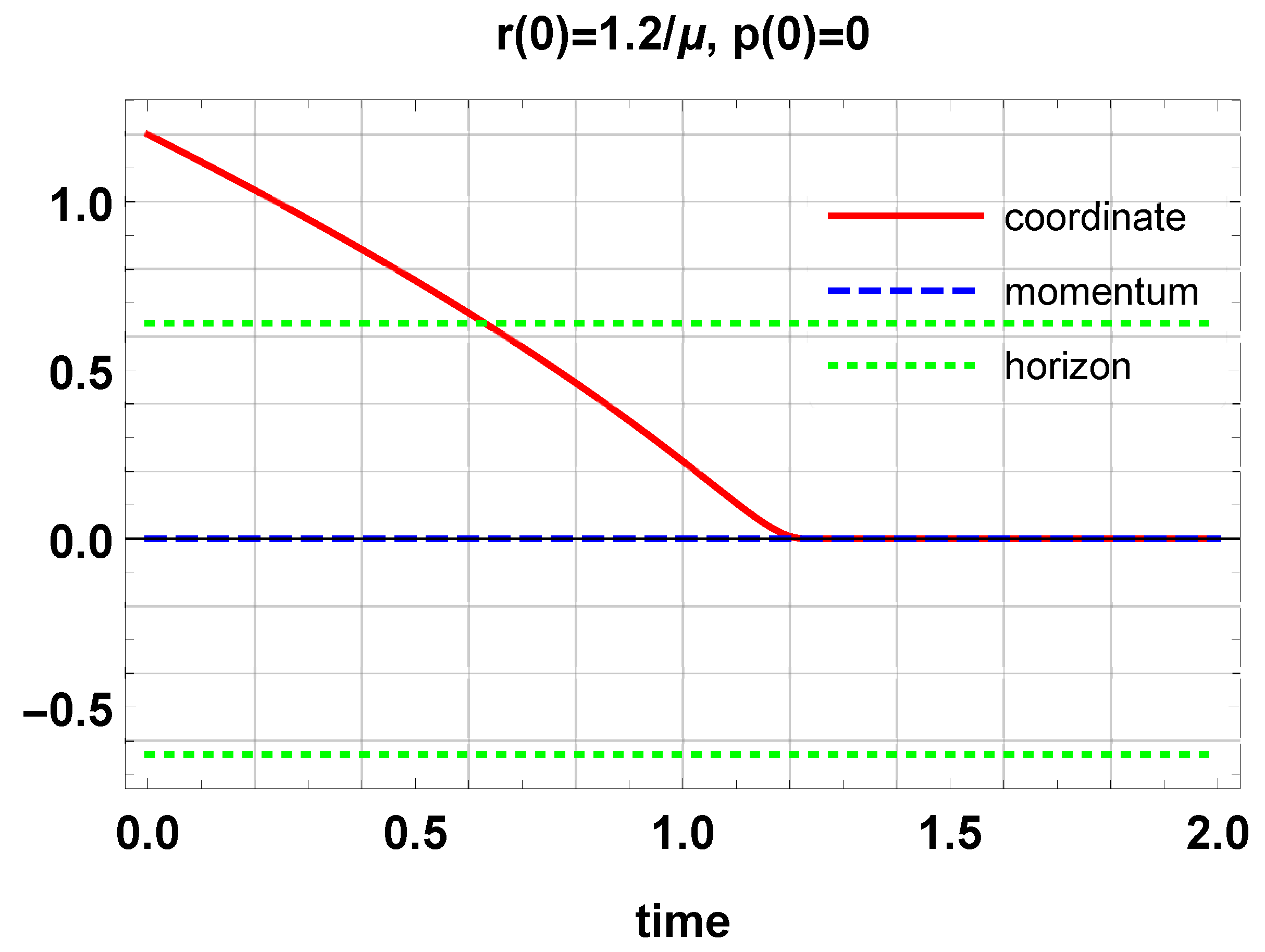
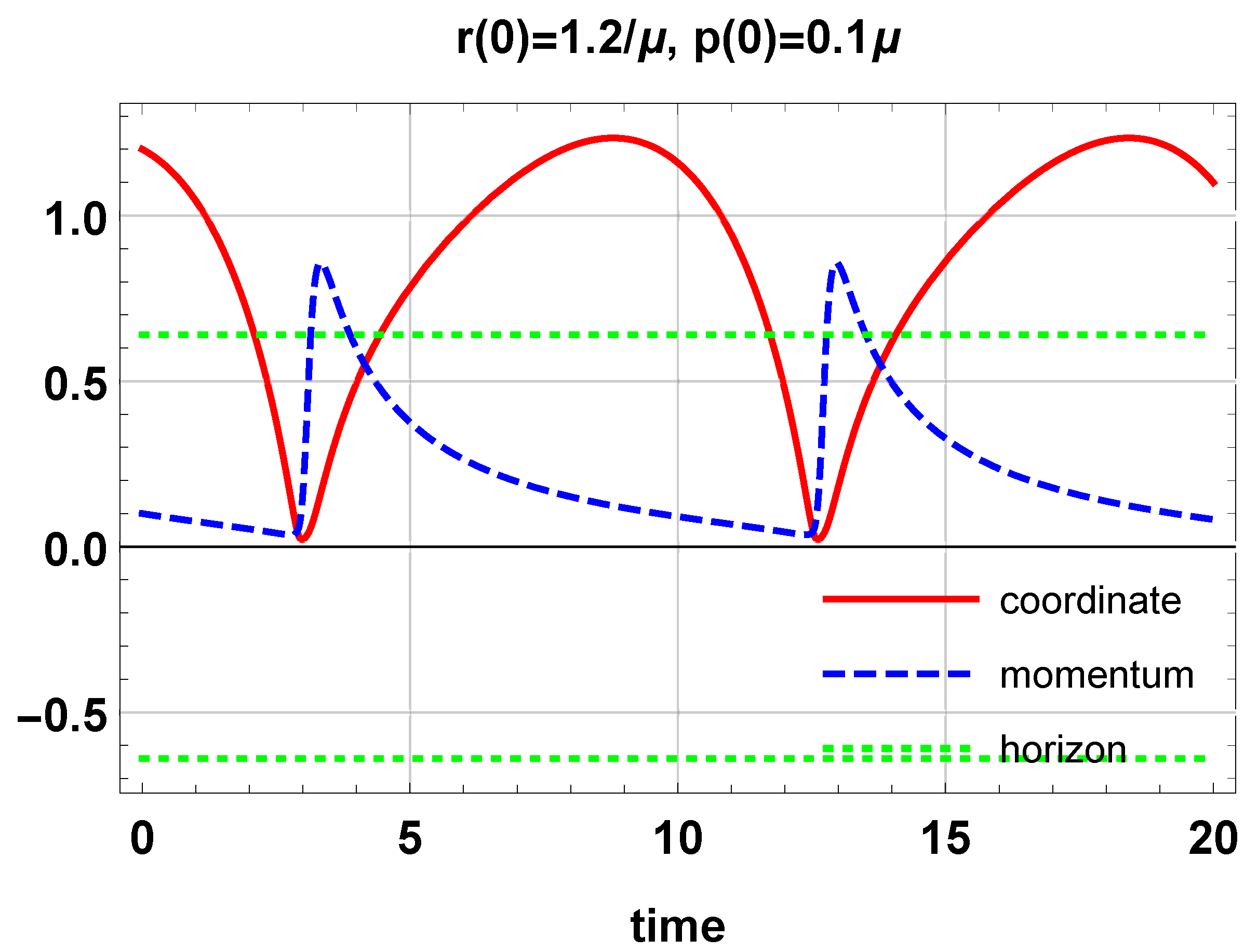
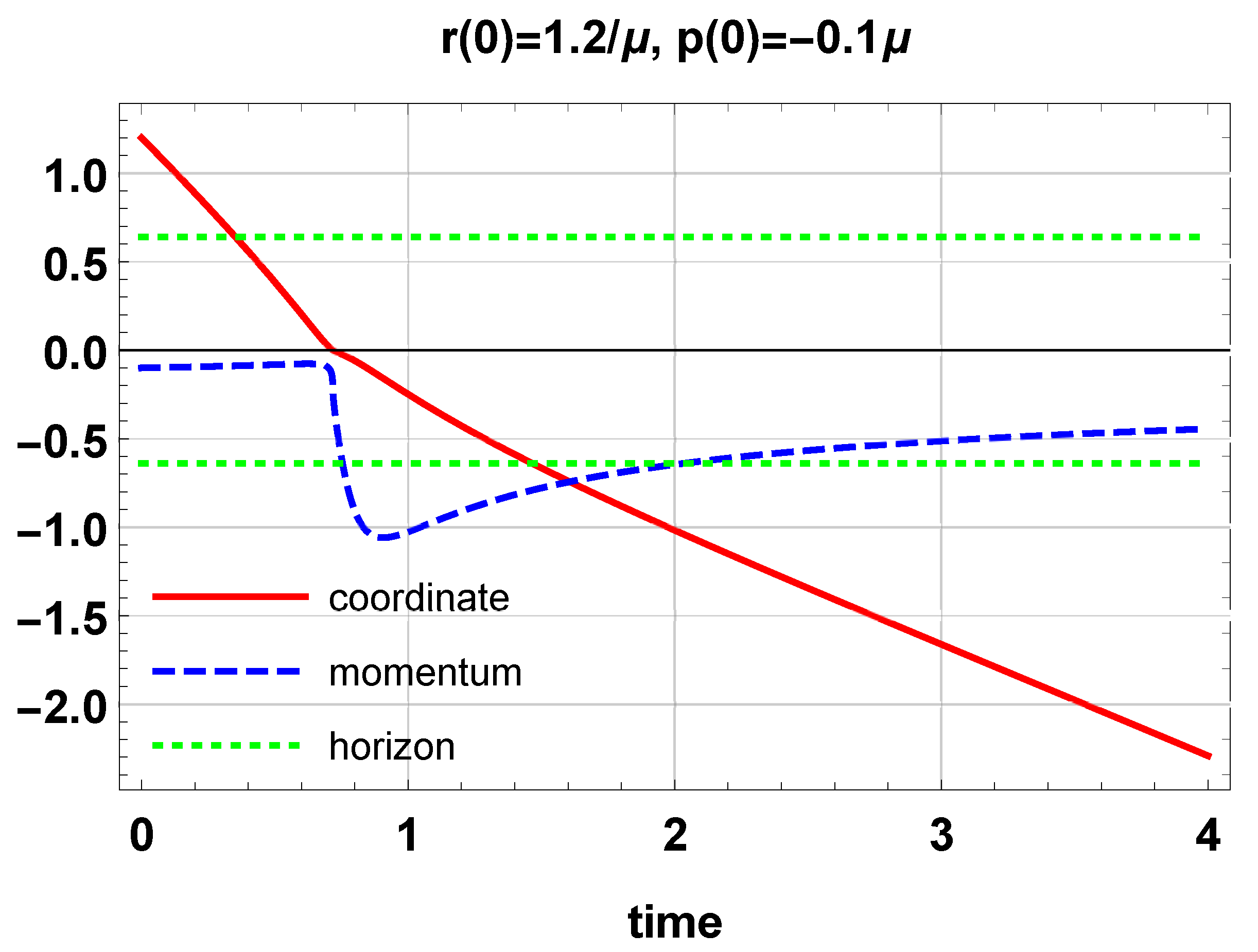
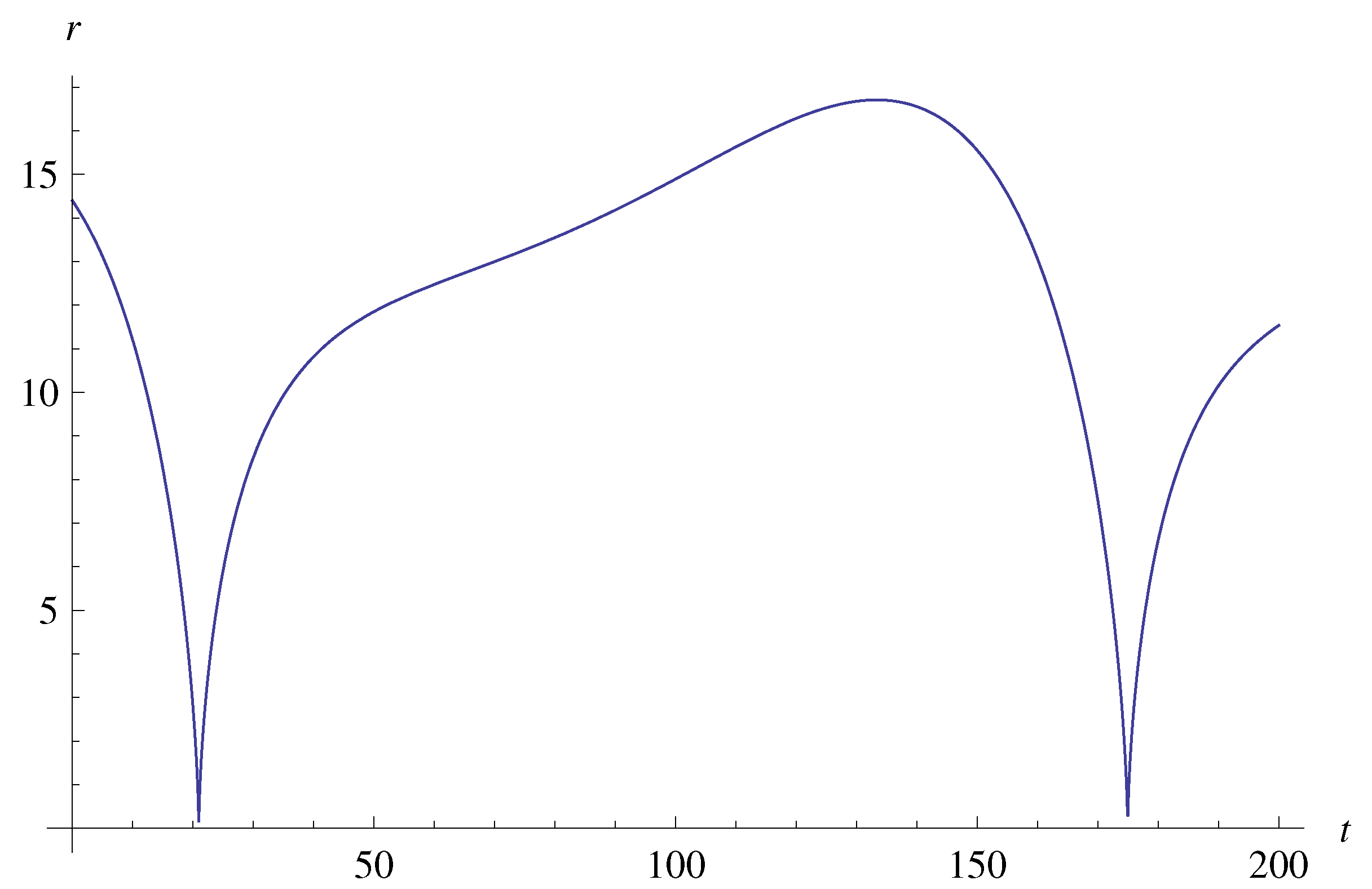
6. Classical Dynamics of Particles
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwarzschild, K. Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie; Sitzungsberichte der Koniglich Preussischen Akademie der Wissenschaften: Berlin, Germany, 1916; pp. 189–196. [Google Scholar]
- Schwarzschild, K. Uber das Gravitationsfeld einer Kugel aus inkompressibler Flussigkeit nach der Einsteinschen Theorie; Sitzungsberichte der Koniglich Preussischen Akademie der Wissenschaften: Berlin, Germany, 1916; pp. 424–434. [Google Scholar]
- Gullstrand, A. Allgemeine Losung des statischen Einkorperproblems in der Einsteinschen Gravitationstheorie. Arkiv. Mat. Astron. Fys. 1922, 16, 1–15. [Google Scholar]
- Painleve, P. La mecanique classique et la theorie de la relativite. C. R. Acad. Sci. (Paris) 1921, 173, 677–680. [Google Scholar]
- Hamilton, A.J.S.; Lisle, J.P. The River model of black holes. Am. J. Phys. 2008, 76, 519. [Google Scholar] [CrossRef]
- Doran, C. A New form of the Kerr solution. Phys. Rev. D 2000, 61, 067503. [Google Scholar] [CrossRef]
- Volovik, G.E. Simulation of Painleve-Gullstrand black hole in thin He-3—A film. JETP Lett. 1999, 69, 705. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Parikh, M.K.; Wilczek, F. Hawking radiation as tunneling. Phys. Rev. Lett. 2000, 85, 5042. [Google Scholar] [CrossRef]
- Akhmedov, E.T.; Akhmedova, V.; Singleton, D. Hawking temperature in the tunneling picture. Phys. Lett. B 2006, 642, 124. [Google Scholar] [CrossRef]
- Jannes, G. Hawking radiation of E < m massive particles in the tunneling formalism. JETP Lett. 2011, 94, 18. [Google Scholar] [CrossRef]
- Volovik, G.E. The Universe in a Helium Droplet; Clarendon Press: Oxford, UK, 2003. [Google Scholar]
- Huhtala, P.; Volovik, G.E. Fermionic microstates within Painleve-Gullstrand black hole. J. Exp. Theor. Phys. 2002, 94, 853–861. [Google Scholar] [CrossRef]
- Parameswaran, S.; Grover, T.; Abanin, D.; Pesin, D.; Vishwanath, A. Probing the chiral anomaly with nonlocal transport in Weyl semimetals. Phys. Rev. X 2014, 4, 031035. [Google Scholar]
- Vazifeh, M.; Franz, M. Electromagnetic response of weyl semimetals. Phys. Rev. Lett. 2003, 111, 027201. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wu, S.; Burkov, A. Axion response in Weyl semimetals. Phys. Rev. B 2013, 88, 125105. [Google Scholar] [CrossRef]
- Chen, Y.; Bergman, D.; Burkov, A. Weyl fermions and the anomalous Hall effect in metallic ferromagnets. Phys. Rev. B 2013, 88, 125110. [Google Scholar] [CrossRef]
- Ramamurthy, S.T.; Hughes, T.L. Patterns of electro-magnetic response in topological semi-metals. arXiv 2014, arXiv:1405.7377. [Google Scholar]
- Zyuzin, A.A.; Burkov, A.A. Topological response in Weyl semimetals and the chiral anomaly. Phys. Rev. B 2012, 86, 115133. [Google Scholar] [CrossRef]
- Goswami, P.; Tewari, S. Axionic field theory of (3+1)-dimensional Weyl semi-metals. Phys. Rev. B 2013, 88, 245107. [Google Scholar] [CrossRef]
- Liu, C.-X.; Ye, P.; Qi, X.-L. Chiral gauge field and axial anomaly in a Weyl semimetal. Phys. Rev. B 2013, 87, 235306. [Google Scholar] [CrossRef]
- Soluyanov, A.A.; Gresch, D.; Wang, Z.; Wu, Q.; Troyer, M.; Dai, X.; Bernevig, B.A. Type-II Weyl Semimetals. Nature 2015, 527, 495–498. [Google Scholar] [CrossRef]
- Schonemann, R.; Aryal, N.; Zhou, Q.; Chiu, Y.-C.; Chen, K.-W.; Martin, T.J.; McCandless, G.T.; Chan, J.Y.; Manousakis, E.; Balicas, L. Fermi surface of the Weyl type-II metallic candidate WP2. Phys. Rev. B 2017, 96, 121108. [Google Scholar] [CrossRef]
- Rhodes, D.; Schonemann, R.; Aryal, N.; Zhou, Q.; Zhang, Q.R.; Kampert, E.; Chiu, Y.-C.; Lai, Y.; Shimura, Y.; McCandless, G.T.; et al. Bulk Fermi-surface of the Weyl type-II semi-metallic candidate MoTe2. Phys. Rev. B 2017, 96, 165134. [Google Scholar] [CrossRef]
- Volovik, G.E.; Zubkov, M.A. Emergent Weyl spinors in multi-fermion systems. Nucl. Phys. B 2014, 881, 514. [Google Scholar] [CrossRef]
- Volovik, G.E. Black hole and Hawking radiation by type-II Weyl fermions. JETP Lett. 2016, 104, 645. [Google Scholar] [CrossRef]
- Nissinen, J.; Volovik, G.E. Type-III and IV interacting Weyl points. JETP Lett. 2017, 105, 447–452. [Google Scholar] [CrossRef]
- Zubkov, M.A. The black hole interior and the type II Weyl fermions. Mod. Phys. Lett. A 2018, 33, 1850047. [Google Scholar] [CrossRef]
- Zubkov, M.A. Analogies between the Black Hole Interior and the Type II Weyl Semimetals. Universe 2018, 4, 135. [Google Scholar] [CrossRef]
- Zubkov, M.A.; Lewkowicz, M. The type II Weyl semimetals at low temperatures: Chiral anomaly, elastic deformations, zero sound. Ann. Phys. 2018, 399, 26–52. [Google Scholar] [CrossRef]
- Babichev, E.; Mukhanov, V.; Vikman, A. k-Essence, superluminal propagation, causality and emergent geometry. JHEP 2008, 0802, 101. [Google Scholar] [CrossRef]
- Dubovsky, S.; Gregoire, T.; Nicolis, A.; Rattazzi, R. Null energy condition and superluminal propagation. JHEP 2006, 2006, 025. [Google Scholar] [CrossRef]
- Dale, R.; Saez, D. Spherical symmetric dust collapse in vector-tensor gravity. Phys.Rev. D 2018, 98, 064007. [Google Scholar] [CrossRef]
- Moffat, J.W. Black holes in Modified Gravity (MOG). Eur. Phys. J. C 2015, 75, 175. [Google Scholar] [CrossRef]
- Arraut, I.; Batic, D.; Nowakowski, M. Velocity and velocity bounds in static spherically symmetric metrics. Central Eur. J. Phys. 2011, 9, 926. [Google Scholar] [CrossRef]
- Alexandrov, S. Immirzi parameter and fermions with non-minimal coupling. Class. Quant. Grav. 2008, 25, 145012. [Google Scholar] [CrossRef]
- Vladimirov, A.A.; Diakonov, D. Phase transitions in spinor quantum gravity on a lattice. Phys. Rev. D 2012, 86, 104019. [Google Scholar] [CrossRef]
- Diakonov, D. Towards lattice-regularized Quantum Gravity. arXiv 2011, arXiv:1109.0091. [Google Scholar]
- Diakonov, D.; Tumanov, A.G.; Vladimirov, A.A. Low-energy general relativity with torsion: A systematic derivative expansion. Phys. Rev. D 2011, 84, 124042. [Google Scholar] [CrossRef]
- Arraut, I. The black hole radiation in massive gravity. Universe 2018, 4, 27. [Google Scholar] [CrossRef]
- Arraut, I. On the apparent loss of predictability inside the de-Rham-Gabadadze-Tolley non-linear formulation of massive gravity: The Hawking radiation effect. EPL 2015, 109, 10002. [Google Scholar] [CrossRef]
- Arraut, I. Path-integral derivation of black-hole radiance inside the de-Rham-Gabadadze-Tolley formulation of massive gravity. Eur. Phys. J. C 2017, 77, 501. [Google Scholar] [CrossRef]
- Arraut, I. Black-hole evaporation from the perspective of neural networks. EPL 2018, 124, 50002. [Google Scholar] [CrossRef]
- Kanai, Y.; Siino, M.; Hosoya, A. Gravitational collapse in Painleve-Gullstrand coordinates. Prog. Theor. Phys. 2011, 125, 1053. [Google Scholar] [CrossRef]
- Krasinski, A.; Bolejko, K. Avoidance of singularities in spherically symmetric charged dust. Phys. Rev. D 2006, 73, 124033. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewkowicz, M.; Zubkov, M. Classical Limit for Dirac Fermions with Modified Action in the Presence of a Black Hole. Symmetry 2019, 11, 1294. https://doi.org/10.3390/sym11101294
Lewkowicz M, Zubkov M. Classical Limit for Dirac Fermions with Modified Action in the Presence of a Black Hole. Symmetry. 2019; 11(10):1294. https://doi.org/10.3390/sym11101294
Chicago/Turabian StyleLewkowicz, Meir, and Mikhail Zubkov. 2019. "Classical Limit for Dirac Fermions with Modified Action in the Presence of a Black Hole" Symmetry 11, no. 10: 1294. https://doi.org/10.3390/sym11101294
APA StyleLewkowicz, M., & Zubkov, M. (2019). Classical Limit for Dirac Fermions with Modified Action in the Presence of a Black Hole. Symmetry, 11(10), 1294. https://doi.org/10.3390/sym11101294




