An Improved Pigeon-Inspired Optimisation Algorithm and Its Application in Parameter Inversion
Abstract
1. Introduction
- An improved PIO algorithm (IPIO) is proposed by introducing the particle swarm optimisation (PSO) algorithm, an inverse factor, and a Gaussian factor into the PIO algorithm. In order to verify the effectiveness of the improvement, the benchmark functions are used to do the experiments and compare the experimental results with other algorithms.
- The improved algorithm for the pre-stack AVO elastic parameter inversion is used. The experimental comparison results with other optimisation algorithms indicate that the proposed IPIO algorithm can achieve better inversion results.
2. PIO Algorithm
2.1. PIO Algorithm and Its Improvement
- Initialise the parameters, initialise the population, calculate the fitness value of each individual in the population, and select the optimal position of the population.
- Update the position and speed of each individual according to the PSO algorithm, and calculate the position of the individual’s corresponding reverse individual.
- Calculate the fitness value, compare the fitness values of the individual and its reverse individual, retain the better one of the two, remove the poor one, and update the global optimum and the historical optimum of each individual.
- Determine whether the maximum number of iterations of the particle swarm operator is reached. If yes, proceed to the next step, otherwise return to Step 2.
- Calculate the centre position of the population using the landmark operator of the PIO algorithm.
- Update the position of each individual based on the improved landmark operator.
- Calculate the fitness value, and update the global optimum.
- Determine whether the maximum number of iterations of the landmark operator is reached. If yes, terminate the operation, otherwise return to Step 6 to operate until the iteration is stopped.
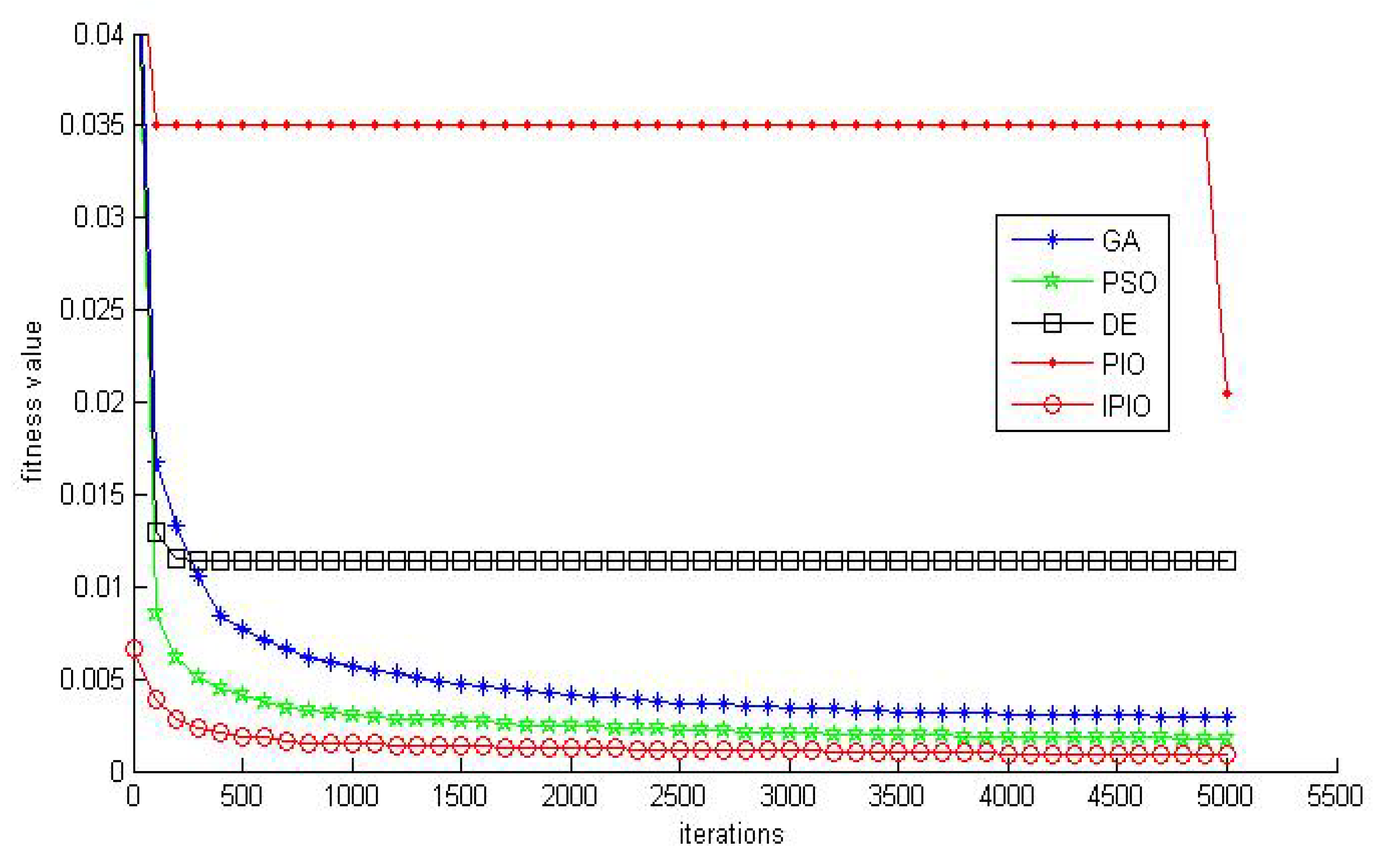
2.2. Experimental Results and Analysis
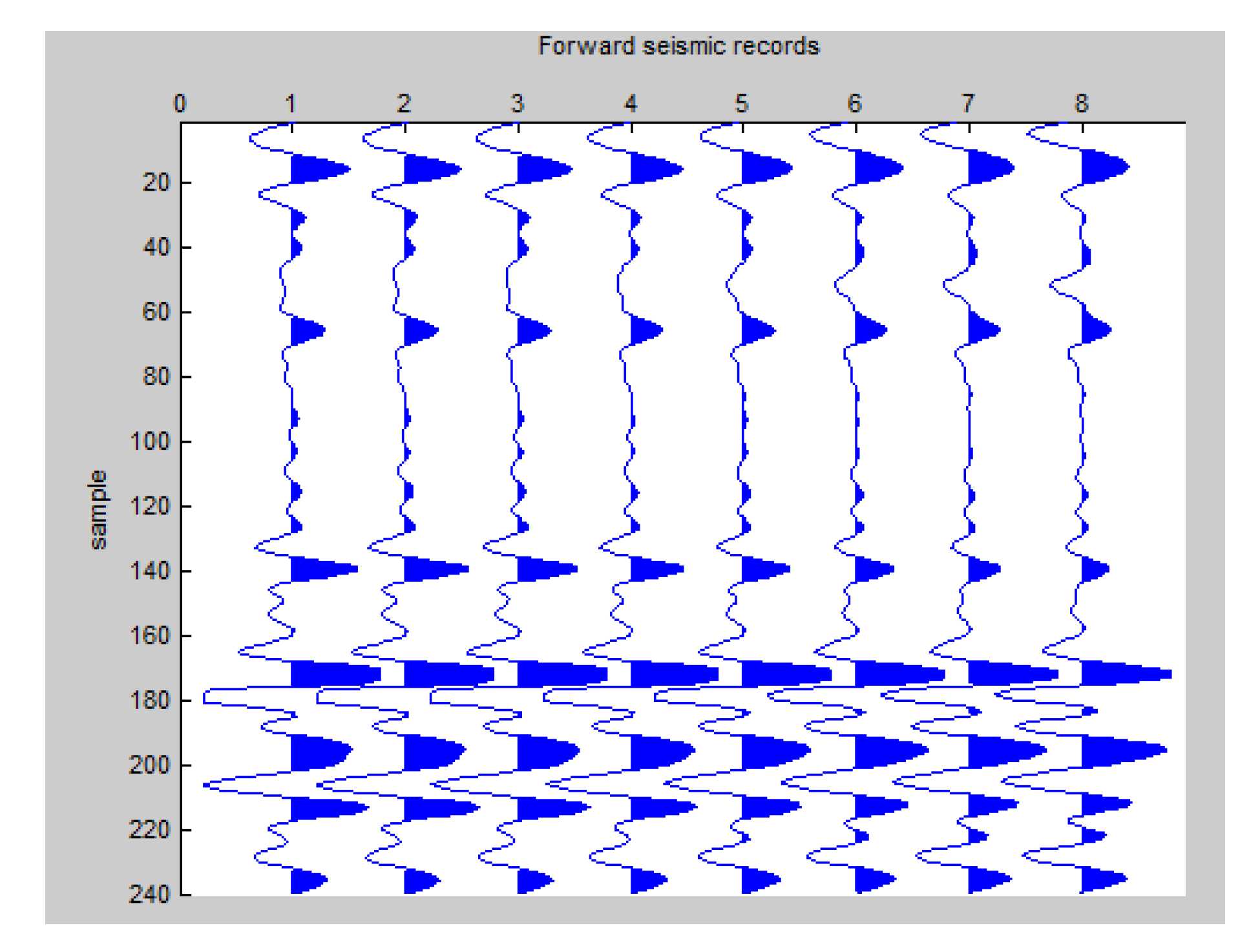
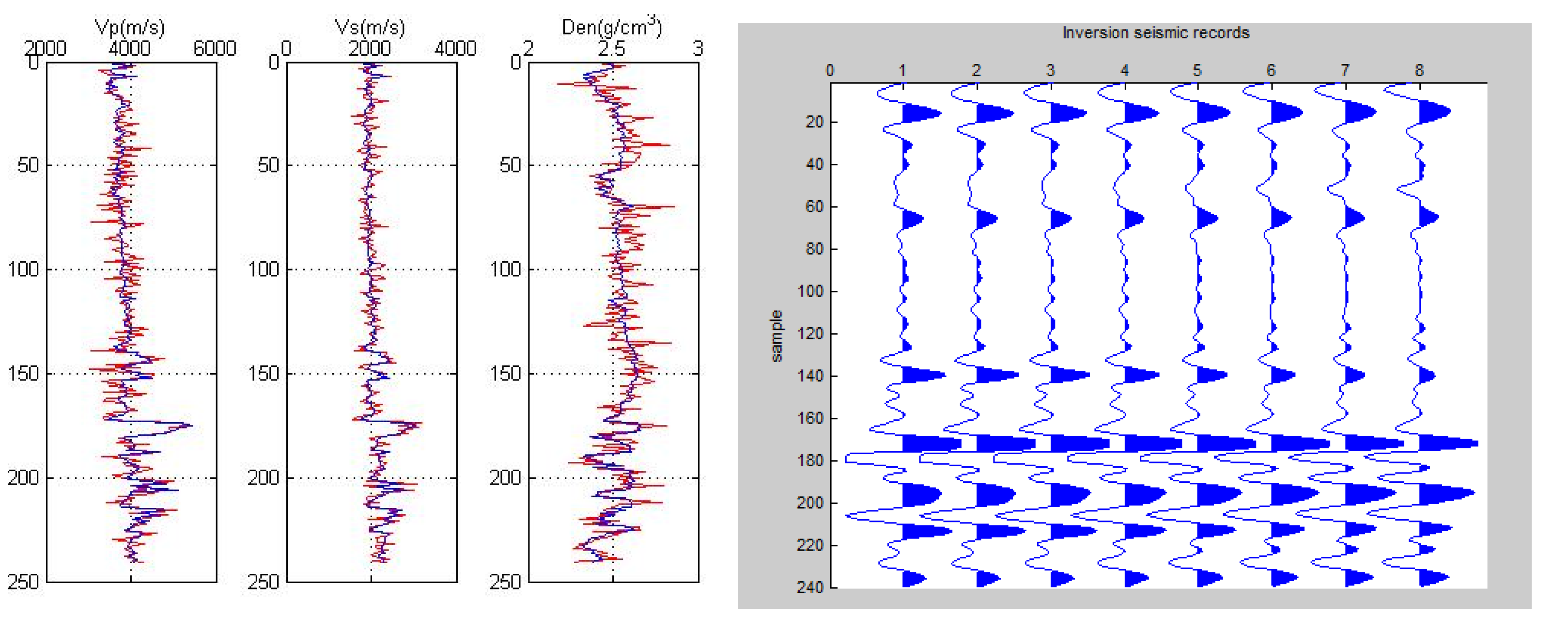
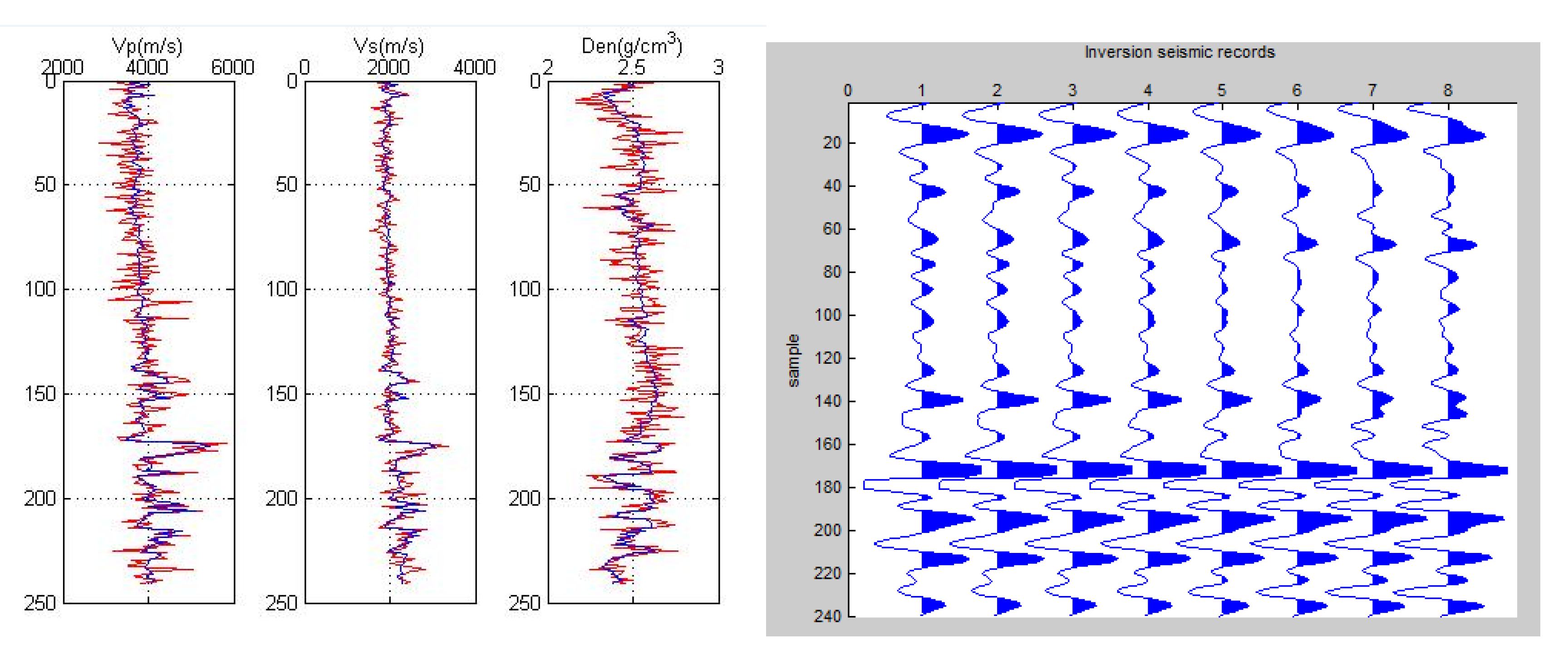
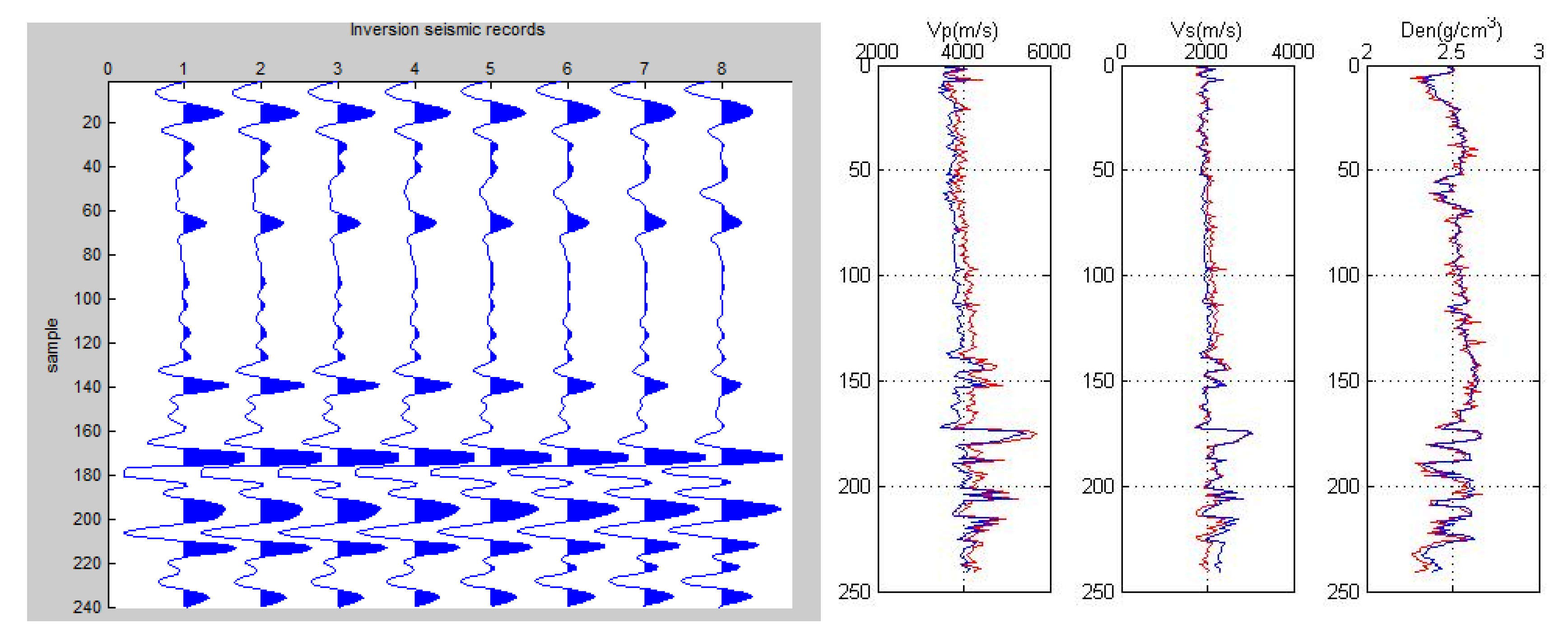
3. Pre-stack AVO Elastic Parameter Inversion Problem
3.1. Inversion Model
3.2. Inversion Results Evaluation
4. Experimental Simulation and Analysis
4.1. Parameter Setting
4.2. Simulation Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kennedy, J. Swarm Intelligence. Swarm Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2001. [Google Scholar]
- Krause, J.; Ruxton, G.D.; Krause, S. Swarm intelligence in animals and humans. Trends Ecol. Evol. 2010, 25, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Dorigo, M.; Stützle, T. Ant Colony Optimization: Overview and Recent Advances. In Handbook of Metaheuristics; Springer: Cham, Switzerland, 2010. [Google Scholar]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the Sixth International Symposium, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Delice, Y.; Aydoğan, E.K.; Özcan, U.; İlkay, M.S. A Modified Particle Swarm Optimization Algorithm to Mixed-Model Two-Sided Assembly Line Balancing. J. Intell. Manuf. 2017, 28, 23–36. [Google Scholar] [CrossRef]
- Chatterjee, S.; Sarkar, S.; Hore, S.; Dey, N.; Ashour, A.S.; Balas, V.E. Particle Swarm Optimization Trained Neural Network for Structural Failure Prediction of Multistoried RC Buildings. Neural Comput. Appl. 2017, 28, 2005–2016. [Google Scholar] [CrossRef]
- Duan, H.; Qiao, P. Pigeon-Inspired Optimization: A New Swarm Intelligence Optimizer for Air Robot Path Planning. Int. J. Intell. Comput. Cybern. 2014, 7, 24–37. [Google Scholar] [CrossRef]
- Duan, H.B.; Qiu, H.X.; Fan, Y.M. Optimal Combat Coordination Control for Unmanned Aerial Vehicle Using Predator-Escaped Pigeon. Chin. Sci. Technol. Sci. 2015, 45, 559–572. [Google Scholar]
- Zhang, B.; Duan, H. Three-Dimensional Path Planning for Uninhabited Combat Aerial Vehicle Based on Predator-Prey Pigeon-Inspired Optimization in Dynamic Environment; IEEE Computer Society Press: Los Alamitos, CA, USA, 2017. [Google Scholar]
- Dou, R.; Duan, H. Pigeon Inspired Optimization Approach to Model Prediction Control for Unmanned Air Vehicles. Aircr. Eng. Aerosp. Technol. Int. J. 2016, 88, 108–116. [Google Scholar] [CrossRef]
- Duan, H.; Wang, X. Echo State Networks with Orthogonal Pigeon-Inspired Optimization for Image Restoration. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 2413–2425. [Google Scholar] [CrossRef] [PubMed]
- Sankareswaran, U.M.; Rajendran, S. A Novel Pigeon Inspired Optimization in Ovarian Cyst Detection. Curr. Med. Imaging Rev. 2016, 12, 43–49. [Google Scholar]
- Lei, X.; Ding, Y.; Wu, F.X. Detecting Protein Complexes from DPINs by Density Based Clustering with Pigeon-Inspired Optimization Algorithm. Sci. China Inf. Sci. 2016, 59, 070103. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06); IEEE: New York, NY, USA, 2005; pp. 695–701. [Google Scholar]
- Zhang, S.; Duan, H. Gaussian Pigeon-Inspired Optimization Approach to Orbital Spacecraft Formation Reconfiguration. Chin. J. Aeronaut. 2015, 28, 200–205. [Google Scholar] [CrossRef]
- Rodriguez-Zalapa, O.; Huerta-Ruelas, J.A.; Rangel-Miranda, D.; Morales-Sanchez, E.; Hernandez-Zavala, A. Csimfs: An Algorithm to Tune Fuzzy Logic Controllers. J. Intell. Fuzzy Syst. 2017, 33, 679–691. [Google Scholar] [CrossRef]
- Alfonso, M.J.F.I.; Milán, D.P.S.; Córdoba, J.V.A.I.; Colmenero, N.P. Some Improvements on Relativistic Positioning Systems. Appl. Math. Nonlinear Sci. 2018, 3, 161–166. [Google Scholar] [CrossRef][Green Version]
- Plata, S.A.; Sáez, S.B. After Notes on Chebyshev’s Iterative Method. Appl. Math. Nonlinear Sci. 2017, 2, 1–12. [Google Scholar]
- Neidell, N.S. Amplitude Variation with Offset. Lead. Edge 1986, 5, 47–51. [Google Scholar] [CrossRef]
- Gao, W.; Zhu, L.; Guo, Y.; Wang, K. Ontology Learning Algorithm for Similarity Measuring and Ontology Mapping Using Linear Programming. J. Intell. Fuzzy Syst. 2017, 33, 3153–3163. [Google Scholar] [CrossRef]
- Jin, J.; Mi, W. An Aimms-Based Decision-Making Model for Optimizing the Intelligent Stowage of Export Containers in a Single Bay. Discret. Contin. Dyn. Syst. Ser. S 2019, 12, 1101–1115. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Z.; Yan, X. Research on the Parameter Inversion Problem of Prestack Seismic Data Based on Improved Differential Evolution Algorithm. Clust. Comput. 2017, 20, 2881–2890. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, Z.; Wu, Q.; Gong, W.; Wang, L. Elastic Parameter Inversion Problem Based on Brain Storm Optimization Algorithm. Memet. Comput. 2019, 11, 143–153. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, Z.; Yan, X.; Gong, W. An Improved Particle Swarm Optimization Algorithm for AVO Elastic Parameter Inversion Problem. Concurr. Comput. Pract. Exp. 2019, 31, 1–16. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, Z.; Hu, C.; Gong, W.; Wu, Q. Spark-Based Intelligent Parameter Inversion Method for Prestack Seismic Data. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Mallick, S. Model-based Inversion of Amplitude-variations-with-offset Data Using a Genetic Algorithm. Geophysics 1995, 60, 939–954. [Google Scholar] [CrossRef]
- Priezzhev, I.; Shmaryan, L.; Bejarano, G. Nonlinear Multitrace Seismic Inversion Using Neural Network and Genetic Algorithm-Genetic Inversion. In Proceedings of the 3rd EAGE St. Petersburg International Conference and Exhibition on Geosciences-Geosciences: From New Ideas to New Discoveries 2008, Saint Petersburg, Russia, 2008. [Google Scholar]
- Soupios, P.; Akca, I.; Mpogiatzis, P.; Basokur, A.T.; Papazachos, C. Applications of Hybrid Genetic Algorithms in Seismic Tomography. J. Appl. Geophys. 2011, 75, 479–489. [Google Scholar] [CrossRef]
- Agarwal, A.; Sain, K.; Shalivahan, S. Traveltime and Constrained AVO Inversion Using FDR PSO. In SEG Technical Program Expanded Abstracts 2016; Society of Exploration Geophysicists: Tulsa, OK, USA, 2016; pp. 577–581. [Google Scholar]
- Sun, S.Z.; Chen, L.; Bai, Y.; Hu, L.G. PSO Non-linear Pre-stack Inversion Method and the Application in Reservoir Prediction. In SEG Technical Program Expanded Abstracts 2012; Society of Exploration Geophysicists: Tulsa, OK, USA, 2012; pp. 1–5. [Google Scholar]
- Sun, S.Z.; Liu, L. A Numerical Study on Non-linear AVO Inversion Using Chaotic Quantum Particle Swarm Optimization. J. Seism. Explor. 2014, 23, 379–392. [Google Scholar]
- Zhou, Y.; Nie, Z.; Jia, Z. An Improved Differential Evolution Algorithm for Nonlinear Inversion of Earthquake Dislocation. Geod. Geodyn. 2014, 5, 49–56. [Google Scholar]
- Song, X.; Li, L.; Zhang, X.; Huang, J.; Shi, X.; Jin, S.; Bai, Y. Differential Evolution Algorithm for Nonlinear Inversion of High-frequency Rayleigh Wave Dispersion Curves. J. Appl. Geophys. 2014, 109, 47–61. [Google Scholar] [CrossRef]
- Lu, Y.F.; Bao, T.F.; Li, J.M.; Wang, T. Inversion of Geotechnical Mechanical Parameters Based on Improved Differential Evolution Algorithm Online Support Vector Regression and ABAQUS. J. Yangtze River Sci. Res. Inst. 2017, 34, 81–87. [Google Scholar]
- Gao, Z.; Pan, Z.; Gao, J. Multimutation Differential Evolution Algorithm and Its Application to Seismic Inversion. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3626–3636. [Google Scholar] [CrossRef]
- Yan, X.; Zhu, Z.; Wu, Q. Intelligent Inversion Method for Pre-stack Seismic Big Data Based on MapReduce. Comput. Geosci. 2018, 110, 81–89. [Google Scholar] [CrossRef]
- Aid, K.; Richards, P.G. Quantitative Seismology: Theory and Methods; W. H. Freeman and Co.: San Francisco, CA, USA, 1980. [Google Scholar]




| Function | Range of Independent Variable | Dimension | Optimal Value | Category |
|---|---|---|---|---|
| f(1) | [−100,100] | 5 | 0 | Single solution |
| f(2) | [−100,100] | 5 | 0 | Single solution |
| f(3) | [−100,100] | 6 | 0 | Single solution |
| f(4) | [−100,100] | 5 | 0 | Single solution |
| f(5) | [−1,4] | 5 | 0 | Single solution |
| f(6) | [0,10] | 5 | 0 | Single solution |
| f(7) | [−100,100] | 5 | 0 | Multiple solutions |
| f(8) | [−100,100] | 5 | 0 | Multiple solutions |
| f(9) | [−100,100] | 6 | 0 | Multiple solutions |
| Function | Algorithm | Minimum Value | Maximum Value | Mean |
|---|---|---|---|---|
| f(1) | GA | 2.56 × 10−3 | 5.14 × 10−1 | 1.01 × 10−1 |
| DE | 3.94 × 10−2 | 45.08599 | 27.59336 | |
| PSO | 3.60 × 10−1 | 4.224161 | 1.934762 | |
| PIO | 1.32 × 10−7 | 3.55 × 10−2 | 8.44 × 10−3 | |
| IPIO | 5.69 × 10−8 | 3.71 × 10−5 | 5.42 × 10−6 | |
| f(2) | GA | 1.19 × 10−1 | 1.604513 | 5.17 × 10−1 |
| DE | 4.63 × 10−7 | 11.1002 | 1.684983 | |
| PSO | 2.213867 | 4.607223 | 3.56288 | |
| PIO | 8.84 × 10−5 | 3.376968 | 1.703053 | |
| IPIO | 3.82 × 10−14 | 2.15 × 10−1 | 1.69 × 10−2 | |
| f(3) | GA | 5.81 × 10−2 | 2.706744 | 1.060794 |
| DE | 2.44 × 10−8 | 55.00046 | 7.248065 | |
| PSO | 7.609825 | 20.19414 | 15.15247 | |
| PIO | 8.81 × 10−9 | 8.328467 | 1.403083 | |
| IPIO | 1.07 × 10−14 | 1.15 × 10−1 | 5.73 × 10−3 | |
| f(4) | GA | 1.90 × 10−2 | 4659.428 | 594.2779 |
| DE | 9.68 × 10−2 | 22078.02 | 3841.383 | |
| PSO | 11827.93 | 3459811 | 362612.9 | |
| PIO | 5.26E + 02 | 114849.4 | 23962.32 | |
| IPIO | 3.88 × 10−8 | 318704.3 | 1.63E+04 | |
| f(5) | GA | 1.67 × 10−11 | 9.68 × 10−6 | 1.81 × 10−6 |
| DE | 2.29 × 10−6 | 4.11 × 10−1 | 3.09 × 10−2 | |
| PSO | 1.21 × 10−4 | 8.53 × 10−4 | 4.84 × 10−4 | |
| PIO | 1.62 × 10−7 | 2.32 × 10−3 | 3.23 × 10−4 | |
| IPIO | 3.87 × 10−24 | 5.45 × 10−19 | 7.82 × 10−20 | |
| f(6) | GA | 6.56 × 10−4 | 7.93 × 10−3 | 3.40 × 10−3 |
| DE | 3.35 × 10−6 | 30.11047 | 7.679355 | |
| PSO | 4.68 × 10−4 | 1.67966 | 8.87 × 10−2 | |
| PIO | 4.02 × 10−1 | 3.06216 | 1.59 | |
| IPIO | 9.86 × 10−32 | 6.99 × 10−15 | 6.79 × 10−16 | |
| f(7) | GA | 2.99 × 10−3 | 2.68 × 10−2 | 1.09 × 10−2 |
| DE | 7.31 × 10−2 | 5.163348 | 1.671903 | |
| PSO | 3.07 × 10−1 | 4.484861 | 1.868947 | |
| PIO | 0.00 | 86.51133 | 33.82977 | |
| IPIO | 7.45 × 10−9 | 6.22 × 10−5 | 4.70 × 10−6 | |
| f(8) | GA | 2.82 × 10−4 | 2.18 × 10−1 | 3.22 × 10−2 |
| DE | 8.06 × 10−6 | 8.353849 | 9.78 × 10−1 | |
| PSO | 1.772018 | 3.991754 | 3.012487 | |
| PIO | 3.02 × 10−5 | 3.41 × 10−2 | 1.66 × 10−4 | |
| IPIO | 3.55 × 10−15 | 3.73 × 10−3 | 2.26 × 10−4 | |
| f(9) | GA | 3.30 × 10−4 | 1.908191 | 4.45 × 10−1 |
| DE | 4.88 × 10−3 | 295.5104 | 21.82682 | |
| PSO | 9.761999 | 47.82482 | 24.92847 | |
| PIO | 3.06 × 10−4 | 2.236064 | 1.41 × 10−1 | |
| IPIO | 5.50 × 10−12 | 0.058537 | 2.93 × 10−3 |
| N | ω | C1 | C2 | p | Max_Iteration1 | Max_Iteration2 |
|---|---|---|---|---|---|---|
| 40 | 0.5 | 2 | 2 | 0.3 | 4000 | 1000 |
| Experimental Environment | Parameter Description |
|---|---|
| JAVA version | 1.8.0_111-b14 |
| Compiler environment | Eclipse-jee-luna-SR1a-win32-x86_64 |
| Processor | Intel(R) Core (TM) i5-6500 CPU @ 3.10 GHZ |
| Installed Memory (RAM) | 8.00 GB |
| System type | 64-bit operating system |
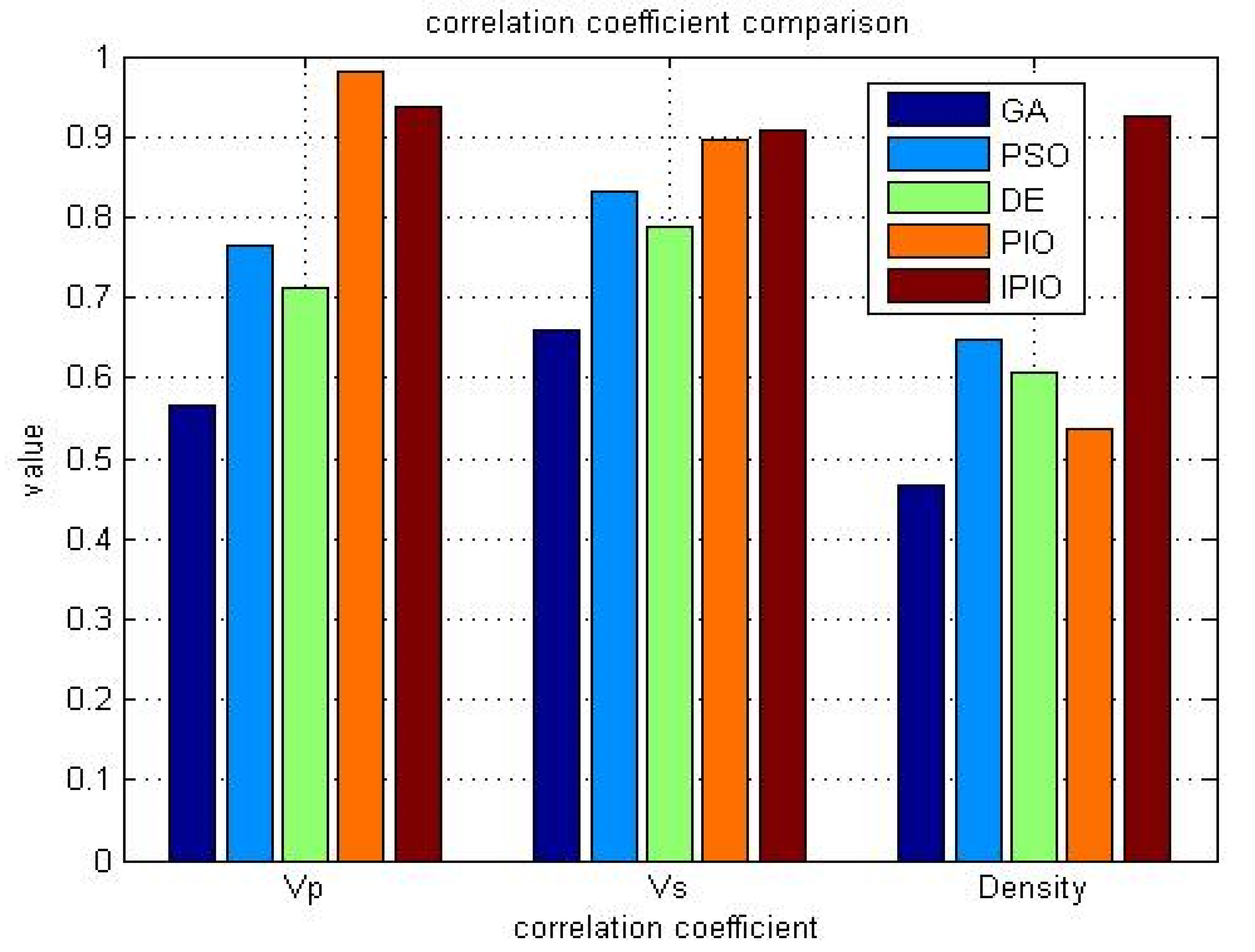
| GA | PSO | DE | PIO | IPIO | |
|---|---|---|---|---|---|
| 0.556364 | 0.765481 | 0.701792 | 0.980645 | 0.937951 | |
| 0.650805 | 0.832094 | 0.787196 | 0.894879 | 0.908213 | |
| 0.462346 | 0.649089 | 0.606702 | 0.537096 | 0.925746 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yan, X.; Wu, Q. An Improved Pigeon-Inspired Optimisation Algorithm and Its Application in Parameter Inversion. Symmetry 2019, 11, 1291. https://doi.org/10.3390/sym11101291
Liu H, Yan X, Wu Q. An Improved Pigeon-Inspired Optimisation Algorithm and Its Application in Parameter Inversion. Symmetry. 2019; 11(10):1291. https://doi.org/10.3390/sym11101291
Chicago/Turabian StyleLiu, Hanmin, Xuesong Yan, and Qinghua Wu. 2019. "An Improved Pigeon-Inspired Optimisation Algorithm and Its Application in Parameter Inversion" Symmetry 11, no. 10: 1291. https://doi.org/10.3390/sym11101291
APA StyleLiu, H., Yan, X., & Wu, Q. (2019). An Improved Pigeon-Inspired Optimisation Algorithm and Its Application in Parameter Inversion. Symmetry, 11(10), 1291. https://doi.org/10.3390/sym11101291




