Split Systems of Nonconvex Variational Inequalities and Fixed Point Problems on Uniformly Prox-Regular Sets

Abstract

In this paper, we studied variational inequalities and fixed point problems in nonconvex cases. By the projection method over prox-regularity sets, the convergence of the suggested iterative scheme was established under some mild rules.

1. Introduction

Variational inequalities theory, introduced and improved by Stampacchia [1], has a tremendous potential in theoretical research and applied fields. For $i\in \{1,2,3,4\}$, given the operator $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$ and $C_i$ nonempty, closed, convex subsets of the Hilbert spaces ${\mathcal{H}}_i$, the variational inequality problem stated in [1] (in short, VIP) is to find $v\in C_1$ such that

$$〈Sv,u-v〉\le 0,\forall u\in C_1,$$

(1)

which helps us to understand a simple, unified, and efficient framework to research the actual problems arising in optimization, engineering, economy, and so on. More specifically, variational inequalities are an important tool for studying some equilibrium problems [2] and convex minimization problems [3]. Various types of equilibrium problems (e.g., Nash and dynamic traffic) can be modeled as VIP. Pang [4] showed that the VIP related to the equilibrium problem can be decomposed into a system of variational inequalities and discussed the convergence of the method of decomposition for a system of variational inequalities.

More specifically, let $f:C_1\times C_2\to {\mathcal{H}}_1$ and $g:C_1\times C_2\to {\mathcal{H}}_2$ be nonlinear bifunctions. The system of variational inequalities (SVI) (please, see [4,5]) is to find $(u,v)\in C_1\times C_2$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{ll}〈f(u,v),w_1-u〉\ge 0,& \forall w_1\in C_1,\\ 〈g(u,v),w_2-v〉\ge 0,& \forall w_2\in C_2.\end{array}\right.\end{array}$$

Using essentially the fixed point formulation and projection technique, many researchers [5,6,7,8,9,10,11] studied related iterative schemes for approximating the solutions to systems of variational inequalities. On the other hand, over the past three decades, there has been quite an activity in the development of powerful and highly efficient numerical methods to solve the VIP and its applications [12,13,14,15,16,17,18]. There is a substantial number of methods, including the linear approximation method [19,20], the auxiliary principle [21,22], the projection technique [9,11], and the descent framework [23]. For applications, numerical techniques and other aspects of variational inequalities and split problems, please see [19,20,24,25,26,27,28].

In 2012, Censor et al. [29] introduced the so called split variational inequality problem (SVIP), as follows. Let $f:{\mathcal{H}}_1\to {\mathcal{H}}_1$ and $g:{\mathcal{H}}_2\to {\mathcal{H}}_2$ be nonlinear operators and A be a bounded linear operator. Find $v\in C_1$ such that

$$\begin{array}{c}\hfill 〈f\left(v\right),w_1-v〉\ge 0,\forall w_1\in C_1,\end{array}$$

and such that $u=Av\in C_2$ solves

$$\begin{array}{c}\hfill 〈g\left(u\right),w_2-u〉\ge 0,\forall w_2\in C_2.\end{array}$$

They also suggested some iterative algorithms for approximating the solutions to the SVIP. This problem is an important improvement of the VIP (1).

In 2016, Kazmi [30] proposed a system of split variational inequalities (SSVI), which is a generalization of the SVIP and the SVI, as follows. Let $\Phi :C_1\times C_2\to {\mathcal{H}}_1$, $\Psi :C_1\times C_2\to {\mathcal{H}}_2$, $\varphi :C_3\times C_4\to {\mathcal{H}}_3$, $\psi :C_3\times C_4\to {\mathcal{H}}_4$ be nonlinear bifunctions and $A:{\mathcal{H}}_1\to {\mathcal{H}}_3$ and $B:{\mathcal{H}}_2\to {\mathcal{H}}_4$ be bounded linear operators. The SSVI is to find $(x,y)\in C_1\times C_2$ such that

$$\begin{array}{c}\hfill \left\{\begin{array}{ll}〈\Phi (x,y),w_1-x〉\ge 0,& \forall w_1\in C_1,\\ 〈\Psi (x,y),w_2-y〉\ge 0,& \forall w_2\in C_2,\end{array}\right.\end{array}$$

and $u=Ax\in C_3$, $v=By\in C_4$ solve

$$\begin{array}{c}\hfill \left\{\begin{array}{ll}〈\varphi (u,v),w_3-u〉\ge 0,& \forall w_3\in C_3,\\ 〈\psi (u,v),w_4-v〉\ge 0,& \forall w_4\in C_4.\end{array}\right.\end{array}$$

He proposed an iteration method for solving SSVI and proved that the sequence produced by the algorithm converges strongly to a solution of SSVI.

It is worth noticing that the results in [29,30] regarding the iterative schemes for approximating the solutions to variational inequalities are considered in underlying convex sets. In many practical cases, the existing results may not be applicable if the convexity assumption is not fulfilled. Thus, in this paper, we extend their results to split systems of nonconvex variational inequalities (SSNVI) in the context of uniformly prox-regular sets, which include the convex sets as special cases.

2. Preliminaries

Let $\mathcal{H}$ be a Hilbert space equipped with its inner product $\langle ·,·\rangle$ and the norm $\parallel ·\parallel$, please, see [9]. Assume that C is a nonempty, closed subset of $\mathcal{H}$. Recall that the projection $Pro{j}_C$ from $\mathcal{H}$ onto C is defined by

$$\begin{array}{c}\hfill Pro{j}_C\left(u\right):=\{v\in C:\parallel u-v\parallel =dis{t}_C\left(u\right)\},\end{array}$$

where $dis{t}_C\left(u\right)={inf}_{w\in C}\parallel u-w\parallel$ is the usual distance related to 2-norm from the point u to the set C.

Definition 1.

[31] Given $v\in \mathcal{H}$, the proximal normal cone of C at v is given by

$$\begin{array}{c}\hfill N_C^P\left(v\right):=\{\tau \in \mathcal{H}:v\in Pro{j}_C(v+\alpha \tau ),\alpha >0\}.\end{array}$$

Proposition 1.

[31] Let C be a nonempty, closed subset of $\mathcal{H}$. Then $\tau \in N_C^P\left(u\right)$ if and only if there exists a constant $\alpha =\alpha (\tau ,u)>0$ such that

$$\begin{array}{c}\hfill 〈\tau ,v-u〉\le \alpha {\parallel v-u\parallel }^2,\forall v\in C.\end{array}$$

We now give the definition of a uniformly l-prox-regular set.

Definition 2.

[32,33] A subset $C_l$ of $\mathcal{H}$, $l\in (0,+\infty ]$, is said to be uniformly l-prox-regular if every nonzero proximal normal to $C_l$ can be realized by a l-ball, that is, for all $u\in C_l$ and all $\mathbf{0}\ne \tau \in N_{C_l}^P\left(u\right)$, one has

$$\begin{array}{c}\hfill 〈\frac{\tau }{\parallel \tau \parallel },v-u〉\le \frac{1}{2l}{\parallel v-u\parallel }^2,\forall v\in C_l.\end{array}$$

Obviously, the convex sets, p-convex sets [34], $C^{1,1}$ submanifolds [35], the images of $C^{1,1}$ diffeomorphism [36] are uniformly prox-regular sets. If we take $l=\infty ,$ the convexity of C and the uniformly prox-regularity of $C_l$ are equivalent. For more details of uniformly prox-regular sets, please see [31,33,37].

Given an operator S, the nonconvex variational inequality problem

$$\mathrm{find}v\in C_l\mathrm{such}\mathrm{that}〈Sv,u-v〉\le 0,\forall u\in C_l,$$

(2)

was introduced by Bounkhel M. [38], and further studied in [37,39,40]. If $C_l=C$, problem (2) and problem (1) are equivalent. We now give an example regarding the nonconvex case.

Example 1.

[37] Let $u=(x,y)$, $v=(t,z)$, and let $Su=(-x,1-y)$, and the set C be the union of two disjoint squares, A and B, having respectively, vertices at the points $(0,1)$, $(2,1)$, $(2,3)$, and $(0,3)$ and at the points $(4,1)$, $(5,2)$, $(4,3)$, and $(3,2)$. The fact that C can be written in the form $\left\{(t,z)\in R^2:max\left\{\right|t-1|,|z-2\left|\right\}\le 1\right\}\cup \left\{\right|t-4|+|z-2|\le 1\}$ shows that it is a uniformly prox-regular set in $R^2$ and the nonconvex variational inequality (2) has a solution on the square B.

Some properties of the uniformly l-prox-regular sets are given below.

Proposition 2.

[37] Let $C_l$, $l\in (0,+\infty ]$, be a nonempty, closed, and uniformly l-prox-regular subset of $\mathcal{H}$. Let $U\left(l\right)=\left\{u\in \mathcal{H}:d_{C_l}\left(u\right)<l\right\}$. Then:

• (i) For all $u\in U\left(r\right)$, $Pro{j}_{C_l}\left(u\right)\ne \varnothing$;
• (ii) For all $l^{\prime }\in (0,l)$, $Proj{C}_l\left(u\right)$ is Lipschitz continuous with constant $\frac{l}{l-l^{\prime }}$ on $U\left(l^{\prime }\right)$;
• (iii) The proximal normal cone $N_{C_l}^P\left(u\right)$ is closed as a set-valued mapping.

The next special operators are needed to develop our results.

Definition 3.

[40] For all u, $v\in \mathcal{H}$, the operator $S:\mathcal{H}\times \mathcal{H}\to \mathcal{H}$ is said to be:

• (i) Monotone in the first variable if

  $$\begin{array}{c}\hfill 〈S(u,·)-S(v,·),u-v〉\ge 0;\end{array}$$
• (ii) α-strongly monotone in the first variable if $\alpha >0$ such that

  $$\begin{array}{c}\hfill 〈S(u,·)-S(v,·),u-v〉\ge \alpha {\parallel u-v\parallel }^2;\end{array}$$
• (iii) β-Lipschitz in the first variable if $\beta >0$ such that

  $$\begin{array}{c}\hfill \parallel S(u,·)-S(v,·)\parallel \le \beta \parallel u-v\parallel .\end{array}$$

Definition 4.

[41] For all u, $v\in \mathcal{H}$, the operator $S:\mathcal{H}\to \mathcal{H}$ is said to be:

• (i) ν-strongly monotone if $\nu >0$ such that

  $$\begin{array}{c}\hfill 〈Su-Sv,u-v〉\ge \nu {\parallel u-v\parallel }^2;\end{array}$$
• (ii) L-Lipschitz if $L>0$ such that

  $$\begin{array}{c}\hfill \parallel Su-Sv\parallel \le L\parallel u-v\parallel ;\end{array}$$
• (iii) Uniformly L-Lipschitz if $L>0$ such that

  $$\begin{array}{c}\hfill \parallel S^{n}u-S^{n}v\parallel \le L\parallel u-v\parallel ,n\ge 1;\end{array}$$
• (iv) Generalized $(L,a)$-Lipschitz if $L,a>0$ such that

  $$\begin{array}{c}\hfill \parallel Su-Sv\parallel \le L(\parallel u-v\parallel +a).\end{array}$$

Now, let us recall the class of the nearly Lipschitz operator, nearly nonexpansive operator, and nearly uniformly L-Lipschitz continuous operator briefly.

Definition 5.

[41] For all u, $v\in \mathcal{H}$, the operator $S:\mathcal{H}\to \mathcal{H}$ is said to be:

• (i) Nearly Lipschitz with respect to $\left\{b_n\right\}\subseteq [0,\infty )$ with $li{m}_{n\to \infty }{b}_n=0$ if $k_n>0$ such that

  $$\parallel S^{n}u-S^{n}v\parallel \le k_n(\parallel u-v\parallel +b_n),n\ge 1.$$

  (3)

The infimum of $\left\{k_n\right\}$ is called nearly Lipschitz constant and is denoted by

$$\begin{array}{c}\hfill \eta \left(S^n\right)=sup\left\{\frac{\parallel S^{n}u-S^{n}v\parallel }{\parallel u-v\parallel +b_n}:u\ne v,u,v\in \mathcal{H}\right\}.\end{array}$$

A nearly Lipschitz operator S with respect to $\left\{(b_n,\eta \left(S^n\right))\right\}$ is said to be:

• (ii) Nearly nonexpansive if $\eta \left(S^n\right)=1$ such that

  $$\begin{array}{c}\hfill \parallel S^{n}u-S^{n}v\parallel \le \parallel u-v\parallel +b_n,n\ge 1;\end{array}$$
• (iii) Nearly asymptotically nonexpansive if $\eta \left(S^n\right)\ge 1$ for all $n\ge 1$ such that ${lim}_{n\to \infty }\eta \left(S^n\right)=1$;
• (iv) Nearly uniformly L-Lipschitz continuous if $\eta \left(S^n\right)\le L$ for all $n\ge 1$.

We need the following proposition in order to get the main result.

Proposition 3.

[41] For $i\in \{1,2\}$, let $S_i:C_l\to C_l$ be nearly uniformly $L_i$-Lipschitz operators with respect to $\left\{b_{i,n}\right\}$. Define a self-mapping S, $S(u,v)=(S_{1}u,S_{2}v)$ for all $(u,v)\in C_l\times C_l$. Then $S=(S_1,S_2):C_l\times C_l\to C_l\times C_l$ is a nearly uniformly $max\{L_1,L_2\}$-Lipschitz operator with respect to $\{b_{1,n}+b_{2,n}\}$. If ${\parallel (u,v)\parallel }_{*}=\parallel u\parallel +\parallel v\parallel$, for any $(u,v),(u^{\prime },v^{\prime })\in C_l\times C_l$, we have

$$\begin{array}{cc}\hfill \parallel S^n(u,v)-S^n(u^{\prime },v^{\prime }){\parallel }_{*}& =\parallel S_1^{n}u-S_1^n{u}^{\prime }\parallel +\parallel S_2^{n}v-S_2^n{v}^{\prime }\parallel \hfill \\ & \le L_1\left(\parallel u-u^{\prime }\parallel +b_{1,n}\right)+L_2\left(\parallel v-v^{\prime }\parallel +b_{2,n}\right)\hfill \\ & \le max\{L_1,L_2\}\left(\parallel (u,v)-(u^{\prime },v^{\prime }){\parallel }_{*}+b_{1,n}+b_{2,n}\right),n\ge 1.\hfill \end{array}$$

Example 2.

Let $\mathcal{H}=[0,a]$, $a\in (0,1]$ and an operator

$$S:\mathcal{H}\times \mathcal{H}\to \mathcal{H}\times \mathcal{H},S(u,v)=(S_{1}u,S_{2}v),(u,v)\in \mathcal{H}\times \mathcal{H},$$

with $S_i\left(x\right)=\left\{\begin{array}{cc}{\lambda }_{i}x,\hfill & x\in [0,a),\hfill \\ 0,\hfill & x=a,\hfill \end{array}\right.$ for $i=1,2,{\lambda }_i\in (0,1)$. Then $S=(S_1,S_2)$ is a nearly uniformly $max\{{\lambda }_1,{\lambda }_2\}$-Lipschitz operator with respect to $\{{\lambda }_1^{n-1}+{\lambda }_2^{n-1}\}$.

Lemma 1.

[9] Let $\left\{a_n\right\}$ be a sequence of nonnegative real numbers and let $\left\{b_n\right\}$ be a sequence in [0,1] such that ${\sum }_{n=1}^{\infty }{b}_n=\infty$, $\left\{c_n\right\}\subset \mathbb{R}$, $c_n\ge 0$, $n\ge n_0$ and ${lim}_{n\to \infty }{c}_n=0$. If $\left\{a_n\right\}$, $\left\{b_n\right\}$ and $\left\{c_n\right\}$ satisfy the property

$$\begin{array}{c}\hfill a_{n+1}\le (1-b_n)a_n+b_n{c}_n,\forall n\ge n_0,\end{array}$$

then ${lim}_{n\to \infty }{a}_n=0$.

In the next sections, we are going to state and prove results regarding the existence and uniqueness of the solutions to a SSNVI, and also propose an iterative algorithm to determine the unique solution to SSNVI which is also a fixed point to some operators with suitable properties.

3. Split Systems of Nonconvex Variational Inequalities

In the section, we consider a SSNVI with several nonlinear operators.

For l, $k>0$, let $C_l\subset {\mathcal{H}}_1$ be uniformly l-prox-regular and $Q_k\subset {\mathcal{H}}_2$ be uniformly k-prox-regular. For $i=1,2$, consider the nonlinear operators ${\Phi }_i:{\mathcal{H}}_1\times {\mathcal{H}}_1\to {\mathcal{H}}_1$, ${\Psi }_i:{\mathcal{H}}_2\times {\mathcal{H}}_2\to {\mathcal{H}}_2$, ${\varphi }_i:C_l\to C_l$, and ${\psi }_i:Q_k\to Q_k$. Let A and B be two bounded linear operators from ${\mathcal{H}}_1$ to ${\mathcal{H}}_2$. The SSNVI is to find $(x,y)\in C_l\times C_l$ such that

$$\left\{\begin{array}{c}〈{\Phi }_1(y,x)+x-{\varphi }_1\left(y\right),{\varphi }_1\left(w_1\right)-x〉+\frac{\parallel {\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)\parallel }{2l}{\parallel {\varphi }_1\left(w_1\right)-x\parallel }^2\ge 0,\forall w_1\in C_l:{\varphi }_1\left(w_1\right)\in C_l,\hfill \\ 〈{\Phi }_2(x,y)+y-{\varphi }_2\left(x\right),{\varphi }_2\left(w_1\right)-y〉+\frac{\parallel {\Phi }_2(x,y)+y-{\varphi }_2\left(x\right)\parallel }{2l}{\parallel {\varphi }_2\left(w_1\right)-y\parallel }^2\ge 0,\forall w_1\in C_l:{\varphi }_1\left(w_1\right)\in C_l,\hfill \end{array}\right.$$

(4)

and such that $(u,v)\in Q_k\times Q_k$ with $u=Ax$, $v=By$ solves

$$\left\{\begin{array}{c}〈{\Psi }_1(v,u)+u-{\psi }_1\left(v\right),{\psi }_1\left(w_2\right)-u〉+\frac{\parallel {\Psi }_1(v,u)+u-{\psi }_1\left(v\right)\parallel }{2k}{\parallel {\psi }_1\left(w_2\right)-u\parallel }^2\ge 0,\forall w_2\in Q_k:{\psi }_1\left(w_2\right)\in Q_k,\hfill \\ 〈{\Psi }_2(u,v)+v-{\psi }_2\left(u\right),{\psi }_2\left(w_2\right)-v〉+\frac{\parallel {\Psi }_2(u,v)+v-{\psi }_2\left(u\right)\parallel }{2k}{\parallel {\psi }_2\left(w_2\right)-v\parallel }^2\ge 0,\forall w_2\in Q_k:{\psi }_2\left(w_2\right)\in Q_k.\hfill \end{array}\right.$$

(5)

To study the existence of solutions to system (4), the following two lemmas are needed.

Lemma 2.

For $i\in \{1,2\}$, $l>0$, let ${\Phi }_i:{\mathcal{H}}_1\times {\mathcal{H}}_1\to {\mathcal{H}}_1$ and ${\varphi }_i:C_l\to C_l$ be nonlinear operators. Then system (4) and the following problem are equivalent:

$$\mathrm{find}(x,y)\in C_l\times C_l\mathrm{such}\mathrm{that}\left\{\begin{array}{c}\mathbf{0}\in {\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)+N_{C_l}^P\left(x\right),\hfill \\ \mathbf{0}\in {\Phi }_2(x,y)+y-{\varphi }_2\left(x\right)+N_{C_l}^P\left(y\right).\hfill \end{array}\right.$$

(6)

Proof. 

Suppose that $(x,y)\in C_l\times C_l$ solves system (4).

If ${\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)=\mathbf{0}$, then:

$$\begin{array}{c}\hfill \mathbf{0}\in {\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)+N_{C_l}^P\left(x\right).\end{array}$$

If ${\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)\ne \mathbf{0}$, the following is always true

$$\begin{array}{c}\hfill -〈{\Phi }_1(y,x)+x-{\varphi }_1\left(y\right),{\varphi }_1\left(w_1\right)-x〉\le \frac{\parallel {\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)\parallel }{2l}\parallel {\varphi }_1\left(w_1\right)-x\parallel .\end{array}$$

By Definition 2 and Proposition 1, we have $-\left({\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)\right)\in N_{C_l}^P\left(x\right),$ and then

$$\begin{array}{c}\hfill \mathbf{0}\in {\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)+N_{C_l}^P\left(x\right).\end{array}$$

Likewise,

$$\begin{array}{c}\hfill \mathbf{0}\in {\Phi }_2(x,y)+y-{\varphi }_2\left(x\right)+N_{C_l}^P\left(y\right).\end{array}$$

Conversely, if $(x,y)\in C_l\times C_l$ solves problem (6), Definition 2 guarantees that $(x,y)\in C_l\times C_l$ solves system (4).  □

We will obtain a uniqueness theorem for the solution to system (4) after verifying the equivalence between the fixed point formulation (7) and system (4).

Lemma 3.

For $i\in \{1,2\}$, $l>0$, let ${\Phi }_i:{\mathcal{H}}_1\times {\mathcal{H}}_1\to {\mathcal{H}}_1$ and ${\varphi }_i:C_l\to C_l$ be nonlinear operators. Suppose that $max\left\{\parallel {\Phi }_1(y,x)\parallel ,\parallel {\Phi }_2(x,y)\parallel \right\}<l^{\prime }$, $(x,y)\in C_l\times C_l$, and $l^{\prime }\in (0,l)$. Then $(x,y)\in C_l\times C_l$ solves system (4) if and only if

$$\left\{\begin{array}{c}x=Pro{j}_{C_l}\left({\varphi }_1\left(y\right)-{\Phi }_1(y,x)\right),\hfill \\ y=Pro{j}_{C_l}\left({\varphi }_2\left(x\right)-{\Phi }_2(x,y)\right),\hfill \end{array}\right.$$

(7)

Proof. 

Suppose that $(x,y)\in C_l\times C_l$ solves system (4). By using ${\varphi }_1:C_l\to C_l$ and the projection operator technique, we have

$$\begin{array}{cc}\hfill dis{t}_{C_l}\left({\varphi }_1\left(y\right)-{\Phi }_1(y,x)\right)& =\underset{w\in C_l}{inf}\parallel {\varphi }_1\left(y\right)-{\Phi }_1(y,x)-w\parallel \hfill \\ & \le \parallel {\varphi }_1\left(y\right)-{\Phi }_1(y,x)-{\varphi }_1\left(y\right)\parallel \le <l^{\prime }.\hfill \end{array}$$

From Proposition 2, we get ${\varphi }_1\left(y\right)-{\Phi }_1(y,x)\in U\left(l^{\prime }\right)$, and then the set $Pro{j}_{C_l}\left({\varphi }_1\left(y\right)-{\Phi }_1(y,x)\right)$ is a singleton. From Lemma 2,

$$\begin{array}{c}\hfill \mathbf{0}\in {\Phi }_1(y,x)+x-{\varphi }_1\left(y\right)+N_{C_l}^P\left(x\right),\end{array}$$

that is,

$$\begin{array}{c}\hfill {\varphi }_1\left(y\right)-{\Phi }_1(y,x)\in (I+N_{C_l}^P)\left(x\right).\end{array}$$

Thus, we get $x=Pro{j}_{C_l}\left({\varphi }_1\left(y\right)-{\Phi }_1(y,x)\right)$.

By the same way, we conclude that $y=Pro{j}_{C_l}\left({\varphi }_2\left(x\right)-{\Phi }_2(x,y)\right)$. Thus, relations (7) are satisfied. It is easy to check the converse.  □

From Lemma 2, we find out the existence of a solution to system (4). By Lemma 3, system (4) admits a unique solution.

Theorem 1.

For $i\in \{1,2\}$, $l>0$, let ${\Phi }_i:{\mathcal{H}}_1\times {\mathcal{H}}_1\to {\mathcal{H}}_1$ be operators which satisfy the conditions from Lemma 3, and ${\varphi }_i:C_l\to C_l$ be nonlinear operators. Suppose that ${\mu }_i$, ${\nu }_i$, ${\zeta }_i$,${\theta }_i>0$. Let the operators ${\Phi }_i$ be ${\mu }_i$-Lipschitz and ${\nu }_i$-strongly monotone in the first variable and the operators ${\varphi }_i$ be ${\zeta }_i$-Lipschitz and ${\theta }_i$-strongly monotone. If the parameters satisfy

$$\left\{\begin{array}{c}1-2{\theta }_i+{\zeta }_i^2\ge 0;\hfill \\ 1-2{\nu }_i+{\mu }_i^2\ge 0,i=1,2;\hfill \\ {\chi }_1+{\chi }_2<1,\hfill \end{array}\right.$$

(8)

where ${\chi }_i:=\frac{l}{l-l^{\prime }}\left(\sqrt{1-2{\theta }_i+{\zeta }_i^2}+\sqrt{1-2{\nu }_i+{\mu }_i^2}\right)$, $i=1,2$, then system (4) admits a unique solution.

Proof. 

Define the operators ${\phi }_1$, ${\phi }_2:{\mathcal{H}}_1\times {\mathcal{H}}_1\to C_l$,

$$\begin{array}{c}{\phi }_1(x,y)=Pro{j}_{C_l}\left({\varphi }_1\left(y\right)-{\Phi }_1(y,x)\right),\hfill \\ {\phi }_2(x,y)=Pro{j}_{C_l}\left({\varphi }_2\left(x\right)-{\Phi }_2(x,y)\right),\hfill \end{array}$$

(9)

for all $(x,y)\in {\mathcal{H}}_1\times {\mathcal{H}}_1$. From Lemma 3, it is easy to check that relations (9) are satisfied. Define ${\parallel ·\parallel }_{*}$ on ${\mathcal{H}}_1\times {\mathcal{H}}_1$ as in Proposition 3, that is

$$\begin{array}{c}\hfill {\parallel (u,v)\parallel }_{*}=\parallel u\parallel +\parallel v\parallel ,\forall (u,v)\in {\mathcal{H}}_1\times {\mathcal{H}}_1.\end{array}$$

Clearly, $({\mathcal{H}}_1\times {\mathcal{H}}_1,\parallel ·{\parallel }_{*})$ is a normed space.

Define a self-mapping $T:C_l\times C_l\to C_l\times C_l$, $T(x,y)=({\phi }_1(x,y),{\phi }_2(x,y))$ for all $(x,y)\in C_l\times C_l$.

Next, we prove that T is a contraction. Let $(x_1,y_1)$, $(x_2,y_2)\in C_l\times C_l$. By Proposition 2, we have

$$\begin{array}{cc}& ∥{\phi }_1(x_1,y_1)-{\phi }_1(x_2,y_2)∥\hfill \\ \hfill =& ∥P_{C_l}\left({\varphi }_1\left(y_1\right)-{\Phi }_1(y_1,x_1)\right)-P_{C_l}\left({\varphi }_1\left(y_2\right)-{\Phi }_1(y_2,x_2)\right)∥\hfill \\ \hfill \le & \frac{l}{l-l^{\prime }}∥{\varphi }_1\left(y_1\right)-{\varphi }_1\left(y_2\right)-\left({\Phi }_1(y_1,x_1)-{\Phi }_1(y_2,x_2)\right)∥\hfill \\ \hfill \le & \frac{l}{l-l^{\prime }}\left(∥y_1-y_2-\left({\varphi }_1\left(y_1\right)-{\varphi }_1\left(y_2\right)\right)∥+∥y_1-y_2-\left({\Phi }_1(y_1,x_1)-{\Phi }_1(y_2,x_2)\right)∥\right).\hfill \end{array}$$

In view of ${\varphi }_1$, ${\Phi }_1$, for the first summand we have

$$\begin{array}{cc}\hfill {∥y_1-y_2-\left({\varphi }_1\left(y_1\right)-{\varphi }_1\left(y_2\right)\right)∥}^2=& {∥y_1-y_2∥}^2-2〈{\varphi }_1\left(y_1\right)-{\varphi }_1\left(y_2\right),y_1-y_2〉+{∥{\varphi }_1\left(y_1\right)-{\varphi }_1\left(y_2\right)∥}^2\hfill \\ \hfill \le & \left(1-2{\theta }_1+{\zeta }_1^2\right){∥y_1-y_2∥}^2,\hfill \end{array}$$

and for the second summand

$$\begin{array}{cc}& {∥y_1-y_2-\left({\Phi }_1(y_1,x_1)-{\Phi }_1(y_2,x_2)\right)∥}^2\hfill \\ \hfill =& {∥y_1-y_2∥}^2-2〈{\Phi }_1(y_1,x_1)-{\Phi }_1(y_2,x_2),y_1-y_2〉+{∥{\Phi }_1(y_1,x_1)-{\Phi }_1(y_2,x_2)∥}^2\hfill \\ \hfill \le & \left(1-{\nu }_1+{\mu }_1^2\right){∥y_1-y_2∥}^2.\hfill \end{array}$$

Thus,

$$\begin{array}{c}\hfill ∥{\phi }_1(x_1,y_1)-{\phi }_1(x_2,y_2)∥\le \frac{l}{l-l^{\prime }}\left(\sqrt{1-2{\theta }_1+{\zeta }_1^2}+\sqrt{1-2{\nu }_1+{\mu }_1^2}\right)∥y_1-y_2∥.\end{array}$$

Similarly, we have

$$\begin{array}{c}\hfill ∥{\phi }_2(x_1,y_1)-{\phi }_2(x_2,y_2)∥\le \frac{l}{l-l^{\prime }}\left(\sqrt{1-2{\theta }_2+{\zeta }_2^2}+\sqrt{1-2{\nu }_2+{\mu }_2^2}\right)∥x_1-x_2∥.\end{array}$$

Therefore, we have obtained

$$\begin{array}{c}\hfill ∥{\phi }_1(x_1,y_1)-{\phi }_1(x_2,y_2)∥+∥{\phi }_2(x_1,y_1)-{\phi }_2(x_2,y_2)∥\le {\chi }_1∥x_1-x_2∥+{\chi }_2∥y_1-y_2∥.\end{array}$$

Finally, we rewrite the inequality above as

$$\begin{array}{c}\hfill {∥T(x_1,y_1)-T(x_2,y_2)∥}_{*}\le \kappa {\parallel (x_1,y_1)-(x_2,y_2)\parallel }_{*},\end{array}$$

(10)

where $\kappa =max\left\{{\chi }_1,{\chi }_2\right\}$. Since the parameters satisfy conditions (8), we get $0\le \kappa <1$. From inequality (10), it follows that the operator T is a contraction. Thus, there exists only one element $(x,y)$ such that $T(x,y)=(x,y)$. Returning to relation (9), we have $x=Pro{j}_{C_l}\left({\varphi }_1\left(y\right)-{\Phi }_1(y,x)\right)$ and $y=Pro{j}_{C_l}\left({\varphi }_2\left(x\right)-{\Phi }_2(x,y)\right)$. From Lemma 3, system (4) admits a unique solution.  □

The SSNVI is to find $(x,y)\in C_l\times C_l$ which solves system (4). Then its image $(u,v)\in Q_k\times Q_k$ has to solve system (5). So, Theorem 1 proved the validity of the existence and uniqueness theorem for the solution to SSNVI.

4. Iterative Algorithm

In this part, the set of solutions to SSNVI is denoted by y $\Xi$ and the set of fixed points of S by $Fix\left(S\right)$. For any given $(x,y)\in C_l\times C_l,$ define $S(x,y)=(S_{1}x,S_{2}y)$ as in Proposition 3. Notice that $x\in Fix\left(S_1\right)$ and $y\in Fix\left(S_2\right)$ if and only if $(x,y)\in Fix\left(S\right)$. If $(x^{*},y^{*})\in \Xi \bigcap Fix\left(S\right)$, from Lemma 3, in relations (9) and for $n\ge 1$, we achieve

$$\left\{\begin{array}{c}{x}^{*}=S_1^n{x}^{*}=Pro{j}_{C_l}\left({\varphi }_1\left(y^{*}\right)-{\Phi }_1(y^{*},x^{*})\right)=S_1^{n}Pro{j}_{C_l}\left({\varphi }_1\left(y^{*}\right)-{\Phi }_1(y^{*},x^{*})\right),\hfill \\ y^{*}=S_2^n{y}^{*}=Pro{j}_{C_l}\left({\varphi }_2\left(x^{*}\right)-{\Phi }_2(x^{*},y^{*})\right)=S_2^{n}Pro{j}_{C_l}\left({\varphi }_2\left(x^{*}\right)-{\Phi }_2(x^{*},y^{*})\right).\hfill \end{array}\right.$$

(11)

We now construct the following iterative algorithm (12) by formulation (11) for approximating the unique common element of the set of fixed points of some nearly uniformly Lipschitz operators and the set of solution to SSNVI.

Theorem 2.

For $i\in \{1,2\}$, $l,k>0$, $C_l\subset {\mathcal{H}}_1$ is a uniformly l-prox-regular and $Q_k\subset {\mathcal{H}}_2$ is a uniformly k-prox-regular. Let ${\Phi }_i$, ${\varphi }_i$ be endowed with the same properties as in Theorem 1. Suppose ${\xi }_i$, ${\vartheta }_i$, ${\lambda }_i$, ${\upsilon }_i>0$. Let the operators ${\Psi }_i:{\mathcal{H}}_2\times {\mathcal{H}}_2\to {\mathcal{H}}_2$ be ${\xi }_i$-Lipschitz and ${\vartheta }_i$-strongly monotone in the first variable and the operators ${\psi }_i:Q_k\to Q_k$ be ${\lambda }_i$-Lipschitz and ${\upsilon }_i$-strongly monotone. A and B are bounded linear operators from ${\mathcal{H}}_1$ to ${\mathcal{H}}_2$, $A^{*}$ and $B^{*}$ are adjoint operators. Let $S_i:C_l\to C_l$ be two nearly uniformly $L_i$-Lipschitz operators with respect to $\left\{{\sigma }_{i,n}\right\}$, $S=(S_1,S_2)$ be the same as in Proposition 3 with $\Xi \bigcap Fix\left(S\right)\ne \varnothing$. Let the sequence $\left\{(x_n,y_n)\right\}$ be computed as follows

$$\left\{\begin{array}{c}{f}_n=Pro{j}_{C_l}({\varphi }_1\left(y_n\right)-{\Phi }_1(y_n,x_n)),\hfill \\ g_n=Pro{j}_{C_l}({\varphi }_2\left(x_n\right)-{\Phi }_2(x_n,y_n)),\hfill \\ h_n=Pro{j}_{Q_k}({\psi }_1\left(B{g}_n\right)-{\Psi }_1(B{g}_n,A{f}_n)),\hfill \\ z_n=Pro{j}_{Q_k}({\psi }_2\left(A{f}_n\right)-{\Psi }_2(A{f}_n,B{g}_n)),\hfill \\ x_{n+1}=(1-{\iota }_n)x_n+{\iota }_n{S}_1^{n}Pro{j}_{C_l}(f_n+\varsigma A^{*}(h_n-A{f}_n)),\hfill \\ y_{n+1}=(1-{\iota }_n)y_n+{\iota }_n{S}_2^{n}Pro{j}_{C_l}(g_n+\varsigma B^{*}(z_n-B{g}_n)),n\ge 1,\hfill \end{array}\right.$$

(12)

where $\left\{{\iota }_n\right\}\subset (0,1)$ with ${\sum }_{n=1}^{\infty }{\iota }_n=\infty$. Suppose that $l^{\prime }\in (0,l)$, $k^{\prime }\in (0,k)$ and

$$max\left\{{\Psi }_1(B{g}_n,A{f}_n),{\Psi }_1(B{y}^{*},A{x}^{*}),{\Psi }_2(A{f}_n,B{g}_n),{\Psi }_2(A{x}^{*},B{y}^{*})\right\}<k^{\prime },$$

(13)

$$\varsigma <min\left\{\frac{2}{{\parallel A\parallel }^2},\frac{2}{{\parallel B\parallel }^2},\frac{r^{\prime }}{1+A^{*}(h_n-A{f}_n)},\frac{r^{\prime }}{1+B^{*}(z_n-B{g}_n)}\right\},n\ge 1.$$

(14)

Suppose that $L=max\left\{L_1,L_2\right\}$, $w=\frac{l}{l-l^{\prime }}$, $M=max\left\{{\chi }_1+2{\chi }_1{\overline{\chi }}_2,{\chi }_2+2{\chi }_2{\overline{\chi }}_1\right\}<1$ with $LwM<1$, ${\chi }_1$ and ${\chi }_2$ are as in Theorem 1 and

$$\begin{array}{c}\hfill {\overline{\chi }}_1=\frac{k}{k-k^{\prime }}\left(\sqrt{1-2{\upsilon }_1+{\lambda }_1^2}+\sqrt{1-2{\vartheta }_1+{\xi }_1^2}\right),{\overline{\chi }}_2=\frac{k}{k-k^{\prime }}\left(\sqrt{1-2{\upsilon }_2+{\lambda }_2^2}+\sqrt{1-2{\vartheta }_2+{\xi }_2^2}\right).\end{array}$$

Then the sequence $\left\{(x_n,y_n)\right\}$ computed by relation (12) converges strongly to an element of $\Xi \bigcap Fix\left(S\right)$.

Proof. 

By Theorem 1, let $(x^{*},y^{*})\in C_l\times C_l$ be the solution to system (4). Therefore, $(x^{*},y^{*})\in C_l\times C_l$ is the unique solution to SSNVI. Let us take $(x^{*},y^{*})\in \Xi \bigcap Fix\left(S\right)$. Since conditions (8) and (13) are satisfied respectively, then we obtain

$$x^{*}=Pro{j}_{C_l}\left({\varphi }_1\left(y^{*}\right)-{\Phi }_1(y^{*},x^{*})\right),$$

(15)

$$y^{*}=Pro{j}_{C_l}\left({\varphi }_2\left(x^{*}\right)-{\Phi }_2(x^{*},y^{*})\right),$$

(16)

$$A{x}^{*}=Pro{j}_{Q_k}\left({\psi }_1\left(B{y}^{*}\right)-{\Psi }_1(B{y}^{*},A{x}^{*})\right),$$

(17)

$$B{y}^{*}=Pro{j}_{Q_k}\left({\psi }_2\left(A{x}^{*}\right)-{\Psi }_2(A{x}^{*},B{y}^{*})\right).$$

(18)

From the definition of ${\Phi }_1$, ${\varphi }_1$, by relations (12), (8), (15) and Proposition 2, we have

$$\begin{array}{cc}\hfill \parallel f_n-x^{*}\parallel \le & \frac{l}{l-l^{\prime }}\left(∥y_n-y^{*}-({\varphi }_1\left(y_n\right)-{\varphi }_1\left(y^{*}\right))∥+∥y_n-y^{*}-({\Phi }_1(y_n,x_n)-{\Phi }_1(y^{*},x^{*}))∥\right)\hfill \\ \hfill \le & {\chi }_1\parallel y_n-y^{*}\parallel ,n\in \mathbb{N}.\hfill \end{array}$$

(19)

In view of ${\Phi }_2$ and ${\varphi }_2$, from relations (12), (8), (16), and Proposition 2, we find

$$\begin{array}{c}\hfill \parallel g_n-y^{*}\parallel \le {\chi }_2\parallel x_n-x^{*}\parallel ,n\in \mathbb{N}.\end{array}$$

(20)

By looking into the definition of ${\Psi }_1$ and ${\psi }_1$, from (12), (13), (17), and Proposition 2, we attain

$$\begin{array}{c}\hfill \parallel h_n-A{x}^{*}\parallel \le {\overline{\chi }}_1\parallel B{g}_n-B{y}^{*}\parallel ,n\in \mathbb{N}.\end{array}$$

(21)

In light of ${\Psi }_2$ and ${\psi }_2$, from (12), (13), (18) and Proposition 2, we conclude

$$\begin{array}{c}\hfill \parallel z_n-B{y}^{*}\parallel \le {\overline{\chi }}_2\parallel A{f}_n-A{x}^{*}\parallel ,n\in \mathbb{N}.\end{array}$$

(22)

By relation (14), we get

$$\begin{array}{cc}\hfill \parallel f_n-x^{*}-\varsigma A^{*}(A{f}_n-A{x}^{*}){\parallel }^2=& \parallel f_n-x^{*}{\parallel }^2-2\varsigma 〈f_n-x^{*},A^{*}(A{f}_n-A{x}^{*})〉+{\varsigma }^2{\parallel A^{*}(A{f}_n-A{x}^{*})\parallel }^2\hfill \\ \hfill \le & \parallel f_n-x^{*}{\parallel }^2-\varsigma \left(2-{\varsigma \parallel A\parallel }^2\right){\parallel A{f}_n-A{x}^{*}\parallel }^2\hfill \\ \hfill \le & \parallel f_n-x^{*}{\parallel }^2,n\in \mathbb{N}.\hfill \end{array}$$

(23)

Using (11), (12), (14), (19)–(21), (23), and Proposition 3, we obtain

$$\begin{array}{cc}& \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill \le & (1-{\iota }_n)\parallel x_n-x^{*}\parallel +{\iota }_n\parallel S_1^{n}Pro{j}_{C_l}(f_n+\varsigma A^{*}(h_n-A{f}_n))-S_1^{n}Pro{j}_{C_l}(x^{*}+\varsigma A^{*}(A{x}^{*}-A{x}^{*}))\parallel \hfill \\ \hfill \le & (1-{\iota }_n)\parallel x_n-x^{*}\parallel +{\iota }_n{L}_1\left(\parallel Pro{j}_{C_l}(f_n+\varsigma A^{*}(h_n-A{f}_n))-Pro{j}_{C_l}(x^{*}+\varsigma A^{*}(A{x}^{*}-A{x}^{*}))\parallel +{\sigma }_{1,n}\right)\hfill \\ \hfill \le & (1-{\iota }_n)\parallel x_n-x^{*}\parallel +{\iota }_n{L}_{1}w\left(\parallel f_n-x^{*}-\varsigma A^{*}(A{f}_n-A{x}^{*})\parallel +\varsigma \parallel A^{*}(h_n-A{x}^{*})\parallel \right)+{\iota }_n{L}_1{\sigma }_{1,n}\hfill \\ \hfill \le & (1-{\iota }_n)\parallel x_n-x^{*}\parallel +{\iota }_n{L}_{1}w\left(\parallel f_n-x^{*}\parallel +\varsigma \parallel A\parallel \parallel h_n-A{x}^{*}\parallel \right)+{\iota }_n{L}_1{\sigma }_{1,n}\hfill \\ \hfill \le & (1-{\iota }_n)\parallel x_n-x^{*}\parallel +{\iota }_n{L}_{1}w\left({\chi }_1\parallel y_n-y^{*}\parallel +2{\chi }_2{\overline{\chi }}_1\parallel x_n-x^{*}\parallel \right)+{\iota }_n{L}_1{\sigma }_{1,n},n\in \mathbb{N}.\hfill \end{array}$$

(24)

Likewise,

$$\begin{array}{c}\hfill \parallel g_n-y^{*}-\varsigma B^{*}(B{g}_n-B{y}^{*})\parallel \le \parallel g_n-x^{*}\parallel ,n\in \mathbb{N}.\end{array}$$

(25)

By using relations (11), (12), (14), (19), (20), (22), (25), and Proposition 3, we have

$$\begin{array}{c}\hfill \parallel y_{n+1}-y^{*}\parallel \le (1-{\iota }_n)\parallel y_n-y^{*}\parallel +{\iota }_n{L}_{2}w\left(s\parallel x_n-x^{*}\parallel +2{\chi }_1{\overline{\chi }}_{2}u\parallel y_n-y^{*}\parallel \right)+{\iota }_n{L}_2{\sigma }_{2,n}.\end{array}$$

(26)

It follows from (24) and (26) that

$$\begin{array}{cc}& {∥(x_{n+1},y_{n+1})-(x^{*},y^{*})∥}_{*}\hfill \\ \hfill \le & (1-{\iota }_n){∥(x_n,y_n)-(x^{*},y^{*})∥}_{*}+{\iota }_{n}Lw\left(M{∥(x_n,y_n)-(x^{*},y^{*})∥}_{*}+{\sigma }_{1,n}+{\sigma }_{2,n}\right)\hfill \\ \hfill =& \left(1-{\iota }_n(1-LwM)\right){∥(x_n,y_n)-(x^{*},y^{*})∥}_{*}+{\iota }_n(1-LwM)\frac{({\sigma }_{1,n}+{\sigma }_{2,n})L}{1-LwM},n\in \mathbb{N}.\hfill \end{array}$$

(27)

By applying Lemma 1 to relation (27), we achieve ${lim}_{n\to \infty }{x}_n=x^{*}$ and ${lim}_{n\to \infty }{y}_n=y^{*}$. Thus, we conclude that the sequence $\left\{(x_n,y_n)\right\}$ computed by (12) converges strongly to an element of $\Xi \bigcap Fix\left(S\right)$.  □

We now have in view a special case of SSNVI, called the split systems of general variational inequalities (SSGVI), which is an improvement of SVIP in [29] and SSVI in [30].

Surely, if $l=\infty ,$ the convexity of C and the uniformly prox-regularity of $C_l$ are equivalent. Thus, in a underlying convex set, the SSGVI is to find $(x,y)\in C\times C$ such that

$$\left\{\begin{array}{c}〈{\Phi }_1(y,x)+x-{\varphi }_1\left(y\right),{\varphi }_1\left(w_1\right)-x〉,\forall w_1\in {\mathcal{H}}_1:{\varphi }_1\left(w_1\right)\in C,\hfill \\ 〈{\Phi }_2(x,y)+y-{\varphi }_2\left(x\right),{\varphi }_2\left(w_1\right)-y〉,\forall w_1\in {\mathcal{H}}_1:{\varphi }_2\left(w_1\right)\in C,\hfill \end{array}\right.$$

and such that $(u,v)\in Q\times Q$ with $u=Ax$, $v=By$ solves

$$\left\{\begin{array}{c}〈{\Psi }_1(v,u)+u-{\psi }_1\left(v\right),{\psi }_1\left(w_2\right)-u〉,\forall w_2\in {\mathcal{H}}_2:{\psi }_1\left(w_2\right)\in Q,\hfill \\ 〈{\Psi }_2(u,v)+v-{\psi }_2\left(u\right),{\psi }_2\left(w_2\right)-v〉,\forall w_2\in {\mathcal{H}}_2:{\psi }_2\left(w_2\right)\in Q.\hfill \end{array}\right.$$

where $C\subset {\mathcal{H}}_1$ and $Q\subset {\mathcal{H}}_2$ are nonempty, closed, convex sets, ${\Phi }_i$, ${\varphi }_i$, ${\Psi }_i$, and ${\psi }_i$ ($i=1,2$) are the same as Theorem 2.

If l, $k=\infty$, then the uniformly prox-regularity of $C_l$, $Q_k$ collapse to convexity, respectively, that is to say $C_l=C$, $Q_k=Q$. Hence, we have the following corollary.

Corollary 1.

Let $C\subset {\mathcal{H}}_1$ and $Q\subset {\mathcal{H}}_2$ be nonempty, closed, convex sets. For $i\in \{1,2\}$, presume that ${\Phi }_i$, ${\varphi }_i$, ${\Psi }_i$ ${\psi }_i$, A, and B are the same as in Theorem 2. For each $n\ge 1,$ let sequence $\left\{(x_n,y_n)\right\}$ be computed as follows

$$\left\{\begin{array}{c}{f}_n=Pro{j}_C({\varphi }_1\left(y_n\right)-{\Phi }_1(y_n,x_n)),\hfill \\ g_n=Pro{j}_C({\varphi }_2\left(x_n\right)-{\Phi }_2(x_n,y_n)),\hfill \\ h_n=Pro{j}_Q({\psi }_1\left(B{g}_n\right)-{\Psi }_1(B{g}_n,A{f}_n)),\hfill \\ z_n=Pro{j}_Q({\psi }_2\left(A{f}_n\right)-{\Psi }_2(A{f}_n,B{g}_n)),\hfill \\ x_{n+1}=(1-{\iota }_n)x_n+{\iota }_{n}Pro{j}_C(f_n+\varsigma A^{*}(h_n-A{f}_n)),\hfill \\ y_{n+1}=(1-{\iota }_n)y_n+{\iota }_{n}Pro{j}_C(g_n+\varsigma B^{*}(z_n-B{g}_n)),\hfill \end{array}\right.$$

(28)

where $\left\{{\iota }_n\right\}\subset (0,1)$ with ${\sum }_{n=1}^{\infty }{\iota }_n=\infty$. Suppose that $\varsigma <min\left\{\frac{2}{{\parallel A\parallel }^2},\frac{2}{{\parallel B\parallel }^2}\right\}$ and $M=max\left\{{\chi }_1+2{\chi }_1{\overline{\chi }}_2,{\chi }_2+2{\chi }_2{\overline{\chi }}_1\right\}<1$ with

$$\begin{array}{c}\hfill {\chi }_1=\sqrt{1-2{\theta }_1+{\zeta }_1^2}+\sqrt{1-2{\nu }_1+{\mu }_1^2},{\chi }_2=\sqrt{1-2{\theta }_2+{\zeta }_2^2}+\sqrt{1-2{\nu }_2+{\mu }_2^2},\end{array}$$

$$\begin{array}{c}\hfill {\overline{\chi }}_1=\sqrt{1-2{\upsilon }_1+{\lambda }_1^2}+\sqrt{1-2{\vartheta }_1+{\xi }_1^2},{\overline{\chi }}_2=\sqrt{1-2{\upsilon }_2+{\lambda }_2^2}+\sqrt{1-2{\vartheta }_2+{\xi }_2^2}.\end{array}$$

Then the sequence $\left\{(x_n,y_n)\right\}$ computed by relation (28) converges strongly to a solution to the SSGVI.

5. Numerical Example

Let ${\mathcal{H}}_1={\mathcal{H}}_2=\mathbf{R}$. Let $\langle x,y\rangle =xy$, ${\Phi }_1(y,x)=\frac{7}{6}y$, ${\Phi }_2(x,y)=\frac{8}{7}x$, ${\Psi }_1(y,x)=\frac{9}{8}y$, ${\Psi }_2(x,y)=\frac{10}{9}x$ for all x, $y\in \mathbf{R}$. Let $C=[0,+\infty )$ and ${\varphi }_1$, ${\varphi }_2:C\to C$, ${\varphi }_1\left(x\right)=\frac{3}{2}x$, ${\varphi }_2\left(x\right)=\frac{4}{3}x$, respectively. Let $Q=\mathbf{R}$ and ${\psi }_1$, ${\psi }_2:Q\to Q$, ${\psi }_1\left(x\right)=\frac{5}{4}x$, ${\psi }_2\left(x\right)=\frac{6}{5}x$, respectively.

Clearly, ${\varphi }_1$, ${\varphi }_2$, ${\psi }_1$, ${\psi }_2$, ${\Phi }_1$, ${\Phi }_2$, ${\Psi }_1$, ${\Psi }_2$ are 1-strongly monotone and 2-Lipschitzian. Let $Ax=\frac{1}{2}x$ and $Bx=\frac{3}{4}x$ from ${\mathcal{H}}_1$ to ${\mathcal{H}}_2$, respectively. For ${\iota }_n=\frac{1}{5}$, $\varsigma =1$. We now rewrite (28) as follows

$$\left\{\begin{array}{c}{f}_n=Pro{j}_C\left(\frac{3}{2}{y}_n-\frac{7}{6}{y}_n\right),\hfill \\ g_n=Pro{j}_C\left(\frac{4}{3}{x}_n-\frac{8}{7}{x}_n\right),\hfill \\ h_n=Pro{j}_C\left(\frac{5}{4}·\frac{3}{4}{g}_n-\frac{9}{8}·\frac{3}{4}{g}_n\right),\hfill \\ z_n=Pro{j}_C\left(\frac{6}{5}·\frac{1}{2}{f}_n-\frac{10}{9}·\frac{1}{2}{f}_n\right),\hfill \\ x_{n+1}=\frac{4}{5}{x}_n+\frac{1}{5}Pro{j}_C(f_n+\frac{1}{2}(h_n-\frac{1}{2}{f}_n)),\hfill \\ y_{n+1}=\frac{4}{5}{y}_n+\frac{1}{5}Pro{j}_C(g_n+\frac{3}{4}(z_n-\frac{3}{4}{g}_n)),n\ge 1.\hfill \end{array}\right.$$

(29)

For every $n\ge 1$, the operators and the parameters satisfy all conditions in Corollary 1. We find that the sequence $\left\{(x_n,y_n)\right\}$ generated by relation (29) converges strongly to (0, 0).

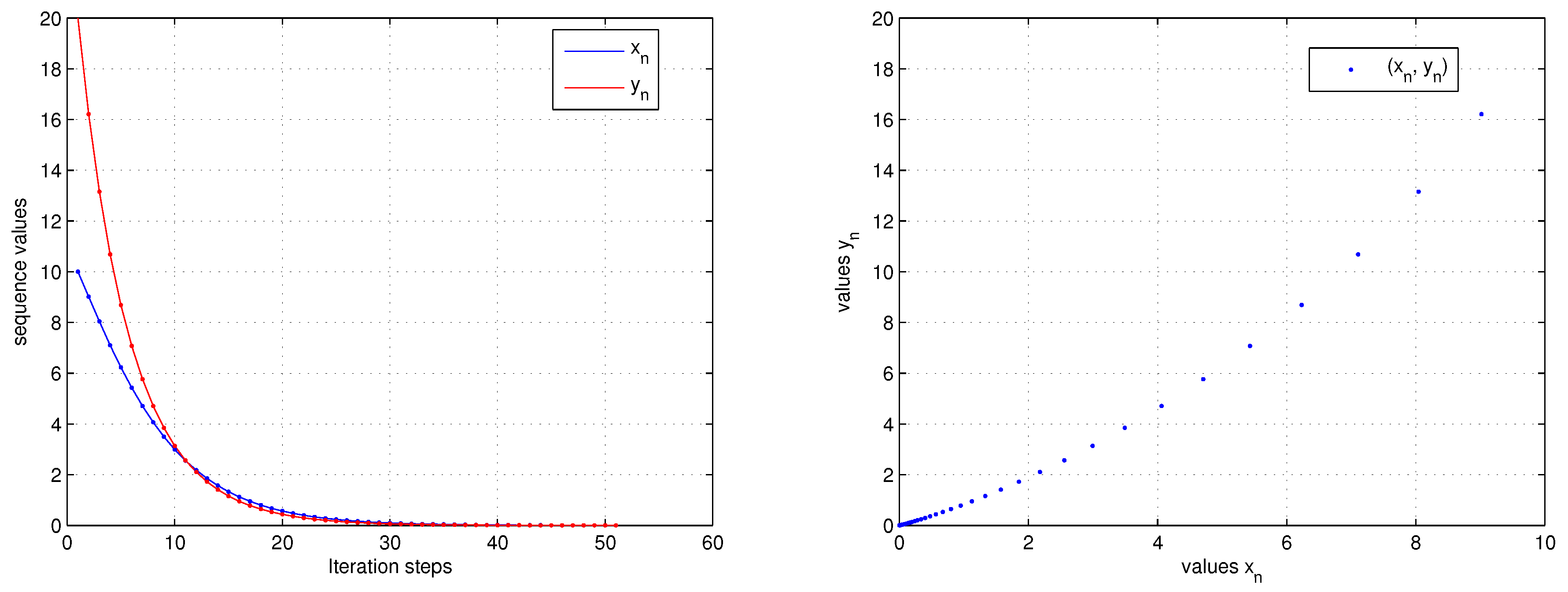
Choosing initial values (10, 20), we see that Figure 1 demonstrates Corollary 1.

6. Conclusions

In this paper, we investigated the split system of nonconvex variational inequalities (SSNVI) in the context of uniformly prox-regular sets, which is an improvement of SSGVI, SSVI, and SVIP. By using an adequate formulation and the projection technique, we constructed an iterative algorithm for approximating the unique common solution to the set of fixed points of nearly uniformly Lipschitz operators and the set of solutions to SSNVI. The results of this paper are expected to be used as further study on numerical techniques.