Weighted h-index for Identifying Influential Spreaders

Abstract

In this paper, we propose weighted h-index $h^w$ and h-index strength $s^h$ to measure spreading capability and identify the most influential spreaders. Experimental results on twelve real networks reveal that $s^h$ was more accurate and more monotonic than $h^w$ and four previous measures in ranking the spreading influence of a node evaluated by the single seed SIR spreading model. We point out that the questions of how to improve monotonicity and how to determine a proper neighborhood range are two interesting future directions.

1. Introduction

Many spreading phenomena, such as the cascading failure [1], rumor diffusion [2], viral advertising [3], etc., in the real world, can be described as the spreading process on complex networks [4,5]. Understanding the significant role that a single node plays provides insights into network structure [6,7,8,9] and function [10,11]. Identifying influential spreaders, whose fundamental problem is how to identify and rank the efficient spreaders in complex networks, has attracted much attention [12].

Degree, the most straightforward indicator, focuses on the number of links per node, and is an often-used measure of the influence of a node in the spreading process. In the early days, people guessed that the node with the maximal degree was the most influential in a network [13,14]. There are also many traditional metrics, such as betweenness [15], closeness [16], Katz [17], etc., which show good performance in distinguishing different influential nodes. However, their computational complexity is unacceptable when we apply them to large-scale networks. Recently, Kitsak et al. [18] found that the most influential spreaders are likely to reside in the core part of a network. However, coreness is a metric based on k-shell decomposition, which assigns many nodes to the same shell. The nodes in the same shell actually have different spreading abilities [19]. The method in Ref. [18] was extended to identify the difference in spreading ability among nodes in the same shell [19,20,21,22,23,24,25,26,27,28,29,30,31]. For example, Zeng et al. proposed a mixed degree decomposition (MDD) method by considering both the residual degree and the exhausted degree [20], but the optimal parameter $\lambda$ is uncertain. Liu et al. took into account the shortest distance from a target node to the node with the highest coreness and presented a more distinguishable identification of influential spreaders [21]. Bae and Kim proposed the neighborhood coreness centrality, which summed the neighbors’ coreness together [22]. Wang et al. utilized the iteration information in the k-shell decomposition process to differentiate the spreading influence of nodes in the same shell [23]. Xu et al. designed an iterative neighbor information gathering (ING) process to rank the node influence [24]. Other measures [25,26,27,28,29,30,31,32,33], such as information index [32] and subgraph centrality [33], also have good performance in finding important nodes. These above-mentioned measures are structural centralities which measure the importance of a node based mainly on the topological structure of a network [10].

In this paper, we argue that edges can be quite different [34] and have different significances when defining the spreading influence of a node. For example, degree and betweenness have good performance for unweighted networks, and they have been extended to weighted networks [29,35,36]. Evidence theory has been employed to identify influential nodes in weighted networks [37]. The different importance of the direction of a link in spreading was taken into account by considering weighted neighborhood centrality [38] and asymmetric link weights [39].

Recently, Lü et al. discussed that h-index as a good tradeoff between degree and coreness when measuring a node’s influence. However, h-index is not the overall best performer when compared with coreness [40]. Investigated by recent work [41], these three fundamental methods (i.e., degree, h-index, and coreness) have the advantage of assessing the performance of identifying the influential node. Inspired by these factors, we propose a weighted h-index ($h^w$) by constructing an operator $\mathcal{H}$ on weighted edges. Furthermore, the sum of weighted h-index ($s^h$) in the node’s neighborhood defines the spreading influence. To evaluate the effectiveness of the proposed measures, we apply the susceptible-infected-recovered (SIR) model for investigating an epidemic spreading process on twelve real-world networks.

The remainder of this paper is organized as follows. Section 2 reviews several centralities and a detailed description of our methods is presented. Then, the SIR model and the evaluation methods are introduced and twelve real networks are employed to test the accuracy and monotonicity of our methods in Section 3. Finally, in Section 4 a simple conclusion is summarized.

2. Methods

Given a network $G\left(V, E\right)$ with $N=\left|V\right|$ nodes and $M=\left|E\right|$ edges, $e_{ij}$ represents the edge linking node $i$ and node $j$, the weight of $e_{ij}$ is $w_{ij}=k_i{k}_j$, and ${\Gamma }_i$ denotes the set of the neighbors of node $i$.

2.1. Measures

The degree of node $i$ is defined as $k_i=\left|{\Gamma }_i\right|$, where $|·|$ indicates the number of the elements in a set.

The betweenness of node $i$ is defined as

$$B_i={\displaystyle \sum }_{j\in V,k\in V, j\ne k}\frac{n_{jk}\left(i\right)}{n_{jk}}$$

(1)

where $n_{jk}$ is the number of shortest paths connecting node $j$ and node $k$, while $n_{jk}\left(i\right)$ is the number of shortest paths connecting node $j$ and node $k$ and passing through node $i$.

The k-shell index ($k_s$) is obtained by k-shell decomposition. During k-shell decomposition, each node will be assigned to a shell with a specific $k_s$ index.

The h-index of node $i$ is defined as [40]

$$h_i=\mathcal{H}\left(k_{j_1},k_{j_2},\cdots ,k_{j_{k_i}}\right).$$

(2)

where $\mathcal{H}(·)$ is an operator, which finds out the maximum integer $h$ such that there are at least $h$ neighbors whose degree is no less than $h$.

To reflect the spreading influence of a node in a network, we design a new measure called weighted h-index ($h^w$). The weight of virtual edges incident with node $i$ is selected to replace the degree of node $i$ in Ref. [40]. Each neighbor $j$ of node $i$ is cloned $k_j$ times. Each cloned neighbor $j_c$ has a virtual edge $e_{i{j}_c}$ whose weight $w_{i{j}_c}=w_{ij}$. The edge weights of all the virtual edges incident with node $j$ are grouped in the descending edge weight sequence of node $i$. This means that $w_{ij}$, which is the weight of the original edge $e_{ij}$, will show up $k_j$ times in the descending edge weight sequence. Then, weighted h-index is

$$h_i^w=\mathcal{H}\left(w_{i{j}_1,1},\cdots ,w_{i{j}_1,k_{j_1}},w_{i{j}_2,1},\cdots ,w_{i{j}_2,k_{j_2}},\cdots ,w_{i{j}_{k_i},1},\cdots ,w_{i{j}_{k_i},k_{j_{k_i}}}\right).$$

(3)

Since the strength of a node [35] is often adopted in identifying the influential nodes [14,39,42], we define the h-index strength of node $i$ as

$$s_i^h={{\displaystyle \sum }}_{j\in \Gamma \left(i\right)}{h}_j^w.$$

(4)

2.2. Single Seed SIR Model

We employed the single seed SIR model to investigate the spreading process on complex networks. Initially, all nodes in a network are in the susceptible state (S) except for the seed node, which is in the infectious state (I). At each time step, the nodes in the I state infect their neighbors in the S state with probability $\beta$, then their state changes from the infectious state (I) to the recovered state (R), which means that they cannot be infected again. The spreading process will stop when any node in the network is in state I. The number of nodes in the recovered state reflects the final infected scope, and this is adopted to measure the infection strength of the seed node.

The higher infection probability $\beta$, the larger the population that will be infected, wherever it locates in a network. According to the previous study [43], we know the critical infection probability ${\beta }_c$ in a network approximately equals to $⟨k⟩/⟨k^2⟩$. In this study, the infection probability $\beta$ is set to larger than ${\beta }_c$.

When node $i$ is the seed for the single seed SIR model, its spreading scope ($S_i$) is quantified by the average number of recovered nodes over 200 independent simulations.

2.3. Evaluation Methods

The Kendall ${\tau }_b$ correlation coefficient is adopted to measure the consistency between two rankings. Given $R_{\mu }$, the rank vector of a measure $\mu$, and $R_{SIR}$, that of the single seed SIR model, the Kendall ${\tau }_b$ correlation coefficient is defined as

$${\tau }_b\left(R_{\mu }, R_{SIR}\right)=\frac{n_c-n_d}{\sqrt{(n_0-n_1)(n_0-n_2)}},$$

(5)

where $n_c$ is the number of concordant pairs, $n_d$ is the number of discordant pairs, and $n_0=n\left(n-1\right)/2$, $n_1={{\displaystyle \sum }}_i{t}_i\left(t_i-1\right)/2$, $n_2={{\displaystyle \sum }}_j{u}_j\left(u_j-1\right)/2$, where $n$ is the size of rank vectors and $t_i$ and $u_j$ are the number of tied values in the $i$th and $j$th group of ties, respectively. Since all measures are evaluated by $R_{SIR}$, ${\tau }_b\left(R_{\mu }, R_{SIR}\right)$ will be denoted by ${\tau }_b\left(\mu \right)$ for short.

To quantify the accuracy of a measure, the imprecision function [10] is employed. Given a selection fraction $p\in \left[0, 1\right]$, $V_{\mathrm{eff}}\left(p\right)$ is the top $p$ fraction of the most influential spreaders, and $V_{\mu }\left(p\right)$ is the $pN$ nodes with the highest value of measure $\mu$. Their average spreading scope is denoted by $S_{\mathrm{eff}}\left(p\right)$ and $S_{\mu }\left(p\right)$, respectively. Then the imprecision function is defined as

$${ϵ}_{\mu }\left(p\right)=1-\frac{S_{\mu }\left(p\right)}{S_{\mathrm{eff}}\left(p\right)}.$$

(6)

A smaller ${ϵ}_{\mu }$ means that the corresponding measure $\mu$ performs more accurately in identifying the most influential spreaders. The measure $\mu$, as discussed in this work, could be $k$, $B$, $k_s$, $h$, $h^w$, and $s^h$.

The monotonicity of ranking vector $R_{\mu }$ is defined as [14]

$$M\left(R_{\mu }\right)={\left(1-\frac{{{\displaystyle \sum }}_{rϵR_{\mu }}N\left(r\right)\left(N\left(r\right)-1\right)}{N\left(N-1\right)}\right)}^2,$$

(7)

where $N$ is the size of ranking vector $R_{\mu }$, which is equal to the number of nodes in a network in this paper. Furthermore, $N\left(r\right)$ is the number of nodes with the same rank $r$ in $R_{\mu }$. If every node is given a distinctive rank, then $M\left(R_{\mu }\right)=1$. This means that $R_{\mu }$ is a complete monotonic ranking, and each node can therefore be differentiated from others. When $M\left(R_{\mu }\right)=0$, all nodes have the same rank, and ranking nodes by the measure $\mu$ cannot distinguish nodes at all. A measure with perfect monotonicity in ranking the nodes of a network will rank each node via an exclusive rank, which means that each node has a different rank from any other nodes.

3. Results

Setting the ranking of nodes by their spreading scope, with the single seed SIR model as the benchmark, we evaluated the accuracy and the monotonicity of ranking nodes by degree ($k$), node betweenness ($B$), k-shell index ($k_s$), h-index of node ($h$), weighted h-index of node ($h^w$) and h-index strength of node ($s^h$) on twelve real networks. The twelve real networks were one power grid network (Power Grid [44]), one computer network in the autonomous systems level (AS), two file-sharing networks (Gnutella06, Gnutella08), one metabolic network (C. elegans [45]), one email communication network (Email [46]), three social networks (PGP [47], Facebook [48] and Hamster [49]), two collaboration networks (CondMat [50] and NetSci [51]) and one protein–protein interaction network (Protein [52]). Their primary features are summarized in Table 1.

Table 1. Properties of twelve real networks. $N$: the number of nodes, $M$: the number of edges, ${\beta }_c$: the critical infection rate for single seed SIR model, $⟨k⟩$: the average degree, $k_{max}$: the maximum degree, and $k_{s,max}$: the maximum k-shell index.

Network	$\mathit{N}$	$\mathit{M}$	${\mathit{\beta }}_{\mathit{c}}$	$⟨\mathit{k}⟩$	${\mathit{k}}_{\mathit{m}\mathit{a}\mathit{x}}$	${\mathit{k}}_{\mathit{s},\mathit{m}\mathit{a}\mathit{x}}$
Power Grid	4941	6594	0.26	2.6691	19	5
AS	3015	5156	0.01	3.4202	590	9
Gnutella06	8717	31,525	0.07	7.2330	115	9
Gnutella08	6301	20,777	0.06	6.5948	97	10
C. elegans	453	2025	0.02	8.9404	237	10
Email	1133	5451	0.05	9.6222	71	11
PGP	10,680	24,316	0.05	4.5536	205	31
Facebook	4039	88,234	0.01	43.6910	1045	115
Hamster	2426	16,630	0.02	13.7098	273	24
CondMat	23,133	93,497	0.05	8.0830	279	25
NetSci	379	914	0.12	4.8232	34	9
Protein	1870	2203	0.15	2.3562	56	5

3.1. Accuracy

Table 2 shows that $s^h$ obtained eleven highest scores, and $h^w$ obtained one highest score in the consistency between ranking by measures and the averaged spreading scope. Compared to the four previous measures, $s^h$ and $h^w$ were better in twelve and ten real networks, respectively. Table 2 suggests that $s^h$ was a better measure than $h^w$ in most networks (except for Hamster). It is noteworthy that similar results can be found in Table 3 when $\beta =1.5{\beta }_c$.

Table 2. Kendall ${\tau }_b$ correlation coefficient for six measures in twelve real networks. In the single seed SIR model, the infection probability $\beta$ is set to slightly larger than ${\beta }_c$, i.e., $\beta =1.005{\beta }_c$. The largest ${\tau }_b$ in each row is marked in boldface.

Network	${\mathit{\tau }}_{\mathit{b}}\left(\mathit{k}\right)$	${\mathit{\tau }}_{\mathit{b}}\left(\mathit{B}\right)$	${\mathit{\tau }}_{\mathit{b}}\left({\mathit{k}}_{\mathit{s}}\right)$	${\mathit{\tau }}_{\mathit{b}}\left(\mathit{h}\right)$	${\mathit{\tau }}_{\mathit{b}}\left({\mathit{h}}^{\mathit{w}}\right)$	${\mathit{\tau }}_{\mathit{b}}\left({\mathit{s}}^{\mathit{h}}\right)$
Power Grid	0.6020	0.4238	0.5142	0.6177	0.7466	0.8060
AS	0.4478	0.2896	0.4540	0.4522	0.3999	0.5023
Gnutella06	0.6715	0.6393	0.6811	0.6940	0.7206	0.7578
Gnutella08	0.6549	0.5987	0.6887	0.6913	0.7139	0.7527
C. elegans	0.5729	0.4361	0.5969	0.5820	0.5868	0.6289
Email	0.7222	0.5862	0.7486	0.7483	0.7694	0.7868
PGP	0.6027	0.4160	0.5707	0.6051	0.6481	0.6566
Facebook	0.6818	0.4491	0.7135	0.7074	0.7320	0.7575
Hamster	0.7477	0.5773	0.7378	0.7523	0.8390	0.8383
CondMat	0.6158	0.3884	0.6337	0.6432	0.7312	0.7564
NetSci	0.6391	0.4071	0.5830	0.6499	0.8256	0.8592
Protein	0.5642	0.5227	0.5598	0.5835	0.7690	0.8246

Table 3. Kendall ${\tau }_b$ correlation coefficient for six measures in twelve real networks. In the single seed SIR model, the infection probability is $\beta =1.5{\beta }_c$. The largest ${\tau }_b$ in each row is marked in boldface.

Network	$\mathit{\tau }\left(\mathit{k}\right)$	$\mathit{\tau }\left(\mathit{B}\right)$	$\mathit{\tau }\left({\mathit{k}}_{\mathit{s}}\right)$	$\mathit{\tau }\left(\mathit{h}\right)$	$\mathit{\tau }\left({\mathit{h}}^{\mathit{w}}\right)$	$\mathit{\tau }\left({\mathit{s}}^{\mathit{h}}\right)$
Power Grid	0.4241	0.2921	0.3987	0.4646	0.6206	0.6893
AS	0.4148	0.2409	0.4412	0.4237	0.5091	0.5927
Gnutella06	0.8135	0.7626	0.8073	0.8438	0.8599	0.8645
Gnutella08	0.7214	0.6597	0.7525	0.7627	0.7844	0.8254
C. elegans	0.5759	0.4137	0.6140	0.5867	0.6355	0.6842
Email	0.7738	0.6171	0.7964	0.8050	0.8438	0.8601
PGP	0.5153	0.3500	0.5118	0.5287	0.6575	0.7099
Facebook	0.6220	0.4251	0.6660	0.6526	0.7353	0.7875
Hamster	0.7151	0.5727	0.7110	0.7232	0.8484	0.8745
CondMat	0.6051	0.3942	0.6316	0.6422	0.7714	0.8152
NetSci	0.5335	0.3443	0.5019	0.5609	0.7747	0.8330
Protein	0.4718	0.4466	0.5147	0.5103	0.7452	0.8429

The imprecision functions of the ranking by six measures are shown in Figure 1. The imprecision of $s^h$ (black) and $h^w$ (red) was less than 0.1 for all $p\in \left[0.01, 0.3\right]$ in all cases. To date, the imprecision of $s^h$ is even less than 0.05 in eleven networks except for Power Grid. Furthermore, $s^h$ is always the most accurate measure in identifying the influential nodes in a network when compared to the other five measures. Similar results are shown in Figure 2 (where $\beta =1.5{\beta }_c$), which proves that $s^h$ is the most accurate measure in identifying the influential spreaders.

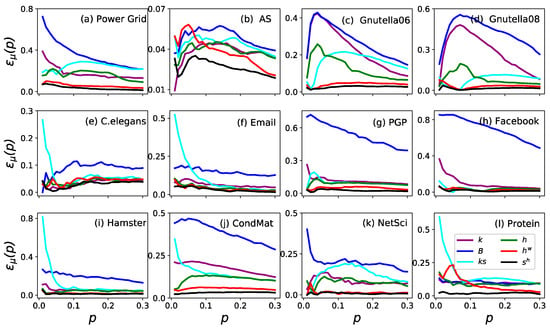
Figure 1. The imprecision functions ${\epsilon }_{\mu }\left(p\right)$ as a function of node fraction $p\in \left[0.01, 0.30\right]$ when $\beta =1.005{\beta }_c$ in the twelve real networks. The six measures are $k$ (purple), $B$ (blue), $k_s$ (cyan), $h$ (green), $h^w$ (red) and $s^h$ (black).

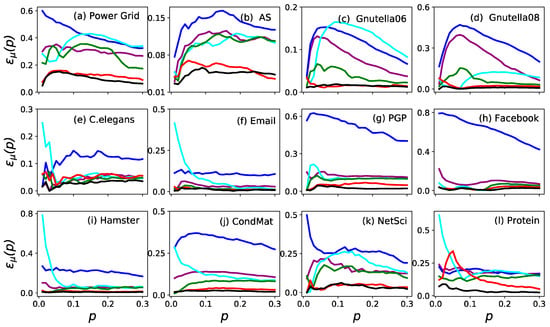
Figure 2. The imprecision functions ${\epsilon }_{\mu }\left(p\right)$ as a function of node fraction $p\in \left[0.01, 0.30\right]$ when $\beta =1.5{\beta }_c$ in the twelve real networks. The six measures are $k$ (purple), $B$ (blue), $k_s$ (cyan), $h$ (green), $h^w$ (red) and $s^h$ (black).

To investigate the robustness of the accuracy of the ranking based on the proposed measures, we show the Kendall ${\tau }_b$ correlation coefficient as a function of the infection probability $\beta$ on six selected real networks in Figure 3. When the infection probability $\beta$ is set around ${\beta }_c$, $s^h$ and $h^w$ show a significantly higher robustness of accuracy. For Power Grid, NetSci and Protein networks in the whole range of $\beta$, $s^h$ is more accurate than $h^w$, and they are both more accurate than the other four measures. When $\beta <{\beta }_c$, the spreading is typically confined to the neighborhood of the initially infected seed node. Since the seed node with a larger degree has a relatively larger neighborhood, it will infect more nodes than other seed nodes with a smaller degree. This is why degree ($k$) always achieves the most significant $\tau$ values when $\beta <{\beta }_c$ for C. elegans and Email. When $\beta$ is increasing, $s^h$ and $h^w$ perform better gradually. The results in Figure 3 demonstrate that $s^h$ is a better measure of the ranking’s robustness for identifying the influential spreaders in a network.

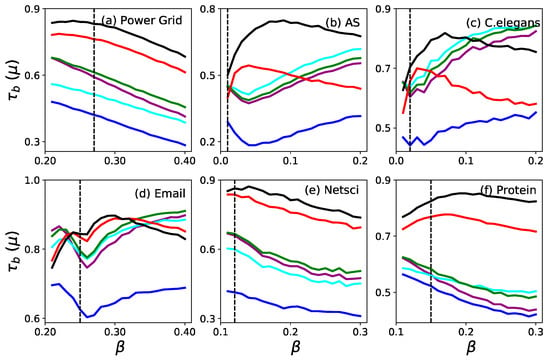
Figure 3. Kendall ${\tau }_b$ correlation coefficient as a function of the infection probability $\beta$ for six real networks. The vertical dash line shows the critical infection rate ${\beta }_c$. The six measures are $k$ (purple), $B$ (blue), $k_s$ (cyan), $h$ (green), $h^w$ (red) and $s^h$ (black).

3.2. Monotonicity

Table 4 shows the monotonicity of the ranking based on six measures. For all the networks, ranking nodes based on $s^h$ achieve the best performance, and $h^w$ gets the second best performance. Both $h^w$ and $s^h$ are more competitive measures than $k$, $B$, $k_s$, and $h$ from monotonicity’s perspective in the global scale of a network.

Table 4. The monotonicity $M$ of node ranking based on six measures was applied to twelve real networks.

Network	$\mathit{M}\left(\mathit{k}\right)$	$\mathit{M}\left(\mathit{B}\right)$	$\mathit{M}\left({\mathit{k}}_{\mathit{s}}\right)$	$\mathit{M}\left(\mathit{h}\right)$	$\mathit{M}\left({\mathit{h}}^{\mathit{w}}\right)$	$\mathit{M}\left({\mathit{s}}^{\mathit{h}}\right)$
Power Grid	0.5927	0.8322	0.2460	0.4776	0.8523	0.9606
AS	0.4506	0.3728	0.3734	0.4336	0.9557	0.9803
Gnutella06	0.8110	0.8990	0.5625	0.7945	0.9738	0.9986
Gnutella08	0.7636	0.8511	0.5990	0.7575	0.9644	0.9979
C. elegans	0.7922	0.8743	0.6962	0.7599	0.9301	0.9961
Email	0.8874	0.9400	0.8088	0.8661	0.9914	0.9996
PGP	0.6193	0.5099	0.4806	0.5836	0.9495	0.9920
Facebook	0.9740	0.9855	0.9419	0.9674	0.9838	0.9998
Hamster	0.8980	0.7128	0.8714	0.8892	0.9796	0.9854
CondMat	0.8524	0.4506	0.7980	0.8268	0.9863	0.9974
NetSci	0.7642	0.3387	0.6421	0.6976	0.9472	0.9907
Protein	0.4264	0.4053	0.2534	0.3825	0.9084	0.9563

To depict the monotonicity in the local scale of a network, the node distribution between ranks is plotted by the complementary cumulative distribution function (CCDF) in Figure 4. The more monotonic a measure is, the slower the distribution in CCDF decreases, and the more significant in distinguishing influential spreaders (nodes). In all twelve real networks, $k$, $k_s$, and $h$ drop quickly at the left beginning, which means that they are poor at distinguishing nodes from each other based on the spreading influence. $s^h$ decreases slower than $h^w$, and both $s^h$ and $h^w$ are slower than $k$, $k_s$, and $h$ in all twelve real networks.

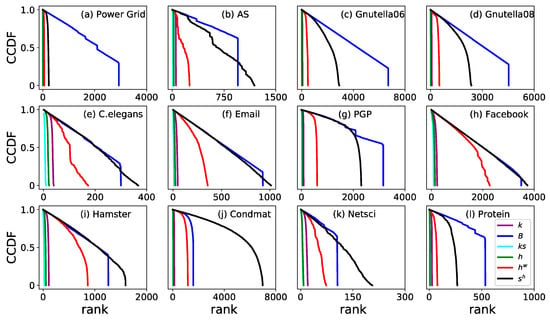
Figure 4. Complementary cumulative distribution function (CCDF) of ranking by six different measures. Six measures are $k$ (purple), $B$ (blue), $k_s$ (cyan), $h$ (green), $h^w$ (red) and $s^h$ (black).

Undoubtedly, $B$ has a competitive performance compared with $s^h$ and $h^w$. For the five real networks including Power Grid, PGP, Gnutella06, Gnutella08, and Protein, $B$ decreases slower than $s^h$ and $h^w$, which means that $B$ shows better monotonicity than $s^h$ and $h^w$. For the other seven networks, $s^h$ always has the best monotonicity. AS is a typical example (Figure 4b), where $B$ decreases slower than $s^h$ at the beginning. However, the black line ($s^h$) goes across the blue line ($B$), which means that ranking nodes by $s^h$ will distinguish nodes into more different ranks, and proves that $s^h$ has a better monotonicity than $B$.

4. Discussion

Spreading like an epidemic, information is a ubiquitous process in social, biological, and technological networks. Identifying influential nodes in the spreading process, as one of the primary problems in network science, remains an open issue. In this study, we propose the weighted h-index $h^w$ and the h-index strength $s^h$ to identify the influential nodes in the spreading process on complex networks. To evaluate the accuracy and monotonicity of the proposed measures, the single seed SIR model was employed and simulated on twelve real networks. The results show that compared to the four previous measures, h-index strength, $s^h$, was the best measure and weighted h-index, $h^w$, was the second best measure to identify the influential nodes in single seed SIR spreading process.

Although the weighted h-index $h^w$ and the h-index strength $s^h$ perform better in most of the conditions, the insufficient monotonicity of the local scale of a network cannot be neglected. The issue of how to improve monotonicity in the local scale of a network requires further studies. Since we only extended a weighted edge to virtual edges according to the degree of the incident neighbor node, how to determine a proper neighborhood range is another noteworthy topic for the future.

Note that the criteria for essential nodes are diverse. For example, the node acts as an articulation point, damage to which will destroy a network into two or more components, and it may therefore be totally unimportant in the spreading process. Although the proposed measures are outstanding in identifying the vital node for the single seed SIR spreading process, it is necessary to conduct further experiments, if one wishes to apply our methods to other situations.