Experimental Study on Plasma Flow Control of Symmetric Flying Wing Based on Two Kinds of Scaling Models
Abstract
1. Introduction
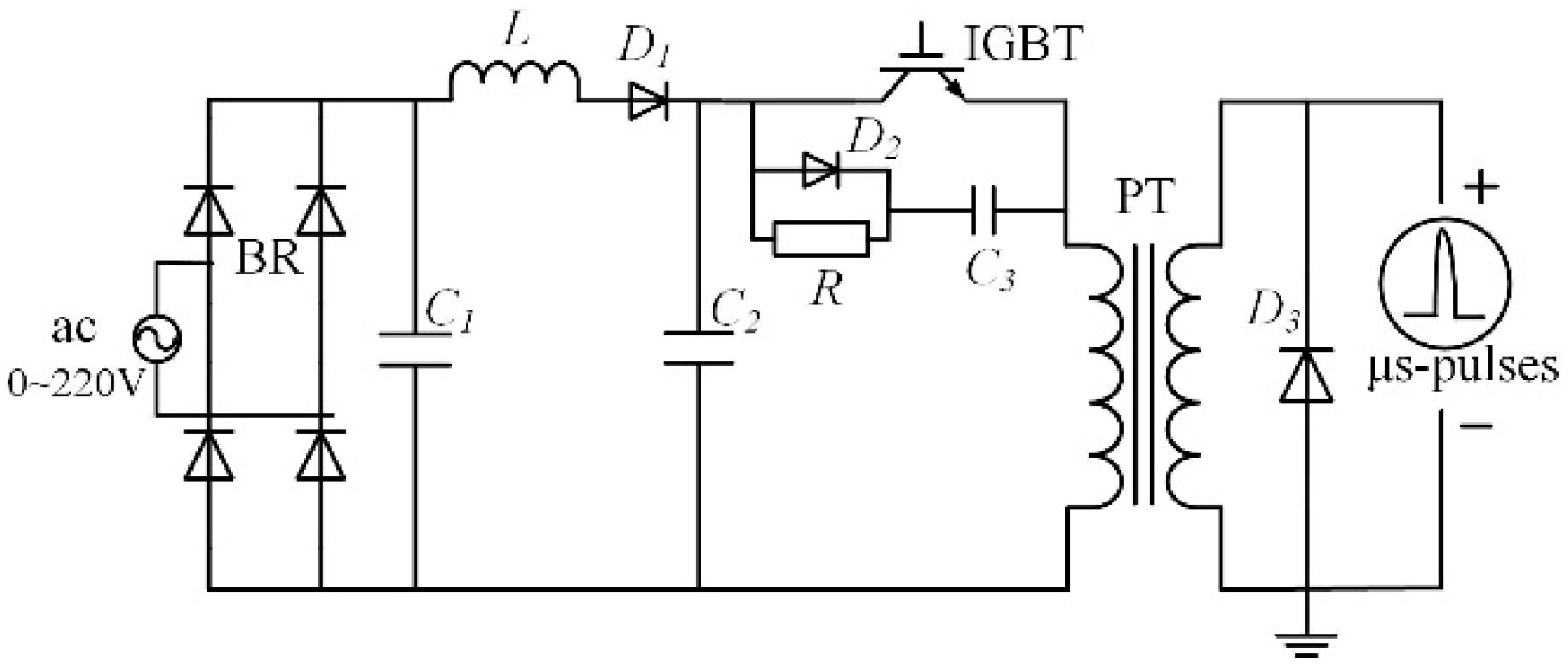
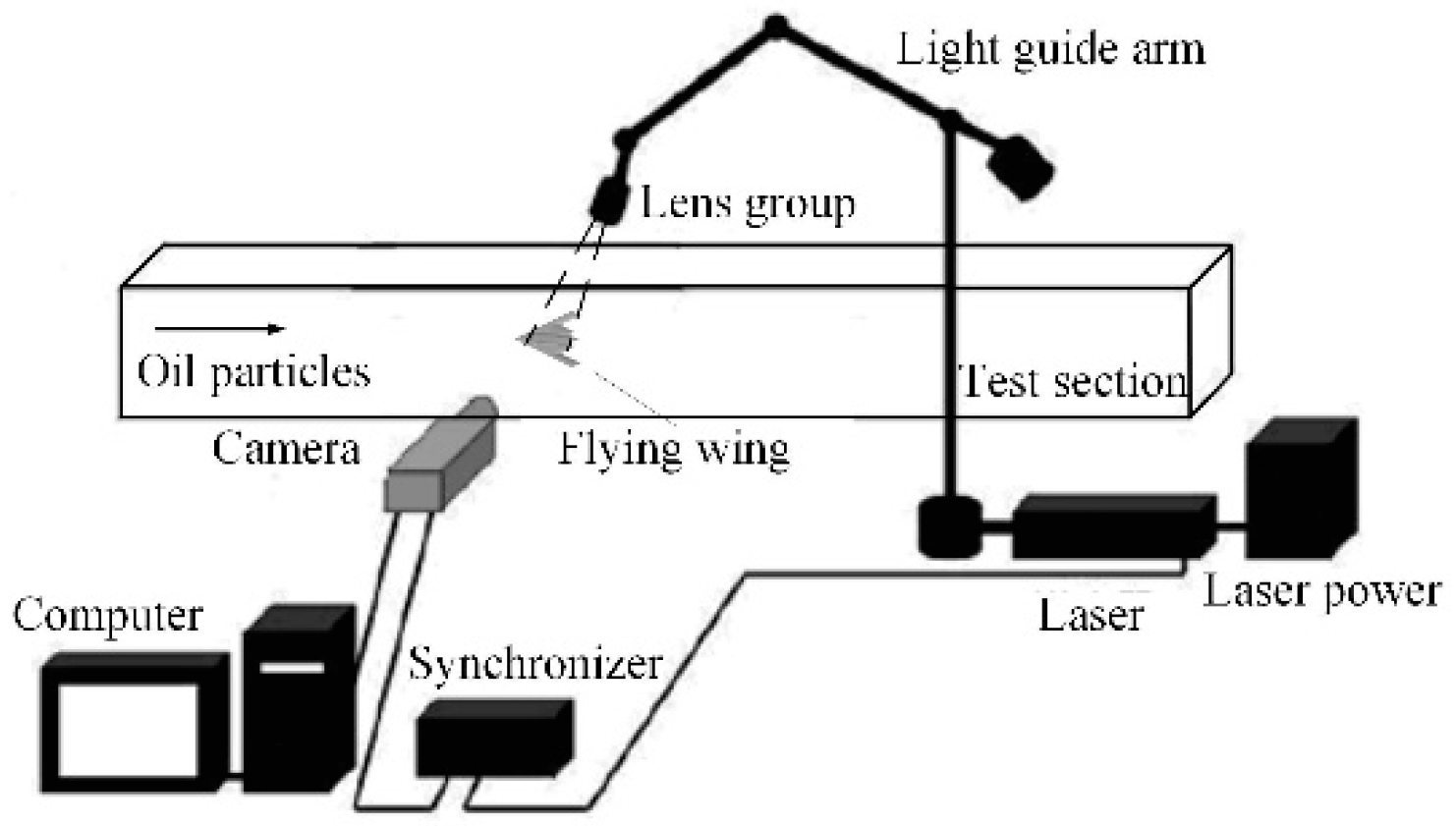
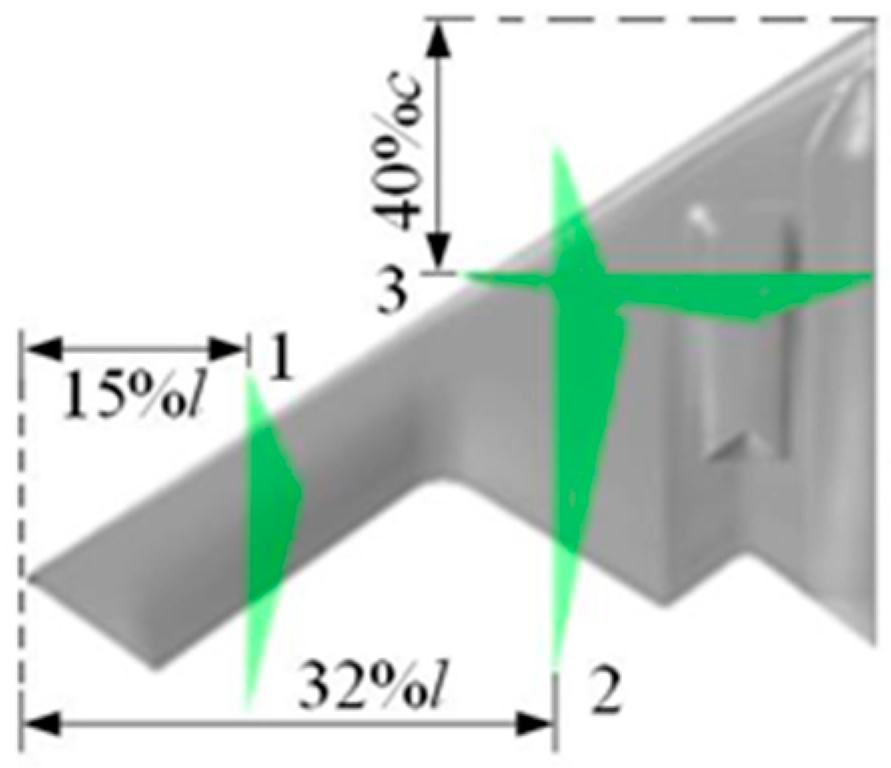
2. Experimental Setup
3. Experimental Results
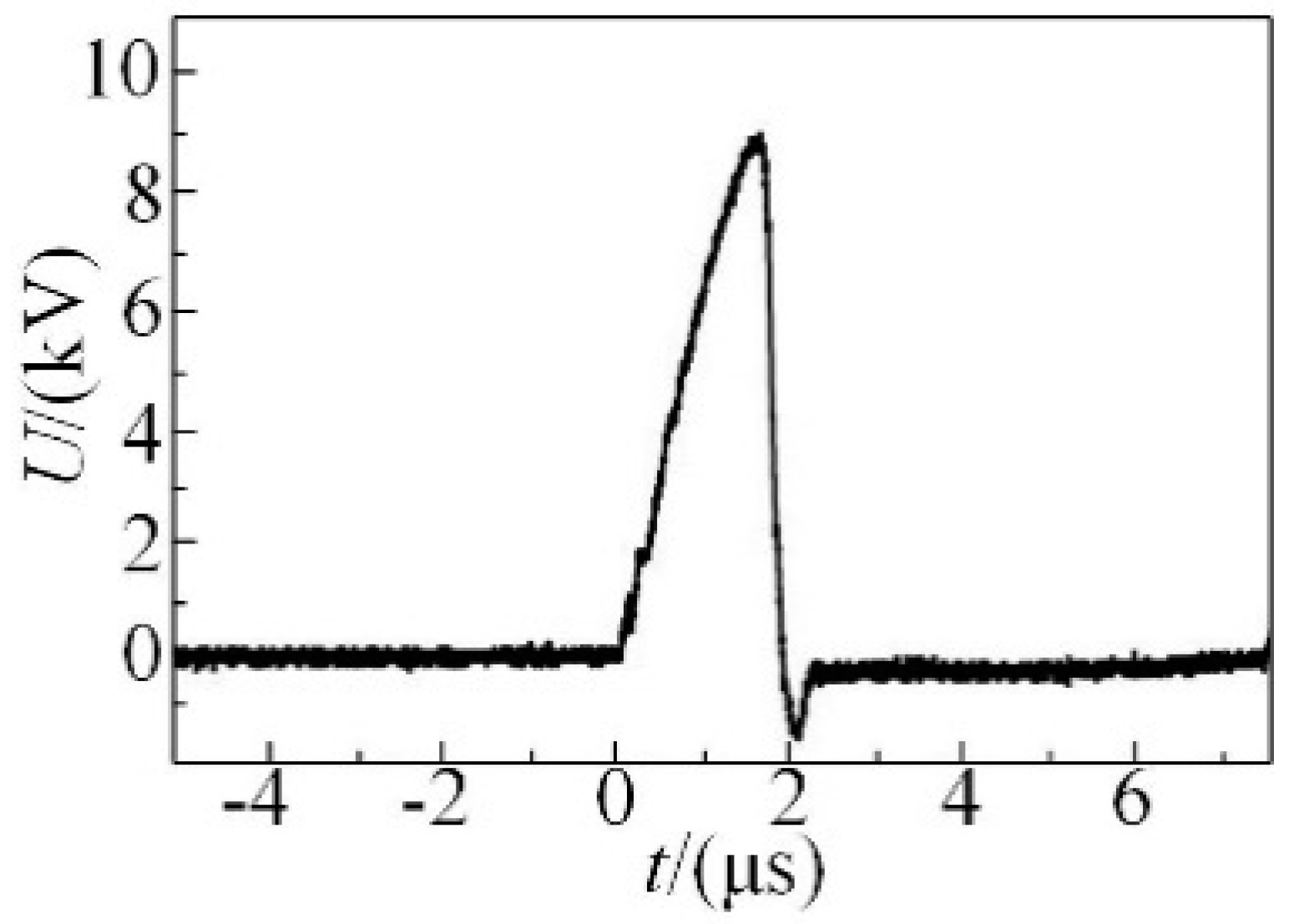
3.1. Analysis of Discharge and Energy
3.1.1. Effect of Actuation Length on Discharge Energy
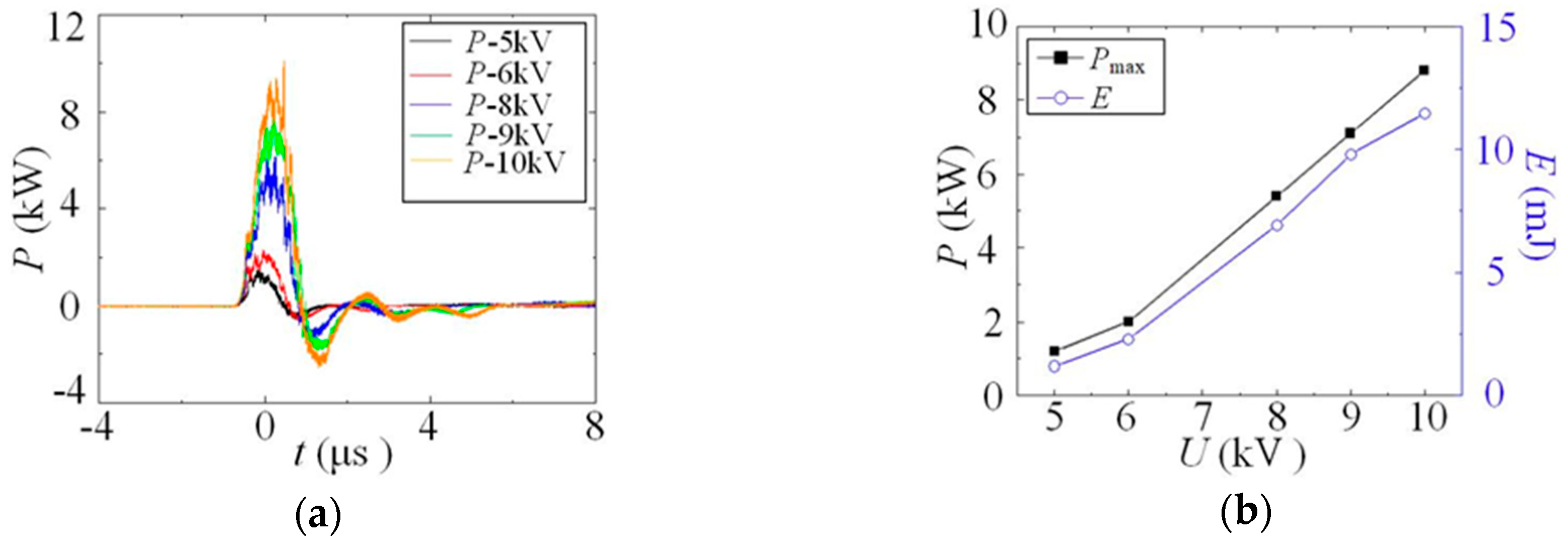
3.1.2. Effect of Actuation Voltage on Discharge Energy
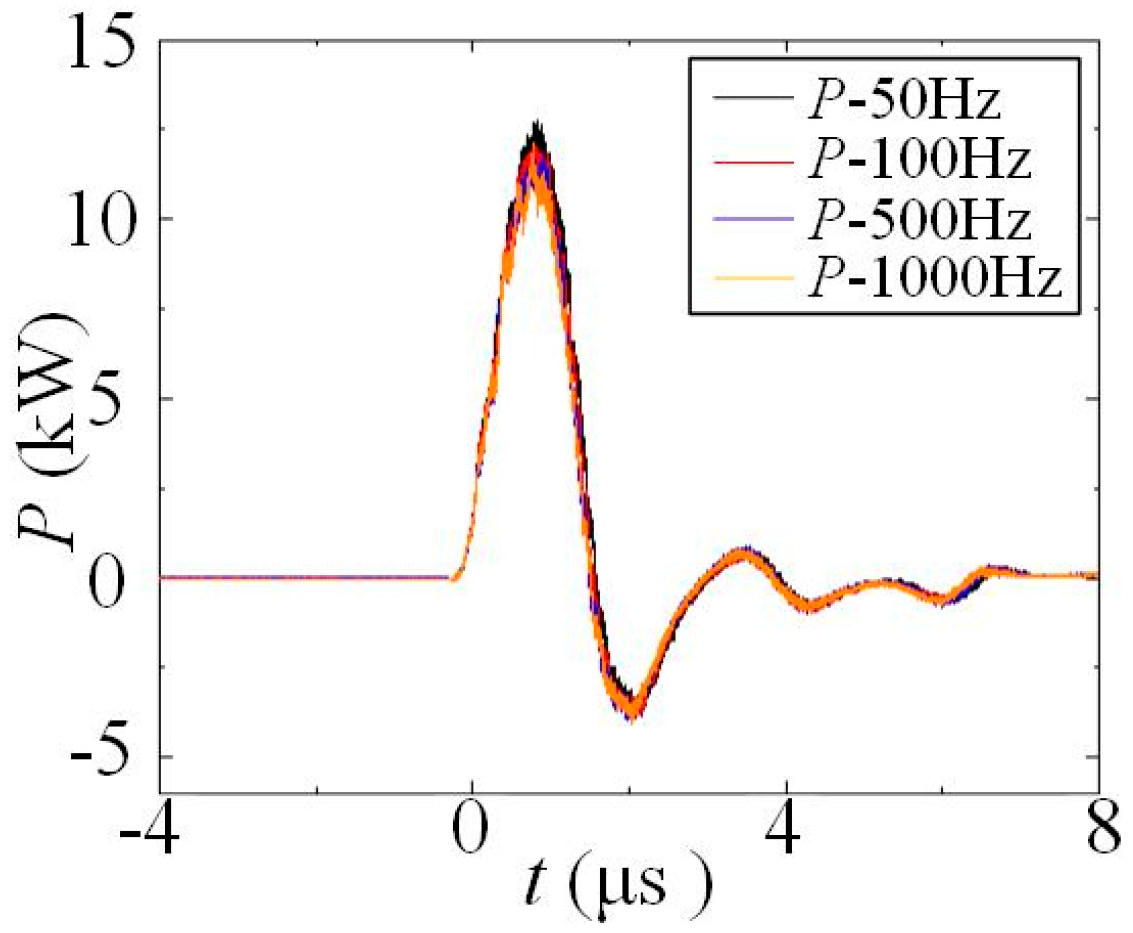
3.1.3. Effect of Actuation Frequency on Discharge Energy
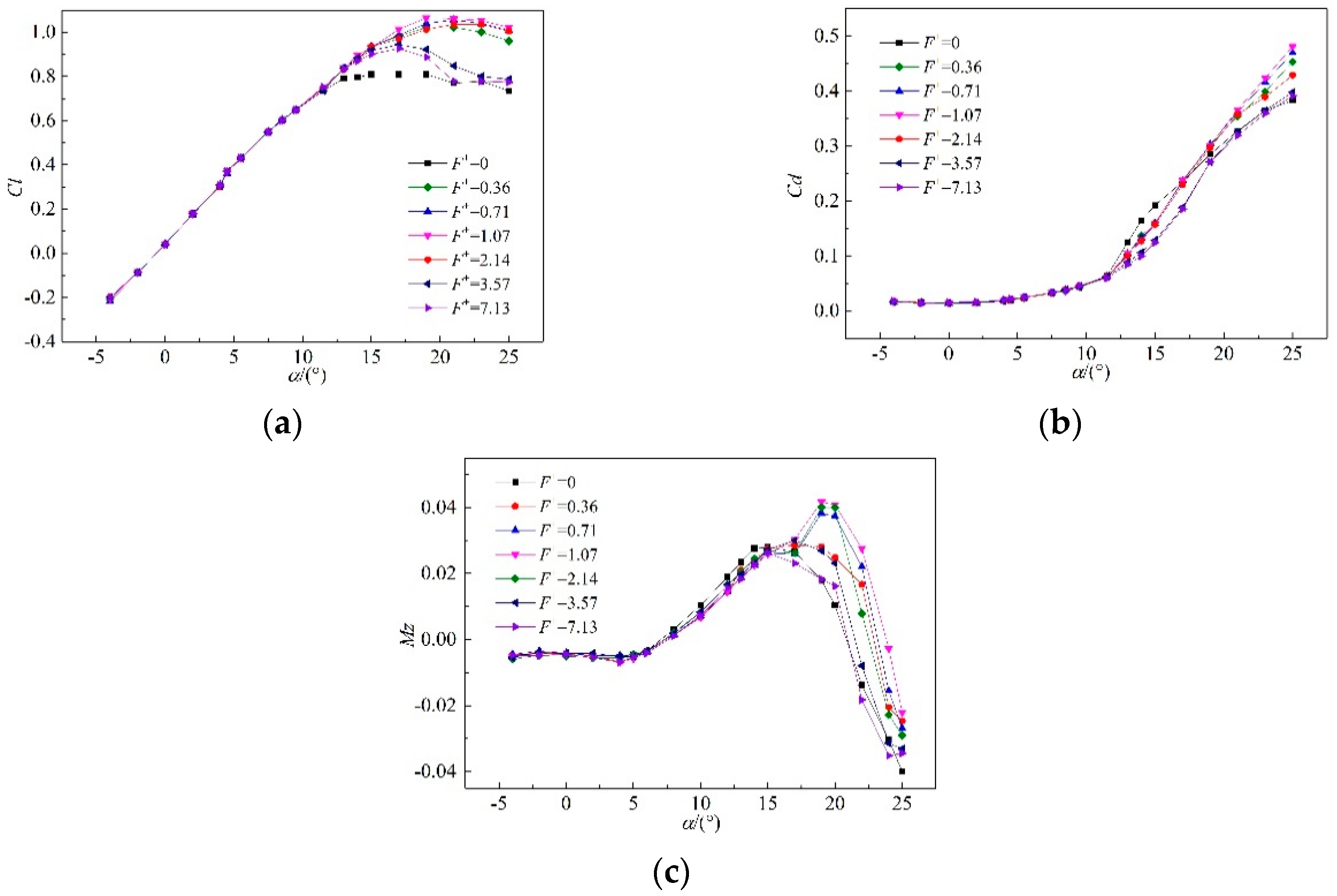
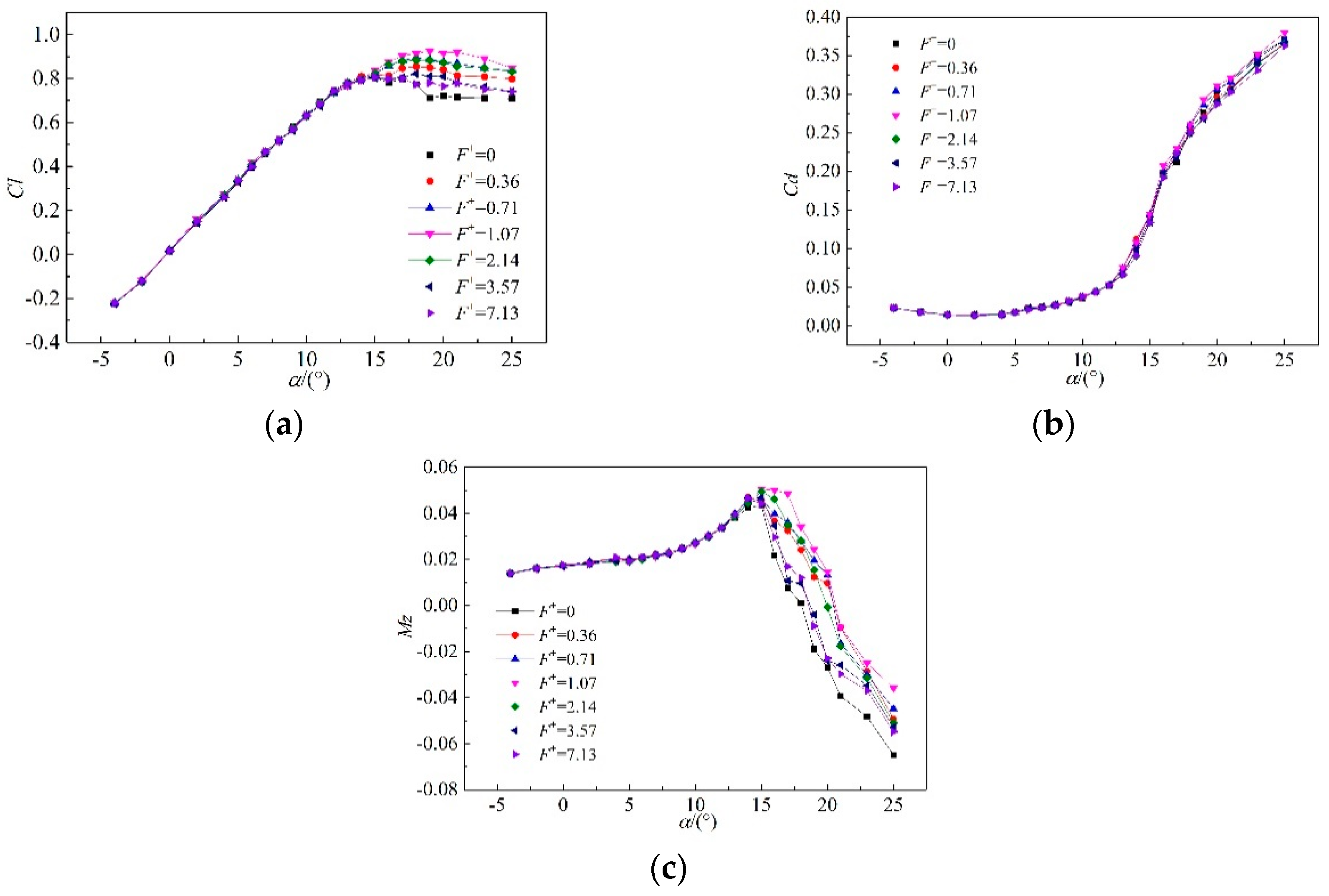
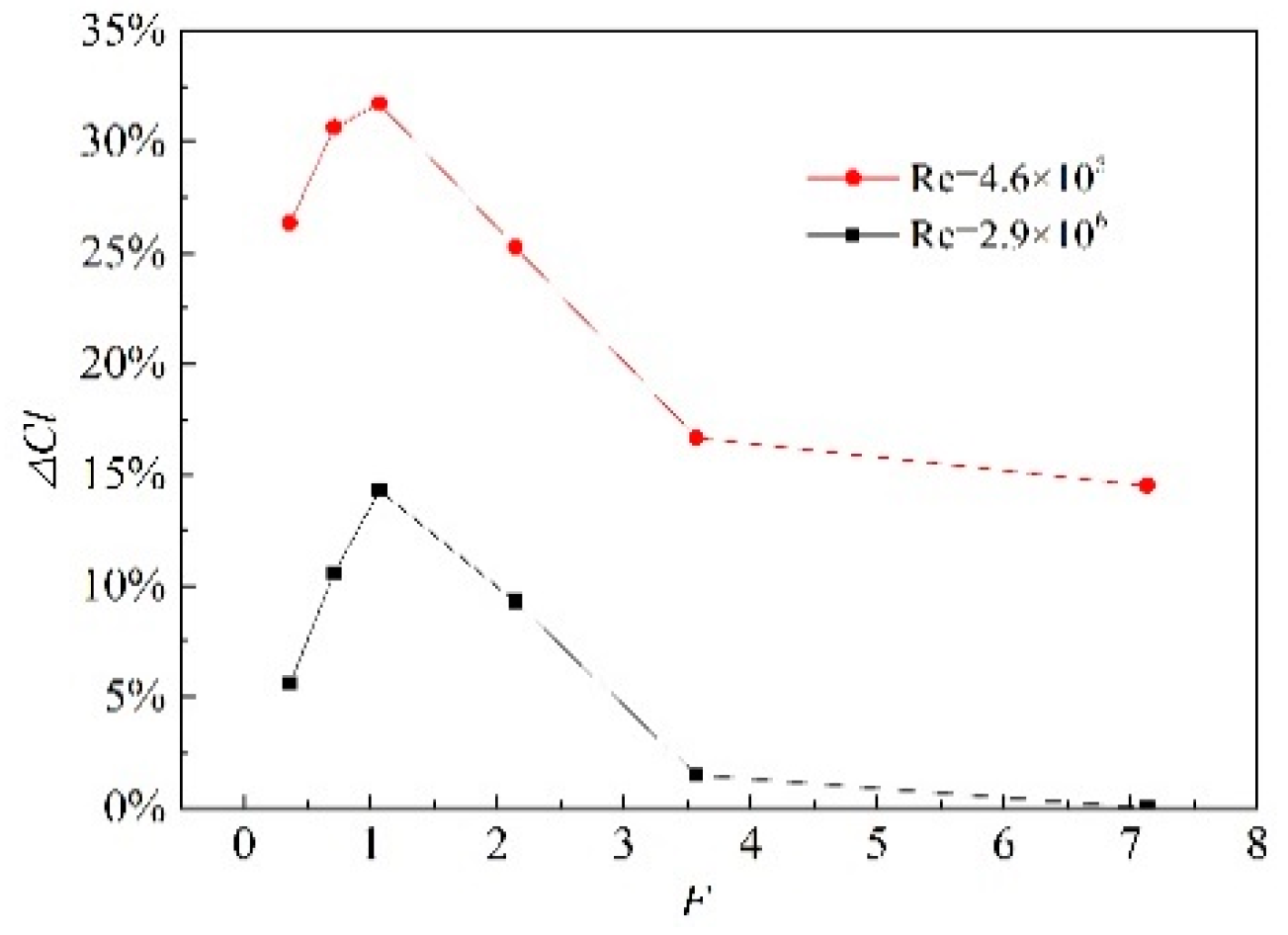
3.2. Force Characteristics
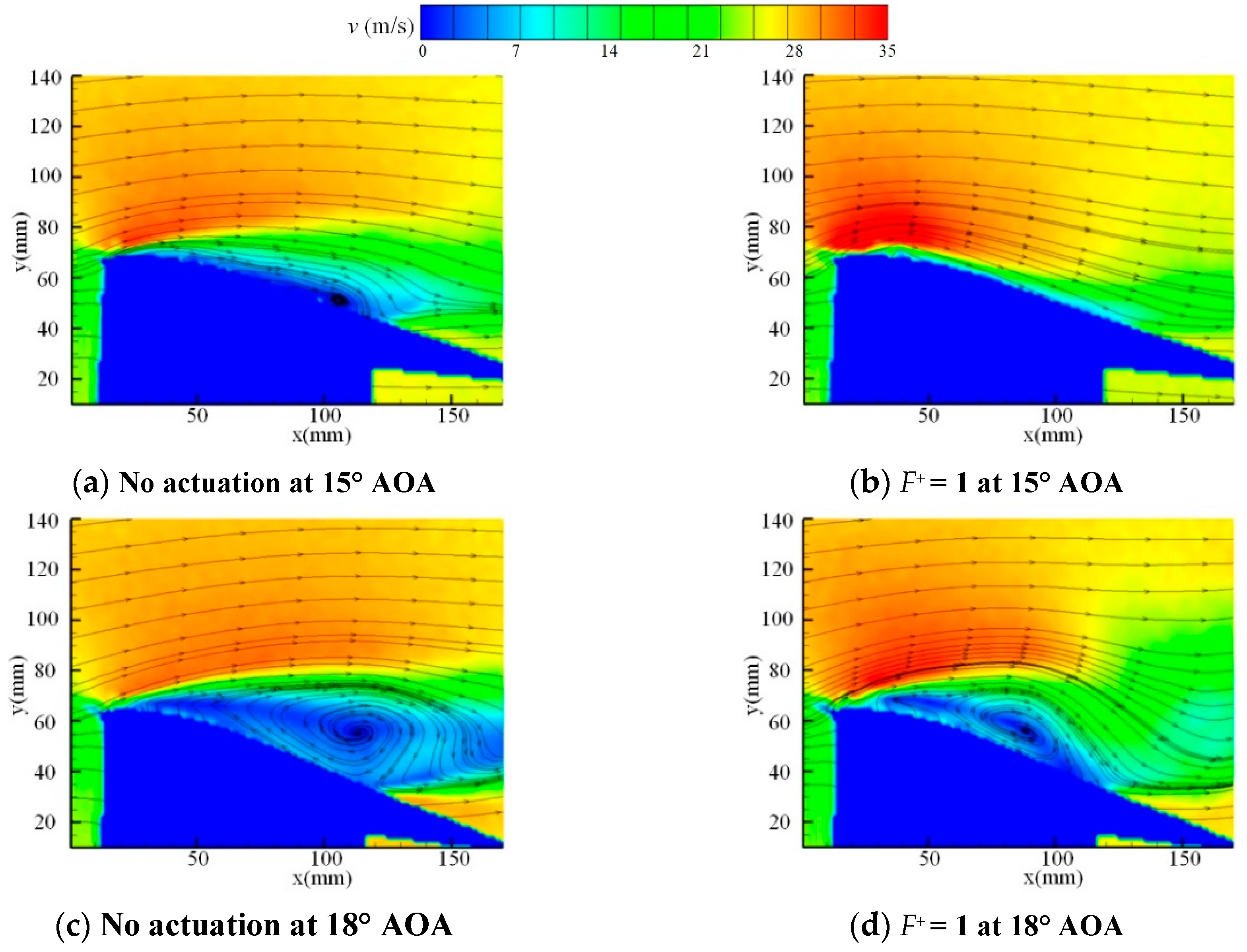
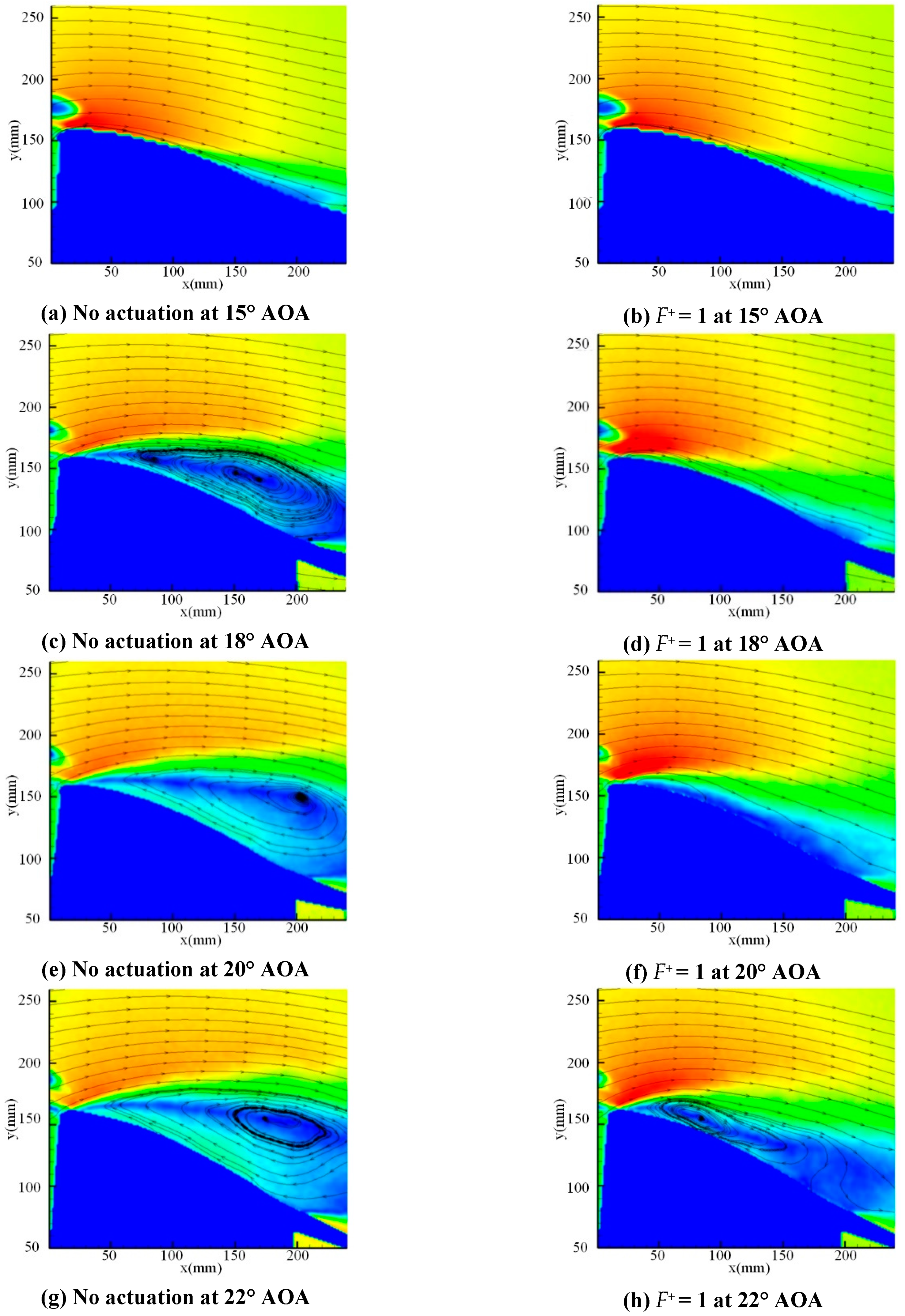
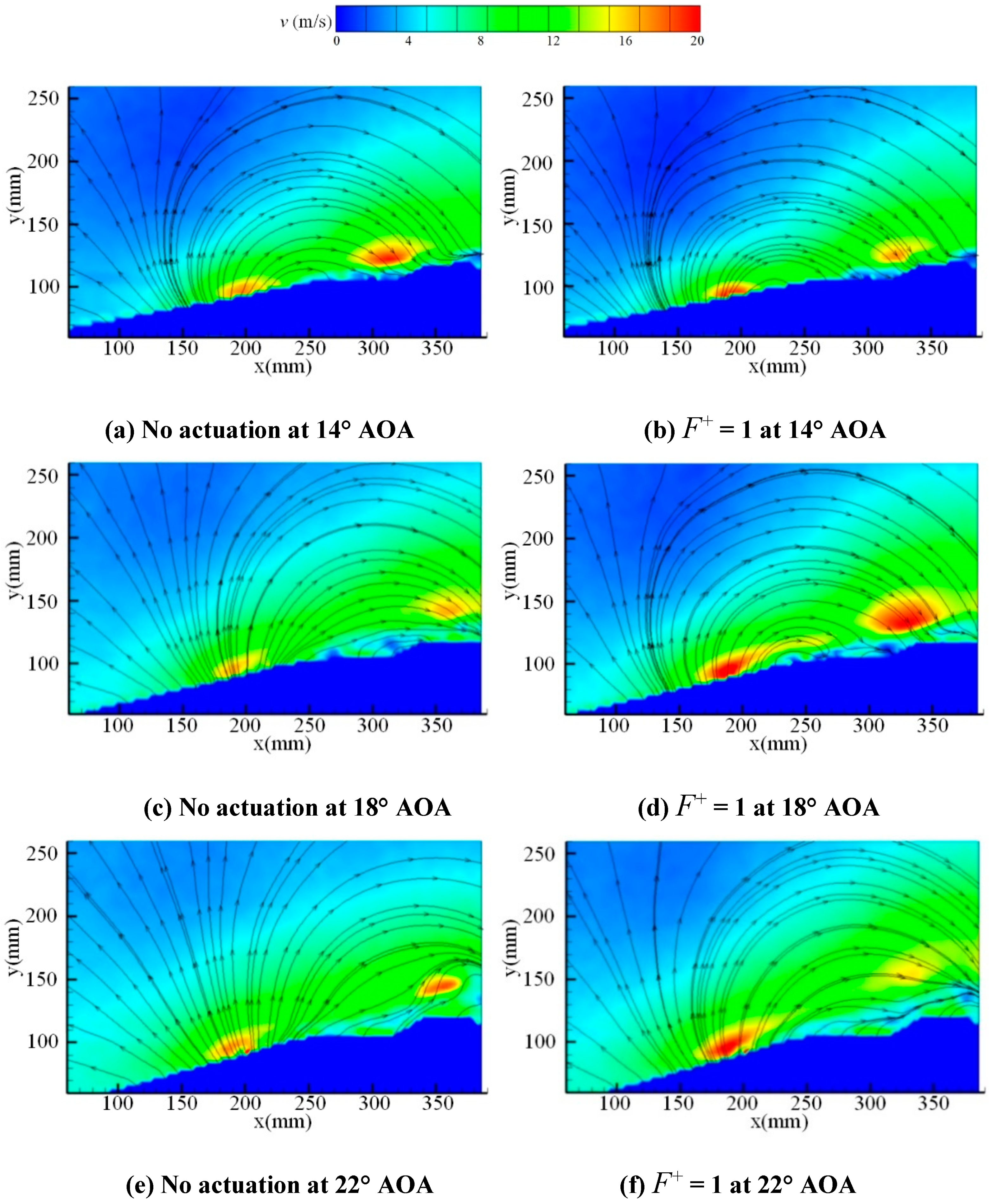
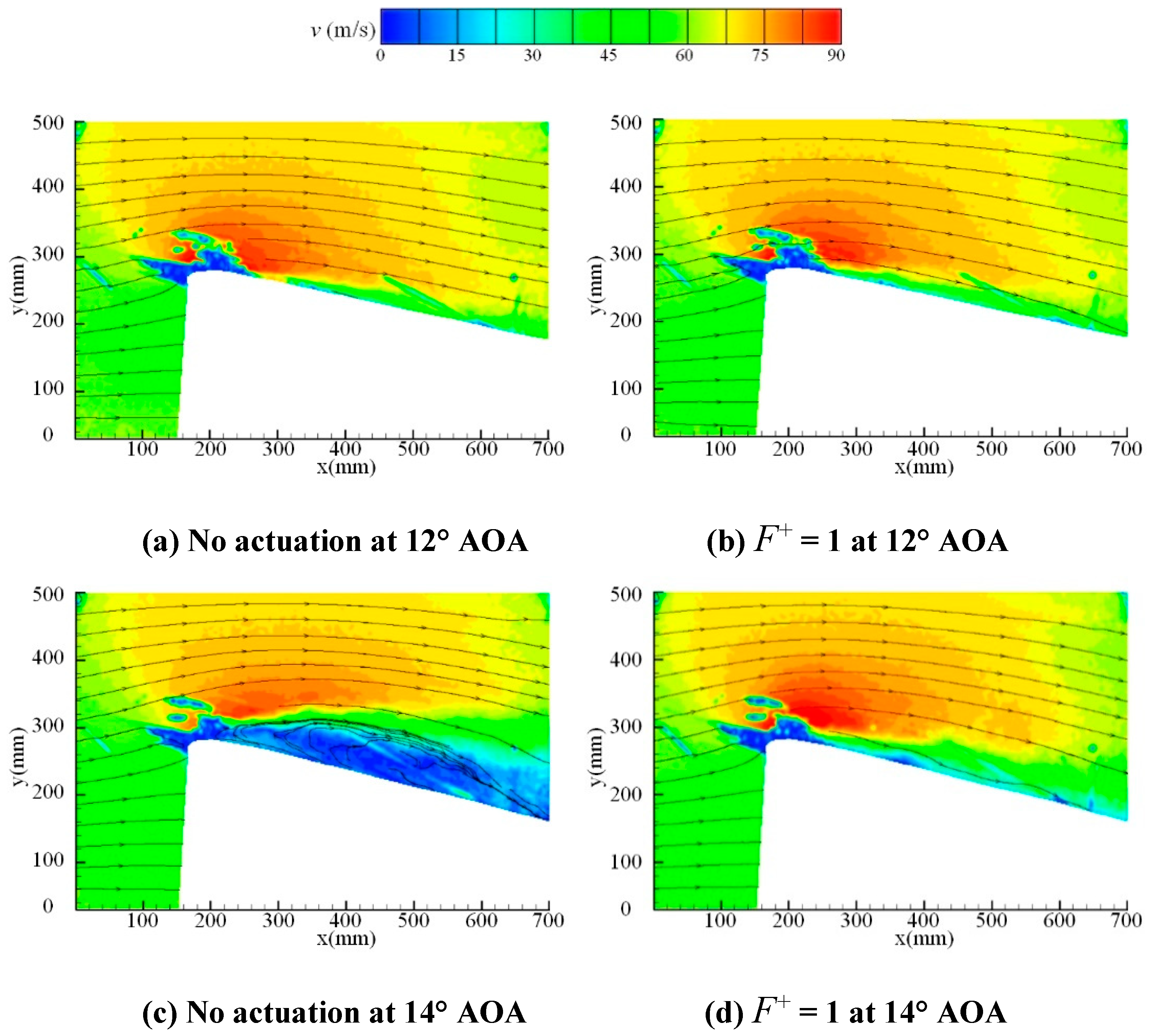
3.3. Flow Field Characteristics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, F. The Comparison of Aerodynamic and Stability Characteristics between Conventional and Blended Wing Body Aircraft. Master’s Thesis, Cranfield University, Cranfield, UK, 2012. [Google Scholar]
- Patil, M.J.; Hodges, D.H. Flight Dynamics of Highly Flexible Flying Wings. J. Aircr. 2006, 43, 1790–1799. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Z.; Xu, X.P.; Wang, H.B. Comparison on aerodynamic and stealthy performance of flying wing unmanned aerial vehicle with three conformal intake inlets. J. Aerosp. Power 2015, 30, 1651–1660. [Google Scholar]
- Chen, S.; Lyu, Z.; Kenway, G.K.; Martins, J.R. Aerodynamic Shape Optimization of the Common Research Model Wing-Body-Tail Configuration. In Proceedings of the AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Nangia, R.; Palmer, M. Flying-Wings (Blended Wing Bodies) with Aft & Forward Sweep, Relating Design Camber & Twist to Longitudinal Control. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference & Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar]
- Mardanpour, P.; Richards, P.W.; Nabipour, O.; Hodges, D.H. Effect of multiple engine placement on aeroelastic trim and stability of flying wing aircraft. J. Fluids Struct. 2014, 44, 67–86. [Google Scholar] [CrossRef]
- Huang, A.; Folk, C.; Silva, C.; Christensen, B.; Chen, Y.F.; Ho, C.M.; Jiang, F.; Grosjean, C.; Tai, Y.C. Applications of MEMS devices to delta wing aircraft: From concept development to transonic flight test. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar]
- Roos, F.W. Microblowing for High-Angle-of-Attack Vortex Flow Control on a Fighter Aircraft. J. Aircr. 2001, 38, 454–457. [Google Scholar] [CrossRef]
- Patel, M.P.; Ng, T.T.; Vasudevan, S.; Corke, T.C.; He, C. Plasma Actuators for Hingeless Aerodynamic Control of an Unmanned Air Vehicle. J. Aircr. 2007, 44, 1264–1274. [Google Scholar] [CrossRef]
- Su, Z.; Li, J.; Liang, H.; Zheng, B.R.; Wei, B.; Chen, J.; Xie, L.K. UAV flight test of plasma slats and ailerons with microsecond dielectric barrier discharge. Chin. Phys. B 2018, 27, 459–468. [Google Scholar] [CrossRef]
- Hsiao, F.B.; Liu, C.F.; Shyu, J.Y. Control of wall-separated flow by internal acoustic excitation. AIAA J. 2012, 28, 1440–1446. [Google Scholar] [CrossRef]
- Krishnappa, S.; Jogi, N.; Nguyen, L.D.; Gudmundsson, S.; MacKunis, W.T.; Golubev, V.V. Towards Experimental Validation of Robust Control of Gust-induced Airfoil Limit Cycle Oscillations Using Synthetic Jet Actuators. In Proceedings of the AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Zong, H.; Kotsonis, M. Effect of slotted exit orifice on performance of plasma synthetic jet actuator. Exp. Fluids 2017, 58, 17. [Google Scholar] [CrossRef]
- Campbell, J.F. Augmentation of Vortex Lift by Spanwise Blowing. J. Aircr. 1976, 13, 727–732. [Google Scholar] [CrossRef]
- Joseph, P.; Amandolese, X.; Edouard, C.; Aider, J.L. Flow control using MEMS pulsed micro-jets on the Ahmed body. Exp. Fluids 2013, 54, 1–12. [Google Scholar] [CrossRef]
- Little, J. High-Lift Airfoil Separation Control with Dielectric Barrier Discharge Plasma Actuators. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2010. [Google Scholar]
- Yun, W.U.; Yinghong, L.I. Progress in Research of Plasma-assisted Flow Control, Ignition and Combustion. High Volt. Eng. 2014, 40, 2024–2038. [Google Scholar]
- Little, J.; Takashima, K.; Nishihara, M.; Adamovich, I.; Samimy, M. Separation Control with Nanosecond-Pulse-Driven Dielectric Barrier Discharge Plasma Actuators. AIAA J. 2012, 50, 350–365. [Google Scholar] [CrossRef]
- Tang, M.; Wu, Y.; Wang, H.; Guo, S.; Sun, Z.; Sheng, J. Characterization of transverse plasma jet and its effects on ramp induced separation. Exp. Therm. Fluid Sci. 2018, 99, 584–594. [Google Scholar]
- Zheng, B.; Xue, M.; Ke, X.; Ge, C.; Wang, Y.; Liu, F.; Luo, S. Unsteady Vortex Structure Induced by a Trielectrode Sliding Discharge Plasma Actuator. AIAA J. 2018, 57, 467–471. [Google Scholar] [CrossRef]
- Sidorenko, A.; Budovsky, A.; Pushkarev, A.; Maslov, A. Flight testing of DBD plasma separation control system. In Proceedings of the AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Wang, J.; Li, Y.; Xing, F. Investigation on oblique shock wave control by arc discharge plasma in supersonic airflow. J. Appl. Phys. 2009, 106, 073307. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control. Exp. Fluids 2014, 55, 1846. [Google Scholar] [CrossRef]
- Roupassov, D.V.; Nikipelov, A.A.; Nudnova, M.M.; Starikovskii, A.Y. Flow Separation Control by Plasma Actuator with Nanosecond Pulsed-Periodic Discharge. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar]
- Durasiewicz, C.; Singh, A.; Little, J. A Comparative Flow Physics Study of Ns-DBD vs. Ac-DBD Plasma Actuators for Transient Separation Control on a NACA 0012 Airfoil. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Sevant, N.E.; Bloor, M.I.G.; Wilson, M.J. Aerodynamic Design of a Flying Wing Using Response Surface Methodology. J. Aircr. 2015, 37, 562–569. [Google Scholar] [CrossRef]
- Huber, K.; Schutte, A.; Rein, M. Numerical Investigation of the Aerodynamic Properties of a Flying Wing Configuration. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Xu, X.; Zhou, Z. Analytical study on the synthetic jet control of asymmetric flow field of flying wing unmanned aerial vehicle. Aerosp. Sci. Technol. 2016, 56, 90–99. [Google Scholar] [CrossRef]
- Han, M.; Li, J.; Niu, Z.; Liang, H.; Zhao, G.; Hua, W. Aerodynamic performance enhancement of a flying wing using nanosecond pulsed DBD plasma actuator. Chin. J. Aeronaut. 2015, 28, 377–384. [Google Scholar] [CrossRef]
- Yao, J.K.; Zhou, D.J.; He, H.B.; He, C.J.; Shi, Z.W.; Du, H. Experimental investigation of lift enhancement for flying wing aircraft using nanosecond DBD plasma actuators. Plasma Sci. Technol. 2017, 19, 11–18. [Google Scholar] [CrossRef]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Liang, H.; Han, M.; Niu, Z.; Wei, B.; Su, Z.; Tang, B. Experimental Study on Plasma Flow Control of Symmetric Flying Wing Based on Two Kinds of Scaling Models. Symmetry 2019, 11, 1261. https://doi.org/10.3390/sym11101261
Xie L, Liang H, Han M, Niu Z, Wei B, Su Z, Tang B. Experimental Study on Plasma Flow Control of Symmetric Flying Wing Based on Two Kinds of Scaling Models. Symmetry. 2019; 11(10):1261. https://doi.org/10.3390/sym11101261
Chicago/Turabian StyleXie, Like, Hua Liang, Menghu Han, Zhongguo Niu, Biao Wei, Zhi Su, and Bingliang Tang. 2019. "Experimental Study on Plasma Flow Control of Symmetric Flying Wing Based on Two Kinds of Scaling Models" Symmetry 11, no. 10: 1261. https://doi.org/10.3390/sym11101261
APA StyleXie, L., Liang, H., Han, M., Niu, Z., Wei, B., Su, Z., & Tang, B. (2019). Experimental Study on Plasma Flow Control of Symmetric Flying Wing Based on Two Kinds of Scaling Models. Symmetry, 11(10), 1261. https://doi.org/10.3390/sym11101261





