1. Introduction
The spectacular success of quantum optics [
1] is based to a considerable extent on the fact that the light quanta do not interact among themselves. On the other hand, the interaction of quantized radiation with matter is quite complicated because even the simplest model, an atomic two-level system coupled to a single radiation mode via a dipole term, does not conserve the excitation number. This model, the quantum Rabi model (QRM) [
2,
3,
4], is of central importance as basically all experimental observations in the field can be traced to a variant of it [
5]. The QRM Hamiltonian reads
Here,
and
a are the creation and annihilation operators of the bosonic mode and energy is measured in units of frequency (
).
denotes the energy splitting of the two-level system, which is coupled linearly to the electric field (
) with interaction strength
g. The QRM has just two degrees of freedom, one continuous (the radiation mode) and one discrete (the two-level system), described by Pauli matrices
. Even better known than the QRM is a famous approximation to it, the Jaynes–Cummings model (JCM),
with
. In this model, the “counter-rotating terms”
are missing, so that it conserves the excitation number
and can be solved analytically in closed form [
4]. The QRM, including these terms, was long considered to be unsolvable by analytical means and also non-integrable [
6], until its exact solution was discovered [
7].
The JCM provides very good agreement with experiments in atom optics where the dipole coupling strength is many orders of magnitude smaller than the mode frequency. Its characteristic feature manifests itself for example in the vacuum Rabi splitting, observable if the coupling is larger than the cavity decay rates. This was achieved in an experiment from 1992 with a ratio
between dipole coupling and mode frequency [
8]. Since then, there has been tremendous progress in the experimental techniques to enhance the coupling strength between light and matter within a wide range of different platforms, ranging from cavity quantum electrodynamics, using optical and microwave frequencies, to circuit QED, which implements the radiation mode in a transmission line, while the coupled two-level system is realized in various ways, e.g. via superconducting qubits or quantum dots, as excitonic or intersubband polaritons [
9,
10]. Within the last 27 years, the ratio
has been raised by eight orders of magnitude, finally reaching the so-called deep strong coupling regime (DSC) [
11],
within a circuit QED framework [
12].
For these coupling strengths, the JCM is no longer applicable and gives even qualitatively wrong results. Already for
, called the perturbative ultra-strong coupling regime (pUSC) [
10], there are measurable deviations [
13], although these can still be accounted for by the Bloch–Siegert Hamiltonian [
14,
15], a solvable extension of the JCM. For
, one enters the non-perturbative ultra-strong coupling regime (USC), where also the Bloch–Siegert Hamiltonian fails.
Part of the interest in the USC and DSC regimes originates in the natural identification of the two-level system with a qubit, the building block of quantum information theory [
16]. The strong coupling between the qubit and light field allows for novel technologies such as nondestructive readout [
17] and remote entanglement [
18] besides the possibility to implement quantum error correcting codes [
19]. However, the strong coupling regimes are also fascinating from the viewpoint of fundamental research, because the light–matter system behaves in unexpected and sometimes counter-intuitive ways: the vacuum state contains virtual photons [
20] and in the DSC the Purcell effect disappears [
21] while the standard collapse and revival dynamics of the two-level system becomes dominated by the mode frequency [
11].
2. The Rotating-Wave Approximation and Its Symmetry
These developments have renewed the interest in the analytical understanding of the QRM beyond a brute-force diagonalization of the Hamiltonian in a truncated, finite-dimensional Hilbert space. To this end, several improvements of the rotating-wave approximation underlying the JCM have been proposed [
22,
23,
24] which should be reliable even for strong coupling. However, all methods, while being quantitatively in reasonable agreement with the numerical diagonalization, deviate qualitatively from it by predicting degeneracies absent in the true spectrum of the QRM.
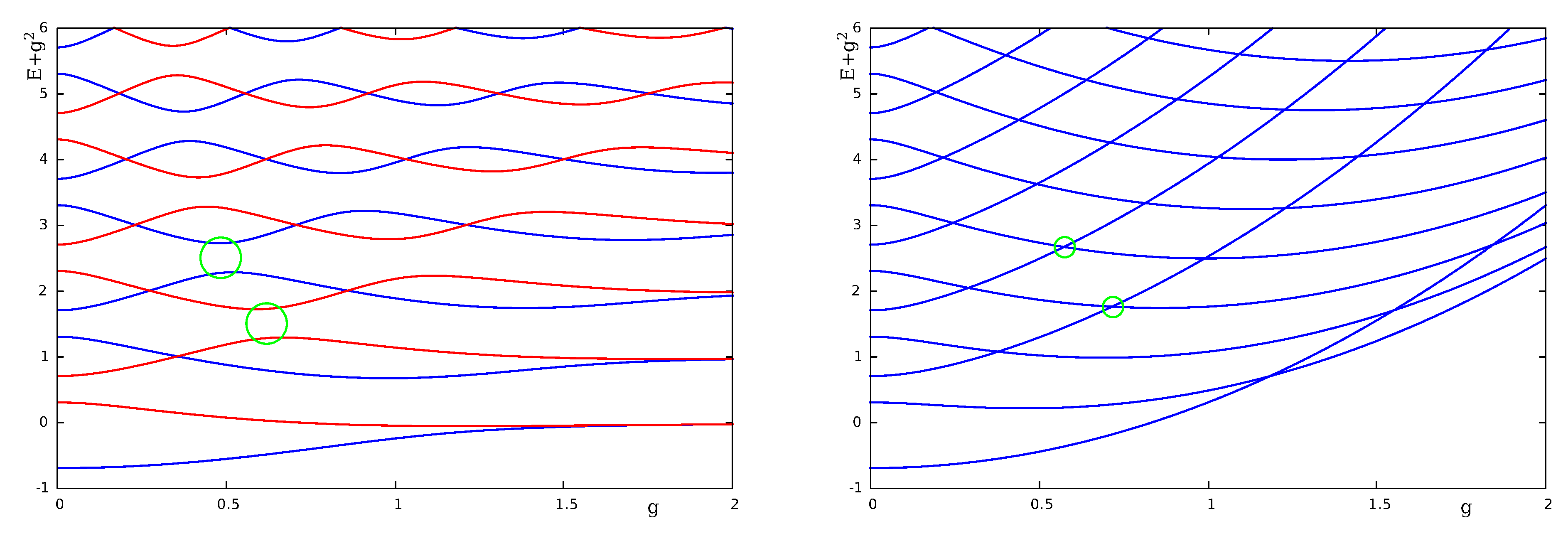
The JCM reproduces the exact spectrum with great accuracy almost up to the first level crossings (counted from the left of the spectral graph in
Figure 1), which is a true crossing, actually the first Juddian solution [
25]. However, the next crossings of the JCM which appear for
(marked with small green circles in
Figure 1) are avoided in the QRM. The reason is the much larger symmetry of the JCM compared to the QRM. Because
, each eigenstate of the JCM is also an eigenstate of
and labeled by corresponding eigenvalue
of
. The eigenspace of
with fixed
for
is two-dimensional while the ground state of the JCM (for sufficiently small
g) is the unique state
with
. In other words, the Hilbert space
decays into a direct sum of dynamically invariant subspaces
where each
is two-dimensional.
Thus, the eigenstates with
can be labeled by two quantum numbers, the first gives the eigenvalue of
, and the second takes just two values 0 and 1, corresponding to the two states in
, forming the so-called Jaynes–Cummings doublets. As the infinitely many subspaces are dynamically disconnected for all values of
g, the energies
and
may become degenerate whenever
. The two crossings selected in
Figure 1 are degeneracies between the JC-states
and
and between
and
, respectively. In contrast to these degeneracies that are lifted by the counter-rotating terms, the crossings between the JC-states
and
are also present in the spectral graph of the QRM.
Because the algebra
generated by
is infinite dimensional, the operators
are linearly independent for all
. However, because the spectrum of
is integer-valued, we have
and the
form an infinite dimensional representation of the continuous compact group
in
with composition law
. We have for any
the relation
, as
This means that the “rotating” interaction term
is invariant for the whole group but the “counter-rotating” term
is invariant only for
. Indeed, the set
forms a discrete subgroup of
. Because
it is the group with two elements
(the sign of the “parity” operator
is chosen here to conform with the convention in [
7]). The QRM is invariant under the finite group
,
.
The character group of
is
, therefore each one-dimensional irreducible representation of
is labeled by an integer
. In the representation in Equation (
4), the space
spanned by the vectors
and
for
is invariant and
acts on it as
. Therefore, the decomposition in Equation (
3) corresponds to the irreducible representations of
in
for integers
and the spectral problem for the JCM reduces to the diagonalization of
-matrices in the spaces
[
4]. If one parameter of the model is varied, say the coupling
g, the spaces
do not change, only the eigenvectors
,
and the eigenenergies
. The spectral graph as function of
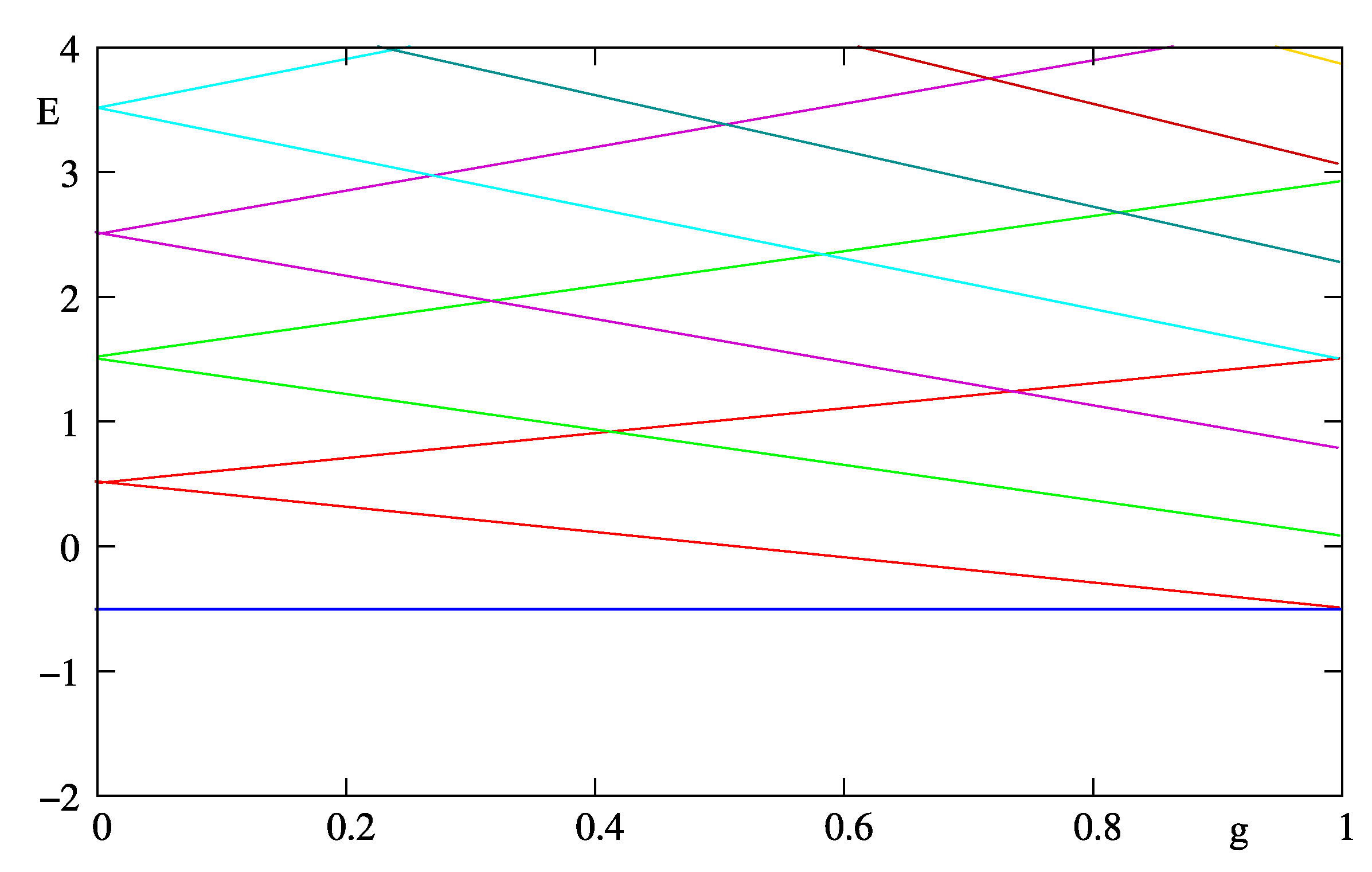
g consists of infinitely many ladders with two rungs, intersecting in the
-plane as shown for
in
Figure 2.
We find that the
continuous symmetry of the JCM allows to classify the eigenstates according to infinitely many irreducible representations, thereby effectively eliminating the
continuous (bosonic) degree of freedom, the radiation mode. The remaining discrete degree of freedom (the two-level system) has a two-dimensional Hilbert space and, after application of the
-symmetry, the Hamiltonian acts non-trivially only in the two-dimensional
. The JCM possesses an additional conserved quantity,
, besides the Hamiltonian
. As it has two degrees of freedom, it is therefore integrable according to the classical criterion by Liouville [
26], because the number of phase-space functions (operators) in involution equals the number of degrees of freedom.
What about the QRM? We have
, but the associated symmetry is discrete and has only two irreducible representations, corresponding to the eigenvalues
of
. It follows that the Hilbert space decomposes into the direct sum
Both
are infinite dimensional and the spectral problem appears as complicated as before. However, in each parity subspace (usually called parity chain [
11]), the discrete degree of freedom has been eliminated and only the continuous degree of freedom remains. According to the standard reasoning, a conservative system with only one degree of freedom is integrable. From this point of view, advocated in [
7], the QRM is integrable because the
discrete -symmetry has eliminated the
discrete degree of freedom. This is only possible because the number of irreducible representations of
matches precisely the dimension of the Hilbert space
of the two-level system. Other models with one continuous and one discrete degree of freedom such as the Dicke models with Hilbert space
are not integrable according to this criterion, because their
-symmetry is not sufficient to reduce the model to a single continuous degree of freedom if
[
27]. On the other hand, the continuous symmetry introduced by the rotating-wave approximation is so strong that it renders the Dicke model integrable for all
n [
28].
The criterion on quantum integrability proposed in [
7] is especially suited to systems with a single continuous and several discrete degrees of freedom and states then that a system is quantum integrable if each eigenstate can be labeled uniquely by a set of quantum numbers
where
corresponds to the continuous degree of freedom and the number of different tuples
equals the dimension
d of the Hilbert space belonging to the discrete degrees of freedom. This unique labeling allows then for degeneracies between states belonging to different tuples
, which characterize the different decoupled subspaces
. Within the space
, which is infinite dimensional and isomorphic to
, the states are labeled with the single number
n and level crossings are usually avoided between states
and
if no continuous symmetry is present. This happens in the QRM, where the spectral graph is composed of two ladders each with infinitely many rungs (see
Figure 1). The situation is in some sense dual to the JCM, where we have infinitely many intersecting ladders with two rungs. The stronger symmetry of the JCM renders it therefore superintegrable [
29].
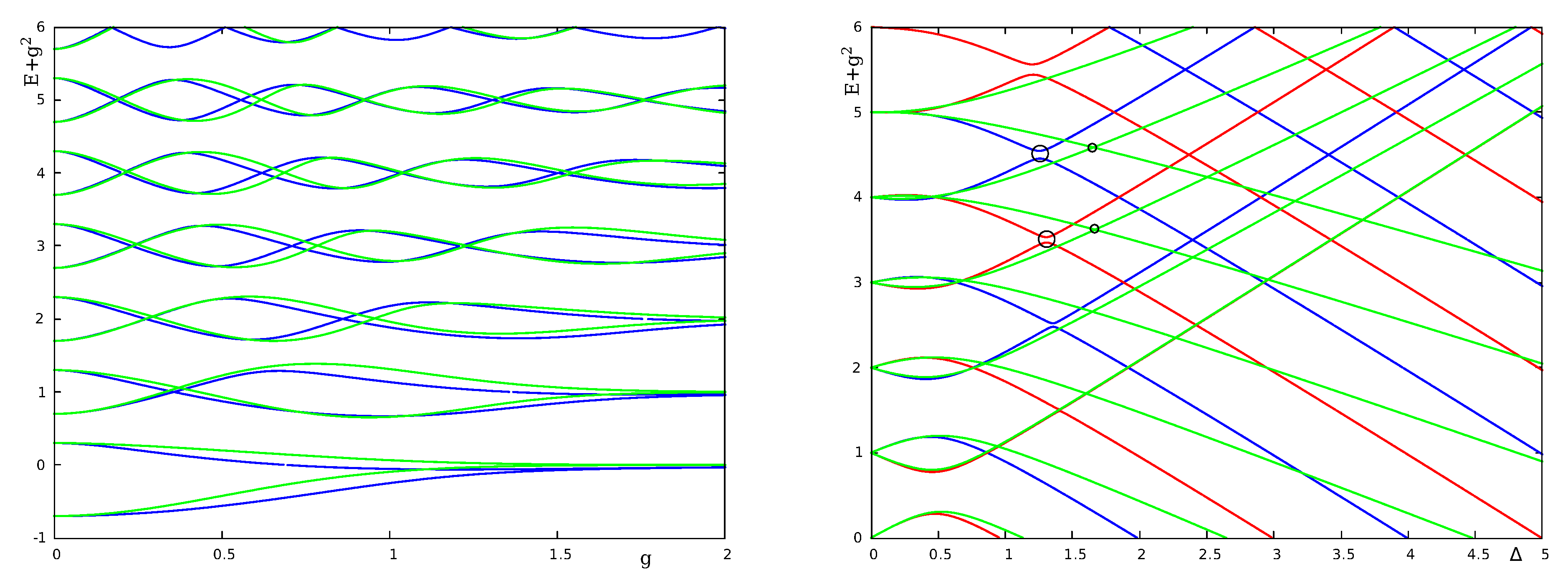
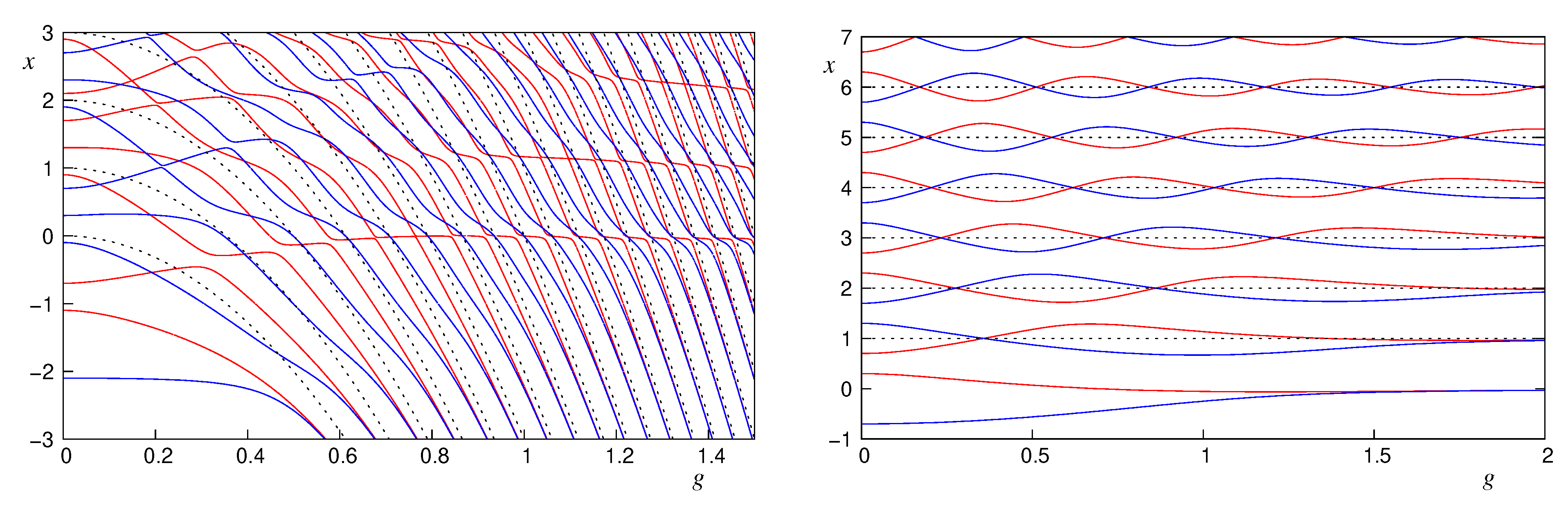
With a stronger symmetry, more degeneracies are to be expected. Especially going from a discrete to a continuous symmetry by applying the rotating-wave approximation inevitably introduces unphysical level crossings in the spectral graph. This applies especially to those methods which apply the rotating-wave approximation on top of unitary transformations such as the GRWA [
22,
23,
24]. In
Figure 3, it is seen that the spectral graph provided by the GRWA indeed reproduces correctly all level crossings of the QRM in the
-plane but exhibits unphysical level crossings in the
-plane.
3. Integrability of Systems with Less Than Two Continuous Degrees of Freedom
The notion of integrability in quantum systems is still controversial [
30] and based mainly either on the Bethe ansatz [
31] or on the statistical criterion by Berry and Tabor [
32]. While it was demonstrated by Amico et al. [
6] and Batchelor and Zhou [
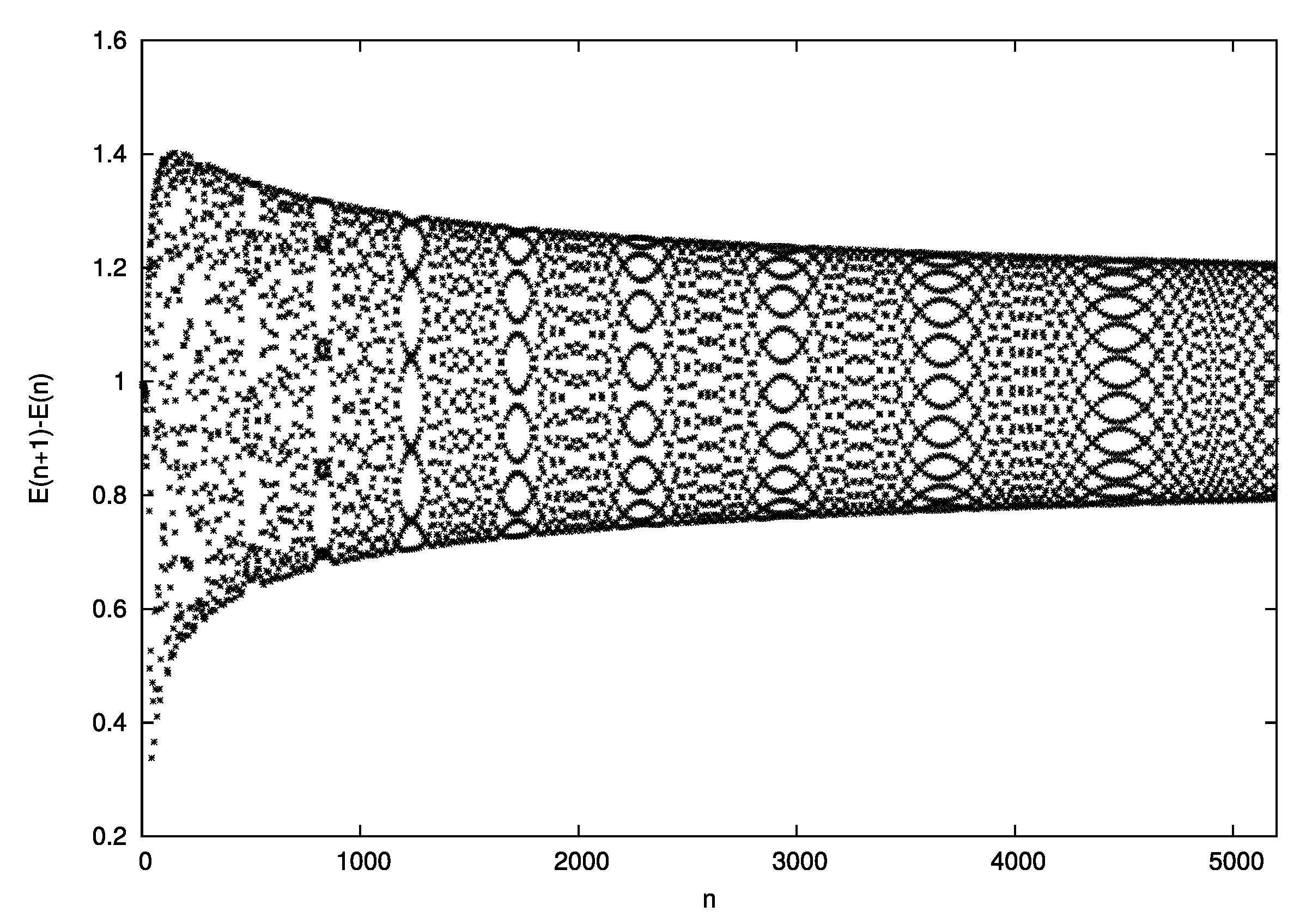
33] that the QRM is not amenable to the Bethe ansatz, its level statistics deviate markedly from the Poissonian form for the average distance
between energy levels. According to Berry and Tabor [
32], the distribution of
in a quantum integrable system should read
, where
is the average level distance in a given energy window. This distribution is not present in the QRM [
34], whose level distances are shown in
Figure 4 up to
.
Due to this deviation from the expected behavior for integrable systems and likewise from the Wigner surmise [
35], it was unclear whether the QRM belongs to the integrable or chaotic systems [
34]. If the QRM is integrable as argued above, why does the Berry–Tabor criterion not apply? The reason lies in the fact that this criterion has been derived for classically integrable systems with
N continuous degrees of freedom, which can be quantized with the Bohr–Sommerfeld method. In this case the energy eigenvalues are labeled by
N integers
. The classical Hamiltonian can be written as an in general non-linear function of
N action variables
,
. Then the quantized energies read
where the
are Maslov indices. The level distance distribution follows then from the statistics of vectors
with integer entries belonging to the energy shell
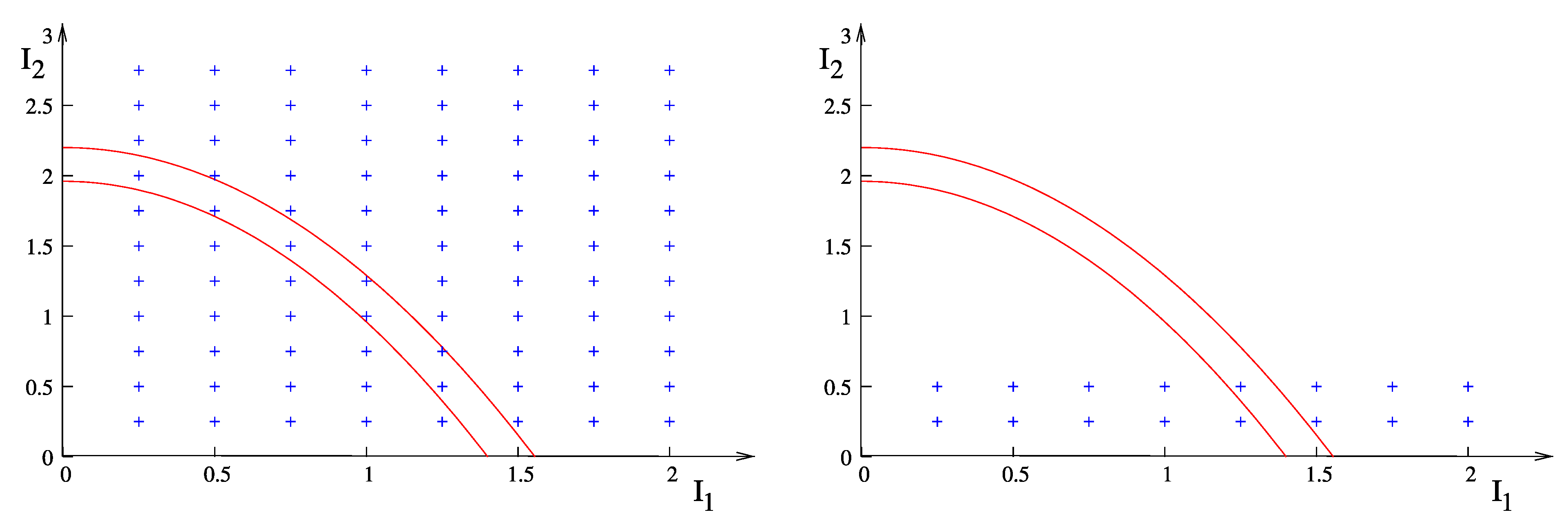
. This is shown for
in
Figure 5.
Berry and Tabor showed that the occurrences of the
in the shell
are essentially uncorrelated provided
is a non-linear function of its arguments and
.
is linear for linearly coupled harmonic oscillators [
32] and in this case the level statistics is not Poissonian. The criterion applies thus only to systems with at least two continuous degrees of freedom. If one of the degrees of freedom is discrete, the corresponding action variable takes only finitely many values. This has the same effect as a linear
. A deviation from Poissonian statistics would therefore be expected even if the QRM would be the quantum limit of a classically integrable system. However, this is not the case. The weak symmetry of the QRM may have a counterpart in the classical limit but then it would not suffice to make the classical model (which must have at least two continuous degrees of freedom) integrable. The QRM is integrable only as a genuine quantum model. The Hilbert space of the quantum degree of freedom must not be larger than two—otherwise the model becomes non-integrable similar to the Dicke model [
27].
Figure 6 shows on the left the spectral graph of the Dicke model for three qubits (which is also exactly solvable by the method described in the next section) with Hamiltonian
where
an
are generators of
in the spin-
representation. The QRM spectrum is depicted on the right. It is apparent that most of the regular features of the Rabi spectrum are absent in the Dicke spectrum, although it has the same
-symmetry.
4. The Global Spectrum of the QRM
As shown in
Figure 6, the spectral graph of the QRM has an intriguingly simple structure. The level lines cross only for different parity on the so-called “baselines” with
for
. Moreover, the degenerate states are quasi-exact solutions whose wave function can be expressed through polynomials [
25]. These features can be explained in a unified way by the properties of the spectral determinant or
G-function of the QRM,
, whose zeroes give the exact eigenvalues of the Hamiltonian in each parity chain [
7]. The
G-function of the QRM is given as the following function (
),
where the
are defined recursively,
with
and initial condition
. Note that
. The
G-functions can be written in terms of confluent Heun functions [
36], namely
where
denotes the derivative of
with respect to
z. The parameters are given as [
37],
From Equations (
11) and (
12) one may deduce that
has simple poles at
and therefore its zeroes are usually not located at integers but pinched between the poles.
can be written as
where
is analytic in
x and
for small
. The coefficients
vanish for
. Indeed, the sign of
determines whether the zero of
in the vicinity of
is located to the right or to the left of
n in the two adjacent intervals
and
. This leads to the following conjecture about the distribution of zeroes of
:
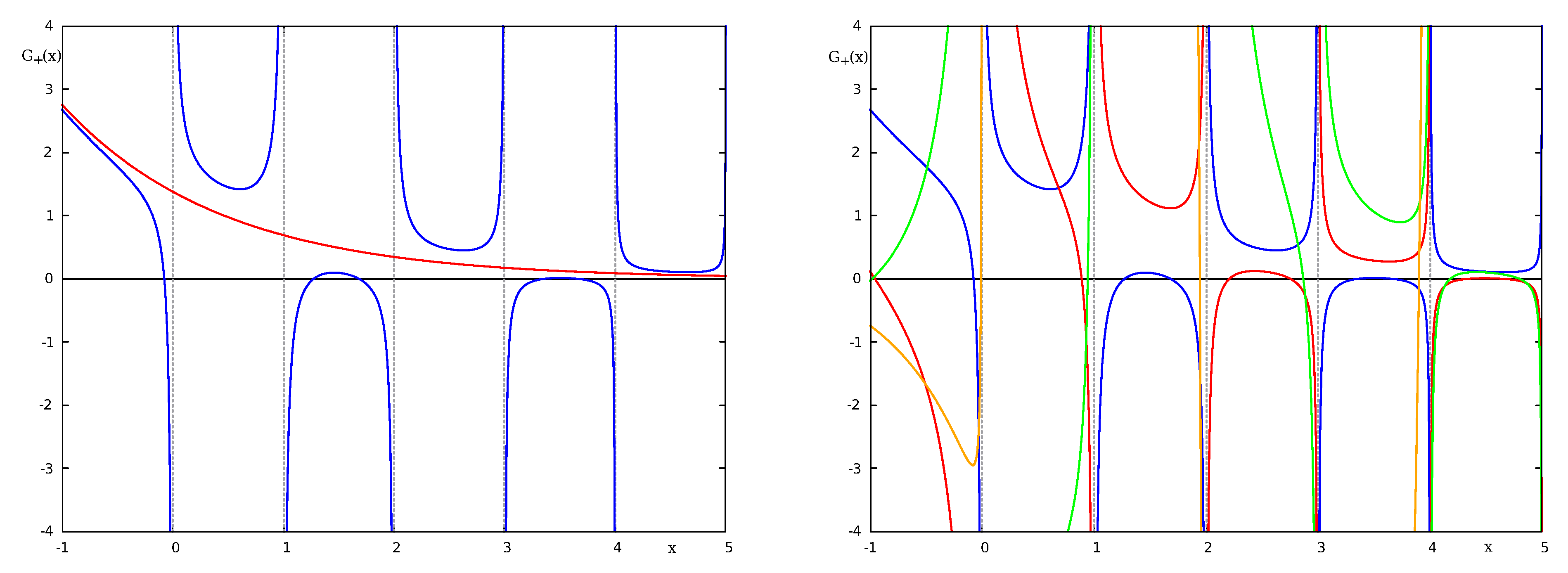
Conjecture 1. The number of zeros in each interval , is restricted to be 0, 1, or 2. Moreover, an interval with two roots of can only be adjacent to an interval with one or zero roots; in the same way, an empty interval can never be adjacent to another empty interval.
Figure 7 shows on the left
for
and
together with the analytic approximation for
. The
G-conjecture appears to be valid for arbitrary
as is shown on the right of
Figure 7.
The
G-conjecture has not yet been proven in general, although it is possible to prove it for small
, which, however, is equivalent with perturbation theory in the operator
, the natural bounded perturbation of the QRM, in contrast to the unbounded coupling operator
. Preliminary steps in the direction of a general proof are given in [
38].
Assuming the
G-conjecture to be valid also for generalizations of the QRM showing the “spectral collapse” phenomenon [
39] allows deriving the continuous spectrum at the collapse point [
40], where numerical methods fail due to the proliferation of low-lying eigenstates.
The
G-functions are derived by using the analyticity properties of the eigenfunctions in the Bargmann space, which also explains the degenerate spectrum (the Juddian solutions) in a natural way simply by doing a Frobenius analysis of the relevant differential equations in the complex domain [
7]. Let
denote
restricted to the subspace with positive parity. In the Bargmann representation, the Schrödinger equation
is equivalent to a linear but non-local differential equation in the complex domain,
With the definition
and
, we obtain the coupled local system,
This system has two regular singular points at
and an (unramified) irregular singular point of s-rank two at
[
36]. With
, the Frobenius exponents of
at the regular singular point
g (
) are
(
), while for
the exponents at
g (
) are
(
) [
41]. The eigenfunctions have to be analytic in all of
, therefore the spectrum of
separates naturally in a
regular part with
and the
exceptional part with
[
7]. For general values of
, the exceptional part is empty and all eigenstates are regular.
For
, one of the two linearly independent solutions for
is not admissible. That means that
will in general develop a branchpoint with exponent
at
even if it is analytic with exponent 0 at
.
vanishes at those
x for which both
and
have exponent 0 at
g and
, rendering
analytic. To find the exceptional spectrum, we define
,
. Then,
A Frobenius solution with exponent 0 at
may be written as
. Then, the integration of Equation (
18) yields
If
,
c must be zero. This determines
uniquely in terms of
and the
are thus given by the recurrence in Equation (
11), leading to the regular spectrum.
Now, let us assume
. In this case, a solution for
analytic at
may be written as
because
[
41]. In this case, the
c in (
20) need not to be zero, the
satisfy still the recurrence in Equation (
11), but with initial condition
,
depending on
c.
reads then
Because
c multiplies both
and
, it may be set to
. The solution will have parity
and be analytic in all of
, if the
G-function
vanishes for parameters
. One sees immediately that
entails
, thus this state is non-degenerate if it exists. States of this type comprise the non-degenerate exceptional spectrum [
42] and are characterized by a lifting of the pole of
(resp.
) at
for special values of
, satisfying
. The exceptional
G-functions in Equation (
22) are given in terms of absolutely convergent series expansions as the regular
G-functions in Equation (
10). The other possible Frobenius solution at
,
, leads to
where the
for
are determined with the same recurrence as above and initial conditions
,
, which fixes the overall factor of the wavefunction. This solution is only independent from the first and admissible if
and
. If so, the
for
are computed recursively via Equation (
11) with initial conditions
,
. Parity symmetry determines now the constant
,
Equation (
24) imposes no additional constraint on
besides
, which is therefore sufficient for the presence of a doubly degenerate solution with
. Because
, this type of degenerate solution cannot occur for
, whereas non-degenerate solutions with
are possible.
For the choice
, one of the degenerate solutions reads
The
are polynomials in
y, therefore Equation (
25) is a quasi-exact solution with polynomial wave function, apart from the factor
multiplying
in
. This quasi-exact solution is not a parity eigenstate but a linear combination of them. The parity eigenstates are in turn a linear combination of Equation (
25) and states having the form of non-degenerate exceptional solutions. It is clear that the possibility of quasi-exact solutions in the QRM depends on the fact that the coefficients of the Frobenius solutions are determined by a three-term recurrence relation (Equation (
11)). Otherwise, the single free integration constant
c would not suffice to break off the series expansions for
at finite order. This is the reason a quasi-exact spectrum does not exist in the isotropic Dicke model [
27] but is possible in the anisotropic Dicke models, where more parameters can be adjusted to eliminate the higher orders in expansions given by recurrence relations with more than three terms [
43].