Abstract
As it is often unavoidable to obtain incomplete data in life testing and survival analysis, research on censoring data is becoming increasingly popular. In this paper, the problem of estimating the entropy of a two-parameter Lomax distribution based on generalized progressively hybrid censoring is considered. The maximum likelihood estimators of the unknown parameters are derived to estimate the entropy. Further, Bayesian estimates are computed under symmetric and asymmetric loss functions, including squared error, linex, and general entropy loss function. As we cannot obtain analytical Bayesian estimates directly, the Lindley method and the Tierney and Kadane method are applied. A simulation study is conducted and a real data set is analyzed for illustrative purposes.
1. Introduction
Lomax distribution, also conditionally known as Pareto Type II distribution, is a heavy tail distribution widely used in reliability analysis, life testing problems, information theory, business, economics, queuing problems, actuarial modeling and biological sciences. It is essentially a Pareto Type II distribution that has been shifted so that it is non-negative. Lomax distribution was first introduced in Reference [1]. Ahsanullah [2] derived some distributional proprieties and presented two types of estimates for the unknown parameters based on the record value for a sequence of Lomax distribution. Afaq [3] derived the Bayesian estimators of Lomax distribution under three different loss functions using Jeffery’s and an extension of Jeffery’s prior, and compared the Bayesian estimates with the maximum likelihood estimate by using mean squared error. Ismail [4] derived the maximum likelihood estimators and interval estimators of the unknown parameters under a step-stress model supposing that the time to failure has a Lomax distribution with failure-censoring and studied the optimal test designs.
The cumulative distribution function of Lomax distribution is given as follows:
The corresponding probability density function of Lomax distribution is given by:
One characteristic of Lomax distribution is that there are many distributions which have a close relationship with it. Lomax distribution is a special case of q-exponential distribution, generalized Pareto distribution, beta prime distribution and F distribution. Plus, it is a mixture of exponential distributions where the mixing distribution of the rate is a gamma distribution. Besides, there are many variants of Lomax distribution, such as the McDonald Lomax distribution with five parameters ([5]), gamma Lomax distribution ([6]) and weighted Lomax distribution ([7]). Apparently, Lomax distribution is of great importance in statistics and probability. Another special characteristic of Lomax distribution is that it plays an important role in information theory. Ahmadi [8] found that on the assumption that (X,Y) has a bivariate Lomax joint survival function, then the bivariate dynamic residual mutual information is constant.
Entropy, which is one of the most significant terms in statistics and information theory, was originally proposed by Gibbs in the thermodynamic system. Shannon [9] re-defined it and introduced the concept of entropy into information theory to quantitatively measure the uncertainty of information. Cover and Thomas [10] extended Shannon’s idea and defined differential entropy (or continuous entropy) of a continuous random variable X with probability density function f as:
Differential entropy can be used to measure the uniformity of a distribution. A distribution that spreads out has a higher entropy, whereas a highly peaked distribution has a relatively lower entropy. Many authors have carried out their studies based on entropy. Siamak and Ehsan [11] proposed Shannon aromaticity based on the concept of Shannon entropy in information theory and applied it to describe the probability of electronic charge distribution between atoms in a given ring. Tahmasebi and Behboodian [12] derived the entropy and the order statistics for the Feller-Pareto family and presented the entropy ordering property for the sample minimum and maximum of Feller-Pareto subfamilies. Cho et al. [13] estimated the entropy for Weibull distribution under three different loss functions based on generalized progressively hybrid censoring scheme. Seo and Kang [14] discussed the entropy of a generalized half-logistic distribution based on Type II censored samples.
The entropy of the Lomax distribution is given by:
As it is often inevitable to lose some experimental units before terminal time in a test, censoring is becoming increasingly popular in lifetime testing and survival analysis. The two most popular censoring schemes in literature are Type I and Type II censoring schemes. Hybrid censoring, which was first proposed in Reference [15], is a mixture of Type I and Type II censoring schemes. The conventional censoring schemes (Type I, Type II, hybrid censoring) do not allow experimental units to be removed other than the terminal time. The early removals are desirable so that some experimental units can be removed and used in other experiments. Accordingly, the progressively censoring scheme was introduced by Reference [16]. The progressively hybrid censoring scheme can be described as follows. Suppose that n identical units are placed on a test. Let be the ordered failure times and be the censoring scheme. Then we have . We refer to Reference [17] for detailed discussion about progressively censoring. The test is terminated either when a pre-assigned number, say m, failures have been observed or when a pre-specified time, say T, has been reached. So clearly the terminal time . When the first failure occurs, units are randomly removed from the test. When the second failure occurs, units are randomly removed. Eventually, when the m-th failure occurs or when the pre-specified time T is reached, all the remaining units are removed from the test.
The disadvantages of progressively hybrid censoring are that it cannot be applied and the accuracy of the estimates can be extremely low if only a few units fail before terminal time . For this reason, Cho et al. [18] proposed a generalized progressively hybrid censoring scheme. Suppose n identical units are placed on an experiment. For the sake of observing at least k (pre-determined) units in the experiment, the terminal time is adjusted to . Similarly, units are randomly removed from the test when the first failure is observed. units are randomly removed when the second failure is observed. This continues until all the units are removed when the has been reached. A representation of the generalized progressively hybrid censoring scheme, the corresponding condition and the expressions of terminal time () and , , , terminal removals are presented as follows.
- Case I ()
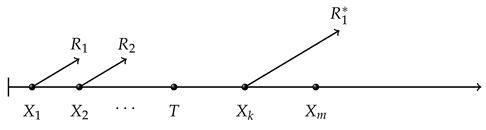 ,
, - Case II ()
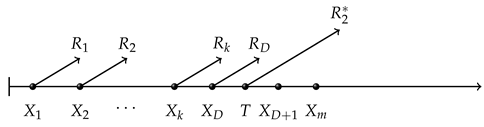 ,
, - Case III ()
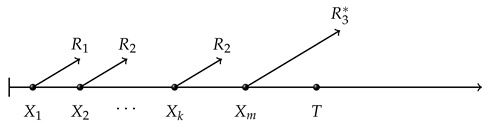 ,
,
The objective of this paper is to derive the maximum likelihood estimator (MLE) and Bayesian estimators of entropy, and to compare the proposed estimates of entropy with respect to mean squared error (MSE) and bias value. We first derive the maximum likelihood estimators of the unknown parameters for the Lomax distribution and calculate the entropy based on the invariance property of the MLE. Next, we consider the Bayesian estimators of the entropy under squared error, linex and general entropy loss function. It is to be noted that it is not easy to obtain explicit expressions of Bayesian estimates and thus the Lindley method and the Tierney and Kadane method are applied. We conduct a simulation study and compare the performance of all the estimates of entropy with respect to MSE and bias values.
The rest of this paper is organized as follows. In Section 2, we deal with computing entropy based on MLEs. Bayesian estimators under squared error, linex and general entropy loss function are derived using the Lindley method and Tierney and Kadane method in Section 3. A simulation study is conducted and presented to study the performance of the estimates in Section 4. In Section 5, a real data set is analyzed for illustrative purposes. Finally, we conclude the paper in Section 6.
2. Maximum Likelihood Estimator
In this section, we obtain the maximum likelihood estimators of entropy based on generalized progressively hybrid censoring. The likelihood functions and log-likelihood functions for cases I, II and III can be found in Appendix A, and the likelihood functions and log-likelihood functions in Case I, Case II and Case III can be combined and written as
where for Case I; for Case II; for Case III.
Let Equation (5) take derivatives with respect to and . We can get
where, =0 for Case I and Case III; for Case II.
Equation (6) can also be written as
where
Therefore, we can use an iterative procedure, which was proposed by Reference [19] and applied in Reference [20], to compute the MLEs. Set an initial guess value of , say , then let , , ⋯, . This iterative process continues until , where is some pre-specified tolerance limit. Then
3. Bayesian Estimation
3.1. Prior and Posterior Distributions
It is to be noticed that both parameters and are unknown, namely no natural conjugate bivariate prior distribution exists. Therefore we assume the independent priors of and are and with corresponding means and , respectively. The priors of and can be written as:
where are the positive hyperparameters containing the prior knowledge.
Thus, the joint prior distribution is given by:
The posterior distribution of and is:
Let be the expectation of a function of and , say . Then we obtain:
In this passage, we only compute the Bayesian estimates for entropy. So particularly, is a function of H.
3.2. Loss Function
In this subsection, we consider Bayesian estimators under symmetric and asymmetric loss functions. One of the most widely used symmetric loss functions is squared error loss function. The loss function is given by:
where is an estimator of .
In this case, the Bayesian estimator (say ) is obtained as:
As for asymmetric loss function, we choose two most commonly used asymmetric loss functions—linex loss function and general entropy loss function. The linex loss function is defined as:
where, is an estimator of , and h is the sign presenting the asymmetry. We refer to Reference [21] for detailed information about linex loss function.
The Bayesian estimator under linex function (say ) is given by:
Next, the general entropy loss function is defined as:
where is an estimator of , and q is the sign presenting the asymmetry. For a detailed information, we refer to Reference [22].
The Bayesian estimator in this situation (say ) is given as:
Using Equations (12)–(14), the Bayesian estimators of entropy under squared error loss function, linex loss function and general entropy loss function can be obtained as:
It is to be noted that all the Bayesian estimates of entropy are in the form of a ratio of two integrals, which cannot be simplified or computed directly. Thus, we apply the Lindley method and Tierney and Knadane method to compute the estimates.
3.3. Lindley Method
In this subsection, we apply the Lindley ([23]) method to compute the approximate Bayesian estimates of entropy. For the two parameters case, the Lindley method can be written as:
The notations in this formula and some basic formulas are omitted here and presented in Appendix B.
- For squared error loss function, we take:Then we can compute that:Then using Equation (18), the Bayesian estimates under squared error loss function can be obtained as:
- Further, for the linex loss function, we take:We can obtain that:Similarly, using Equation (18), we can derive the Bayesian estimates of entropy under the linex loss function as:
- For general entropy loss function, we take:We can derive that:Thus, the Bayesian estimate under general entropy loss function can be computed using:
In the next subsection, we apply the Tierney and Kadane method to compute the approximate Bayesian estimate.
3.4. Tierney and Kadane Method
An alternative to the Lindley method to approximate the integrals is using the method proposed by Tierney and Kadane. Detailed information about the Tierney and Kadane method can be found in Reference [24], and a comparision between the Tierney and Kadane method and Lindley method can be found in [25]. In this subsection, we use the Tierney and Kadane method to estimate the entropy. We consider the function of and , say . The formulas in the Tierney and Kadane method are as follows:
where and are the inverse of the negative Hessian matrix of and , respectively.
In order to compute and , we need to solve the following equations:
We can also find that
Thus, we can compute at
- For squared error loss function, we take:Let take derivatives with respect to and , we obtain:According to the equations above, we can obtain . In order to compute at , we also need to compute:So the Bayesian estimate under squared error loss function is:
- Further, for linex loss function, we take:Thus, we have:We can also compute that:Thus, we can compute at . The Bayesian estimate under linex loss function can be derived as:
- As for general entropy loss function, we take:We can compute that:We can also compute that:Then, we can obtain at .Obviously, the Bayesian estimate under the general entropy loss function can be derived as:
4. Simulation Results
In this section, a simulation study is conducted in order to compare different estimates of entropy with respect to MSEs and bias values. First, we describe how to generate a generalized progressively hybrid censored sample for Lomax distribution.
Let be the Type II progressively censored sample for Lomax distribution with censoring scheme . Then
is the Type II progressively censored sample for a standard exponential distribution. According to the transformation proposed by [16], let
Then are the independent random variables from standard exponential distribution. Further, after generating Type II progressively censored sample , we need to convert it to generalized progressively hybrid censored sample. For fixed T and k, if , then the generalized progressively hybrid censored sample X is ; if , then the corresponding generalized progressively hybrid censored sample X is ; and if , then the corresponding generalized progressively hybrid censored sample X is . The algorithm for generating generalized hybrid censored sample can be described as:
- generate , where is the random variable from standard exponential distribution.
- Let , , then is the Type II progressively censored sample from standard exponential distribution.
- Further, let , where is the inverse of the cumulative distribution function. Then is the Type II progressively censored sample for Lomax distribution.
- For pre-fixed T and k, if , then the generalized progressively hybrid censored sample X is ; if , then the corresponding generalized progressively hybrid censored sample X is ; if , then the corresponding generalized progressively hybrid censored sample X is .
Without loss of generality, we take , and . The desired MLEs of entropy is obtained based on the MLEs of unknown parameters. The Bayesian estimates under squared error, linex and general entropy loss function are derived using the Lindley method and the Tierney and Kadane method. Under the linex loss function, we choose and . Under general entropy loss function, we choose and . For computing proper Bayesian estimates, we assign the value of hyperparameters as . Besides, we also computed Bayesian estimates with respect to non-informative prior distribution. This corresponds to the case when hyperparameters take values . The simulation results with non-informative priors are presented in Table 1 and the results with informative priors are presented in Table 2. We apply two different types of censoring scheme (Sch). Sch I: . for ; Sch II: . for .

Table 1.
The relative MSEs and biases of entropy estimates with MLE and the Bayes estimates with non-informative priors ( for the MLEs, for the Bayesian estimates under the squared error loss function, for the Bayesian estimates under the linex loss function, for the Bayesian estimates under general entropy loss function, Lindley for the Lindley method and TK for the Tierney and Kadane method).

Table 2.
The relative MSEs and biases of entropy estimates with MLE and the Bayes estimates with informative priors ( for the MLEs, for the Bayesian estimates under the squared error loss function, for the Bayesian estimates under the linex loss function, for the Bayesian estimates under general entropy loss function, Lindley for the Lindley method and TK for the Tierney and Kadane method).
In all the tables, the bias values and the MSEs of the MLES of entropy are presented in the fifth column. All other columns uniformly contain four values. The first value denotes the bias value of the Bayesian estimate using the Lindley method and the second value denotes the corresponding MSE of the estimate using the Lindley method. The third and forth values represent the bias value and MSE of the estimates obtained by the Tierney and Kadane method.
In general, we can observe that the MSE values decrease as the sample size n increases. For fixed n and m, the MSEs decrease as k increases. Plus, the Bayesian estimate with informative prior performs much better than that with non-informative prior with respect to bias value and MSE. Further, it is observed that Bayesian estimates with proper priors usually perform better than the MLEs, while MLEs compete really well with Bayesian estimates with non-informative priors. When the prior is informative, both the methods perform well; while when the prior is non-informative, the Tierney and Kadane method is a better choice. For linex loss function, seems to be a better choice than , and for general entropy loss function, compete well with . Overall, the Bayesian estimates with proper prior under the linex loss function behave better than the other estimates.
5. Data Analysis
In this section, a real data set is analyzed for illustrative purposes. We consider the data set obtained from a meteorological study in Reference [26] and analyzed by Reference [27]. The data were based on the radar-evaluated rainfall from 52 cumulus clouds (26 seeded clouds and 26 control clouds), namely the sample size n is 52. We apply the Akaike information criterion (AIC), defined by , Bayesian information criterion (BIC), defined by , where p is the number of parameters, n is the number of observations, and L is the maximized value of the likelihood function and Kolmogorov-Smirnov (K-S) statistics with its p-value. The competing model is gamma distribution and generalized inverted exponential distribution. If the Lomax model fits well with the data, it will have low AIC, BIC, K-S statistics value and high p value. Plus, we also draw quantile-quantile plots to test the goodness of the model. The results are presented in Table 3 and Figure 1.

Table 3.
AIC, BIC K-S statistics with p value for competing lifetime models.
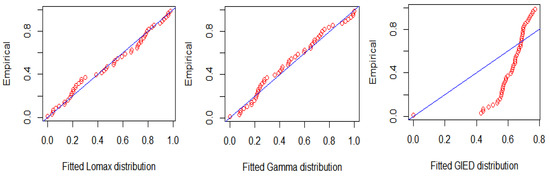
Figure 1.
Quantile-quantile plots.
Although Gamma distribution competes well with Lomax distribution, its second parameter is too small. Plus, compared with gamma distribution, Lomax distribution is easier to handle with respect to the computational aspect. So, Lomax distribution is a better choice. We choose to apply the same censoring scheme as Reference [28], which is , and and the ordered progressively type-II censored sample generated by Reference [28] is: 1, 4.1, 4.9, 4.9, 7.7, 11.5, 17.3, 17.5, 21.7, 26.3, 28.6, 29, 31.4, 36.6, 40.6, 41.1, 68.5, 81.2, 92.4, 95, 115.3, 118.3, 119, 163, 198.6. Take Case I (k = 15, T = 80), Case II (k = 15, T = 100), and Case III (k = 18, T = 80). For Case I, the generalized progressively hybrid censored sample is 1.0, 4.1, 4.9, 4.9, 7.7, 11.5, 17.3, 17.5, 21.7, 26.3, 28.6, 29.0, 31.4, 36.6, 40.6, 41.1, 68.5; for Case II, the generalized progressiveky hybrid censored sample is 1.0, 4.1, 4.9, 4.9, 7.7, 11.5, 17.3, 17.5, 21.7, 26.3, 28.6, 29.0, 31.4, 36.6, 40.6, 41.1, 68.5, 81.2, 92.4, 95.0, and for Case III, the generalized progressively hybrid censored sample is 1.0, 4.1, 4.9, 4.9, 7.7, 11.5, 17.3, 17.5, 21.7, 26.3, 28.6, 29.0, 31.4, 36.6, 40.6, 41.1, 68.5, 81.2.
For the Bayesian estimation, we apply the non-informative prior . Besides, for the linex loss function, we choose and . For the general loss function, we assign and . The results are shown in Table 4. We can observe that, although using different methods under different loss functions, the estimates of entropy are pretty close to each other.

Table 4.
Estimation of entropy based on a real data from a meteorological study.
6. Conclusions
The problem of estimating the entropy for Lomax distribution is considered in this paper, based on generalized progressively hybrid censoring. The maximum likelihood estimator of entropy is derived. Further, we apply the Lindley method and the Tierney and Kadane method to compute Bayesian estimates under squared error loss function, linex loss function and general entropy loss function. Then the proposed estimates are compared with respect to bias values and MSEs. It is observed that Bayesian estimates with proper priors behave better than the corresponding MLEs. However, MLEs compete very well with Bayesian estimates when the priors of the Bayesian estimates are non-informative. Overall, the Bayesian estimates with proper priors under the linex loss function behave better than other estimates according to the simulation results presented in this passage.
Much research has been done based on traditional censoring schemes and progressively censoring schemes, while few studies have been conducted based on generalized hybrid censoring schemes. Besides, compared with the parameters, entropy has a wider use in many fields now. Therefore, the estimation of entropy from other distributions based on generalized progressively hybrid censoring is still of great potential for future study.
Author Contributions
Investigation, S.L.; Supervision, W.G.
Funding
This research was supported by Project 202010004004 which was supported by National Training Program of Innovation and Entrepreneurship for Undergraduates.
Acknowledgments
The authors would like to thank the four referees and the editor for their careful reading and constructive comments which led to this substantive improved version.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Likelihood and Log-Likelihood Functions
The likelihood functions and log-likelihood functions are presented in this Section as follows:
Case I:
Case II:
Case III:
Appendix B. Lindley Method
Notations and basic expressions in (18) in Lindley method are as follows:
denotes the -th element of the inverse of the negative Hessian matrix of log-likelihood function.
For Lomax distribution based on generalized progressively hybrid censoring sample, we have:
where, , , for Case II, for Case I and Case III.
We also have:
References
- Lomax, K.S. Business Failures: Another Example of the Analysis of Failure Data. Publ. Am. Stat. Assoc. 1987, 49, 847–852. [Google Scholar] [CrossRef]
- Ahsanullah, M. Record values of the Lomax distribution. Stat. Neerl. 2010, 45, 21–29. [Google Scholar] [CrossRef]
- Afaq, A.; Ahmad, S.P.; Ahmed, A. Bayesian analysis of shape parameter of Lomax distribution using different loss functions. Int. J. Stat. Math. 2015, 2, 55–65. [Google Scholar]
- Ismail, A.A. Optimum Failure-Censored Step-Stress Life Test Plans for the Lomax Distribution. Strength Mater. 2016, 48, 1–7. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Cordeiro, G.M. An extended Lomax distribution. Statistics 2013, 47, 800–816. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.M.; Popovic, B.V. The gamma-Lomax distribution. J. Stat. Comput. Simul. 2015, 85, 305–319. [Google Scholar] [CrossRef]
- Kilany, N.M. Weighted Lomax distribution. Springerplus 2016, 5, 1862–1880. [Google Scholar] [CrossRef]
- Ahmadi, J.; Crescenzo, A.D.; Longobardi, M. On dynamic mutual information for bivariate lifetimes. Adv. Appl. Probab. 2015, 47, 1157–1174. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Siamak, N.; Ehsan, S. Shannon entropy as a new measure of aromaticity, Shannon aromaticity. Phys. Chem. Chem. Phys. 2010, 12, 4742–4749. [Google Scholar]
- Tahmasebi, S.; Behboodian, J. Shannon Entropy for the Feller-Pareto (FP) Family and Order Statistics of FP Subfamilies. Appl. Math. Sci. 2010, 4, 495–504. [Google Scholar]
- Cho, Y.; Sun, H.; Lee, K. Estimating the Entropy of a Weibull Distribution under Generalized Progressive Hybrid Censoring. Entropy 2015, 17, 102–122. [Google Scholar] [CrossRef]
- Seo, J.I.; Kang, S.B. Entropy Estimation of Generalized Half-Logistic Distribution (GHLD) Based on Type-II Censored Samples. Entropy 2014, 16, 443–454. [Google Scholar] [CrossRef]
- Epstein, B. Truncated life-tests in the expotential case. Ann. Math. Stat. 1954, 25, 555–564. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring; Birkhauser: Boston, MA, USA, 2000. [Google Scholar]
- Kundu, D.; Joarder, A. Analysis of Type-II progressively hybrid censored data. Comput. Stat. Data Anal. 2006, 50, 2509–2528. [Google Scholar] [CrossRef]
- Cho, Y.; Sun, H.; Lee, K. An Estimation of the Entropy for a Rayleigh Distribution Based on Doubly-Generalized Type-II Hybrid Censored Samples. Entropy 2014, 16, 3655–3669. [Google Scholar] [CrossRef]
- Kundu, D. On hybrid censored Weibull distribution. J. Stat. Plan. Inference 2007, 137, 2127–2142. [Google Scholar] [CrossRef]
- Ma, Y.; Shi, Y. Inference for Lomax Distribution Based on Type-II Progressively Hybrid Censored Data; Vidyasagar University: Midnapore, India, 2013. [Google Scholar]
- Parsian, A.; Kirmani, S. Handbook of Applied Econometrics and Statistical Inference; Chapter Estimation Under LINEX Loss Function; Marcel Dekker Inc.: New York, NY, USA, 2002; pp. 53–76. [Google Scholar]
- Singh, P.K.; Singh, S.K.; Singh, U. Bayes Estimator of Inverse Gaussian Parameters Under General Entropy Loss Function Using Lindley’s Approximation. Commun. Stat. Simul. Comput. 2008, 37, 1750–1762. [Google Scholar] [CrossRef]
- Lindley, D.V. Approximate Bayesian methods. Trab. Estad. Investig. Oper. 1980, 31, 223–245. [Google Scholar] [CrossRef]
- Tierney, L.; Kadane, J. Accurate Approximations for Posterior Moments and Marginal Densities. Publ. Am. Stat. Assoc. 1986, 81, 82–86. [Google Scholar] [CrossRef]
- Howlader, H.A. Bayesian survival estimation of Pareto distribution of the second kind based on failure-censored data. Comput. Stat. Data Anal. 2002, 38, 301–314. [Google Scholar] [CrossRef]
- Simpson, J. Use of the gamma distribution in single-cloud rainfall analysis. Mon. Weather Rev. 1972, 100, 309–312. [Google Scholar] [CrossRef]
- Giles, D.; Feng, H.; Godwin, R.T. On the bias of the maximum likelihood estimator for the two parameter Lomax distribution. Commun. Stat. Theory Methods 2013, 42, 1934–1950. [Google Scholar] [CrossRef]
- Helu, A.; Samawi, H.; Raqab, M.Z. Estimation on Lomax progressive censoring using the EM algorithm. J. Stat. Comput. Simul. 2015, 85, 1035–1052. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).