Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform
Abstract
:1. Introduction
2. Related Works
3. Proposed Methodology
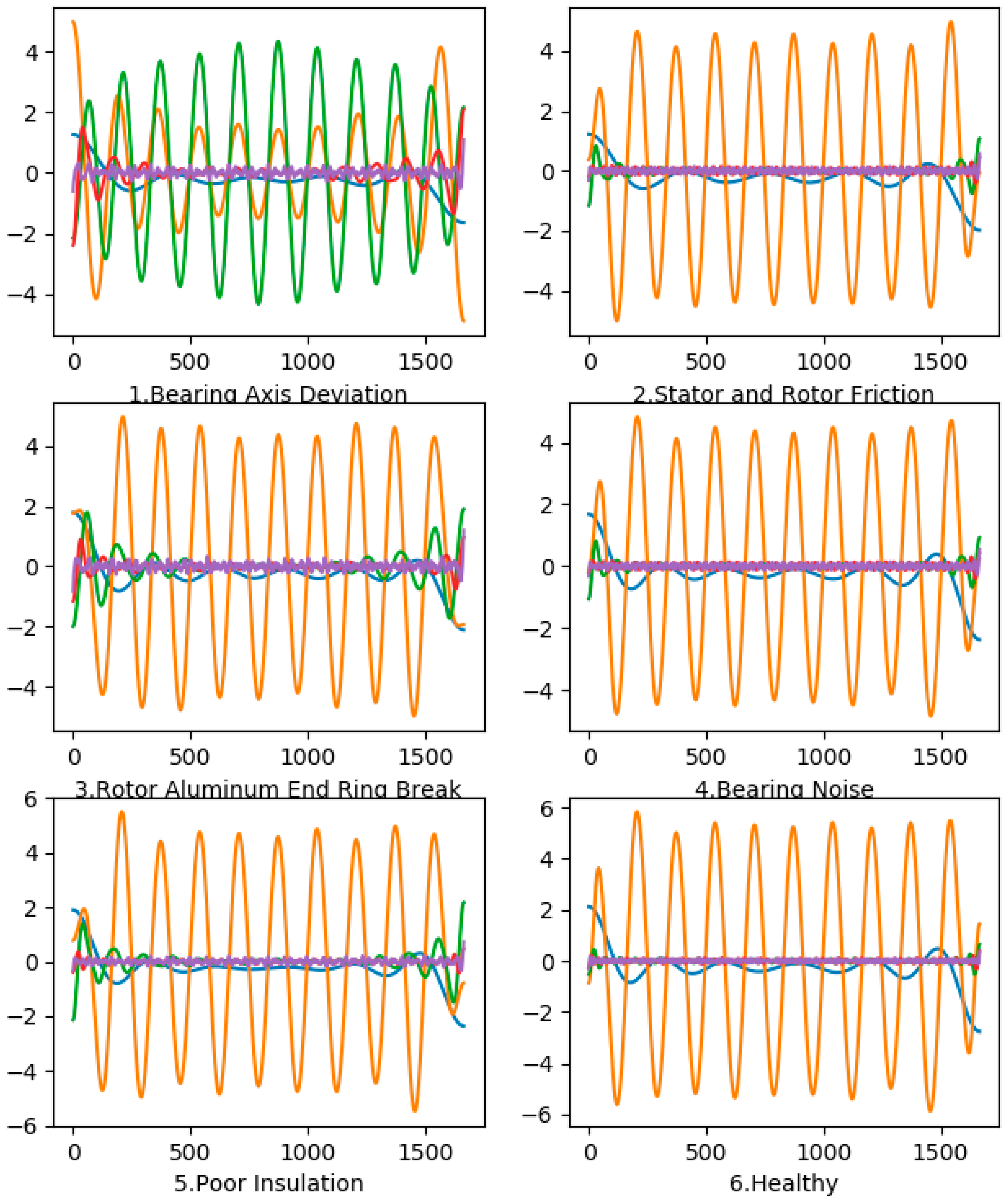
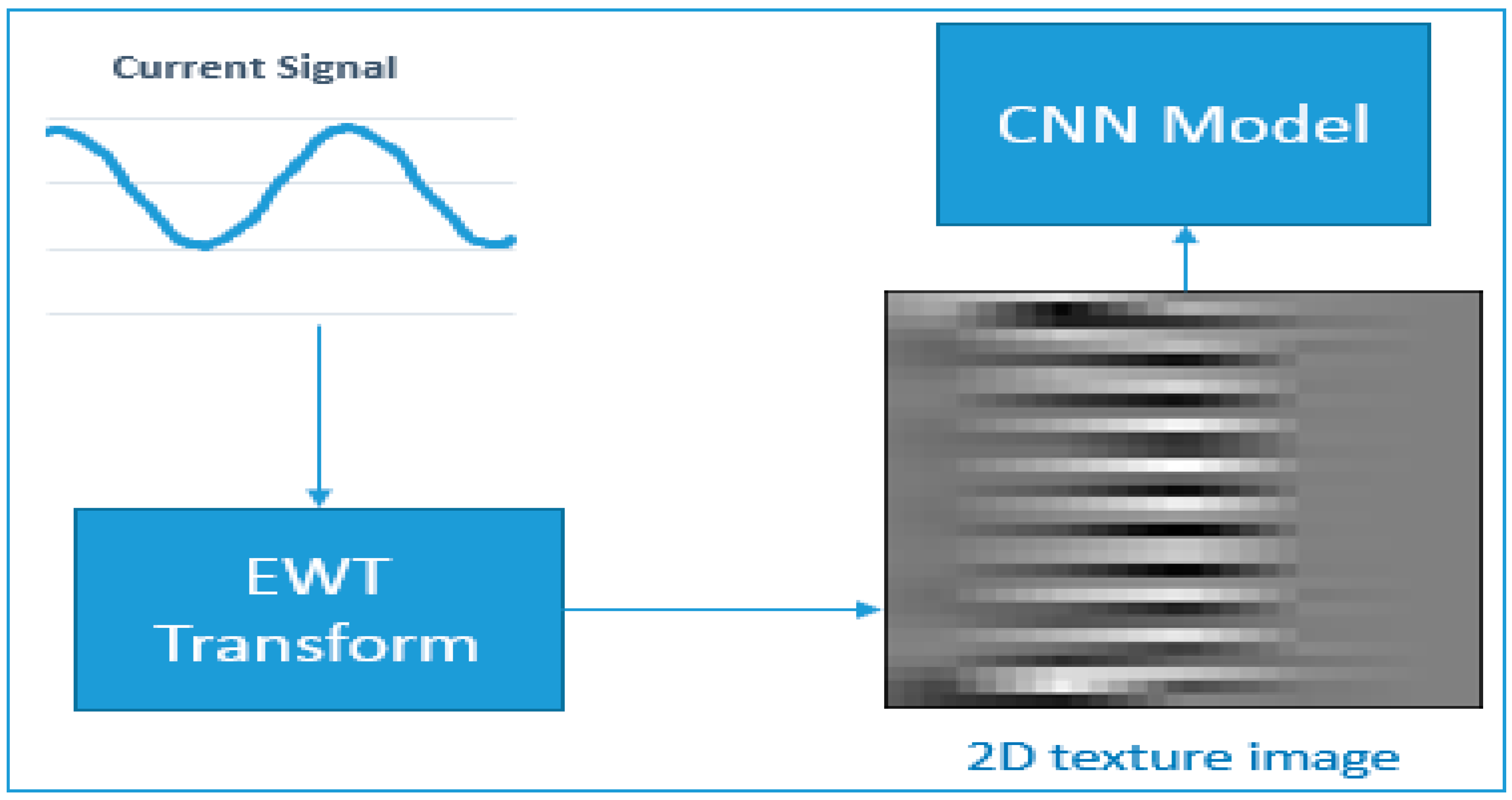
3.1. Pattern Recognition Technique
- Step 1: Find the Fourier transform of the processed input signal.
- Step 2: Segment the Fourier spectrum by detecting the local maxima in the spectrum.
- Step 3: Sort the local maxima in decreasing order
- Step 4: Define the boundaries of every segment as the center between two successive maxima.
- Step 5: Follow the construction idea of Meyer’s wavelet to obtain a tight frameset
- Step 6: Obtain the corresponding signal filters (modes as defined in [24]).
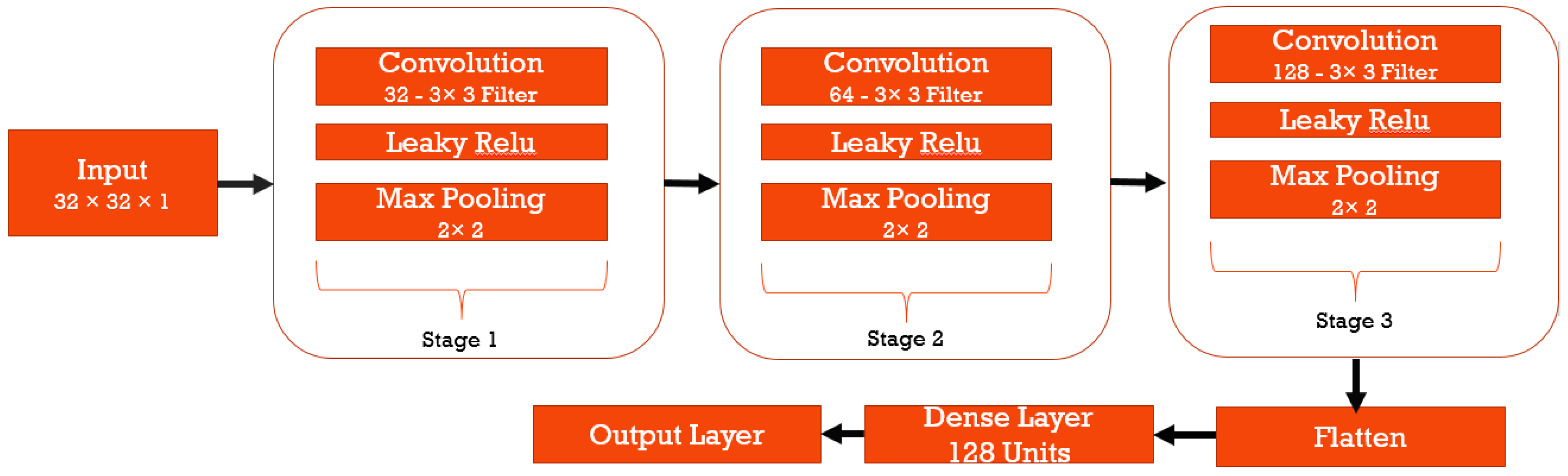
3.2. Proposed Deep Convolutional Neural Network
4. Experimental Results and Discussion
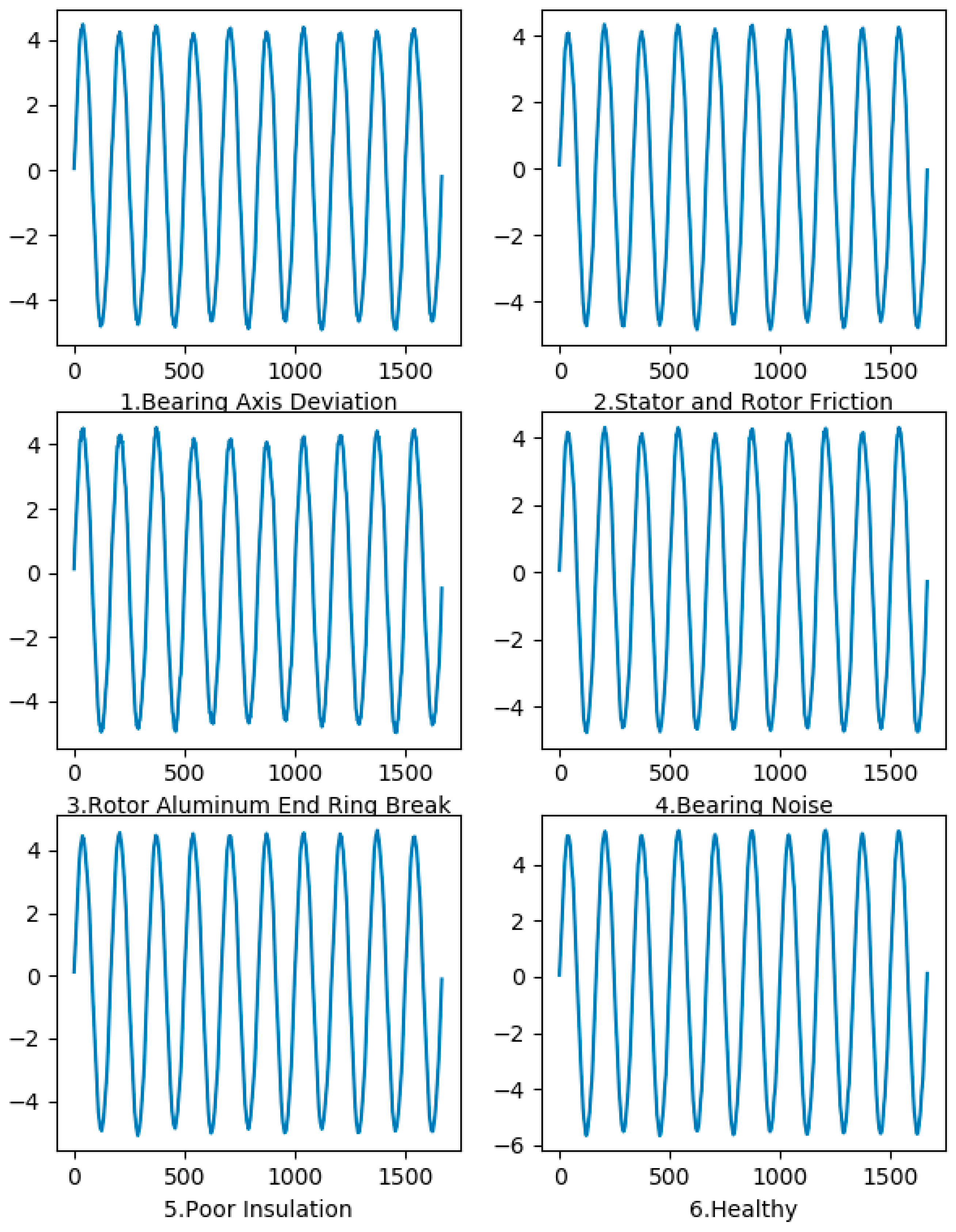
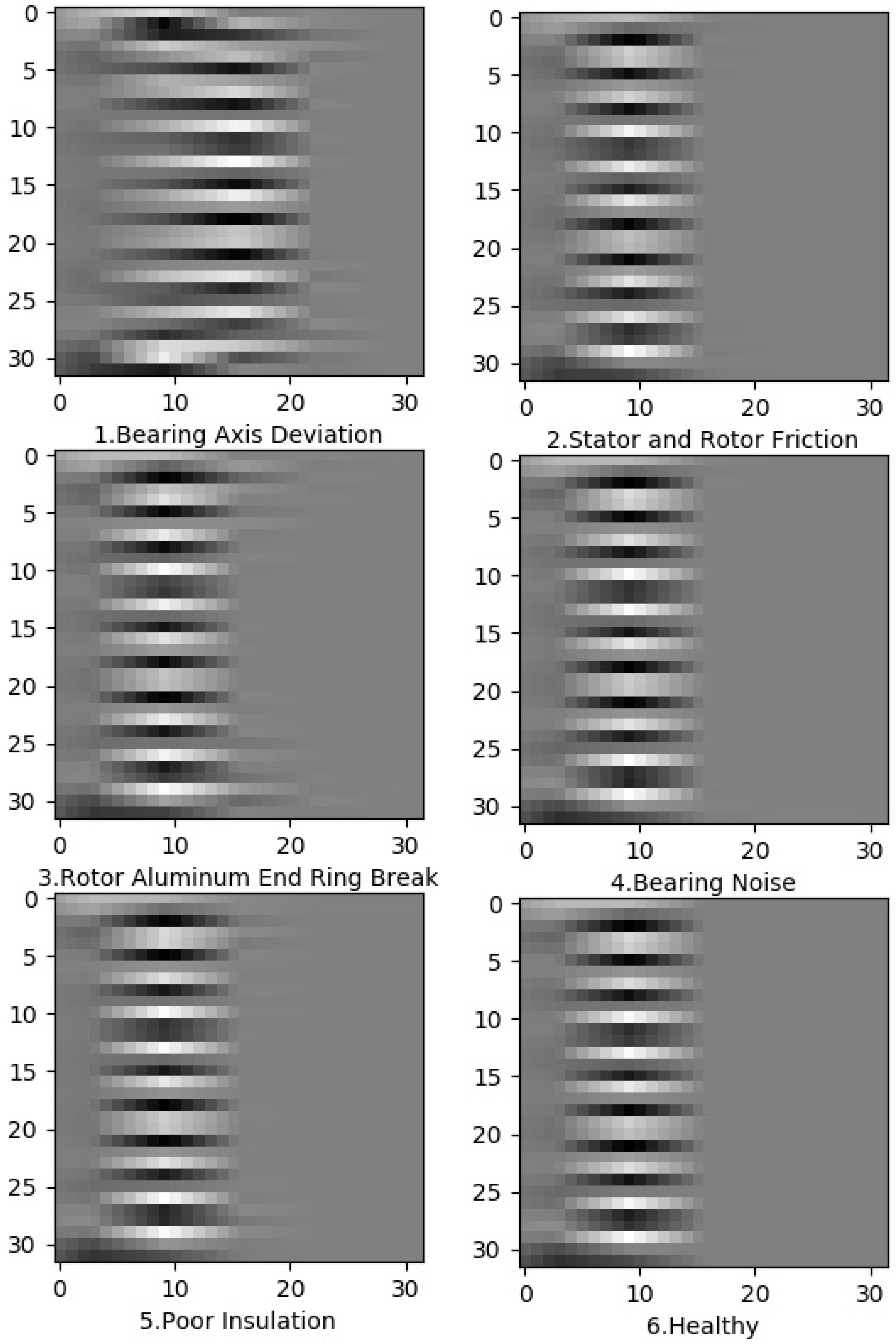
4.1. Faults in Induction Motors
- Bearing Axis Deviation: The structure of the bearing is precise. If it is disturbed by some external forces, the structure of the bearing may be affected. After connecting the motor to the load, an earthquake, collision, and the assembly process may introduce an offset of midpoints on both ends of the connection, which causes heating problems and unwanted noise. A normal motor with a full load is used, and, for this experiment, the coupling is shifted 0.5 mm upward to imitate the deviation condition. The experimental motor model is shown in Figure 6d.
- Stator and Rotor Friction and Poor Insulation: Because of friction, overheating, insulation aging, dampness and corona, the stator or rotor coil is short-circuited, and hence it will break down if not diagnosed. The insulation of the adjacent turns in the stator coil will be damaged, causing a short circuit, as shown in the Figure 6a. When the motor is started, the short-circuit current value will be high due to the difference in excessive voltage caused by different wound turns in the stator, and the motor will be burnt. The experimental motor model is shown in Figure 6a.
- Rotor Aluminum End Ring Break: The outer ring damage is one of the most common faults. If the starting frequency is very high and/or the motor is overloaded, the rotor bar will break due to the excessive current. For this experiment, a hole with a diameter of 7 mm and a depth of 30 mm is made on the rotor bar to simulate the fault condition. The experimental motor model is shown in Figure 6b.
- Bearing Noise: Damage to the bearing’s outer race is considered one of the constant faults observed in bearings. The structure of the bearing is always kept precise. However, if the structure is disturbed by an external force or some other structures of bearing, this causes messy and numerous harmonics in the measured spectrum. A hole with a diameter and depth of 1 mm is made in the outer race to simulate the fault condition for this experiment. The experimental motor model is shown in Figure 6c.
4.2. Dataset
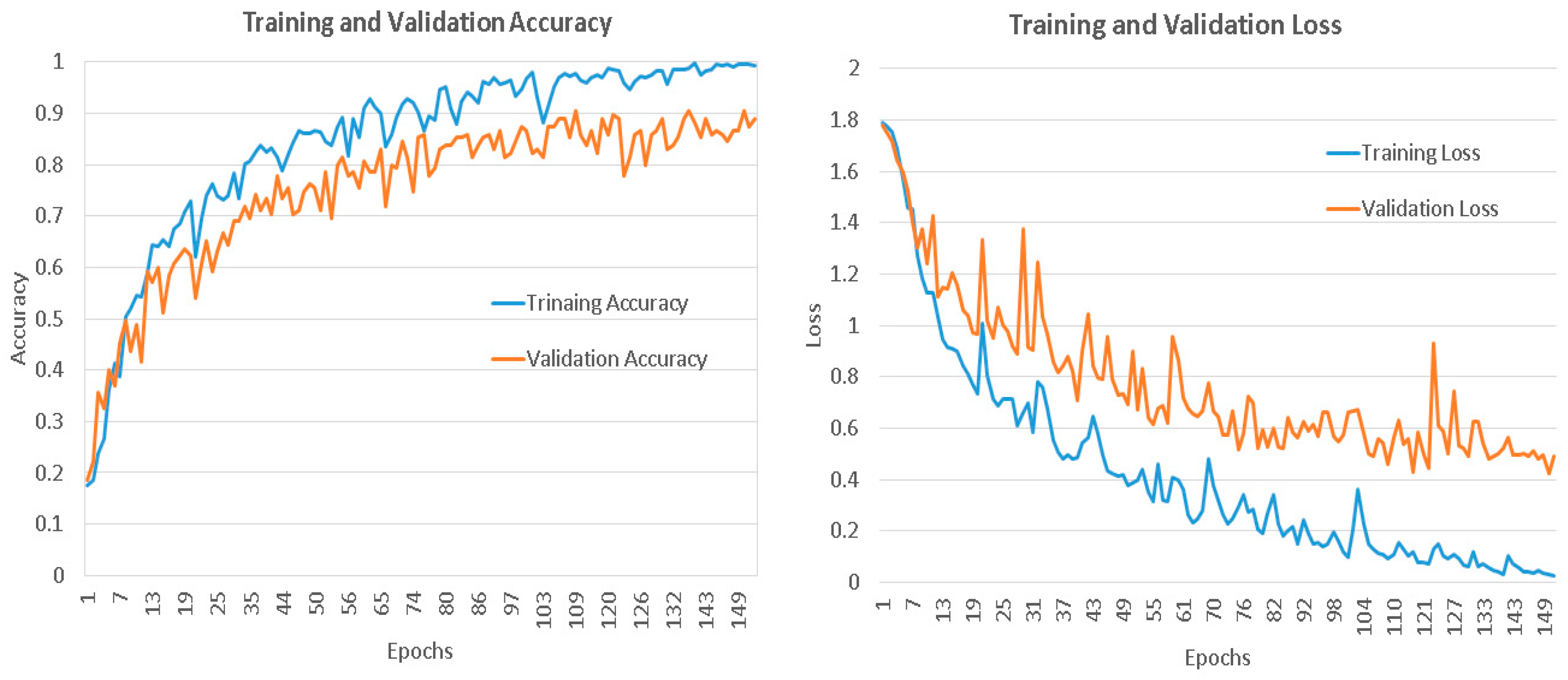
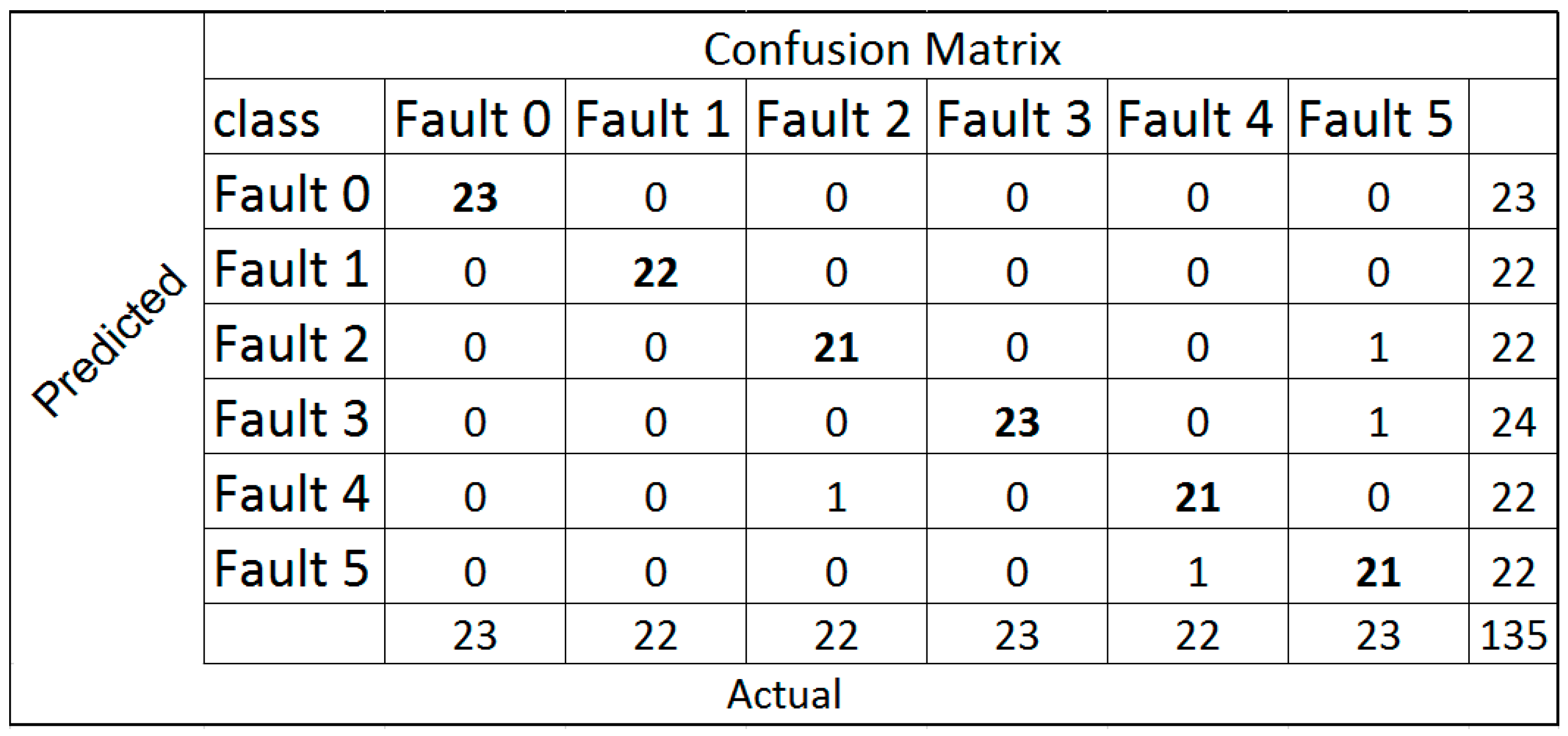
4.3. CNN Performance Evaluation Results
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Albrecht, P.F.; Appiarius, J.C.; McCoy, R.M.; Owen, E.L.; Sharma, D.K. Assessment of the Reliability of Motors in Utility Applications—Updated. IEEE Trans. Energy Convers. 1986, EC-1, 39–46. [Google Scholar] [CrossRef]
- Bonnett, A.H.; Soukup, G.C. Cause and Analysis of Stator and Rotor Failures in Three-Phase Squirrel-Cage Induction Motors. IEEE Trans. Ind. Appl. 1992, 28, 921–937. [Google Scholar] [CrossRef]
- Dai, X.; Gao, Z. From model signal to knowledge: A data-driven perspective of fault detection and diagnosis. IEEE Trans. Ind. Inform. 2013, 9, 2226–2238. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques-Part I: Fault diagnosis with model-based and signal-based approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Cecati, C. A survey of fault diagnosis and fault-tolerant techniques-Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Lamim Filho, P.C.M.; Pederiva, R.; Brito, J.N. Detection of stator winding faults in induction machines using flux and vibration analysis. Mech. Syst. Signal Process. 2014, 42, 377–387. [Google Scholar] [CrossRef]
- Sun, W.; Chen, J.; Li, J. Decision tree and PCA-based fault diagnosis of rotating machinery. Noise Vib. Worldw. 2007, 21, 1300–1317. [Google Scholar] [CrossRef]
- Ngaopitakkul, A.; Bunjongjit, S. An application of a discrete wavelet transform and a back-propagation neural network algorithm for fault diagnosis on single-circuit transmission line. Int. J. Syst. Sci. 2013, 44, 1745–1761. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, D.; Cheng, J. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM. Measurement 2007, 40, 943–950. [Google Scholar] [CrossRef]
- Pandya, D.H.; Upadhyay, S.H.; Harsha, S.P. Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN. Expert Syst. Appl. 2013, 40, 4137–4145. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Shen, C.; Wang, D.; Shi, J.; Jiang, X.; Zhu, Z. Stacked Sparse Autoencoder-Based Deep Network for Fault Diagnosis of Rotating Machinery. IEEE Access 2017, 5, 15066–15079. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; Silva, C.W. Fault Diagnosis for Rotating Machinery Using Multiple Sensors and Convolutional Neural Networks. IEEE/ASME Trans. Mechatron. 2018, 23, 101–110. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A New Deep Transfer Learning Based on Sparse Auto-Encoder for Fault Diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2017, 99, 1–9. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 115002. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Wang, F.; Zhao, H. An enhancement deep feature fusion method for rotating machinery fault diagnosis. Knowl. Based Syst. 2017, 119, 200–220. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Lee, K.B.; Cheon, S.; Chang, O.K. A Convolutional Neural Network for Fault Classification and Diagnosis in Semiconductor Manufacturing Processes. IEEE Trans. Semicond. Manuf. 2017, 30, 135–142. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; She, M.; Nahavandi, S.; Kouzani, A. Bag-of-words representation for biomedical time series classification. Biomed. Signal Process. Control 2016, 8, 634–644. [Google Scholar] [CrossRef]
- Hatami, N.; Chira, C. Classifiers with a reject option for early time-series classification. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence and Ensemble Learning (CIEL), Singapore, 16–19 April 2013; pp. 9–16. [Google Scholar]
- Wang, Z.; Oates, T. Pooling sax-bop approaches with boosting to classify multivariate synchronous physio-logical time series data. In Proceedings of the 28th International FLAIRS Conference, Hollywood, FL, USA, 18–20 May 2015; pp. 335–341. [Google Scholar]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-time motor fault detection by 1-D convolutional neural networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Jerome, G. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar]
- Wang, J.; Zhuang, J.; Duan, L.; Cheng, W. A multi-scale convolution neural network for featureless fault diagnosis. In Proceedings of the International Symposium on Flexible Automation (ISFA′16), Cleveland, OH, USA, 1–3 August 2016. [Google Scholar]
- Lee, D.; Siu, V.; Cruz, R.; Yetman, C. Convolutional neural net and bearing fault analysis. In Proceedings of the International Conference on Data Mining Series (ICDM) Barcelona, San Diego, CA, USA, 12–15 December 2016; pp. 194–200. [Google Scholar]
- Ge, H.; Chen, G.; Yu, H.; Chen, H.; An, F. Theoretical Analysis of Empirical Mode Decomposition. Symmetry 2018, 10, 623. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. EEMD method and WNN for fault diagnosis of locomotive roller bearings. Expert Syst. Appl. 2011, 38, 7334–7341. [Google Scholar] [CrossRef]
- Ma, F.; Zhan, L.; Li, C.; Li, Z.; Wang, T. Self-Adaptive Fault Feature Extraction of Rolling Bearings Based on Enhancing Mode Characteristic of Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. Symmetry 2019, 11, 513. [Google Scholar] [CrossRef]
- Ge, M.; Wang, J.; Xu, Y.; Zhang, F.; Bai, K.; Ren, X. Rolling Bearing Fault Diagnosis Based on EWT Sub-Modal Hypothesis Test and Ambiguity Correlation Classification. Symmetry 2018, 10, 730. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Yang, X.; Dong, C. A Fault Feature Extraction Method for Motor Bearing and Transmission Analysis. Symmetry 2017, 9, 60. [Google Scholar] [CrossRef]
- Agrawal, P.; Jayaswal, P. Diagnosis and Classifications of Bearing Faults Using Artificial Neural Network and Support Vector Machine. J. Inst. Eng. India Ser. C 2019, 1–12. [Google Scholar] [CrossRef]
- Jayaswal, P.; Wadhwani, A.K. Application of artificial neural networks, fuzzy logic and wavelet transform in fault diagnosis via vibration signal analysis: A review. Aust. J. Mech. Eng. 2015, 7, 157–171. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets-Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring: A survey. arXiv 2016, arXiv:1612.07640. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Cho, H.C.; Knowles, J.; Fadali, M.S.; Lee, K.S. Fault detection and isolation of induction motors using recurrent neural networks and dynamic Bayesian modeling. IEEE Trans. Control Syst. Technol. 2009, 18, 430–437. [Google Scholar] [CrossRef]
- Xu, Y.; Liang, F.; Zhang, G.; Xu, H. Image Intelligent Detection Based on the Gabor Wavelet and the Neural Network. Symmetry 2016, 8, 130. [Google Scholar] [CrossRef]
- OAbdeljaber; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Chong, U.P. Signal model-based fault detection and diagnosis for induction motors using features of vibration signal in two-dimension domain. Stroj. Vestn. J. Mech. Eng. 2011, 57, 655–666. [Google Scholar]
- Xu, G.; Liu, M.; Jiang, Z.; Söffker, D.; Shen, W. Bearing fault diagnosis method based on deep convolutional neural network and random forest ensemble learning. Sensors 2019, 19, 1088. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Wang, Y.; Ragulskis, M.; Cheng, Y. Fault diagnosis for rotating machinery: A method based on image processing. PLoS ONE 2016, 11, e0164111. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.M. Reliable fault diagnosis of multiple induction motor defects using a 2-D representation of Shannon wavelets. IEEE Trans. Magn. 2014, 50, 1–13. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1971, 454, 903–995. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; ser. CBMS-NSF Regional Conference Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Jaffard, S.; Meyer, Y.; Ryan, R.D. Wavelets: Tools for Science and Technology; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing: The Sparse Way, 3rd ed.; Elsevier/Academic: New York, NY, USA, 2009. [Google Scholar]
- Huang, S.J.; Hsieh, C.T. High-impedance fault detection utilizing a Morlet wavelet transform approach. IEEE Trans. Power Deliv. 1999, 14, 1401–1410. [Google Scholar] [CrossRef]
- Lin, J.; Qu, L. Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Peng, Z.K.; Chu, F.L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography. Mech. Syst. Signal Process. 2004, 18, 199–221. [Google Scholar] [CrossRef]
- Verstraete, D.; Ferrada, A.; Droguett, E.L.; Meruane, V.; Modarres, M. Deep Learning Enabled Fault Diagnosis Using Time-Frequency Image Analysis of Rolling Element Bearings. Shock Vib. 2017, 2017, 5067651. [Google Scholar] [CrossRef]
- Image Processing in Python. Available online: http://scikit-image.org/docs/dev/auto_examples/transform/plot_rescale.html (accessed on 12 May 2019).
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation Functions: Comparison of Trends in Practice and Research for Deep Learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Conference on Neural Information Processing Systems (NIPS12), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Park, S.; Kwak, N. Analysis on the Dropout Effect in Convolutional Neural Networks. In Computer Vision—ACCV 2016; Lecture Notes in Computer Science; Lai, S.H., Lepetit, V., Nishino, K., Sato, Y., Eds.; Springer: Cham, Switzerland, 2017; Volume 10112, pp. 189–204. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chang, H.; Kuo, C.; Hsueh, Y.; Wang, Y.; Hsieh, C. Fuzzy-Based Fault Diagnosis System for Induction Motors on Smart Grid Structures. In Proceedings of the IEEE International Conference on Smart Energy Grid Engineering, Oshawa, ON, Canada, 14–17 August 2017. [Google Scholar]
- The Dataset Used for This Study. Available online: https://drive.google.com/drive/u/0/folders/1Cvs-1LYagNmEQcj-s395dZflh3L4JWTO (accessed on 12 May 2019).
- Zhang, X.; Liang, Y.; Zhou, J. A novel bearing fault diagnosis model integrated permutation entropy ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]

| Bearing Axis Deviation | Stator and Rotor Friction | Rotor Aluminum End Ring Break | Bearing Noise | Poor Insulation | Healthy | Total |
|---|---|---|---|---|---|---|
| 150 | 150 | 150 | 150 | 150 | 150 | 900 |
| Data Split Ratio | ||
|---|---|---|
| Training | 70% | 630 |
| Validation | 15% | 135 |
| Test | 15% | 135 |
| Classification Report | ||||
|---|---|---|---|---|
| CLASS | Precision | Recall | F1-Score | Support |
| Healthy | 1.00 | 1.00 | 1.00 | 23 |
| Bearing Axis Deviation | 0.97 | 0.96 | 0.94 | 22 |
| Stator and Rotor Friction | 0.95 | 0.97 | 0.96 | 22 |
| Rotor Aluminum End Ring Break | 1.00 | 1.00 | 1.00 | 23 |
| Bearing Noise | 0.93 | 1.00 | 0.96 | 22 |
| Poor Insulation | 0.96 | 0.89 | 0.95 | 23 |
| Accuracy | 0.97 | 135 | ||
| Macro avg | 0.97 | 0.97 | 0.97 | 135 |
| Weighted avg | 0.97 | 0.97 | 0.97 | 135 |
| Methods | Accuracy (%) |
|---|---|
| DBN | 92.2 |
| SVM | 89.8 |
| Sparse filter | 96.4 |
| ANN | 81.8 |
| ADCNN | 96.2 |
| Proposed CNN | 97.37 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsueh, Y.-M.; Ittangihal, V.R.; Wu, W.-B.; Chang, H.-C.; Kuo, C.-C. Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry 2019, 11, 1212. https://doi.org/10.3390/sym11101212
Hsueh Y-M, Ittangihal VR, Wu W-B, Chang H-C, Kuo C-C. Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry. 2019; 11(10):1212. https://doi.org/10.3390/sym11101212
Chicago/Turabian StyleHsueh, Yu-Min, Veeresh Ramesh Ittangihal, Wei-Bin Wu, Hong-Chan Chang, and Cheng-Chien Kuo. 2019. "Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform" Symmetry 11, no. 10: 1212. https://doi.org/10.3390/sym11101212
APA StyleHsueh, Y.-M., Ittangihal, V. R., Wu, W.-B., Chang, H.-C., & Kuo, C.-C. (2019). Fault Diagnosis System for Induction Motors by CNN Using Empirical Wavelet Transform. Symmetry, 11(10), 1212. https://doi.org/10.3390/sym11101212






