A Study of the Effect of Medium Viscosity on Breakage Parameters for Wet Grinding

Abstract

The rheological behavior of mineral slurries shows the level of interaction or aggregation among particles, being a process control variable in processes such as slurry transportation, dehydration, and wet grinding systems. With the aim to analyze the effect of medium viscosity in wet grinding, a series of monosize grinding ball mill tests were performed to determine breakage parameters, according to the generally accepted kinetic approach of grinding processes. A rheological modifier (polyacrylamide, PAM) was used to modify solutions viscosity. A model was proposed by means of dimensional analysis (Buckingham’s Pi theorem) in order to determine the behavior of the specific breakage rate (S_j) for a ball grinding process in terms of the rheology of the system. In addition to this, a linear adjustment was established for the relationship between specific breakage rates with and without PAM addition, based on the reduced viscosity, μ_r. Furthermore, within a certain interval of viscosity, it was proved that an increment of viscosity can increase the specific breakage rate, and consequently the grinding degree.

1. Introduction

The importance of comminution operations in the mineral processing industry has bolstered in the last decades the search for greater process knowledge. More accurate models have been proposed [1,2,3,4,5,6,7,8,9] with the aim to get a better phenomenological processes description and to overcome the apparent technological barriers related to energy efficiency in grinding operations. In the last decades, considerable work has been done on the optimization of energy consumption in grinding mills using phenomenological grinding kinetics models based on population balance (PB) considerations [10]. PB modeling is based on first order kinetics and uses two functions, namely the specific rate of breakage S_i and the breakage function (b_ij), which provide the fundamental size-mass balance equation for fully mixed batch grinding operations.

The rheological behavior of mineral slurries shows the level of interaction or aggregation among particles, being a process control variable in processes such as slurry transportation, dehydration, and wet grinding systems [11]. Ball mill grinding is one of the most used industrial comminution solutions [12,13,14], and it is a process that depends on different conditions such as mill dimensions, rotation speed, filling degree, ball size distribution in the charge, feed size distribution, etc. An exhaustive and broad review of the importance of rheology in mineral processing has been recently published by Cruz et al. [15].

The importance of solids concentration and slurry viscosity to determine the operating conditions has been remarked by Yin et al. [16]. It seems proven that the physic–chemical properties in the slurry can be modified in wet grinding due to changes in physical and chemical conditions (such as size distribution, concentration of solids, temperature, shear rate, pH value, the use of grinding aids, etc.). The use of polyacrylamide (PAM) in water as a viscosity modifier has been broadly studied previously [17,18].

The main goal of this study was to set a model by means of dimensional analysis in order to analyze the behavior of the specific breakage rate (S_j) for a ball grinding process in terms of the rheology of the system. In addition to this, a linear adjustment could be established for the relationship between specific breakage rates with and without PAM addition, based on the reduced viscosity, μ_r. Furthermore, within the validity interval of viscosity, it will be studied whether an increment of viscosity can increase the specific breakage rate, and consequently the grinding degree.

2. Methodology

2.1. Materials

To carry out the tests, representative samples in a quartz ore quarry were selected and characterized with X-ray fluorescence in a Bruker XRF, model S-4 Pioneer. Trace element detection was performed through ICP-OES, after digestion in aqua regia, in a Varian, model Vista-PRO. To perform the mineralogical characterization through X-ray diffraction, a Bruker XRD device, model D8 Advance was used. Results of XRF characterization are shown in Table 1, and ICP-OES results are shown in Table 2.

Table 1. Mineralogical composition of the quartz sample by XRF (%).

Al2O3	SiO2	Fe2O3	TiO2	CaO	MgO	Na2O	K2O	P2O5	LOI
6.49	89.42	0.73	0.67	<0.1	<0.1	0.03	1.10	<0.1	1.54

Table 2. Trace elements in the quartz sample by ICP-OES (ppb).

As	Ba	Sr	Sb	Co	Cr	Cu	Cd	Hg	Pb	Zn	Zr	Ni	Mn	Sn
18	142	15	<10	14	31	22	<10	<10	<10	<10	85	<10	17	<10

Mineralogical analysis results are shown in Figure 1, in which it is clear the abundance of quartz, with the presence of clay components as illite and nacrite. This sample has been used in previous research work and further information about it can be found in Menendez-Aguado et al. [19].

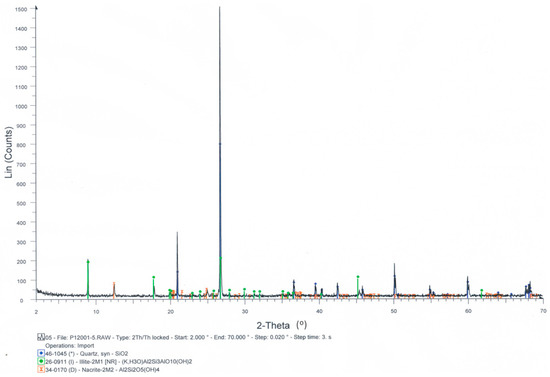
Figure 1. Results from XRD characterization.

2.2. Methods

To carry out the grinding tests, quartz monosize slurries were carefully prepared through sieving, and ASTM standard sieves were used to prepare the samples and determine the particle sizes. Quartz monosizes were prepared through careful wet sieving within the intervals 53/45, 45/38, and 38/30 microns, naming each monosize with the greater size in the interval. Slurries with different viscosity fluids were prepared (1, 4, 6 y 8 cP); suspension liquid viscosity was modified with different levels of PAM addition to the suspending liquid, distilled water. The PAM used was commercial grade (Sigma-Aldrich, CAS number 9003-05-8), with average molecular weight 40,000 g/mol. It is important to remark here that the low value of the molecular weight dismiss the possibility of aggregation effects on particles [20,21]. Viscosity measurements were carried out in a Brookfield viscometer with accessories, and specific gravity of suspensions was determined using a Marcy scale.

In order to determine breakage parameters, more specifically the specific breakage rate, a series of grinding tests were carried out at each fluid viscosity (including dry grinding test) and at each grinding time (0.5, 1, 3, 5, and 10 min) in laboratory a jar mill (Figure 2). Each test was repeated for each ball size diameter. A block diagram depicting the grinding tests performed for each monosize is shown in Figure 3. The grinding parameters that were fixed during the tests are shown in Table 3. Grinding tests were performed in a laboratory ball mill (0.16 m in diameter and 0.18 m long), with grinding charge made of manganese steel alloy balls, with diameters 2, 3, and 4 cm. To carry out the viscosity measurements, a Brookfield RVDV-2 +Pro device was used (Figure 4), with a shear rate of 66.93 s⁻¹. This value was experimentally determined considering a fixed rotational speed of 100 rpm, and according to the Brookfield recommendations for the selected configuration.

Figure 2. Jar mill.

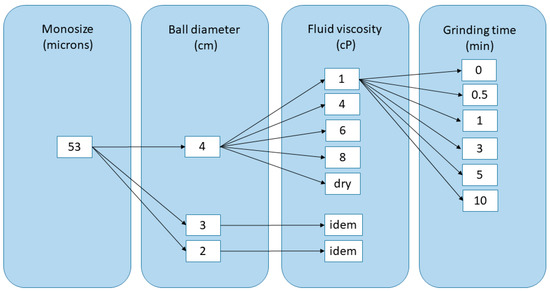
Figure 3. Block diagram, monosize 53 microns.

Table 3. Mill operating conditions.

Sample	Quartz
Solids concentration, ϕ (%w/v)	60
Mill lentgh, L (m)	0.18
Mill diameter, D (m)	0.16
L/D ratio	1.16
Fraction of critical speed, ϕC	0.75
Ball filling fraction, J	0.3
Hole fraction, U	1.0
Bed normal porosity	0.4

Figure 4. Viscometer.

Buckingham’s Pi theorem was used to determine the final model. It states that if there are n variables in a problem and these variables contain m primary dimensions the equation relating all the variables will have (n−m) dimensionless groups, which are referred to as Π groups. The Π groups must be independent of each other and no one group should be formed by multiplying together powers of other groups. [22,23,24].

The objective was to analyze the specific breakage rate, S_j, in terms of the variables that it is expected to have more influence on its behavior:

• viscosity of the suspending fluid, μ_l;
• viscosity of the suspension, μ_s;
• particle diameter, d_p;
• density of the grinding media, ρ_b.

3. Results and Discussion

Table 4 shows the specific breakage rates found for the different grinding tests, in the case of 2, 3, and 4 cm ball diameter. The correlation coefficients show that the results of the tests follow a first order law. These values are similar to those mentioned by Tangsathitkulchai [25,26], who found values of specific breakage rate for quartz grinding between 0.21 and 0.24 min⁻¹.

Table 4. Specific breakage rates for the different tests.

		Ball Diameter (cm)
		2		3		4
Monosize (μm)	Suspension Fluid Viscosity (cP)	Sj (min−1)	R2	Sj (min−1)	R2	Sj (min−1)	R2
53	1	0.112	0.9793	0.152	0.9771	0.205	0.9826
53	4	0.215	0.9843	0.171	0.9455	0.155	0.9612
53	6	0.220	0.9739	0.175	0.9892	0.252	0.9890
53	8	0.198	0.9860	0.213	0.9796	0.271	0.9809
45	1	0.108	0.9532	0.153	0.9640	0.044	0.9820
45	4	0.141	0.9814	0.151	0.9834	0.092	0.9869
45	6	0.178	0.9619	0.158	0.9620	0.177	0.9871
45	8	0.087	0.9567	0.165	0.9829	0.199	0.9896
38	1	0.057	0.9638	0.107	0.9797	0.030	0.921
38	4	0.113	0.9824	0.130	0.9891	0.077	0.9706
38	6	0.161	0.9885	0.155	0.9870	0.100	0.9780
38	8	0.044	0.9820	0.163	0.9723	0.053	0.9891

Figure 5, Figure 6 and Figure 7 show the effect of suspension viscosity on the specific breakage rate, S_j, in the case of each monosize. Greater values of S_j pose higher probability of particle breakage, so in general terms it seems that, within certain intervals, an increase in the viscosity of suspension can entail an increase in the breakage probability. This effect is more evident in the case of monosize 53 microns (Figure 5), while in the case of monosizes 45 and 38 microns over some value of suspension viscosity, an increase in suspension viscosity reduces the probability of particle breakage (Figure 6 and Figure 7). This behavior is different in the case of different ball sizes in the grinding charge, although in the case of 3 cm the variations in S_j due to suspension viscosity changes is less noticeable. This probably can be caused by hydrodynamic reasons due to the combination of particle and ball dimensions, and rheological conditions, but this way of analysis evidences that the relationships among variables and their influence cannot be easily analyzed and understood, for further research should be performed to define a clear picture of the phenomenological model. This is the reason why an alternative way of analyzing these data was tried and introduced in this paper. To do this, the following notation is going to be used: We will refer as S_jw in the case of specific breakage rate when the fluid is just water, and S_jd in the rest of the cases in which the water properties have been modified with the dissolution of the abovementioned reagent.

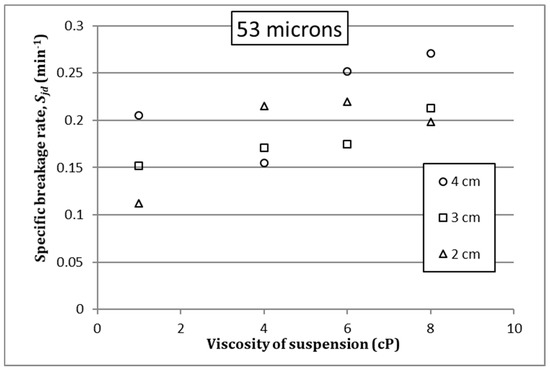
Figure 5. Effect of suspension viscosity on S_jd, monosize 53 microns.

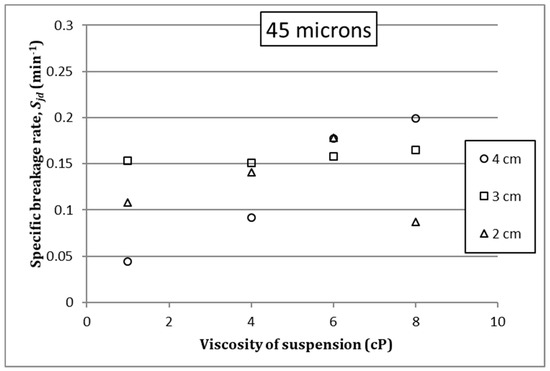
Figure 6. Effect of suspension viscosity on S_jd, monosize 45 microns.

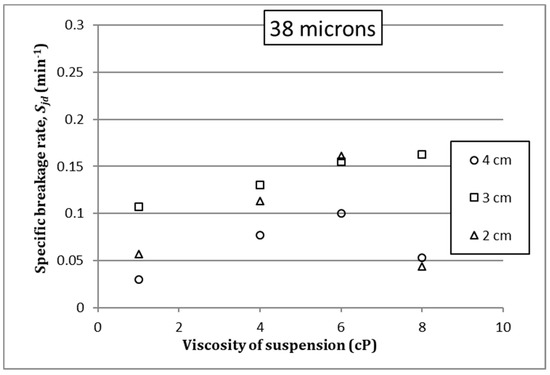
Figure 7. Effect of suspension viscosity on S_jd, monosize 38 microns.

With the aim of performing an analysis of the data obtained in the laboratory tests, the effect of different variables was considered when defining the Π groups. According to the Buckingham’s Pi theorem, the following non-dimensional Π groups were defined:

$${\Pi }_1=\frac{S_{jw}}{S_{jd}}$$

(1)

$${\Pi }_2=\frac{{\mu }_s}{{\rho }_b·S_{jd}·d_p^2}$$

(2)

$${\Pi }_3=\frac{{\mu }_l}{{\rho }_b·S_{jd}·d_p^2}$$

(3)

Being dimensionless parameters, the following relationship can be considered:

$$\frac{{\Pi }_2}{{\Pi }_3}=\frac{{\mu }_s}{{\mu }_l}={\mu }_r$$

(4)

where μ_r is the reduced viscosity.

According to the expressions above, when plotting Π₁ versus Π₂/Π₃ (see Figure 8) we can analyze the behavior the specific grinding rate at different specific gravities as a function of μ_r. Figure 8, Figure 9 and Figure 10 show the behavior of the abovementioned relationship for the systems studied. In all cases, an increase of μ_r poses a decrease in Π₁, that is, an increase in S_jd. In most of the cases the linearity obtained can be satisfactory, although in the case of 2 cm diameter balls, the R² values are lower in the case of the monosizes 45 and 38 microns.

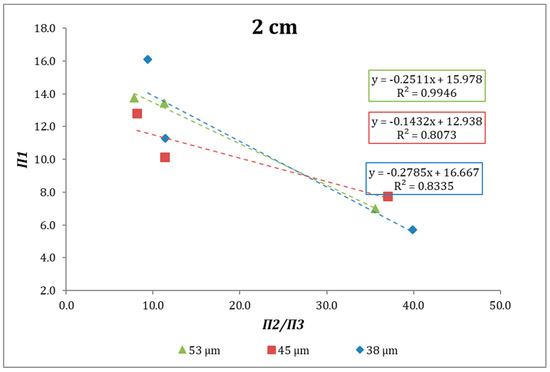
Figure 8. Fitting to the developed model, ball size 2 cm.

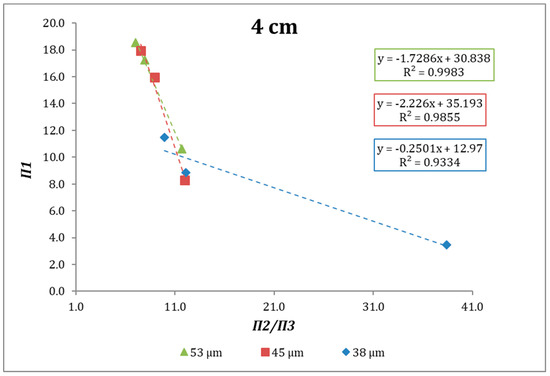
Figure 9. Fitting to the developed model, ball size 3 cm.

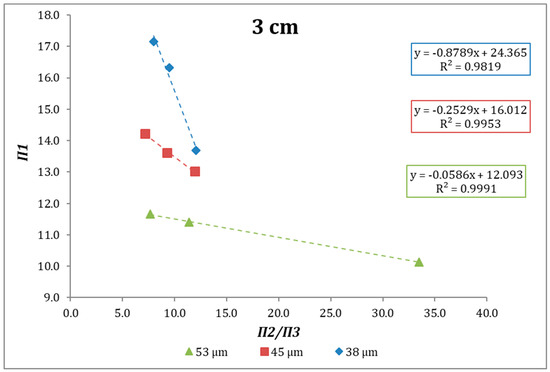
Figure 10. Fitting to the developed model, ball size 4 cm.

It can be observed that there is a reduced viscosity range for which the relationship between the specific fracture rates can be considered linear. The coefficients of the models that represent each system and the suspending fluid viscosity range for which it is valid are shown in Table 5 below.

Table 5. Linear adjustment parameters for the relationship S_jw/S_jd as a function of μ_r.

Ball Size (cm)	Monosize (μm)	a	b	R2	Range of Linearity
2	53	−0.2511	15.9780	0.9946	1–6 cp
	45	−0.1432	12.9380	0.8073	1–6 cp
	38	−0.2785	16.6670	0.8335	1–6 cp
3	53	−0.0586	12.0930	0.9991	1–6 cp
	45	−0.2529	16.0120	0.9953	4–8 cp
	38	−0.8789	24.3650	0.9819	4–8 cp
4	53	−1.7286	30.8380	0.9983	4–8 cp
	45	−2.2260	35.1930	0.9855	4–8 cp
	38	−0.2501	12.9700	0.9334	1–6 cp

Results suggest that the viscosity of the suspension fluid influences the specific breakage rate, and that this influence is different depending on some other conditions, as is the case of ball diameter. The explanation to this phenomenon is that within a given range, an increase in the viscosity increases the chance of particle breakage as the mobility decreases within the slurry. Besides, when the viscosity is increased over a given range, the positive effect of decreasing particle mobility on grinding kinetics is reduced due to energy dissipation in ball dynamics, resulting in an inefficient fragmentation process. Thus, it could be stated that under any grinding conditions there can be defined a fluid viscosity that maximizes the breakage kinetics, and this can be an interesting strategy to optimize the grinding process from the point of view of power efficiency. Nevertheless, further research is needed to get a better understanding of the process and to set a reliable conceptual background in the development of that optimization strategy.

4. Conclusions

The influence of fluid viscosity on specific breakage rate has been studied under different test conditions. In general terms, specific breakage rate can be modified when increasing the suspension viscosity, within certain ranges. For the test conditions, that relationship could be established using the dimensional analysis by means of Pi-Buckingham’s theorem for different grinding conditions. Results suggest that there is a reduced viscosity range for which the relationship between the specific fracture rates can be considered linear. Furthermore, it can be stated that under any grinding conditions a fluid viscosity that maximizes the breakage kinetics can be defined, and this can be an interesting strategy to optimize the grinding process from the point of view of power efficiency. Nevertheless, further research is needed to get a better understanding of the process and to set a reliable conceptual background in the development of that optimization strategy.