The Circular Hill Problem Regarding Arbitrary Disturbing Forces: The Periodic Solutions that are Emerging from the Equilibria

Abstract

In this work, sufficient conditions for computing periodic solutions have been obtained in the circular Hill Problem with regard to arbitrary disturbing forces. This problem will be solved by means of using the averaging theory for dynamical systems as the main mathematical tool that has been applied in this work.

1. Introduction

The three-body problem, as it is known, is a special case of the n—body problem where the motion of three point masses under their mutual gravitational interactions is described. This classical problem represents a large range of astronomical situations. Because a general solution of the problem exists but it is unusable in practice, some simplifications to it have been made. The Hill problem is an example of this. There are many studies on the Hill problem [1,2,3,4,5,6,7,8,9,10,11], and many modifications of this classic problem have appeared in the mathematical, astronomical, and mechanical literature. For example, in [6], Markellos and Roy introduced a photogravitational Hill problem as a simplified, non-trivial form of the photogravitational restricted three-body problem. In [8], Papadakis made a mainly numerical study of this problem on the planar case. On the other hand, in [2], the authors focused their attention on the case of a perturbed spatial Hill lunar problem using the averaging theory, and in [3], Chavineau and Mignard studied the trajectories of the Hill problem to describe the effect of solar perturbations on the relative motion of a binary asteroid. In a central force field, the binary objects case can be approached from potential [4].

Our main goal in this study was to find, using the averaging theory, sufficient conditions for the existence of periodic orbits that come from the Lagrangian points of the circular Hill problem with arbitrary disturbing forces.

Firstly, we assumed that the first two masses were small, compared to the third one (i.e., we assumed $m_1$ and $m_2$ were small as compared to M), and that the two small masses were close together, as compared to their separation from the third mass.

In the case of the circular Hill problem, the equations of the relative motion are [3,4]:

$$\begin{array}{c}{\ddot{q}}_1-2\omega {\dot{q}}_2-3{\omega }^2{q}_1+\frac{Gm{q}_1}{{(q_1^2+q_2^2+q_3^2)}^{3/2}}=0,\hfill \\ {\ddot{q}}_2+2\omega {\dot{q}}_1+\frac{Gm{q}_2}{{(q_1^2+q_2^2+q_3^2)}^{3/2}}=0,\hfill \\ {\ddot{q}}_3+{\omega }^2{q}_3+\frac{Gm{q}_3}{{(q_1^2+q_2^2+q_3^2)}^{3/2}}=0,\hfill \end{array}$$

(1)

where G is the gravitational constant, $m=m_1+m_2$, and $\omega$ is the angular velocity of the motion of the barycenter of the $m_1$-$m_2$ system around M.

The equilibrium solutions of the differential system (1) are given by

$${\mathcal{L}}_1=\left({\left(\frac{Gm}{3{\omega }^2}\right)}^{1/3},0,0\right),{\mathcal{L}}_2=\left(-{\left(\frac{Gm}{3{\omega }^2}\right)}^{1/3},0,0\right).$$

In this work, we provide sufficient conditions for the existence of periodic solutions coming from the equilibrium point, ${\mathcal{L}}_1$. The same conditions are valid for the equilibrium, ${\mathcal{L}}_2.$

Making the change of variables $x=q_1-{\left(\frac{Gm}{3{\omega }^2}\right)}^{1/3}$, $y=q_2$ and $z=q_3$, and linearizing, we can rewrite the unperturbed system of differential Equations (1) in the form:

$$\begin{array}{c}\ddot{x}-9{\omega }^{2}x-2\omega \dot{y}=0,\hfill \\ \ddot{y}+2\omega \dot{x}+3{\omega }^{2}y=0,\hfill \\ \ddot{z}+4{\omega }^{2}z=0.\hfill \end{array}$$

(2)

Using the averaging theory, we will provide a system of nonlinear equations whose simple zeros provide periodic solutions of the perturbed system:

$$\begin{array}{c}\ddot{x}-9{\omega }^{2}x-2\omega \dot{y}=\epsilon F_1(t,x,\dot{x},y,\dot{y},z,\dot{z}),\hfill \\ \ddot{y}+2\omega \dot{x}+3{\omega }^{2}y=\epsilon F_2(t,x,\dot{x},y,\dot{y},z,\dot{z}),\hfill \\ \ddot{z}+4{\omega }^{2}z=\epsilon F_3(t,x,\dot{x},y,\dot{y},z,\dot{z}),\hfill \end{array}$$

(3)

where the parameter $\epsilon$ is small, and $F_1,F_2$ and $F_3$ are the smooth and periodic functions in the variable t in resonance $p:q,(p,q$ positive integers relatively prime) with some of the periodic solutions for $\epsilon =0$.

The unperturbed system (2) has a unique singular point, the origin, with eigenvalues $\pm {\omega }_{1}i,\pm {\omega }_{2}i,$ $\pm {\omega }_3$ with

$${\omega }_1=2\omega ,{\omega }_2=\omega \sqrt{2\sqrt{7}-1}\mathrm{and}{\omega }_3=\omega \sqrt{2\sqrt{7}+1},$$

and thus, the phase space $\left(x,\dot{x},y,\dot{y},z,\dot{z}\right)$ has two planes (excluding the origin) covered by periodic solutions, with periods

$$T_1={\displaystyle \frac{2\pi }{{\omega }_1}}or{T}_2={\displaystyle \frac{2\pi }{{\omega }_2}}.$$

Accordingly, they belong to the plane associated to the eigenvectors with eigenvalues $\pm {\omega }_{1}i$ or $\pm {\omega }_{2}i$, respectively. Now, we are going to study if and when the parameter $\epsilon$ is sufficiently small, and when the perturbed functions $F_i$ for $i\in \{1,2,3\}$ have a period of either $p{T}_1/q$ or $p{T}_2/q$, whether these solutions still exist for the perturbed system (3).

Let $\mathcal{G}=({\mathcal{G}}_1,{\mathcal{G}}_2)$ be the Malkin bifurcation function (see [12]) for the system (3) and $X^0=(X_1^0,X_2^0)$. Then:

$$\begin{array}{c}\hfill {\mathcal{G}}_1\left(X^0\right)=\frac{1}{p{T}_1}{\int }_0^{p{T}_1}cos\left({\omega }_{1}t\right)F_1^{*}\left(t\right)dt,\\ \hfill {\mathcal{G}}_2\left(X^0\right)=\frac{1}{p{T}_1}{\int }_0^{p{T}_1}sin\left({\omega }_{1}t\right)F_1^{*}\left(t\right)dt,\end{array}$$

(4)

where

$$F_1^{*}\left(t\right)=F_3$$

with $F_3=F_3({\sigma }_1^1\left(t\right),\cdots ,{\sigma }_6^1\left(t\right))$, and ${\sigma }_j^1\left(t\right)=0,j=1,\cdots 4$,

$$\begin{array}{cc}\hfill {\sigma }_5^1\left(t\right)& =\frac{X_{1}sin\left(2t\omega \right)-X_{2}cos\left(2t\omega \right)}{2\omega }\hfill \\ \hfill {\sigma }_6^1\left(t\right)& =X_{1}cos\left(2t\omega \right)+X_{2}sin\left(2t\omega \right).\hfill \end{array}$$

As usual, we are going to call a simple zero of the system $\mathcal{G}\left(X^0\right)=0$ to any solution $X^{0*}=(X_1^{0*},X_2^{0*})$, such that $det\left(\frac{\partial \mathcal{G}}{\partial X^0}{|}_{X^0=X^{0*}}\right)\ne 0$.

If $X^{0*}$ is a simple zero, then the $T_1$-periodic solution of the unperturbed system with $X^{0*}$ as the initial value gives a $T_1$-periodic solution of the perturbed system (see Appendix A).

Given an initial condition, we can use this result in order to find sufficient conditions for the existence of families of periodic orbits.

Theorem 1.

Suppose that the functions of the equations of motion of (3), $F_1$, $F_2$, and $F_3$ are smooth and periodic functions of the $p{T}_1/q$ period in the variable t, with p and q being positive integers that are relatively prime, and where the ratio of the frequencies ${\omega }_2/{\omega }_1$ are not resonant with π. If $\epsilon \ne 0$ is sufficiently small, then for every simple zero that is not null, $X^{0*}$, of the nonlinear system $\mathcal{G}\left(X^0\right)=0$, the system (3) has a periodic solution $\left(x\right(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon \left)\right)$ such that $(x(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon ))\to (x\left(t\right),y\left(t\right),z\left(t\right))=({\sigma }_1^1\left(t\right),{\sigma }_3^1\left(t\right),{\sigma }_5^1\left(t\right)){|}_{X^0=X^{0*}}$, when $ϵ\to 0$—that is, when the periodic solution for the unperturbed system (2) travelled p times.

In Section 2, Theorem 1 will be proved using the averaging theory (see [13,14,15,16,17,18]).

In the next corollary, an application of Theorem 1 is shown, whose proof is implemented in Section 3.

Corollary 1.

Assume that $f_i(t,x,\dot{x},y,\dot{y},z,\dot{z}),i=1,2,3$, are arbitrary, smooth functions, and

$$\begin{array}{cc}\hfill F_1(t,x,\dot{x},y,\dot{y},z,\dot{z})& =f_1(t,x,\dot{x},y,\dot{y},z,\dot{z}),\hfill \\ \hfill F_2(t,x,\dot{x},y,\dot{y},z,\dot{z})& =f_2(t,x,\dot{x},y,\dot{y},z,\dot{z}),\hfill \\ \hfill F_3(t,x,\dot{x},y,\dot{y},z,\dot{z})& =sin\left({\omega }_{1}t\right)+\omega \dot{z}+f_3(t,x,\dot{x},y,\dot{y},z,\dot{z})xyz+1.\hfill \end{array}$$

If $\epsilon \ne 0$ is sufficiently small, the perturbed system (3) has one periodic solution $\left(x\right(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon \left)\right)$ such that, whenever $\epsilon \to 0$, $\left(x\right(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon \left)\right)$ tends to the periodic solution of the unperturbed system $(x\left(t\right),y\left(t\right),z\left(t\right))=({\sigma }_1^1\left(t\right),{\sigma }_3^1\left(t\right),{\sigma }_5^1\left(t\right)){|}_{X^0=\left(0,\sqrt[3]{\frac{4}{3\omega }}\right)}$.

This corollary will be proved in Section 3.

Figure 1 shows the solution of the system (3) for the smooth function $F_1$, $F_2$ and $F_3$.

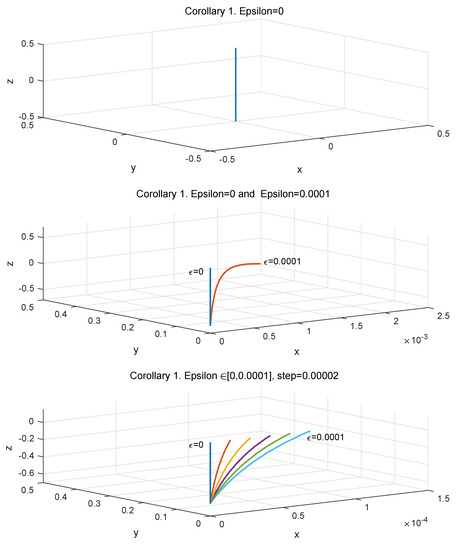
Figure 1. Solutions of the differential system (3) for the smooth functions $F_1=1-x{\dot{x}}^2-sin\left({\omega }_{1}t\right)y$, $F_2=sin\left({\omega }_{1}t\right){\dot{x}}^2-yz+z^2$, and $F_3=sin\left({\omega }_{1}t\right)+\omega \dot{z}+\dot{x}xyz+1$ for Corollary 1 with $\epsilon >0$, $w=1$, ${\omega }_1=2\omega$, $t=[0,2\pi /{\omega }_1]$, and $X^{0*}=\left(0,\sqrt[3]{\frac{4}{3\omega }}\right)$.

Let $\overline{\mathcal{G}}=({\mathcal{G}}_3,{\mathcal{G}}_4)$ be the Malkin bifurcation function (see [12]) for system (3) and $Y^0=(Y_1^0,Y_2^0)$. Then:

$$\begin{array}{c}\hfill {\mathcal{G}}_3\left(Y^0\right)=\frac{1}{p{T}_2}{\int }_0^{p{T}_2}[cos\left({\omega }_{2}t\right)F_3^{*}\left(t\right)-sin\left({\omega }_{2}t\right)F_4^{*}\left(t\right)]dt,\\ \hfill {\mathcal{G}}_4\left(Y^0\right)=\frac{1}{p{T}_2}{\int }_0^{p{T}_2}[cos\left({\omega }_{2}t\right)F_4^{*}\left(t\right)+sin\left({\omega }_{2}t\right)F_3^{*}\left(t\right)]dt,\end{array}$$

where

$$F_3^{*}\left(t\right)=\left(\frac{1}{2}+\frac{2}{\sqrt{7}}\right)F_2\mathrm{and}{F}_4^{*}\left(t\right)=-\frac{1}{2}\sqrt{\frac{2}{\sqrt{7}}-\frac{1}{7}}{F}_1$$

with $F_i=F_i({\sigma }_1^2\left(t\right),\cdots ,{\sigma }_6^2\left(t\right)),i=1,2,$ and

$$\begin{array}{cc}\hfill {\sigma }_1^2\left(t\right)& =-\frac{1}{9\omega }\left(4-\sqrt{7}\right)\left(Y_{1}cos\left(\sqrt{2\sqrt{7}-1}\omega t\right)+Y_{2}sin\left(\sqrt{2\sqrt{7}-1}\omega t\right)\right)\hfill \\ \hfill {\sigma }_2^2\left(t\right)& =-\frac{\left(\sqrt{7}-2\right)\left(Y_{2}cos\left(\sqrt{2\sqrt{7}-1}\omega t\right)-Y_{1}sin\left(\sqrt{2\sqrt{7}-1}\omega t\right)\right)}{\sqrt{2\sqrt{7}-1}}\hfill \\ \hfill {\sigma }_3^2\left(t\right)& =-\frac{Y_{2}cos\left(\sqrt{2\sqrt{7}-1}\omega t\right)-Y_{1}sin\left(\sqrt{2\sqrt{7}-1}\omega t\right)}{\sqrt{2\sqrt{7}-1}\omega }\hfill \\ \hfill {\sigma }_4^2\left(t\right)& =Y_{1}cos\left(\sqrt{2\sqrt{7}-1}\omega t\right)+Y_{2}sin\left(\sqrt{2\sqrt{7}-1}\omega t\right)\hfill \end{array}$$

and ${\sigma }_j^2\left(t\right)=0,j=5,6$.

As has been stated before, if $Y^{0*}$ is a simple zero of $\overline{\mathcal{G}}\left(Y^{0*}\right)=0$, then the $T_2$-periodic solution of the unperturbed system with $Y^{0*}$ as the initial value gives a $T_2$-periodic solution of the perturbed system (see Appendix A).

Theorem 2.

Suppose that the functions of the equations of motion of (3), $F_1$, $F_2$, and $F_3$, are smooth and periodic functions of the $p{T}_2/q$ period in the variable t, with p and q positive integers relatively prime, and the ratio of the frequencies ${\omega }_2/{\omega }_1$ not resonant with π. If $\epsilon \ne 0$ is sufficiently small, then for every simple and not null zero, $Y^{0*}$ of the nonlinear system $\overline{\mathcal{G}}\left(Y^0\right)=0$, the system (3) has a periodic solution $\left(x\right(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon \left)\right)$ such that $(x(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon ))\to (x\left(t\right),y\left(t\right),z\left(t\right))=({\sigma }_1^2\left(t\right),{\sigma }_3^2\left(t\right),{\sigma }_5^2\left(t\right)){|}_{Y^0=Y^{0*}}$, when $ϵ\to 0$—that is, when the periodic solution for the unperturbed system (2) travelled p times.

The proof of Theorem 2 is given in Section 2.

In the next corollary, an application of Theorem 2 is shown, whose proof is implemented in Section 3.

Corollary 2.

Let $g\left(t\right)$ be the arbitrary and smooth function, and thus consider:

$$\begin{array}{cc}\hfill F_1(t,x,\dot{x},y,\dot{y},z,\dot{z})& =(1+x\dot{z})sin\left({\omega }_{2}t\right),\hfill \\ \hfill F_2(t,x,\dot{x},y,\dot{y},z,\dot{z})& =x+\dot{y}+2z,\hfill \\ \hfill F_3(t,x,\dot{x},y,\dot{y},z,\dot{z})& =x^3+{\dot{y}}^2+g\left(t\right).\hfill \end{array}$$

If $\epsilon \ne 0$ is sufficiently small, the perturbed system (3) has one periodic solution, $\left(x\right(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon \left)\right)$ such that, whenever $\epsilon \to 0$, $\left(x\right(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon \left)\right)$ tends to the periodic solution of the unperturbed system $(x\left(t\right),y\left(t\right),z\left(t\right))=({\sigma }_1^2\left(t\right),{\sigma }_3^2\left(t\right),{\sigma }_5^2\left(t\right)){|}_{Y^0=\left(\frac{\sqrt{14\sqrt{7}-7}w}{\sqrt{7}-\left(7+4\sqrt{7}\right)w},0\right)}$, $\omega \ne \frac{1}{9}\left(4-\sqrt{7}\right)$.

Corollary 2 will be proved in Section 3.

Figure 2 shows the solution of the system (3) for the smooth function, $F_1$, $F_2$ and $F_3$.

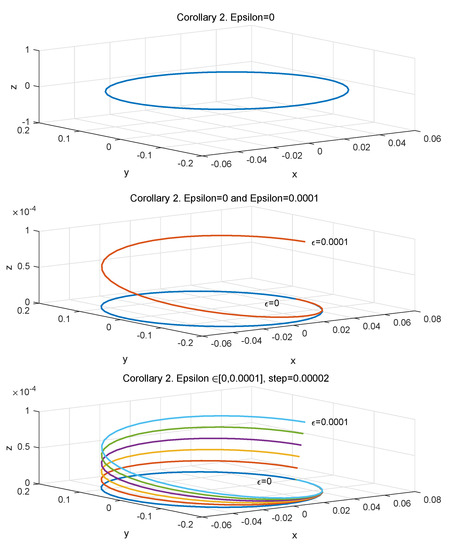
Figure 2. Solutions of the differential system (3) for the smooth functions $F_1=(1+x\dot{z})sin\left({\omega }_{2}t\right)$, $F_2=x+\dot{y}+2z$ and $F_3=x^3+{\dot{y}}^2+t$ for Corollary 2 with $\epsilon >0$, $w=1$, ${\omega }_2=\omega \sqrt{2\sqrt{7}-1}$, $t=[0,2\pi /{\omega }_2]$ and $Y^{0*}=\left(\frac{\sqrt{14\sqrt{7}-7}w}{\sqrt{7}-\left(7+4\sqrt{7}\right)w},0\right)$.

2. Proof of Theorems 1 and 3

The differential system (3) must be written as a first-order differential system defined in ${\mathbb{R}}^6$. For that, the variables $(x_1,x_2,y_1,y_2,z_1,z_2)=(x,\dot{x},y,\dot{y},z,\dot{z})$ have been introduced in the following form, this being:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{x}_1}{dt}}& =x_2\hfill \\ \hfill {\displaystyle \frac{d{x}_2}{dt}}& =9{\omega }^2{x}_1+2\omega y_2+\epsilon F_1(x_1,x_2,y_1,y_2,z_1,z_2)\hfill \\ \hfill {\displaystyle \frac{d{y}_1}{dt}}& =y_2\hfill \\ \hfill {\displaystyle \frac{d{y}_2}{dt}}& =-2\omega x_2-3{\omega }^2{y}_1+\epsilon F_2(x_1,x_2,y_1,y_2,z_1,z_2)\hfill \\ \hfill {\displaystyle \frac{d{z}_1}{dt}}& =z_2\hfill \\ \hfill {\displaystyle \frac{d{z}_2}{dt}}& =-4{\omega }^2{z}_1+\epsilon F_3(x_1,x_2,y_1,y_2,z_1,z_2).\hfill \end{array}$$

(5)

It must be remarked that if $\epsilon =0$, the differential system (5) is equivalent to the differential system (2), well-known as the unperturbed system. Otherwise, when $\epsilon \ne 0$, this is known as the perturbed system

The change of variables $({\overline{x}}_1,{\overline{x}}_2,{\overline{y}}_1,{\overline{y}}_2,{\overline{z}}_1,{\overline{z}}_2)\to (x_1,x_2,y_1,y_2,z_1,z_2)$ given by

$$\left(\begin{array}{c}{x}_1\\ x_2\\ y_1\\ y_2\\ z_1\\ z_2\end{array}\right)=\left(\begin{array}{cccccc}0& 0& \frac{\sqrt{7}-4}{9w}& 0& -\frac{4+\sqrt{7}}{9w}& -\frac{4+\sqrt{7}}{9w}\\ 0& 0& 0& \frac{2-\sqrt{7}}{\sqrt{-1+2\sqrt{7}}}& -\frac{2+\sqrt{7}}{\sqrt{1+2\sqrt{7}}}& \frac{2+\sqrt{7}}{\sqrt{1+2\sqrt{7}}}\\ 0& 0& 0& -\frac{1}{\sqrt{-1+2\sqrt{7}}w}& \frac{1}{\sqrt{1+2\sqrt{7}}w}& -\frac{1}{\sqrt{1+2\sqrt{7}}w}\\ 0& 0& 1& 0& 1& 1\\ 0& -\frac{1}{2w}& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0\end{array}\right)\left(\begin{array}{c}{\overline{x}}_1\\ {\overline{x}}_2\\ {\overline{y}}_1\\ {\overline{y}}_2\\ {\overline{z}}_1\\ {\overline{z}}_2\end{array}\right)$$

(6)

writes the linear part of the differential system (5) in its real Jordan normal form, and this system in the new variables $\overline{x}=({\overline{x}}_1,{\overline{x}}_2,{\overline{y}}_1,{\overline{y}}_2,{\overline{z}}_1,{\overline{z}}_2)$ becomes

$$\begin{array}{cc}\hfill {\dot{\overline{x}}}_1& ={\omega }_1{\overline{x}}_2+\epsilon F_1^{*}\hfill \\ \hfill {\dot{\overline{x}}}_2& =-{\omega }_1{\overline{x}}_1+\epsilon F_2^{*}\hfill \\ \hfill {\dot{\overline{y}}}_1& ={\omega }_2{\overline{y}}_2+\epsilon F_3^{*}\hfill \\ \hfill {\dot{\overline{y}}}_2& =-{\omega }_2{\overline{y}}_1+\epsilon F_4^{*}\hfill \\ \hfill {\dot{\overline{z}}}_1& ={\omega }_3{\overline{z}}_1+\epsilon F_5^{*}\hfill \\ \hfill {\dot{\overline{z}}}_2& =-{\omega }_3{\overline{z}}_2+\epsilon F_6^{*},\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill F_1^{*}& =F_3\hfill \\ \hfill F_2^{*}& =0\hfill \\ \hfill F_3^{*}& =\left(\frac{1}{2}+\frac{2}{\sqrt{7}}\right)F_2\hfill \\ \hfill F_4^{*}& =-\frac{1}{2}\sqrt{\frac{2}{\sqrt{7}}-\frac{1}{7}}{F}_1\hfill \\ \hfill F_5^{*}& =\left(\frac{1}{4}-\frac{1}{\sqrt{7}}\right)F_2-\frac{1}{4}\sqrt{\frac{1}{7}+\frac{2}{\sqrt{7}}}{F}_1\hfill \\ \hfill F_6^{*}& =\left(\frac{1}{4}-\frac{1}{\sqrt{7}}\right)F_2+\frac{1}{4}\sqrt{\frac{1}{7}+\frac{2}{\sqrt{7}}}{F}_1\hfill \end{array}$$

with $F_i=F_i({\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4,{\sigma }_5,{\sigma }_6)$, and

$$\begin{array}{cc}\hfill {\sigma }_1& =\frac{\left(\sqrt{7}-4\right){\overline{y}}_1-\left(4+\sqrt{7}\right)({\overline{z}}_1+{\overline{z}}_2)}{9w}\hfill \\ \hfill {\sigma }_2& =\frac{\sqrt{5+2\sqrt{7}}({\overline{z}}_2-{\overline{z}}_1)-\sqrt{2\sqrt{7}-5}{\overline{y}}_2}{\sqrt{3}}\hfill \\ \hfill {\sigma }_3& =\frac{\sqrt{2\sqrt{7}-1}({\overline{z}}_1-{\overline{z}}_2)-\sqrt{1+2\sqrt{7}}{\overline{y}}_2}{3\sqrt{3}w}\hfill \\ \hfill {\sigma }_4& ={\overline{y}}_1+{\overline{z}}_1+{\overline{z}}_2\hfill \\ \hfill {\sigma }_5& =-\frac{{\overline{x}}_2}{2\omega }\hfill \\ \hfill {\sigma }_6& ={\overline{x}}_1.\hfill \end{array}$$

In order to prove Theorems 1 and 2, in the following lemma we are going to obtain the general expressions of the periodic orbits of the unperturbed system.

Lemma 1.

If $ϵ=0$, the $T_1$—periodic solutions of the system of the differential Equations (7) are

$$\begin{array}{cc}\hfill {\overline{x}}_1\left(t\right)& =X_1^{0}cos\left({\omega }_{1}t\right)+X_2^{0}sin\left({\omega }_{1}t\right),\hfill \\ \hfill {\overline{x}}_2\left(t\right)& =X_2^{0}cos\left({\omega }_{1}t\right)-X_1^{0}sin\left({\omega }_{1}t\right),\hfill \\ \hfill {\overline{y}}_1\left(t\right)& =0,\hfill \\ \hfill {\overline{y}}_2\left(t\right)& =0,\hfill \\ \hfill {\overline{z}}_1\left(t\right)& =0,\hfill \\ \hfill {\overline{z}}_2\left(t\right)& =0,\hfill \end{array}$$

(8)

and the $T_2$—periodic solutions are

$$\begin{array}{cc}\hfill {\overline{x}}_1\left(t\right)& =0,\hfill \\ \hfill {\overline{x}}_2\left(t\right)& =0,\hfill \\ \hfill {\overline{y}}_1\left(t\right)& =Y_1^{0}cos\left({\omega }_{2}t\right)+Y_2^{0}sin\left({\omega }_{2}t\right),\hfill \\ \hfill {\overline{y}}_2\left(t\right)& =Y_2^{0}cos\left({\omega }_{2}t\right)-Y_1^{0}sin\left({\omega }_{2}t\right),\hfill \\ \hfill {\overline{z}}_1\left(t\right)& =0,\hfill \\ \hfill {\overline{z}}_2\left(t\right)& =0.\hfill \end{array}$$

Proof of Lemma 1.

If $\epsilon =0$, the system (7) is a system of linear differential equations, and the proof follows easily. □

Proof of Theorem 1.

Since the positive integers p and q are relatively prime, and the functions $F_i,i=1,2,3,$ of the system (3) are $p{T}_1/q$—periodic in the variable t, we can consider that the system (7) and the solutions (8) are $p{T}_1$—periodic.

Now, we shall study what periodic solutions of the unperturbed system (7) with $\epsilon =0$ of the type (8) persist as periodic solutions, with the perturbed one for $\epsilon \ne 0$ being sufficiently small.

If we write the system (7) in the form

$$\dot{\mathrm{x}}\left(t\right)=G_0(t,\overline{\mathrm{x}})+ϵG_1(t,\overline{\mathrm{x}})+{ϵ}^2{G}_2(t,\overline{\mathrm{x}},ϵ),$$

where

$$\overline{\mathrm{x}}=\left(\begin{array}{c}{\overline{x}}_1\\ {\overline{x}}_2\\ {\overline{y}}_1\\ {\overline{y}}_2\\ {\overline{z}}_1\\ {\overline{z}}_2\end{array}\right),G_0(t,\overline{\mathrm{x}})=\left(\begin{array}{c}{\omega }_1{\overline{x}}_2\\ -{\omega }_1{\overline{x}}_1\\ {\omega }_2{\overline{y}}_2\\ -{\omega }_2{\overline{y}}_1\\ {\omega }_3{\overline{z}}_1\\ -{\omega }_3{\overline{z}}_2\end{array}\right),G_1(t,\overline{\mathrm{x}})=\left(\begin{array}{c}{F}_1^{*}\\ F_2^{*}\\ F_3^{*}\\ F_4^{*}\\ F_5^{*}\\ F_6^{*}\end{array}\right),G_2(t,\overline{\mathrm{x}},\epsilon )=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right),$$

we can apply Theorem A1 of the Appendix A. Our starting point is the description of the different elements which appear in this theorem for the particular case of the differential system (7). In this case, $\mathsf{\Omega }={\mathbb{R}}^6,k=2$, and $n=6$. Now, let $r_1>0$ be arbitrarily small, and let $r_2>0$ be arbitrarily large. If V is the open and bounded subset of the plane ${\overline{x}}_i=0,i=3,\cdots ,6$, of the form $V=\{(X_1^0,X_2^0,0,0,0,0)\in {\mathbb{R}}^6:r_1<\sqrt{{\displaystyle \sum _{i=1}^2}{\left(X_i^0\right)}^2}<r_2\}$. If $\alpha =(X_1^0,X_2^0)$, then we identify V with the set $\{\alpha \in {\mathbb{R}}^2:r_1<|\left|\alpha \right||<r_2\}$, where $\left|\right|·\left|\right|$ is the Euclidean norm in ${\mathbb{R}}^2$. If we denote by Cl$\left(V\right)$, the closure of V, the function $\beta :\mathrm{Cl}\left(\mathrm{V}\right)\to {\mathbb{R}}^4$ is $\beta \left(\alpha \right)=(0,0,0,0)$. Using all these elements in our system, we have

$$\begin{array}{cc}\hfill \mathcal{Z}& =\{{\mathrm{z}}_{\alpha }=(\alpha ,\beta \left(\alpha \right)),\alpha \in \mathrm{Cl}\left(V\right)\}=\hfill \\ & =\{(X_1^0,X_2^0,0,0,0,0)\in {\mathbb{R}}^6:r_1\le \sqrt{{\displaystyle \sum _{i=1}^2}{\left(X_i^0\right)}^2}\le r_2\}\hfill \end{array}$$

Now, for each ${\mathrm{z}}_{\alpha }\in \mathcal{Z}$, we consider the $p{T}_1$—periodic solution

$$\mathrm{x}(t,{\mathrm{z}}_{\alpha })=(X_1\left(t\right),X_2\left(t\right),0,0,0,0)$$

given by (8).

The fundamental matrix $M_{{\mathrm{z}}_{\alpha }}\left(t\right)$ of the linear differential system (7) with $\epsilon =0$, that is, associated to the $p{T}_1$—periodic solution ${\mathrm{z}}_{\alpha }=(X_1^0,X_2^0,0,0,0,0)$ and such that $M_{{\mathrm{z}}_{\alpha }}\left(0\right)=Id$ in ${\mathbb{R}}^6$, is

$$M_{{\mathrm{z}}_{\alpha }}\left(t\right)=M\left(t\right)=$$

$$=\left(\begin{array}{cccccc}cos\left({\omega }_{1}t\right)& sin\left({\omega }_{1}t\right)& 0& 0& 0& 0\\ -sin\left({\omega }_{1}t\right)& cos\left({\omega }_{1}t\right)& 0& 0& 0& 0\\ 0& 0& cos\left({\omega }_{2}t\right)& sin\left({\omega }_{2}t\right)& 0& 0\\ 0& 0& -sin\left({\omega }_{2}t\right)& cos\left({\omega }_{2}t\right)& 0& 0\\ 0& 0& 0& 0& e^{{\omega }_{3}t}& 0\\ 0& 0& 0& 0& 0& e^{-{\omega }_{3}t}\end{array}\right),$$

where $M\left(t\right)$ does not depend on the particular periodic solution $\mathrm{x}(t,{\mathrm{z}}_{\alpha },0)$.

Computing the matrix $M=M^{-1}\left(0\right)-M^{-1}\left(p{T}_1\right)$, we get

$$M=\left(\begin{array}{cccccc}2{sin}^2\left(p\pi \right)& sin\left(2p\pi \right)& 0& 0& 0& 0\\ -sin\left(2p\pi \right)& 2{sin}^2\left(p\pi \right)& 0& 0& 0& 0\\ 0& 0& 2{sin}^2\left(\frac{p\pi {\omega }_2}{{\omega }_1}\right)& sin\left(\frac{2p\pi {\omega }_2}{{\omega }_1}\right)& 0& 0\\ 0& 0& -sin\left(\frac{2p\pi {\omega }_2}{{\omega }_1}\right)& 2{sin}^2\left(\frac{p\pi {\omega }_2}{{\omega }_1}\right)& 0& 0\\ 0& 0& 0& 0& 1-e^{-\frac{2p\pi {\omega }_3}{{\omega }_1}}& 0\\ 0& 0& 0& 0& 0& 1-e^{\frac{2p\pi {\omega }_3}{{\omega }_1}},\end{array}\right)$$

and M satisfies the assumptions of statement (ii) of Theorem A1, since the determinant

$$\left|\begin{array}{cccc}2{sin}^2\left(\frac{p\pi {\omega }_2}{{\omega }_1}\right)& sin\left(\frac{2p\pi {\omega }_2}{{\omega }_1}\right)& 0& 0\\ -sin\left(\frac{2p\pi {\omega }_2}{{\omega }_1}\right)& 2{sin}^2\left(\frac{p\pi {\omega }_2}{{\omega }_1}\right)& 0& 0\\ 0& 0& 1-e^{-\frac{2p\pi {\omega }_3}{{\omega }_1}}\\ 0& 0& 0& 1-e^{\frac{2p\pi {\omega }_3}{{\omega }_1}}\end{array}\right|=$$

$$=-16{sinh}^2\left(\frac{p\pi {\omega }_3}{{\omega }_1}\right){sin}^2\left(\frac{p\pi {\omega }_2}{{\omega }_1}\right)\ne 0,$$

owing to the ratio of the frequencies, is non-resonant with $\pi$. In other words, all the assumptions of Theorem A1 are satisfied by the system (7).

In our particular system, if $\overline{x}=({\overline{x}}_1,{\overline{x}}_2,{\overline{y}}_1,{\overline{y}}_2,{\overline{z}}_1,{\overline{z}}_2)$, the map $\xi$: ${\mathbb{R}}^6\to {\mathbb{R}}^2$ is given by $\xi \left(\overline{x}\right)=({\overline{x}}_1,{\overline{x}}_2)$, and if we calculate the function $\mathcal{G}(X_1^0,X_2^0)$

$$\mathcal{G}(X_1^0,X_2^0)=\mathcal{G}\left(\alpha \right)=\xi \left(\frac{1}{p{T}_1}{\int }_0^{p{T}_1}{M}_{{\mathrm{z}}_{\alpha }}^{-1}\left(t\right)G_1(t,\overline{\mathrm{x}}(t,{\mathrm{z}}_{\alpha },0))dt\right),$$

we obtain $\mathcal{G}\left(X^0\right)=({\mathcal{G}}_1\left(X^0\right),{\mathcal{G}}_2\left(X^0\right))$, where the functions ${\mathcal{G}}_1,{\mathcal{G}}_2$ are given in (4). Then, by means of Theorem A1 of the Appendix A, for every simple zero $X^{0*}\in V$ of the system of nonlinear functions $\mathcal{G}\left(X^0\right)=0$, there is a periodic solution $({\overline{x}}_1(t,\epsilon ),{\overline{x}}_2(t,\epsilon ),{\overline{y}}_1(t,\epsilon ),{\overline{y}}_2(t,\epsilon ),{\overline{z}}_1(t,\epsilon ),{\overline{z}}_2(t,\epsilon ))$ of system (7), so that

$$({\overline{x}}_1(0,\epsilon ),{\overline{x}}_2(0,\epsilon ),{\overline{y}}_1(0,\epsilon ),{\overline{y}}_2(0,\epsilon ),{\overline{z}}_1(0,\epsilon ),{\overline{z}}_2(0,\epsilon ))\stackrel{\epsilon \to 0}{\to }(X_1^{0*},X_2^{0*},0,0,0,0).$$

Going back through the change of variables (6), the periodic solution $(x_1(t,\epsilon ),x_2(t,\epsilon ),y_1(t,\epsilon ),y_2(t,\epsilon ),z_1(t,\epsilon ),z_2(t,\epsilon ))$ of system (7) has been obtained, so that

$$\left(\begin{array}{c}{x}_1(t,\epsilon )\\ x_2(t,\epsilon )\\ y_1(t,\epsilon )\\ y_2(t,\epsilon )\\ z_1(t,\epsilon )\\ z_2(t,\epsilon )\end{array}\right)\to \left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ \frac{X_{1}sin\left(2t\omega \right)-X_{2}cos\left(2t\omega \right)}{2\omega }\\ X_{1}cos\left(2t\omega \right)+X_{2}sin\left(2t\omega \right)\end{array}\right)\mathrm{when}\epsilon \to 0.$$

Consequently, a periodic solution $\left(x\right(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon \left)\right)$ of system (3) has been achieved, so that

$$(x(t,\epsilon ),y(t,\epsilon ),z(t,\epsilon ))\to \left(\begin{array}{c}0\\ 0\\ \frac{X_{1}sin\left(2t\omega \right)-X_{2}cos\left(2t\omega \right)}{2\omega }\end{array}\right)\mathrm{when}\epsilon \to 0.$$

This completes the proof of Theorem 1. □

Proof of Theorem 2.

The proof is analogous to the proof of Theorem 1 changing the roles of $T_1$ for $T_2$, and we obtain the periodic solution

$$\left(\begin{array}{c}-\frac{\left(4-\sqrt{7}\right)\left(Y_{1}cos\left(\sqrt{2\sqrt{7}-1}t\omega \right)+Y_{2}sin\left(\sqrt{2\sqrt{7}-1}t\omega \right)\right)}{9\omega }\\ -\frac{\left(\sqrt{7}-2\right)\left(Y_{2}cos\left(\sqrt{2\sqrt{7}-1}t\omega \right)-Y_{1}sin\left(\sqrt{2\sqrt{7}-1}t\omega \right)\right)}{\sqrt{2\sqrt{7}-1}}\\ -\frac{Y_{2}cos\left(\sqrt{2\sqrt{7}-1}t\omega \right)-Y_{1}sin\left(\sqrt{2\sqrt{7}-1}t\omega \right)}{\sqrt{2\sqrt{7}-1}\omega }\\ Y_{1}cos\left(\sqrt{2\sqrt{7}-1}t\omega \right)+Y_{2}sin\left(\sqrt{2\sqrt{7}-1}t\omega \right)\\ 0\\ 0\end{array}\right)\mathrm{when}\epsilon \to 0.$$

In consequence, a periodic solution $(x,y,z)(t,\epsilon )$ of system (3) has been obtained, so that

$$(x,y,z)(t,\epsilon )\to \left(\begin{array}{c}-\frac{\left(4-\sqrt{7}\right)\left(Y_{1}cos\left(\sqrt{2\sqrt{7}-1}t\omega \right)+Y_{2}sin\left(\sqrt{2\sqrt{7}-1}t\omega \right)\right)}{9\omega }\\ -\frac{Y_{2}cos\left(\sqrt{2\sqrt{7}-1}t\omega \right)-Y_{1}sin\left(\sqrt{2\sqrt{7}-1}t\omega \right)}{\sqrt{2\sqrt{7}-1}\omega }\\ 0\end{array}\right)\mathrm{when}\epsilon \to 0.$$

□

3. Proof of Corollaries 1 and 2

Proof of Corollary 1.

Under the assumptions of Corollary 1, we have the function

$$\begin{array}{cc}\hfill {\mathcal{G}}_1\left(X^0\right)& =\frac{1}{p{T}_1}{\int }_0^{p{T}_1}cos\left({\omega }_{1}t\right)F_1^{*}\left(t\right)dt=\frac{3}{8}{X}_1^0\left[{\left(X_1^0\right)}^2+{\left(X_2^0\right)}^2\right]\omega ,\hfill \\ \hfill {\mathcal{G}}_2\left(X^0\right)& =\frac{1}{p{T}_1}{\int }_0^{p{T}_1}sin\left({\omega }_{1}t\right)F_1^{*}\left(t\right)dt=\frac{1}{8}[4+3{\left(X_1^0\right)}^2{X}_2^0\omega +3{\left(X_2^0\right)}^3\omega ]\hfill \end{array}$$

and

$$det{\left.\left(\frac{\partial \mathcal{G}}{\partial X^0}\right)\right|}_{X^{0*}=(X_1^0,X_2^0)}=\frac{3}{8}\sqrt[3]{\frac{9{\omega }^2}{2}}\ne 0,\forall X_1^0,X_2^0\in \mathbb{R},\omega \ne 0$$

Therefore, the solution $X^{0*}=\left(0,\sqrt[3]{\frac{4}{3\omega }}\right)$ of the nonlinear system $\mathcal{G}\left(X^0\right)=0$ is simple, and by Theorem 1 we only have one periodic solution for the system of this corollary. □

Proof of Corollary 2.

Under the assumptions of Corollary 2, we have the function

$$\begin{array}{cc}\hfill {\mathcal{G}}_3\left(Y^0\right)& =\frac{1}{p{T}_2}{\int }_0^{p{T}_2}\left[cos\left({\omega }_{2}t\right)F_3^{*}\left(t\right)-sin\left({\omega }_{2}t\right)F_4^{*}\left(t\right)\right]dt=\hfill \\ \hfill & =\frac{w\left(\left(7+4\sqrt{7}\right)Y_1^0+\sqrt{14\sqrt{7}-7}\right)-\sqrt{7}{Y}_1^0}{28w}\hfill \\ \hfill {\mathcal{G}}_4\left(Y^0\right)& =\frac{1}{p{T}_2}{\int }_0^{p{T}_2}\left[cos\left({\omega }_{2}t\right)F_4^{*}\left(t\right)+sin\left({\omega }_{2}t\right)F_3^{*}\left(t\right)\right]dt=\hfill \\ \hfill & =\frac{1}{28}{Y}_2^0\left(-\frac{\sqrt{7}}{w}+4\sqrt{7}+7\right),\hfill \end{array}$$

and, if $\omega \ne \frac{1}{9}(4-\sqrt{7})$,

$$det{\left.\left(\frac{\partial \overline{\mathcal{G}}}{\partial Y^0}\right)\right|}_{Y^{0*}=(Y_1^0,Y_2^0)}=\frac{1}{112}\left(\frac{1}{w^2}-\frac{2\left(4+\sqrt{7}\right)}{w}+8\sqrt{7}+23\right)\ne 0.$$

Therefore, the solution $Y^{0*}=\left(\frac{\sqrt{14\sqrt{7}-7}w}{\sqrt{7}-\left(7+4\sqrt{7}\right)w},0\right)$ of the nonlinear system $\overline{\mathcal{G}}\left(Y^0\right)=0$ is simple. By means of Theorem 1, the system of this Corollary has only this periodic solution. □