1. Introduction
A graph is a tool for describing the complex systems, such as biological [
1], chemical [
2], and electronic interactive systems [
3]. In many cases, these systems are accompanied by the temporal information. One example is that in the social network the time when people send the messages is always recorded [
4]. Another example is that the chronological order of the packet transmission is also concerned in cyber network [
5]. Obviously, the temporal information is a key component of such systems. For the purpose of analysis, the complex systems are usually represented by the networks (graphs). However, the static networks cannot describe the complex systems that contain the temporal information. Therefore, the temporal network, in which each edge has a timestamp, is proposed [
6].
Graph pattern counting is a fundamental problem in network analysis, including anomaly detection [
7], community detection [
8], internet traffic classification [
9] and so on. Usually, the graph pattern refers to small and induced subgraph, which is also called motif or graphlet. In particular, for the temporal network, if the graph pattern has temporal information, then the pattern becomes temporal graph pattern (TGP). TGP has been widely studied and is more commonly known as temporal motif in many studies. According to the application scenario, there are two kinds of definitions about temporal motif. The first definition is the network motif for the graph snapshots at different time points, in which the edges have continuous timestamps [
10]. The second definition is the temporal motif of a whole temporal graph. In this paper, we consider the second type of temporal motif.
The counting problem of small graph pattern in static network has been proposed for a long time and attracted widespread attention, especially the triangle counting in social network analysis [
11,
12,
13]. Until now, most of the triangle counting algorithms are estimation algorithms, and the graph stream model has been applied in the algorithms to optimize memory usage [
12,
14]. In recent years, more and more scholars have shown interest in the problem of counting a large graph pattern (i.e., the pattern with more than three vertexes) [
15,
16,
17]. The counting algorithms can be divided into two categories: the exact algorithms and the estimation algorithms. The former is designed for the graph pattern with no more than five vertexes and has low efficiency [
15,
16,
17,
18,
19,
20,
21]. Even for the fastest exact algorithm, the Efficient Subgraph Counting Algorithmic PackagE (ESCAPE) [
15], it takes a week to count the five-vertex graph pattern in a graph with a million vertexes. Compared to the exact algorithms, the estimation algorithms reduce the search space by sampling the graph and thus improve the computational efficiency [
18,
19,
20,
21]. Rahman et al. [
22] reduced the counting time by sampling the edges. Bhuiyan et al. [
21] used a Markov chain to uniformly sample motifs and obtained the counts of three-, four-, and five-vertex graphlets. In the existing estimation algorithm, the most frequently used sampling methods are path sampling [
23], random walk [
19] and color coding [
20,
24], where the path sampling can not be applied to count the graph pattern with more than five vertexes, while the other two methods can be used for larger graph patterns.
The above algorithms are designed for graph pattern counting in static network. They cannot be directly applied to the temporal network because the problems in temporal network and static network are totally different. Firstly, the temporal network has temporal information, while the static network does not. Secondly, the edges of the TGP have a chronological order, while the edges of the static graph pattern do not. Thirdly, the graph isomorphism of the temporal network, which is more complex than that of the static network, considering not only the topology structure isomorphism but also the chronological order of the edges in the temporal graph.
At present, there are many studies on the graph pattern counting problem in temporal network. At the early stage, TGP (known as temporal motif) was usually defined as the network motif of graph snapshots at different time points [
10,
25]. On the basis of this definition, Bajardi et al. [
25] further defined the dynamic motif of the cattle trade movement. Recently, temporal motif is no longer limited by snapshots, but extends to the network motifs with temporal attribute [
26]. Inspired by this idea, Kovanan et al. [
27] proposed a temporal motif definition that is widely used in Wikipedia network [
28] and combat system coordination [
29], and Paranjape et al. [
30] put forward the
-temporal motif. Although both definitions have temporal attribute, there are still some differences between them. On the one hand,
-temporal motif stipulates that the edges must be sorted according to the timestamps, i.e., there is no edge of the same time, while the definition in [
27] may have several edges with the same time. On the other hand, all the edges of
-temporal motif should be in a fixed time window, while the temporal motif in [
27] only requires that the time difference between adjacent edges does not exceed the threshold. Afterwards, Mackey et al. [
31] used the
-temporal motif and designed a chronological edge-driven method to search all matched subgraphs of a given temporal graph. Liu et al. [
32] proposed a sampling framework for counting the
-temporal motif. Since these counting methods are based on the
-temporal motif, it is hard for them to count the temporal motif in [
27].
Although there are many algorithms for counting different kinds of TGP (or temporal motifs), the TGP counting still has two challenges. Firstly, the counting algorithm for the TGP defined in [
27] is lacking. Secondly, the existing algorithms do not consider the TGP that has multiple edges with the same time. To solve the challenges, here we study the counting problem for the TGP defined in [
27], and propose an exact algorithm and an estimation algorithm. The exact algorithm first partitions the graph into several temporal subgraphs according to the time threshold, and then counts the TGP of each temporal subgraph. The key problem in the counting process is the temporal graph isomorphism, which is actually a typical NP-complete problem. To fix this problem, we produce an edge order via the time first search (TFS) algorithm, and match the temporal motif according to the order. Since the TFS algorithm considers both the temporal and topological information simultaneously, the intermediate results in the isomorphism are reduced and the efficiency of the algorithm is improved. Based on the exact algorithm, the estimation algorithm which can achieve an unbiased estimation is proposed. Because of the use of edge sampling, this algorithm can greatly reduce the running time while guaranteeing the accuracy. Moreover, both algorithms are suitable for the TGP that has multiple edges with the same time. The main contributions of this paper are as follows:
(1) The paper studies the problem of counting the temporal graph pattern defined in [
27] and proposes the corresponding problem model. Since all the counting algorithms in the existing literature are designed for the TGP defined in [
30], the problem here has not been discussed before and is of great significance.
(2) The paper provides a strategy of the TFS algorithm to process the temporal graph pattern that has multiple edges with the same time. The TFS algorithm gives an edge order determined according to the topology when there exist such edges. The edge order is used to match the edges, and makes the proposed algorithms suitable for any TGP.
(3) The paper proposes an exact algorithm and an estimation algorithm to count the TGP in temporal graph. Both algorithms are computationally efficient because they can match the topology and temporal information simultaneously.
The rest of this manuscript is organized as follows.
Section 2 gives some definitions and describes the temporal graph counting problem for the temporal network. In
Section 3, we propose an exact algorithm and an estimation algorithm for the TGP counting.
Section 4 presents a variety of experiments to demonstrate the effectiveness of the algorithms.
Section 5 gives some discussions. Finally, conclusions are provided in
Section 6.
2. Definitions and Problem
In this section, we give the fundamental definitions of the temporal graph, the temporal graph pattern, the temporal graph isomorphism and so on. Then, according to these definition, we briefly describe the counting problem of the temporal graph pattern.
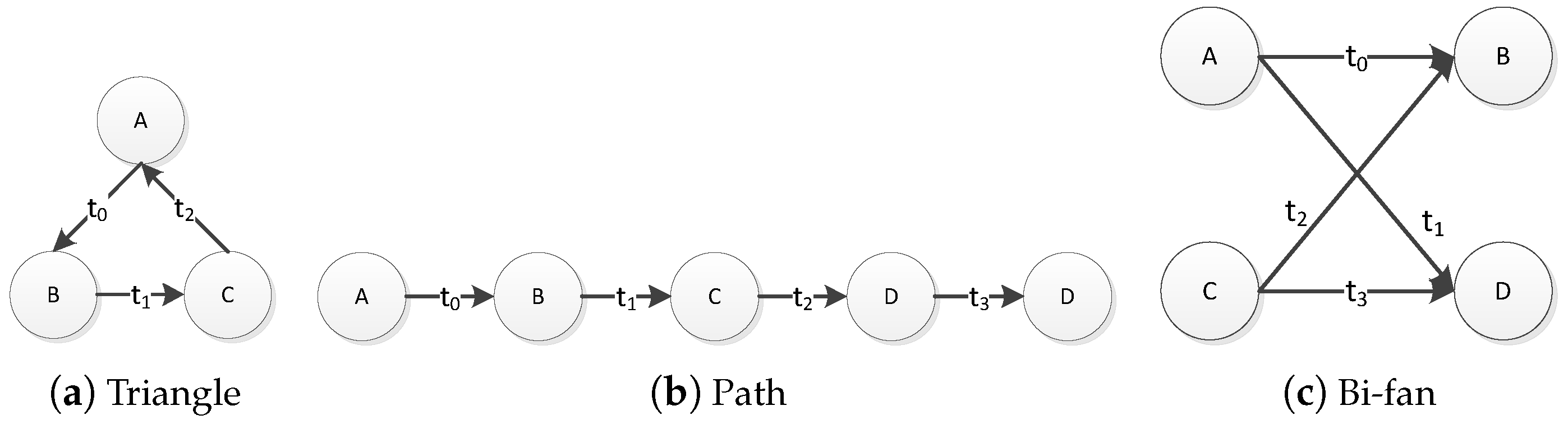
Definition 1. Temporal Graph. A temporal graph consists of a set of vertices V and a set of temporal edges , where t is the timestamp of the edge.
Definition 2. -Temporally Related Edges. Given two edges and , the edge is -temporally related to edge if they are temporally adjacent, i.e., and .
Definition 3. -Temporally Connected Graph.
A temporal graph is -temporally connected graph if and only if the graph is weakly connected and all the adjacent edges are -temporally related edges.
Definition 4. Temporal Graph Pattern. A temporal graph pattern , also known as the temporal motif, is a -temporally connected graph .
Definition 4 is just one of the TGP definitions, and we aim at counting the number of this pattern in a large temporal graph. Since the TGP contains the temporal information, the graph isomorphism needs to satisfy both the isomorphic conditions of static graph and the temporal conditions. In the following, we further give the definition of temporal graph isomorphism and the conditions that need to be satisfied.
Definition 5. Temporal Graph Isomorphism. If a temporal subgraph is temporally isomorphic to the temporal graph pattern , where , then there exists an injective function which satisfies the following conditions:| (1) |
| (2) |
| (3) |
| |
| |
| . |
Condition (3) describes the temporal relationship among the edges. In addition to the above conditions, all the adjacent edges in the matched subgraph G must be the -temporally related edges.
Therefore, given a temporal graph G and the TGP H, the problem here is to count the number of subgraphs that are temporally isomorphic to H in G.
5. Discussion
In this section, we discuss the application scope and limitations of the algorithm.
(1) The type of network: In
Section 3, we propose two algorithms for the counting problem in the static temporal network. Similar to all algorithms based on such network, the proposed algorithm cannot be applied to the dynamic network or the static network whose edges do not have the temporal information. It is worth noting that no algorithm can be applied to two different networks at the same time.
(2) The definition of TGP: In this paper, we consider the TGP defined in [
27], which is different from the other definitions discussed in the Introduction. This definition is relatively suitable for communication networks [
36], wikipedia network [
28], and mobile cohesive groups [
37].
(3) The algorithms: Since our algorithms partition the large graph into multiple subgraphs, the algorithms can be implemented in parallel, i.e., each subgraph is processed independently and the total result is obtained by adding the parallel results.
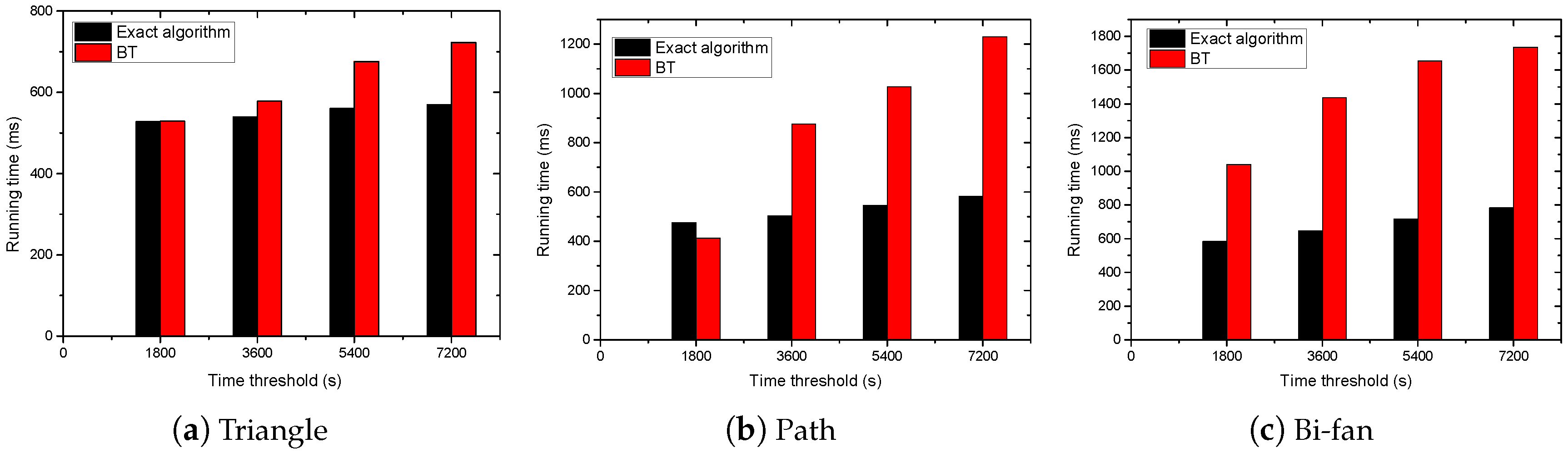
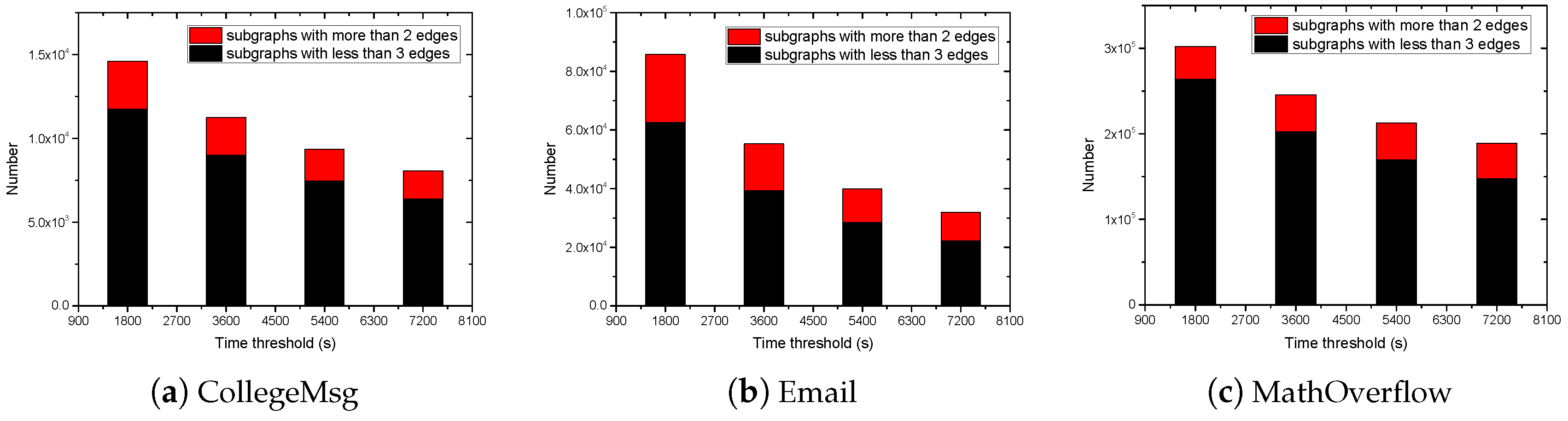
(4) The edge sampling: In the estimation algorithm, we use the edge sampling strategy to estimate the number of TGP. Since the increase in the edge number of TGP reduces the probability of the isomorphic subgraphs being sampled, the number of sampled isomorphic subgraphs will be small when is large. Therefore, the algorithm has high relative error when counting the TGP with many edges. This indicates that it is only suitable for the TGP with a small number of edges. In the future, the problem of estimating the number of large TGP in the temporal graph can be further studied.