Abstract
The interval neutrosophic set (INS) can make it easier to articulate incomplete, indeterminate, and inconsistent information, and the Schweizer-Sklar (Sh-Sk) t-norm (tm) and t-conorm (tcm) can make the information aggregation process more flexible due to a variable parameter. To take full advantage of INS and Sh-Sk operations, in this article, we expanded the Sh-Sk and to IN numbers (INNs) in which the variable parameter takes values from , develop the Sh-Sk operational laws for INNs and discussed its desirable properties. After that, based on these newly developed operational laws, two types of generalized prioritized aggregation operators are established, the generalized IN Sh-Sk prioritized weighted averaging (INSh-SkPWA) operator and the generalized IN Sh-Sk prioritized weighted geometric (INSh-SkPWG) operator. Additionally, we swot a number of valuable characteristics of these intended aggregation operators (AGOs) and created two novel decision-making models to match with multiple-attribute decision-making (MADM) problems under IN information established on INSh-SkPWA and INSh-SkPRWG operators. Finally, an expressive example regarding evaluating the technological innovation capability for the high-tech enterprises is specified to confirm the efficacy of the intended models.
1. Introduction
The most important utility of multiple-attribute decision-making (MADM) problems is to go for the preeminent alternative from the set of finite alternatives as stated to the partiality values specified by decision makers (DMs) with admiration to the attributes. However, despite the complication of the decision situation, it is hard for DMs to convey the partiality values by a particular real number in realistic problems. To agree with such circumstances, an intuitionistic fuzzy set (IFS) initiated by Atanassov [1] is one of the most promising simplifications of the fuzzy set (FS) initiated by Zadeh [2] to articulate unsure and inaccurate information perfectly [3,4,5]. Yet, in several circumstances, only a positive-membership degree (TMD) and negative-membership degree (FMD) cannot depict the incompatible information precisely. To agree with the corresponding circumstances, Smarandache [6] created a neutrosophic set (NS) which depicts the vague, inaccurate, and incompatible information by TMD, neutral-membership degree (IMD), and FMD. The values of the said functions are taken independently and are standard or nonstandard subsets of . As the NS consists of the IMD, it can explain the vague information much better than FS and IFS, and in addition, it is more reliable when it comes to individual expected opinions and perceptions. However, NS is difficult to exploit in factual problems due to the included nonstandard subsets of . As a result, to employ NS effortlessly in factual problems, Wang et al. [7,8] initiated the conceptions of single-valued NS and interval neutrosophic set (INS), which are subclasses of NS.
In factual decision making, we require aggregation operators (AGOs) to incorporate the specified information. In a neutrosophic environment, a lot of researchers have anticipated a number of AGOs. For example, the operational laws of single-valued neutrosophic numbers (SVNNs) was initially anticipated by Ye [9] and established the SVN weighted averaging (SVNWA) operator and SVN weighted geometric (SVNWG) operator. Afterwards, Peng et al. [10] located various drawbacks in the operational laws presented by Ye [9] and established enhanced operational rules for SVNNs and anticipated various SVN ordered weighted averages and SVN ordered weighted geometric operators. Ye [11] further presented a number of SVN hybrid averaging (SVNHA) and SVN hybrid geometric (ACNHG) operators and used these AGOs to solve MADM problems. Zhang et al. [12] initiated operational laws for IN numbers and established some IN weighted averaging and IN weighted geometric AGOs and applied these AGOs to solve MADM problems. Ye [13] initiated some IN ordered weighted averaging operators and a possibility ranking method and initiated an approach established based on these AGOs and a possibility ranking method to solve a MADM problem under an IN environment. Sun et al. [14] studied some Choquet integral AGOs for INNs. Garg and Nancy [15] initiated a nonlinear programming model established on TOPSIS to solve MAM problems. Wei et al. [16] initiated several generalized IN Bonferroni mean operators and applied them in the evaluation of high-tech technology enterprises. Tan et al. [17] established various exponential AGOs and specified their application in typhoon disaster evaluation. Wang et al. [18] established a MADM method with IN probability established based on regret theory. Khan et al. [19] initiated the concept of IN power Bonferroni mean operators and applied these to solve MADM problems under IN information. Zhou et al. [20] established several Frank IN weighted and geometric averaging operators. Rani and Garg [21] discovered various drawbacks in division and subtraction operations of INS and established modified division and subtraction operations for INS. Liu et al. [22] presented a MAGDM established on IN power Hamy mean operators. Yang et al. [23] initiated various new similarities and entropies for INS. Meng et al. [24] presented the concept of IN preference and its application in the selection of virtual enterprise partners. Kakati et al. [25] presented various IN hesitant Choquet integral AGOs established on Einstein operational laws and applied them to MADM. Liu et al. [26] presented a number of generalized Hamacher AGOs for NS and applied them to MAGDM. Liu et al. [27] introduced the generalized IN power averaging (GINPA) operator by combining power AGOs with INS to gain the full advantage of power AGOs under an IN environment. Yang et al. [28] established various IN linguistic power AGOs based on Einstein’s operational laws.
All the above-presented AGOs are recognized on the anticipation that the input arguments to be aggregated are independent. These managing AGOs have not measured the condition where the attributes have a priority relationship between them. To resolve this difficulty, Yager [29] initiated the concept of PA operator. Wei et al. [30] presented the concept of generalized PA operators. These AGOs were further enlarged by several researchers, such as Wu et al. [31], who enlarged PA operators to the SVN environment by anticipating the notions of SVN prioritized WA (SVNPWA) and SVN prioritized WG (SVNPWG) operators and used them on MADM problems with SVN information. Additionally, Liu et al. [32] anticipated a number of prioritized ordered WA/geometric operators to agree with IN information. Ji et al. [33] fused PA operators with BM operators and presented a number of SVN Frank prioritized BM AGOs by exploiting Frank operations. Recently, Wei et al. [34] put forward a number of PA operators established on Dombi TN and TCN and used them on MADM problems with SVN information. Sahin [35] anticipated some generalized PA operators for normal NS and applied these aggregation operators to MADM. Liu and You [36] studied some IN Muirhead mean operators and applied them to solve MADM problems with IN information. Sarkar et al. [37] developed an optimization technique for a national income determination model with stability analysis of differential equations in discrete and continuous processes under uncertain environment.
From the mentioned AGOs, the majority of these AGOs for NS or INS are established on algebraic, Hamacher, Frank, and Dombi operational rules, which are particular cases of Archimedean tn (Atn) and tcn (Atcn). Atn and Atcn are definitely the expansions of numerous TNs and TCNs, which have a number of particular cases which are preferrable for articulating the union and intersection of SVNS [38]. Sh–Sk operations [39] are the particular cases from Atn and Atcn, and they are with a changeable parameter, so they are additionally supple and better than the former operations. Still, the majority of research concerning Sh–Sk mostly determined the elementary theory and types of Sh-Sk TN (Sh-Sktn) and TCN (Sh-Sktcn) [40,41]. Recently, Liu et al. [42] and Zhang [43] merged Sh-Sk operations with interval-valued IFS (IVIFS) and IFS and anticipated power WA/geometric AGOs and weighted power WA/geometric AGOs for IVIFSs and IFSs, respectively. Wang and Liu [44] anticipated a Maclaurin symmetric mean operator for IFS established on Sh–Sk operational laws. Liu et al. [45] further presented Sh-Sk operational laws for SVNS and presented some Sh-Sk prioritized AGOs and applied these AGOs to solve MADM problems. Later on, Zhang et al. [46] anticipated some Muirhead mean operators for SVNS established on Sh-Sk operational laws and applied them to MADM problems. Nagarajan et al. [47] presented some Sh-Sk operational laws for INNs by taking the values of the variable parameter from . They also anticipated some weighted averaging and geometric AOs based on these Sh–Sk operational laws for INNs. In recent years, INSs have gained much attention from the researchers and a great number of achievement have been made, such as VIKOR [48,49,50], cross entropy [51], MABAC, EDAS [52], out ranking approach [53], distance and similarity measures [54], TOPSIS [55].
2. Literature Review
In this section, the literature discussing IN MADM aggregation operators is reviewed. It has been noticed that research of IN MADM aggregation operators has been rapidly published since 2013. Table 1 provides the recent literature of IN MADM based on different types of aggregation operators.

Table 1.
Multiple-attribute decision-making (MADM) methods based on different aggregation operators.
It can be seen that no research attempted to merge Sh-Sk operational laws and generalized prioritized aggregation operators to deal with IN information. Therefore, we suggest that:
- (1)
- INNs are superior in depicting tentative information by identifying the interval TMD, interval IMD, and interval FMD than FSs and IFSs in dealing with MADM problems.
- (2)
- The Sh-Sk operations are too flexible and better than the former operations by a variable parameter;
- (3)
- Conveniently, several MADM problems exist in which the attributes have a priority relationship, and a number of existing AGOs can moderate these circumstances only when the attributes take the form of real numbers. So far, there are no such AGOs to handle MADM problems under IN information established on Sh-Sktn and Sh-Sktcn. In response to this limitation, we merged the ordinary generalized PA operator with Sh-Sk operations to handle MADM problems with the IN information.
Therefore, from the above research inspirations, the objectives and offerings of this article are revealed as follows.
- (1)
- Anticipating a generalized IN Sh-Sk prioritized weighted averaging (GIN Sh-Sk PWA) operator and generalized IN Sh-Sk prioritized weighted geometric (GIN Sh-Sk PWG) operator.
- (2)
- Examining properties and precise cases of these anticipated AGOs.
- (3)
- Put forward two novel MADM approaches based on the anticipated AGOs.
- (4)
- Confirming the efficacy and realism of the anticipated approaches.
To achieve these objectives, this article is structured as follows. In Section 3, we initiate some basic ideas of INSs and score and accuracy functions of PA operators. In Section 4, we examine a number of Schweizer-Sklar operational laws for INNs where the variable parameter takes values from . In Section 5, we propose INSSPWA and INSSPWG operators and examine a number of properties and particular cases of the anticipated AGOs. In Section 6, we present two MADM approaches established on these AGOs. In Section 7, we resolve a numerical example to confirm the soundness and compensations of the anticipated approaches by contrasting with other existing approaches. Finally, a short conclusion is made in Section 8.
3. Preliminaries
In this part, some basic definitions about INSs, INN, the PA operator, Schweizer-Sklar TN and TCN, and their associated properties are argued. These definitions are given in Appendix A and Appendix B.
4. Sh-Sk Operations for INNs
The Sh-Sk (SS) operations contain Sh-Sk product and Sh-Sk sum, which are particular cases of Att.
Definition 1
[12]. Assume that and are any two arbitrary INSs, then the generalized union and intersection are identified as follows:
where and respectively represent TN and TCN.
The Sh-Sktn and TCN are explained as follows:
where
Moreover, when , Sh-Sktn and Sh-Sktcn degenerate into algebraic TN and TCN.
Based on the tn and tcn of Sh-Sk operations, we can provide the following definition for Sh-Sk operations for INNs.
Definition 2
[12]. Let and be any two arbitrary INNs, then the following generalized union and generalized intersection of INN are established on the basis of Sh-Sk operations:
On the basis of Definitions 1 and 2, we can develop the SS operational laws of INNs shown as follows :
Theorem 1.
Let and be any three INNs. Then:
5. Some Generalized Prioritized Aggregation Operators for INNs
In this part, we develop some generalized prioritized aggregation operators based on the developed operational laws for INNs.
5.1. Generalized Interval Neutrosophic Schweizer-Sklar Prioritized Aggregation (GINSh-SkPA) Operator
In this subpart, we develop a generalized interval neutrosophic Schweizer-Sklar prioritized weighted averaging (GINSh-SkPWA) operator and discuss its enviable properties and some particular cases.
Definition 3.
For a group of INNs the GINSh-SkPWA operator is a function
where , , andis the score of INN .
Theorem 2.
Letbe a set of INNs, then the aggregated value employing Definition (3) is still INN, and we have:
Proof.
In the following, we first prove:
by utilizing mathematical induction on .
For .
From the operational rules defined for INNs in Definition (2), we have:
and:
Similarly:
Then:
If Equation (23) holds for :
Then, when by the operational rules given in Definition (5), we have:
That is, Equation (19) is true for Thus, Equation (19), is true for all Then:
Therefore:
which completes the proof of Theorem 2. □
Theorem 3.
Idempotency: If allthen:
Proof.
(1). Since for all then:
□
Theorem 4.
Boundedness: Letbe a group of INNs, whereandis the score of INN. Moreover, letand, whereandthen:
Proof.
Since, . First, when , then:
Similarly, we have:
and as , we have:
and:
Similarly, the same process is for the falsity-membership function, that is:
Thus, on the other hand, we have:
Let , then:
and:
If , then:
If , that is:
then:
If , that is:
then:
From the above established analysis, we have:
□
Theorem 5.
Monotonicity: Letand be two groups of INNs, where and and are the scores of INNs and . Then:
Proof.
The proof of Theorem (5) directly follows from Theorem (4).
Further, we shall discuss a few cases of the developed AGO with respect to parameter , which are listed below:
- (1)
- If , then the GINSh–SkPWA operator reduces into an INSS prioritized weighted average (PWA) operator:
- (2)
- If and , then the GINSh-SkPWA operator reduces to an IN prioritized weighted average operator based on algebraic operation. That is:
□
5.2. Some Generalized Interval Neutrosophic Schweizer-Sklar Power Geometric Aggregation Operators
In this subsection, we develop a generalized interval neutrosophic Schweizer-Sklar prioritized weighted geometric (GINSh-SkPWG) operator and discuss its desirable properties and some particular cases.
Definition 4.
For a group of INNs the GIFSh–SkPWG operator is a mapping
where , , andis the score of INN.
Theorem 6.
Let be a group of INNs, then the value aggregated employing Definition (4) is still INN, and we have:
Proof.
In the following, we first prove:
by utilizing a mathematical induction on .
For .
From the operational rules defined for INNs in Definition (5), we have:
and:
Similarly:
Then:
If Equation (30) holds for :
Then, when by the operational rules given in Definition (5), we have:
That is, Equation (30) is true for Thus, Equation (30), is true for all Then:
Therefore:
which completes the proof of Theorem 2. □
Similar to the GINSh-SkPWA operator, the GINSh-SkPWGA operators have the properties of idempotency, boundedness, and monotonicity.
Further, we shall discuss a few cases of the developed aggregation operator with respect to parameter , which are listed below:
- (1)
- If , then the GINSh-SkPWGA operator reduces to an INSS prioritized weighted geometric average (INPWGA) operator:
- (2)
- If and , then the GINSSPWGA operator reduces to an IN prioritized weighted geometric average operator based on algebraic operation. That is:
6. Models for Multiple-Attribute Decision Making Established on Proposed Aggregation Operators
In this section, we develop MADM methods based on GINSh-SkPWA and GINSh-SkPWGA operators to deal with interval neutrosophic information. The following assumptions or notions are employed to state the MADM problems. Let be the set of alternatives, and be the set of attributes with a prioritization along with the attributes signified by the linear-ordering , then the specific attribute has a superior priority than if Assume that is the INN decision matrix, where and state the interval neutrosophic TM function, interval neutrosophic IM function, and interval neutrosophic FM function, respectively, such that . The aim of this problem is to rank the alternatives.
6.1. The Model Established on GINSh-SkPWA Operator
Subsequently, a procedure for positioning and picking of the mainly superior alternative(s) is offered as follows.
Step 1. Equalize the decision matrix.
First, the decision-making information in matrix must be equalized. Accordingly, the criteria can be categorized into the benefit and cost types. For the criterion of benefit type, the evaluation information does not need to be distorted, but for the criterion of cost type, it should be customized with the complement set.
Thus, the decision matrix can be equalized by exploiting the formula:
Step 2. Find out the values of by exploiting the following formula:
where
Step 3. Exploit the decision information from decision matrix and the INSh-SkPWA operator specified in Equation (18):
to acquire the overall INN .
Step 4. Discover the score values of the overall INNs by utilizing Definition A2 given in Appendix A to rank all the alternatives .
Step 5. Rank all the alternatives and pick the preeminent one exploiting Definition A3 given in Appendix A.
Step 6. End.
6.2. The Model Established on GINSh–SkPWGA Operator
Steps 1 and 2 are same as those given for the GINSh-SkPWA operator.
Step 3. Exploit the decision information from decision matrix and the INSh-SkPWG operator specified in Equation (26):
to acquire the overall INN .
Step 4. Discover the score values of the overall INNs using Definition A2 given in Appendix A to order all the alternatives .
Step 5. Rank all the alternatives and pick the preeminent one exploiting Definition A3 given in Appendix A.
Step 6. End.
7. Numerical Example
In this part, a numerical example is modified from [16] about assessing technological innovation competency for high-tech enterprises with INNs.
Assume that signifies the promising five high-tech enterprises (alternatives), which are to be evaluated. The experts exploit the following four attributes to evaluate the promising five high-tech enterprises: (1) the innovative culture signified by ; (2) the infrastructure and funding for the enlargement of industry signified by ; (3) the organizational learning and knowledge management signified by ; and (4) support for technological innovation signified by The following priority relationship between the four attributes is considered. The experts evaluated the promising five high-tech enterprises with respect to the above four attributes and provide the evaluation information in the form of INNs listed in Table 2.

Table 2.
Interval neutrosophic number (INN) decision matrix .
Now, we exploit the developed approach to solve the MADM problem.
Step 1. Since all the attributes are of same type, there is no need to equalize decision matrix .
Step 2. Discover the values of by exploiting Formula (34), and we have:
Step 3. Exploit the decision information from decision matrix and the INSSPWA operator specified in Formula (35):
Step 4. Discover the score values of the overall INNs by Definition 2 to rank all the alternatives . We have:
Step 5. According to the score values, the ranking order of the alternatives is Hence, the best high-tech enterprise is , while the worst one is .
Now, we exploit the method established on the GINSh-SkPWGA operator.
Steps 1 and 2 are the same.
Step 3. Exploit the decision information from decision matrix and the INSSPWA operator specified in Formula (36), and we have:
Step 4. Discover the score values of the overall INNs by Definition 2 to order all the alternatives . We have:
Step 5. According to the score values, the ranking order of the alternatives is Hence, the best high-tech enterprise is , while the worst one is .
7.1. Effect of the Parameters and on Decision Result
Firstly, we fix the value of the parameter and give different values to parameter . The effect of parameter on the decision results exploiting the GINSh–SkPWA operator and GINSh-SkPWG operator is revealed in Figure 1 and Figure 2, respectively. Secondly, we fix the value of parameter and give different values to parameter . The effect of parameter on the decision results exploiting the GINSh-SkPWA operator and GINSh-SkPWG operator is revealed in Figure 3 and Figure 4, correspondingly.
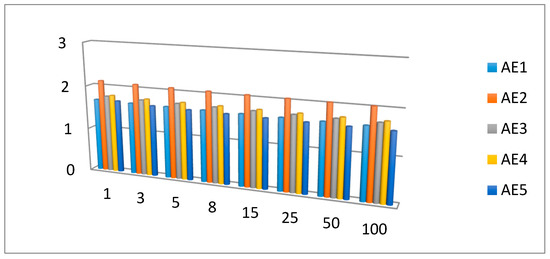
Figure 1.
Score values of the alternatives for different values of parameter .
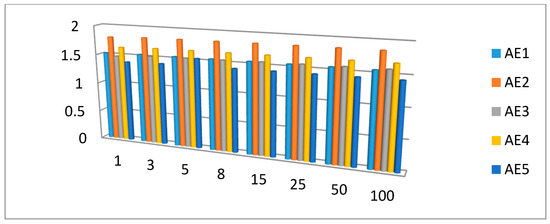
Figure 2.
Score values of the alternatives for different values of parameter .
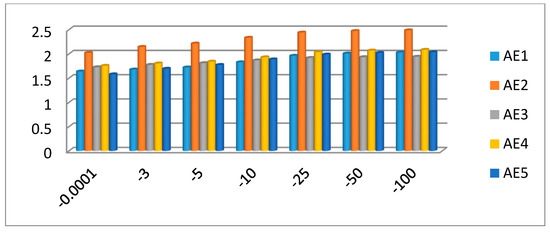
Figure 3.
Score values of the alternatives for different values of parameter .
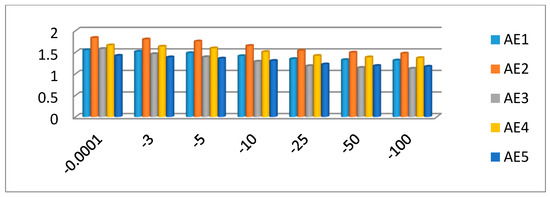
Figure 4.
Score values of the alternatives for different values of parameter .
From Figure 1 and Figure 2, one can perceive that although the ranking order for dissimilar values of parameter may be diverse, the best and worst alternatives stay the same. From Figure 1 and Figure 2, we can also perceive that, when the values of parameter go up, exploiting the INSh-SkPWA operator, the score values of the alternatives are reduced, while when exploiting the INSh-SkPWG operator, the score values of the alternatives raises.
Similarly, from Figure 3 and Figure 4, one can perceive that the ranking order for dissimilar values of the parameter may be different, but the best and worst alternatives remain the same. From Figure 3 and Figure 4, we can also perceive that, when the values of parameter reduce, exploiting the INSh-SkPWA operator, the score values of the alternatives go up, while when exploiting the INSh-SkPWG operator, the score values of the alternatives are reduced.
7.2. Comparison with Existing Approaches
In the following, we compare our developed approach established on these innovative developed AGOs with some existing approaches, such as the approaches developed by Zhang et al. [12], Nagarajan et al. [47], TOPSIS [55], and MABAC [52]. The score values and ranking orders are specified in Table 3.

Table 3.
Comparison with different approaches.
From Table 3, we can perceive that the ordering acquired from the INWA [16], INSh-SkWA, and INSh–SkWG operators [47] and TOPSIS is the same. While solving the same problem utilizing the MABAC method [51], the ranking order is different. The best alternative remains the same, and only the worst alternative is changed. In the above methods, the weight vector of the criteria is calculated using PA operators. However, the existing AGOs do not judge the priority relationship among attributes. Thus, the proposed aggregation operators have some advantages over these aggregation operators. Firstly, they developed Sh-Sk operational rules that consist of variable parameters, which makes the decision process suppler. Secondly, the anticipated AGOs can judge the priority relationship along with attributes. Therefore, the enlarged AGOs in this article are more realistic and supple to be employed in the decision-making procedure.
8. Conclusions
In practical decision making, accessible information is frequently imperfect and incompatible, and the INS is a superior tool to signify such types of information. In this article, initially, a number of Schweizer-Sklar operational rules for INNs were developed. Secondly, we created two new AGOs, an INSh-SkPWA operator and an INSh-SkPWG operator, and discussed their desirable properties. The leading qualities of these enlarged Schweizer-Sklar AGOs are that they can consider the priority relationship among attributes and are more flexible due to variable parameters. Moreover, based on these Schweizer-Sklar prioritized aggregation operators, two novel MADM approaches we are instituted. The novelty of the proposed method is compared to other methods. It is shown in Table A1 of Appendix C. The proposed method is illustrated by a numerical example. This example is specified to confirm the realism and efficacy of the proposed approach, and a comparison with the presented approaches is also given. In future research, we will apply the proposed approach to some new applications, such as evaluation of traffic control management [46], tourism recourses [47], enterprise green technology innovation behavior [48], mobile robot navigation [56,57], and so on, or extend the proposed method to some more extended form of INSs.
Author Contributions
Idea and conceptualization, Q.K. and L.A.; Methodology, Q.K. and M.N.; Collection of data and result calculation, T.M.; Writing—review and editing, S.R. and L.A.
Funding
This study was funded by Fundamental Research Grant Scheme (FGRS), No. 59522, Ministry of Education Malaysia and Universiti Malaysia Terengganu.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Some Concepts about INS
In this subsection, the definition of INS adapted from [8], score and accuracy functions, and comparison rules [36] are given.
Definition A1
[8]. Let be the universe of a discourse set, with a common element articulated by . An INS in is mathematically symbolized as:
where and , respectively, represent an interval truth-membership (ITM) function, interval indeterminacy-membership (IIM) function, and interval falsity-membership (IFM) function, and these three mappings are subsets of . The sum of the upper bound of these three functions should assure the condition The triplet is called an IN number (INN. To be easily understood, we shall symbolize INN by , and the set of all INNs is designated by .
Definition A2
[36]. Let be an INN. Subsequently, the score function and accuracy function can be classified as follows:
To compare any two INNs, Liu et al. [36] described the following comparison terms, which can be stated as follows.
Definition A3
[36]. Let and be any two INNs. Then, we have:
- (1)
- Ifthenis better thanand denoted by
- (2)
- Ifandthenis better thanand denoted by
- (3)
- Ifandthenis equal toand denoted by
Appendix B
Prioritized Average (PA) Operator
The PA operator was initially developed by Yager [29] for a crisp number. The main advantage of the PA operator is its capacity of considering a prioritization relationship among attributes.
Definition A4
[29]. Let be the collection of criteria and pledge that there is a prioritization between the criterion articulated by a linear ordering , which signifies that the attribute has a superior priority than , if is an assessment value articulating the act of the choice under the criteria and assures . If
The PA operators have successfully handled the situation where the values of criterion are real numbers.
Appendix C

Table A1.
Comparison between the contributions of different authors to interval neutrosophic MADM methods.
Table A1.
Comparison between the contributions of different authors to interval neutrosophic MADM methods.
| Author Years | Interval Neutrosophic MADM Methods Based on Different Aggregation operators | Generalized Parameter | Schweizer-Sklar Operational Laws | Consider Priority Relationship among the Attributes |
|---|---|---|---|---|
| Zhang et al. [12] (2014) | IN weighted averaging and geometric operators | No | No | No |
| Ye and Du [54] (2019) | Similarity Measures | No | No | No |
| Zhang et al. [53] (2016) | An outranking approach | No | No | No |
| Tain et al. [51] (2016) | Cross entropy | No | No | No |
| Liu and Wang [32] (2016) | Prioritized OWA operators | No | No | Yes |
| Liu and Tang [27] (2016) | Power generalized aggregation operators | Yes | No | No |
| Peng and Dia [52] (2017) | MABAC and EDAS methods | No | No | No |
| Huang et al. [49] and Hu et al. [50] (2017) | VIKOR methods | No | No | No |
| Liu and You [36] (2017) | Muirhead Mean Operators | No | No | No |
| Khan et al. [19] (2018) | Dombi Power Bonferroni Mean operators | Yes | No | No |
| Liu et al. [22] | Power Hamy mean operators | Yes | No | No |
| Wei et al. [16] (2019) | Generalized Bonferroni mean Operators | No | No | No |
| Proposed Method | Generalized Schweitzer-Sklar prioritized Operators | Yes | Yes | Yes |
References
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Aggregation Operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Liu, P.; Mahmood, T.; Khan, Q. Multi-attribute decision-making based on prioritized aggregation operator under hesitant intuitionistic fuzzy linguistic environment. Symmetry 2007, 9, 270. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic. In Philosophy; American Research Press: Santa Fe, NM, USA, 1999; pp. 1–141. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistructure 2010, 4, 410–413. [Google Scholar]
- Wang, H.; Smarandache, F.; Sunderraman, R.; Zhang, Y.Q. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing: Theory and Applications in Computing; Hexis: Phoenix, AZ, USA, 2005. [Google Scholar]
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Lu, Z.; Ye, J. Single-Valued Neutrosophic Hybrid Arithmetic and Geometric Aggregation Operators and Their Decision-Making Method. Information 2017, 8, 84. [Google Scholar] [CrossRef]
- Zhang, H.-Y.; Wang, J.-Q.; Chen, X.-H. Interval Neutrosophic Sets and Their Application in Multicriteria Decision Making Problems. Sci. World J. 2014. [Google Scholar] [CrossRef]
- Ye, J. Multiple attribute decision-making method based on the possibility degree ranking method and ordered weighted aggregation operators of interval neutrosophic numbers. J. Intell. Fuzzy Syst. 2015, 28, 1307–1317. [Google Scholar]
- Sun, H.-X.; Yang, H.-X.; Wu, J.-Z.; Ouyang, Y. Interval neutrosophic numbers Choquet integral operator for multi-criteria decision making. J. Intell. Fuzzy Syst. 2015, 28, 2443–2455. [Google Scholar] [CrossRef]
- Garg, H. Non-linear programming method for multi-criteria decision making problems under interval neutrosophic set environment. Appl. Intell. 2018, 48, 2199–2213. [Google Scholar] [CrossRef]
- Wei, G.; Wang, R.; Wang, J.; Wei, C.; Zhang, Y. Methods for Evaluating the Technological Innovation Capability for the High-Tech Enterprises With Generalized Interval Neutrosophic Number Bonferroni Mean Operators. IEEE Access 2019, 7, 86473–86492. [Google Scholar] [CrossRef]
- Tan, R.; Zhang, W.; Chen, S. Exponential Aggregation Operator of Interval Neutrosophic Numbers and Its Application in Typhoon Disaster Evaluation. Symmetry 2018, 10, 196. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.-Q.; Wang, T.-L. Fuzzy stochastic multi-criteria decision-making methods with interval neutrosophic probability based on regret theory. J. Intell. Fuzzy Syst. 2018, 35, 2309–2322. [Google Scholar] [CrossRef]
- Khan, Q.; Liu, P.; Mahmood, T.; Smarandache, F.; Ullah, K. Some Interval Neutrosophic Dombi Power Bonferroni Mean Operators and Their Application in Multi–Attribute Decision–Making. Symmetry 2018, 10, 459. [Google Scholar] [CrossRef]
- Zhou, L.-P.; Dong, J.-Y.; Wan, S.-P. Two New Approaches for Multi-Attribute Group Decision-Making with Interval-Valued Neutrosophic Frank Aggregation Operators and Incomplete Weights. IEEE Access 2019, 7, 102727–102750. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Some modified results of the subtraction and division operations on interval neutrosophic sets. J. Exp. Theor. Artif. Intell. 2019, 31, 677–698. [Google Scholar] [CrossRef]
- Liu, P.; Khan, Q.; Mahmood, T. Application of Interval Neutrosophic Power Hamy Mean Operators in MAGDM. Informatica 2019, 30, 293–325. [Google Scholar] [CrossRef]
- Yang, H.; Wang, X.; Qin, K. New Similarity and Entropy Measures of Interval Neutrosophic Sets with Applications in Multi-Attribute Decision-Making. Symmetry 2019, 11, 370. [Google Scholar] [CrossRef]
- Meng, F.; Wang, N.; Xu, Y. Interval neutrosophic preference relations and their application in virtual enterprise partner selection. J. Ambient. Intell. Hum. Comput. 2019, 1–30. [Google Scholar] [CrossRef]
- Kakati, P.; Borkotokey, S.; Rahman, S.; Davvaz, B. Interval neutrosophic hesitant fuzzy Einstein Choquet integral operator for multicriteria decision making. Artif. Intell. Rev. 2019, 1–36. [Google Scholar] [CrossRef]
- Liu, P.; Chu, Y.; Li, Y.; Chen, Y. Some Generalized Neutrosophic Number Hamacher Aggregation Operators and Their Application to Group Decision Making. Int. J. Fuzzy Syst. 2016, 16, 242–255. [Google Scholar]
- Liu, P.; Tang, G. Some power generalized aggregation operators based on the interval neutrosophic sets and their application to decision making. J. Intell. Fuzzy Syst. 2016, 30, 2517–2528. [Google Scholar] [CrossRef]
- Yang, L.; Li, B.; Xu, H. Novel Power Aggregation Operators Based on Einstein Operations for Interval Neutrosophic Linguistic Sets. IAENG Int. J. Appl. Math 2018, 48, 475–484. [Google Scholar]
- Yager, R.R. Prioritized aggregation operators. Int. J. Approx. Reason. 2008, 48, 263–274. [Google Scholar] [CrossRef]
- Wei, C.; Tang, X. Generalized prioritized aggregation operators. Int. J. Intell. Syst. 2012, 27, 578–589. [Google Scholar] [CrossRef]
- Wu, X.-H.; Wang, J.-Q.; Peng, J.-J.; Chen, X.-H. Cross-Entropy and Prioritized Aggregation Operator with Simplified Neutrosophic Sets and Their Application in Multi-Criteria Decision-Making Problems. Int. J. Fuzzy Syst. 2016, 18, 1104–1116. [Google Scholar] [CrossRef]
- Liu, P.; Wang, Y. Interval neutrosophic prioritized OWA operator and its application to multiple attribute decision making. J. Syst. Sci. Complex. 2016, 29, 681–697. [Google Scholar] [CrossRef]
- Ji, P.; Wang, J.Q.; Zhang, H. Frank prioritized Bonferroni mean operator with single-valued neutrosophic sets and its application in selecting third-party logistics providers. Neural Comput. Appl. 2018, 30, 799–823. [Google Scholar] [CrossRef]
- Wei, G.; Wei, Y. Some single-valued neutrosophic dombi prioritized weighted aggregation operators in multiple attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 1–13. [Google Scholar] [CrossRef]
- Şahin, R. Normal neutrosophic multiple attribute decision making based on generalized prioritized aggregation operators. Neural Comput. Appl. 2018, 30, 3095–3115. [Google Scholar] [CrossRef]
- Liu, P.; You, X. Interval neutrosophic muirhead mean operators and their application in multiple attribute group decision-making. Int. J. Uncertain. Quantif. 2017, 7, 303–334. [Google Scholar] [CrossRef]
- Sarkar, B.; Mondal, S.P.; Hur, S.; Ahmadian, A.; Salahshour, S.; Guchhait, R.; Iqbal, M.W. An optimization technique for national income determination model with stability analysis of differential equation in discrete and continuous process under the uncertain environment. Rairo Oper. Res. 2018. [Google Scholar] [CrossRef]
- Liu, P. The Aggregation Operators Based on Archimedean t-Conorm and t-Norm for Single-Valued Neutrosophic Numbers and their Application to Decision Making. Int. J. Fuzzy Syst. 2016, 18, 849–863. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. A generalization of operators on intuitionistic fuzzy sets using triangular norms and conorms. Notes Intuit. Fuzzy Sets 2002, 8, 19–27. [Google Scholar]
- Deschrijver, G. Generalized arithmetic operators and their relationship to t-norms in interval-valued fuzzy set theory. Fuzzy Sets Syst. 2009, 160, 3080–3102. [Google Scholar] [CrossRef]
- Zhang, X.; He, H.; Xu, Y. A fuzzy logic system based on Schweizer-Sklar t-norm. Sci. China Ser. F Inf. Sci. 2006, 49, 175–188. [Google Scholar] [CrossRef]
- Liu, P.; Wang, P. Some interval-valued intuitionistic fuzzy Schweizer–Sklar power aggregation operators and their application to supplier selection. Int. J. Syst. Sci. 2018, 49, 1188–1211. [Google Scholar] [CrossRef]
- Zhang, L. Intuitionistic fuzzy averaging Schweizer-Sklar operators based on interval-valued intuitionistic fuzzy numbers and its applications. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 2194–2197. [Google Scholar]
- Wang, P.; Liu, P. Some Maclaurin symmetric mean aggregation operators based on Schweizer-Sklar operations for intuitionistic fuzzy numbers and their application to decision making. J. Intell. Fuzzy Syst. 2019, 36, 3801–3824. [Google Scholar] [CrossRef]
- Liu, P.; Khan, Q.; Mahmood, T. Multiple-attribute decision making based on single-valued neutrosophic Schweizer-Sklar prioritized aggregation operator. Cogn. Syst. Res. 2019, 57, 175–196. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Geng, Y. Multi-Criteria Decision-Making Method Based on Single-Valued Neutrosophic Schweizer–Sklar Muirhead Mean Aggregation Operators. Symmetry 2019, 11, 152. [Google Scholar] [CrossRef]
- Nagarajan, D.; LathaMaheswari, M.; Broumi, S.; Kavikumar, J. A new perspective on traffic control management using triangular interval type-2 fuzzy sets and interval neutrosophic sets. Oper. Res. Perspect. 2019, 6, 100099. [Google Scholar] [CrossRef]
- Guan, H.; Zhao, A.; Du, J. Enterprise Green Technology Innovation Behaviour; Economic Science Press: Beijing, China, 2017. [Google Scholar]
- Huang, Y.-H.; Wei, G.-W.; Wei, C. VIKOR Method for Interval Neutrosophic Multiple Attribute Group Decision-Making. Information 2017, 8, 144. [Google Scholar] [CrossRef]
- Hu, J.; Pan, L.; Chen, X. An Interval Neutrosophic Projection-Based VIKOR Method for Selecting Doctors. Cogn. Comput. 2017, 9, 801–816. [Google Scholar] [CrossRef]
- Tian, Z.P.; Zhang, H.Y.; Wang, J.; Wang, J.Q.; Chen, X.H. Multi-criteria decision-making method based on a cross-entropy with interval neutrosophic sets. Int. J. Syst. Sci. 2016, 47, 3598–3608. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. Algorithms for interval neutrosophic multiple attribute decision-making based on mabac, similarity measure, and edas. Int. J. Uncertain. Quantif. 2017, 7, 395–421. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Chen, X. An outranking approach for multi-criteria decision-making problems with interval-valued neutrosophic sets. Neural Comput. Appl. 2016, 27, 615–627. [Google Scholar] [CrossRef]
- Ye, J.; Du, S. Some distances, similarity and entropy measures for interval-valued neutrosophic sets and their relationship. Int. J. Mach. Learn. Cybern. 2019, 10, 347–355. [Google Scholar] [CrossRef]
- Chi, P.; Liu, P. An extended TOPSIS method for the multiple attribute decision making problems based on interval neutrosophic set. Neutrosophic Sets Syst. 2013, 1, 63–70. [Google Scholar]
- Kretzschmar, H.; Spies, M.; Sprunk, C.; Burgard, W. Socially compliant mobile robot navigation via inverse reinforcement learning. Int. J. Robot. Res. 2016, 35, 1289–1307. [Google Scholar] [CrossRef]
- Omrane, H.; Masmoudi, M.S.; Masmoudi, M. Fuzzy Logic Based Control for Autonomous Mobile Robot Navigation. Comput. Intell. Neurosci. 2016. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).