Abstract
E-lottery schemes have attracted much interest from both industry and academia recently, because they are not only useful to raise funds for charity institutions, but also can be used as the major building blocks to design micro-payment systems. In the literature, a number of e-lottery schemes have been introduced over the last two decades. However, most of these schemes rely on some computational assumptions. In this paper, we introduce a novel e-lottery scheme that achieves information theoretical security. Our proposed scheme is designed using symmetric bivariate polynomials, and it satisfies the required security properties, such as correctness, unpredictability, verifiability, and robustness. Moreover, the winning number is generated in a distributed fashion, so that no trusted third party needs to be involved and the danger of a single point of failure is minimized.
1. Introduction
Today, the lottery has grown into a multi-billion dollar industry, and it is very popular in peoples’ daily life. In one aspect, it allows the players to bet on a small amount of money and get the chance to win a large fortune, and meanwhile, funds raised by the lottery are indispensable sources for various charity institutions. In another aspect, Rivest has shown in [1] that the lottery can be used as the major building block to design micro-payment systems. Therefore, it has attracted much interest from both industry and academia recently because of its practical importance, as well as theoretical potentials.
In general, a lottery scheme consists of the following participants, as shown in Figure 1: lottery issuers, players, and drawing centers. If a player wants to participate in a lottery game, she/he purchases the lottery tickets from some lottery issuer. Note that the player can purchase as many tickets as she/he likes, and each ticket costs her/him a small amount of money. Depending on the rules, in the lottery ticket, the player chooses either one number within some pre-defined large domain or several numbers in some pre-defined small domain. In this paper, we only consider the first case, since a lottery scheme designed in this case can be easily transformed into one that handles the second case, e.g., running the scheme several times in parallel. Once the ticket purchase phase finishes, the winning number is then generated by the drawing centers. If the player’s selected number matches with the winning number, she/he wins, and the lottery ticket that contains the winning number can be used to claim the prize from the lottery issuer.
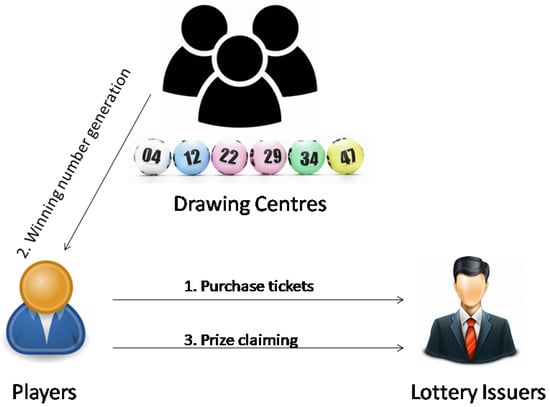
Figure 1.
An illustration of the lottery game.
With the rapid development of technologies, designing the lottery systems using information technologies and implementing them over computer networks have become inevitable trends, and these systems are called e-lotteries. Although the e-lottery is helpful to simplify the ticket purchase experience (i.e., with computer-aided user interfaces) and makes the system more accessible by ordinary users (i.e., the tickets can be purchased remotely at the users’ most convenient time), it also brings many new security issues compared with the traditional lottery systems. For example, a lottery system should guarantee that the winning number is randomly distributed in the pre-defined large domain, and it is unpredictable before its announcement. Note that these requirements ensure that each ticket will have a fair chance to win the prize. Moreover, the drawing phase should be transparent so that the validity of the winning number can be verified. Because computer networks are publicly accessible and they allow the users to communicate with each other without physical contact, the harmonization of these conflicting security requirements is challenging and needs the dedicated design and proper use of some advanced cryptographic techniques.
1.1. Related Works
The first e-lottery scheme was proposed by Goldschlag et al. [2], in which the winning number is generated using the delay function with the purchased tickets as its inputs. Informally, the delay function is a deterministic function that is not hard to compute, but still requires a significant amount of time to complete the computation. Therefore, the drawing phase can be verified by re-computing the delay function with the same inputs, and the unpredictability of the winning number relies on the fact that the players cannot compute the delay function effectively. To guarantee that the winning number is randomly distributed, the scheme requires an early registration of the players, and this step is later used to ensure that the number of participating players is not too small. Otherwise, the winning number may not contain enough entropy, and its distribution can be biased. However, this scheme has several limitations. Firstly, each player is allowed to purchase only one ticket. Secondly, it is not suitable to be used in some real-world e-lottery systems in which the winning number is generated periodically no matter how many tickets have been purchased. Thirdly, the delay function could be a single point of failure, and it may not be robust over time. A related e-lottery scheme has been introduced by Syverson [3] around the same time using weakly-secret bit commitment (WSBC). Note that WSBC has similar properties as the delay function such that once a secret has been committed, it can be read only after a pre-determined amount of time. In [4], Kushilevitz et al. introduced an e-lottery scheme in which the delay function is used in the winning number verification rather than the winning number generation. This scheme does not need to employ a trusted third party (TTP), and the correctness of execution can be verified. Moreover, the early registration of players is not required, and each player is allowed to purchase multiple tickets.
The above schemes mainly focus on the generation of the winning number. In [5], Zhou et al. introduced an e-lottery scheme that focuses on fair payment for lottery tickets and prize claim. Moreover, the players’ anonymity is considered to enhance the participation rate. The downside is that this scheme needs to employ an off-line TTP. The players and the lottery issuers exchange messages using verifiable encrypted signatures, and an off-line TTP needs to be involved if there is any dispute in the exchange. In this scheme, the delay function is also suggested to be used to prevent the last participating player from biasing the distribution of the winning number. Some other e-lottery schemes based on delay functions can be found in [6,7,8]. The design and implementation of large-scale lottery systems have been described in [9,10].
In the literature, several e-lottery schemes also have been introduced without using the delay function. In [11], the winning number is generated by aggregating the drawing centers’ random values. The scheme relies on the homomorphic property of the Paillier encryption [12], and the winning number is retrieved in the drawing phase using the verifiable threshold decryption. Its benefit is that the winning number is independent of the players’ tickets; hence, the e-lottery scheme is more versatile and suits more real-world applications. In [13,14], Lee et al. introduced two e-lottery schemes that further consider the protection of players’ privacy and anonymity. This property is achieved using blind signatures. However, some TTP needs to be involved in the drawing phase to generate the winning number. In [15], Liu et al. extended Lee’s schemes in two aspects. First, players’ privacy is protected using an efficient oblivious transfer rather than blind signatures. Second, the drawing phase is carried out by a number of drawing centers in a distributed fashion using Lagrange interpolation of polynomials. Each drawing center can verify that her/his input has contributed to the winning number by checking whether her/his point satisfies the resulting polynomial. The benefit is that neither the delay function nor any TTP is required in the drawing phase.
1.2. Our Contributions
To the best of our knowledge, most of the existing e-lottery schemes rely on some computational assumptions. In other words, if the adversary has infinite computational power, the security properties in these existing schemes will be violated. In this paper, we introduce a novel e-lottery scheme that achieves information theoretical security. Our proposed scheme is designed using symmetric bivariate polynomials, and its security properties, such as correctness, unpredictability, verifiability, and robustness, can be guaranteed against the adversary who has unlimited resources. Moreover, the winning number is generated in a distributed fashion so that neither TTP nor the delay function needs to be involved; hence, the danger of a single point of failure is minimized. Note that our suggested method also can be used to improve some existing e-lottery schemes. For example, when it is used to generate the winning number in Lee’s schemes [13,14], the TTP can be removed in the drawing phase.
1.3. Organization of the Paper
The rest of the paper is organized as follows: In Section 2, we outline some preliminaries. The models and definitions of e-lottery schemes are described in Section 3. In Section 4, we introduce our proposed e-lottery scheme, and its security and efficiency analyses are presented in Section 5. Finally, we conclude in Section 6.
2. Preliminaries
Symmetric bivariate polynomials have been widely used in the research of information technologies [16,17,18,19,20]. In this section, we describe the symmetric bivariate polynomial, as well as its properties that will be used in our proposed e-lottery scheme. Denote p as some large prime, and all the computations are modulo p unless otherwise stated. The dealer first chooses a random symmetric bivariate polynomial over with degree at most in both x and y as:
such that for all . Moreover, denote as a set of players and as the public parameters associate with these players. computes the shares for and sends them to the players through the secure channel. Note that each share is a univariate polynomial with degree at most in x.
Pairwise key establishment: The players can use their shares to establish pairwise secret keys among them without interaction [21]. For example, the player and the player can establish a secret key between them as . This is because in the symmetric bivariate polynomial , we always have . Note that in [22,23], Stinson et al. also used this property to authenticate whether the shares have been generated consistently.
Secret recovery: If t or more than t of these players work together and all these players are honest, they can recover the value using their shares through Lagrange interpolation. Without loss of generality, we assume that the players are involved. The value can be recovered as , where is the Lagrange coefficient. Here, each is a value within .
Robust secret recovery: Even if some players are dishonest, the value still can be correctly recovered under some conditions [24]. The basic idea is as follows: suppose n players are all involved and that they reveal the values for , but some dishonest players might reveal incorrect values. Now, every set containing t of the values can be interpolated into a possible value of , and there are in total number of such sets. If a particular value of appears in more than half of these sets, it can be treated as the correct value without ambiguity. The remaining issue is how many dishonest players can be tolerated in this method, and we denote this number as b. Obviously, must hold. Otherwise, these dishonest players can recover by themselves. Moreover, any two different univariate polynomials with degree agree on at most points. Recall that there are n players and that each player can generate one point; these two polynomials must differ at least points. By information theory, the error correction codes have the ability to correct less than errors. Hence, we have , which further implies that . Under this condition, either the Euclidean decoder or the Berlekamp–Massey decoder can be used to recover the value efficiently.
Homomorphic property in secret sharing: Note that the values for can be considered as the shares of the secret using Shamir secret sharing [25]. In [26], Benaloh discovered the homomorphic property in secret sharing schemes. Denote as a set of shares encoding the secret s and as another set of shares encoding the secret . Moreover, ⊕ and ⊗ are denoted as the operation of shares and operation of the secret, respectively. Then, the set encodes the secret . Obviously, Shamir secret sharing enjoys the homomorphic property.
3. Models and Definitions
Participants: There are four types of participants in an e-lottery system:
- Lottery issuers: They sell tickets to the players and provide the prize to the winner. We assume that the lottery issuers are honest.
- Players: They buy tickets and hope to win a large fortune.
- Drawing centers: They follow the public procedure to generate the winning number.
- Adversary: The adversary is assumed to have unlimited computational resources, and can control at most b of the drawing centers. Controlling a drawing center means learning its internal states, modifying its messages, disconnecting it, changing its intended behavior, and so on.
Communication model: We assume that the drawing centers are connected by pairwise secure channels, so that the messages exchanged among them cannot be intercepted or modified by the adversary . We also assume that there exists a common authenticated broadcast channel that is accessible by every participant. Moreover, we assume that the system is synchronized. Each drawing center can access a common global clock, and it can access some local source of randomness.
System model: An e-lottery scheme consists of the following three phases:
- Purchasing phase: The players can only purchase the tickets in this phase. To purchase a ticket, the player chooses a number in a pre-defined large domain and bets a small amount of money on it. Note that each player can purchase as many tickets as she/he likes. The purchased tickets are physically signed by these lottery issuers, so that they cannot be counterfeited by the players.
- Drawing phase: This phase begins after the purchasing phase. The drawing centers generate the winning number in a distributed fashion. The winning number is required to be randomly distributed in the pre-defined large domain, and it is unpredictable before its announcement. Moreover, this phase should be transparent so that the generation of the winning number can be verified.
- Claiming phase: Once the winning number is announced, the player who has selected the wining number can use her/his ticket to claim the prize from the lottery issuers.
Security properties: The following security properties are advocated in the majority of e-lottery schemes:
- Correctness: The proposed scheme will output the winning number that is randomly distributed in the pre-defined domain in the drawing phase.
- Unpredictability: The adversary cannot predict the winning number before it is announced. Note that the correctness property together with the unpredictability property guarantee that each player will have a fair chance to win the prize.
- Verifiability: It can be verified that the winning number is generated according to the public procedure.
- Robustness: The winning number is generated in a distributed fashion, so that neither TTP nor the delay function needs to be employed.
4. An E-Lottery Scheme with Information Theoretical Security
In this section, we describe our proposed e-lottery scheme with information theoretical security. Its design is inspired by the unconditionally-secure, verifiable secret sharing [22] and privacy preserving data aggregation [27,28], and we have incorporated the techniques in [29] to improve its round complexity.
4.1. The Proposed Scheme
Suppose n drawing centers are involved in generating the winning number in the drawing phase, and are the public parameters associate with these drawing centers, respectively. The static adversary can control at most b of these drawing centers, where and . The word “static” means that chooses the corruption drawing centers at the beginning of the scheme. Moreover, p is denoted as some large prime, and all the computations are assumed to be modulo p unless otherwise stated. The winning number is generated as follows:
- Each drawing center chooses a random symmetric bivariate polynomial with degree at most in both x and y:where for all . Then, computes and sends it to every other drawing center through the pairwise secure channel. Note that each is a univariate polynomial with degree at most in x. At the same time, each sends to every a random value through the pairwise secure channel for .
- After receiving from and from the other drawing centers, each computes the value for every and broadcasts these values.
- Each computes the maximum subset such that any ordered pair satisfies the equation . If , then broadcasts a bit and puts the value k in a list . Otherwise, simply broadcasts .
- If , then each broadcasts a bit and computes her/his aggregated share as:Otherwise, simply broadcasts and stops.
- If , each computes and sends it to the other drawing centers in through the pairwise secure channels.
- Finally, after receiving the values from the other drawing centers in , each computes the winning number for at least of the values she/he has received. Note that this operation can be computed efficiently using the error-correction codes.
4.2. Some Discussions
In order to simplify the above description, we have assumed in Step 1 that every drawing center can access some local source of randomness, and they can choose the random symmetric bivariate polynomial, as well as the random values in . However, in some real-world environments, this assumption is too strong, and it will restrict the applications of the proposed e-lottery scheme. Here, we discuss how the leftover hash lemma [30] can be used to weaken this assumption.
Definition 1 (Universal hash function).
For a keyed hash function defined over , where is its key space, is its message space, and is its digest space, given an adversary , the attack game works as follows: the challenger first randomly selects a key and keeps k private and then outputs two distinct messages . We say that wins the game if . ’s advantage of winning the above game is denoted as . We say that is an ϵ-bounded universal hash function (or ϵ-), if for all adversaries (even inefficient ones).
Lemma 1 (Leftover hash lemma).
Let be a - defined over , where . Let be mutually independent random variables, where k is randomly distributed in , and each can be guessed with probability at most γ. Let δ be the statistical difference between and the uniform distribution on . Then, we have:
To see how the leftover hash lemma can be used to weaken the above assumption, suppose and the value s cannot be guessed with probability at most . Then, the leftover hash lemma says that given whatever side information about s, for any adversary (even with unlimited computational resources), the advantage in distinguishing from , where t is a truly-random element of , is bounded by . In other words, if are sufficiently small, the output of will be indistinguishable from a truly random value. Therefore, when using the leftover hash lemma, we only need to assume that the drawing centers are able to generate some values that cannot be guessed with some small probability (e.g., passwords with enough entropy), but there is no need to assume that these values are randomly distributed in some pre-defined domain. In the following section, we still assume that every drawing center can access some local source of randomness in order to simplify the security analysis.
5. Security and Efficiency Analysis
In this section, we analyze the proposed e-lottery scheme and compare it with some existing schemes with respect to the security properties. Moreover, we analyze the computation and communication costs of generating the winning number in our proposed scheme.
5.1. Security Analysis
Theorem 1 (Correctness).
If and , the proposed e-lottery scheme will output a winning number that is randomly distributed in .
Proof.
Firstly, suppose the drawing center is good in Step 1. In this case, will randomly select a symmetric bivariate polynomial over with degree at most , and every other drawing center will receive a univariate polynomial from . Because is symmetric, we have for all good drawing centers and . This further implies that the broadcast values and will match in Step 2. Hence, the good drawing centers and will be in the subset . Therefore, for all good drawing centers in Step 3, and k will be included in the list . Otherwise, if a good drawing center outputs , then the size of the maximum subset is at most . Thus, every good drawing center outputs . In this case, k will not be included in the list .
Next, suppose there are T univariate polynomials with degree at most , where , and these polynomials are consistent, i.e., for all . Then, there exists a univariate polynomial with degree at most such that for all , and any t of the values can determine the value without ambiguity. To see this, suppose and are two different t-subsets of . The univariate polynomial can be computed such that for all . In particular, can be computed using the Lagrange interpolation as , where is the Lagrange coefficient. Note that similar properties also hold for the set . Moreover, the equation always holds because:
Furthermore, suppose at least drawing centers output . Then, we have . Because it is assumed that there are at most b bad drawing centers, there must exist more than good ones in , and these good drawing centers have consistent shares . Using the error correction codes, can always be efficiently recovered by interpolating the values. Similarly, thanks to the homomorphic property of secret sharing schemes, the interpolation of the values (where is the aggregated share) using the error correction codes can recover the winning number . If there exists at least one good drawing center in , the winning number s will be randomly distributed in . In summary, based on the assumption that , our proposed scheme satisfies the correctness property. □
Theorem 2 (Unpredictability).
If , the adversary controlling at most b of the drawing centers cannot guess the winning number with probability better than before it is announced in the drawing phase.
Proof.
We first assume that the symmetric bivariate polynomial over is generated by a trusted dealer , and each drawing center for receives the univariate polynomial . We show that the adversary who controls at most drawing centers cannot recover the polynomial because its threshold is t. To see this, has coefficients, and since for all , has different coefficients. Each drawing center can evaluate her/his univariate polynomial at t independent points. Therefore, can obtain t independent equations. Although also can obtain t equations, one of the equations is the same as ’s equations; hence, can obtain independent equations. Similarly, can obtain independent equations, and so on. To solve the system of equations with unknowns, independent equations are needed. t shareholders can obtain equations, which is enough, but shareholders can obtain equations, which is not enough. Moreover, we show that cannot predict the value with probability better than . Note that each pair of drawing centers and can establish a pairwise key without interaction as . Denote as a Vandermonde matrix that is publicly known and as a private matrix representing the coefficients of , and is a matrix representing the pairwise keys:
We have , and ’s univariate polynomial is the column in the matrix . Without loss of generality, we assume that controls the drawing centers . Hence, learns the first rows, as well as the first columns of , because is symmetric. However, cannot learn the value . For every possible value , not only the entire matrix can be determined since the rank of is t, but also one can use the relationship to construct a symmetric bivariate polynomial , such that for all and for . Moreover, each different value maps to a unique value . Therefore, this proves that if is honest, cannot guess the value with probability better than .
In our proposed e-lottery scheme, each drawing center serves as the dealer to execute the above dealing phase once, and all these dealing phases are executed independently. Hence, if the drawing center is good, cannot guess the value with probability better than . Moreover, the winning number is , where contains more than good drawing centers. Therefore, cannot guess the winning number s with probability better than , and this finishes the proof for the unpredictable property. □
Theorem 3 (Verifiability).
In the proposed e-lottery scheme, it can be verified that the winning number is generated according to the public procedure.
Proof.
In the proposed e-lottery scheme, each drawing center first serves as the dealer to share a symmetric bivariate polynomial among all drawing centers, and then, these drawing centers work together to recover the wining number through polynomial interpolation. In the first phase, the drawing centers can verify whether their received univariate polynomials are consistent by checking whether the broadcast values for all . The following two properties are employed in this process: (1) if the dealer follows the protocol, all good drawing centers will output the bit ; (2) if one good drawing center outputs the bit , all good drawing centers will output the same bit, and the dealer has violated the protocol. In the second phase, given that there are more than drawing centers in , the winning number always can be efficiently recovered using the error correction codes. This is because more than of the drawing centers in are good. Moreover, once the winning number is recovered, the bad drawing centers in can be identified, i.e., the winning number can be interpolated by the set that only contains good drawing centers, but it cannot be interpolated by the set that contains some bad ones. Therefore, it can be verified that the winning number is generated according to the public procedure. □
Theorem 4 (Robustness).
The proposed e-lottery scheme employs neither TTP nor the delay function, and the winning number is generated in a distributed fashion.
Proof.
The proof is obvious. Note that because neither TTP nor the delay function has been used in the proposed e-lottery scheme, the danger of a single point of failure is minimized. □
5.2. Comparison with Some Existing Works
Table 1 summarizes the comparison of our proposed e-lottery scheme with some existing schemes in the literature regarding the security properties (the abbreviation “IT security” stands for information theoretical security). To the best of our knowledge, our proposed scheme is the first e-lottery scheme that achieves information theoretical security.

Table 1.
Comparison with some existing works IT, information theoretical.
5.3. Efficiency Analysis
In Step 1, each drawing center serves as the dealer to select a random symmetric bivariate polynomial over . There are in total coefficients in , but since for all , only coefficients need to be selected in . Furthermore, needs to evaluate , where . The evaluation needs to perform times, and each evaluation requires t multiplications and additions using Horner’s algorithm. Therefore, the total computational cost in this step is multiplications and additions in . Moreover, sends the univariate polynomial over to each other drawing center. The communication cost in this step is bits. In Step 2, each drawing center has n univariate polynomials over (one generated by herself/himself and received from the other drawing centers). For each of these univariate polynomial, evaluates it times. Using Horner’s algorithm, each evaluation takes t multiplications and t additions. Therefore, the total computational cost in this step is multiplications and additions in . Moreover, each drawing center broadcasts values in . Hence, the communication cost in this step is bits. In Step 3, each drawing center compares pairs of values in and broadcasts n bits. In Step 4, each performs at most additions in and broadcasts 1 bit. In Step 5, each sends a value in to all other drawing centers. The communication cost in this step is bits. In Step 6, each recovers the winning number using the error correction codes.
Our proposed e-lottery scheme is very efficient for use in real-world applications because of the following two reasons. Firstly, in our scheme, the modular p can be set as 128 bits or 256 bits; while in many existing works that use public key cryptosystems, this modular needs to be set as several thousand bits in order to achieve the same security level. Secondly, most of the computations in our scheme are modular multiplications and modular additions, and they are much more efficient compared with the modular exponentiations that are required in many existing works. To illustrate this, suppose the security level is set as 128 bits in some application. In other words, the adversary with unlimited computational resources cannot predict the winning number with probability better than . Moreover, suppose and so that is satisfied. Using these system parameters, in Step 1, the computational cost for each drawing center is 24 multiplications and 72 additions in , where the modular p is a 128-bit prime, and the communication cost is 3072 bits. In Step 2, each drawing center needs to compute 216 multiplications and additions in , and she/he needs to sends 9216 bits to the other drawing centers. In Step 3, each drawing center needs to compare 36 pairs of values in and broadcasts nine bits. In Step 4, each drawing center performs 27 additions in and broadcasts 1 bit. In Step 5, the communication cost is 1024 bit. To achieve the same security level, Liu’s scheme [15] needs to use a subgroup with order q, where q is a 256-bit prime, and the modular needs to be set as a 3072-bit prime according to the NIST recommendations. Each drawing center needs to perform nine full modular exponentiations in . Using the square-and-multiply algorithm, these modular exponentiations cost roughly 3456 multiplications in . Recall that is much larger than p; our proposed method therefore has computational advantages over Liu’s scheme. Regarding the communication complexity, in Liu’s scheme, each drawing center needs to broadcast a 3072-bit value and sends 2048-bit values to the other drawing centers. Although our proposed scheme is less efficient in communication costs, it is still acceptable for real-world applications. Moreover, our proposed scheme does not rely on any computational assumption, and this is a property that is not enjoyed in Liu’s scheme.
We have to note that the degree t of the polynomial will affect both the security and efficiency of our proposed scheme. In one aspect, the degree of the polynomial defines the maximum allowed drawing centers controlled by the adversary. Hence, the polynomial with a higher degree can be used to design a scheme with better security. In another aspect, the polynomial with a higher degree will increase the computational costs of the proposed scheme. Therefore, this parameter needs to be selected carefully based on specific requirements.
6. Conclusions
In this paper, we have introduced an e-lottery scheme with the desirable security properties. In particular, the winning number is generated by a number of drawing centers in a distributed fashion, and this procedure can be verified. Before the winning number is announced, it cannot be guessed with a probability better than a pre-defined small value. These properties ensure that the scheme is transparent and every player will have a fair chance to win the prize. Moreover, these properties are guaranteed without relying on computational assumptions. To the best of our knowledge, our scheme is the first e-lottery scheme that satisfies information theoretical security.
Author Contributions
Conceptualization: Z.X. and Y.L.; methodology: Z.X. and Y.L.; formal analysis: Z.X. and C.-F.H.; writing–original draft preparation: Z.X., Y.L., C.-F.H.; writing–review and editing: Z.X. and C.-C.C.; supervision: C.-C.C.; funding acquisition: Y.L.
Funding
This work was partially supported by the National Natural Science Foundation of China (Grant No. 61662016, 61772224), the Natural Science Foundation of Hubei Province (Grant No. 2017CFB303), and the Key Projects of Guangxi Natural Science Foundation (Grant No. 2018JJD170004).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rivest, R.L. Electronic lottery tickets as micropayments. In Lecture Notes in Computer Science, Proceedings of the International Conference on Financial Cryptography, Anguilla, Anguilla, 24–28 February 1997; Springer: Berlin, Germany, 1997; pp. 307–314. [Google Scholar]
- Goldschlag, D.M.; Stubblebine, S.G. Publicly verifiable lotteries: Applications of delaying functions. In Lecture Notes in Computer Science, Proceedings of the International Conference on Financial Cryptography, Anguilla, Anguilla, 23–25 February 1998; Springer: Berlin, Germany, 1998; pp. 214–226. [Google Scholar]
- Syverson, P. Weakly Secret Bit Commitment: Applications to Lotteries and Fair Exchange; Technical Report, NAVAL Research Lab Washington DC Center for High Assurance Computing Systems (CHACS); NAVAL Research Lab: Washington, DC, USA, 1998. [Google Scholar]
- Kushilevitz, E.; Rabin, T. Fair e-lotteries and e-casinos. In Lecture Notes in Computer Science, Proceedings of the Cryptographers’ Track at the RSA Conference, San Francisco, CA, USA, 8–12 April 2001; Springer: Berlin, Germany, 2001; pp. 100–109. [Google Scholar]
- Zhou, J.; Tan, C. Playing lottery on the Internet. In Lecture Notes in Computer Science, Proceedings of the International Conference on Information and Communications Security, Singapore, 9–12 December 2001; Springer: Berlin, Germany, 2001; pp. 189–201. [Google Scholar]
- Chow, S.S.; Hui, L.C.; Yiu, S.M.; Chow, K. Practical electronic lotteries with offline TTP. Comput. Commun. 2006, 29, 2830–2840. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, L.; Liu, H. Using an efficient hash chain and delaying function to improve an e-lottery scheme. Int. J. Comput. Math. 2007, 84, 967–970. [Google Scholar] [CrossRef]
- Goldschlag, D.M.; Stubblebine, S.G.; Syverson, P.F. Temporarily hidden bit commitment and lottery applications. Int. J. Inf. Secur. 2010, 9, 33–50. [Google Scholar] [CrossRef]
- Sako, K. Implementation of a digital lottery server on WWW. In Secure Networking—CQRE [Secure]’99; Springer: Berlin, Germany, 1999; pp. 101–108. [Google Scholar]
- Konstantinou, E.; Liagkou, V.; Spirakis, P.; Stamatiou, Y.C.; Yung, M. Electronic national lotteries. In Lecture Notes in Computer Science, Proceedings of the International Conference on Financial Cryptography, Key West, FL, USA, 9–12 February 2004; Springer: Berlin, Germany, 2004; pp. 147–163. [Google Scholar]
- Fouque, P.A.; Poupard, G.; Stern, J. Sharing decryption in the context of voting or lotteries. In Lecture Notes in Computer Science, Proceedings of the International Conference on Financial Cryptography, Anguilla, Anguilla, 20-24 February 2000; Springer: Berlin, Germany, 2000; pp. 90–104. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Lecture Notes in Computer Science, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; Springer: Berlin, Germany, 1999; pp. 223–238. [Google Scholar]
- Lee, J.S.; Chan, C.S.; Chang, C.C. Non-iterative privacy preservation for online lotteries. IET Inf. Secur. 2009, 3, 139–147. [Google Scholar] [CrossRef]
- Lee, J.S.; Chang, C.C. Design of electronic t-out-of-n lotteries on the Internet. Comput. Stand. Interfaces 2009, 31, 395–400. [Google Scholar] [CrossRef]
- Liu, Y.N.; Cheng, C.; Jiang, T.; Chang, C.C. A practical lottery using oblivious transfer. Int. J. Commun. Syst. 2016, 29, 277–282. [Google Scholar] [CrossRef]
- Marszałek, Z. Parallelization of modified merge sort algorithm. Symmetry 2017, 9, 176. [Google Scholar] [CrossRef]
- Allem, L.E.; Hoppen, C. A pre-test for factoring bivariate polynomials with coefficients in F2. Inf. Process. Lett. 2017, 121, 22–28. [Google Scholar] [CrossRef]
- Marszałek, Z.; Woźniak, M.; Połap, D. Fully Flexible Parallel Merge Sort for Multicore Architectures. Complexity 2018, 2018, 8679579. [Google Scholar] [CrossRef]
- Nakatsukasa, Y.; Noferini, V.; Townsend, A. Vector spaces of linearizations for matrix polynomials: A bivariate polynomial approach. SIAM J. Matrix Anal. Appl. 2017, 38, 1–29. [Google Scholar] [CrossRef]
- Plestenjak, B. Minimal determinantal representations of bivariate polynomials. Linear Algebra Its Appl. 2017, 532, 550–569. [Google Scholar] [CrossRef]
- Blom, R. An optimal class of symmetric key generation systems. In Lecture Notes in Computer Science, Proceedings of the Workshop on the Theory and Application of of Cryptographic Techniques, Paris, France, 9–11 April 1984; Springer: Berlin, Germany, 1984; pp. 335–338. [Google Scholar]
- Stinson, D.R.; Wei, R. Unconditionally secure proactive secret sharing scheme with combinatorial structures. In Lecture Notes in Computer Science, Proceedings of the International Workshop on Selected Areas in Cryptography, Kingston, ON, Canada, 9–10 August 1999; Springer: Berlin, Germany, 1999; pp. 200–214. [Google Scholar]
- D’Arco, P.; Stinson, D.R. On unconditionally secure robust distributed key distribution centers. In Lecture Notes in Computer Science, Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Queenstown, New Zealand, 1–5 December 2002; Springer: Berlin, Germany, 2002; pp. 346–363. [Google Scholar]
- Ben-Or, M.; Goldwasser, S.; Wigderson, A. Completeness theorems for non-cryptographic fault-tolerant distributed computation. In Proceedings of the ACM Twentieth Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 2–4 May 1988; pp. 1–10. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Benaloh, J.C. Secret sharing homomorphisms: Keeping shares of a secret secret. In Lecture Notes in Computer Science, Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Santa Barbara, CA, USA, 11–15 August 1986; Springer: Berlin, Germany, 1986; pp. 251–260. [Google Scholar]
- Liu, Y.; Guo, W.; Fan, C.I.; Chang, L.; Cheng, C. A practical privacy-preserving data aggregation (3PDA) scheme for smart grid. IEEE Trans. Ind. Inform. 2018. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Wang, X.; Xia, Z.; Xu, J.F. Privacy-preserving raw data collection without a trusted authority for IoT. Comput. Netw. 2018. [Google Scholar] [CrossRef]
- Gennaro, R.; Ishai, Y.; Kushilevitz, E.; Rabin, T. The round complexity of verifiable secret sharing and secure multicast. In Proceedings of the ACM Thirty-Third Annual ACM Symposium on Theory of Computing, Santa Barbara, CA, USA, 16–20 August 2001; pp. 580–589. [Google Scholar]
- Håstad, J.; Impagliazzo, R.; Levin, L.A.; Luby, M. Construction of a pseudo-random generator from any one-way function. SIAM J. Comput. Citeseer 1993, 28, 12–24. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).