An Efficient Essential Secret Image Sharing Scheme Using Derivative Polynomial

Abstract

As a popular technology in information security, secret image sharing is a method to guarantee the secret image’s security. Usually, the dealer would decompose the secret image into a series of shadows and then assign them to a number of participants, and only a quorum of participants could recover the secret image. Generally, it is assumed that every participant is equal. Actually, due to their position in many practical applications, some participants are given special privileges. Therefore, it is desirable to give an approach to generate shadows with different priorities shadows. In this paper, an efficient essential secret image sharing scheme using a derivative polynomial is proposed. Compared with existing related works, our proposed scheme can not only create the same-sized shadows with smaller size but also removes the concatenation operation in the sharing phase. Theoretical analysis and simulations confirm the security and effectiveness of the proposed scheme.

1. Introduction

With the growth of multimedia technology and sharing, publishing and communication of multimedia data on the Internet have become more and more popular. Obviously, it is an easy way to share multimedia data on the Internet and, therefore, people should concern the privacy and security of secret data like commercial or military images during sharing and transmitting. Secret image sharing is an image protection technology that can prevent the secret image from being lost or modified during storage and transmission. In the era of big data, the technology of secret image sharing can be applied in various flied-like information hiding, access control and so on.

The concept of secret sharing [1] proposed by Shamir is a fundamental way to solve the problem if there is only one authority who is not trustworthy in the real world. This concept has drawn many researchers’ attention so that it has been developed into a significant role in the field of information security [2,3,4]. To protect the secret image, Thien and Lin [5] proposed a $(k,n)$ secret image sharing (SIS) scheme. In Thien and Lin’s scheme, the dealer constructs a sharing function based on Lagrange interpolation and the sharing function $f(x)$ processes on the modulus a prime number $p$; usually $p$ is set as $p=251$. In addition, all the pixel values from 251–255 should be truncated to 250, which would result in the recovered image being distorted. To overcome this drawback, many schemes with a similar approach include: Wu [6] set the prime number $p=257$ to replace 251 to achieve low information overhead. Kanso et al. [7] proposed a scheme which reduces the effect on the truncated secret pixel values. Besides, in order to acquire a distortion-less secret image, there are many existing works [8,9,10] which use Galois Field $GF(2^8)$ instead of modulus $251$. In addition, visual cryptographic is another technology designed to protect the security of secret images, which is used in the visual system of human to recognize images. In 2018, Jia et al. [11] proposed a verifiable visual cryptographic scheme to achieve reconstruction without cheating shares. Meanwhile, Jia et al. [12] designed a collaborative visual cryptography scheme to avoid the risk of leaking the secret from the collection of noncommon participants.

All the above schemes assume that each participant is considered to have the same priority. However, in real life, many examples require to assign the different privileges to different participants, such as the teachers and students in school and managers and staff in a company. It is highlighted to generate shadows with different priorities. In fact, there are many ways to generate different important shadows such as weighted SIS (WSIS) schemes, hierarchical SIS (HSIS) schemes and essential SIS (ESIS) schemes. In 2009, Shyu et al. [13] utilized the Chinese remainder theorem to construct a WSIS scheme. In the sharing phase, the weight of the shadow for a participant is determined by its own privilege. In the reconstruction phase, the secret image can be recovered only if the total weights of the collected shadows reach the pre-defined threshold. Afterwards, Chen et al. [14], Li et al. [15] and Lin et al. [16] also improved the WSIS scheme in different ways. The HSIS scheme uses polynomial derivatives and Birkhoff interpolation to generate shadows with different priorities. In 2007, Tassa [17] provided a method for constructing a hierarchical secret sharing scheme that constructs a polynomial from a set of unstructured points and derivative values. Guo et al. [18] provided a method to construct a hierarchical structure. Unfortunately, there exists the problem that some non-authorized participants may partially restore the secret information. Subsequently, Pakniat et al. [19] utilized cellular automata and the hash function to enhance Guo et al.’s scheme. Unlike WSIS schemes and HSIS schemes, the generated shadows in ESIS schemes are divided into two categories, one is the essential shadow with higher priority and the other is the non-essential shadow. For essential participants, the ESIS schemes have an additional essentiality condition which is smaller than the threshold condition. In 2013, Li et al. [20] firstly presented a $(t,s,k,n)$-ESIS scheme, where the generated shadows contain $s$ essential shadows and $(n-s)$ non-essential shadows. To recover the secret image, it still requires $k$ shadows including $t$ or more essential shadows. After that, Yang et al. [21] proposed a $(t,s,k,n)$-ESIS scheme with a smaller total size of shadows. To generate shadows with different importance, two different thresholds of SIS scheme are adopted in Chen’s [22] scheme. It is unlikely that there exists a weakness of threshold fulfillment. Chen and Chen [23] enhanced Chen’s [22] scheme by constructing a two-layered structure. However, all the ESIS schemes mentioned above ignore two critical problems. The first one is the different sizes among shadows. The other is the final shadows are concatenated of multiple sub-shadows. The former would allow the attacker to judge the status of the shadow from its size, which leads to the leak of some sensitive information about the corresponding participant’s privileged status. The latter would complicate the reveal process in practice. If a scheme applies multiple SIS, the dealer needs to concatenate the sub-shadows in some way so that the location of each sub-shadow needs to be recorded and each sub-shadow needs to be extracted in the reconstruction. To solve these problems, Li et al. [24] proposed a $(t,s,k,n)$-ESIS scheme aimed to generate equal-sized shadows, which solves the problem of the different shadows’ size. Besides, by constructing an expandable ESIS structure, Chen et al. [25] could not only make the generated shadows with equal size but also avoid concatenation operation in the sharing process. Chen [26] presented a three-layered $(t,s,k,n)$-ESIS scheme in 2018. However, Chen’s scheme only when parameters are properly chosen can achieve the goal of generating equal-sized shadows. Li et al. [27] presented a $(t,k,n)$-ESIS scheme which solves the problem of different sizes of shadows and has no concatenation operation in the sharing process, while this scheme is a special case of $(t,s,k,n)$-ESIS scheme when $t=s$.

The main contributions of the proposed scheme are listed as follows. First, based on Li et al.’s scheme [27], the proposed scheme extends the range of the essentiality threshold from $t=s$ to $0<t\le s$, which is more suitable in the real world. Second, compared with other existing $(t,s,k,n)$-ESIS schemes, the main advantages of the proposed scheme are listed as follows:

(1)

Same-sized shadows.

(2)

Smaller-sized shadows.

(3)

Effectiveness.

The outline of this paper is organized as follows. Section 2 presents the descriptions about the $(k,n)$-SIS scheme and $(t,s,k,n)$-ESIS scheme. Section 3 presents a review and analysis of Li et al.’s scheme [27]. The proposed scheme is introduced in Section 4. Section 5 presents a theoretical analysis of the proposed scheme. Section 6 presents the simulation results and comparison, and the conclusion is presented in Section 7.

2. Preliminaries

2.1. $\left(k,n\right)$ Secret Image Sharing Scheme

Thien and Lin [5] proposed a $(k,n)$ secret image sharing (SIS) scheme to protect the secret image. This scheme has a threshold condition which requires only at least $k$ out of $n$ participates’ cooperation could reconstruct the secret image.

2.1.1. Sharing Phase

Giving a secret image $I$ and a pair of the parameters $(k,n)$, where $0<k\le n$. The dealer will share $I$ to $n$ participates $P_1$, $P_2$, …, $P_n$ as the follow’s step.

Step 1: Set a prime number $p$; usually $p$ is set as 251.

Step 2: Permute each pixel’s position in $I$ by a permutation sequence. Then, all the pixels larger than 250 should be truncated to 250.

Step 3: The processed permuted image is divided into some units with $k$ pixels. These $k$ pixels then are to be used to construct a sharing function $f\left(x\right)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{k-1}{x}^{k-1}\mathrm{mod}p$, where $a_0$, $a_1$, …, $a_{k-1}$ are the pixels values in each unit.

Step 4: The output $f\left(1\right)$, $f\left(2\right)$, …, $f\left(n\right)$ are pixel values sequentially assigned to $n$ shadows $O_1$, $O_2$, …, $O_n$.

Step 5: Repeat step 3 and step 4 until each unit has been processed, the generated shadows $O_1$, $O_2$, …, $O_n$ are shared to $n$ participates $P_1$, $P_2$, …, $P_n$ respectively.

2.1.2. Recovery Phase

Supposing there are at least $k$ participates satisfying the threshold condition. These $k$ participates could recover the secret image through the following steps.

Step 1: By collecting $k$ shadows from $k$ participates, the $\left(k-1\right)$ degree polynomial $f\left(x\right)$ can be reconstructed based on Lagrange’s interpolation. Therefore, the pixels in each unit can be recovery and the permuted secret image.

Step 2: Employ the corresponding inverse-permutation and the permuted secret image can obtain the secret image.

2.2. $\left(t,s,k,n\right)$ Essential Secret Image Sharing Scheme

In 2013, Li et al. [20] firstly presented a $(t,s,k,n)$-ESIS scheme. In fact, both the $(t,s,k,n)$-ESIS scheme and the $(k,n)$-SIS scheme have the same threshold condition. The difference of these two kinds of schemes is that the $(t,s,k,n)$-ESIS scheme constructs an essentiality condition which is smaller than the threshold condition. In the $(t,s,k,n)$-ESIS scheme, the generated $n$ shadows are endowed with two different important elements: $s$ essential shadows and $\left(n-s\right)$ non-essential shadows. Note that the essential shadows with higher importance are shared to the corresponding essential participants such as the teachers in the school and the managers in a company. Similarly, the other non-essential shadows are shared to the corresponding non-essential participants, such as the students in the school and the staff in a company. In the recovery phase, the collected shadows have to meet both the threshold condition and the essentiality condition. In other words, in the $(t,s,k,n)$-ESIS scheme, it requires that $k$ shadows including $t$ or more essential shadows can reconstruct the secret image.

2.2.1. Sharing Phase

Giving a secret image $I$ and a pair of the parameters $(t,s,k,n)$, where $0<t\le s$, $0<k\le n$, $t\le k$, $s\le n$. The secret image $I$ is shared to $n$ participates $P_i$, where $1\le i\le n$. Supposing that the essential participates are $P_i$, where $1\le i\le s$ and non-essential participates $P_i$, where $s+1\le i\le n$.

Step 1: Encrypt $I$ by $(k,s+k-t)$-SIS scheme to generate $\left(s+k-t\right)$ shadows $I_j$ as intermediate shadows, where $1\le j\le s+k-t$. Set $I_j\left(1\le j\le s\right)$ as $s$ essential shadows $O_i\left(1\le i\le s\right)$ shared to corresponding essential participates $P_i$.

Step 2: Each remaining intermediate shadows $I_j\left(s+1\le j\le s+k-t\right)$ are further encrypted by $(j,n-s)$-SIS scheme and obtain $(n-s)$ sub-shadows $S_{j,1},$, $S_{j,2}$, …, $S_{j,n-s}$.

Step 3: The $(n-s)$ non-essential shadows $O_i\left(s+1\le i\le n\right)$ can be obtained by $O_i=S_{j,i-s}\parallel S_{j+1,i-s}\parallel \cdots \parallel S_{s+k-t,i-s}$, and then shared to the corresponding non-essential participates $P_i\left(s+1\le i\le n\right)$.

2.2.2. Recovery Phase

Supposing there are $t$ essential participates (say $P_1$, $P_2$, …, $P_t$) and $(k-t)$ non-essential participates (saying $P_{s+1}$, $P_{s+2}$, …, $P_{s+k-t}$) satisfying the threshold requirement and essentiality requirement. These $k$ participates can recover the secret image through the following steps.

Step 1: Employ the Lagrange’s interpolation, the $(k-t)$ intermediate shadows $I_j\left(s+1\le j\le s+k-t\right)$ can be recovered by $(k-t)$ non-essential participates.

Step 2: Employ the Lagrange’s interpolation, the secret image can be recovered by $t$ essential shadows $I_j\left(1\le j\le t\right)$ from essential participates $P_1$, $P_2$, …, $P_t$.

3. Review and Analysis of Li et al.’s Scheme

3.1. Review Li et al.’s Scheme

Li et al. [27] considered a special case of $(t,s,k,n)$-ESIS scheme where $t=s$ and provided an efficient method to construct the $(t,k,n)$-ESIS scheme. In this scheme, the secret image can generate $t$ essential shadows and $\left(n-t\right)$ non-essential shadows, when they collected no less than $k$ shadows including all $t$ essential shadows could make a reconstruction of secret image. The pseudo-code of the encryption and decryption phase is described in Algorithm 1 and Algorithm 2, respectively.

3.1.1. Sharing Phase

Giving a secret image $I$ and a pair of the parameter $(t,k,n)$, where $0<t\le k\le \mathrm{n}$. The secret image $I$ is shared to $t$ essential participants $P_i\left(1\le i\le t\right)$ and $\left(n-t\right)$ non-essential participates $P_i\left(t+1\le i\le n\right)$.

Step 1: Permute each pixel’s position in $I$ by a permutation sequence to obtain the permuted secret image $\widehat{I}$.

Step 2: Employ the $(k,n)$-SIS scheme on $\widehat{I}$ to obtain $n$ intermediate shadows $T_i\left(1\le i\le n\right)$. And the mask shadow $R$ can be generated as $R=T_1\oplus T_2\oplus \cdots \oplus T_t$, where $\oplus$ is denoted as the bit-wise XOR operation.

Step 3: The $t$ essential shadows $O_i=T_i$ are shared to $t$ essential participants $P_i\left(1\le i\le t\right)$. And $\left(n-t\right)$ non-essential shadows $O_i=\left(T_i+R\right)\mathrm{mod}\left(256\right)$ are shared to $\left(n-t\right)$ non-essential participates $P_i\left(t+1\le i\le n\right)$.

Algorithm 1 Sharing phase of Li et al.’s scheme

Input: A secret image $\widehat{I}=P\left(I\right)$ and a pair of the parameter. Output: $n$ shadows: $O_1$, $O_2$, …, $O_t$ are essential shadows; $O_{t+1}$, $O_{t+2}$, …, $O_n$ are non-essential shadows.

(A1-1): Permute $I$ to $\widehat{I}$ by $\widehat{I}=P\left(I\right)$; /*$P(\cdot )$: a reversible permutation operation */ (A1-2): Generate the intermediate shadows $T_1$, $T_2$, …, $T_n$, by applying $(k,n)$-SIS scheme on $\widehat{I}$; (A1-3): Compute the mask shadow $R=T_1\oplus T_2\oplus \cdots \oplus T_t$, where $\oplus$ denotes the bit-wise XOR operation; (A1-4): Generate $t$ essential shadows $O_1=T_1$, $O_2=T_2$, …, $O_t=T_t$ and $\left(n-t\right)$ non-essential shadows $O_{t+1}=\left(T_{t+1}+R\right)\mathrm{mod}\left(256\right)$, $O_{t+2}=\left(T_{t+2}+R\right)\mathrm{mod}\left(256\right)$, …, $O_n=\left(T_n+R\right)\mathrm{mod}\left(256\right)$;

3.1.2. Recovery Phase

Supposing there are $t$ essential participates (say $P_1$, $P_2$, …, $P_t$) and $(k-t)$ non-essential participates (saying $P_{s+1}$, $P_{s+2}$, …, $P_{s+k-t}$) satisfying the threshold requirement and essentiality requirement. The detail of the revealing process is listed as follows.

Step 1: By collecting $t$ essential shadows from $t$ essential participates, the mask shadow $R$ can be reconstructed by computing $R=O_1\oplus O_2\oplus \cdots \oplus O_t$.

Step 2: Reconstruct $\left(n-t\right)$ non-essential shadows by $(k-t)$ non-essential participates $T_i=\left(O_i-R+256\right)\mathrm{mod}256$ from $(k-t)$ non-essential participates, where $t+1\le i\le k$.

Step 3: By collecting $t$ essential shadows $T_i=O_i\left(1\le i\le t\right)$ and $(k-t)$ non-essential shadows $T_i\left(t+1\le i\le k\right)$, the permuted secret image $\widehat{I}$ can be recovered by Lagrange’s interpolation.

Step 4: The secret image can be recovered by employing the corresponding inverse-permutation on the permuted secret image.

Algorithm 2 Recovery phase of the Li et al.’s scheme

Input: $t$ essential shadows and any $\left(k-t\right)$ non-essential shadows. /* say $t$ essential shadows are $O_1$, $O_2$, …, $O_t$ and $(k-t)$ non-essential shadows are $O_{t+1}$, $O_{t+2}$, …, $O_k$*/ Output: The secret image $I$.

(A2-1): Collect $t$ essential shadows to compute the mask shadow $R=O_1\oplus O_2\oplus \cdots \oplus O_t$; (A2-2): Compute $k$ intermediate shadows $T_1$, $T_2$, …, $T_k$, as: $T_1=O_1$, $T_2=O_2$, …, $T_t=O_t$ and $T_{t+1}=\left(O_{t+1}-R+256\right)\mathrm{mod}\left(256\right)$, …, $T_k=\left(O_k-R+256\right)\mathrm{mod}\left(256\right)$; (A2-3): Since there are $T_1$, $T_2$, …, $T_n$, the permuted image $\widehat{I}$ can be obtained by employing Lagrange’s interpolation; (A2-4): Acquire the secret image by $I=P^{-1}(\hat{I})$; $/*P^{(-1)}(\cdot ):$ the corresponding inverse-permutation of $P(\cdot )*/$

3.2. Analysis Li et al.’s Scheme

Li et al.’s $(t,k,n)$-ESIS scheme [27] is a special case of $(t,s,k,n)$-ESIS scheme when $t=s$. If and only if there are $k$ shadows including $t$ essential shadows in the reconstruction process can the secret image be recovered, which would result in some limitations in some real-life situations.

Besides, the generated non-essential shadows have the homomorphic property in Li et al.’s scheme [27]; in some special cases, it may lead to leaking some sensitive information of the secret image. The specific reasons are as follows. In Step 3, in the sharing phase of Li et al.’s scheme [27], each non-essential shadow is acquired in the same approach by employing the additive modulo operation between each $T$ and $R$, that would lead to the scheme having the homomorphic property for 8 bit-based XOR operation is similarly with the additive operation in $GF\left(2^8\right)$. However, the additive modulo operation also has the homomorphic property in generated shadows. When the attacker collecting $k$ non-essential shadows with the homomorphic property attempts to reconstruct the secret image, he would obtain a fuzzy secret image, which would lead to information leakage of the secret image. There are some simulations to demonstrate it. We did a simulation based on Li et al.’s scheme [27] as an example, and the simulation results are shown in Figure 1. Figure 1a shows the test’s secret image and Figure 1b shows the result of the revealed image which only utilizes two non-essential shadows in (1, 2, 3)-ESIS. The simulation result shows that it is not secure to use additive modulo operation to generate non-essential shadows.

4. The Proposed Scheme

An efficient essential secret image sharing scheme using a derivative polynomial is proposed in this paper. In the proposed scheme, the Lagrange interpolation is used to construct the threshold condition, and the derivative polynomial is used to construct the essentiality condition to fit the requirement of the $(t,s,k,n)$-ESIS scheme. The process of constructing the essential condition would be more simple by combining the derivative polynomial and would not increase the size of the generated shadows. Therefore, an efficient essential secret image sharing scheme using a derivative polynomial is proposed in this paper. Instead of some related $(t,s,k,n)$-ESIS schemes adopting multiple SIS schemes and concatenating the sub-shadows, the proposed scheme has removed the concatenation operation which can simplify the reveal process in practice.

4.1. Sharing Phase

Giving a secret image $I$ and a pair of the parameters $(t,s,k,n)$, the secret image $I$ is shared to $s$ essential participants $P_i\left(1\le i\le s\right)$ and $\left(n-s\right)$ non-essential participates $P_i\left(s+1\le i\le n\right)$.

Step 1: Permute each pixel’s position in $I$ by a permutation sequence to obtain the permuted secret image $\widehat{I}$.

Step 2: Employ the $\left(k,k\right)$-SIS scheme on $\widehat{I}$ to obtain $k$ intermediate shadows $T_i\left(1\le i\le k\right)$.

Step 3: Construct the $(k-1)$-degree function $g\left(x\right)=w_0+w_{1}x+\dots +w_{k-1}{x}^{k-1}\mathrm{mod}\left(2^8\right)$; the coefficients in $g\left(x\right)$ are the pixel values at the same position in each intermediate shadow. And the outputs $O_i=g\left(i\right)$ are $s$ essential shadows shared to essential participates $P_i$, where $1\le i\le s$.

Step 4: Calculate $t$-th derivative of $g\left(x\right)$, a $(k-t-1)$-degree polynomial $g^{(t)}(x)$ can be constructed, and the outputs $O_i=g^{\left(t\right)}\left(x\right)$ are non-essential shadows shared with the other non-essential participates $P_i$, where $s+1\le i\le n$.

Algorithm 3 Sharing phase of the proposed scheme

Input: A secret image $I$ and a pair of the parameters $(t,s,k,n)$. Output: $n$ shadows: $O_1$, $O_2$, …, $O_s$ are essential shadows; $O_{s+1}$, $O_{s+2}$, …, $O_n$ are non-essential shadows.

(A3-1): Obtain the permuted image $\widehat{I}$ by $\widehat{I}=P\left(I\right)$; (A3-2): Generate the intermediate shadows by applying $(k,k)$-SIS scheme on $\widehat{I}$; (A3-3): Construct the function $g\left(x\right)$, and the outputs $O_i=g\left(i\right)$ are $s$ essential shadows, where $1\le i\le s$; (A3-4): Calculate $t$-th derivative of $g\left(x\right)$ to obtain $g^{(t)}(x)$, and the outputs $O_i=g^{\left(t\right)}\left(x\right)$ are non-essential shadows, where $s+1\le i\le n$;

4.2. Recovery Phase

The secret image can be recovered when there are no less than $k$ shadows, and these $k$ involved shadows need to have at least $t$ essential shadows. The details of the revealing process are listed as follows:

Step 1: By collecting no less than $k$ shadows involved at least $t$ essential shadows form participants, the $k$ coefficients in the function $g\left(x\right)$ can be reconstructed by employing Lagrange interpolation, so that $k$ intermediate shadows $T_i$ also can be reconstructed.

Step 2: Employ the Lagrange interpolation to obtain the permuted secret image $\widehat{I}$ by at least $k$ intermediate shadows $T_i$.

Step 3: The secret image $I$ can be recovered by employing the corresponding inverse-permutation on the permuted secret image $\widehat{I}$.

Algorithm 4 Recovery phase of the proposed scheme

Input: Any at least $k$ shadows and no less than $t$ essential shadows included. Output: The secret image $I$.

(A4-1): The function $g\left(x\right)$ can be reconstructed by any $k$ involved shadows including at least $t$ essential shadows; (A4-2): The intermediate shadows $T_1$, $T_2$, …, $T_k$ can be reconstructed by the function $g\left(x\right)$; (A4-3): The permuted secret image $\widehat{I}$ can be reconstructed by $T_1$, $T_2$, …, $T_k$; (A4-4): Acquire the original secret image by $I=P^{-1}(\widehat{I})$;

5. Analysis

5.1. The Security Analysis

The security of the $(t,s,k,n)$-ESIS schemes is always judged on whether the threshold property is satisfied or not. In the $(t,s,k,n)$-ESIS scheme, supposing that $P$, $Q$, $EP$, and $NEP$ denote the set of all participants, the set of participates involved in reconstruction, the set of essential participates, and the set of non-essential participates, respectively, where $Q\subseteq P$ and $P=EP\cup NEP$. Supposing that $|*|$ represents the number of elements in the set $*$, so that the cardinalities of $EP$ and $NEP$ are $\left|EP\right|=s$ and $\left|NEP\right|=\left(n-s\right)$. Let $Q\backslash NEP$ denote the set having elements in $Q$ but not in $NEP$. A qualified subset of participates $Q$ in a $\left(t,s,k,n\right)$-ESIS scheme must satisfy two conditions:

(1)

Threshold condition: $\left|Q\right|\ge k$.

(2)

Essentiality condition: $\left|Q\backslash NEP\right|\ge t$.

Theorem 1. 

The proposed scheme satisfies the threshold condition and the essentiality condition.

Proof. 

Supposing that $l=l_1+l_2$ shadows are involved in reconstruction, with essential shadows (say $S_1$, $S_2$, …, $S_{l_1}$) and $l_2$ non-essential shadows (say $S_{s+1}$, $S_{s+2}$, …, $S_{s+l_2}$). First, we certify that the secret image cannot be reconstructed when against any one of following condition: (i) threshold condition: $\left|Q\right|\ge k$ and (ii) essentiality condition: $\left|Q\backslash NEP\right|\ge t$. □

Case 1. 

When the involved shadows against the threshold condition while satisfy the essentiality condition.

This case implies that $l\ge k$, $l_1<t$, $l_2>k-t$. In the revealing process, since there are $l_2$ non-essential shadows, the $\left(k-t-1\right)$-degree polynomial $g^{\left(t\right)}\left(x\right)$ can be reconstructed and the $\left(k-t\right)$ coefficients in $g^{\left(t\right)}\left(x\right)$ can be recovered. However, there are also $t$ coefficients in $g\left(x\right)$ unknown and another $t$ essential shadows are needed to solve them. Since $l_1<t$, the $g\left(x\right)$ cannot be reconstructed correctly and the secret image cannot be recovered correctly further.

Case 2. 

When the involved shadows against the essentiality condition while satisfy the threshold condition.

This case implies that $l<k$, $l_1\ge t$, $l_2<k-t$. In the revealing process, the $\left(k-1\right)$-degree function $g\left(x\right)$ cannot be reconstructed correctly for $l<k$, that means the intermediate shadows $T_i$ cannot be reconstructed correctly; the secret image cannot be recovered correctly further.

Second, we certify that both the threshold condition and essentiality condition are satisfied; therefore, the secret image can be recovered.

Supposing that $l\ge k$ and $l_1\ge t$. In the proposed scheme, the $\left(k-1\right)$-degree function $g\left(x\right)$ can be reconstructed correctly by collecting $l_1$ essential shadows and $l_2$ non-essential shadows $\left(l_1+l_2=l\ge k\right)$, and the $k$ intermediate shadows can be reconstructed. Employing the Lagrange interpolation, the permuted secret image can be reconstructed. By employing the corresponding inverse-operation, the secret image can be recovered finally.

5.2. The Analysis of Shadow Size Ratio

Supposing that the size ratio of the essential shadow, non-essential shadow, total shadow and the total required shadows for reconstruction are $SE$, $SN$, $ST$, and $SR$, respectively.

Theorem 2. 

$SE=SN=1/k$, $ST=n/k$, $ST=n/k$.

Proof. 

According to the proposed scheme in Section 4, the secret image must firstly be decrypted to generate $k$ intermediate shadows $T_1$, $T_2$, …, $T_k$. These intermediate shadows are equal to $1/k$ times of the secret image. After that, the $\left(k-1\right)$-degree function $g\left(x\right)$ can be constructed, where the coefficients in $g\left(x\right)$ are the pixel values at the same position in each intermediate shadow; the outputs $O_1$, $O_2$, …, $O_s$ are $s$ essential shadows with the same size as the intermediate shadow. Therefore, $SE=1/k$. Then, the dealer calculates the $t$-th derivative of $g\left(x\right)$ to obtain $f^{\left(t\right)}\left(x\right)$, the outputs $O_{s+1}$, $O_{s+2}$, …, $O_n$ are $\left(n-s\right)$ non-essential shadows with the same size as the essential shadow. Therefore $SE=SN=1/k$. It can be seen that $ST=SE+SN=s/k+\left(n-s\right)/k=n/k$. In the recovery phase, collecting $k$ shadows including $t$ essential shadows can reconstruct the original secret image. Hence, $SR=t/k+\left(k-t\right)/k=1$. □

6. Simulation Results and Comparison

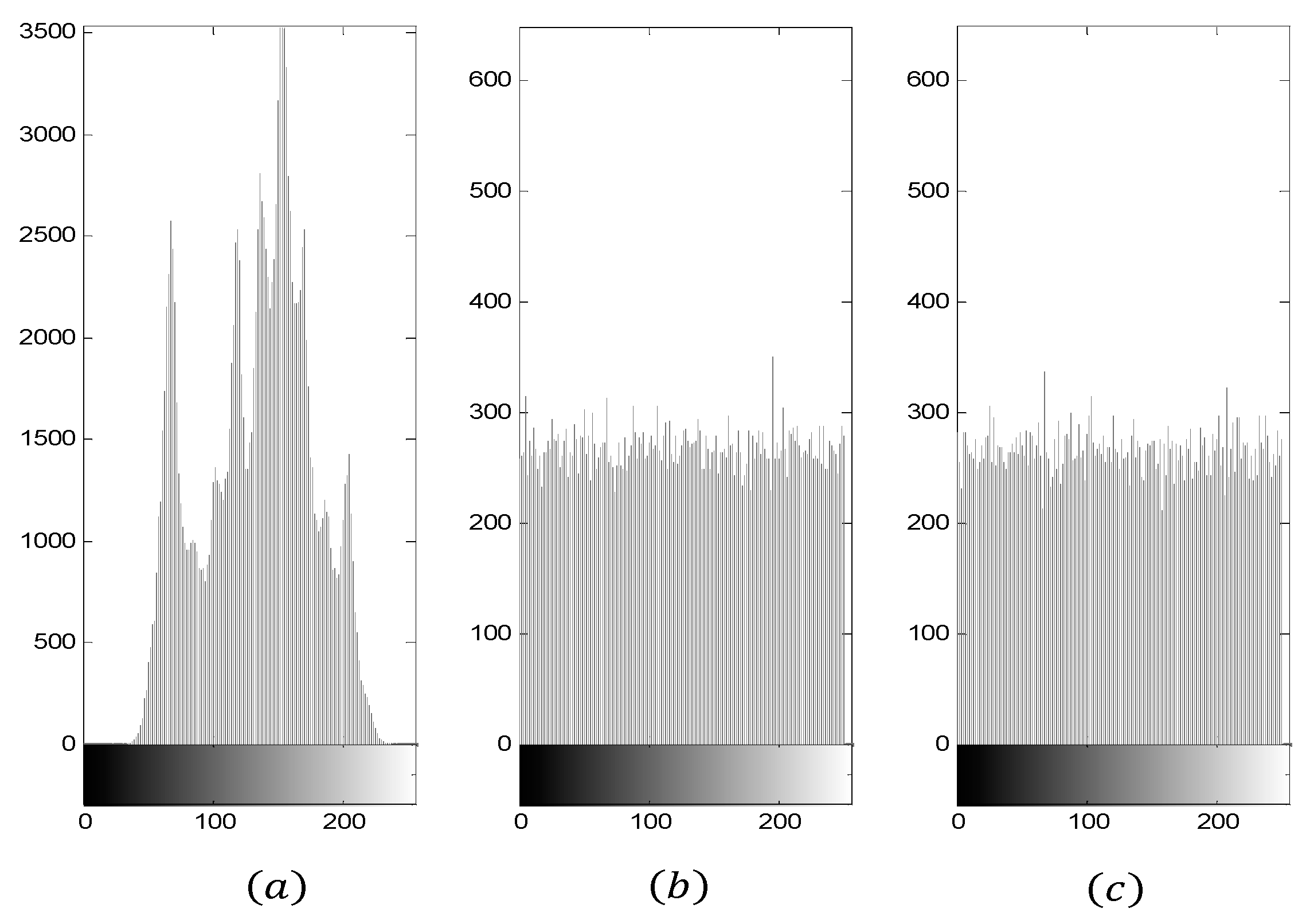
6.1. Simulation Results

First, we experiment the $(2,3,4,6)$-ESIS as an example to verify the proposed scheme, the simulation results are shown in Figure 2. Figure 2a shows the test secret image named ‘Lena’. Figure 2b shows the result of the permutated secret image. Figure 2c shows the intermediate shadows $T_1$, $T_2$, $T_3$, $T_4$. Three essential shadows $O_1$, $O_2$, $O_3$ and three non-essential shadows $O_4$, $O_5$, $O_6$ are shown in Figure 2d and Figure 2e, respectively.

Second, we conduct some experiment in order to demonstrate the security of the proposed scheme. Corresponding to the theoretical analysis of Theorem 1 in Section 5, there are three simulation results presented in Figure 3. As shown in Figure 3a, the secret image cannot be reconstructed when the collected shadows violate the threshold condition. Figure 3b shows that the secret image cannot be reconstructed when the collected shadows violate the essentiality condition. Figure 3c shows that the secret image can be recovered when the collected shadows satisfy both the threshold condition and the essentiality condition.

To highlight the security of the proposed scheme, there are some statistical analyses of the secret image which generated essential and non-essential shadows. Figure 4a shows the histogram of the test secret image ‘Lena’; Figure 4b,c shows the histogram of the essential shadow and non-essential shadow, respectively. It is clearly seen that the histogram of the secret image does not satisfy the uniform distribution but the generated shadows satisfy the uniform distribution. Therefore, it reduces the probability of information leakage when the shadows be attacked.

Meanwhile, we conduct a $(2,2,4,6)$-ESIS as an example to demonstrate the generated non-essential shadows in the proposed scheme which do not have the homomorphic property. Figure 5a shows the test secret image ‘Lena’; Figure 5b shows the generated two essential shadows $O_1$, $O_2$ and four non-essential shadows $O_3-O_6$. Figure 5c shows the reconstructed image with four non-essential shadows $O_3-O_6$, which can be seen as a disorganized image and verify that the proposed scheme does not have the homomorphic property. Figure 5d shows the recovered secret image with two essential shadows and two non-essential shadows.

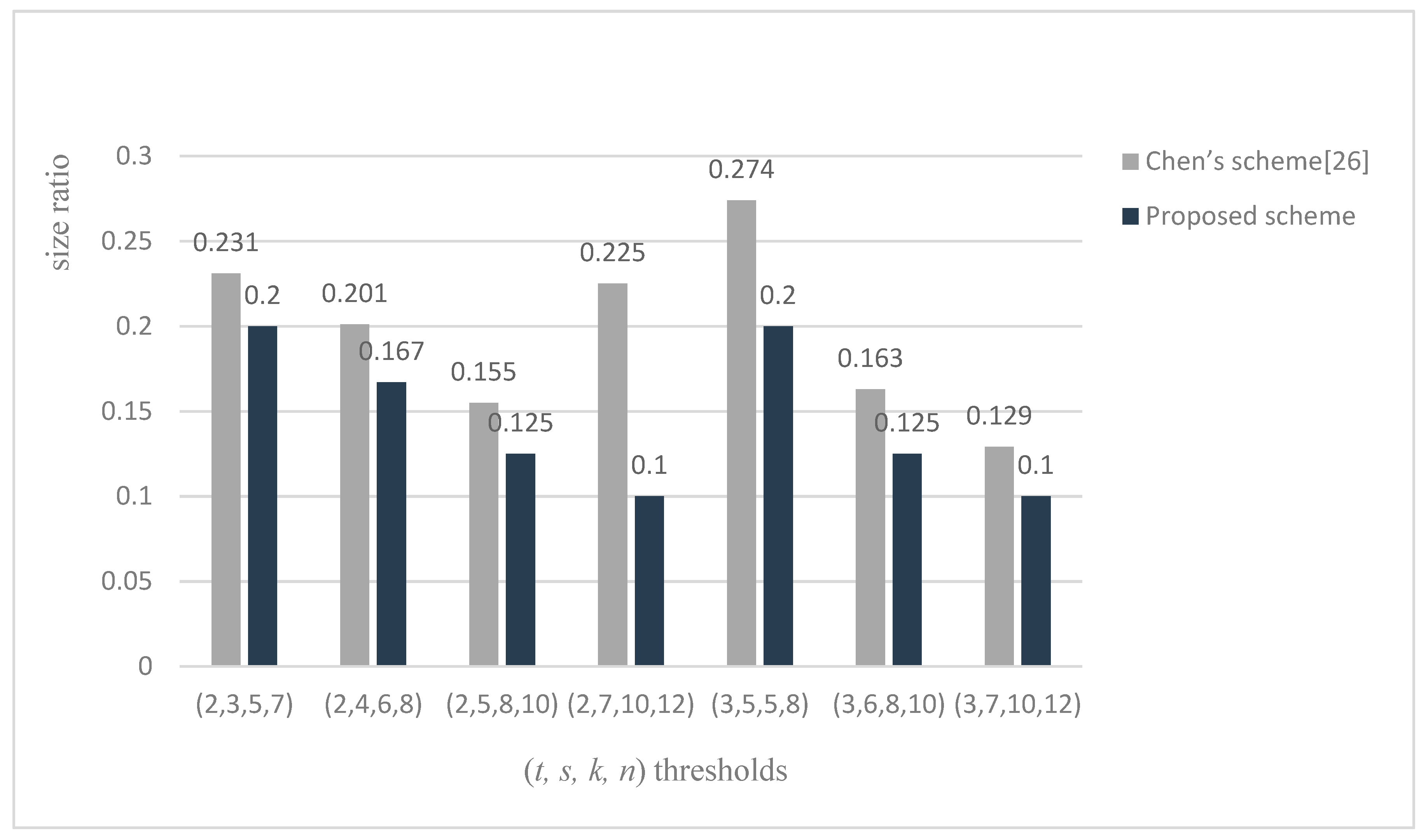
6.2. Comparison

This subsection presents some properties comparison between the proposed $(t,s,k,n)$-ESIS scheme and some other existing $(t,s,k,n)$-ESIS schemes. In this subsection, there is no comparison between the proposed scheme and Li et al.’s scheme, because Li et al.’s $(t,k,n)$-ESIS scheme [27] is a special case of $(t,s,k,n)$-ESIS schemes when $s=t$.

First, there is a comparison on whether the generated shadows have the same size between the proposed scheme and some other related ESIS schemes. Note that: ‘Yes’ same-size shadows are better than ‘No’ for the same-size shadows, which is important to guarantee the shadows are indistinguishable when they are shared to two different privileged participants. As shown in

Table 1. Comparison on whether the generated shadows are same-sized.

	[21]	[23]	[24]	[25]	[26]	Proposed Scheme
Same-size shadows	No	No	Yes	Yes	Yes	Yes

, the proposed scheme can generate same-sized essential shadows and non-essential shadows, which is better than Yang et al.’s [21] and Chen and Chen’s [23].

Second, there is a comparison on the generated shadows’ size ratio. Note: The smaller size of the shadows is better during storage and transmission.

Table 2. Comparison on shadows’ size ratio among the proposed scheme and the other three related works.

	[24]	[25]	[26]	Proposed Scheme
Essential shadow size ratio	$\frac{1}{t}$	$\frac{1}{t}$	$\frac{ry}{\left(k-t\right)\times \left(x+y\right)}$	$\frac{1}{k}$
Non-essential shadow size ratio	$\frac{1}{t}$	$\frac{1}{t}$	$\frac{ry}{\left(k-t\right)\times \left(x+y\right)}$	$\frac{1}{k}$

shows the proposed scheme has a better performance on shadows’ size than Li et al.’s scheme [24] and Chen et al.’s scheme [25]. Figure 6 also shows that the proposed scheme has a smaller size ratio than Chen’s scheme [26].

Table 3. Size ratios among the proposed scheme and the other three related works.

$(\mathit{t},\mathit{s},\mathit{k},\mathit{n})$		[24]	[25]	[26] a	Proposed Scheme
$(2,3,4,6)$	Essential shadow size ratio	$0.5$	0.5	$0.3$	$0.25$
	Non-essential shadow size ratio	$0.5$	0.5	$0.3$	$0.25$
$(3,6,8,10)$	Essential shadow size ratio	$0.333$	0.333	$0.163$	$0.125$
	Non-essential shadow size ratio	$0.333$	0.333	$0.163$	$0.125$
$(5,7,9,11)$	Essential shadow size ratio	$0.2$	0.2	$0.538$	$0.111$
	Non-essential shadow size ratio	$0.2$	0.2	$0.538$	$0.111$

[26] ^a: The $(t,s,k,n)$-ESIS scheme in [26] when $r=1$.

shows the example of shadows’ size ratio in different thresholds among the proposed scheme and three related works. Hence, the proposed scheme has a better performance on shadows’ size.

Third, there is a comparison regarding the properties on the concatenation of sub-shadows. If a scheme concatenates the sub-shadows in some way, the location of each sub-shadow needs to be recorded and each sub-shadows need to be extracted in the reconstruction, which would complicate the reveal process in practice. Hence, ‘No’ concatenation of sub-shadows is better than ‘Yes’. As shown in

Table 4. Comparison of concatenation of sub-shadows.

	[21]	[23] a	[24]	[25]	[26]	Proposed Scheme
Concatenation of sub-shadows	Yes	Yes	Yes	No	Yes	No

, only the proposed scheme and Chen et al.’s scheme [25] do not need the concatenation operation in the sharing process, which is better than Yang et al.’s scheme [21], Chen and Chen’s [23], Li et al.’s scheme [24], and Chen’s scheme [26].

7. Conclusions

In this paper, an efficient essential secret image sharing scheme using a derivative polynomial is proposed. In contrast to the conventional $(t,s,k,n)$-ESIS scheme which only utilizes Lagrange interpolation, the process of constructing the essential condition would be more simple by combining the derivative polynomial and would not increase the size of the generated shadows. In addition, the proposed scheme not only overcomes the shortcomings of previous works such as different-sized shadows and concatenation of sub-shadows, but is also superior in generating the smaller essential shadows and non-essential shadows. Future work will include the appropriate improvement of the proposed scheme, which is expected to reduce system complexity. Besides, the method provided in this paper may be applied in other fields of research to achieve a better performance, such as verifiable secret image sharing, scalable secret image sharing, etc.