Harmonic Superspace Approach to the Effective Action in Six-Dimensional Supersymmetric Gauge Theories
Abstract
Contents
| 1 | Introduction | 2 | |
| 2 | Harmonic Superspace Formulation of 6D Supersymmetric Gauge Theories | 3 | |
| 3 | Quantum Corrections in 6D, = (1, 0) Supersymmetric Electrodynamics | 6 | |
| 3.1 | Quantization, Feynman Rules, and Ward Identities in the Abelian Case . . . . . . . . . . . . . | 6 | |
| 3.2 | One-Loop Divergences and Their Gauge Dependence . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 9 | |
| 4 | Quantum Corrections in Non-Abelian 6D, = (1, 0) and = (1, 1) Supersymmetric | ||
| Theories | 12 | ||
| 4.1 | Quantization of Non-Abelian 6D Gauge Theories in the Harmonic Superspace by the | ||
| Background Field Method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 12 | ||
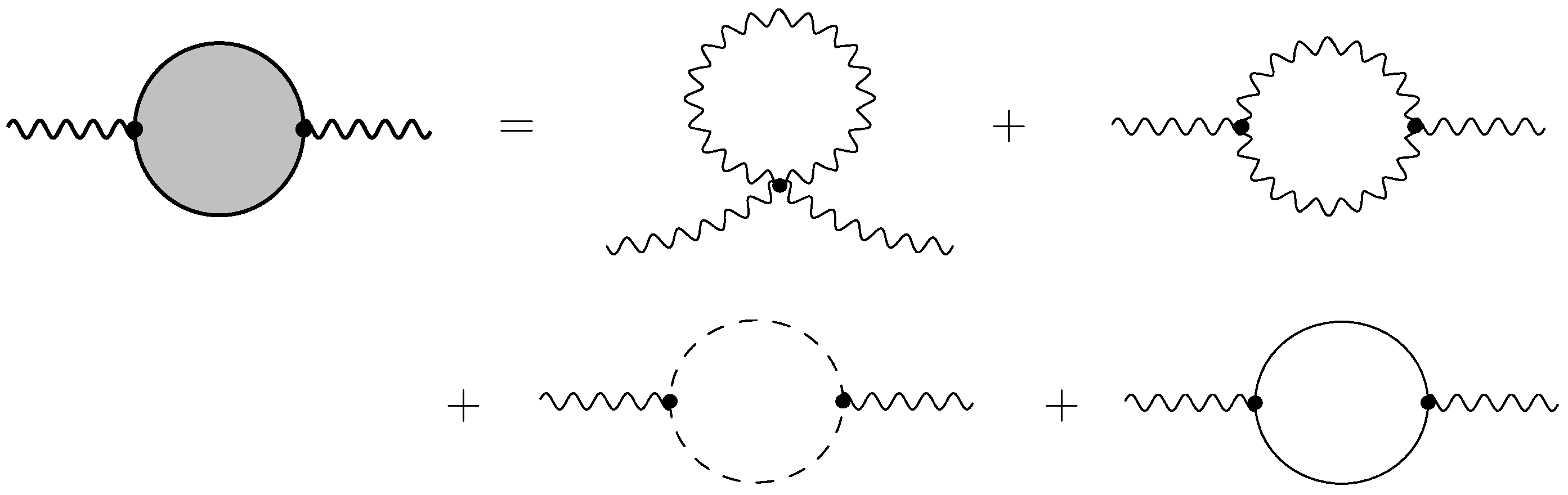
| 4.2 | One-Loop Divergences in Harmonic Superspace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 15 | |
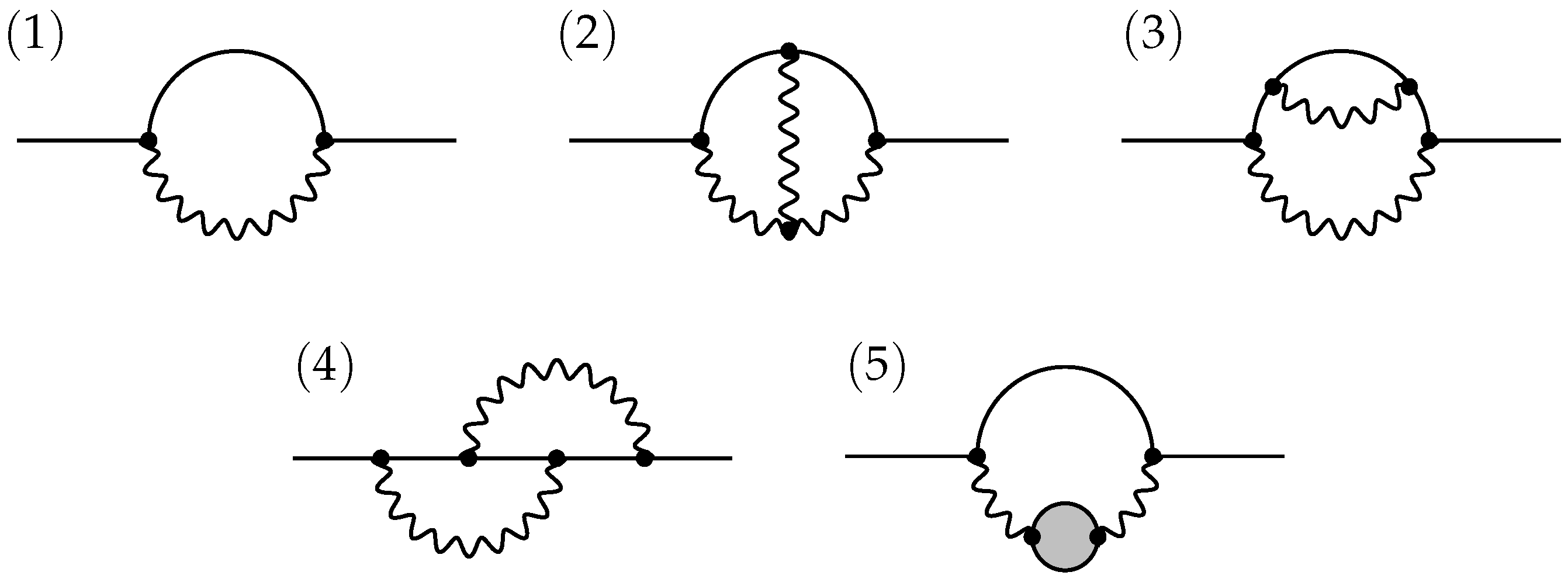
| 4.3 | Two-Loop Divergent Part of the Hypermultiplet Two-Point Green Function of 6D SYM | ||
| Theories . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 18 | ||
| 4.4 | Manifestly Gauge Covariant Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 20 | |
| 4.5 | Low-Energy Effective Action . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | 22 | |
| 5 | Conclusions | 25 | |
| References | 26 | ||
1. Introduction
2. Harmonic Superspace Formulation of 6D Supersymmetric Gauge Theories
3. Quantum Corrections in 6D, Supersymmetric Electrodynamics
3.1. Quantization, Feynman Rules, and Ward Identities in the Abelian Case
3.2. One-Loop Divergences and Their Gauge Dependence
4. Quantum Corrections in Non-Abelian , and Supersymmetric Theories
4.1. Quantization of Non-Abelian Gauge Theories in the Harmonic Superspace by the Background Field Method
4.2. One-Loop Divergences in Harmonic Superspace
4.3. Two-Loop Divergent Part of the Hypermultiplet Two-Point Green Function of SYM Theories
4.4. Manifestly Gauge Covariant Analysis
4.5. Low-Energy Effective Action
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Smilga, A. Ultraviolet divergences in non-renormalizable supersymmetric theories. Phys. Part. Nucl. Lett. 2017, 14, 245–260. [Google Scholar] [CrossRef]
- Bork, L.V.; Kazakov, D.I.; Kompaniets, M.V.; Tolkachev, D.M.; Vlasenko, D.E. Divergences in maximal supersymmetric Yang-Mills theories in diverse dimensions. J. High Energy Phys. 2015, 1511, 59. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Quantum properties of higher dimensional and dimensionally reduced supersymmetric theories. Nucl. Phys. B 1983, 227, 252–290. [Google Scholar] [CrossRef]
- Marcus, N.; Sagnotti, A. A Test of Finiteness Predictions for Supersymmetric Theories. Phys. Lett. B 1984, 135, 85–90. [Google Scholar] [CrossRef]
- Howe, P.S.; Stelle, K.S. Ultraviolet Divergences in Higher Dimensional Supersymmetric Yang-Mills Theories. Phys. Lett. B 1984, 137, 175–180. [Google Scholar] [CrossRef]
- Howe, P.S.; Stelle, K.S. Supersymmetry counterterms revisited. Phys. Lett. B 2003, 554, 190–196. [Google Scholar] [CrossRef]
- Bossard, G.; Howe, P.S.; Stelle, K.S. The Ultra-violet question in maximally supersymmetric field theories. Gen. Relat. Gravit. 2009, 41, 919–981. [Google Scholar] [CrossRef]
- Bossard, G.; Howe, P.S.; Stelle, K.S. A Note on the UV behavior of maximally supersymmetric Yang-Mills theories. Phys. Lett. B 2009, 682, 137–142. [Google Scholar] [CrossRef]
- Gates, S.J.; Grisaru, M.T.; Rocek, M.; Siegel, W. Superspace or one thousand and one lessons in supersymmetry. Front. Phys. 1983, 58, 1–548. [Google Scholar]
- Buchbinder, I.L.; Kuzenko, S.M. Ideas and Methods of Supersymmetry and Supergravity: Or a Walk through Superspace; IOP: Bristol, UK, 1998; 656p, ISBN 0750305061. [Google Scholar]
- Marcus, N.; Sagnotti, A. The Ultraviolet Behavior of N = 4 Yang-Mills and the Power Counting of Extended Superspace. Nucl. Phys. B 1985, 256, 77–108. [Google Scholar] [CrossRef]
- Galperin, A.; Ivanov, E.; Kalitzin, S.; Ogievetsky, V.; Sokatchev, E. Unconstrained N = 2 matter, Yang-Mills and supergravity theories in harmonic superspace. Class. Quantum Gravity 1984, 1, 469–498, Erratum in 1985, 2, 127. [Google Scholar] [CrossRef]
- Galperin, A.; Ivanov, E.A.; Ogievetsky, V.; Sokatchev, E. Harmonic supergraphs: Green functions. Class. Quantum Gravity 1985, 2, 601–616. [Google Scholar] [CrossRef]
- Galperin, A.; Ivanov, E.; Ogievetsky, V.; Sokatchev, E. Harmonic supergraphs: Feynman rules and examples. Class. Quantum Gravity 1985, 2, 617–630. [Google Scholar] [CrossRef]
- Galperin, A.S.; Ivanov, E.A.; Ogievetsky, V.I.; Sokatchev, E.S. Harmonic Superspace; Cambridge University Press: Cambridge, UK, 2001; 306p, ISBN 0521801648. [Google Scholar]
- Buchbinder, E.I.; Ovrut, B.A.; Buchbinder, I.L.; Ivanov, E.A.; Kuzenko, S.M. Low-energy effective action in N = 2 supersymmetric field theories. Phys. Part. Nucl. 2001, 32, 641–674. [Google Scholar]
- Buchbinder, I.L.; Ivanov, E.A.; Pletnev, N.G. Superfield approach to the construction of effective action in quantum field theory with extended supersymmetry. Phys. Part. Nucl. 2016, 47, 291–369. [Google Scholar] [CrossRef]
- Howe, P.S.; Sierra, G.; Townsend, P.K. Supersymmetry in six-dimensions. Nucl. Phys. B 1983, 221, 331–348. [Google Scholar] [CrossRef]
- Howe, P.S.; Stelle, K.S.; West, P.C. N = 1, d = 6 harmonic superspace. Class. Quantum Gravity 1985, 2, 815–821. [Google Scholar] [CrossRef]
- Zupnik, B.M. Six-dimensional supergauge theories in the harmonic superspace. Sov. J. Nucl. Phys. 1986, 44, 512–517. [Google Scholar]
- Ivanov, E.A.; Smilga, A.V.; Zupnik, B.M. Renormalizable supersymmetric gauge theory in six dimensions. Nucl. Phys. B 2005, 726, 131–148. [Google Scholar] [CrossRef]
- Ivanov, E.A.; Smilga, A.V. Conformal properties of hypermultiplet actions in six dimensions. Phys. Lett. B 2006, 637, 374–381. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Pletnev, N.G. Construction of 6D supersymmetric field models in N = (1,0) harmonic superspace. Nucl. Phys. B 2015, 892, 21–48. [Google Scholar] [CrossRef]
- Townsend, P.K.; Sierra, G. Chiral anomalies and constraints on the gauge group in higher dimensional supersymmetric Yang-Mills theories. Nucl. Phys. B 1983, 222, 493–506. [Google Scholar] [CrossRef]
- Smilga, A.V. Chiral anomalies in higher-derivative supersymmetric 6D theories. Phys. Lett. B 2007, 647, 298–304. [Google Scholar] [CrossRef]
- Kuzenko, S.M.; Novak, J.; Samsonov, I.B. The anomalous current multiplet in 6D minimal supersymmetry. J. High Energy Phys. 2016, 2016, 132. [Google Scholar] [CrossRef]
- Kuzenko, S.M.; Novak, J.; Samsonov, I.B. Chiral anomalies in six dimensions from harmonic superspace. J. High Energy Phys. 2017, 2017, 145. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Buchbinder, E.I.; Kuzenko, S.M.; Ovrut, B.A. The background field method for N = 2 superYang-Mills theories in harmonic superspace. Phys. Lett. B 1998, 417, 61–71. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Merzlikin, B.S.; Stepanyantz, K.V. One-loop divergences in the 6D, = (1,0) Abelian gauge theory. Phys. Lett. B 2016, 763, 375–381. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Merzlikin, B.S.; Stepanyantz, K.V. One-loop divergences in 6D, = (1,0) SYM theory. J. High Energy Phys. 2017, 2017, 128. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Merzlikin, B.S.; Stepanyantz, K.V. Supergraph analysis of the one-loop divergences in 6D, = (1,0) and = (1,1) gauge theories. Nucl. Phys. B 2017, 921, 127–158. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Merzlikin, B.S.; Stepanyantz, K.V. On the two-loop divergences of the 2-point hypermultiplet supergraphs for 6D, = (1,1) SYM theory. Phys. Lett. B 2018, 778, 252–255. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Merzlikin, B.S.; Stepanyantz, K.V. Gauge dependence of the one-loop divergences in 6D, = (1,0) Abelian theory. Nucl. Phys. B 2018, 936, 638–660. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Merzlikin, B.S. Leading Low-Energy Effective Action in 6D, = (1,1) SYM Theory. arXiv, 2017; arXiv:1711.03302 [hep-th]. [Google Scholar]
- Cederwall, M. Pure spinor superfields—An overview. In Springer Proceedings in Physics; Springer: Cham, Switzerland, 2014; Volume 153, pp. 61–93. [Google Scholar] [CrossRef]
- Cederwall, M. Pure spinor superspace action for D = 6, N = 1 super-Yang-Mills theory. J. High Energy Phys. 2018, 2018, 115. [Google Scholar] [CrossRef]
- Schwinger, J.S. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- DeWitt, B.S. Dynamical theory of groups and fields. Conf. Proc. 1964, C630701, 585–820. [Google Scholar] [CrossRef]
- Aleshin, S.S.; Kazantsev, A.E.; Skoptsov, M.B.; Stepanyantz, K.V. One-loop divergences in non-Abelian supersymmetric theories regularized by BRST-invariant version of the higher derivative regularization. J. High Energy Phys. 2016, 2016, 14. [Google Scholar] [CrossRef]
- Kutasov, D. Introduction to little string theory. ICTP Lect. Notes Ser. 2002, 7, 165–209. [Google Scholar]
- Chang, C.M.; Lin, Y.H.; Shao, S.H.; Wang, Y.; Yin, X. Little String Amplitudes (and the Unreasonable Effectiveness of 6D SYM). J. High Energy Phys. 2014, 2014, 176. [Google Scholar] [CrossRef]
- Lin, Y.H.; Shao, S.H.; Wang, Y.; Yin, X. Interpolating the Coulomb Phase of Little String Theory. J. High Energy Phys. 2015, 2015, 22. [Google Scholar] [CrossRef]
- Bossard, G.; Ivanov, E.; Smilga, A. Ultraviolet behavior of 6D supersymmetric Yang-Mills theories and harmonic superspace. J. High Energy Phys. 2015, 2015, 85. [Google Scholar] [CrossRef]
- Grisaru, M.T.; Siegel, W. Supergraphity. 2. Manifestly Covariant Rules and Higher Loop Finiteness. Nucl. Phys. B 1982, 201, 292–314, Erratum in Nucl. Phys. B 1982, 206, 496–497. [Google Scholar] [CrossRef]
- Mandelstam, S. Light Cone Superspace and the Ultraviolet Finiteness of the N = 4 Model. Nucl. Phys. B 1983, 213, 149–168. [Google Scholar] [CrossRef]
- Brink, L.; Lindgren, O.; Nilsson, B.E.W. N = 4 Yang-Mills Theory on the Light Cone. Nucl. Phys. B 1983, 212, 401–412. [Google Scholar] [CrossRef]
- Howe, P.S.; Stelle, K.S.; Townsend, P.K. Miraculous Ultraviolet Cancellations in Supersymmetry Made Manifest. Nucl. Phys. B 1984, 236, 125–166. [Google Scholar] [CrossRef]
- Ward, J.C. An Identity in Quantum Electrodynamics. Phys. Rev. 1950, 78, 182. [Google Scholar] [CrossRef]
- Taylor, J.C. Ward Identities and Charge Renormalization of the Yang-Mills Field. Nucl. Phys. B 1971, 33, 436–444. [Google Scholar] [CrossRef]
- Slavnov, A.A. Ward Identities in Gauge Theories. Theor. Math. Phys. 1972, 10, 99–107. [Google Scholar] [CrossRef]
- Siegel, W. Supersymmetric dimensional regularization via dimensional reduction. Phys. Lett. B 1979, 84, 193–196. [Google Scholar] [CrossRef]
- Slavnov, A.A. Invariant regularization of nonlinear chiral theories. Nucl. Phys. B 1971, 31, 301–315. [Google Scholar] [CrossRef]
- Slavnov, A.A. Invariant regularization of gauge theories. Theor. Math. Phys. 1972, 13, 1064–1066. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Pletnev, N.G.; Stepanyantz, K.V. Manifestly N = 2 supersymmetric regularization for N = 2 supersymmetric field theories. Phys. Lett. B 2015, 751, 434–441. [Google Scholar] [CrossRef]
- Boulware, D.G. Gauge Dependence of the Effective Action. Phys. Rev. D 1981, 23, 389–396. [Google Scholar] [CrossRef]
- Voronov, B.L.; Tyutin, I.V. On Renormalization of the Einsteinian Gravity. Yad. Fiz. 1981, 33, 1710–1722. (In Russian) [Google Scholar]
- Voronov, B.L.; Lavrov, P.M.; Tyutin, I.V. Canonical Transformations And The Gauge Dependence In General Gauge Theories. Yad. Fiz. 1982, 36, 498–508. (In Russian) [Google Scholar]
- Voronov, B.L.; Tyutin, I.V. Formulation Of Gauge Theories Of General Form. II. Gauge Invariant Renormalizability And Renormalization Structure. Theor. Math. Phys. 1982, 52, 628–637. [Google Scholar] [CrossRef]
- Lavrov, P.M.; Tyutin, I.V. Effective Action In General Gauge Theories. Yad. Fiz. 1985, 41, 1658–1666. (In Russian) [Google Scholar]
- Becchi, C.; Rouet, A.; Stora, R. Renormalization of the Abelian Higgs-Kibble Model. Commun. Math. Phys. 1975, 42, 127–162. [Google Scholar] [CrossRef]
- Tyutin, I.V. Gauge Invariance in Field Theory and Statistical Physics in Operator Formalism. arXiv, 2008; arXiv:0812.0580 [hep-th]. [Google Scholar]
- Shakhmanov, V.Y.; Stepanyantz, K.V. New form of the NSVZ relation at the two-loop level. Phys. Lett. B 2018, 776, 417–423. [Google Scholar] [CrossRef]
- Slavnov, A.A. Regularization-independent gauge-invariant renormalization of the Yang-Mills theory. Theor. Math. Phys. 2002, 130, 1–10. [Google Scholar] [CrossRef]
- Slavnov, A.A.; Stepanyantz, K.V. Universal invariant renormalization of supersymmetric Yang-Mills theory. Theor. Math. Phys. 2004, 139, 599–608. [Google Scholar] [CrossRef]
- Kazakov, D.I. Towards a consistent SUSY QFT in extra dimensions. arXiv, 2002; arXiv:hep-ph/0202150. [Google Scholar]
- Kazakov, D.I. Ultraviolet fixed points in gauge and SUSY field theories in extra dimensions. J. High Energy Phys. 2003, 2003, 20. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Pletnev, N.G. Hypermultiplet dependence of one-loop effective action in the N = 2 superconformal theories. J. High Energy Phys. 2007, 2007, 96. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Kuzenko, S.M. Comments on the background field method in harmonic superspace: Nonholomorphic corrections in N = 4 SYM. Mod. Phys. Lett. A 1998, 13, 1623–1636. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A. Complete N = 4 structure of low-energy effective action in N = 4 super Yang-Mills theories. Phys. Lett. B 2002, 524, 208–216. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Petrov, A.Y. Complete low-energy effective action in N = 4 SYM: A Direct N = 2 supergraph calculation. Nucl. Phys. B 2003, 653, 64–84. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Petrov, A.Y.; Tseytlin, A.A. Two loop N = 4 superYang-Mills effective action and interaction between D3-branes. Nucl. Phys. B 2002, 621, 179–207. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Kuzenko, S.M.; Tseytlin, A.A. On low-energy effective actions in N = 2, N = 4 superconformal theories in four-dimensions. Phys. Rev. D 2000, 62, 045001. [Google Scholar] [CrossRef]
- Buchbinder, I.L.; Ivanov, E.A.; Samsonov, I.B. The low-energy N = 4 SYM effective action in diverse harmonic superspaces. Phys. Part. Nucl. 2017, 48, 333–388. [Google Scholar] [CrossRef]
- Giveon, A.; Kutasov, D. Brane dynamics and gauge theory. Rev. Mod. Phys. 1999, 71, 983–1084. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Kors, B.; Lust, D.; Stieberger, S. Four-dimensional String Compactifications with D-Branes, Orientifolds and Fluxes. Phys. Rep. 2007, 445, 1–193. [Google Scholar] [CrossRef]
- Kuzenko, S.M.; McArthur, I.N. Effective action of N = 4 superYang-Mills: N = 2 superspace approach. Phys. Lett. B 2001, 506, 140–146. [Google Scholar] [CrossRef]
- Kuzenko, S.M. Self-dual effective action of N = 4 SYM revisited. J. High Energy Phys. 2005, 2005, 8. [Google Scholar] [CrossRef]



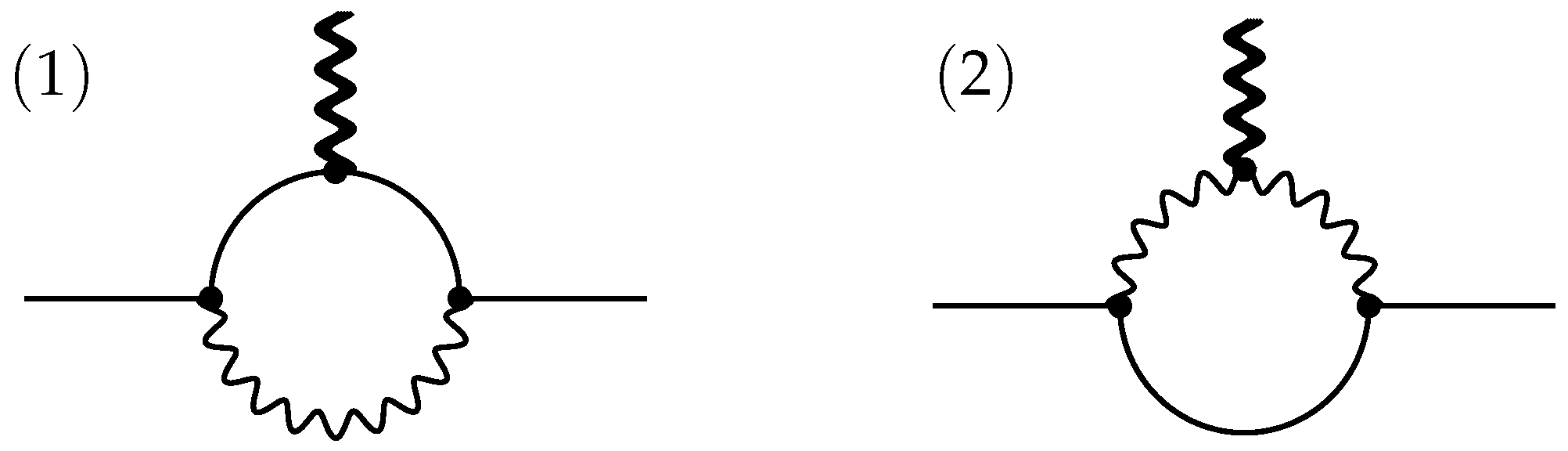
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buchbinder, I.; Ivanov, E.; Merzlikin, B.; Stepanyantz, K. Harmonic Superspace Approach to the Effective Action in Six-Dimensional Supersymmetric Gauge Theories. Symmetry 2019, 11, 68. https://doi.org/10.3390/sym11010068
Buchbinder I, Ivanov E, Merzlikin B, Stepanyantz K. Harmonic Superspace Approach to the Effective Action in Six-Dimensional Supersymmetric Gauge Theories. Symmetry. 2019; 11(1):68. https://doi.org/10.3390/sym11010068
Chicago/Turabian StyleBuchbinder, Ioseph, Evgeny Ivanov, Boris Merzlikin, and Konstantin Stepanyantz. 2019. "Harmonic Superspace Approach to the Effective Action in Six-Dimensional Supersymmetric Gauge Theories" Symmetry 11, no. 1: 68. https://doi.org/10.3390/sym11010068
APA StyleBuchbinder, I., Ivanov, E., Merzlikin, B., & Stepanyantz, K. (2019). Harmonic Superspace Approach to the Effective Action in Six-Dimensional Supersymmetric Gauge Theories. Symmetry, 11(1), 68. https://doi.org/10.3390/sym11010068





