Anti-Cavitation Design of the Symmetric Leading-Edge Shape of Mixed-Flow Pump Impeller Blades
Abstract
1. Introduction
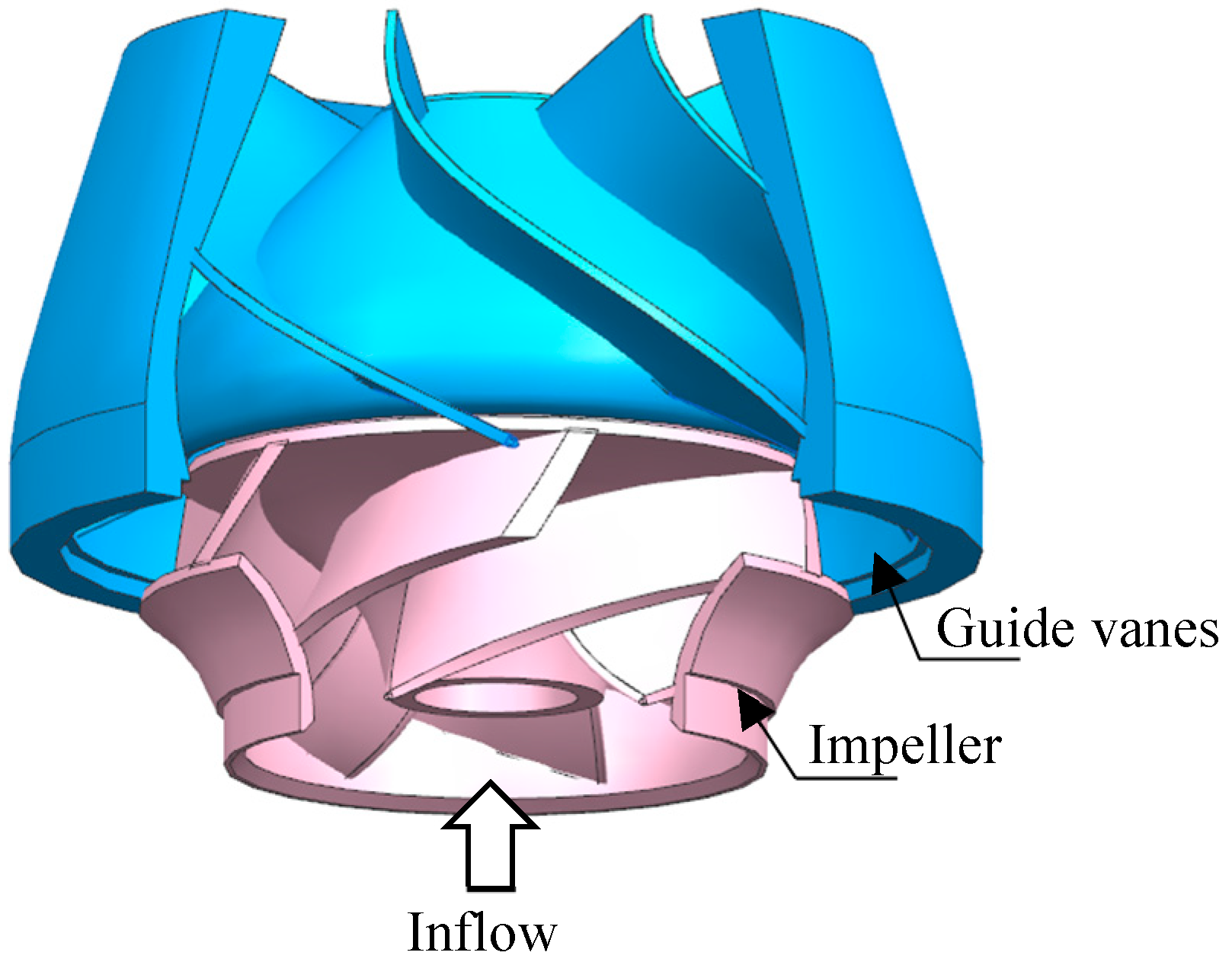
2. Mixed-Flow Pump Object
3. Mathematical Methods
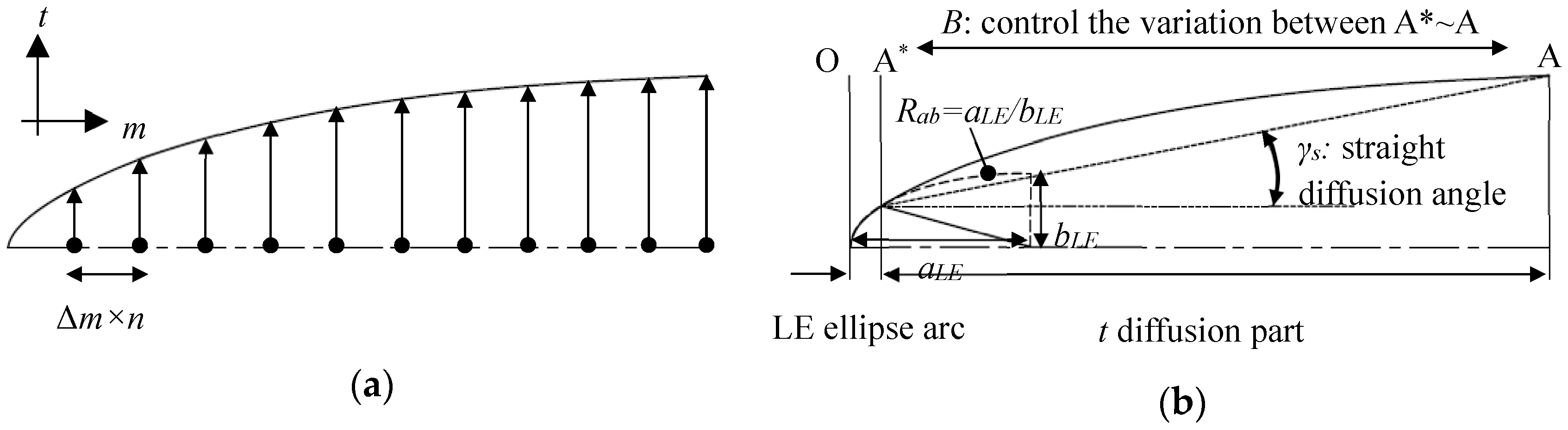
3.1. Brief Introduction of the Diffusion-Angle Integral Method
3.2. Genetic Algorithm and Setup
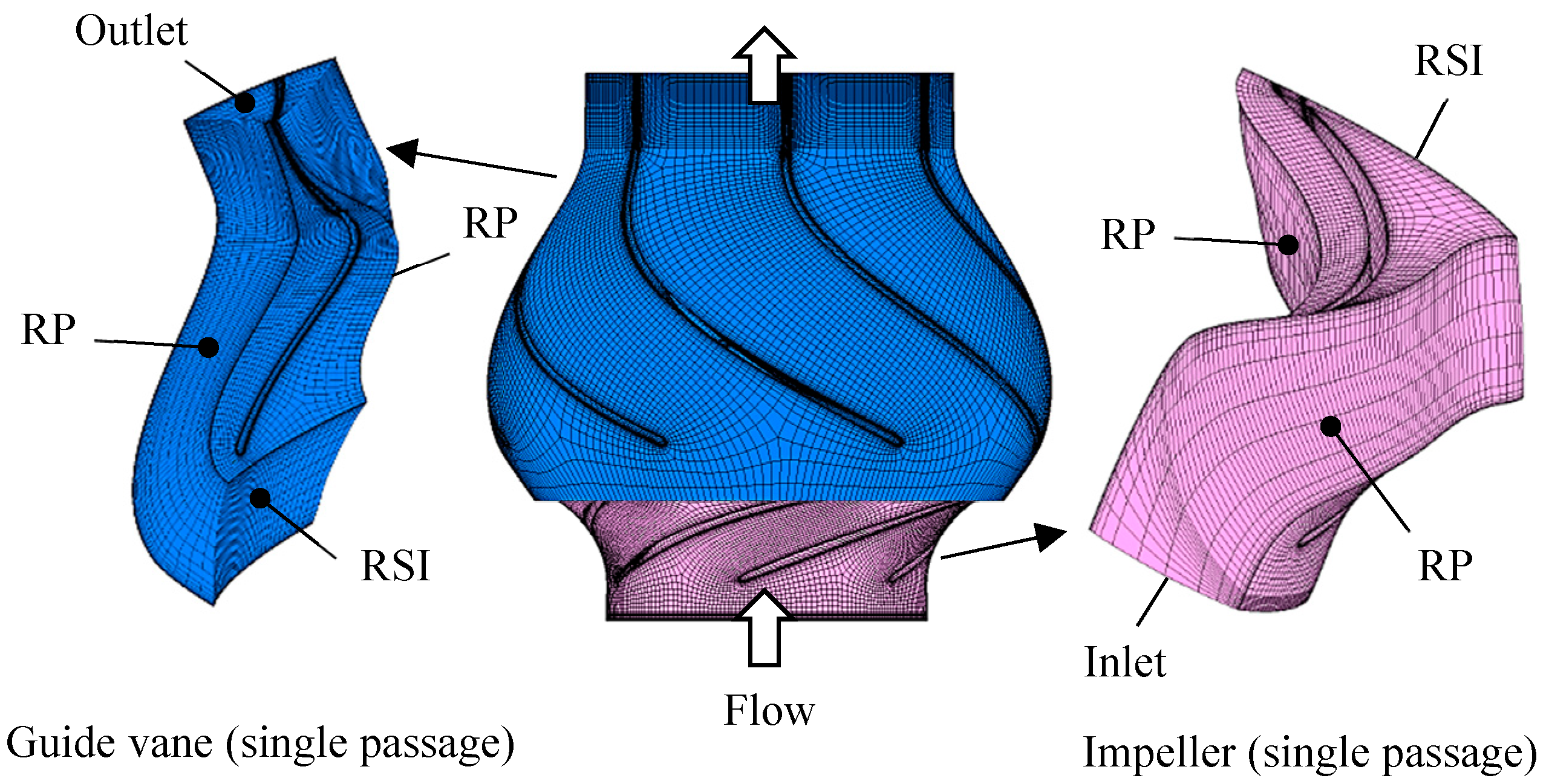
3.3. CFD Simulation Setup
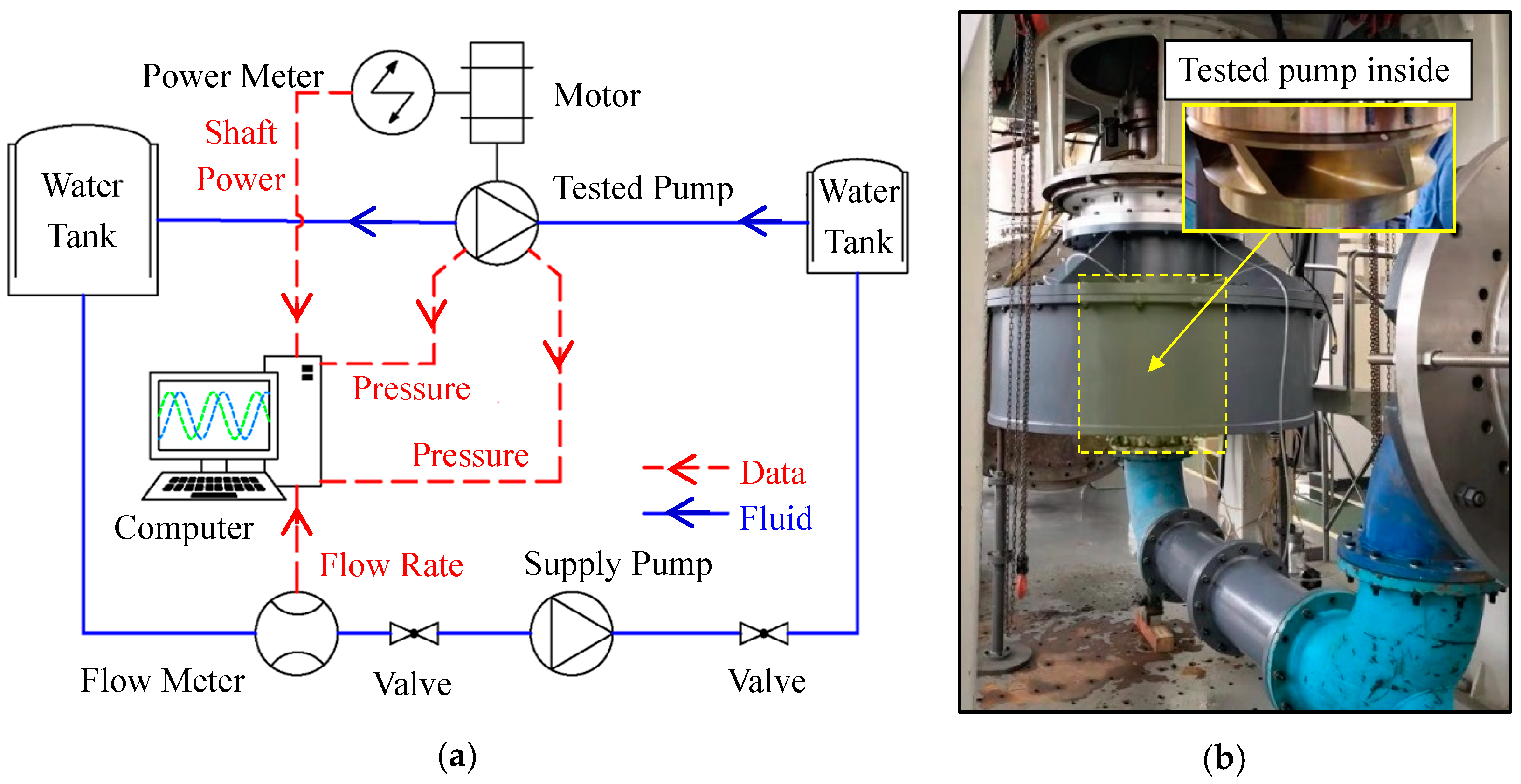
3.4. Model Test for Verification
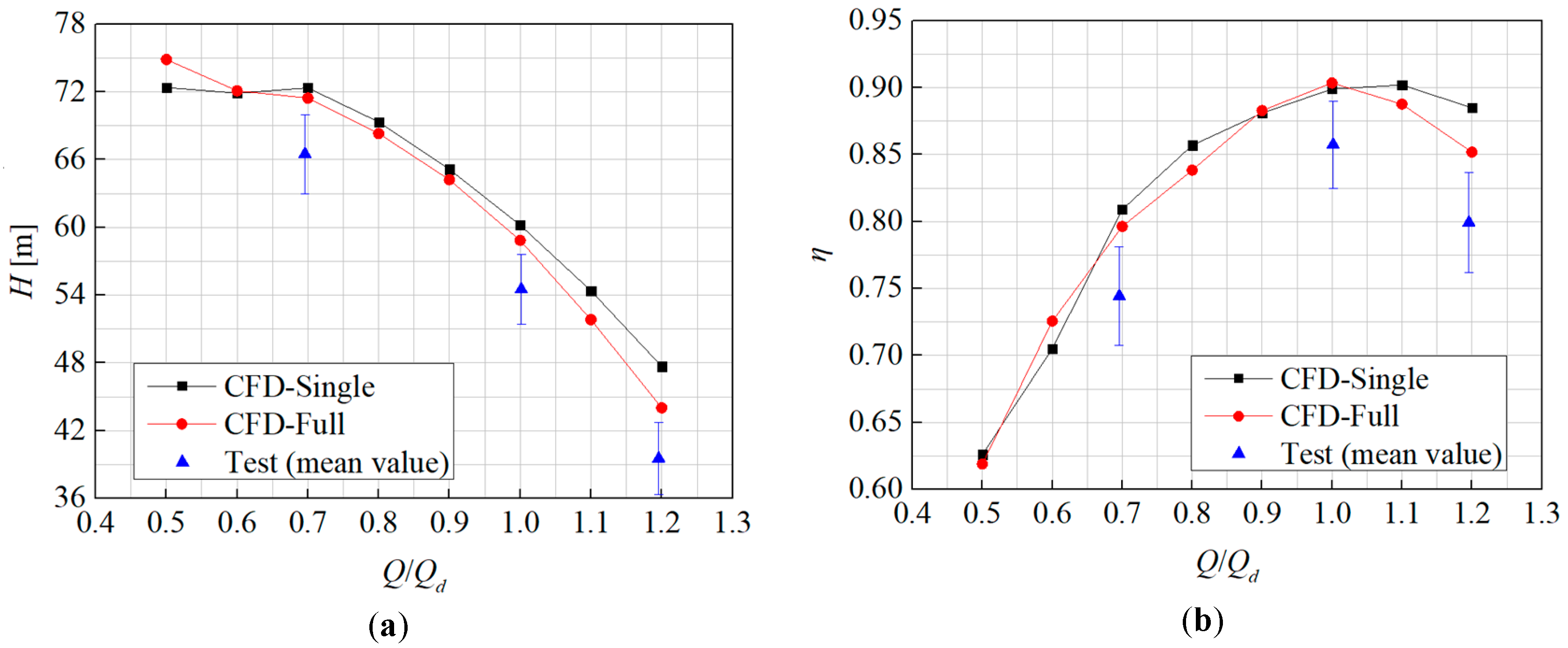
4. Experimental Verification of Computation
5. Results of Optimization Design
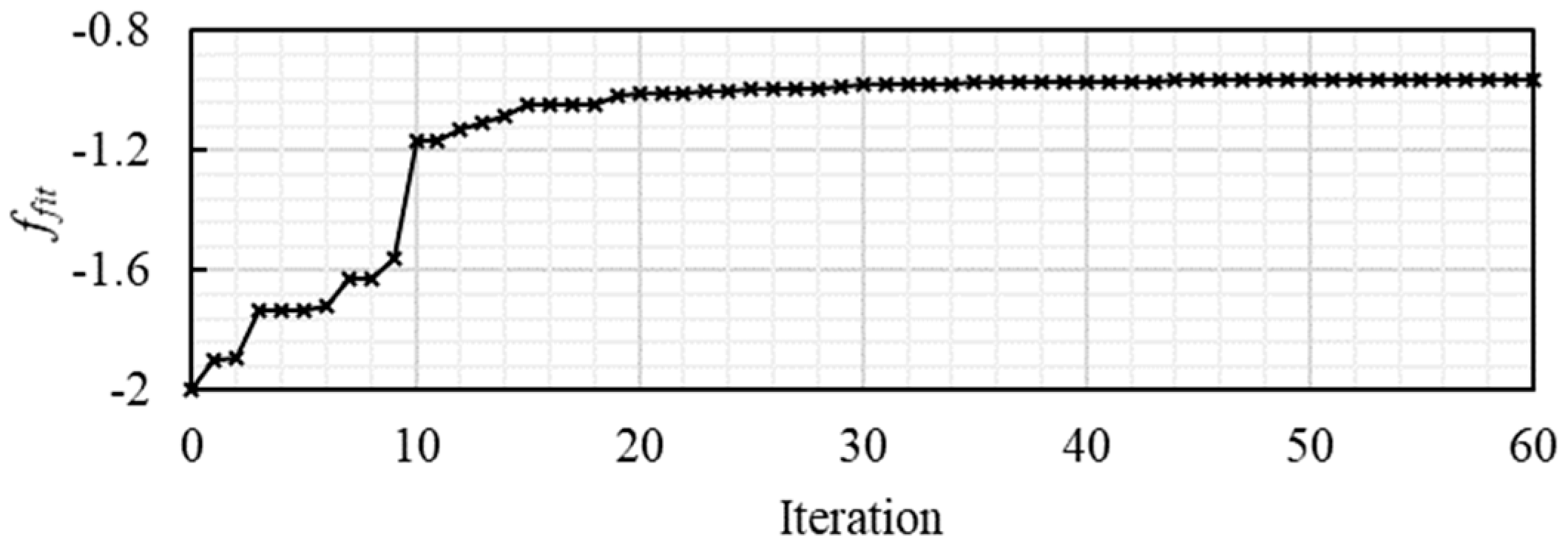
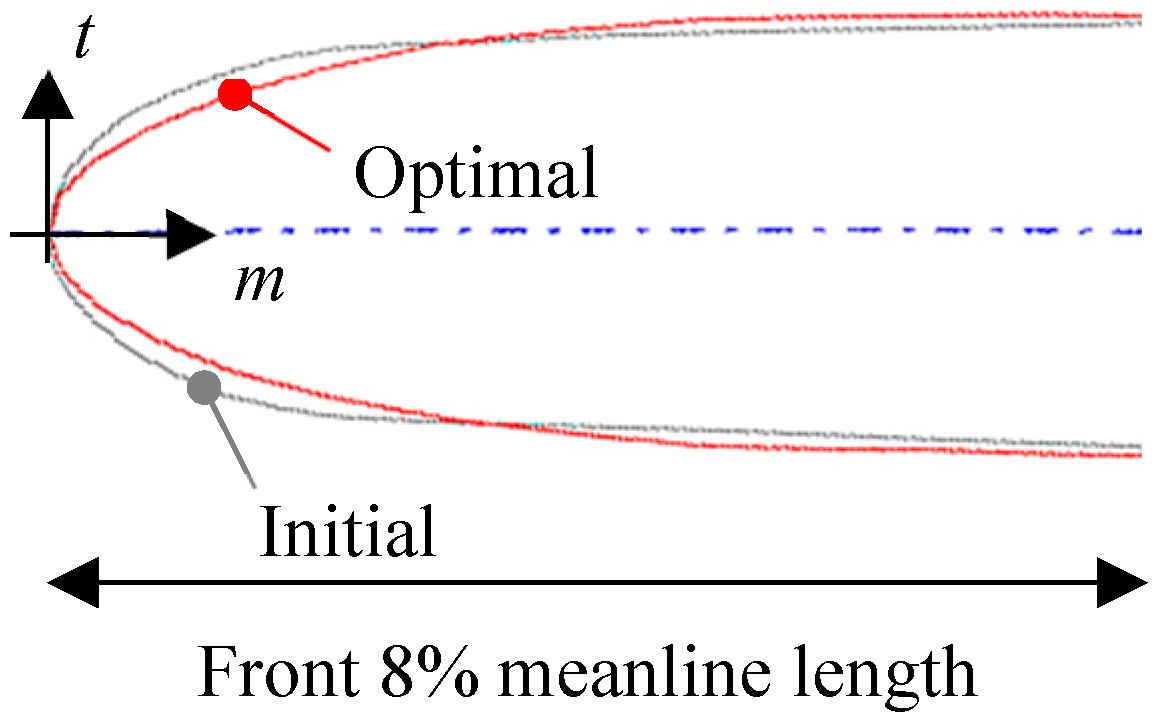
5.1. Optimization Process
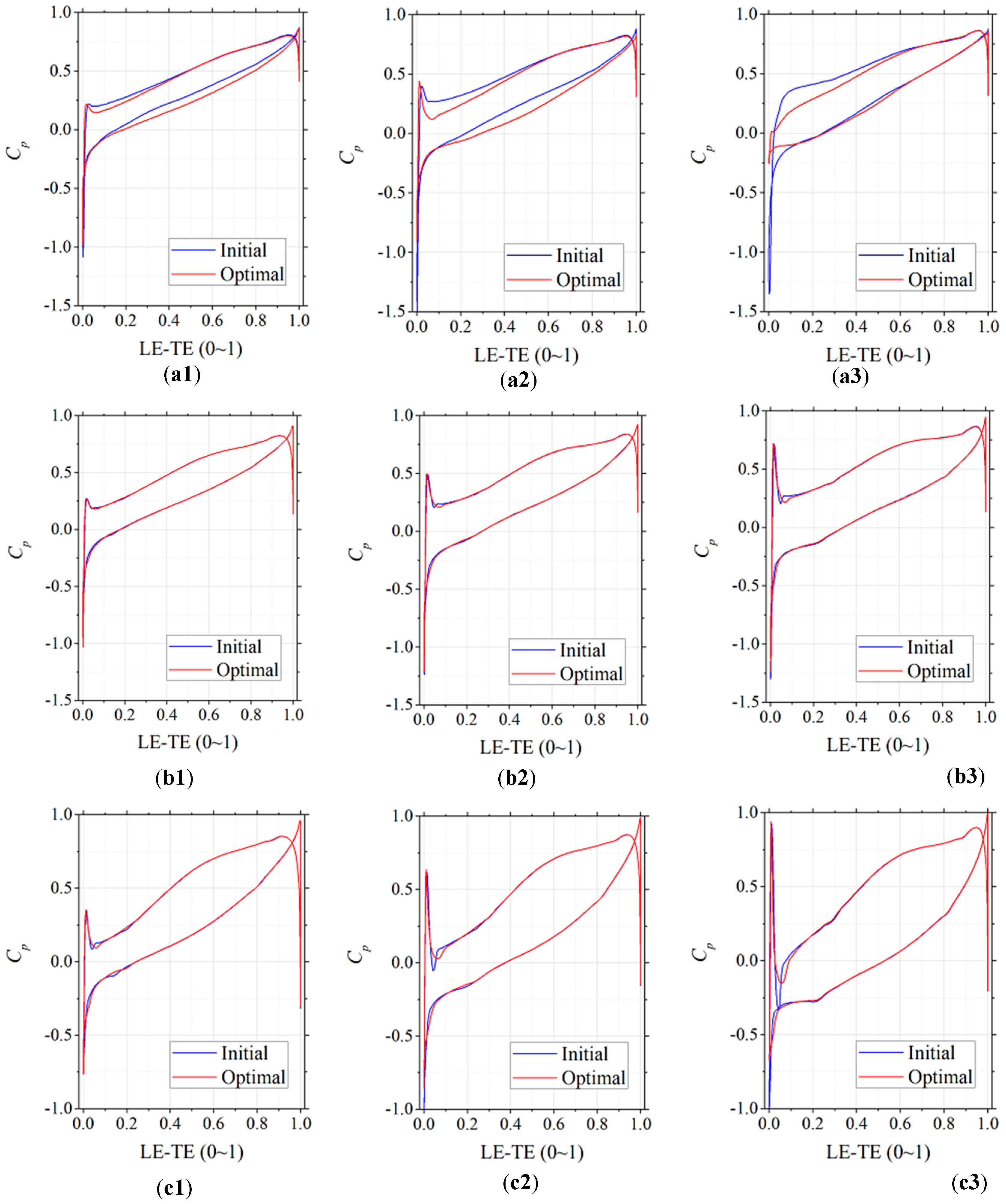
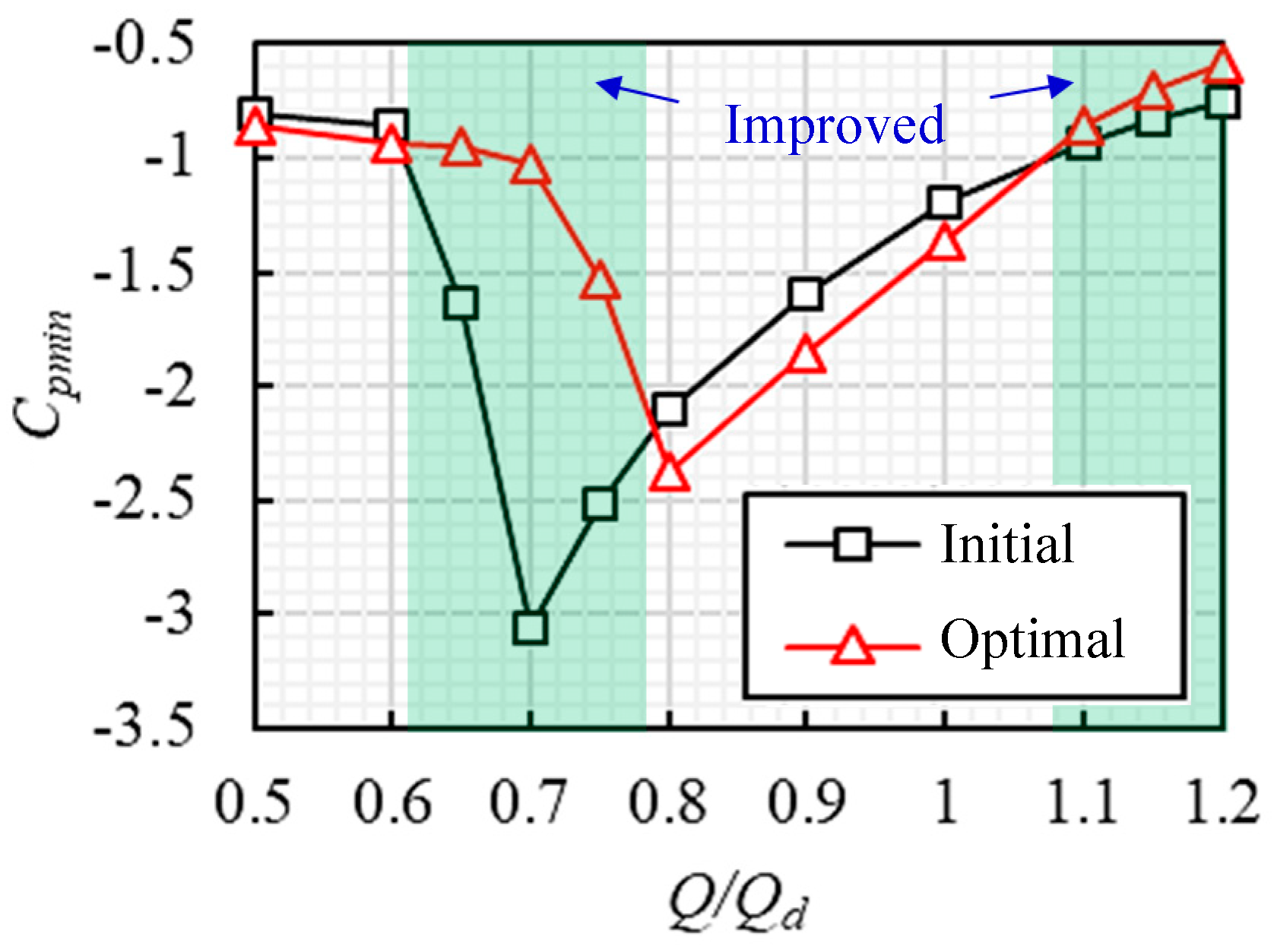
5.2. Analysis of Cavitation Performance
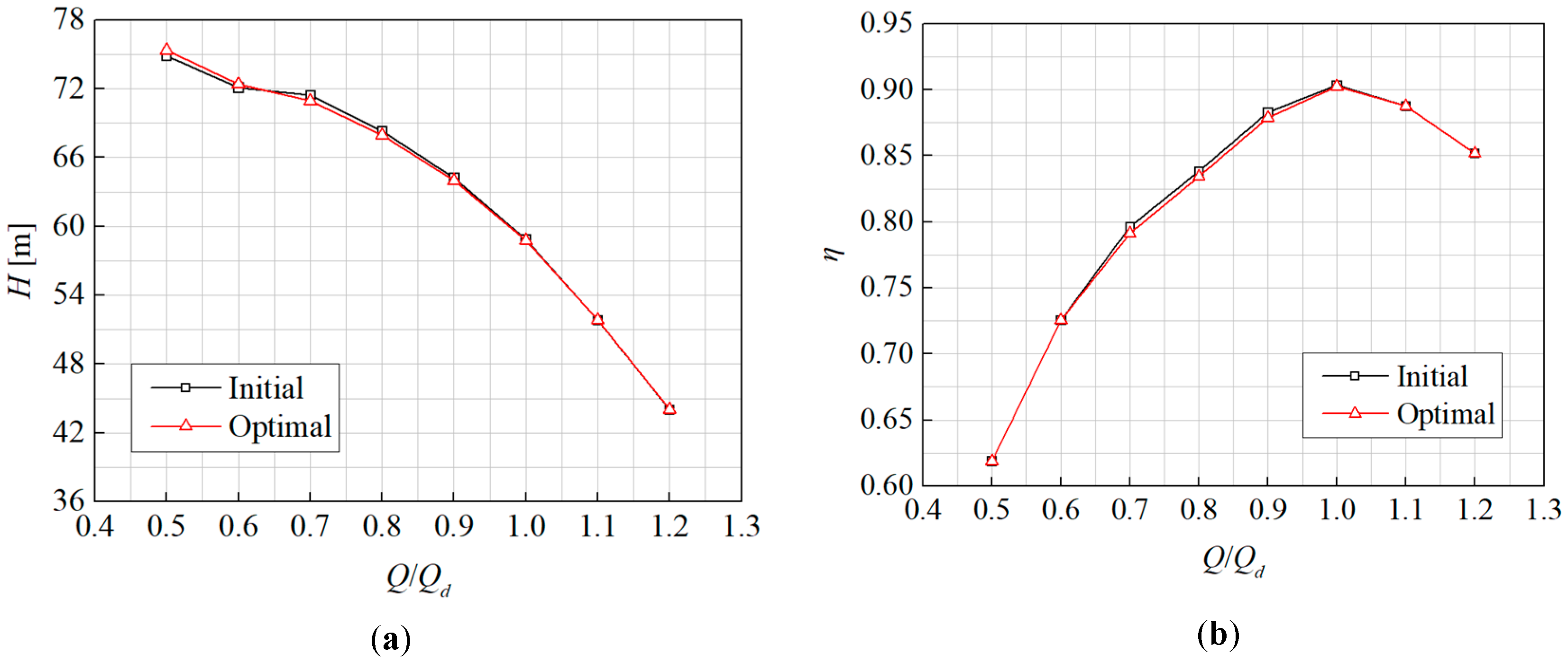
5.3. Comparison of Head and Efficiency
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Wu, Q.; Huang, B.; Wang, G.; Cao, S.; Zhu, M. Numerical modelling of unsteady cavitation and induced noise around a marine propeller. Ocean Eng. 2018, 160, 143–155. [Google Scholar] [CrossRef]
- Valentín, D.; Presas, A.; Egusquiza, M.; Valero, C.; Egusquiza, E. Transmission of high frequency vibrations in rotating systems. Application to cavitation detection in hydraulic turbines. Appl. Sci. 2018, 8, 451. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, Z.; Stone, H.A.; Liu, S. Motion of a Free-Settling Spherical Particle Driven by a Laser-Induced Bubble. Phys. Rev. Lett. 2017, 119, 084501. [Google Scholar] [CrossRef] [PubMed]
- Mouvanal, S.; Chatterjee, D.; Bakshi, S.; Burkhardt, A.; Mohr, V. Numerical prediction of potential cavitation erosion in fuel injectors. Int. J. Multiph. Flow 2018, 104, 113–124. [Google Scholar] [CrossRef]
- Pan, Z.; Yuan, S. Fundamentals of Cavitation in Pumps; Jiangsu University Press: Zhenjiang, China, 2013. [Google Scholar]
- Hao, Y.; Tan, L. Symmetrical and unsymmetrical tip clearances on cavitation performance and radial force of a mixed flow pump as turbine at pump mode. Renew. Energy 2018, 127, 368–376. [Google Scholar] [CrossRef]
- Hirschi, R.; Dupont, P.; Avellan, F.; Favre, J.N.; Guelich, J.F.; Parkinson, E. Centrifugal pump performance drop due to leading edge cavitation: Numerical predictions compared with model tests. J. Fluids Eng. Trans. ASME 1998, 120, 705–711. [Google Scholar] [CrossRef]
- Koukouvinis, P.; Gavaises, M.; Supponen, O.; Farhat, M. Simulation of bubble expansion and collapse in the vicinity of a free surface. Phys. Fluids 2016, 28, 052103. [Google Scholar] [CrossRef]
- Susan-Resiga, R.; Vu, T.C.; Muntean, S.; Ciocan, G.D.; Nennemann, B. Jet control of the draft tube vortex rope in Francis turbines at partial discharge. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Yang, W.; Xiao, R.; Wang, F.; Wu, Y. Influence of splitter blades on the cavitation performance of a double suction centrifugal pump. Adv. Mech. Eng. 2014, 6, 963197. [Google Scholar] [CrossRef]
- Yao, Z.; Xiao, R.; Wang, F.; Yang, W. Numerical investigation of cavitation improvement for a francis turbine. In Proceedings of the 9th International Symposium on Cavitation, Lausanne, Switzerland, 6–10 December 2015. [Google Scholar]
- Liu, Y.; Li, Y.; Han, W.; Song, H.D.; Chen, J.X. Effect of geometric parameters of centrifugal pump inlet on its cavitation performance. J. Lanzhou Univ. Technol. 2011, 37, 50–53. [Google Scholar]
- Visser, F.C.; Dijkers, R.J.H.; Op De Woerd, J.G.H. Numerical flow-field analysis and design optimization of a high-energy first-stage centrifugal pump impeller. Comput. Vis. Sci. 2000, 3, 103–108. [Google Scholar] [CrossRef]
- Toyoda, M.; Nishida, M.; Maruyama, O.; Yamane, T.; Tsutsui, T.; Sankai, Y. Geometric optimization for non-thrombogenicity of a centrifugal blood pump through flow visualization. JSME Int. J. 2002, 45, 1013–1019. [Google Scholar] [CrossRef]
- Liu, H.; Wang, K.; Yuan, S.; Tan, M.; Wang, Y.; Dong, L. Multicondition optimization and experimental measurements of a double-blade centrifugal pump impeller. J. Fluids Eng. 2013, 135, 111031. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Xiao, R.; Wang, F.; Liu, W. Cavitation behavior study in the pump mode of a reversible pump-turbine. Renew. Energy 2018, 125, 655–667. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Wang, Z. Influence of blade leading-edge shape on cavitation in a centrifugal pump impeller. Energies 2018, 11, 2588. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.; Wang, F.; Liu, W. Improving the cavitation inception performance of a reversible pump-turbine in pump mode by blade profile redesign: Design concept, method and applications. Renew. Energy 2019, 133, 325–342. [Google Scholar] [CrossRef]
- Xuan, G. Genetic Algorithms and Engineering Optimization; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Menter, F.R. Ten years of experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Spalart, P.R. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 203–229. [Google Scholar] [CrossRef]
- Zhong, L.; Lai, X.; Liao, G.; Zhang, X. Analysis on the relationship between swirling flow at outlet of a Francis turbine runner and vortex rope inside draft tube. J. Hydroelectr. Eng. 2018, 37, 40–46. [Google Scholar]
- Tao, R.; Xiao, R.; Yang, W.; Wang, F.; Liu, W. Optimization for cavitation inception performance of pump-turbine in pump mode based on genetic algorithm. Math. Probl. Eng. 2014, 2014, 234615. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. Hydraulic Turbines, Storage Pumps and Pump-Turbines-Model Acceptance Tests, 2nd ed.; International Standard IEC 60193; IEC: Geneva, Switzerland, 1999. [Google Scholar]
| Parameter | Value |
|---|---|
| Rotation speed nd | 1470 [rpm] |
| Design flow rate Qd | 1 [m3/s] |
| Design head Hd | 55 [m] |
| Specific speed nq | 72.8 |
| Impeller blade number | 6 |
| Guide vane blade number | 7 |
| Impeller inlet diameter D1 | 0.4 [m] |
| Operation | Copy/Eliminate | Crossover | Mutation |
|---|---|---|---|
| Probability | 1.0 | 0.6 | 0.1 |
| Parameter | Rab | γs [°] | B |
|---|---|---|---|
| Range | 1–5 | 1–10 | 1–6 |
| Number of Mesh Nodes [×106] | 0.3180 | 0.5594 | 0.8269 | 1.2056 | 1.7427 | 2.3546 |
| Residual [%] | 100 | 1.1862 | 0.7266 | 0.0809 | 0.3019 | 0.3782 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Tao, R.; Xiao, R. Anti-Cavitation Design of the Symmetric Leading-Edge Shape of Mixed-Flow Pump Impeller Blades. Symmetry 2019, 11, 46. https://doi.org/10.3390/sym11010046
Zhu D, Tao R, Xiao R. Anti-Cavitation Design of the Symmetric Leading-Edge Shape of Mixed-Flow Pump Impeller Blades. Symmetry. 2019; 11(1):46. https://doi.org/10.3390/sym11010046
Chicago/Turabian StyleZhu, Di, Ran Tao, and Ruofu Xiao. 2019. "Anti-Cavitation Design of the Symmetric Leading-Edge Shape of Mixed-Flow Pump Impeller Blades" Symmetry 11, no. 1: 46. https://doi.org/10.3390/sym11010046
APA StyleZhu, D., Tao, R., & Xiao, R. (2019). Anti-Cavitation Design of the Symmetric Leading-Edge Shape of Mixed-Flow Pump Impeller Blades. Symmetry, 11(1), 46. https://doi.org/10.3390/sym11010046





