Edge-Version Atom-Bond Connectivity and Geometric Arithmetic Indices of Generalized Bridge Molecular Graphs

Abstract

Topological indices are graph invariants computed by the distance or degree of vertices of the molecular graph. In chemical graph theory, topological indices have been successfully used in describing the structures and predicting certain physicochemical properties of chemical compounds. In this paper, we propose a definition of generalized bridge molecular graphs that can model more kinds of long chain polymerization products than the bridge molecular graphs, and provide some results of the edge versions of atom-bond connectivity ($AB{C}_e$) and geometric arithmetic ($G{A}_e$) indices for some generalized bridge molecular graphs, which have regular, periodic and symmetrical structures. The results of this paper offer promising prospects in the applications for chemical and material engineering, especially in chemical industry research.

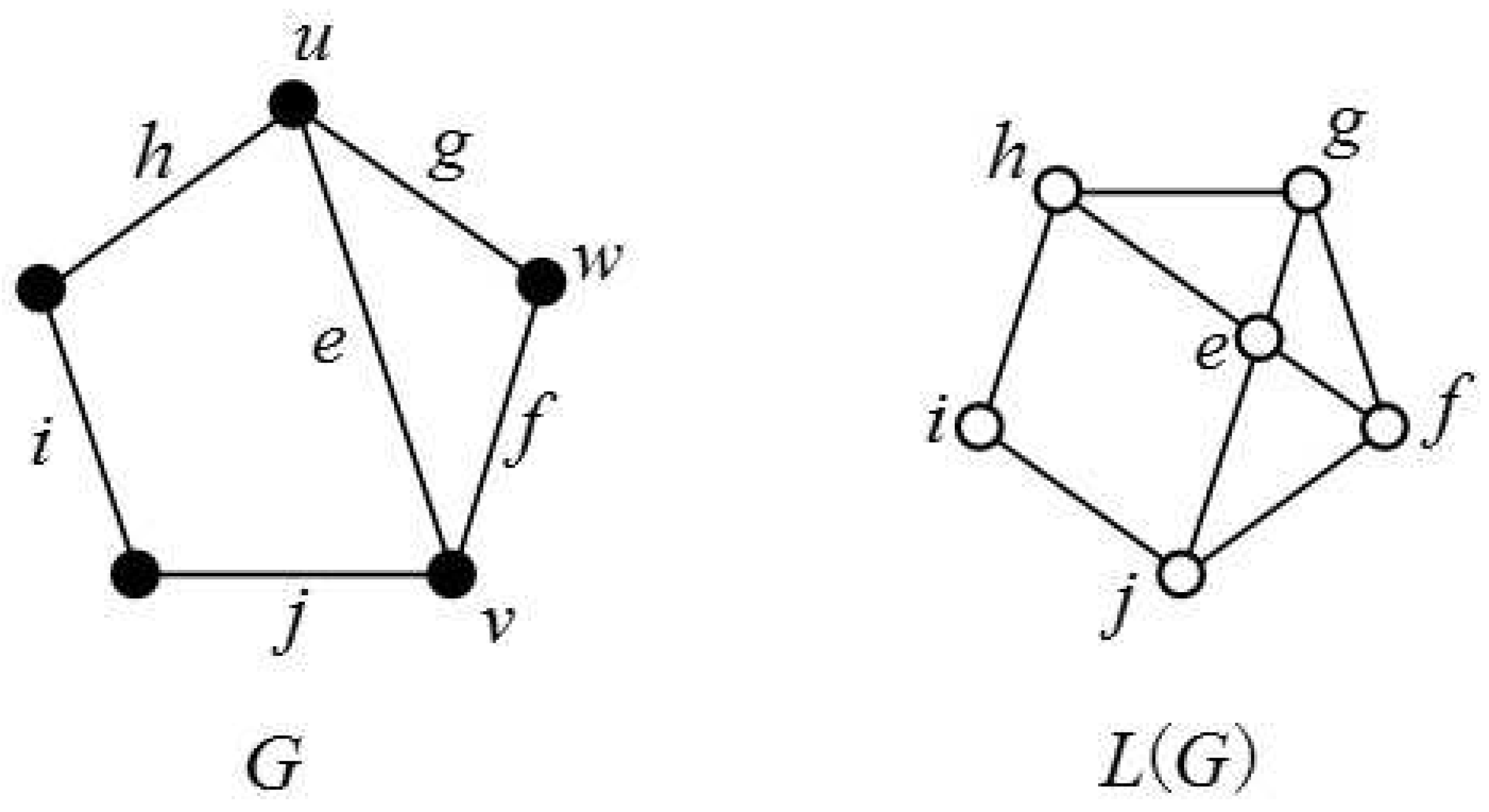
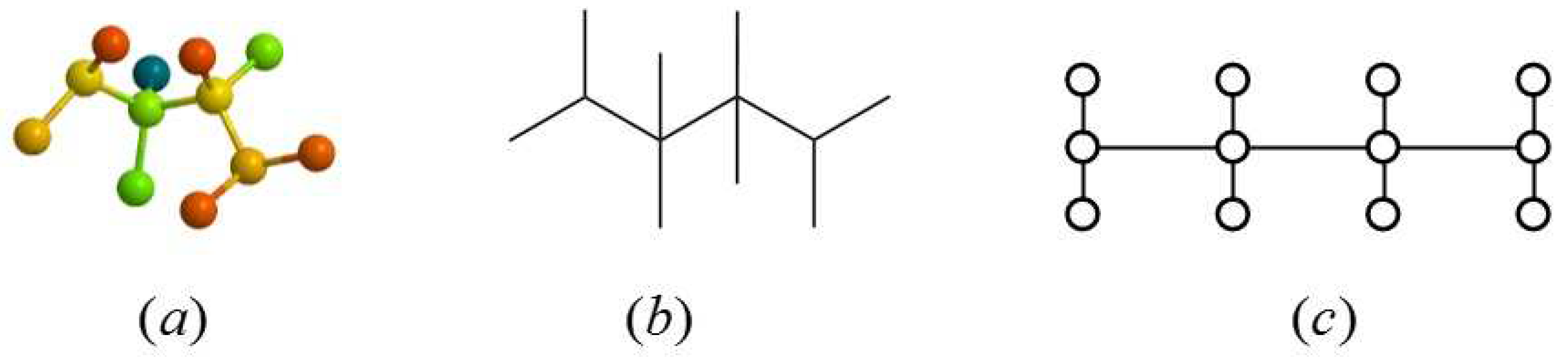
1. Introduction

Let G be an undirected simple graph without loops or multiple edges. We denote by $V(G)$ the vertex set of G and we denote by $E(G)$ the edge set of G. We denote by $e=uv$ the edge connect vertices u and v or vertices u and v adjacent. We denote by $P_n$, $C_n$, and $S_n$ the path, cycle, and star of n vertices, respectively. We denote by $N(v)$ the open neighborhood of vertex v, i.e., $N(v)=\{u|uv\in E(G)\}$. We denote by $d(v)$ or $d_G(v)$ the degree of a vertex v of a graph G, i.e., $d(v)=|\{u\in N(v)\}|$. Let $L(G)$ or $G^L$ be a line graph of G, so each vertex of $L(G)$ corresponds an edge of G. Two vertices of $L(G)$ are adjacent if and only if a common endpoint is shared by their corresponding edges in G [1]. The degree of edge e in G is denoted by $d_{L(G)}(e)$, which is the number of edges that share common endpoint with edge e in G; it is also the degree of vertex e in $L(G)$. We give simple a illustration to explain the relationship of original graph and corresponding line graph in Figure 1. We can see $u,v,w$ denote corresponding vertexes, and $e,f,g,h,i,j$ denote corresponding edges in original graph G and denote corresponding vertices in line graph $L(G)$. We get $d(u)=d(v)=3,d(w)=2$. $d_{L(G)}(e)$, which is the degree of vertex e in $L(G)$, is also the degree of edge e in G, thus $d_{L(G)}(e)=4$ in Figure 1.

Figure 1. The original graph G and corresponding line graph $L(G)$.

Topological indices are graph invariants, which are obtained by performing some numerical operations on the distance or degree of vertices of the molecular graph. In chemical graph theory, topological indices are the molecular descriptors. They have been successfully used in describing the structures and predicting certain physicochemical properties of chemical compounds. To study the relationship between molecular structure and physical properties of saturated hydrocarbons, Wiener index was first published in 1947 [2], and the edge version of Wiener index, which can be considered as the Wiener index of line graph of G, was proposed by Iranmanesh et al. in 2009 [3]. As the important role of topological indices in chemical research has been confirmed, more topological indices appeared, which include atom-bond connectivity index and geometric arithmetic index.

In chemical graph theory, hydrogen atoms are usually ignored when the topological indices are calculated, which is very similar to how organic chemists usually simply write a benzene ring as a hexagon [4]. Now, three types of graphs of $C_{24}{H}_{28}$ are illustrated in Figure 2.

Figure 2. (a) $C_{24}{H}_{28}$ ball and stick model graph in $3D$; (b) $C_{24}{H}_{28}$ chemical structure graph; and (c) $C_{24}{H}_{28}$ model graph in chemical graph theory.

To explore the properties of simple short chain compound products, Gao et al. [5] defined some join graphs such as $P_n+C_m$, $P_n+S_m$, $C_m+P_n+C_m$, $S_m+P_n+S_m$, and $C_m+P_n+S_r$, created by $P_n$, $C_n$ and $S_n$ and obtained the $AB{C}_e$ and $G{A}_e$ indices of these graphs. In another paper, Gao et al. [6] defined the bridge molecular structures, which can be used to research some long chain polymerization products, and the forgotten indices ($F(G)$) formulae of some simple bridge molecular structures constructed by $P_2$, $C_6$ or $K_3$ are presented. The forgotten index is defined as $F(G)={\displaystyle \sum _{v\in V(G)}}(d{(v)}^3)$ [7]. In this paper, we define generalized bridge molecular graphs that could cover more kinds of long chain polymerization products, and the edge-version atom-bond connectivity and geometric arithmetic indices of generalized bridge molecular graphs are calculated.

To facilitate the reader, the topological indices discussed in this thesis are all given in Table 1.

Table 1. The definition of topological indices.

Index Name	Definition	Proposed	Recent Studied
atom-bond connection index	$ABC(G)={\displaystyle \sum _{uv\in E(G)}}\sqrt{\frac{d(u)+d(v)-2}{d(u)d(v)}}$	[8]	[9,10,11]
edge version of ABC index	$AB{C}_e(G)={\displaystyle \sum _{e_1{e}_2\in E(L(G))}}\sqrt{\frac{d_{L(G)}(e_1)+d_{L(G)}(e_2)-2}{d_{L(G)}(e_1)\times d_{L(G)}(e_2)}}$	[12]	[5,13,14]
geometric arithmetic index	$GA(G)={\displaystyle \sum _{uv\in E(G)}}\frac{2\sqrt{d_G(u)d_G(v)}}{d_G(u)+d_G(v)}$	[15]	[16,17,18]
edge version of GA index	$G{A}_e(G)={\displaystyle \sum _{e_1{e}_2\in E(L(G))}}\frac{2\sqrt{d_{L(G)}(e_1)d_{L(G)}(e_2)}}{d_{L(G)}(e_1)+d_{L(G)}(e_2)}$	[19]	[5,12,19,20,21]

In Table 1, $d_G(u)$ and $d_G(v)$ are the degrees of the vertices u and v in G, and $d_{L(G)}(e_1)$ and $d_{L(G)}(e_2)$ are the degrees of the edges $e_1$ and $e_2$ in G.

2. Main Results and Proofs

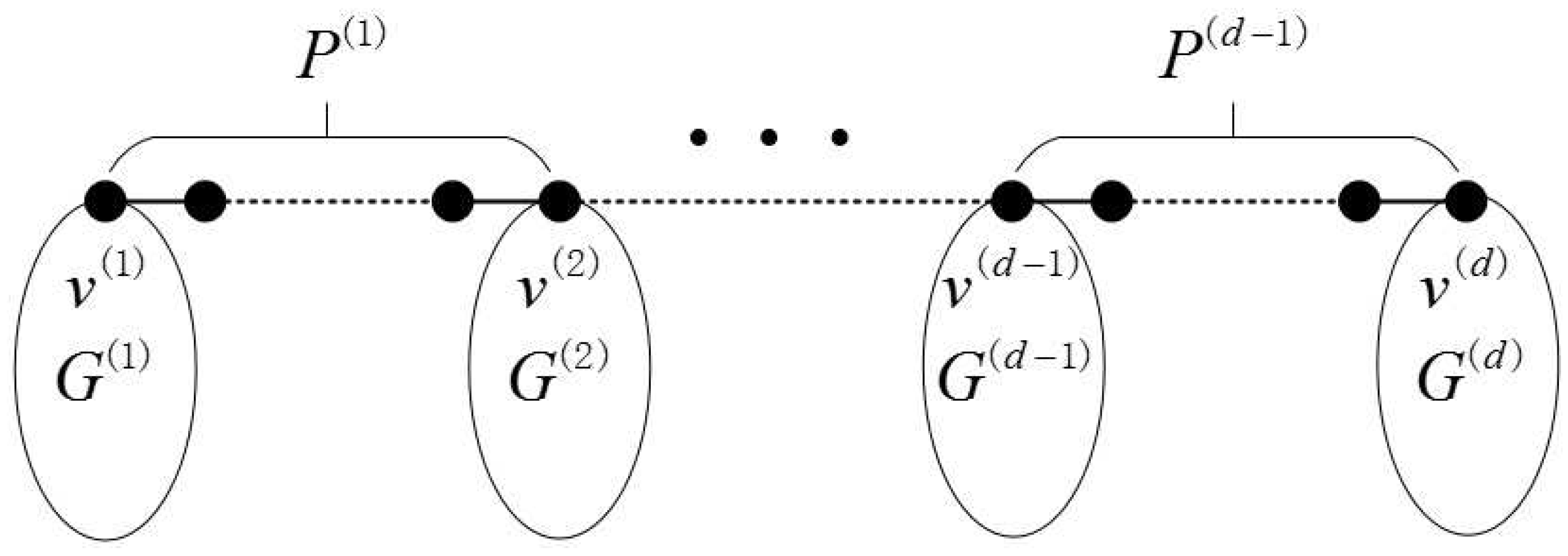
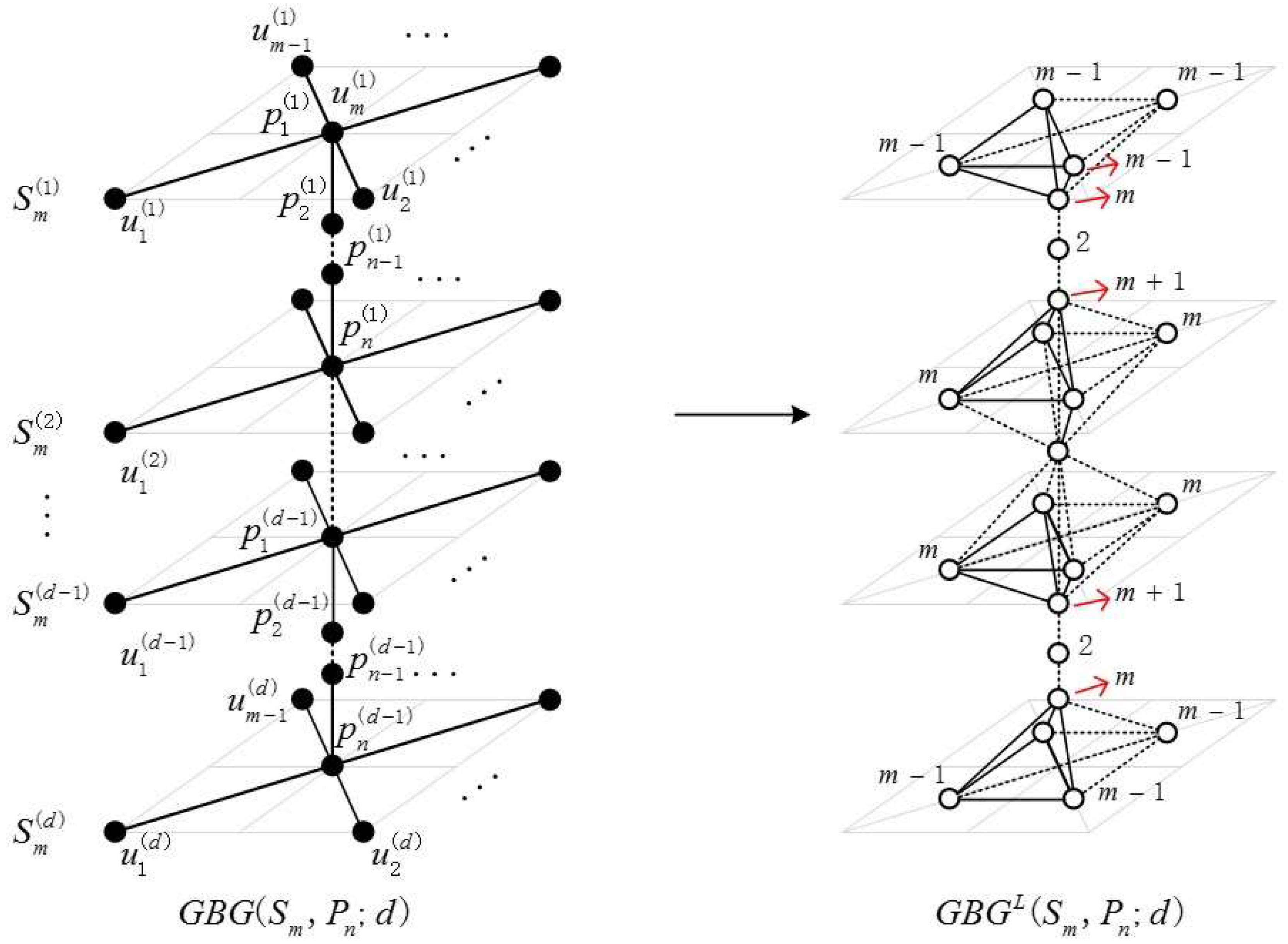
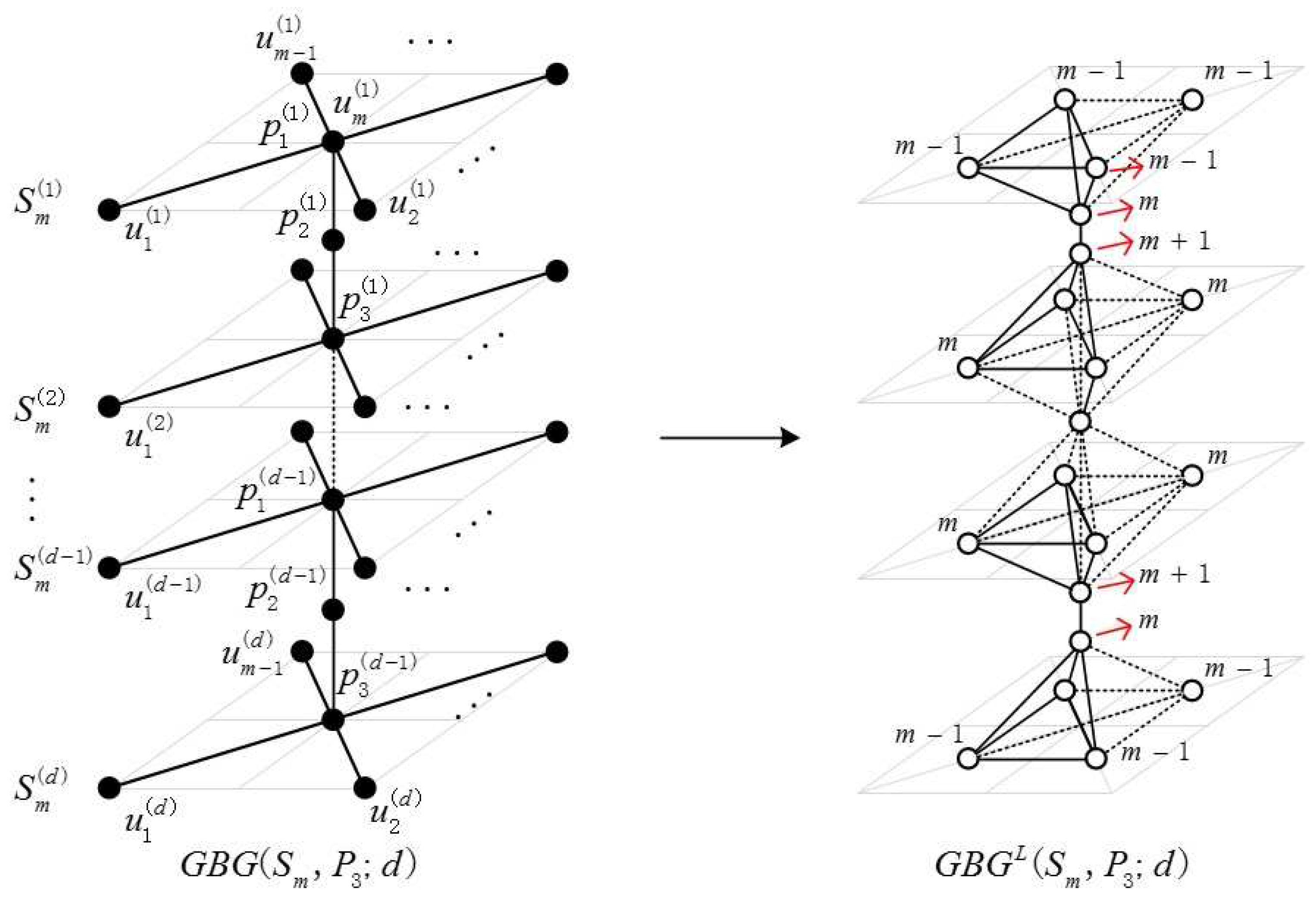
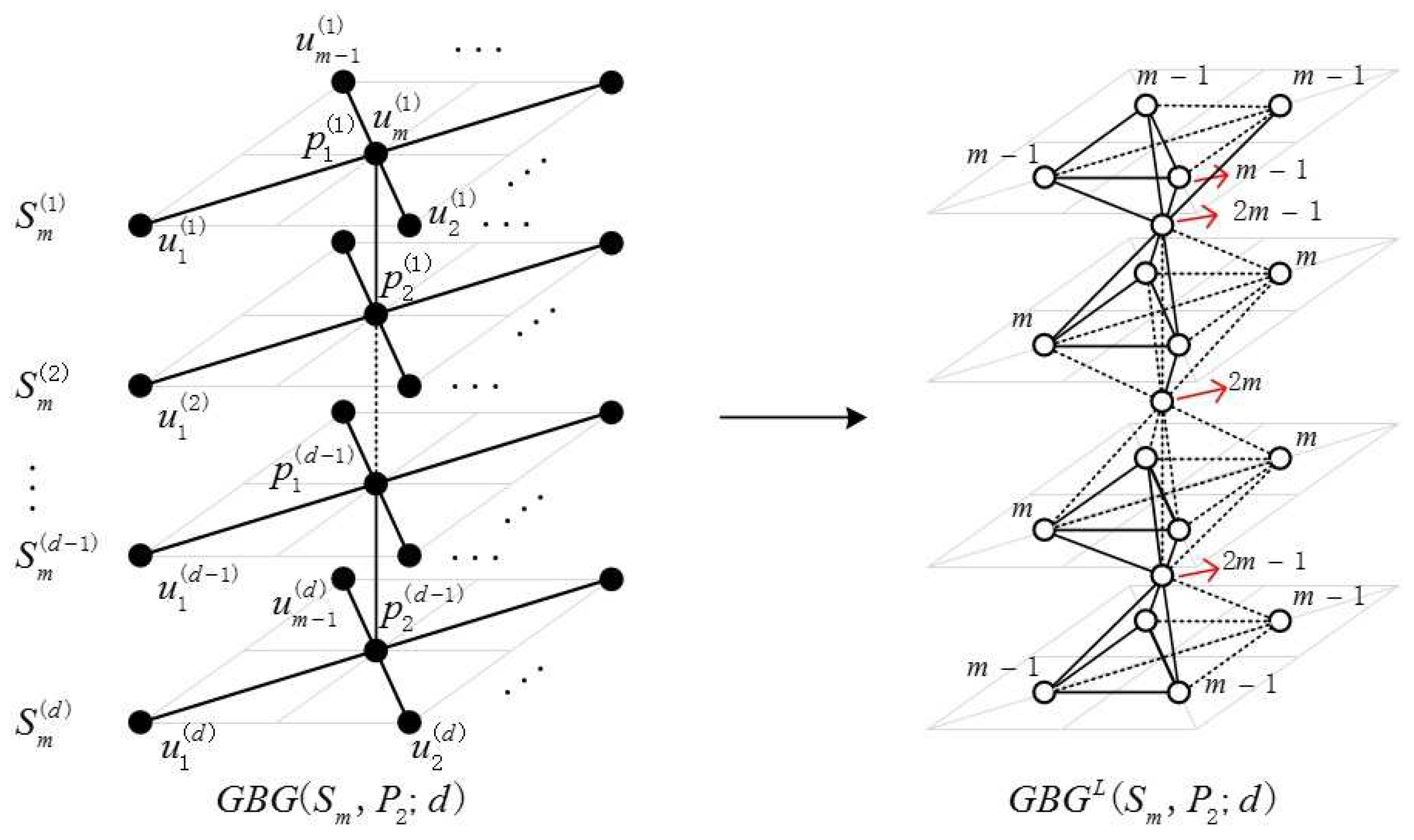
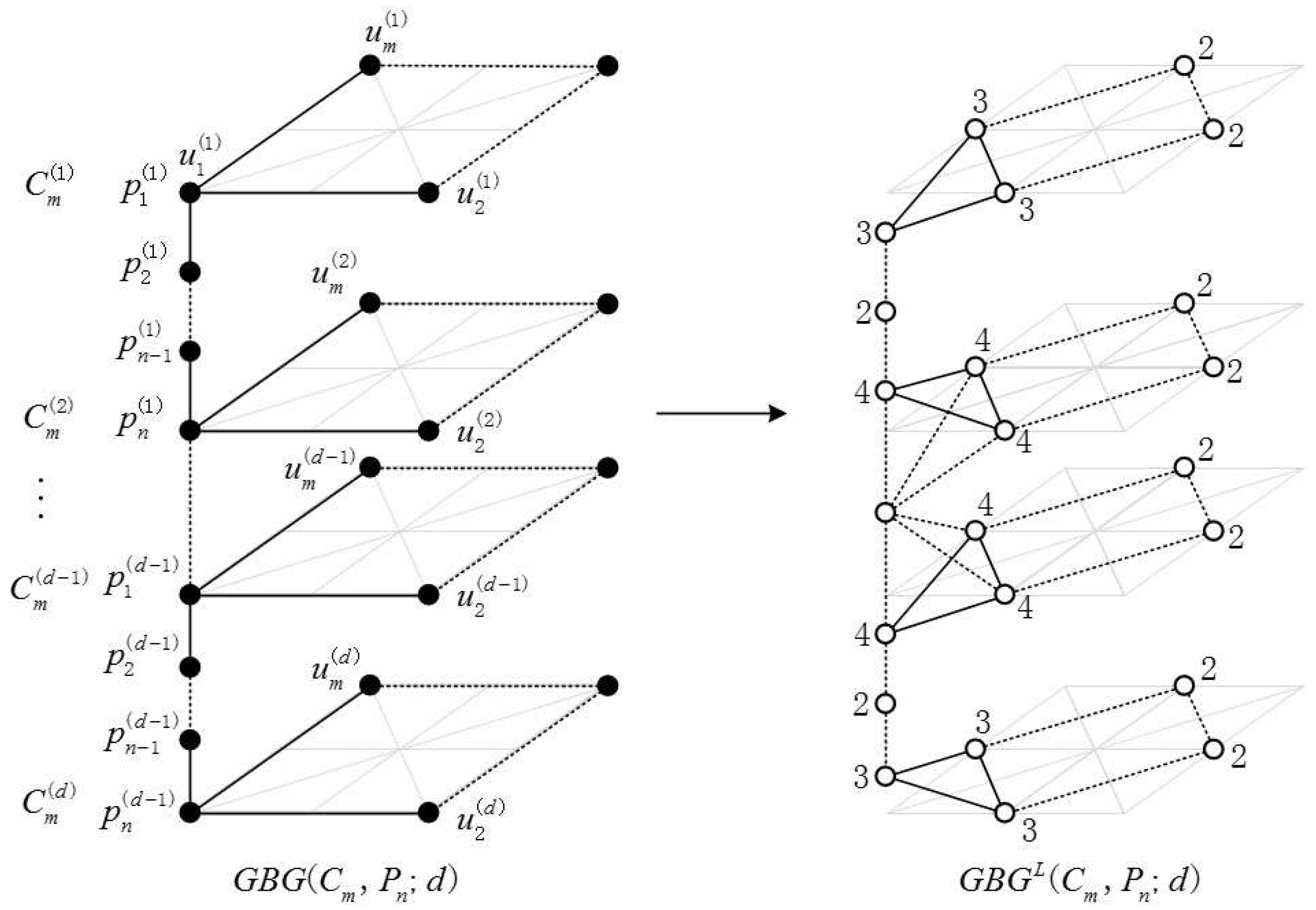
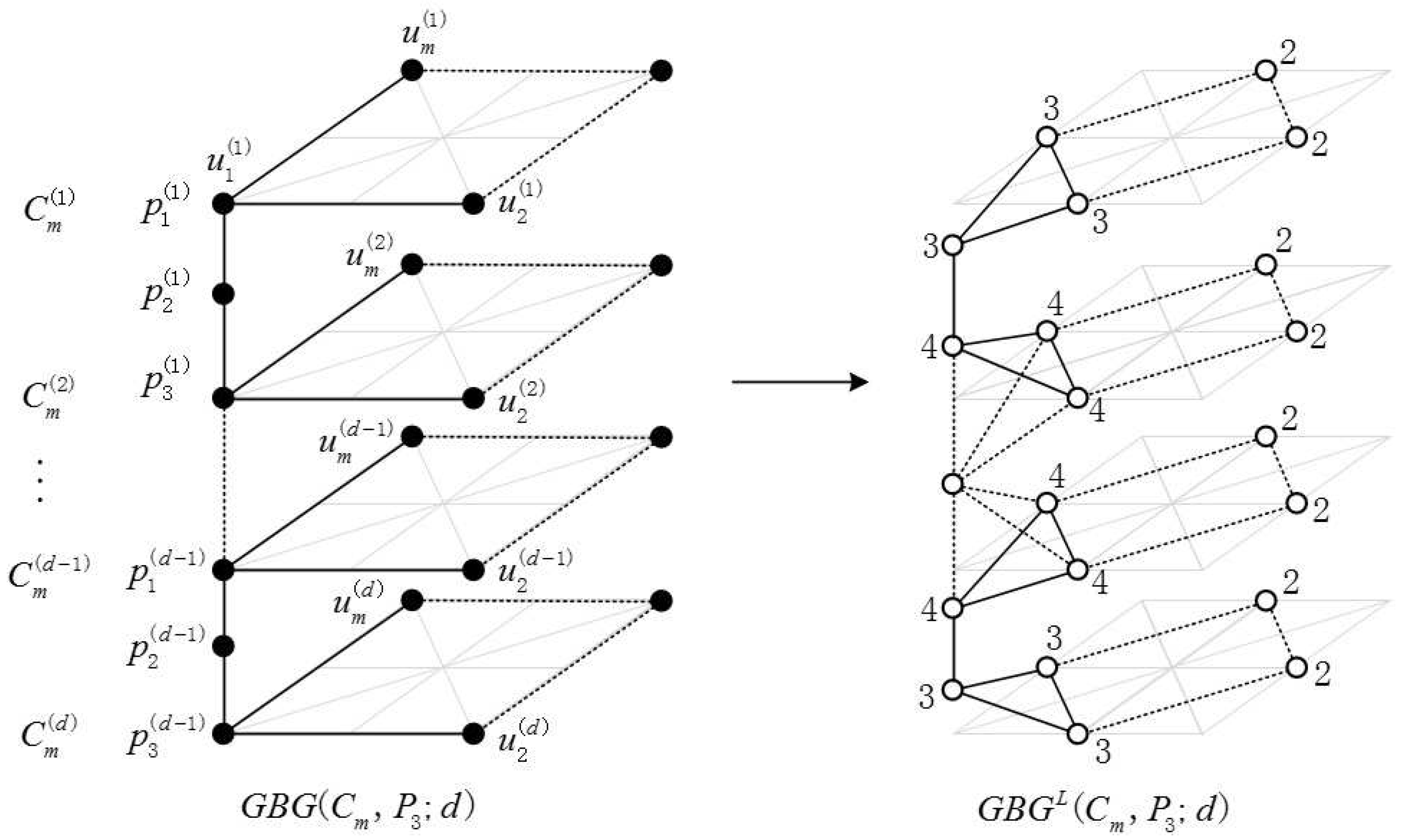
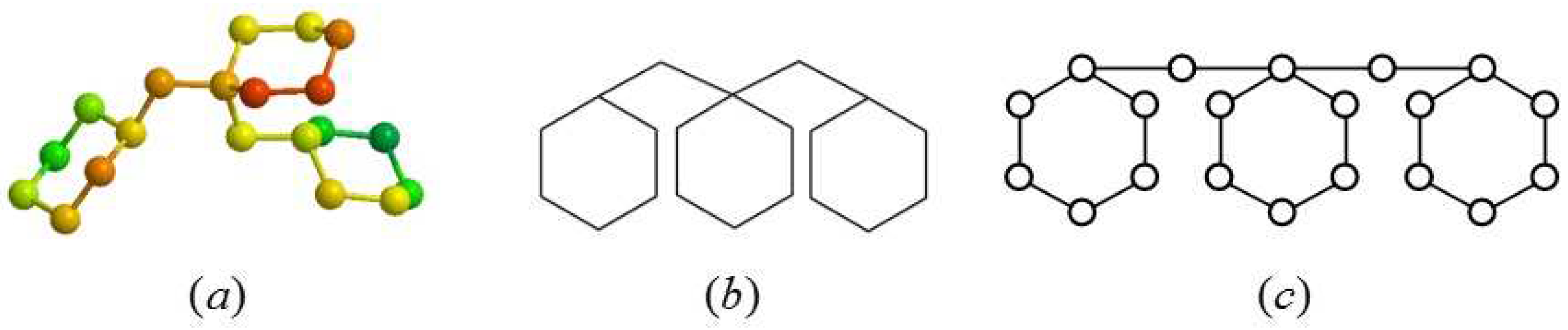
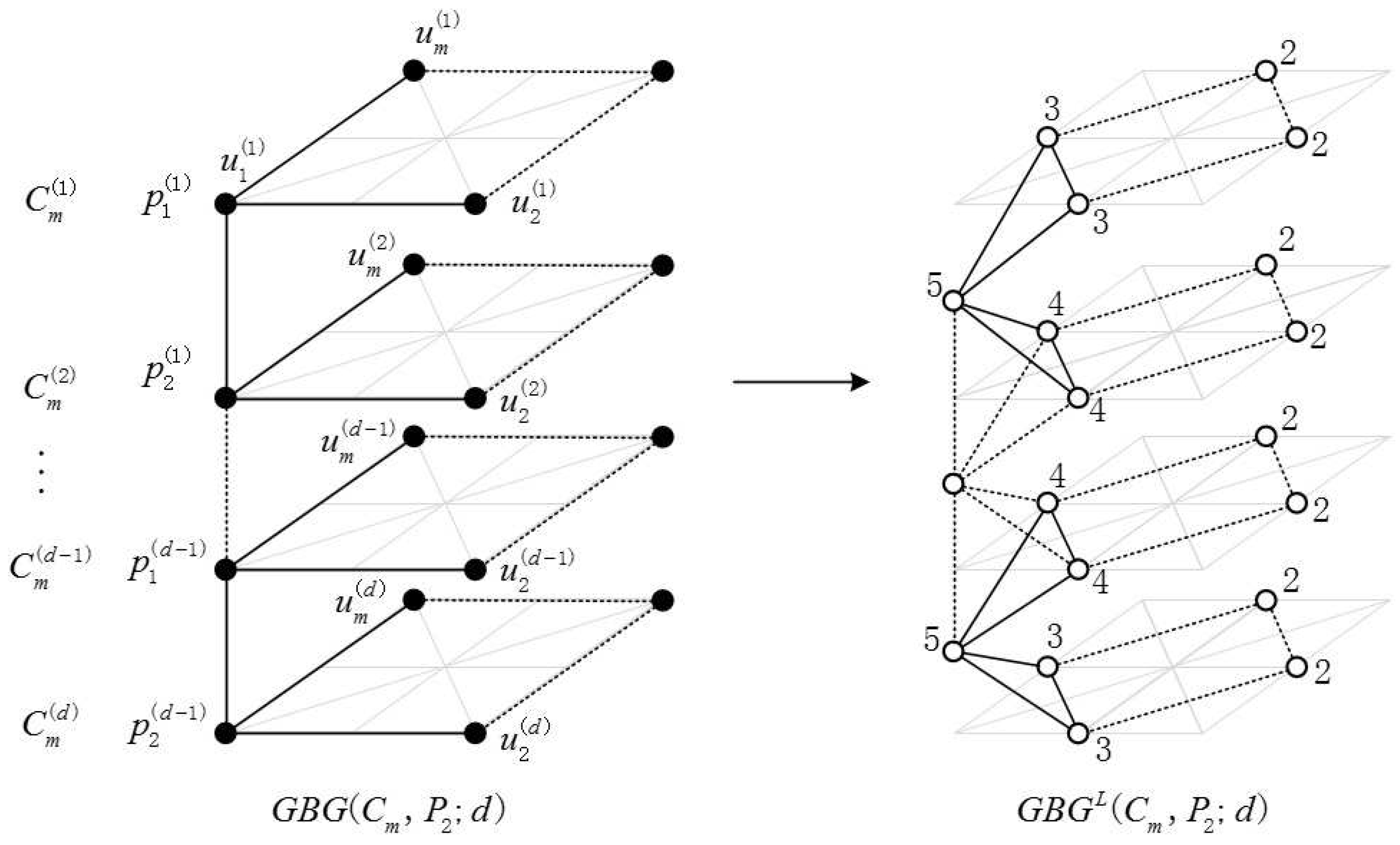
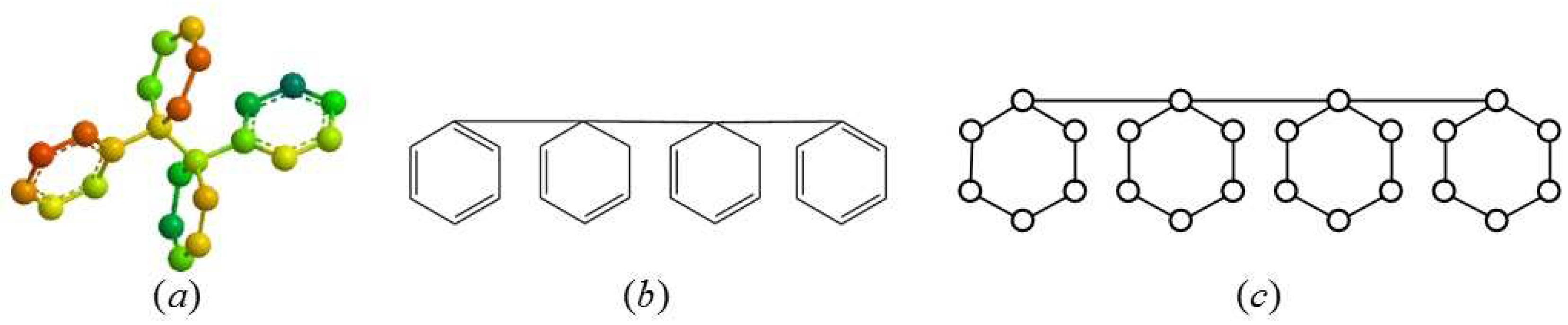
2.1. Definition of the Generalized Bridge Molecular Graph

Before we start a discussion, we give the definition of the generalized bridge molecular graph as follows. For a positive integer d, d pairwise disjoint molecular graphs $\{G^{(1)},G^{(2)},\cdots ,G^{(d)}\}$ with $v^{(i)}\in V(G^{(i)})$ for each $i=1,2,\cdots ,d$, and $d-1$ pairwise disjoint path molecular graphs $P^{(1)},P^{(2)},\cdots ,P^{(d-1)}$ (called bridges), the generalized bridge molecular graph $GBG(G^{(1)}$, $v^{(1)}$, $G^{(2)}$, $v^{(2)}$, ⋯, $G^{(d)}$, $v^{(d)};P^{(1)}$, $P^{(2)}$, ⋯, $P^{(d-1)})$ is the graph obtained by connecting the vertices $v^{(i)}$ and $v^{(i+1)}$ by a path $P^{(i)}$ for which two end vertices are identified with $v^{(i)}$ and $v^{(i+1)}$ for $i=1,2,\dots ,d-1$ (See Figure 3). When $G:=G^{(i)}$, $P:=P^{(i)}$, $v:=v^{(i)}$ for each i, we simplify $GBG(G^{(1)}$, $v^{(1)}$, $G^{(2)}$, $v^{(2)}$, ⋯, $G^{(d)}$, $v^{(d)};P^{(1)}$, $P^{(2)}$, ⋯, $P^{(d-1)})$ to be $GBG(G,v;P;d)$. In this paper, if G is a star, then v is the central vertex and if G is a cycle, v is considered as any vertex. In such cases, we further simplify $GBG(G,v;P;d)$ to be $GBG(G,P;d)$. The bridge molecular graph’s bridge is strictly $P_2$ in [6], which limits the scope of modeling objects. The generalized bridge molecular graphs can model more kinds of long chain polymerization products than the bridge molecular graphs, because the bridge can be either $P_2$ or $P_n$ and $n\ge 3$.

Figure 3. The generalized bridge molecular graph $GBG(G^{(1)},v^{(1)},G^{(2)},v^{(2)},\dots ,G^{(d)},v^{(d)};P^{(1)},P^{(2)},\dots ,P^{(d-1)})$.

2.2. Results and Discussion

In the following, we discuss the edge-version atom-bond connectivity and geometric arithmetic indices of some generalized bridge molecular graph. The line graph $GB{G}^L(S_m,P_n;d)$ of $GBG(S_m,P_n;d)$ is illustrated in Figure 4.

Figure 4. The generalized bridge molecular graph of $GBG(S_m,P_n;d)$ and $GB{G}^L(S_m,P_n;d)$.

Theorem 1.

Let $GBG(S_m,P_n;d)$ be the generalized bridge molecular graph for $n\ge 4$, $d\ge 2$ and $m\ge 2$ (see Figure 4), then the $AB{C}_e$ and $G{A}_e$ of $GBG(S_m,P_n;d)$ are

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(S_m,P_n;d))& =& \frac{\sqrt{2}}{2}(d-1)(n-2)+\frac{d-2}{m+1}\sqrt{2m}\hfill \\ & & +2(m-1)\sqrt{\frac{2m-3}{m^2-m}}+2(d-2)(m-1)\sqrt{\frac{2m-1}{m^2+m}}\hfill \\ & & +(m-2)\sqrt{2m-4}+\frac{(d-2)(m-1)(m-2)\sqrt{2m-2}}{2m},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(S_m,P_n;d))& =& \frac{4\sqrt{2m}}{m+2}+\frac{4(d-2)\sqrt{2m+2}}{m+3}+(d-1)(n-4)+(d-2)\hfill \\ & & +4(m-1)\frac{\sqrt{m^2-m}}{2m-1}+4(d-2)(m-1)\frac{\sqrt{m^2+m}}{2m+1}\hfill \\ & & +\frac{d}{2}(m-1)(m-2).\hfill \end{array}$$

Proof. 

This line graph has $2-2m-n+\frac{d}{2}(m^2+m+2n-4)$ edges. If $d_{L(G)}(e_1)$ and $d_{L(G)}(e_2)$ are the degree of edge of $e_1$ and $e_2$, then there are 2 edges of type $d_{L(G)}(e_1)=m$, $d_{L(G)}(e_2)=2$, $2(d-2)$ edges of type $d_{L(G)}(e_1)=m+1$, $d_{L(G)}(e_2)=2$, $(d-1)(n-4)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=2$, $d-2$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=m+1$, $2(m-1)$ edges of type $d_{L(G)}(e_1)=m$, $d_{L(G)}(e_2)=m-1$, $2(d-2)(m-1)$ edges of type $d_{L(G)}(e_1)=m$, $d_{L(G)}(e_2)=m+1$, $(m-1)(m-2)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=m-1$, and $\frac{d-2}{2}(m-1)(m-2)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=m$. Hence, we get

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(S_m,P_n;d))& =& 2\left(\sqrt{\frac{m+2-2}{m\times 2}}\right)+2(d-2)\left(\sqrt{\frac{m+1+2-2}{(m+1)\times 2}}\right)\hfill \\ & & +(d-1)(n-4)\left(\sqrt{\frac{2+2-2}{2\times 2}}\right)\hfill \\ & & +(d-2)\left(\sqrt{\frac{m+1+m+1-2}{(m+1)\times (m+1)}}\right)\hfill \\ & & +2(m-1)\left(\sqrt{\frac{m+m-1-2}{m\times (m-1)}}\right)\hfill \\ & & +2(d-2)(m-1)\left(\sqrt{\frac{m+m+1-2}{m\times (m+1)}}\right)\hfill \\ & & +(m-1)(m-2)\left(\sqrt{\frac{m-1+m-1-2}{(m-1)\times (m-1)}}\right)\hfill \\ & & +\frac{d-2}{2}(m-1)(m-2)\left(\sqrt{\frac{m+m-2}{m\times m}}\right)\hfill \\ & =& \frac{\sqrt{2}}{2}(d-1)(n-2)+\frac{d-2}{m+1}\sqrt{2m}\hfill \\ & & +2(m-1)\sqrt{\frac{2m-3}{m^2-m}}+2(d-2)(m-1)\sqrt{\frac{2m-1}{m^2+m}}\hfill \\ & & +(m-2)\sqrt{2m-4}+\frac{(d-2)(m-1)(m-2)\sqrt{2m-2}}{2m},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(S_m,P_n;d))& =& 2\left(\frac{2\sqrt{m\times 2}}{m+2}\right)+2(d-2)\left(\frac{2\sqrt{(m+1)\times 2}}{m+1+2}\right)\hfill \\ & & +(d-1)(n-4)\left(\frac{2\sqrt{2\times 2}}{2+2}\right)\hfill \\ & & +(d-2)\left(\frac{2\sqrt{(m+1)\times (m+1)}}{m+1+m+1}\right)\hfill \\ & & +2(m-1)\left(\frac{2\sqrt{m\times (m-1)}}{m+m-1}\right)\hfill \\ & & +2(d-2)(m-1)\left(\frac{2\sqrt{m\times (m+1)}}{m+m+1}\right)\hfill \\ & & +(m-1)(m-2)\left(\frac{2\sqrt{(m-1)\times (m-1)}}{m-1+m-1}\right)\hfill \\ & & +\frac{d-2}{2}(m-1)(m-2)\left(\frac{2\sqrt{m\times m}}{m+m}\right)\hfill \\ & =& \frac{4\sqrt{2m}}{m+2}+\frac{4(d-2)\sqrt{2m+2}}{m+3}+(d-1)(n-4)+(d-2)\hfill \\ & & +4(m-1)\frac{\sqrt{m^2-m}}{2m-1}+4(d-2)(m-1)\frac{\sqrt{m^2+m}}{2m+1}\hfill \\ & & +\frac{d}{2}(m-1)(m-2).\hfill \end{array}$$

The proof is complete. □

For Example 1, in Figure 5, $2,7,7,12-tetramethyltridecane$ can be modeled by $GBG(S_3,P_6;3)$, so $AB{C}_e(GBG(S_3,P_6;3))\approx 13.76052$ and $G{A}_e(GBG(S_3,P_6;3))\approx 19.72337$.

Figure 5. (a) $2,7,7,12$-$tetramethyltridecane$ ball and stick model graph in $3D$; (b) $2,7,7,12$-$tetramethyltridecane$ chemical structure graph; and (c) $2,7,7,12$-$tetramethyltridecane$ model graph in chemical graph theory.

Theorem 2.

Let $GBG(S_m,P_3;d)$ be the generalized bridge molecular graph for $n=3$, $d\ge 3$ and $m\ge 2$ (see Figure 6), then the $AB{C}_e$ and $G{A}_e$ of $GBG(S_m,P_3;d)$ are

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(S_m,P_3;d))& =& 2\sqrt{\frac{2m-1}{m^2+m}}+\frac{2d-5}{m+1}\sqrt{2m}+2(m-1)\sqrt{\frac{2m-3}{m^2-m}}\hfill \\ & & +2(d-2)(m-1)\sqrt{\frac{2m-1}{m^2+m}}+(m-2)\sqrt{2m-4}\hfill \\ & & +\frac{(d-2)(m-1)(m-2)}{2m}\sqrt{2m-2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(S_m,P_3;d))& =& \frac{4}{2m+1}\sqrt{m^2+m}+(2d-5)\hfill \\ & & +\frac{4}{2m-1}(m-1)\sqrt{m^2-m}\hfill \\ & & +\frac{4}{2m+1}(d-2)(m-1)\sqrt{m^2+m}\hfill \\ & & +\frac{d}{2}(m-1)(m-2).\hfill \end{array}$$

Figure 6. The generalized bridge molecular graph of $GBG(S_m,P_3;d)$ and $GB{G}^L(S_m,P_3;d)$.

Proof. 

This line graph has $\frac{d}{2}(m^2+m+2)-2m-1$ edges. If $d_{L(G)}(e_1)$ and $d_{L(G)}(e_2)$ are the degree of edge of $e_1$ and $e_2$, then there are 2 edges of type $d_{L(G)}(e_1)=m$, $d_{L(G)}(e_2)=m+1$, $2d-5$ edges of type $d_{L(G)}(e_1)=m+1$, $d_{L(G)}(e_2)=m+1$, $2(m-1)$ edges of type $d_{L(G)}(e_1)=m$, $d_{L(G)}(e_2)=m-1$, $2(d-2)(m-1)$ edges of type $d_{L(G)}(e_1)=m$, $d_{L(G)}(e_2)=m+1$, $(m-1)(m-2)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=m-1$, and $\frac{d-2}{2}(m-1)(m-2)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=m$. Hence, we get

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(S_m,P_3;d))& =& 2\left(\sqrt{\frac{m+m+1-2}{m\times (m+1)}}\right)+(2d-5)\left(\sqrt{\frac{m+1+m+1-2}{(m+1)\times (m+1)}}\right)\hfill \\ & & +2(m-1)\left(\sqrt{\frac{m+m-1-2}{m\times (m-1)}}\right)\hfill \\ & & +2(d-2)(m-1)\left(\sqrt{\frac{m+m+1-2}{m\times (m+1)}}\right)\hfill \\ & & +(m-1)(m-2)\left(\sqrt{\frac{m-1+m-1-2}{(m-1)\times (m-1)}}\right)\hfill \\ & & +\frac{d-2}{2}(m-1)(m-2)\left(\sqrt{\frac{m+m-2}{m\times m}}\right)\hfill \\ & =& 2\sqrt{\frac{2m-1}{m^2+m}}+\frac{2d-5}{m+1}\sqrt{2m}+2(m-1)\sqrt{\frac{2m-3}{m^2-m}}\hfill \\ & & +2(d-2)(m-1)\sqrt{\frac{2m-1}{m^2+m}}+(m-2)\sqrt{2m-4}\hfill \\ & & +\frac{(d-2)(m-1)(m-2)}{2m}\sqrt{2m-2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(S_m,P_3;d))& =& 2\left(\frac{2\sqrt{m\times (m+1)}}{m+m+1}\right)+(2d-5)\left(\frac{2\sqrt{(m+1)\times (m+1)}}{m+1+m+1}\right)\hfill \\ & & +2(m-1)\left(\frac{2\sqrt{m\times (m-1)}}{m+m-1}\right)\hfill \\ & & +2(d-2)(m-1)\left(\frac{2\sqrt{m\times (m+1)}}{m+m+1}\right)\hfill \\ & & +(m-1)(m-2)\left(\frac{2\sqrt{(m-1)\times (m-1)}}{m-1+m-1}\right)\hfill \\ & & +\frac{d-2}{2}(m-1)(m-2)\left(\frac{2\sqrt{m\times m}}{m+m}\right)\hfill \\ & =& \frac{4}{2m+1}\sqrt{m^2+m}+(2d-5)\hfill \\ & & +\frac{4}{2m-1}(m-1)\sqrt{m^2-m}\hfill \\ & & +\frac{4}{2m+1}(d-2)(m-1)\sqrt{m^2+m}\hfill \\ & & +\frac{d}{2}(m-1)(m-2).\hfill \end{array}$$

The proof is complete. □

For Example 2, in Figure 7, $2,4,4,6-tetramethylheptane$ can be modeled by $GBG(S_3,P_3;3)$, so $AB{C}_e(GBG(S_3,P_3;3))\approx 9.394663$ and $G{A}_e(GBG(S_3,P_3;3))\approx 13.85764$.

Figure 7. (a) $2,4,4,6$-$tetramethylheptane$ ball and stick model graph in $3D$; (b) $2,4,4,6$-$tetramethylheptane$ chemical structure graph; and (c) $2,4,4,6$-$tetramethylheptane$ model graph in chemical graph theory.

Theorem 3.

Let $GBG(S_m,P_2;d)$ be the generalized bridge molecular graph for $n=2$, $d\ge 4$ and $m\ge 2$ (see Figure 8), then the $AB{C}_e$ and $G{A}_e$ of $GBG(S_m,P_2;d)$ are

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(S_m,P_2;d))& =& 2(m-1)\sqrt{\frac{3m-4}{2m^2-3m+1}}+2(m-1)\sqrt{\frac{3m-3}{2m^2-m}}\hfill \\ & & +2\frac{(d-3)(m-1)}{m}\sqrt{\frac{3m-2}{2}}+(m-2)\sqrt{2m-4}\hfill \\ & & +\frac{(d-2)(m-1)(m-2)}{2m}\sqrt{2m-2}\hfill \\ & & +2\sqrt{\frac{4m-3}{4m^2-2m}}+\frac{d-4}{2m}\sqrt{4m-2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(S_m,P_2;d))& =& \frac{4(m-1)}{3m-2}\sqrt{2m^2-3m+1}+\frac{4(m-1)}{3m-1}\sqrt{2m^2-m}\hfill \\ & & +\frac{4\sqrt{2}}{3}(d-3)(m-1)+\frac{d}{2}(m-1)(m-2)\hfill \\ & & +\frac{4\left(\sqrt{4m^2-2m}\right)}{4m-1}+(d-4).\hfill \end{array}$$

Figure 8. The generalized bridge molecular graph of $GBG(S_m,P_2;d)$ and $GB{G}^L(S_m,P_2;d)$.

Proof. 

This line graph has $\frac{1}{2}m(dm+d-4)$ edges. If $d_{L(G)}(e_1)$ and $d_{L(G)}(e_2)$ are the degree of edge of $e_1$ and $e_2$, then there are $2(m-1)$ edges of type $d_{L(G)}(e_1)=2m-1$,$d_{L(G)}(e_2)=m-1$, $2(m-1)$ edges of type $d_{L(G)}(e_1)=2m-1$,$d_{L(G)}(e_2)=m$, $2(d-3)(m-1)$ edges of type $d_{L(G)}(e_1)=2m$,$d_{L(G)}(e_2)=m$, $(m-1)(m-2)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=m-1$, $\frac{d-2}{2}(m-1)(m-2)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=m$, 2 edges of type $d_{L(G)}(e_1)=2m-1$,$d_{L(G)}(e_2)=2m$, and $d-4$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=2m$. Hence, we get

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(S_m,P_2;d))& =& 2(m-1)\left(\sqrt{\frac{2m-1+m-1-2}{(2m-1)\times (m-1)}}\right)\hfill \\ & & +2(m-1)\left(\sqrt{\frac{2m-1+m-2}{(2m-1)\times m}}\right)\hfill \\ & & +2(d-3)(m-1)\left(\sqrt{\frac{2m+m-2}{2m\times m}}\right)\hfill \\ & & +(m-1)(m-2)\left(\sqrt{\frac{m-1+m-1-2}{(m-1)\times (m-1)}}\right)\hfill \\ & & +\frac{d-2}{2}(m-1)(m-2)\left(\sqrt{\frac{m+m-2}{m\times m}}\right)\hfill \\ & & +2\left(\sqrt{\frac{2m-1+2m-2}{(2m-1)\times 2m}}\right)\hfill \\ & & +(d-4)\left(\sqrt{\frac{2m+2m-2}{2m\times 2m}}\right)\hfill \\ & =& 2(m-1)\sqrt{\frac{3m-4}{2m^2-3m+1}}+2(m-1)\sqrt{\frac{3m-3}{2m^2-m}}\hfill \\ & & +2\frac{(d-3)(m-1)}{m}\sqrt{\frac{3m-2}{2}}+(m-2)\sqrt{2m-4}\hfill \\ & & +\frac{(d-2)(m-1)(m-2)}{2m}\sqrt{2m-2}\hfill \\ & & +2\sqrt{\frac{4m-3}{4m^2-2m}}+\frac{d-4}{2m}\sqrt{4m-2},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(S_m,P_2;d))& =& 2(m-1)\left(\frac{2\sqrt{(2m-1)\times (m-1)}}{2m-1+m-1}\right)\hfill \\ & & +2(m-1)\left(\frac{2\sqrt{(2m-1)\times m}}{2m-1+m}\right)\hfill \\ & & +2(d-3)(m-1)\left(\frac{2\sqrt{2m\times m}}{2m+m}\right)\hfill \\ & & +(m-1)(m-2)\left(\frac{2\sqrt{(m-1)\times (m-1)}}{m-1+m-1}\right)\hfill \\ & & +\frac{d-2}{2}(m-1)(m-2)\left(\frac{2\sqrt{m\times m}}{m+m}\right)\hfill \\ & & +2\left(\frac{2\sqrt{(2m-1)\times 2m}}{2m-1+2m}\right)\hfill \\ & & +(d-4)\left(\frac{2\sqrt{2m\times 2m}}{2m+2m}\right)\hfill \\ & =& \frac{4(m-1)}{3m-2}\sqrt{2m^2-3m+1}+\frac{4(m-1)}{3m-1}\sqrt{2m^2-m}\hfill \\ & & +\frac{4\sqrt{2}}{3}(d-3)(m-1)+\frac{d}{2}(m-1)(m-2)\hfill \\ & & +\frac{4\left(\sqrt{4m^2-2m}\right)}{4m-1}+(d-4).\hfill \end{array}$$

The proof is complete. □

For Example 3, in Figure 9, $2,3,3,4$-$tetramethylpentane$ can be modeled by $GBG(S_3,P_2;4)$, so $AB{C}_e(GBG(S_3,P_2;4))\approx 11.69568$ and $G{A}_e(GBG(S_3,P_2;4))\approx 17.24996952$.

Figure 9. (a) $2,3,3,4$-$tetramethylpentane$ ball and stick model graph in $3D$; (b) $2,3,3,4$-$tetramethylpentane$ chemical structure graph; and (c) $2,3,3,4$-$tetramethylpentane$ model graph in chemical graph theory.

Theorem 4.

Let $GBG(C_m,P_n;d)$ be the generalized bridge molecular graph for $n\ge 4$, $d\ge 2$ and $m\ge 3$ (see Figure 10), then the $AB{C}_e$ and $G{A}_e$ of $GBG(C_m,P_n;d)$ are

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(C_m,P_n;d))& =& \frac{\sqrt{2}}{2}(d(m-3)+(d-1)(n-4))+(2\sqrt{2}+\frac{3\sqrt{6}}{2})d\hfill \\ & & -\sqrt{2}-3\sqrt{6}+4,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(C_m,P_n;d))& =& d(m-3)+(d-1)(n-4)\hfill \\ & & +(\frac{8\sqrt{2}}{3}+6)(d-2)+\frac{12\sqrt{6}}{5}+5.\hfill \end{array}$$

Figure 10. The generalized bridge molecular graph of $GBG(C_m,P_n;d)$ and $GB{G}^L(C_m,P_n;d)$.

Proof. 

In Figure 10, the degrees of vertices in line graph $G^L(G_d(C_m+P_n))$ are displayed near by the corresponding vertices. This line graph has $d(m+n+3)-n-4$ edges. In addition, there are $d(m-3)+(d-1)(n-4)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=2$, 6 edges of type $d_{L(G)}(e_1)=2$ and $d_{L(G)}(e_2)=3$, 6 edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=3$, $4(d-2)$ edges of type $d_{L(G)}(e_1)=2$ and $d_{L(G)}(e_2)=4$, and $6(d-2)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=4$. Hence, we have

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(C_m,P_n;d))& =& \left(d(m-3)+(d-1)(n-4)\right)\left(\sqrt{\frac{2+2-2}{2\times 2}}\right)\hfill \\ & & +6\left(\sqrt{\frac{2+3-2}{2\times 3}}\right)+6\left(\sqrt{\frac{3+3-2}{3\times 3}}\right)\hfill \\ & & +4(d-2)\left(\sqrt{\frac{2+4-2}{2\times 4}}\right)+6(d-2)\left(\sqrt{\frac{4+4-2}{4\times 4}}\right)\hfill \\ & =& \frac{\sqrt{2}}{2}(d(m-3)+(d-1)(n-4))+(2\sqrt{2}+\frac{3\sqrt{6}}{2})d\hfill \\ & & -\sqrt{2}-3\sqrt{6}+4,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(C_m,P_n;d))& =& \left(d(m-3)+(d-1)(n-4)\right)\left(\frac{2\sqrt{2\times 2}}{2+2}\right)\hfill \\ & & +6\left(\frac{2\sqrt{2\times 3}}{2+3}\right)+6\left(\frac{2\sqrt{3\times 3}}{3+3}\right)\hfill \\ & & +4(d-2)\left(\frac{2\sqrt{2\times 4}}{2+4}\right)+6(d-2)\left(\frac{2\sqrt{4\times 4}}{4+4}\right)\hfill \\ & =& d(m-3)+(d-1)(n-4)\hfill \\ & & +(\frac{8\sqrt{2}}{3}+6)(d-2)+\frac{12\sqrt{6}}{5}+5.\hfill \end{array}$$

The proof is complete. □

For Example 4, in Figure 2, $C_{24}{H}_{28}$ is $(cyclohexa$-$2,4$-$diene$-$1,1$-$diylbis(propane$-$3,1$-$diyl))dibenzene$, which can be modeled by $GBG(C_6,P_5;3)$, so $AB{C}_e(GBG(C_6,P_5;3))\approx 22.52347702$ and $G{A}_e(GBG(C_6,P_5;3))\approx 31.65001155$.

Theorem 5.

Let $GBG(C_m,P_3;d)$ be the generalized bridge molecular graph for $n=3$, $d\ge 3$, and $m\ge 3$ (see Figure 11), then the $AB{C}_e$ and $G{A}_e$ of $GBG(C_m,P_3;d)$ are

Figure 11. The generalized bridge molecular graph of $GBG(C_m,P_3;d)$ and $GB{G}^L(C_m,P_3;d)$.

$AB{C}_e(GBG(C_m,P_3;d))=\frac{\sqrt{2}}{2}d(m-3)+(\sqrt{2}+7\frac{\sqrt{6}}{4})d+4+\frac{\sqrt{15}}{3}-\frac{15\sqrt{6}}{4}$,

$G{A}_e(GBG(C_m,P_3;d))=d(m-3)+(\frac{4\sqrt{2}}{3}+7)d+\frac{8\sqrt{6}}{5}+6+\frac{8\sqrt{3}}{7}-\frac{8\sqrt{2}}{3}-15$.

Proof. 

In Figure 11, the degrees of vertices in line graph $G^L(GBG(C_m,P_3;d))$ are displayed near by the corresponding vertices. This line graph has $d(m+6)-7$ edges. In addition, there are $d(m-3)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=2$, 4 edges of type $d_{L(G)}(e_1)=2$ and $d_{L(G)}(e_2)=3$, $2(d-2)$ edges of type $d_{L(G)}(e_1)=2$ and $d_{L(G)}(e_2)=4$, 6 edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=3$, 2 edges of type $d_{L(G)}(e_1)=3$ and $d_{L(G)}(e_2)=4$, and $7d-15$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=4$. Hence, we have

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(C_m,P_3;d))& =& d(m-3)\left(\sqrt{\frac{2+2-2}{2\times 2}}\right)+4\left(\sqrt{\frac{2+3-2}{2\times 3}}\right)\hfill \\ & & +2(d-2)\left(\sqrt{\frac{2+4-2}{2\times 4}}\right)+6\left(\sqrt{\frac{3+3-2}{3\times 3}}\right)\hfill \\ & & +2\left(\sqrt{\frac{3+4-2}{3\times 4}}\right)+(7d-15)\left(\sqrt{\frac{4+4-2}{4\times 4}}\right)\hfill \\ & =& \frac{\sqrt{2}}{2}d(m-3)+(\sqrt{2}+7\frac{\sqrt{6}}{4})d+4\hfill \\ & & +\frac{\sqrt{15}}{3}-\frac{15\sqrt{6}}{4},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(C_m,P_3;d))& =& d(m-3)\left(\frac{2\sqrt{2\times 2}}{2+2}\right)+4\left(\frac{2\sqrt{2\times 3}}{2+3}\right)\hfill \\ & & +2(d-2)\left(\frac{2\sqrt{2\times 4}}{2+4}\right)+6\left(\frac{2\sqrt{3\times 3}}{3+3}\right)\hfill \\ & & +2\left(\frac{2\sqrt{3\times 4}}{3+4}\right)+(7d-15)\left(\frac{2\sqrt{4\times 4}}{4+4}\right)\hfill \\ & =& d(m-3)+(\frac{4\sqrt{2}}{3}+7)d+\frac{8\sqrt{6}}{5}+6\hfill \\ & & +\frac{8\sqrt{3}}{7}-\frac{8\sqrt{2}}{3}-15.\hfill \end{array}$$

The proof is complete. □

For Example 5, in Figure 12, $(cyclohexane$-$1,1$-$diylbis(methylene))dicyclohexane$ can be modeled by $GBG(C_6,P_3;3)$, so $AB{C}_e(GBG(C_6,P_3;3))\approx 19.57183078$ and $G{A}_e(GBG(C_6,P_3;3))\approx 28.78428831$.

Figure 12. (a) $(cyclohexane$-$1,1$-$diylbis(methylene))dicyclohexane$ ball and stick model graph in $3D$; (b) $(cyclohexane$-$1,1$-$diylbis(methylene))dicyclohexane$ chemical structure graph; and (c) $(cyclohexane$-$1,1$-$diylbis(methylene))dicyclohexane$ model graph in chemical graph theory.

Theorem 6.

Let $GBG(C_m,P_2;d)$ be the generalized bridge molecular graph for $n=2$, $d\ge 4$, and $m\ge 3$ (see Figure 13), then the $AB{C}_e$ and $G{A}_e$ of $GBG(C_m,P_2;d)$ are

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(C_m,P_2;d))& =& \frac{\sqrt{2}}{2}dm+(\sqrt{2}+\frac{\sqrt{6}}{4}+\frac{4\sqrt{3}}{3}+\frac{\sqrt{10}}{6}-\frac{3\sqrt{2}}{2})d\hfill \\ & & +\frac{4}{3}+4\sqrt{\frac{2}{5}}+2\sqrt{\frac{7}{5}}+2\sqrt{\frac{3}{10}}-\frac{\sqrt{6}}{2}-4\sqrt{3}-\frac{2\sqrt{10}}{3},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(C_m,P_2;d))& =& dm+(\frac{4\sqrt{2}}{3}+\frac{8\sqrt{6}}{5}-1)d+\sqrt{15}+\frac{16\sqrt{5}}{9}+\frac{4\sqrt{30}}{11}\hfill \\ & & -\frac{16\sqrt{6}}{5}-\frac{8\sqrt{2}}{3}-4.\hfill \end{array}$$

Figure 13. The generalized bridge molecular graph of $GBG(C_m,P_2;d)$ and $GB{G}^L(C_m,P_2;d)$.

Proof. 

In Figure 13, the degrees of vertices in line graph $G^L(GBG(C_m,P_2;d))$ are displayed near by the corresponding vertices. This line graph has $d(m-5)-6$ edges. In addition, there are $d(m-3)$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=2$, 4 edges of type $d_{L(G)}(e_1)=2$, $d_{L(G)}(e_2)=3$, $2(d-2)$ edges of type $d_{L(G)}(e_1)=2$,$d_{L(G)}(e_2)=4$, 2 edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=3$, 4 edges of type $d_{L(G)}(e_1)=3$, $d_{L(G)}(e_2)=5$, $d-2$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=4$, 4 edges of type $d_{L(G)}(e_1)=4$, $d_{L(G)}(e_2)=5$, $4(d-3)$ edges of type $d_{L(G)}(e_1)=4$, $d_{L(G)}(e_2)=6$, 2 edges of type $d_{L(G)}(e_1)=5$, $d_{L(G)}(e_2)=6$, and $d-4$ edges of type $d_{L(G)}(e_1)=d_{L(G)}(e_2)=6$. Hence, we have

$$\begin{array}{ccc}\hfill AB{C}_e(GBG(C_m,P_2;d))& =& d(m-3)\left(\sqrt{\frac{2+2-2}{2\times 2}}\right)+4\left(\sqrt{\frac{2+3-2}{2\times 3}}\right)\hfill \\ & & +2(d-2)\left(\sqrt{\frac{2+4-2}{2\times 4}}\right)+2\left(\sqrt{\frac{3+3-2}{3\times 3}}\right)\hfill \\ & & +4\left(\sqrt{\frac{3+5-2}{3\times 5}}\right)+(d-2)\left(\sqrt{\frac{4+4-2}{4\times 4}}\right)\hfill \\ & & +4\left(\sqrt{\frac{4+5-2}{4\times 5}}\right)+4(d-3)\left(\sqrt{\frac{4+6-2}{4\times 6}}\right)\hfill \\ & & +2\left(\sqrt{\frac{5+6-2}{5\times 6}}\right)+(d-4)\left(\sqrt{\frac{6+6-2}{6\times 6}}\right)\hfill \\ & =& \frac{\sqrt{2}}{2}dm+(\sqrt{2}+\frac{\sqrt{6}}{4}+\frac{4\sqrt{3}}{3}+\frac{\sqrt{10}}{6}-\frac{3\sqrt{2}}{2})d\hfill \\ & & +\frac{4}{3}+4\sqrt{\frac{2}{5}}+2\sqrt{\frac{7}{5}}+2\sqrt{\frac{3}{10}}-\frac{\sqrt{6}}{2}-4\sqrt{3}-\frac{2\sqrt{10}}{3},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill G{A}_e(GBG(C_m,P_2;d))& =& d(m-3)\left(\frac{2\sqrt{2\times 2}}{2+2}\right)+4\left(\frac{2\sqrt{2\times 3}}{2+3}\right)\hfill \\ & & +2(d-2)\left(\frac{2\sqrt{2\times 4}}{2+4}\right)+2\left(\frac{2\sqrt{3\times 3}}{3+3}\right)\hfill \\ & & +4\left(\frac{2\sqrt{3\times 5}}{3+5}\right)+(d-2)\left(\frac{2\sqrt{4\times 4}}{4+4}\right)\hfill \\ & & +4\left(\frac{2\sqrt{4\times 5}}{4+5}\right)+4(d-3)\left(\frac{2\sqrt{4\times 6}}{4+6}\right)\hfill \\ & & +2\left(\frac{2\sqrt{5\times 6}}{5+6}\right)+(d-4)\left(\frac{2\sqrt{6\times 6}}{6+6}\right)\hfill \\ & =& dm+(\frac{4\sqrt{2}}{3}+\frac{8\sqrt{6}}{5}-1)d+\sqrt{15}+\frac{16\sqrt{5}}{9}+\frac{4\sqrt{30}}{11}\hfill \\ & & -\frac{16\sqrt{6}}{5}-\frac{8\sqrt{2}}{3}-4.\hfill \end{array}$$

The proof is complete.${\gamma }_i(C_6\square C_n)$ □

For Example 6, in Figure 14, $2^{\prime }H,2^{″}H$-$1,1^{\prime }:1^{\prime },1^{″}:1^{″},1^{‴}$-$quaterphenyl$ can be modeled by $GBG(C_6,P_2;4)$, so $AB{C}_e(GBG(C_6,P_2;4))\approx 25.00131406$ and $G{A}_e(GBG(C_6,P_2;4))\approx 37.44953704$.

Figure 14. (a) $2^{\prime }H,2^{″}H$-$1,1^{\prime }:1^{\prime },1^{″}:1^{″},1^{‴}$-$quaterphenyl$ ball and stick model graph in $3D$; (b) $2^{\prime }H,2^{″}H$-$1,1^{\prime }:1^{\prime },1^{″}:1^{″},1^{‴}$-$quaterphenyl$ chemical structure graph; and (c) $2^{\prime }H,2^{″}H$-$1,1^{\prime }:1^{\prime },1^{″}:1^{″},1^{‴}$-$quaterphenyl$ model graph in chemical graph theory.

3. Conclusions

Topological indices are proven to be very helpful to test the chemical properties of new chemical or physical materials. To describe more kinds of long chain polymerization products than the bridge molecular graphs, we propose the generalized bridge molecular graph structures. In this paper, we focus on some generalized bridge molecular graphs such as $GBG(S_m,P_n;d)$ and $GBG(C_m,P_n;d)$ and give the formulas of the edge version ABC and GA indices of these generalized bridge molecular graphs. By demonstrating the calculation of real molecules, we find that some long chain molecular graphs can be quickly modeled and their topological indices can be calculated using generalized bridge molecular graphs. The results of this paper also offer promising prospects in the applications for chemical and material engineering, especially in chemical industry research.