1. Introduction
Creating aesthetic representations is part of the process of the construction and acquisition of knowledge [
1]. Rarely is this more apparent than in scientific endeavour. The pioneering drawings of sunspots depicted by the monk John of Worcester at the beginning of the High Medieval Period [
2] or, the microscopic illustrations of a flea that Robert Hooke revealed in his book
Micrographia [
3], as well as the detailed descriptions of the plants’ sexual system that the Swedish naturalist Carl Linnaeus included in his seminal work
Systema Naturae [
4], might be among those of the numerous significant examples that spring to mind when reflecting on the connection that graphical representation has with scientific knowledge. Needless to say, nowadays visual representation and, more specifically, drawing-based techniques continue to be a significant part of the construction and communication of scientific knowledge, as the evidence stemming from different fields of science bears witness to; for instance, from immunology [
5], astronomy [
6] and also, from medical sciences [
7], to name but a few.
On a separate but not unrelated matter, drawings are also a distinctive feature of children’s expressivity [
8]. By their depictions and painting activities, children represent their thoughts and knowledge [
9] and, not surprisingly, drawing-based research techniques have proved to be useful to gain insight into children’s views, experiences and perceptions about the world around them [
10,
11]. Different aspects of young children’s drawings have been subject to particular interest among scholars; for instance, the content of the illustrations that children create [
12], the palette of colours that children choose when colouring their illustrations [
13] and, also, the geometrical shapes that they freely depict in their representations [
14].
Little attention, however, has been attached to the fact that when a free-hand is given to pre-schoolers and children at the initial stages of primary education, they depict symmetrical motifs spontaneously [
15] and to the best of our knowledge, no quantitative study has been undertaken regarding the spontaneous occurrence of symmetry in young children’s drawing. This lack of research is, in itself, not unimportant, given the relevant connections that symmetry has proved to have not only with education-related topics but, also, with the study of human perception and aesthetic experience [
16].
Accordingly, the following is a research project on the issue of the symmetrical motifs that a sample of young children freely depict concerning a general natural topic and represents an attempt to provide the scientific community with preliminary data regarding the spontaneous occurrence of symmetrical patterns in early pictorial activities.
2. Theoretical Background
Drawing activities are pointed out as an effective way to encourage children to express their thoughts and feelings [
17,
18]. Not surprisingly, the study of their depictions has proved to be useful to gain an insight into how children acquire the comprehension of a variety of topics, such as, the microbial world and its implications on health [
19], the structure of plants [
20], earthquakes [
21], the ecological relationships between animals and plants [
22], as well as the concept of living things [
23] and even pre-schooler’s ideas about magnetism [
24]. In addition, studies in line with this field of research have also been successfully conducted to better understand how children grasp geoscience related themes [
25,
26], elementary astronomy [
27] and even conceptions about science [
28].
As far as the examination of children’s drawings is concerned, some research pays particular attention to the content displayed in the drawings, that is to say, the pictorial motifs that the child includes in their illustration [
12,
29]. The undoubted usefulness that this line of research has when it comes to unveiling children’s comprehension on a large range of topics notwithstanding, some scholars also highlight the value of looking into more general pictorial features, that is, those characteristics related to the process of creating the depictions. Thus, the examination of the colour that children choose when painting their drawings has proved to be a relevant feature that leads to a better understanding of their comprehension of the natural world. Moreover, the study of the shapes appearing in children’s drawings paves the way to the achievement of a more comprehensive picture about their geometrical thinking [
14].
In this sense, spontaneous symmetry is a significant pictorial feature of young children’s drawings which has not been subject to examination in previous research. Educators, parents and children’s caregivers might be no strangers to the symmetrical patterns that young children, well before receiving formal education about geometry, naturally include in their drawings; but the fact is that previous research has devoted very little attention to the examination of this phenomena. To the best of our knowledge, the qualitative study undertaken by Professor Ha [
15] has been the only attempt to gain an insight into the natural depiction of symmetrical motifs in early childhood.
This lack of study regarding the natural emergence of symmetry in graphic expression in early childhood is in contrast with the remarkable development that the study of symmetry has experienced in the field of cognitive science. In this respect, current research indicates that the sensibility to symmetry emerges very early in children’s development in such a way that even infants show the capability of spotting and paying attention to vertical symmetry in patterns [
30,
31]. It is not altogether certain that this early cognitive ability means early aesthetic preferences to symmetry. Thus, current evidence points out that young children’s attentional choices in favour of symmetrical patterns are dissociated from their aesthetic preference [
32]. Accordingly, it seems more plausible to consider that one’s prior experience and educational background may be behind aesthetic judgements related to symmetrical patterns [
33]. Nevertheless it is a fact that not only do infants and young children show sensibility to symmetry, but also older children [
34], adults [
35] and even non-human primates [
36] together with other kinds of animals [
37].
In this respect, it is worth noting that symmetrical stimuli is encoded more quickly than those with asymmetrical arrangements, due to the fact that redundant information embodied in symmetrical patterns enhances the process of grouping perceptual items and discriminating them from the background [
38].
Symmetry has also been the subject of particular attention in the educational arena in line with the emphasis that is currently devoted to spatial thinking [
39]. What is actually behind this interest is the observation that spatial reasoning abilities underpin more general mathematical skills as well as people’s performance in the domains of science, technology, engineering, and mathematics [
40]. Accordingly, applying transformations to shapes and objects, seeing and producing geometric shapes in the mind, rearranging shapes into different perspectives, developing ties between geometry and numeracy are among those symmetry-linked objectives that children are supposed to cover during their school years [
41].
More salient, schoolchildren as young as four and five benefit from being involved in activities related to spatial thinking [
42] and in this connection, symmetry is one of the topics that has been pointed out due to the crucial role that it plays in the development of geometrical thinking in early childhood [
43].
However, the truth is that spatial thinking barely appears as a significant component of early education [
39] and it is believed that there is untapped potential in designing teaching interventions that take into consideration young children’s insights, preferences and attraction towards symmetry, with a strong focus on painting and drawing activities [
44].
Of special relevance in this context is the phenomenon of the spontaneous depiction of symmetrical motifs by young children. Drawing is a natural activity for most children that allows them to communicate and demonstrate their understandings, even when oral expression might not be as easy, as well as providing parents, educators and researchers with a window into children’s view of the world [
45,
46,
47]. Accordingly, studying the fact that young children instinctively represent symmetrically arranged pictorial motifs should provide developmental information in connection with the conceptualisation of symmetry in early years. However, no research has been undertaken to quantitatively examine the representation of symmetrical patterns in early childhood apart from the only qualitative study conducted some time ago by Professor Ha [
15] which provides a collection of symmetrical patterns illustrated by children.
In accordance with the theoretical background presented, this study poses the research question of whether young schoolchildren naturally express a tendency to draw symmetries in their illustrations and, if so, what kind of symmetrical patterns and with what frequency they appear in their pictures.
3. Objectives
This research project aims to study the spontaneous occurrence of symmetrical motifs in young children’s pictorial production when they graphically tackle the challenge of conveying their understanding of a particular natural phenomena.
Specifically, the study intends to follow these objectives:
To quantify the occurrence of cyclic and dihedral symmetrical motifs in a sample of pictures drawn by children aged between 4 and 7, when they are given a free hand to illustrate their understanding of plant life.
To analyse whether girls and boys in the sample under examination draw cyclic and dihedral symmetric motifs differently.
To study whether the educational level variable displays any connection with the tendency to draw cyclic and dihedral motifs in the pictorial production undertaken by the children in the sample.
To examine whether the children’s level of proficiency when it comes to depicting basic geometrical shapes (viz. closed curves, quadrilaterals and triangles) relates to the frequency of occurrence of the drawing of cyclic and dihedral motifs in the spontaneous representation of plant life undertaken by the participants in the study.
Ultimately, the relevance on the presented study lies in the fact that the data collected might help clarify the issue of how symmetry is conceptualised during early childhood. This must certainly be a major enabler for the design of didactic strategies aiming to improve the grasp of symmetry and, more generally, to enhance spatial thinking in basic education.
4. Method
4.1. Sample
The sample under examination in this study consists of 116 drawings undertaken by young children.
Table 1 accounts for the educational level of the children as well as their age at the moment of being involved in the study. Besides that, 56% of the participants were girls and 44%, boys.
The drawings were collected in accordance with the method described in the data collection section, during a series of visits to three state-run schools in the region of Uribe-Kosta (the Basque Country, Spain). The schools are located in medium-sized towns with less than 15,000 inhabitants and the distance between them does not exceed 20 km. The schools were selected under the criteria of accessibility and proximity to the research group.
4.2. Data Collection
The drawings comprising the sample were collected within a more general research framework aimed at studying the understanding of plant life in early childhood [
23]. The rationale for having chosen this particular sample is that its initial research purpose and design as well as the fieldwork carried out had no immediate connection with topics related to either geometry or symmetry. Accordingly, this study can guarantee that no indication, even inadvertently, concerning the depiction of symmetrical motifs or geometric shapes were given to the participants during their drawing activity.
Moreover, one individual interviewer of the panel of signatories with this paper undertook the meetings with the children during the 2012–2013 academic year and the procedure followed was as outlined below. Firstly, the researcher, accompanied by the classroom teacher, carried out a general presentation of the pictorial activity with all the children attending the same class. The objective of the presentation was to familiarise the children with the researcher as well as with the artistic activity. In the presentation, the researcher introduced the children to a puppet that he had brought with him and he narrated a tale to the children related to the puppet. Through the story, the researcher explained to the children that the puppet knew very little about plants and it was looking forward to learning more about them. The children were encouraged to help the puppet find out more about plants by drawing an illustration about them and representing what plants look like, where they live and what might be beneficial to them. No additional information was given about the content of the drawings.
After this presentation, individual meetings with each child were conducted in a place adjacent to the classroom or, without this, in an area within the same classroom which had been prepared for this objective. The interview always began with a reminder about the objective of the drawing activity (that is to say, to help the puppet to learn more about plants) and asking the children whether they wished to go ahead with the activity. No child refused to be involved in the activity. Afterwards, sheets of paper, pencils as well as felt-tip pens were offered to the child to start the drawing. After the child expressed that the drawing was finished, the researcher reviewed the content of the drawing with the child to ensure that he was able to recognise the meaning of the motifs drawn. During the meeting, the researcher gave no information on the issue of the plants world and no comment was made regarding symmetry or geometrical shapes. The pictorial activity rarely took more than 10 min.
The research protocol utilised in the study was agreed to and approved by the head and teachers of each of the schools collaborating in this study. The parents of the children were also notified in writing regarding the objectives and method of the research as well as how they could refuse to allow their children to join in the study. No recordings or photographs connected with the activity of the children were made or taken.
4.3. Target Study Variables and Data Encoding
Information on the gender of the children engaged in the activity along with the course in which they were enrolled at the moment of the study was registered. In addition, data linked to the frequency of the occurrence of pictorial motifs showing either cyclic or dihedral symmetries, as well as, the level of geometric proficiency when it comes to depicting closed curves, quadrilaterals and triangles was also recorded. The following is a detailed explanation of the criteria used to encode these variables.
4.4. Regarding the Encoding Criteria on Symmetrical Motifs
The process of pinpointing symmetries in the children’s drawings was based on the examination of the pictorial motifs appearing in their pictures. A pictorial motif, in accordance with previous research linked to the analysis of the content of young children’s drawings [
22,
29,
47], is considered to be the graphical representation of a certain entity, both physical (e.g., a tree) or abstract (e.g., a decorative pattern), which displays a distinctive level of independence in the picture. Thus, for instance, a flower appearing in a picture is regarded as a pictorial motif as it represents a particular physical entity, which, plausibly, looks to be singled out from the other parts of the drawing. However, the petals and the stems of the flowers were considered constituent elements that shape the motif. Similarly, a certain depiction of a house is considered a pictorial motif but the windows and the doors of the house are regarded as pictorial elements contained in the motif.
Moving onto the identification of the symmetries, the pictures in the sample were examined in pursuit of forms of cyclic and dihedral symmetries. The criteria utilised to define both kinds of symmetries are those that are conventional in the studies linked to the recognition of geometrical patterns [
48,
49,
50]. Therefore, a cyclic symmetry was considered in the case where a particular pictorial motif displays only rotational symmetry around a centre point; that is to say, the points on the figure are equally positioned around a point, referred to as the central point. Moreover, a dihedral symmetry was recognised in the case where a pictorial motif displays a rotational symmetry around a centre point with reflection lines through the centre point. In the results section of this paper the reader may find several examples of the symmetrical motifs identified in accordance with these criteria in the sample under study.
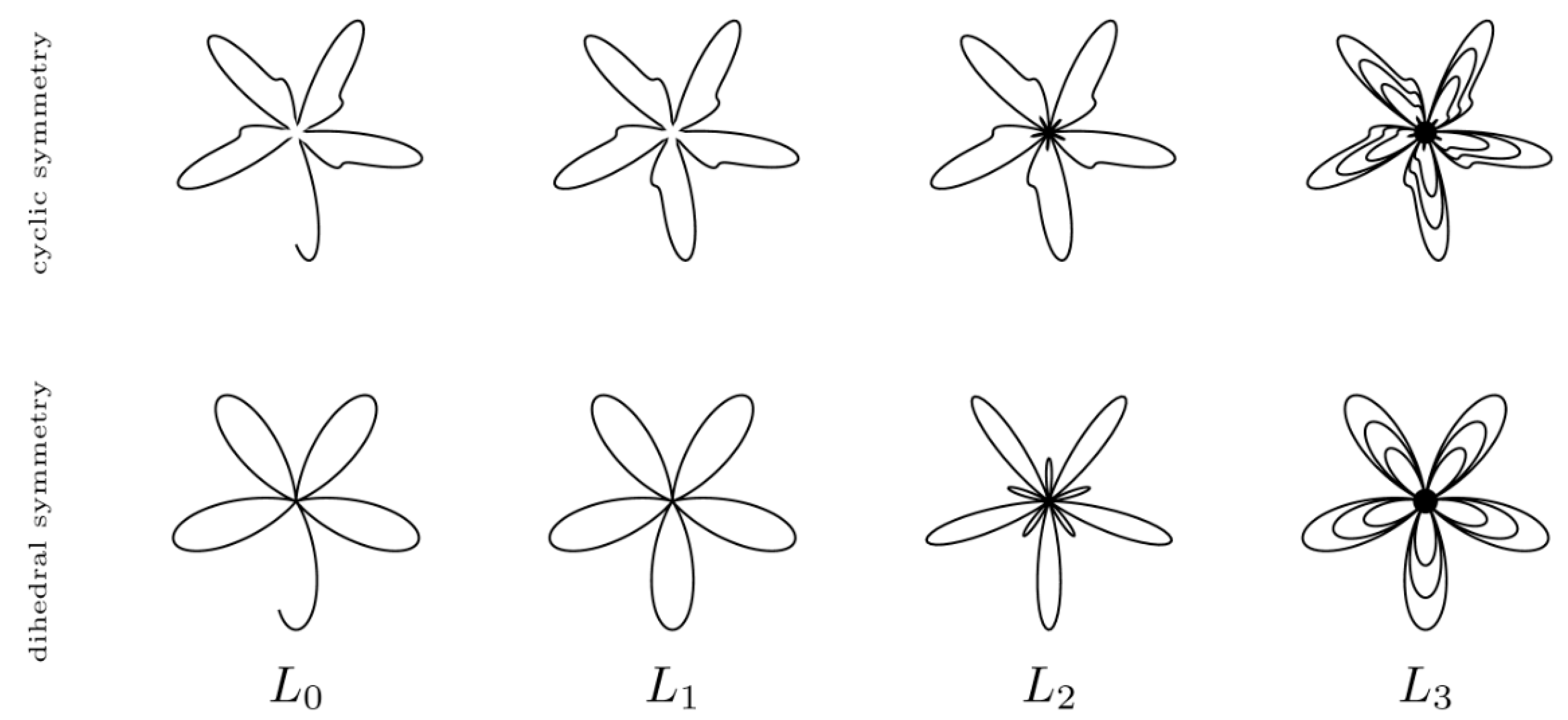
Finally the complexity level of the symmetrical motifs was also registered. To that end, four different complexity levels were defined according to the number of pictorial elements comprising the motifs: no symmetry (
L0), only one pictorial element constitutes the motif (
L1), two or three pictorial elements (
L2) and, more than three (
L3).
Figure 1 provides theoretical models of illustrations of flowers displaying cyclic as well as dihedral symmetries with different levels of complexity. It should also be noted that in the case that a certain drawing displays several motifs with different complexity levels, the highest one is recorded.
4.4.1. Regarding the Encoding Criteria on Geometrical Shapes
The study of the level of proficiency with respect to the depiction of closed curves, quadrilaterals and triangles, was conducted in accordance with Villarroel and Sanz’s work [
14].
Table 2 displays the criteria used to classify the drawings in the sample.
In agreement with the criteria stated by Villarroel and Sanz [
14], when a particular drawing shows examples that fit in well with both the incomplete and completed patterns, the criterion applied is to consider the best shape drawn by the child. Therefore, in the case that a particular picture displays well-defined triangles and also, triangle-like shapes, similar to those that are classified as incomplete patterns, the geometric proficiency level allocated to the picture is the completed pattern, since the participant has, at least on one occasion, confirmed their competence for this proficiency.
4.4.2. Regarding the Process of Encoding
The study of both the occurrence of the symmetries and the level of proficiency over the geometrical shapes displayed in the pictures was undertaken in three phases. Firstly, the research team carried out a preliminary test with a sample of 40 drawings that children of the same age as the participants involved in the present research project had also undertaken on the issue of plant life. The purpose of this introductory examination was to standardise the criteria among the researchers when it comes to both pinpointing the occurrence of symmetries and assessing the level of proficiency linked to the geometrical shapes. The results of this initial analysis were not included in the outcomes of the study presented in this paper. Subsequently, the three members of the research team independently analysed the 116 drawings comprising the sample under examination in this study. Finally, the results achieved were analysed with the group and the agreement between the observers was measured. The discrepancies found were discussed until reaching an agreement over the analysis undertaken.
4.5. Statistical Methodology
The inter-rater agreement between the three observers was assessed by the coefficient and test of concordance of Kendall [
51] for all the variables. The hypothesis tests to contrast the dependence between gender and educational level variables with the occurrence and complexity level of symmetries, as well as the geometric proficiency, were carried out by the Fisher exact test (FET) [
52]. Additionally, the effect size was measured by Cramer’s V [
53], where only medium and large size effects were considered. The level of significance considered for rejecting null hypotheses was 5%. The statistical methods were performed by R software [
54], version 3.5.0.
5. Results
The outcomes of the study are presented in four sections. Firstly, the data provided by the analysis of the interobserver agreement is introduced. Then, the findings related to the occurrence of symmetry for the whole of the sample, irrespective of the gender and educational level variables, are presented. Together with this, a selection of the pictures exhibiting some form of symmetry is also displayed. Subsequently, the results of the examination of the relationship that the gender and educational level variables show with the presence of symmetry in the drawings are detailed. The final part of the subsection reports the outcomes linked to the study of the connection that depicting circular, rectangular and triangular shapes has with the occurrence of symmetry in the pictures.
5.1. The Agreement between the Observers
Regarding the results of the examination of the agreement among the three researchers in charge of the process of coding the pictures in the sample,
Table 3 displays the data linked to the interobserver consistency when it comes to spotting the occurrence of both cyclic and dihedral symmetries. Additionally, the table also shows the agreement among the observers concerning the assigning of the level of complexity of the symmetries identified (viz. the pictorial motifs presenting symmetry include one unique element,
L1; or two or three elements,
L2; or more than three elements,
L3). The p-values displayed in
Table 3 suggest that the null hypothesis indicating that there is no agreement between the observers should be rejected in all of the cases.
As for the study of the accord among the three researchers when appraising the geometric pattern displayed in the drawings included in the sample, the results are broken down in
Table 4. Once again, the
p-value sought indicates that the assumption of no agreement between the observers should be excluded.
5.2. The Occurrence and Complexity of Symmetry in the Whole of the Sample
Some examples taken from the pictures under study illustrating cyclic and dihedral symmetric motifs are introduced in
Figure 2 and
Figure 3, respectively.
Figure 2 presents four examples of the representation of the sun found as part of the illustrations undertaken by four different children. From top to bottom and left to right, they display C
20, C
11, C
14 and C
7 cyclic symmetries.
Figure 3 shows 16 examples of dihedral symmetries encountered as part of the pictures of the children. More specifically, the examples presented from top to bottom are as follows: in the first column, a cloud (D
2), a star (D
6), a heart (D
1), rainbow (D
1), a start (D
6); in the second column, a tree (D
1), a butterfly (D
1), a daisy-like flower (D
1), a fruit tree (D
1), a house (D
1) and a tulip-like flower (D
1) and, finally, in the third column, a child (D
1), a tree (D
1), a flower (D
1), an inflorescence (D
10) and a house (D
1).
Additionally, some examples of completed pictures belonging to the drawings analysed are presented in the
Appendix of the paper.
Moreover, among the pictorial motifs depicted, 81.9% of the 116 drawings analysed showed one kind of symmetry (either cyclic or dihedral) and 14.7% presented both kinds of symmetries.
Furthermore, some sort of dihedral symmetry was found in 95.7% of the drawings, while cyclic symmetry was found in 15.5% of the pictures.
Table 5 spells out in more detail the frequency of each of the complexity levels considered in this study when it comes to both cyclic and dihedral symmetry.
5.3. The Connection between the Gender and Educational Level Variables with the Occurrence of Symmetry
No differences have been found between girls and boys when it comes to the frequency of the depiction of symmetries, cyclic as well as dihedral symmetry, in their drawings. However, as regards to the level of complexity, it is worth noting that, in comparison with their male classmates, girls were significantly more prone to draw dihedral symmetries involving more than three elements. Accordingly, 66% of those that depicted the most complex dihedral symmetry were girls (FET; p < 0.001; Cramer’s V =0.33).
As far as the educational level variable is concerned, the data collected indicates that as the drawings of children in higher educational levels are considered, the occurrence of the cyclic symmetry, the dihedral symmetry and both types of symmetries together become significantly more frequent (cyclic symmetry: FET;
p < 0.05; Cramer’s V = 0.24; dihedral symmetry: FET;
p < 0.01; Cramer’s V = 0.32 and the both symmetries: FET;
p < 0.01; Cramer’s V = 0.27).
Table 6 introduces the data related to the frequencies of the presence of each of both kinds of symmetries in accordance with the educational level of the children in the sample.
Moving onto the study of whether the pictures undertaken by children in different educational levels are different in connection with the levels of complexity that the symmetrical motifs show,
Table 7 accounts for the figures related to the frequency of each of the complexity levels of both kinds of symmetry within the three educational levels considered in the present study.
In the case of cyclic symmetry, all the pictorial motifs found in the sample consist of two or three pictorial elements; that is, the second level of complexity considered in this study. This particular level of complexity turns out to be substantially more frequent in the drawings of the children in the higher educational levels (FET;
p < 0.05; Cramer’s V = 0.24). It is worth noting that all the motifs found linked to cyclic symmetry were illustrations of the sun, a topic that has been pointed out as very significant feature in young children’s depiction of natural phenomena [
29].
In addition, the frequency of the levels of complexity linked to dihedral symmetry are also different among the educational levels involved in the study (FET; p < 0.01; Cramer’s V = 0.26) in the sense that the drawings undertaken by those in the higher educational levels are also more likely to present more complex dihedral symmetries.
5.4. The Connection between the Drawing of closed Curves, Quadrilaterals and Triangles and the Occurrence of Symmetry
The following are the results of the study concerning the relationship that the depiction of circular, rectangular and triangular shapes displays with the occurrence of symmetries in the children’s drawings under study.
Firstly,
Table 8 breaks down the data linked to the frequency of the children’s drawings categorised in each of the three levels of geometric competence for each of the three geometric shapes considered in the study.
Furthermore, the data collected indicates no differences between boys and girls regarding the frequency of occurrence of the three kinds of geometrical shapes in their drawings. However, there is evidence of a connection between the depiction of closed curves, quadrilaterals and triangles and the educational level of the children in such a way that the higher the children’s level, the more likely it is that they draw circular, rectangular and triangular shapes (FET; p < 0.01; Cramer’s V =0.27 for closed curves; p < 0.001; Cramer’s V = 0.29 for quadrilaterals and p < 0.001; Cramer’s V =0.38 for triangles).
Finally, the analysis of the connection between the occurrence of symmetries and the depiction of the geometric shapes indicates that the frequency of closed curves, quadrilaterals and triangles recorded in drawings showing cyclic symmetry is indistinguishable from the frequency registered in the pictures that do not display this form of symmetry.
However, the frequency of closed curves found in drawings displaying dihedral symmetry differs from the frequency observed in the depictions that do not present this kind of symmetry (FET; p < 0.01; Cramer’s V = 0.41). Thus, among the 111 pictures that present some kind of dihedral symmetry, 92.8% of them include forms of completed patterns of closed curves, whilst the proportion of pictures without dihedral symmetry (N = 5) containing closed curves drops to 40%.
In addition, the data indicates that the more complex the dihedral symmetry depicted by the children is, the more likely it is to appear as closed curves in their drawings, which is reflected in
Table 9 (FET;
p < 0.001; Cramer’s V = 0.33).
The aforementioned relationship between the occurrence of dihedral symmetry and the frequency of closed curves notwithstanding, it is worth noting that this study cannot report any substantial connection between the drawing of quadrilaterals and triangles and the occurrence of symmetrical pictorial elements.
6. Summary of the Results
The discussion of the results provided in this study is introduced in two sections. The first part synthesises the findings linked to the occurrence of the symmetrical motifs in the drawings under examination, and the second part details the connexion that symmetry shows with the independent variables considered in the study, id est, the gender and educational level.
Regarding the first point, the data provided in this study indicates that symmetry is a common pictorial phenomenon in the pictures that the children in the sample spontaneously presented on the issue of plant life. This seems to be the case given that virtually, every child drew at least one symmetrical motif during the artistic activity undertaken. This overwhelming tendency to depict symmetrical patterns notwithstanding, some particular aspects should be pointed out as regards the symmetrical motifs found in the drawings examined.
First and foremost, it is noteworthy that cyclic and dihedral symmetries do not occur with the same frequency. Thus, the children in the sample opted by far to draw dihedral symmetries (more than 9 out of 10 drawings show this feature), while cyclic symmetries were substantially scarcer, so that hardly 2 out of 10 children displayed this kind of symmetry in their illustrations.
Moreover, children draw on cyclic and dihedral symmetries to illustrate different entities. Thus, cyclic symmetry exclusively happens in the picture of the sample when depicting the sun. However, dihedral symmetry appears linked to the representation of a wide variety of real instances, particularly when the children illustrate the plant world (flowers and tress), human environment (e.g., houses and people) and decorative items (e.g., hearts, stars).
Another substantial difference appearing in the sample under study concerning the utilisation of cyclic and dihedral symmetries is related to the complexity of the motifs. Thus, 7 out of 10 of the pictures in the sample included at least one motif showing a dihedral symmetry composed of more than three pictorial elements. However, no child depicted any cyclic symmetry with such level of complexity and, therefore, cyclic symmetry only appears linked to motifs formed by two or three pictorial elements.
On another development, and with respect to the connection between symmetry and geometrical shapes, it should be noted that 9 out of 10 of the children in the sample drew circles, ellipses or ovals and this study gives evidence of the strong connection that the occurrence of these geometric shapes has with the depictions of symmetrical motifs showing dihedral symmetry. Thus, the children in the sample very often draw dihedral symmetry in tandem with closed curves, as the large size effect found points out (0.41), and, more interestingly, they particularly draw closed curves with a completed pattern (0.33). However, no relationship can be reported between the representation of dihedral motifs and the occurrence of the other two geometric shapes; that is to say, quadrilaterals and triangles (which appear well-shaped in two fifths and one fifth of the pictures, respectively). The data examined also fails to confirm any connection between the drawings of motifs displaying cyclic symmetry and the depiction of any one of the geometric shapes considered in the study.
Moving onto results connected to the analysis of how the depiction of symmetrical motifs is related to the independent variables, this study accounts for differences linked to both the gender and educational level variables. Regarding the former, the differences found are not connected with the occurrence of symmetries in the pictures but with the level of complexity of the motifs showing dihedral symmetry. Thus, girls turn out to be in the majority (nearly 7 out of 10) among those who depicted dihedral symmetries with more than three pictorial elements (viz. the highest level of complexity considered in this study, L3). Contrarily, the boys are more prone to depict dihedral symmetries with only two or three pictorial elements (L2).
With respect to the differences associated with the educational level, both the frequency of appearing cyclic and dihedral symmetries and, also, the level of complexity of the motifs depicted seem to be related to this independent variable.
More specifically, nearly 3 out of 10 of the pictures undertaken by the children in primary education display a motif showing cyclic symmetry (always attached to the intermediate level of complexity, L2) but this proportion decreases dramatically as the drawings of the children in lower educational levels are considered. In addition, all the children in primary education as well as those in their final academic year in preschool education drew at least one dihedral symmetry in their pictures and, once again, the proportion of pictures with, in this case, dihedral symmetries, importantly falls when the drawings of the younger children are considered.
Perhaps even more salient is the fact that the level of complexity of the dihedral symmetries presented in the pictures strongly relates to the educational levels of the children (24). Thus the younger children are characterized by depicting dihedral symmetries more often with two or three pictorial elements; while 8 out of 10 of those in higher educational levels drew motifs presenting dihedral symmetries with more than three pictorial elements (the highest level of complexity, L3).
7. Discussion and Conclusions
The present study aims to examine the occurrence of symmetrical motifs that young children spontaneously create in their pictures of plant life. The data collected shows that dihedral symmetry is overwhelmingly utilised in the sample and, specifically, to illustrate flowers, trees, vegetables, houses, people and also decorative items. To the best of our knowledge, no previous research has accounted quantitatively for this pictorial tendency in young children’s drawings.
With a view to explaining this observation, it could be understood that the children in the sample are enthusiastic about symmetry and that aesthetic reasons might be behind their interest in depicting dihedral symmetries in their pictures, a point that might be in line with the rules of neuroesthetics described by Ramachandran [
55]. Although this rationale cannot be completely ruled out with the data presented, the truth is that recent studies cast doubts regarding the assumption that human beings might be hard-wired to consider symmetry as aesthetically pleasing [
32] or that symmetry could be a universal standard of beauty [
33] and it seems more likely that aesthetic preferences related to symmetry might be shaped by our own personal and educational experiences [
38]. Bearing in mind this line of thought, it seems reasonable to look for further explanations, apart from aesthetic preferences, that might help account for the inclination shown by the children in the sample to draw motifs with dihedral symmetries.
In this regard, it is worth noting that previous research underscores that even infants are capable of encoding symmetrical patterns more quickly than asymmetrical stimuli [
30] and also that the redundant information involved in symmetrical patterns is what enables them to make a faster distinction between the two [
32,
38].
One might consider that the redundant information included in symmetrical patterns might play a key role not only in the processing of visual input, as previously stated, but, also, in facilitating drawings. More specifically, depicting pictorial motifs that show a dihedral symmetry implies the representation of redundant information; viz, the information appearing on both sides of its line of symmetry. As a result, the depiction of the shapes placed on one side of the axis might act as a guide that enables the drawing of the other symmetrical side and young children might make use of dihedral symmetry to carry out their depiction more quickly and effectively. It conveys the point that dihedral symmetry might act as an enabler for graphical expression in early childhood.
This perspective might offer a possible explanation not only for the fact that the dihedral symmetry occurs so often in the sample studied but, also, for the relationship found between dihedral symmetry and the educational level variable. Thus, previous research gives evidence to the fact that as children advance to higher levels of education in the time period between the end of preschool and the beginning of primary education, this increases their graphical expressivity, drawing more pictorial elements [
22,
23] and with more complex shapes [
14]. Arguably, the observation provided by this study in the sense that dihedral symmetries are more frequent and also more complex as the pictures of the children in the highest educational levels are considered, could be linked to the fact that the children in these levels need to extend their graphical expressivity and, to that end, they more often draw on their representation of motifs with dihedral symmetry, and, presumably, with more complex structures.
On another development, cyclic symmetry might play a different role in young children’s pictorial activity. The evidence collected in this study indicates that the children in the sample drew on this kind of symmetry much less often compared with dihedral symmetry. It might be that the children find this technique less useful, more complex or perhaps less appropriate to illustrate their own thoughts and ideas as well as to represent the objects around them. Further research aimed at studying the graphical occurrence of cyclic symmetry on young children’s depictions seems all the more necessary to clarify why this kind of symmetry might turn out to be significantly less utilised by the children.
Remarkably, in addition, the occurrence of symmetry does not relate in the sample under study to the depiction of quadrilaterals and triangles. One might expect a connection between the enhancement of the depiction of geometrical shapes and the occurrence of symmetrical motifs, as both variables appear closely related in the children’s educational experiences [
41,
44]. However, the truth is that in the sample studied the children make use of cycle and dihedral symmetries regardless of their level of competence to depict quadrilaterals and triangles. This observation might suggest that the development of symmetry-based pictorial representations in early childhood might happen to some extent independently of the process of children’s learning of the depiction of geometrical shapes.
On a separate but not unconnected issue, some of the findings provided in this study seem to have interesting implications in the educational arena. Thus, previous research indicates the importance that young children’s spontaneous artistic activity has when it comes to examining their comprehension of geometrical-related concepts [
14]. This seems to be the case in this study, since the children in the sample, spontaneously and without having received further instruction or explanation regarding symmetry, show their capacity to create symmetrical motifs in their pictures. This necessarily implies that the children have some kind of internal representation or an implicit understanding regarding the symmetries that they draw (mainly, dihedral symmetry but also, to a lesser extent, cyclic symmetry) because, otherwise, explaining how the children can depict pictorial elements that present a symmetrical arrangement would be particularly difficult. In the light of these considerations, Ausubel’s words appealing to the importance of the skills that learners bring to the learning environment are particularly pertinent, when the author stated that “The most important single factor influencing learning is what the learner already knows. Ascertain this and teach him accordingly” [
56]. Accordingly, exploring the implicit knowledge that young children have on the issue of symmetry seems recommendable for the design of teaching activities intending to improve geometrical thinking in early childhood and, in this regard, pictorial activities may be a good option for checking out this particular issue [
44].
Finally, the data related to gender differences that this study presents, deserves a special mention. These differences refer exclusively to the fact that girls seem to be more prone to depict more complex dihedral symmetries. Previous research involving the examination of children’s drawings gives evidence of the differences between girls and boys regarding their graphical explanations [
18,
21], even though there are also studies that fail to show evidence in this same sense [
22,
57]. Nevertheless, no preceding study has examined the issue of gender differences in relation to the depiction of symmetry, so there is no way to put the presented data into perspective with other completed studies. In any event, it is worth noting that the influence that gender stereotypes have on girls’ perceptions seems to begin at the age of 6 [
58]; precisely the age that some of the children in the sample under study. Further research is required to shed light on the gender-related differences regarding the complexity and also the occurrence of the symmetry in young children’s drawings, particularly to clarify if the differences provided by this study are confirmed with the examination of larger samples.
The authors of the present study cannot ignore some limitations related to the research project undertaken. On the one hand, the fact that the topic of the pictorial activity proposed to the children in the sample was the plant world, might have an influence on their depictions. Plant life is symmetric by its nature and there are plenty of floral examples that display dihedral symmetry. Further research might consider the study of the drawings that children of the same age range carry out on different themes to confirm whether the same model of occurrence of symmetry is found. Moreover, this study mentions nothing regarding the influence that cultural and contextual variables might have in the kind of symmetrical patterns that young children draw, a topic that previous research has proved to have an impact on children’s graphical expression [
47]. In addition, further research should also examine the opportunities that continuous symmetry measures offer to analyse quantitatively the symmetry of the motifs that young children display in their pictures [
59,
60]. Accordingly, all this is a potential avenue for fresh research with a view to gaining an insight into how symmetry is conceptualised in early childhood.