Modeling and Control for a Multi-Rope Parallel Suspension Lifting System under Spatial Distributed Tensions and Multiple Constraints
Abstract
:1. Introduction
2. Modeling and Preliminaries
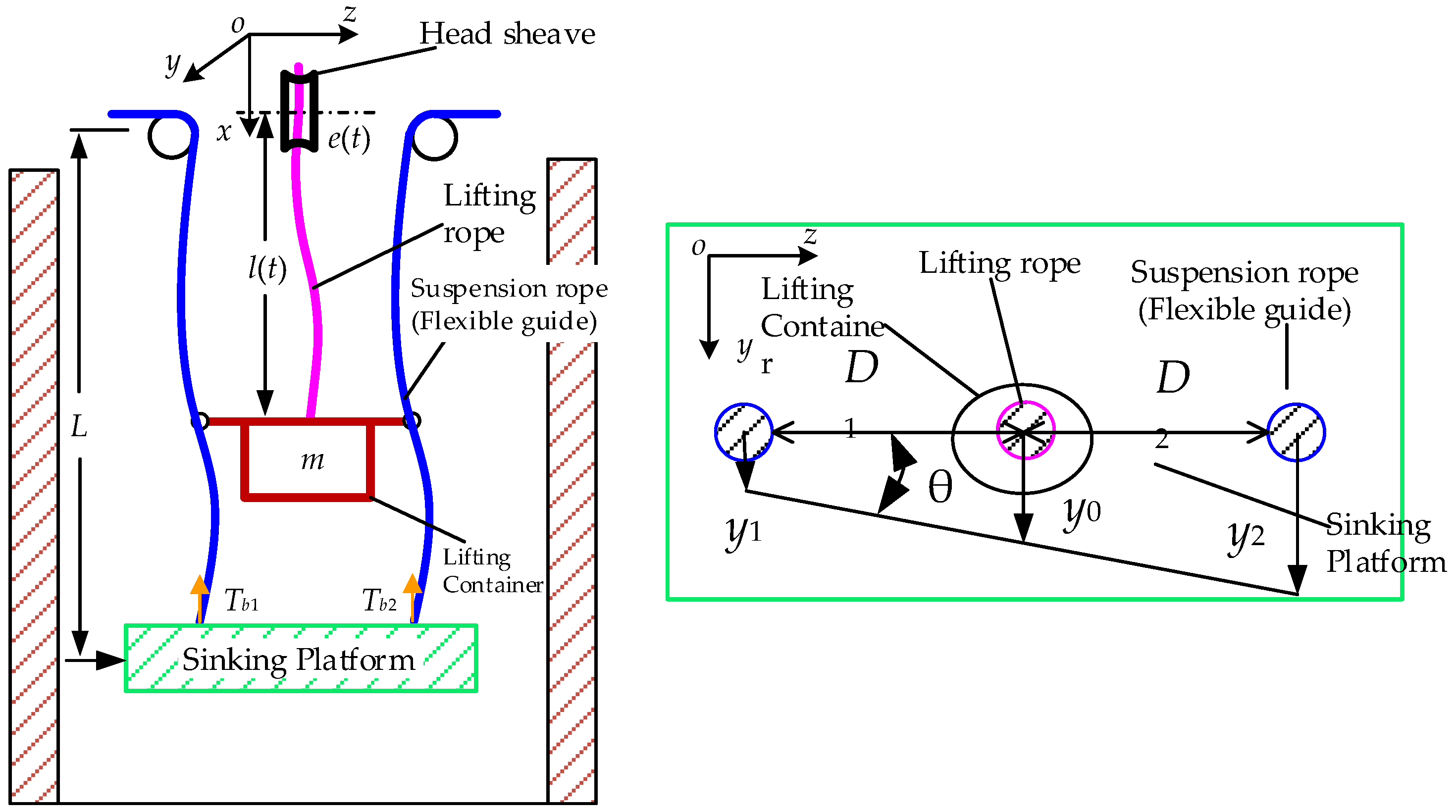
2.1. Modeling
2.2. Preliminaries
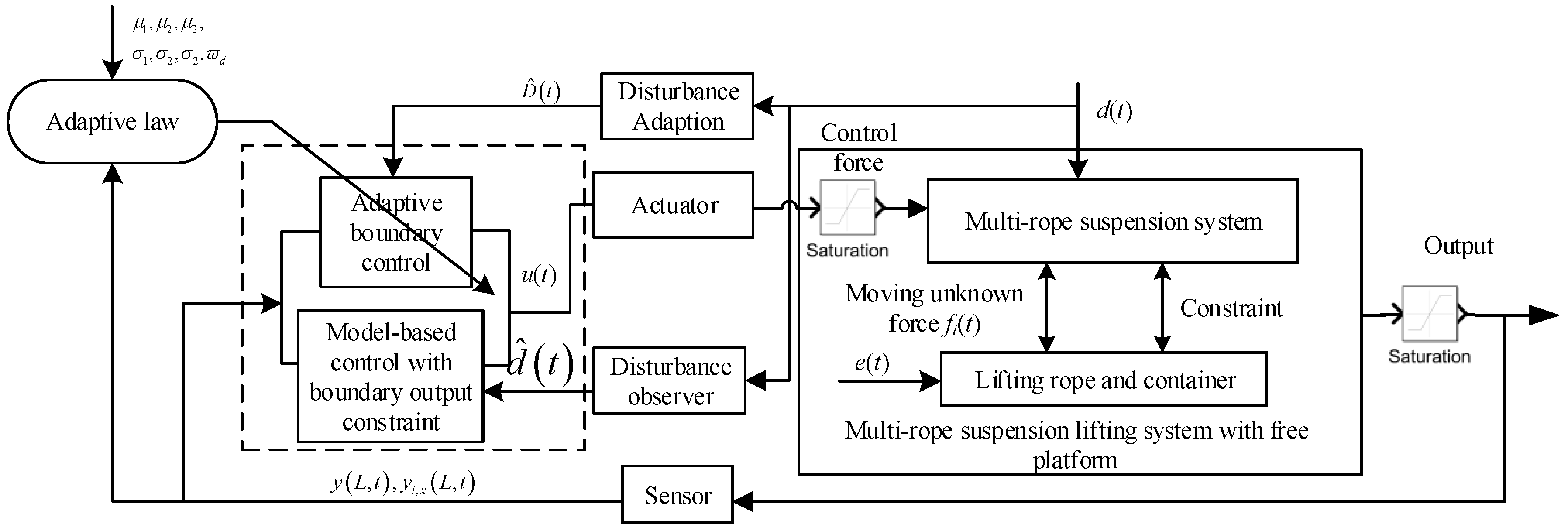
3. Control Design and Analysis
3.1. Model-Based Boundary Control
3.2. Robust Adaptive Boundary Control
4. ADAMS Simulation and Numerical Calculation
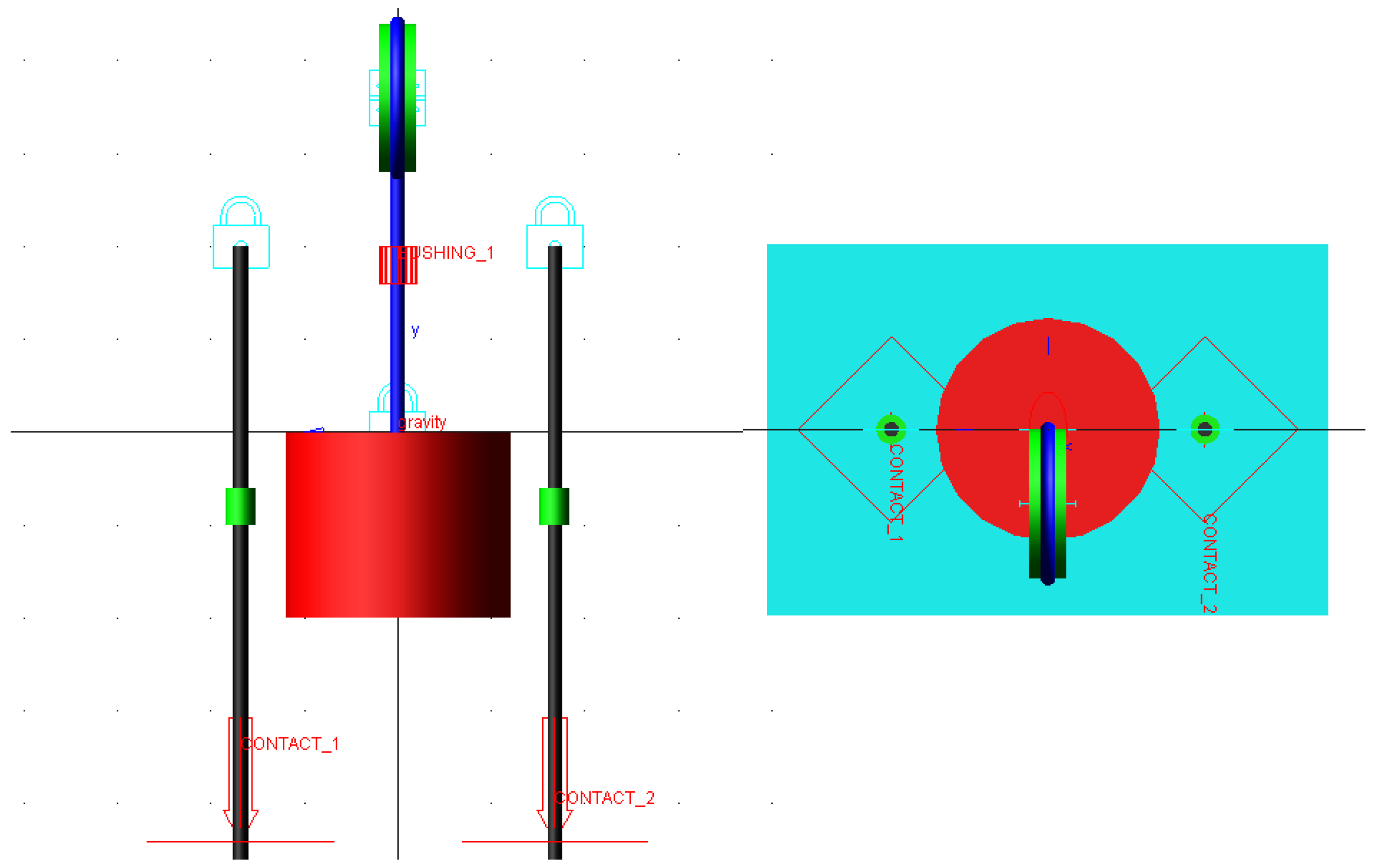
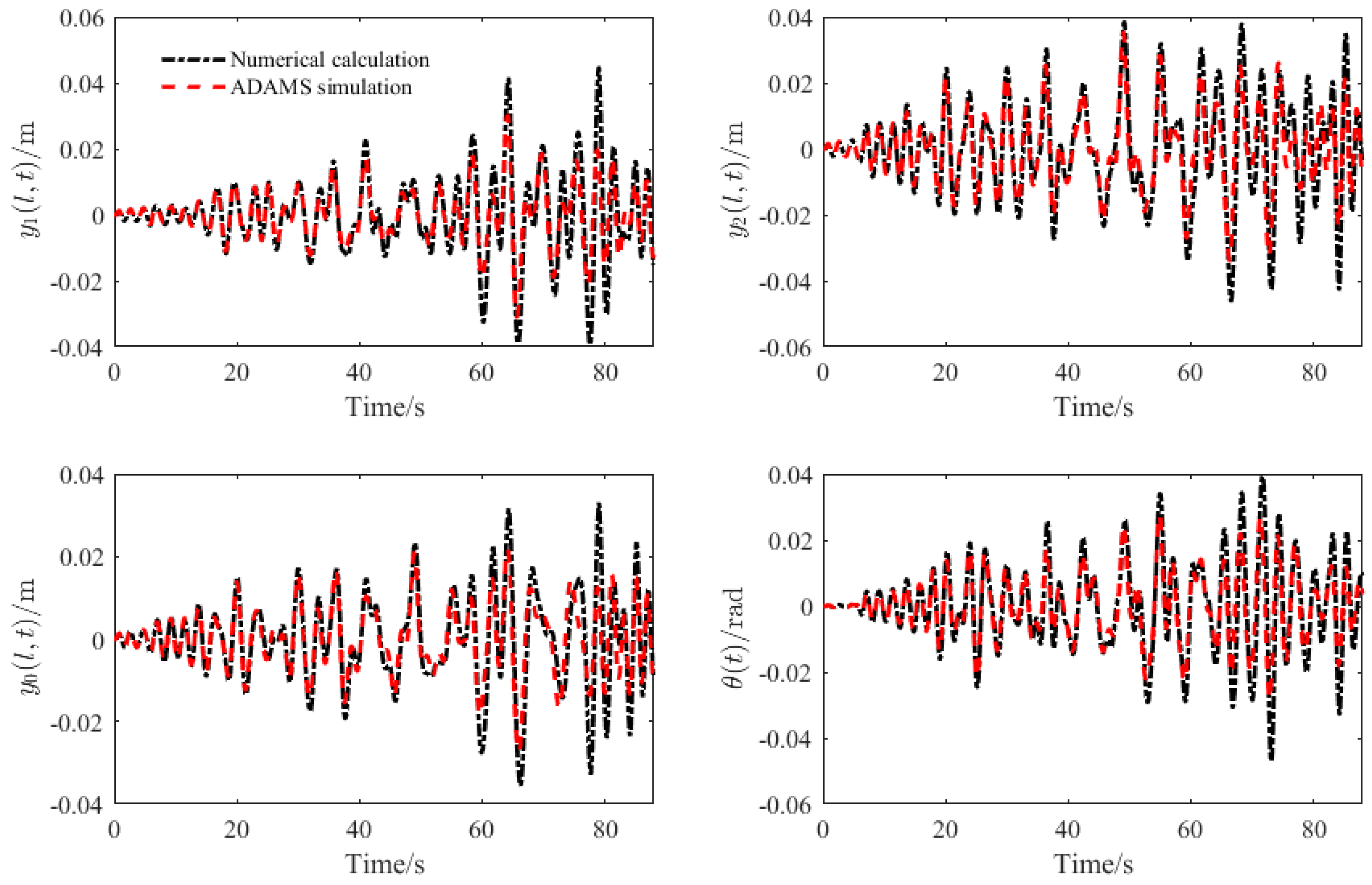
4.1. ADAMS Simulation
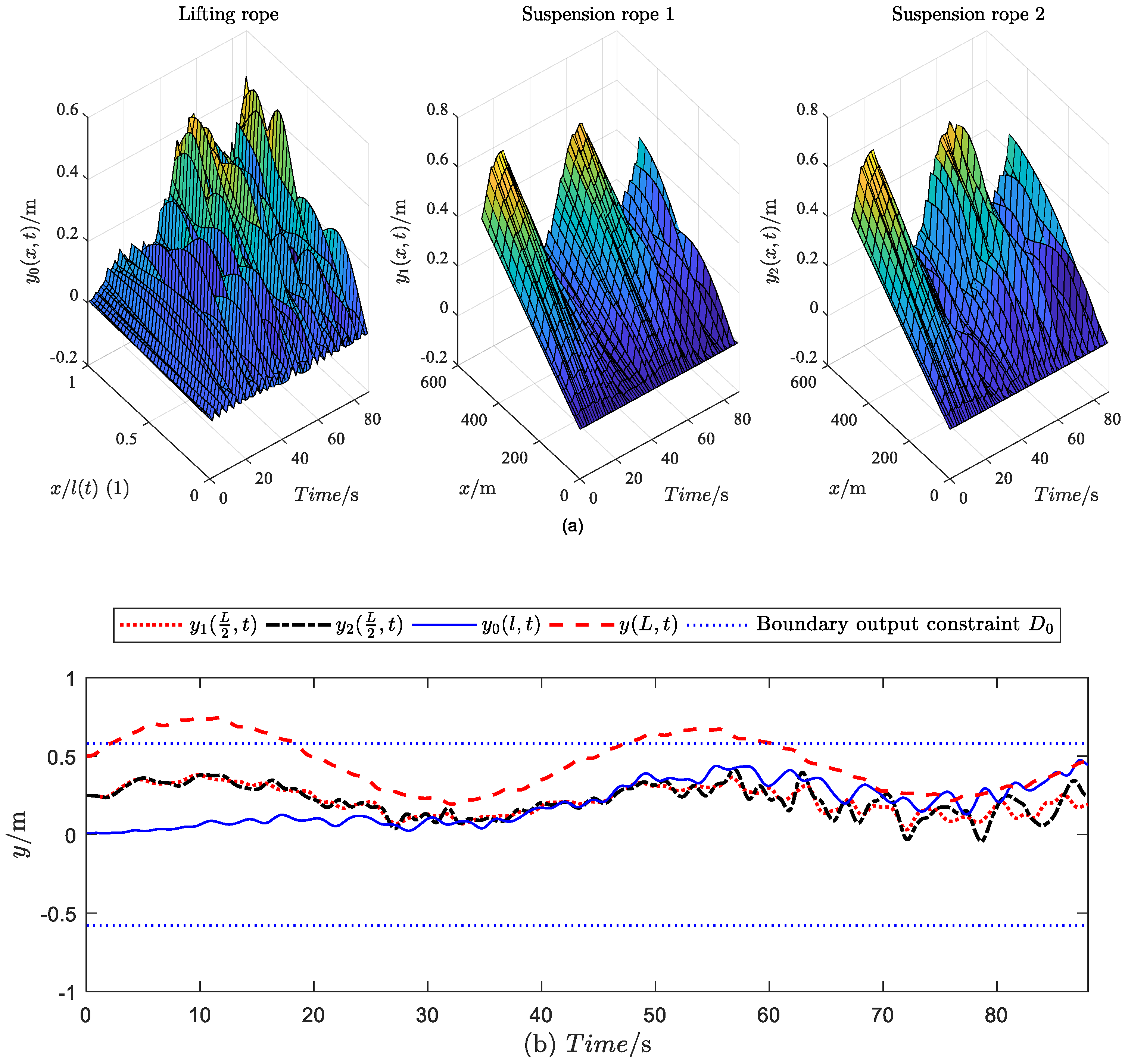
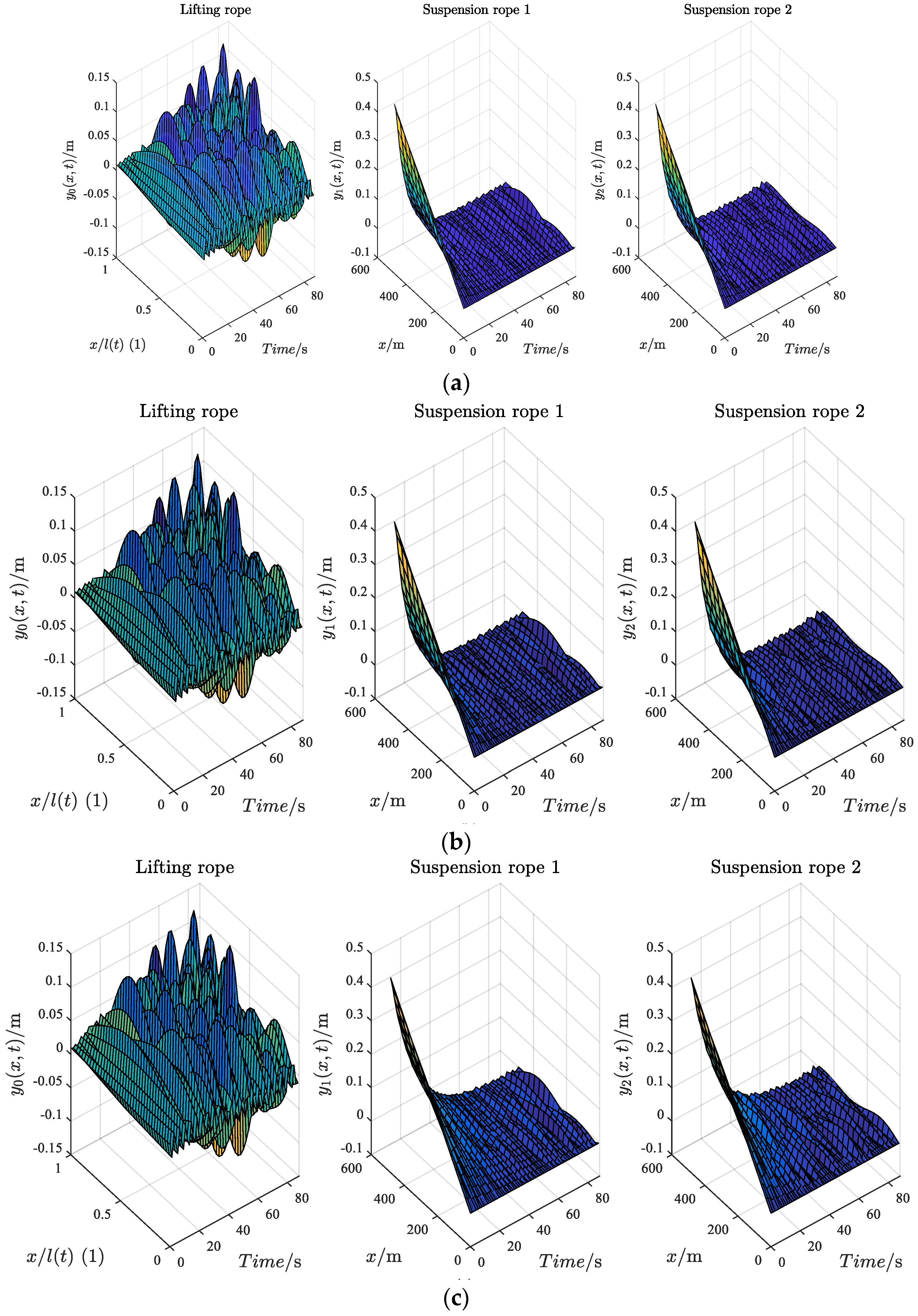
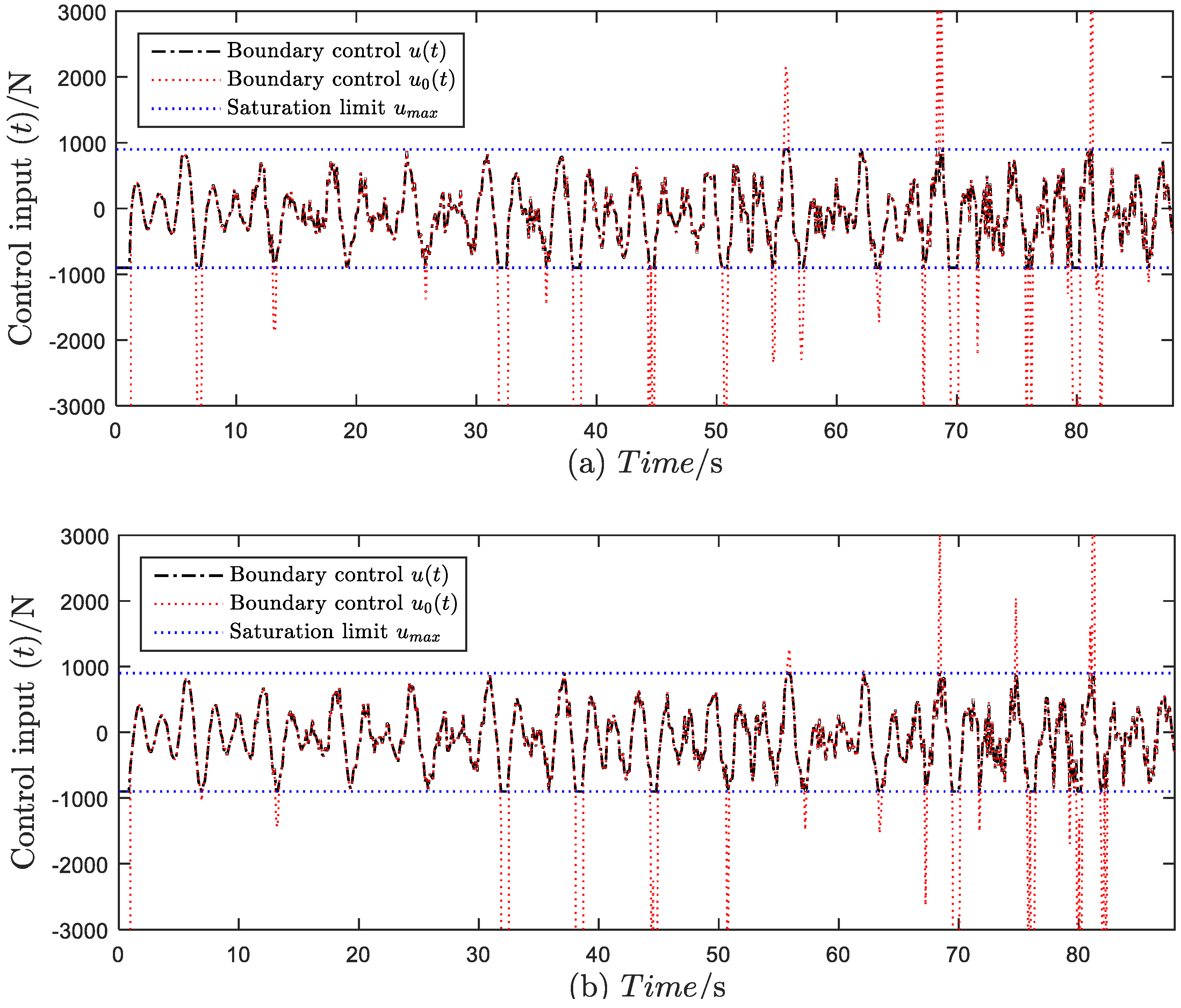
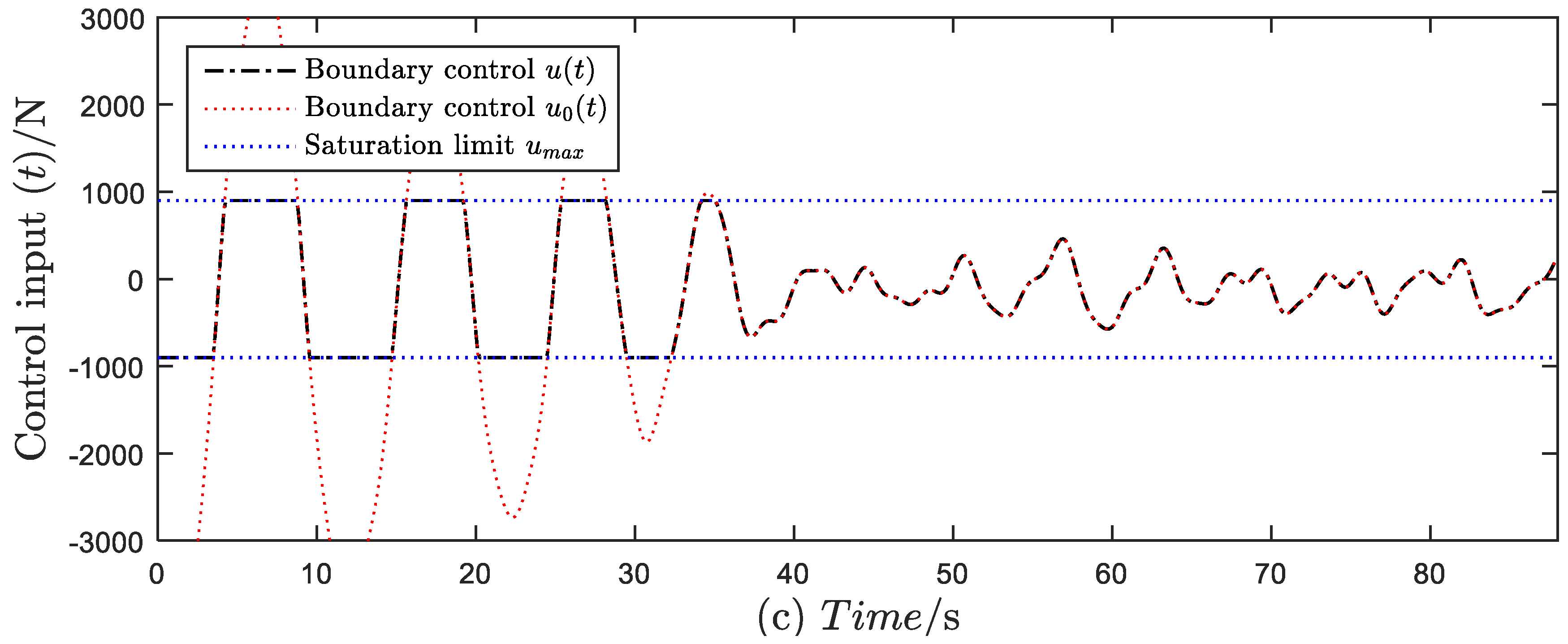
4.2. Different Cases
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Transverse displacement | |
| Arbitrary axial acceleration | |
| Arbitrary axial velocity | |
| The length of the lifting rope | |
| Total length of the suspension rope | |
| Inertia of the lifting container | |
| Mass of the lifting container | |
| Tension of suspension rope | |
| The gravitational acceleration | |
| Kinetic energy | |
| Virtual work | |
| Potential energy | |
| Unknown boundary disturbance | |
| Control command | |
| The saturation limit | |
| Line density of the lifting rope | |
| Line density of the suspension rope | |
| Geometric length | |
| Transverse boundary disturbance | |
| Rotation of the lifting container | |
| Time variable | |
| Space variable | |
| Tension in lifting rope | |
| The bottom tension of the suspension rope | |
| , | The damping coefficient |
| The viscous damping of the sinking platform | |
| Dirac delta generalized function | |
| Unknown moving force | |
| The control input | |
| Signum function |
Appendix A
Appendix B
Appendix C
Appendix D
References
- Michael, N.; Fink, J.; Kumar, V. Cooperative manipulation and transportation with aerial robots. Auton. Robot. 2011, 30, 73–86. [Google Scholar] [CrossRef]
- Mao, Y.; Jin, X.; Gera Dutta, G.; Scholz, J.P.; Agrawal, S.K. Human movement training with a cable Driven ARm EXoskeleton (CAREX). IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Andréa-Novel, B.D.; Coron, J.M. Exponential stabilization of an overhead crane with flexible cable via a back-stepping approach. Automatica 2000, 36, 587–593. [Google Scholar] [CrossRef]
- Elbadawy, A.A.; Shehata, M.M.G. Anti-sway control of marine cranes under the disturbance of a parallel manipulator. Nonlinear Dyn. 2015, 82, 1–20. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Boundary control of three-dimensional inextensible marine risers. J. Sound Vib. 2009, 327, 299–321. [Google Scholar] [CrossRef]
- Fung, R.F.; Liao, C.C. Application of variable structure control in the nonlinear string system. Int. J. Mech. Sci. 1995, 37, 985–993. [Google Scholar] [CrossRef]
- Pi, Y.; Ouyang, H. Vibration control of beams subjected to a moving mass using a successively combined control method. Appl. Math. Model. 2016, 40, 4002–4015. [Google Scholar] [CrossRef]
- He, W.; Yan, Z.; Sun, C.; Chenm, Y. Adaptive neural network control of a flapping wing micro aerial vehicle with disturbance observer. IEEE Trans. Cybern. 2017, 47, 3452–3465. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Huang, H.; Ge, S.S. Adaptive neural network control of a robotic manipulator with time-varying output constraints. IEEE Trans. Cybern. 2017, 47, 3136–3147. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z. Robust and adaptive boundary control of a stretched string on a moving transporter. IEEE Trans Automat. Control 2001, 46, 470–476. [Google Scholar]
- Baz, A. Dynamic boundary control of beams using active constrained layer damping. Mech. Syst. Signal. Process. 1997, 11, 811–825. [Google Scholar] [CrossRef]
- Meirovitch, L.; Kwak, M. convergence of the classical rayleigh-ritz method and the finite element method. AIAA J. 1990, 28, 1509–1516. [Google Scholar] [CrossRef]
- Balas, M.J. Active control of flexible systems. J. Optim. Theor. Appl. 1978, 25, 415–436. [Google Scholar] [CrossRef]
- He, W.; Ge, S.S. Robust adaptive boundary control of a vibrating string under unknown time-varying disturbance. IEEE Trans. Control Syst. Technol. 2011, 20, 48–58. [Google Scholar] [CrossRef]
- How, B.V.E.; Ge, S.S.; Choo, Y.S. Active control of flexible marine risers. J. Sound Vib. 2009, 320, 758–776. [Google Scholar] [CrossRef]
- Yang, K.; Hong, K.; Matsuno, F. Robust adaptive boundary control of an axially moving string under a spatiotemporally varying tension. J. Sound Vib. 2004, 273, 1007–1029. [Google Scholar] [CrossRef]
- Guo, B.; Jin, F. The active disturbance rejection and sliding mode control approach to the stabilization of the Euler-Bernoulli beam equation with boundary input disturbance. Automatica 2013, 49, 2911–2918. [Google Scholar] [CrossRef]
- Azinheira, J.R.; Moutinho, A. Hover control of an UAV with backstepping design including input saturations. IEEE Trans. Control Syst. Technol. 2008, 16, 517–526. [Google Scholar] [CrossRef]
- Zhong, Y.S. Globally stable adaptive system design for minimum phase SISO plants with input saturation. Automatica 2005, 41, 1539–1547. [Google Scholar] [CrossRef]
- Zhang, T.P.; Ge, S.S. Adaptive dynamic surface control of nonlinear systems with unknown dead zone in pure feedback form. Automatica 2008, 44, 1895–1903. [Google Scholar] [CrossRef]
- Tee, K.P.; Ren, B.; Ge, S.S. Control of nonlinear systems with time-varying output constraints. Automatica 2011, 47, 2511–2516. [Google Scholar] [CrossRef]
- He, W.; Ma, T. Adaptive neural network control of a vessel with output constraints using the asymmetric barrier lyapunov function. IFAC Proc. Vol. 2013, 46, 246–251. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; He, W. Vibration control of a flexible aerial refuelling hose with input saturation. Int. J. Syst. Sci. 2017, 48, 971–983. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C. Adaptive Backstepping Control of Uncertain Systems Nonsmooth Nonlinearities, Interactions or Time-Variations; Springer: Berlin, Germany, 2008; ISBN 3540778063. [Google Scholar]
- He, W.; Yan, Z.; Sun, Y.; Ou, Y.; Sun, C. Neural-learning-based control for a constrained robotic manipulator with flexible joints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 1–11. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Dong, Y. Adaptive fuzzy neural network control for a constrained robot using impedance learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1174–1186. [Google Scholar] [CrossRef] [PubMed]
- He, W.; He, X.; Ge, S.S. Modeling and vibration control of a coupled vessel-mooring-riser system. IEEE/ASME Trans. Mechatron. 2015, 20, 2832–2840. [Google Scholar] [CrossRef]
- He, W.; Zhang, S.; Ge, S.S. Robust adaptive control of a thruster assisted position mooring system. Automatica 2014, 50, 1843–1851. [Google Scholar] [CrossRef]
- Cai, X.; Krstic, M. Nonlinear stabilization through wave PDE dynamics with a moving uncontrolled boundary. Automatica 2016, 68, 27–38. [Google Scholar] [CrossRef]
- Krstic, M. Boundary Control. of PDEs: A Course on Backstepping Designs; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008; ISBN 9780898716504. [Google Scholar]
- Rahn, C.D. Mechatronic Control of Distributed Noise and Vibration; Springer: Berlin/Heidelberg, Germany, 2001; ISBN 978-3-642-07536-0. [Google Scholar]
- Queiroz, M.S.D.; Dawson, D.M.; Nagarkatti, S.P.; Zhang, F. Lyapunov-Based Control. of Mechanical Systems; Birkhäuser: Boston, NY, USA, 2000; ISBN 978-1-4612-7108-6. [Google Scholar]
- Yang, K.J.; Hong, K.S.; Matsuno, F. Energy-based control of axially translating beams: Varying tension, varying speed, and disturbance adaptation. IEEE Trans. Control Syst. Technol. 2005, 13, 1045–1054. [Google Scholar] [CrossRef]
- Yang, K.; Hong, K.; Matsuno, F. Robust adaptive control of a cantilevered flexible structure with spatiotemporally varying coefficients and bounded disturbance. JSME Int J. Ser. C 2005, 47, 812–822. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice-Hall: Saddle River, NJ, USA, 1996; ISBN 0134391004. [Google Scholar]
- Yang, D.-H.; Kim, K.-Y.; Kwak, M.K.; Lee, S. Dynamic modeling and experiments on the coupled vibrations of building and elevator ropes. J. Sound Vib. 2017, 390, 164–191. [Google Scholar] [CrossRef]


| Parameter | Description | Value |
|---|---|---|
| Total length of the suspension rope | 500 m | |
| Initial length of lifting rope | 10 m | |
| Mass of the lifting container | 500 kg | |
| Mass of the sinking platform | 10 t | |
| Inertia of the lifting container | 70 kg m2 | |
| Mass per unit length of the rope | 2 kg/m, 1.5 kg/m | |
| Maximum acceleration of the lifting rope | 0.75 m/s2 | |
| Maximum velocity of the lifting rope | 6 m/s | |
| Total duration time | 88 s | |
| Damping coefficient | ||
| Geometrical distance | 0.54 m, 0.66 m | |
| Constrained positive constant | 0.58 m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Cao, G.; Yan, L.; Wang, L. Modeling and Control for a Multi-Rope Parallel Suspension Lifting System under Spatial Distributed Tensions and Multiple Constraints. Symmetry 2018, 10, 412. https://doi.org/10.3390/sym10090412
Wang N, Cao G, Yan L, Wang L. Modeling and Control for a Multi-Rope Parallel Suspension Lifting System under Spatial Distributed Tensions and Multiple Constraints. Symmetry. 2018; 10(9):412. https://doi.org/10.3390/sym10090412
Chicago/Turabian StyleWang, Naige, Guohua Cao, Lu Yan, and Lei Wang. 2018. "Modeling and Control for a Multi-Rope Parallel Suspension Lifting System under Spatial Distributed Tensions and Multiple Constraints" Symmetry 10, no. 9: 412. https://doi.org/10.3390/sym10090412
APA StyleWang, N., Cao, G., Yan, L., & Wang, L. (2018). Modeling and Control for a Multi-Rope Parallel Suspension Lifting System under Spatial Distributed Tensions and Multiple Constraints. Symmetry, 10(9), 412. https://doi.org/10.3390/sym10090412





