1. Introduction
The discovery of the structure of DNA [
1] and the decipherment of the Standard Genetic Code (SGC) [
2,
3] are landmarks of scientific achievements. The elucidation of the origin and evolution of the SGC is a central problem in evolutionary biology. The SGC is nearly universal, with some minor exceptions. Crick proposed the frozen accident hypothesis to account for the universality of the SGC [
4]. The universality of the SGC immediately implied a Last Universal Common Ancestor (LUCA). Therefore, evolution has to do with preserving or fixing some necessary properties of life. Given the astonishing diversity of life in the history of the biosphere, the fact that the SGC is frozen indicates that all organisms are phylogenetically related.
Attempts at thawing the origin and evolution of the frozen SGC have been numerous. Symmetries in the SGC have been analyzed by examining the transfer RNA (tRNA) [
5,
6], the aminoacyl-tRNA-synthetases (aaRSs) [
7,
8,
9,
10], and mathematical models searching hidden symmetries [
11,
12]. The hypercube algebraic representation has allowed the analysis of the evolution of the SGC and a variety of its biological properties. The SGC, as derived from the primeval genetic code [
5], and the Rodin–Ohno model [
9] are one and the same, that is, these seemingly different models of the genetic code are mathematically equivalent [
13]. Hence, the 6D algebraic model unifies different models of the genetic code [
13].
The genetic code is a dictionary composed of words three letters long, known as codons or triplets, each letter a nucleotide base. There are four basic nucleotides in the DNA, to wit, adenine (A), cytosine (C), guanine (G), and thymine (T). During the translation process of the DNA, thymine nucleotides are replaced by uracil (U) in the RNA. This constitutes a set of 64 possible codons, which codify for 20 canonical amino acids and a stop signal. The genetic code is degenerated, as more than one codon can codify for a given amino acid. This degeneracy property usually occurs in the third base of a codon and is known as the wobble property [
14,
15,
16].
The nucleotide bases can be divided according to their chemical properties into: strong S = {G, S} and weak W = {U, A}; amino nucleotides M = {C, A}, keto nucleotides K = {U, G}, and nucleotide bases of the same chemical kind: pyrimidines Y= {C, U} and purines R = {A, G} [
17].
Diverse genetic codes occur in a cell, for example, the SGC, the genetic code of mitochondria, the genetic code of chloroplasts, the anticodon code of tRNAs, ribosomal codes.
The mitochondrion is the major energy provider of the Eukaryotic cell [
18]. Mitochondria produces ATP by oxidizing the major products of glucose: pyruvate, and NADH [
18]. This type of cellular respiration known as aerobic respiration, is dependent on the presence of oxygen. When oxygen is scarce, the glycolytic products will be metabolized by anaerobic fermentation, a process that is independent of the mitochondria [
18]. Mitochondria also contribute to many physiological processes, such as calcium homeostasis, apoptosis, lipid and amino acid metabolism [
19,
20,
21].
The different genetic codes that have been encountered so far (e.g., mitochondrial,
Euplotes, some ciliate protozoans,
Tetrahymena) are considered to have evolved from the SGC [
22]. Most of the noncanonical codes arise from alterations in the transfer RNA (tRNA) by post-transcriptional modifications, such as base modification or RNA editing, rather than by substitutions within tRNA anticodons. Typically, variations occur in the unicoded amino acids (Met and Trp) and in the stop codons UAG (amber), UGA (opal), and UAA (ochre). However, the freezing of the code is supported by the fact that the 20 natural amino acids have been stringently selected over the course of the evolution (with the notable exception of selenocysteine and pyrrolysine [
23]). Then, the SGC can evolve but at a glacial rate.
To examine the symmetries of the SGC, it is necessary to unleash it from the traditional 2D representation of the Table of the Genetic Code [
4].
The SGC exhibits an exact symmetry under a Galois Field of 4 elements, also known as the Klein Four-Group (an Abelian (commutative) group of order 4 where each element is its own inverse) [
24]. The Klein Four-Group emerges from the primeval RNY code that evolved until the formation of the SGC. This symmetry has been selected since the origin and during the evolution of the genetic code. The SGC has been derived by assuming a primeval genetic code, RNY [
25]. This primeval RNY code was composed of 16 codons that codify for 8 amino acids (slight degeneration) and was proposed by Eigen 40 years ago [
25]. Two evolutionary paths have been established to reach the SGC from the RNY code [
17,
26]. These paths consist in permitting frame-shift reading-mistranslations or transversions in the first and third base of the codons. The SGC has been modeled as a six-dimensional (6D) binary hypercube
, where
is the binary field of 2 elements, also known as
GF(2) the Galois Field of 2 elements. The binary hypercube is a 2
6—Klein Group [
27]. In the 6D hypercube, the vertices are indexed by the codons [
13,
26]. The hypercube of codons has been further transformed into its phenotypic graph representation [
13,
28,
29,
30], where the new vertices are the amino acids and the stop signal.
One goal of the present work is to determine if these symmetries were selected since the origin of the primeval code and preserved during its evolution until the formation of the SGC. In this work, the hypothesis that the symmetry groups must allow us to predict the possible symmetry breaking groups to determine the evolvability of the SGC is put forward. To this end, we examine how the SGC has led to new genetic codes by determining their symmetries. We analyze the symmetries of the graphs of codons and their respective phenotypic graph representation spanned by the RNY code, the two RNA Extended codes, and the complete code of 64 codons that comprises the SGC, as well as three different mitochondrial genetic codes from yeast, invertebrates, and vertebrates. In general, the SGC has evolved into more symmetrical mitochondrial codes.
2. Material and Methods
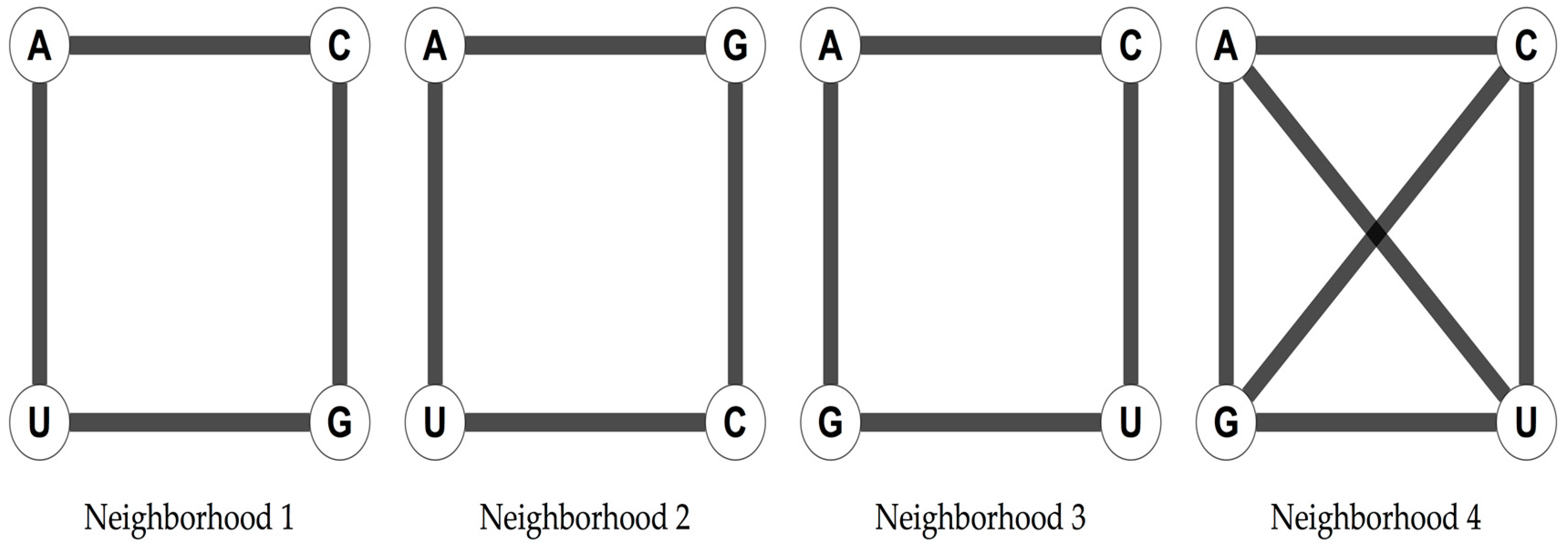
The four nucleotides of the RNA alphabet, A, U, C, and G, can be arranged in three different ways as the vertices of a square that are not symmetrically equivalent, and in one extra way considering the two diagonals of the square (
Figure 1).
The arrangement in a square has been shown to yield a 6D hypercube when considering the 64 possible triplets [
13,
26]. The genetic code is then represented as a 6D hypercube, which can be interpreted as a graph of vertices, representing the codons, and edges, joining the codons at distance one, making it possible to analyse its symmetries through the group of automorphisms of the graph [
13]. This group consists of all the bijective functions of the graph
G, that preserve its adjacencies. These automorphisms comprise all the isometric transformations of the cube. The 6D hypercube arises when the triplets are used as vertices of a graph. Two vertices, or triplets, will be joined by an edge if they differ by one letter, and the different letters are joined in the given nucleotide neighborhood type. The resulting graph is isomorphic to a 6D hypercube [
13,
26]. This high-dimensional cubic graph of the 64 triplets is a natural extension of the nucleotides arranged in a square. A codon graph is a graph in which the vertices represent codons and are joined according to a nucleotide neighborhood type. Codon graphs can be constructed for any subset of the 64 possible triplets. The RNY code has been modeled as a 4D hypercube [
26,
29,
30]. Two genetic codes from which the primeval RNA code [
25] could have originated the SGC have been derived [
26]. Given the RNY code, the necessary transformations that are needed to obtain the SGC are simple algebraic operations: rotations (for the Extended RNA code type I) and translations (for the Extended RNA code type II) in the vector space
GF(4) in 3 dimensions [
26].
The Extended RNA code type I consists of RNY, NYR and YRN codons. The extended RNA code type II comprises all codons of the type RNY, YNY and RNR [
26]. Then, by performing frame-reading mistranslations (Extended code I), 48 codons that specify 17 amino acids and the three stop codons are obtained. If transversions in the 1st or 3rd nucleotide bases of the RNY pattern are permitted, then there are also 48 codons that encode for 18 amino acids without stop codons (Extended code II). The codons in each of the subsets of both Extended RNA codes were represented by 4D symmetrical hypercubes [
26], whose union comprised precisely the already-known 6D hypercube of the SGC of 64 triplets [
31]. Evolutionary analysis of SGC based upon 3D algebraic models, dubbed Genetic Hotels, leads more clearly to the same conclusions [
32]. The composition of both evolutionary paths yields to the complete set of 64 codons of the SGC. Mitochondrial codes present variations principally in the codons for the stop signals and unicoded amino acids. The mitochondrial genetic codes of yeast, invertebrates, and vertebrates are shown in
Table 1. They were downloaded from:
https://www.ncbi.nlm.nih.gov/Taxonomy/Utils/wprintgc.cgi?chapter=tgencodes#SG24 (accessed on July 31 2018).
Note that in the mitochondrial genetic codes (
Table 1) every amino acid has a set of coding triplets with an even number of elements. Note that Ile is tricodonic in SGC but it is dicodonic in all mitochondrial codes; Leu is tetracodonic in all codes except in yeast’s mitochondria, which is dicodonic; Trp is unicoded only in SGC whilst it is tricodonic in all mitochondrial codes. Met is unicoded in SGC, but it is dicodonic in all mitochondrial codes. Ser is hexacodonic in SGC, vertebrate, and yeast mitochondria, but octacodonic in invertebrate mitochondria. The stop codons are tricodonic in SGC, tetracodonic in vertebrate mitochondria, and dicodonic in invertebrate and yeast mitochondria.
Genetic codes induce a natural partition of the codons and determine an equivalence relation. In this equivalence relation, two codons are considered equivalent if they codify for the same amino acid or stop signal. A graph and an equivalence relation can be combined to construct a quotient graph [
33]. The set of vertices of the quotient graph are the equivalent classes, and two vertices of the quotient graph are joined if there are elements of the equivalence classes that are joined in the original graph. The quotient graph derived from the codon graphs and a genetic code are known as phenotypic graphs [
27,
28,
29,
30]. The phenotypic graph represents the phenotypic expression of the codon hypercube; the vertices represent the 20 amino acids and the stop signal [
22].
The symmetries of the codon graphs of the RNY code, the extended codes, and the complete codes are analyzed for the four neighborhood types of the nucleotides. A description of the codon graphs is provided (
Table 2). Labeling the vertices by the codons, the symmetries are analyzed by determining the automorphisms that keep invariant all the sets of equivalence classes for each of the genetic codes. The phenotypic graphs are constructed for the four genetic codes, in each of the evolutionary steps for the SGC and for the complete code for the mitochondrial codes. Loops in the phenotypic graphs are considered if there is a pair of elements in an equivalence class that are adjacent in the codon graph. The automorphisms group of the phenotypic graphs is determined for the four genetic codes in the four neighborhood types of nucleotides.
3. Results
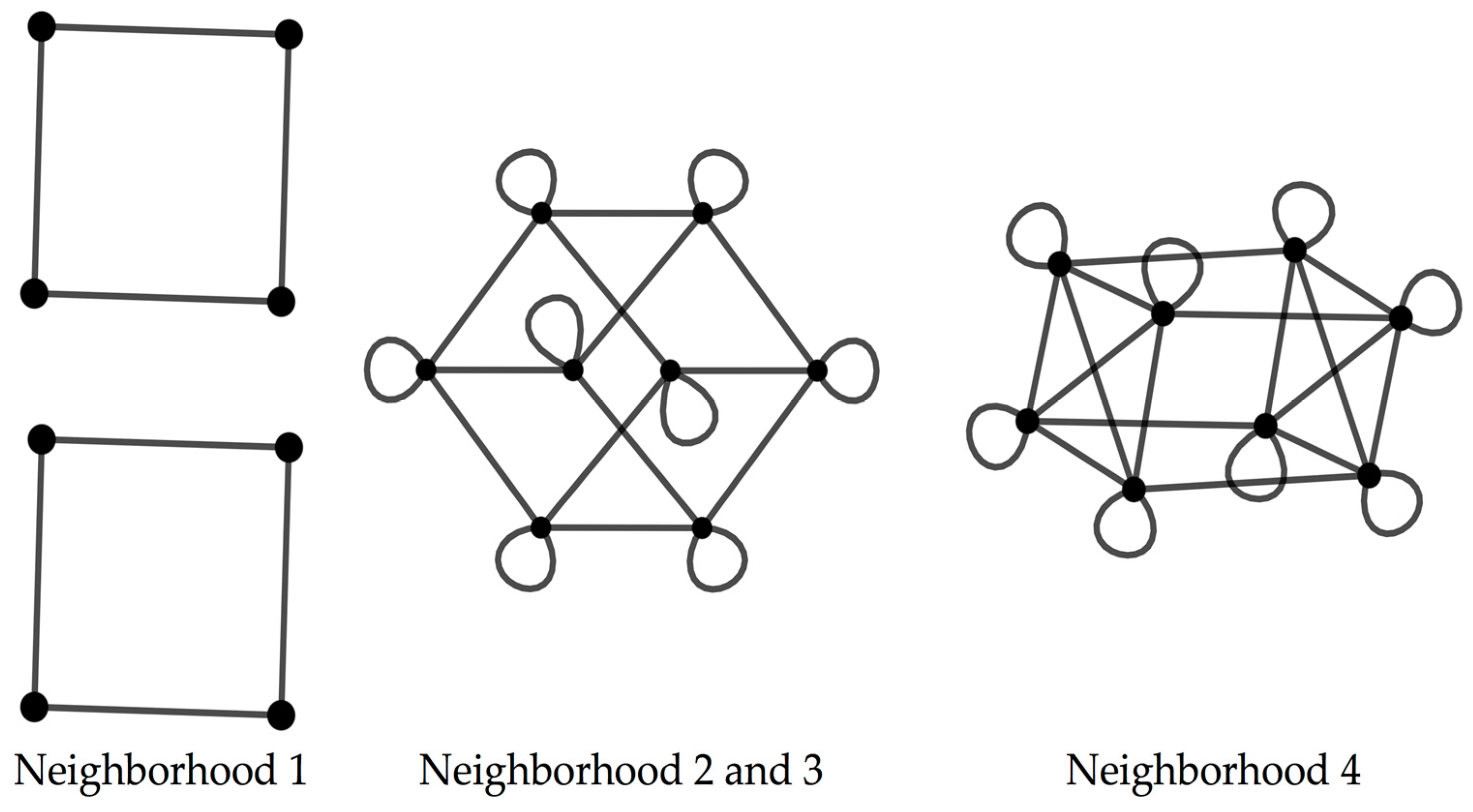
The codon graphs constructed for the RNY for the four nucleotide neighborhood types result in three different graphs (
Figure 2).
When considering the codon graphs with the vertices unlabeled, the neighborhood type 1 yields a graph composed by four disjoint squares; the neighborhood types 2 and 3 result in a graph isomorphic to a 4D hypercube; the neighborhood type 4 produces a 4D hypercube with four marked diagonals, where this graph is isomorphic to the graph resulting from the Cartesian product [
34], denoted by □ of the graphs
K4 and
C4, where
Kn is the complete graph of n vertices and
Cn is the cyclic graph of n vertices (
Table 2).
For the Extended code 1, the codon graph resulting from the neighborhoods type 2 and type 3 is isomorphic to the Cartesian product of the graphs
C6 and
Q3 where
Qn is the hypercube of dimension n (
Table 2). The adjacency matrices for the codon graphs of the Extended code 1 based on the nucleotide neighborhoods type 1 and type 4 are provided in
Supplementary Materials I. For the Extended code 2, the codon graph from the nucleotide neighborhoods type 2 and type 3 are isomorphic to the Cartesian product of the graphs
Q4 and
P3 where
Pn is the path graph of n vertices (
Table 2). The adjacency matrices for the codon graphs of the Extended code 2 based on the nucleotide neighborhoods type 1 and type 4 are provided in
Supplementary I.
With the vertices of the codon graphs labeled with the corresponding set of codons, these labeled codon graphs are analyzed for the four genetic codes. As these genetic codes are different, the automorphisms group that keeps invariant all the equivalent classes for each genetic code is also different. The RNY code is the same in the SGC and the three mitochondrial codes analyzed. The corresponding automorphisms group for the four nucleotide neighborhood types are
for the neighborhood type 1, and
for the rest of the nucleotide neighborhood types (
Table 3).
For the Extended codes in the SGC, the nucleotide neighborhoods type 2 and type 3 possess no symmetries, as the automorphisms group is the trivial one. For the neighborhood type 1, the automorphisms groups for the Extended codes 1 and 2 are
and
, respectively. Considering the nucleotide neighborhood type 4, the automorphisms groups for both extended codes are
(
Table 3). The three mitochondrial codes exhibit the same automorphisms groups in the codon graphs for the Extended codes (
Table 3). For the complete code, the codon graph for the SGC only possesses a symmetry given by the group
in the nucleotide neighborhoods type 1 and type 4. In the three mitochondrial codes, the codon graphs for the complete code present as automorphisms group, the group
for the neighborhoods type 1 and type 4; the group
is the symmetry group for the neighborhoods type 2 and type 3 (
Table 3). The codon graphs for the three mitochondrial codes not only share the same amino-acid-preserving symmetries, but the elements of these groups are the same. This result shows that the codons that the three mitochondrial codes have in common, which are different from the SGC, are the source of symmetry. Specifically, the swap of the codon AUA from Ile to Met increases the symmetries of the mitochondrial codes. This codon is neighbor to the Met codon AUG in the nucleotide neighborhood types 2, 3, and 4. The codons AUA and AUG are present in both Extended codes, hence, the codon graphs for mitochondrial codes are more symmetric than the SGC. A detailed description of the automorphisms groups in permutation representation is provided in
Supplementary II.
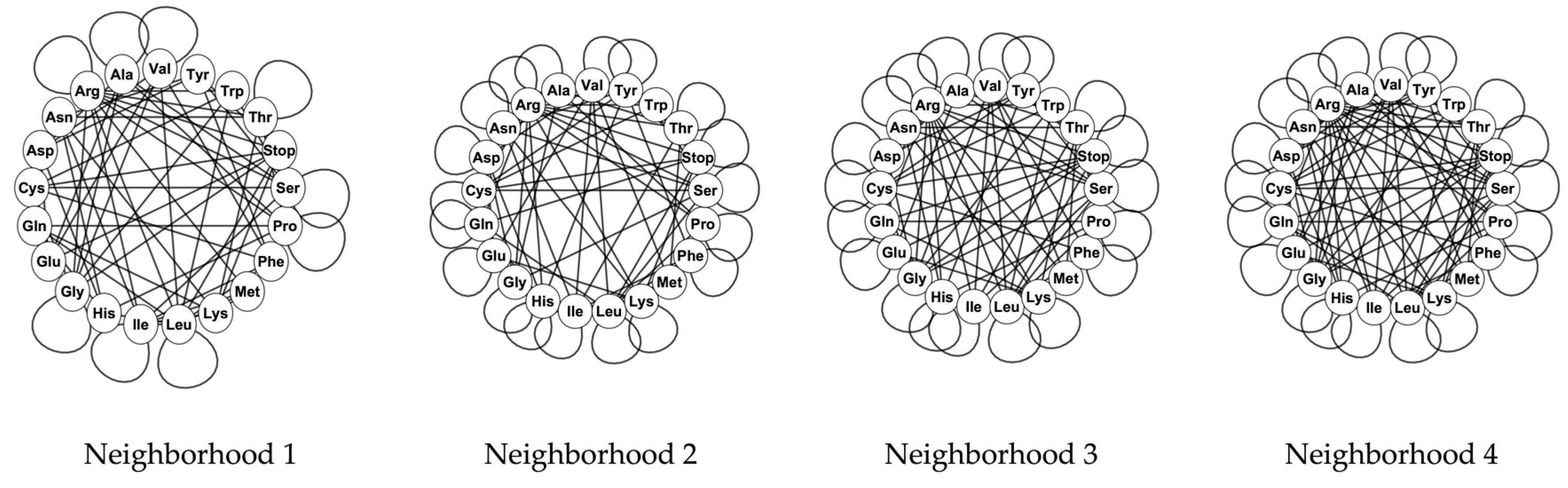
The phenotypic graphs were constructed for all the nucleotide neighborhood types, at the four evolutionary stages and for the four genetic codes analyzed. The phenotypic graphs for the RNY code present nontrivial automorphisms groups. For the nucleotide neighborhood type 1, the automorphisms group is given by D4 × D4 × S2 where Dn is the dihedral group of a regular n-gon and Sn is defined as the symmetric group of n elements; for the rest of the nucleotide neighborhood types, the automorphisms group is the octahedral group Oh.
For the rest of the evolutionary stages and genetic codes, only the phenotypic graph of the complete code for the invertebrate mitochondrial code, based on the nucleotide neighborhood type 3, has as automorphisms group, the group
, whereas the rest of the phenotypic graphs hold no symmetries. The reflection on the phenotypic graph for the complete invertebrate mitochondrial code on the nucleotide neighborhood type 3 is given by the permutation that interchanges the amino acids of Ile and Met. Note that the codons of these two amino acids generate the symmetries of the codon graphs for the mitochondrial codes. Phenotypic graphs for the SGC for the four nucleotide neighborhood types are shown in
Figure 3 4. Discussion
In this work, we analyzed the symmetric structure of different genetic codes with graph theory. With codon graphs and phenotypic graphs, we analyzed both sides of a genetic code, the genotype and its phenotype. Our method is a novel approach to analyse any genetic code, even synthetic ones.
The codon graphs allow us to analyze the structure and evolution of the genetic code through its evolutionary stages. Each nucleotide neighborhood type spans a different graph in each evolutionary step of a genetic code, both for codons and amino acids. The automorphisms group of the codon graphs that keep invariant the sets of codons for all the amino acids reflects the symmetric assignation of the codons to the phenotype. The degeneracy of the genetic code, given by the wobble property, coupled with the codonicity of each amino acid, produce the symmetric assignations of codons to amino acids. The symmetries of the phenotypic graphs, given by their automorphisms group, determine codon swaps that maintain the distribution of amino acids in a genetic code. These codon swaps are codon reassignations that interchange the codification of whole sets of codons for given amino acids. The reassignation of the codon AUA to Met in the analyzed mitochondrial codes emerges as the source of the symmetry of the mitochondrial codes. The stop codons of vertebrate mitochondria are different from the stop codons in invertebrate and yeast mitochondria. Yet these differences do not explain the increase of symmetry in mitochondrial codes. We remark that despite differences among mitochondrial codes, they display the same type of symmetry. Despite that mitochondrial codes are different among them and different from the SGC, they display at least the symmetries observed in the SGC. Even more, they show a more symmetrical structure than the SGC and at the same time they conserve the basic symmetrical structure of the SGC. Indeed, we proved that mitochondrial codes are more symmetrical than the SGC. Then, the Four-Klein group can be found in all codes, and interestingly, we also found the group in the mitochondrial codes analyzed, notwithstanding the differences among them. We point out that the origin of the increase in symmetry is due to changes in the unicoded amino acids but not in the stop codons or in the octacodonic amino acids. Our work does not allow us to discern if the mitochondrial code is the result of evolutionary progress or because of retrogression. What we can safely say is that changes in the mitochondrial code are restricted to certain codons and not all changes seem to be allowed.
Evolving codes tend to freeze into structures like that of the standard code and having similar levels of robustness. Departures involve only a few codons, so that the structure of the code has remained almost frozen at least since the time of LUCA of all modern (cellular) life forms. These changes were adaptations that kept anticodon sequences fixed to have a universal code and facilitated the diversification of living organisms. This universality of the genetic code and the manifest non-randomness are inherent features of the evolving codes. The life forms that probably obeyed the Extended RNA code types I and II were progenotes intermediate between the ribo-organisms of the RNA World and LUCA. They pertained to the Ribonucleoprotein World. Therefore, genomes are systems that are constantly under a critical state and they may show universal properties of scale invariance [
35].
The 6D hypercube has been used to analyze different biological properties of the SGC. Woese’s [
36] polar requirement property broadly distinguishes the amino acids into four categories. The polar requirement is a physico-chemical property of the amino acids and is directly associated to the organization of the SGC [
37]. Polar requirement is related to the division of amino acids in a polar–nonpolar interface [
38]. The relation between the assignations in the SGC and the polar requirements is reflected in the symmetrical pattern that arises when the polar requirement categories are used to color the codon graphs of the SGC [
13]. Genetic codes are implemented via tRNA molecules and their anticodons. These molecules bind the codons in mRNA to their corresponding anticodons, then link the appropriate amino acids as determined by the mRNA. There are 20 different tRNAs, one for each amino acid. A tRNA is charged with its corresponding amino acid with the action of the aaRSs. The aaRSs are divided into two families, class I and class II, according to the groove of tRNA with which they interact, minor groove or major groove. The Rodin–Ohno model of the genetic codes divides the codon table into two categories by which class of aaRSs is responsible to charge the amino acid associated with each codon [
39,
40]. The division of the SGC table by the two classes of aaRSs was argued as “almost symmetrical” [
40], although, this symmetrical partition of the SGC was shown with the codon graphs of the SGC [
13].
Given the set of 64 codons that codify for 20 canonical amino acids and a stop signal, there are 21
64 ≈ 4 × 10
84 possible genetic codes. This calculation does not assume the evolution and degeneracy of the SGC. Coupling codon graphs of the SGC with different biological properties have allowed the analysis of several biological properties that uniquely determine the current SGC [
29].
The robustness and optimality of the SGC have been widely analyzed [
30,
41,
42,
43] and found suboptimal according to its error correction properties. Phenotypic graphs of random codes that maintain specific properties of the SGC have been analyzed for their connectivity properties. It was shown that despite the current SGC being suboptimal (regarding error tolerance, for example), it is optimal if its evolutionary history is considered [
30]. For the SGC to reach its optimal state of error tolerance, it would require codon swaps that are evolutionarily incompatible as these paths fix the SGC in each stage.
Other nucleotide models represent them by using a bijection from the nucleotides to the elements of the Galois field of four elements
GF(4) [
17,
27,
32]. With this bijection, an algebraic structure is given to the nucleotides. Representing the field
GF(4) with the integer numbers from one to four, it is possible to represent the nucleotides in the real line
and the codons in the space
. There are 24 possible assignations of the elements of the
GF(4) to the set {1,2,3,4} [
17]. These representations of the genetic code have been widely studied for their biological and mathematical properties [
17,
27,
32]. Phenotypic graphs of these 3D representations have been constructed to analyze the SGC and compare it with the human tRNA code and the standard tRNA code for its centrality measures, and the role of the stop codons and different degeneracy patterns have been described [
27]. Representations of the primeval RNY code have been constructed based on the bijection to the
GF(4) and their phenotypic graphs have been derived and analyzed for their symmetries based on polar requirement [
28]. Recall that phenotypic graphs can be constructed from any graph representation of the 64 codons, or any subset of it. The graph representation of the nucleotides in a square generalizes the bijection to the
GF(4) and allows using group actions that represent the biological mutations, transitions and transversions, to represent the symmetries of the genetic code [
13].
The two evolutionary paths arise from transformations of the primeval RNY code based on mistranslations on the early translation mechanisms and mutations on this small set of codons [
26]. Geometrically, these extended codes arise from symmetry breakings and translations of an RNY four-dimensional hypercube [
26,
32]. The composition of both evolutionary paths completes the set of 64 codons of a genetic code.
The codon graphs constitute a useful approach to analyze the evolvability of the genetic code. All in all, the codon graphs and their derived phenotypic graphs constitute a mathematical framework to theoretically analyze the SGC, the mitochondrial code, or any noncanonical code, including custom-designed codes.