1. Introduction
Given a key ring of apparently identical keys to open different doors, how many colors are needed to identify them? This puzzle was given by Rubin [
1] for the first time. In this puzzle, there is no need for coloring to be a proper one. Indeed, one cannot find a reason why adjacent keys must be assigned different colors, whereas in other problems, like storing chemicals and scheduling meetings, a proper coloring is needed with a small number of colors required.
Inspired by this puzzle, Albertson and Collins [
2] introduced the concept of the distinguishing number of a graph as follows: a labeling
is called
t-
distinguishing if no non-trivial automorphism of a graph
G preserves the vertex labels. The least integer
t such that a graph
G has a labeling which is
t-distinguishing for the graph
G, is called the
distinguishing number of
G and it is denoted by
. For example, the distinguishing number of a complete graph
is
n, the distinguishing number of a path graph
is 2 and the distinguishing number of a cyclic graph
is 2. For a graph
G of order
n,
[
2].
Harary [
3] gave different methods (orienting some of the edges, coloring some of the vertices with one or more colors and same for the edges, labeling vertices or edges, adding or deleting vertices or edges) of destroying the symmetries of a graph. Collins and Trenk [
4] defined the distinguishing chromatic number where the authors used proper
t-distinguishing for vertex labeling. The authors have given a comparison between the distinguishing number, the distinguishing chromatic number and the chromatic number of families like complete graphs, path graphs, cyclic graphs, Petersen graph and trees, etc. Kalinowski and Pilsniak [
5] defined similar graph parameters, the distinguishing index and the distinguishing chromatic index where the authors labeled edges instead of vertices. The authors also gave a comparison between the distinguishing number and the distinguishing index of a connected graph
G of order
. Boutin [
6] introduced the concept of determining sets. Albertson and Boutin [
7] proved that a graph has a
-distinguishable determining set if and only if the graph is
t-distinguishable. The authors also proved that every Kneser graph
with
and
is 2-distinguishable. A considerable amount of literature has been developed in this area—for example, see [
8,
9,
10,
11,
12].
Unless otherwise specified, all graphs considered in this paper are simple, non-trivial and connected. The set of all vertices that are adjacent to a vertex
is called the
open neighborhood of
u and it is denoted by
. The set of vertices
is called the
closed neighborhood of
u and it is denoted by
. If two distinct vertices
of a graph
G have the same open neighborhood, then these are called
non-adjacent twins. If the two vertices have the same closed neighborhood, then these are called
adjacent twins. In the both cases,
u and
v are called
twins. A vertex
v of a graph
G is called
saturated, if it is adjacent to all other vertices of
G. A graph
H whose vertex set
and edge set
are subsets of
and
, respectively, then
H is called a
subgraph of graph
G. Let
be any subset of vertices of
G. The
induced subgraph, denoted by
, is the graph whose vertex set is
S and whose edge set is the set of all those edges in
which have both end vertices in
S. A
spanning subgraphH of a graph
G is a subgraph such that
and
. An
automorphism of
G,
is a bijective mapping such that
if and only if
Thus, each automorphism
of
G is a permutation of the vertex set
which preserves adjacencies and non-adjacencies. The
automorphism group of a graph
G, denoted by
, is the set of all automorphisms of a graph
G. A graph with a trivial automorphism group is called a
rigid (or asymmetric) graph. The minimum number of vertices in a rigid graph is 6 [
13]. The distinguishing number of a rigid graph is 1.
The idea of a permutation graph was introduced by Chartrand and Harary [
14] for the first time. The authors defined a permutation graph as follows: a permutation graph consists of two identical disjoint copies of a graph
G, say
and
, along with
additional edges joining
and
according to a given permutation on
. Dorfler [
15] defined a mapping graph as follows: a
mapping graph of a graph
G on
n vertices consists of two disjoint identical copies of graph
G with
n additional edges between the vertices of two copies, where the additional edges are defined by a function. The mapping graph was rediscovered and studied by Chen et al. [
16], where it was called the functigraph. A functigraph is an extension of a permutation graph. Formally, the functigraph is defined as follows: let
and
be disjoint copies of a connected graph
G and let
be a function. A
functigraph of a graph
G consists of the vertex set
and the edge set
. Linda et al. [
17,
18] and Kang et al. [
19] studied the functigraphs for some graph invariants like metric dimension, domination and zero forcing number. In [
20], we have studied the fixing number of some functigraphs. The aim of this paper is to study the distinguishing number of functigraphs.
Network science and graph theory are two interconnected research fields that have synonymous structures, problems and their solutions. The notions ‘network’ and ‘graph’ are identical and these can be used interchangeably subject to the nature of application. The roads network, railway network, social networks, scholarly networks, etc are among the examples of networks. In the recent past, the network science has imparted to a functional understanding and the analysis of the complex real world networks. The basic premise in these fields is to relate metabolic networks, proteomic and genomic with disease networks [
21] and information cascades in complex networks [
22]. Real systems of quite a different nature can have the same network representation. Even though these real systems have different nature, appearance or scope, they can be represented as the same network. Since a functigraph consists of two copies of the same graph (network) with the additional edges described by a function, a mathematical model involving two systems with the same network representation and additional links (edges) between nodes (vertices) of two systems can be represented by a functigraph. The present study is useful in distinguishing the nodes of such pair of the same networks (systems) that can be represented by a functigraph.
Throughout the paper, we denote the functigraph of G by , , , g denotes a function , f denotes the distinguishing labeling, and , .
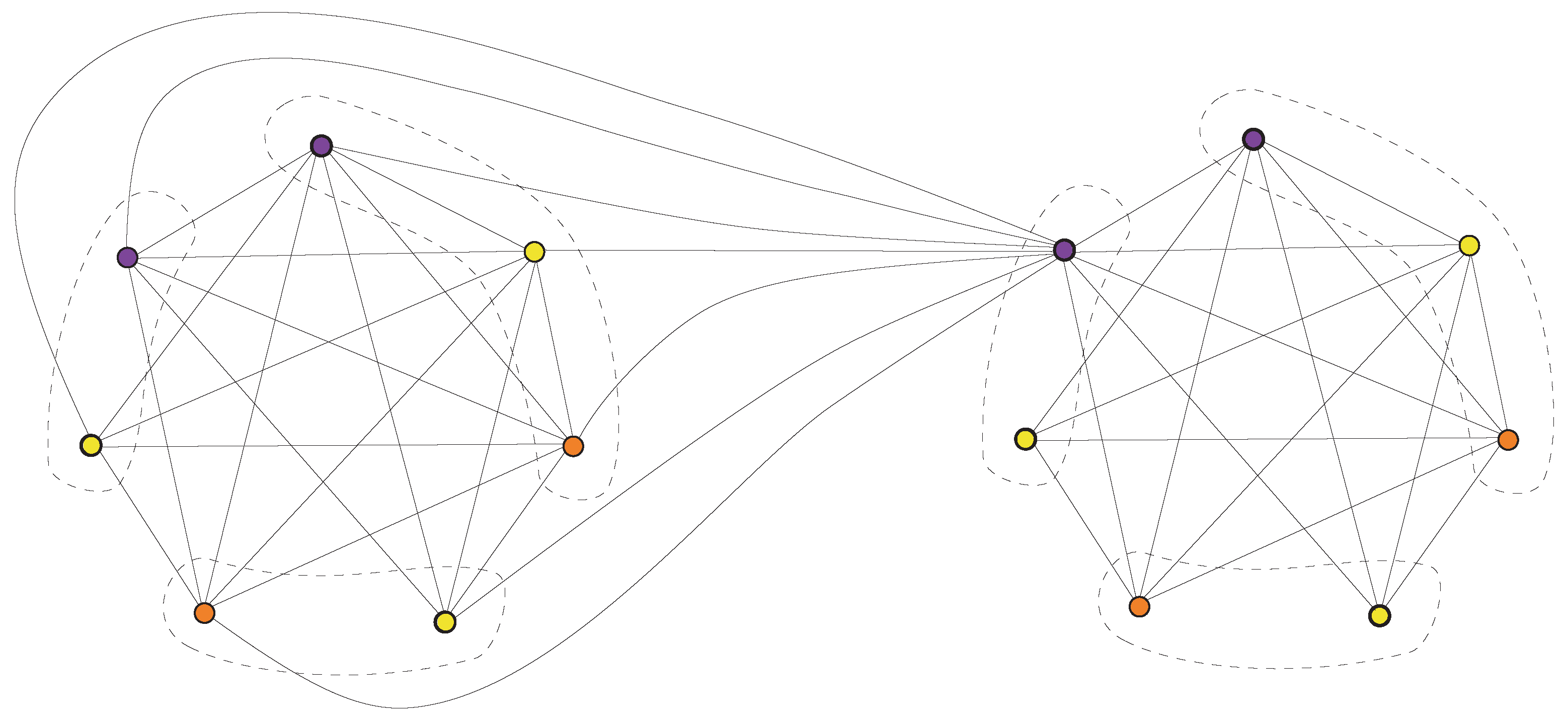
In order to understand the concept of functigraphs, we consider an example of a functigraph of
. Take
and
and function
g is defined as follows:
The corresponding functigraph is shown in
Figure 1.
This paper is organized as follows: in
Section 2, we give sharp lower and upper bounds for the distinguishing number of functigraphs. This section also establishes connections between the distinguishing number of graphs and their corresponding functigraphs in the form of realizable results. In
Section 3, we compute the distinguishing number of functigraphs of complete graphs and joining of path graphs. Some useful results related to these families have also been presented in this section.
2. Bounds and Realizable Results
The sharp lower and upper bounds on the distinguishing number of functigraphs are given in the following result.
Proposition 1. Let G be a connected graph of order ; then,Both bounds are sharp. Proof. Obviously, by definition. Let and f be a t-distinguishing labeling for the graph G. In addition, let and , . We extend labeling f to as: for all . We have the following two cases for g:
If g is not bijective, then f as defined earlier is a t-distinguishing labeling for . Hence, .
If g is bijective, then f as defined earlier destroys all non-trivial automorphisms of except possible flipping of and in . Let and be the functigraph of G when g is an identity function, i.e., for all i, and when g is not identity function, respectively. The flipping of and is possible in the cases when either g is an identity function or when g is not the identity function but the corresponding functigraph is isomorphic to . In order to break this automorphism (flipping), only one vertex of either or must be labeled with an extra color, and hence .
For the sharpness of bounds, we consider a rigid graph G on vertices. For the sharpness of the lower bound, take a functigraph in which g is a constant function. For the sharpness of the upper bound, take functigraph in which g is an identity function. ☐
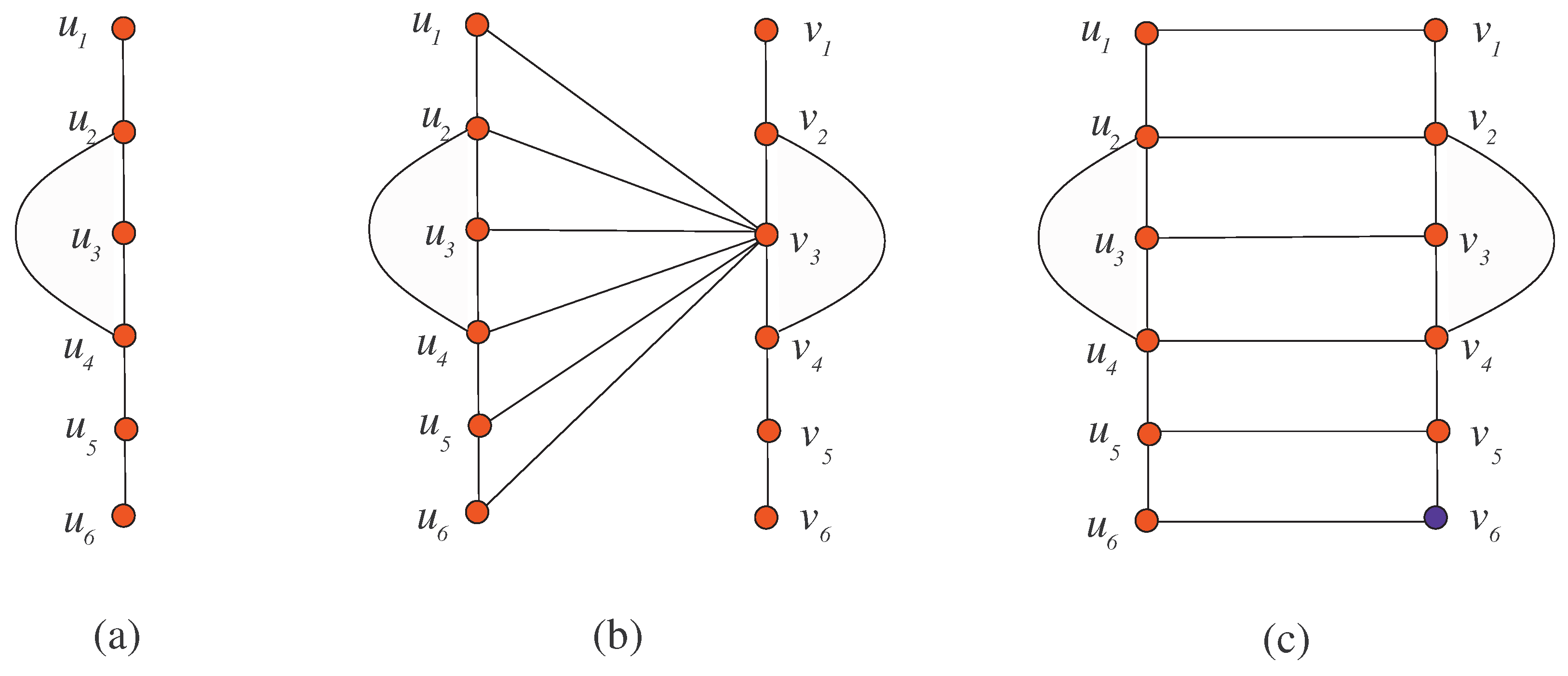
We discuss an example for Proposition 1, where we consider a rigid graph
G with the smallest number of vertices i.e.,
as shown in
Figure 2a. Since
, we label its vertices with a red color.
Figure 2b shows
, when
g is a constant function. In this case,
is a rigid graph and hence
.
Figure 2c shows
, when
g is the identity function. In this case,
has a non-trivial automorphism i.e., horizontal flipping of
. We label vertex
of copy
with blue color to break the non-trivial automorphism. Hence,
.
Since at least m colors are required to break all automorphisms of a twin-set of cardinality m, we have the following proposition.
Proposition 2. Let be disjoint twin-sets in a connected graph G of order and ,
- (i)
,
- (ii)
If , then .
Two vertices in a graph G are said to be similar vertices, if both can be mapped on each other under some automorphism of graph G.
Lemma 1. Let G be a connected graph of order and g be a constant function, then .
Proof. Let
. In the functigraph
, we label the vertices in copy
of
G with
colors. Now,
v is the only vertex of
with the largest degree (as we can see in
Figure 2b
and
is the vertex of
with the largest degree); therefore, it is not similar to any other vertex of
and hence it can also be labeled with one of
colors. Thus, vertices in
are labeled by
colors. Since
g is a constant function, all vertices in
are not similar to any vertex in
in functigraph
. If two disjoint subsets of vertices of a graph are such that every vertex of one set is not similar to any vertex of the other set, then the vertices of both sets can be labeled by the same set of colors; therefore, the vertices in
and
can be labeled by
colors. Hence,
. ☐
Remark 1. Let G be a connected graph and , if g is constant and , if g is not constant; then,
Now, we discuss a special type of connected subgraph H of a connected graph G such that . We define a set is similar to for some . If the graph G has a connected subgraph H in which all vertices in are either adjacent to all vertices in or non-adjacent to all vertices in , then we discuss in Remark 2 that .
Lemma 2. Let H be a connected subgraph of a connected graph G such that all vertices in are either adjacent to all vertices in or non-adjacent to all vertices in , then every automorphism of H can be extended to an automorphism of G.
Proof. Let
be an arbitrary automorphism. We define an extension
of
on
as:
Since for all , being an identity function preserves the relation of adjacency among the vertices in . In addition, being an automorphism of the subgraph H preserves the relation of adjacency among the vertices in . Next, we will prove that also preserves the relation of adjacency among the vertices in . Suppose and , where both y and u are arbitrary vertices of their sets. Since , . We discuss two cases for the subgraph H in graph G:
All vertices in are adjacent to all vertices in ; then, u is adjacent to y in G. In addition, being a vertex of H is adjacent to . Hence, preserves the relation of adjacency among the vertices in .
All vertices in are non-adjacent to all vertices in ; then, u is non-adjacent to y in G. In addition, being a vertex of H is non-adjacent to . Hence, preserves the relation of adjacency among the vertices in .
Thus, preserves the relation of adjacency among the vertices of . ☐
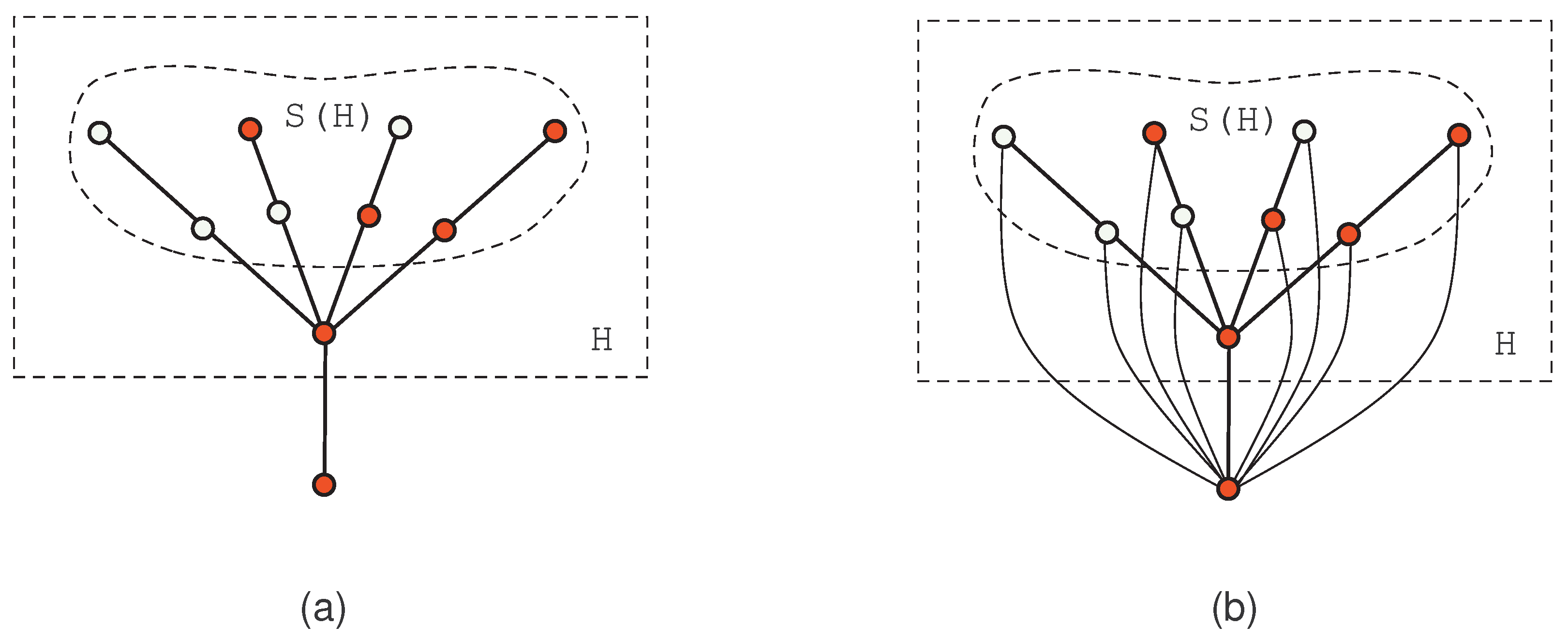
Let
H be a connected subgraph of a graph
G such that
H satisfies the hypothesis of Lemma 2, then every distinguishing labeling of
G requires at least
colors to break the extended automorphism
of
G, therefore
for the subgraph
H. It can be seen in
Figure 3 that subgraph
H of graph
G satisfies the hypothesis of Lemma 2 and
. We label the vertices of the graph with red and white colors.
Remark 2. Let H be a connected subgraph of a connected graph G such that all vertices in are either adjacent to all vertices in or non-adjacent to all vertices in , then .
A vertex v of degree at least three in a connected graph G is called a major vertex. Two paths rooted from the same major vertex and having the same length are called the twin stems.
We define a function as , where k is the least number such that . For example, . Note that is well-defined.
In the following lemma, we find a lower bound of the distinguishing number of a graph having twin stems of length 2 rooted at the same major vertex, in terms of the function .
Lemma 3. If a graph G has twin stems of length 2 rooted at the same major vertex, then .
Proof. Let
be a major vertex and
where
are the twin stems of length 2 attached with
x. Let
and
. Since
where
are twin stems in the graph
G, the subgraph
H satisfies the hypothesis of Lemma 2. We define a labeling
as:
Using this labeling, one can see that f is a t-distinguishing labeling for H. With permutations with a repetition of k colors, when two of them are taken at a time equal to , at least k colors are needed to label the vertices in t-stems. Thus, k is the least integer for which subgraph H has k-distinguishing labeling, and hence . Thus, by Remark 2. ☐
It can be seen that the graph
G as shown in
Figure 3a has four twin stems of length 2 rooted at the same major vertex; therefore, by Lemma 3,
. The following result gives the existence of a graph
G and its functigaph
, such that both have the same distinguishing number.
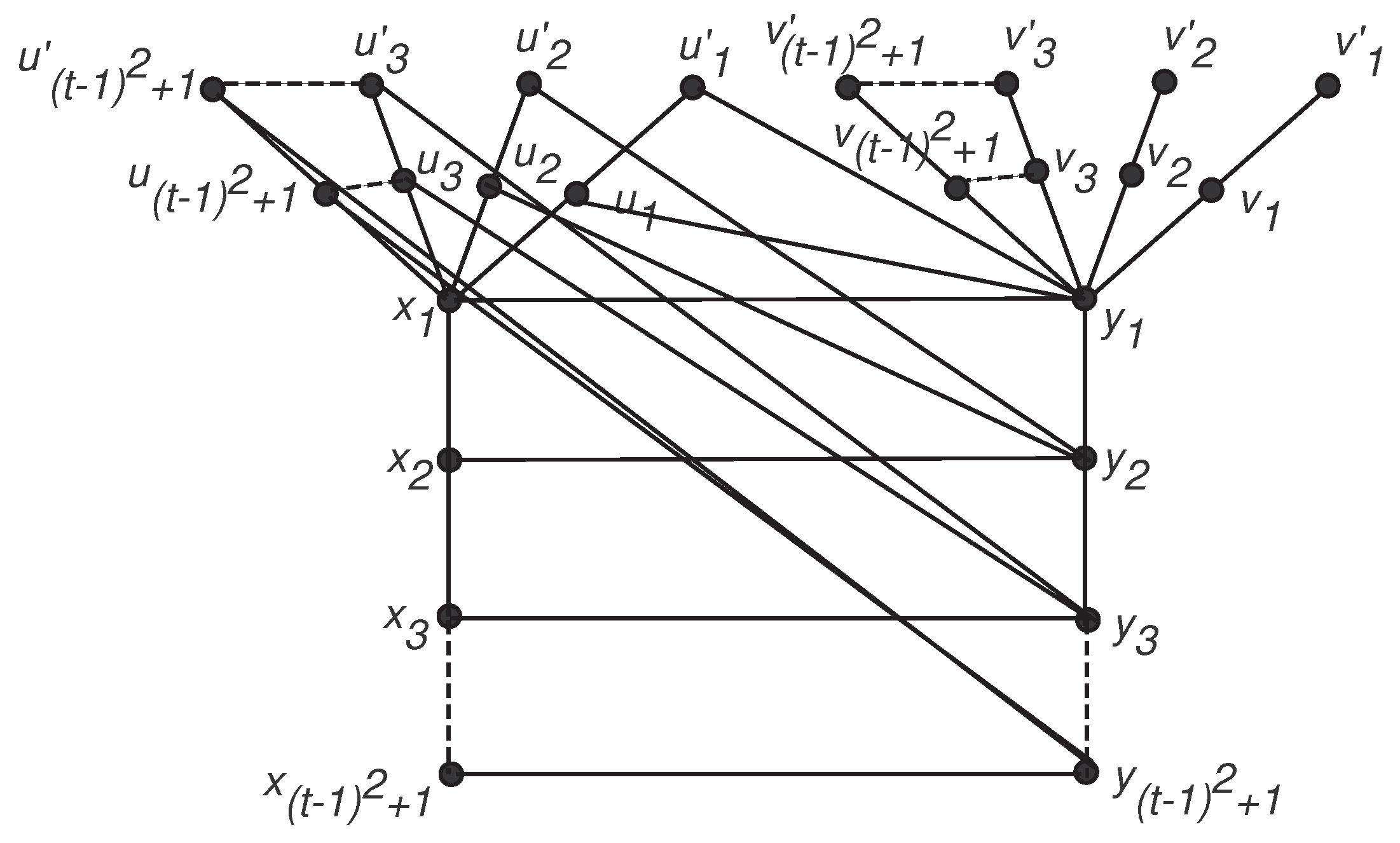
Lemma 4. For any integer , there exists a connected graph G and a function g such that .
Proof. Construct a graph
G as follows: let
be a path graph. Join
twin stems
where
each of length two with vertex
of
. This completes construction of
G. We first show that
. For
, we have two twin stems attached with
, and hence
. For
, we define a labeling
as follows:
, for all
i, where
Using this labeling, one can see the unique automorphism preserving this labeling is the identity automorphism. Hence,
f is a
t-distinguishing. With permutations with a repetition of
colors, when two of them are taken at a time,
,
twin stems can be labeled by at least
t colors. Hence,
t is the least integer such that
G has a
t-distinguishing labeling. Now, we denote the corresponding vertices of
as
for all
i, where
and construct a functigraph
by defining
as follows:
, for all
i, where
and
, for all
i, where
as shown in
Figure 4. Thus,
has only symmetries of
twin stems attached with
. Hence,
☐
Consider an integer
. We construct a graph
G similarly as in the proof of Lemma 4 by taking a path graph
and attach
twin stems
where
with any one of its end vertex, say,
. Using the similar labeling and arguments as in the proof of Lemma 4, one can see that
f is
distinguishing and
is the least integer such that
G has
distinguishing labeling. Define functigraph
, where
is defined by:
, for all
i, where
,
, for all
i, where
,
, for all
i, where
. From this construction,
has only symmetries in which two twin stems attached with
can be mapped on each other under some automorphism of
, and hence
. Thus, we have the following result, which shows that
can be arbitrarily large:
Lemma 5. For any integer , there exists a connected graph G and a function g such that .
Consider
. We construct a graph
G similarly as in the proof of Lemma 4 by taking a path graph
:
and attach
twin stems
, where
with
. Using the similar labeling and arguments as in the proof of Lemma 4, one can see that
f is
distinguishing labeling and
is the least integer such that
G has
distinguishing labeling. Let us now define
g as
, for all
i, where
,
, for all
i, where
and
, for all
i, where
Thus,
has only symmetries of
twin stems attached with
, and hence
. After making this type of construction, we have the following result which shows that
can be arbitrarily large:
Lemma 6. For any integer , there exists a connected graph G and a function g such that .
3. The Distinguishing Number of Functigraphs of Some Families of Graphs
In this section, we discuss a distinguishing number of functigraphs on complete graphs, edge deletion graphs of complete graph and joining of path graphs.
Let G be the complete graph of order . We use the following terminology for in the proof of Theorem 1: Let and for all i, where . In addition, let and . From the definitions of l and m, we note that and .
In the next result, we find the distinguishing number of functigraphs of complete graphs, when g is bijective, in terms of function as defined in the previous section.
Lemma 7. Let G be the complete graph of order and g be a bijective function; then, .
Proof. Let
and
. In addition, let
. Let
be a labeling in which
is defined as in Equation (
1) and
as in Equation (
3) in the proof of Lemma 4. Using this labeling, one can see that
f is a
k-distinguishing labeling for
. With permutations with repetitions of
k colors, when two of them are taken at a time equal to
, at least
k colors are needed to label the vertices in
. Hence,
k is the least integer for which
has
k-distinguishing labeling. ☐
Let G be a complete graph and let be a function such that . Without loss of generality, assume are those vertices of A such that , where in B. In addition, for all , where . By using the similar labeling f as defined in Lemma 7, at least colors are needed to break these automorphisms in . Thus, we have the following proposition:
Proposition 3. Let G be a complete graph of order and g be a function such that ; then, .
The following result gives the distinguishing number of functigraphs of complete graphs.
Theorem 1. Let be the complete graph of order , and let ; then, Proof. We discuss the following cases for l:
If , then A contains twin vertices and B contains twin vertices (except for where B contains no twin vertices). In addition, there are vertices in A which have distinct images in B. By Proposition 3, these m vertices and their distinct images are labeled by at least colors (only 1 color if ). Since is the largest among , and , is the least number such that has —distinguishing labeling. Thus, .
If , then , and hence .
If , then B contains the largest set of twin vertices in . In addition, there are vertices in A, each of which have distinct images in B. Since , .
If , then both A and B contain the largest set of twin vertices in . In addition, there are vertices in A that have distinct images in B. Since , .
If , then we have the following two subcases:
- (a)
If , then both A and B contain the largest set of twin vertices in . In addition, there are vertices in A that have distinct images in B. Since (if exists), .
- (b)
If , then , and hence .
☐
We define a function as , where k is the least number such that . For instance, . Note that is well defined.
The following result gives the distinguishing number of functigraphs of a family of spanning subgraphs of complete graphs.
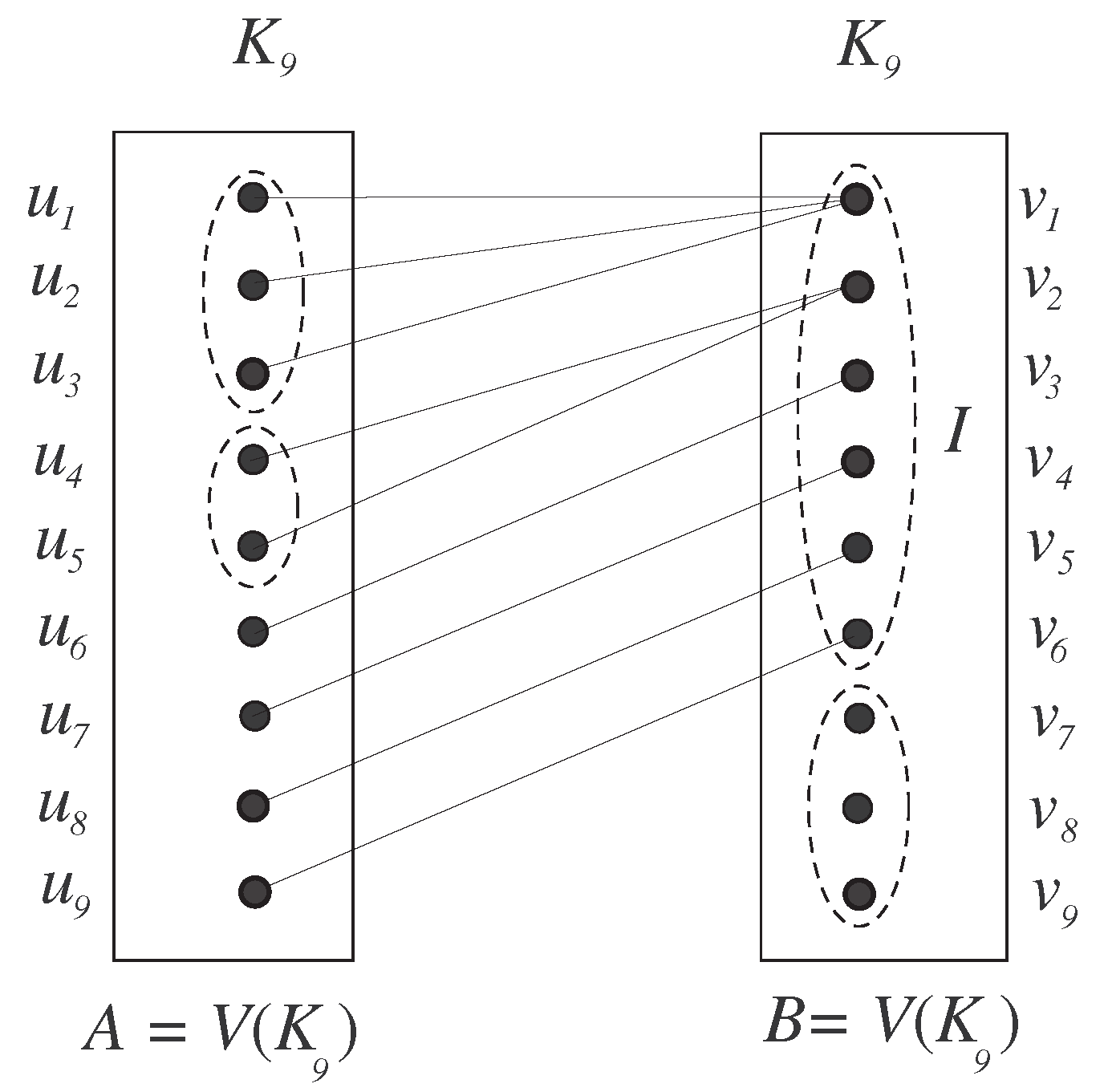
Theorem 2. For a complete graph G of order and , where is the graph deduced from G by deleting i edges with no common end vertices that join two saturated vertices of G for all i. If g is a constant function, then Proof. On deleting
i edges from
G, we have
saturated vertices and
i twin-sets each of cardinality two (as shown in
Figure 5 where
G is the complete graph on 7 vertices,
and
g is a constant function). We will now show that exactly
colors are required to label vertices of all
i twin-sets. We observe that all vertices in twin sets of cardinality 2 are similar to each other in
G. Since two vertices in a twin-set are labeled by a unique pair of colors out of
pairs of
k colors, at least
k colors are required to label vertices of
i twin-sets. Now, we discuss the following two cases for
:
If , then the number of colors required to label saturated vertices is greater than or equal to the number of colors required to label the vertices of i twin-sets. Thus, we label saturated vertices with exactly colors and out of these colors, colors will be used to label vertices of i twin-sets.
If , then the number of colors required to label saturated vertices is less than the number of colors required to label vertices of i twin-sets. Thus, we label vertices of i twin-sets with colors and, out of these colors, colors will be used to label saturated vertices in .
Since g is constant, by using the same arguments as in the proof of Lemma 1, ☐
Suppose that and are two graphs with disjoint vertex sets and and disjoint edge sets and . The join of G and is the graph , in which and : , .
Proposition 4. Let be a path graph of order ; then, for all and , .
Proof. Let and . We discuss the following cases for .
If and , then , and hence by Theorem 1.
If and , then has three saturated vertices. Thus, by Proposition 1. However, for all s where and all possible definitions of g in , one can see .
If
and
, then a labeling
defined as:
is a distinguishing labeling for
, and hence
. Thus,
by Proposition 1. However, for all
s where
and all possible definitions of
g in
, one can see
.
If
and
, then a labeling
defined as:
is a distinguishing labeling for
, and hence
. Thus, the result follows by Proposition 1.
☐