1. Introduction
The classification of finite subgroups in
derives attention from various research areas in mathematics. Especially when
, it is related to McKay correspondence and ADE singularity theory [
1].
The list of finite subgroups of
consists of cyclic groups (
), binary dihedral groups corresponded to the symmetry group of regular
-gons, and binary polyhedral groups related to regular polyhedra. These are related to the classification of regular polyhedrons known as Platonic solids. There are five platonic solids (tetrahedron, cubic, octahedron, dodecahedron, icosahedron), but, as a regular polyhedron and its dual polyhedron are associated with the same symmetry groups, there are only three binary polyhedral groups (binary tetrahedral group
, binary octahedral group
, binary icosahedral group
) related to regular polyhedrons. Moreover, it is a well-known fact that there is a correspondence between binary polyhedral groups and vertices of 4-polytopes as follows:
where the dual compound of 24-cell means by the compound polytopes obtained from 24-cell and its dual polytope, which is also a 24-cell [
2,
3,
4,
5].
As the symmetries of polyhedrons are isometries, the related finite subgroups are also considered as the subgroups of
. As
is a spin group of
, we can regard
,
, and
as subgroups of quaternions
. From this point of view, it is also well known that the vertices of 24 cell correspond to roots of
, and the set of vertices of the dual compound of 24-cell, which is the union of a 24-cell and a dual 24-cell forms a roots of
. The 600-cell is a complicated case of a reflection group of
-type [
3,
6].
The aim of this article is to provide explicit description of a binary icosahedron group as a 600-cell. By applying spin covering map from to , we introduce a method to construct the binary polyhedral groups in terms of quaternions from the symmetries of regular polyhedrons. Then, by applying the theory of reflection groups along the Coxeter–Dynkin diagram, we show that the subgroup in is indeed the set of vertices of a 600-cell. We also discuss related to 24-cell, but, because the dual compound of a 24-cell is not regular, its relation to will be discussed in another article.
2. Binary Polyhedral Groups in Quaternions
Every finite subgroup of is conjugate to a finite subgroup of so that the classification of the finite subgroup of including binary polyhedral groups corresponds to the classification of the finite subgroup of . As , we can identify the binary polyhedral groups as certain subsets in quaternions . In fact, is not only a unit sphere in but also the spin group which is a 2-covering map of . In this section, we explain how an element in lifts to quaternions in .
The algebra of quaternions
is the four-dimensional vector space over
defined by
satisfying relations
. The quaternionic conjugate of
is defined by
and the corresponding norm
is also defined by
. Along this norm, quaternions satisfy
, which implies that it is one of the normed algebras whose classification consists of real numbers
, complex numbers
, quaternions
, and octonions
. A quaternion
q is called
if
and is called
if
. According to these facts, we can divide
into a real part and an imaginary part:
It is well known that the set of unit sphere
in
is a Lie group
which is also isomorphic to
as follows:
Below, we use the identification between and . Along this, a vector in (resp. a quaternion in ) is corresponded to a quaternion in (resp. a vector in ).
Now, we define a map
which is given by an action of
on
As a matter of fact, the map
must be defined as
so that
is in
. However, we use a simpler definition instead. It is well known that
is a 2-covering map, which is also a group homomorphism.
In the next section, we will consider the preimage of to define the lifting of symmetry groups of polyhedrons in which are subgroups of . For this purpose, we consider further in below.
We observe that the multiplication of two pure quaternions
p,
in
can be written by the cross product × and the standard inner product · on
:
After we denote
(
),
can be written as
Here, since , we denote where and for some
Now, to understand the meaning of , we consider two cases for case (1) and case (2) .
- (1)
(Case
) Since
, we have
- (2)
(Case
) After we denote
for some
,
By the two cases above, we conclude presents the rotation of vector in with respect to the axis by .
By applying the above, we have the following lemma.
Lemma 1. For each element A in presenting a rotation with respect to a unit vector for angle , the preimage of is given as Note if we choose unit vector instead in the lemma, then the rotation performed for angle . Therefore, the related lifting is given by . Hence is well defined.
By applying Lemma 1, we can consider the preimage of any subset in . We call the preimage the lift of in . When is one of the symmetry groups of regular polyhedrons, the lift is called binary polyhedral group. In particular, we consider binary tetrahedral group , binary octahedral group , and binary icosahedral group , which are lifts of symmetry groups of tetrahedron, octahedron and icosahedron with order , respectively.
2.1. Symmetry Groups of Regular Polyhedrons
A polyhedron considered here is convex and regular. According to convention, we denote a regular polyhedron by
which means that the polyhedron has only one type of face which is a
p-gon, and each vertex is contained in
q faces. It is well known that there are only five regular polyhedrons, which are also called
Platonic solids. Up to duality, we consider three classes of regular polyhedrons as follows:
As the special linear group
is generated by rotations on
, we consider rotations of
preserving a regular polyhedron to study the symmetry group of it. When the axis of the rotation crosses a vertex (the barycenter of an edge, the barycenter or a face resp.), we call the rotation
vertex symmetry (
edge symmetry,
face symmetry resp.). For instance, the tetrahedron has two different types of axes of rotations. One is the line passing through a vertex and the barycenter of the opposite face, and the other is the line connecting barycenters of the edges at the opposite position. We also say that a symmetry has
order if the order of the corresponding rotation is
n. Note that the order of each edge symmetry is 2. One can figure all the possible orders of each type of symmetry for regular polyhedrons, as shown in
Table 1.
Construction of binary polyhedral groups
Now, we will introduce a construction which provides a way to find the elements of binary polyhedral groups related to regular polyhedrons when the set of vertices of regular polyhedrons are given.
Assume we have a regular polyhedron whose barycenter is the origin of and let be the set of vertices of the regular polyhedron:
- (1)
Find the barycenters of vertices, edges and faces (The barycenter of each vertex is itself).
- (2)
For each barycenter, derive all the related symmetries in by identifying corresponding axis of rotations and its order.
- (3)
For each symmetry obtained from step 2, we get related lifts in by applying Lemma 1. It is useful to observe that we obtain the axis of rotation and its order instead of related angle where there can be more than one related angle.
- (4)
The union of lifts is a subset of binary polyhedral groups. In fact, its union with is the binary polyhedral group by counting elements.
Note: From the above, it is clear that two regular polyhedrons which are dual to each other are associated with the same binary polyhedral groups.
For example, let
be a barycenter of order 3. Then, there are two related angles
and
. Thus, the corresponding lift is
Here, we also observe that, if we begin with instead of B, the corresponding lifts are still the same.
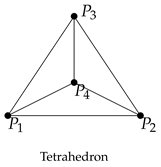
Binary tetrahedral group
We consider a tetrahedron consisting of vertices
.
- (1)
Since vertex symmetry has order 3, each vertex symmetry has two angles
and
and the union of lifts of vertex symmetries is
- (2)
As the edge symmetry has order 2, each edge symmetry has only one angle
so that the related lift is
and the union is given as
Since
, two barycenters
and
of edges have the same lifts of edge symmetries. Similarly, the pairs of edges produce the same lifts of edge symmetries, and we get
- (3)
For a barycenter of face consisting of
, we have a relation
since
. Thus, the related lift of face symmetry is the same as the lift of vertex lift for a vertex
. Similarly, each lift of face symmetry corresponds to the lift of vertex symmetry.
Finally, the union
of lifts of symmetries of a tetrahedron is a subset binary tetrahedral group
in
. Since
the union
is a binary tetrahedral group, namely
If we choose vertices
of a tetrahedron as
the corresponding binary tetrahedral group is obtained as
Remark: The subset
is the unit integral quaternions which is also known as
Hurwitz integral quaternions. ([
7,
8])
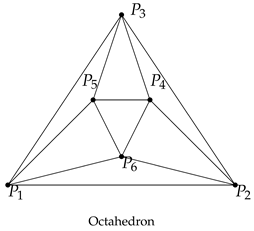
Binary Octahedral Group
We consider an octahedron consisting of vertices
as below.
- (1)
The possible orders of vertex symmetry are
and 4. The vertex symmetry with order 4 has two angles
and
and one with order
has one angle
. Thus, the union of lifts of vertex symmetries is
Since two antipodal vertices produce the same lifts of vertex symmetries, we obtain that
- (2)
As the edge symmetry has order 2, each edge symmetry has only one angle
so that the union of the related lift is
where the union is performed for all the pairs of
and
form an edge. For the barycenter of an edge given by
, there is exactly one edge whose barycenter is antipodal to
. Moreover, the pair of edges produce the same lifts of edge symmetries. Therefore, we get
- (3)
For a barycenter of face given as
, the face symmetry has order 3 and it is related to two angles
and
. Thus, the lifts of a face symmetry is
and the union of lifting of face symmetries is
Since the octahedron is symmetric for origin, for the barycenter of a face given by
, there is exactly one face whose barycenter is antipodal to
, and the pair of faces produce the same lifts of face symmetries. Therefore, we deduce
Finally, the union
of lifts of symmetries of an octahedron is a subset of the binary octahedral group
in
. Since
the union
is a binary octahedral group, namely
One can take
s as follows:
so as to obtain
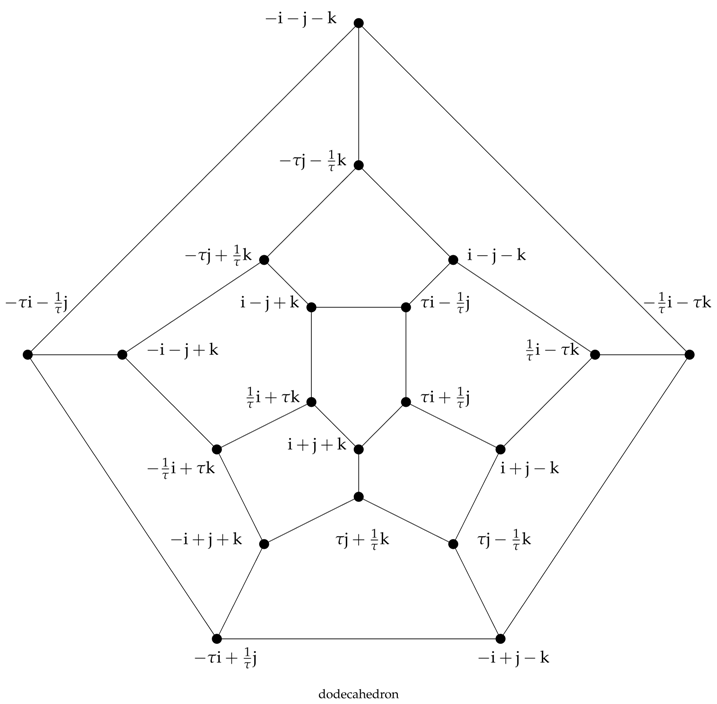
Binary Icosahedral Group
Since both the regular icosahedron and its dual regular dodecahedron produce the binary icosahedral group, we consider a regular dodecahedron in
instead of a regular icosahedron. Moreover, for the sake of convenience, one can choose specific coordinates of vertices of a dodecahedron in
such as
where
and
. It is also useful to know
and
.
In the following diagram, we consider the given set of vertices as a subset in
and depict the configuration among the vertices.
For the above dodecahedron, we denote the set of vertices as without a specific choice of order.
- (1)
Since the possible order of each vertex symmetry is 3, the vertex symmetry has two angles
and
. Thus, the union of lifts of vertex symmetries is
Since the dodecahedron is symmetric for origin, each vertex and its antipodal vertex produce the same lifts of vertex symmetries. Thus, we obtain that
- (2)
As before, the edge symmetry has order 2, and each edge symmetry has only one angle
so that the union of the related lifts is
where the union is performed for all the pairs of
and
form an edge. Just like the lifts of edge symmetries for an octahedron, the pair of antipodal edges produce the same lifts of edge symmetries. Therefore, we get
- (3)
For a barycenter of face given as
where
(
) forms a face, the face symmetry has order 5 and it is related to four angles
. Thus, the lifts of a face symmetry are
and the union of lifts of face symmetries is
Since a pair of antipodal faces produce the same lifts of face symmetries, we deduce
Finally, the union
of lifts of symmetries of a dodecahedron is a subset of a binary icosahedral group
in
. Since
the union
is a binary icosahedral group, namely
For the given vertices we have, we can obtain
As a result, we can identify all the elements of the binary icosahedral group as
Theorem 1. The finite subsets , and in defined as above are a binary tetrahedral group, a binary octahedral group, and a binary icosahedral group, respectively.
Note that it is well known that the a subset in is the vertices of 24-cell and the complementary subset in is the vertices of a snub 24-cell.
3. 600-Cell
The Coxeter–Dynkin diagrams are the way of describing the group generated by reflections. For each graph,
node represents a mirror (or a reflection hypersurface) and the label
attached to a branch between nodes marks the dihedral angle
between two mirrors. By convention, no label is attached to a branch if the corresponding dihedral angle is
. When all the dihedral angles are
, the diagram is called
simply laced. Ringed nodes present so called active mirrors where there is a point
not to sit in the hyperplanes of reflections corresponded to the mirrors. By successive applying the reflections in the diagram to the point
P, we obtain a polytope whose symmetry group is the Weyl group generated by the Coxeter–Dynkin diagram. Moreover, the combinatorics of subpolytopes can also be decoded by the Coxeter–Dynkin diagram when it is simply laced with one ringed node (see [
7,
9,
10]). In fact, a similar method can be applied for the diagram, which is not simply laced or has more than one ringed node.
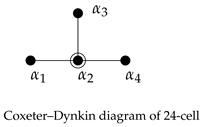
The Coxeter–Dynkin diagram of 24-cell is an example of simply laced with one ringed node.
The Weyl group associated with this diagram is
-type. In [
7], the subpolytopes of 24-cell as shown in
Table 2 are described by using the Coxeter–Dynkin diagram.
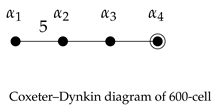
The Coxeter–Dynkin diagram of 600-cell is given by
whose Weyl group is
-type. Thus, the diagram is not simply laced and has one ringed node.
By removing a ringed node, we obtain the isotropy subgroup in the Weyl group of
which fixed a vertex in the 600-cell. Here, the corresponding isotropy group is
and we can compute the total number of vertices as
For the remaining diagram above, we ring a node connected to the removed node. Then, we obtain the Coxeter–Dynkin diagram of an Icosahedron, which implies that the vertex figure of
cell is an icosahedron.
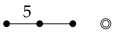
(2) Edges
For edges, we consider the ringed node that performs one reflection corresponding to an edge.
For the isotropy subgroup of the edge, we remove the unringed node connected to the ringed node. In addition, the remaining diagram generates the isotropy subgroup
. Thus, we compute the total number of edges as
(3) Faces
For faces, we consider the ringed node and extend the diagram to unringed nodes so as to obtain a subdiagram of
-type. The subdiagram of
with one ringed node generate
, namely a triangle. Thus, the faces of 600-cell are all triangles.
For the isotropy subgroup of a face, we remove any unringed node connected to the subdiagram of a face. The remaining subdiagram generates the isotropy subgroup of a face, which is
. Thus, we compute the total number of faces as
(4) Cells
To obtain a cell in a 600-cell, we consider an extended diagram from the ringed nodes to unringed nodes so as to obtain a subdiagram of
. The diagram of type
with one ringed node on one side represents a tetrahedron.
For the isotropy subgroup of a cell, we consider that any unringed node connected to the subdiagram of
, and the subdiagram given by removing the node generates the isotropy subgroup, which is
. Thus, we compute the total number of cells,
Table 3 shows the subpolytopes of 600:
4. Binary Polyhedral Groups as Polytopes
In this section, we show that the binary icosahedral group in is the set of vertices of a 600-cell. Thus, the convex hull of in is a 600-cell.
For each
in
with
, we define a reflection on
as
Since
is a normed division algebra,
is also written as
via quaternionic multiplication (see Ref. [
7]). Since
is a reflection for a vector
,
has eigenvalues
where
is an eigenvector of
and the hyperplane perpendicular to
is the eigenspace of 1. Moreover, it is not an element in
.
Binary tetrahedral groupinand 24-cell
For 24-cell, we consider the Coxeter–Dynkin diagram of type
given in
Section 3, where
In Ref. [
7], the Weyl group generated by the Coxeter–Dynkin diagram acts on the binary tetrahedral group
. Moreover, it is shown that
is the set of vertices of a 24-cell. In fact, it is also the subset of unit integral quaternions.
Binary icosahedral groupinand 600-cell
Similarly, for 600-cell, we consider the Coxeter–Dynkin diagram of Type
given in
Section 3, where
The Weyl group generated by the reflections is denoted by . In below, we want to show that (1) the Weyl group acts on the binary icosahedral group , and (2) is a single orbit, where it corresponds to the set of vertices of 600-cell.
Lemma 2. The Weyl group acts on the binary icosahedral group in .
Proof. Since the Weyl group
is generated by the reflections
(
), we show that each
acts on
. For an arbitrary element
, the reflections are written as follows:
It is easy to see that
and
act on
. By choosing
as an ordered orthonormal basis of
,
and
can be written as
In addition, these are similar because
where
is an orthogonal matrix
In fact,
S is an element in
defined by
and one can check that
acts on
by simple calculation. Thus, it suffices to show that
acts on
to check
and
act on
. For
, we consider
submatrix
A of
defined as
This is a automorphism of
which satisfies
and
. Moreover,
also acts on
which is our choice of the vertices of a dodecahedron. Since
is a reflection, it is also a symmetry of the dodecahedron so that it also acts on the set of edges and the set of faces. According to the construction of binary icosahedral group
in
Section 2.1, the action of
on the icosahedron induces the action of
on
. For example, an edge symmetry given by an edge
is sent to another given by
because
Similarly, we conclude that
acts on
. ☐
By applying the above lemma, we obtain the following theorem.
Theorem 2. The set of a binary icosahedral group is an orbit of the Weyl group , and it is the set of vertices of a 600-cell.
Proof. By Lemma 2, the Weyl group
acts on
. Now, we consider an element
in
and its orbit
. Since
is perpendicular to
,
and
, the orbit
is given by the following Coxeter–Dynkin diagram 3 of 600-cell. By
Section 3, we have
. Therefore, we conclude
and this gives the theorem. ☐