Fermion Scattering in a CPT-Even Lorentz Violation Quantum Electrodynamics

Abstract

In this work, we reassess two known processes of Quantum Electrodynamics involving electrons and muons. The photon propagator is modified by a CPT-even Lorentz-violating (LV) tensor, while fermion lines and the vertex interaction are not altered. Using the Feynman rules, the associated cross sections for unpolarized scatterings are evaluated, revealing the usual energy dependence and Lorentz-violating contributions that induce space anisotropy. A possible route to constraining the LV coefficients is presented and the results properly commented.

1. Introduction

Particle physics has received a lot of attention in the so-called LHC (Large Hadron Collider) era, in which several predictions of the standard model of elementary particles (SM) were confirmed, including the very significant detection of the Higgs particle. Despite this history of success, the SM is still an incomplete model, motivating the search for new theories that explain the actual issues not well described by it, the so-called physics beyond the standard model. A model in this direction is the standard model extension (SME) [1], which proposes the possibility of violating Lorentz symmetry by including fixed terms in all sectors of the original SM Lagrangian. During the last two decades, efforts have been made to impose upper bounds on the Lorentz-violating (LV) coefficients [2]. CPT-odd [3] and CPT-even [4,5,6,7,8,9] modifications on the electromagnetic field were considered and analyzed in several respects, as quantum electrodynamics corrections [10,11,12,13,14,15] and consistency analysis about causality, stability, and unitarity [16,17,18,19]. Aspects about the covariant quantization of the LV quantum electrodynamics were recently addressed and analyzed [20], including a small photon mass factor. An alternative analysis keeping the photon massless but considering a modified gauge fixing was also performed [21,22].

Out of the broad framework of the SME, a nonminimal CPT-odd interaction between fermions and photons was proposed [23], with interesting consequences in the nonrelativistic limit of Dirac equation concerning topological effects and geometrical phases [24,25,26,27,28,29,30], Landau level [31] and on the high energy Bhabha cross section [32]. Similar types of CPT-odd nonminimal coupling were also investigated in the context of radiative generation evaluations [33,34,35], as well as fermion scattering at zero temperature [36] and at finite temperature [37]. New types of CPT-even nonminimal interaction were proposed in the context of the Dirac equation [38], with repercussions on the study of electron magnetic and electric dipole moments [39] and shifts of the energy levels of particles confined to a Penning trap [40]. Nonminimal couplings composed by CPT-even and CPT-odd higher-derivative operators were also investigated in an extension of the SME, both for the photon [7,41,42] and the fermion sector [43].

In the present paper, we consider two quantum electrodynamics processes, mediated by a photon propagator modified by CPT-even LV coefficients in a minimal way, in such a way that the vertices are not altered. Using the Feynman rules, we evaluate the corrected cross section for two processes with electrons and muons, identifying the way Lorentz violation affects the results.

2. Aspects of the Photonic SME Minimal Sector

The Lagrangian of the CPT-even electrodynamics of the minimal SME,

$$\mathcal{L}=-\frac{1}{4}{F}_{\mu \nu }{F}^{\mu \nu }-\frac{1}{4}{\left(K_F\right)}^{\mu \nu \alpha \beta }{F}_{\mu \nu }{F}_{\alpha \beta },$$

(1)

contains the usual Maxwell term, with $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$, and an LV structure, composed of the constant background tensor field ${\left(K_F\right)}^{\mu \nu \alpha \beta },$ endowed with the same symmetries as the Riemann’s tensor and a null double trace, ${\left(K_F\right)}_{\mu \nu }^{\mu \nu }=0$, which implies a total of 19 components, being 10 birefringent and nine non birefringent ones. This theory obviously preserves gauge invariance.

In general, light birefringence in vacuum is a characteristic of the SME electrodynamics, but the coefficients associated with this phenomenon are strongly constrained by astrophysical data [6]. Thus, we can consider only the nine nonbirefringent components represented by ${\kappa }^{\mu \nu }$, which is a symmetrical traceless tensor, related to the $\left(K_F\right)$ tensor by the following parameterization [44]:

$${\left(K_F\right)}_{\mu \nu \alpha \beta }=\frac{1}{2}\left(g_{\mu \alpha }{\kappa }_{\nu \beta }-g_{\mu \beta }{\kappa }_{\nu \alpha }+g_{\nu \beta }{\kappa }_{\mu \alpha }-g_{\nu \alpha }{\kappa }_{\mu \beta }\right).$$

(2)

Thus, Lagrangian (1) is rewritten as:

$$\mathcal{L}=-\frac{1}{4}{F}_{\mu \nu }{F}^{\mu \nu }-\frac{1}{2}{\kappa }_{\alpha \beta }{F}^{\mu \alpha }{F_{\mu }}^{\beta }.$$

(3)

The non birefringent components can be classified in accordance with the behavior under parity operation, so that one identifies: the parity-even isotropic ${\kappa }_{tr}$ component, the parity-odd ${\kappa }_i$ part and anisotropic parity-even ${\left({\kappa }_{e-}\right)}_{ij}$ components, read as below:

$$\left\{\begin{array}{c}{\kappa }_{00}=\frac{3}{2}{\kappa }_{tr},\\ {\kappa }_{0i}=-{\kappa }_i,\\ {\kappa }_{ij}=\frac{1}{2}{\kappa }_{tr}{\delta }_{ij}-{\left({\kappa }_{e-}\right)}_{ij}.\end{array}\right.$$

(4)

An alternative way to parameterize the ${\kappa }^{\mu \nu }$ tensor was proposed in Ref. [19], using two four-vectors,

$${\kappa }^{\mu \nu }=\frac{1}{2}\left(U^{\mu }{V}^{\nu }+U^{\nu }{V}^{\mu }\right)-\frac{1}{4}{g}^{\mu \nu }\left(U·V\right),$$

(5)

which is useful to represent the main configurations of this tensor. The isotropic sector is recovered by two timelike four-vectors, $U^{\mu }=\left(U^0,0\right),V^{\nu }=\left(V^0,0\right)$, the anisotropic parity-even sector is parameterized by two pure spacelike ones, $U^{\mu }=\left(0,\mathbf{u}\right),$ $V^{\nu }=\left(0,\mathbf{v}\right),$ with $\mathbf{u}·\mathbf{v}=0$, while the anisotropic parity-odd sector is represented by $U^{\mu }=\left(0,\mathbf{u}\right),V^{\nu }=\left(V^0,0\right)$.

Photon Propagator and a Lorentz Violation Gauge Choice

A modified proposal of an LV gauge condition yielding a satisfactory covariant quantization of the electromagnetic field (in the absence of photon mass) was recently developed [21,22]. This is an alternative route to some gauge fixing relations defined in the presence of a small photon mass [45,46]. However, it differs at second order in the LV parameters when small birefringent effects in the parity-odd sector are taken into account. The standard Lorenz gauge was used to exactly calculate the photon propagator, which provided the dispersion relations and allowed the consistency analysis of this electrodynamics [19]. In the present work, we will work with the generalized Lorenz condition,

$${\mathcal{L}}_{GF}=\frac{1}{2\xi }{\left({\partial }_{\alpha }{A}^{\alpha }+{\kappa }_{\alpha \beta }{\partial }^{\alpha }{A}^{\beta }\right)}^2,$$

(6)

choosing $\xi =1$. It is important to mention that the physical results remains gauge independent, since this new gauge is based on longitudinal terms (in momentum) that provide null contributions to the scattering matrix or amplitudes. We then can calculate the propagator, $D^{\delta \epsilon },$ in the momentum space, which fulfills the relation

$$-\left(\left(q^2+{\kappa }_{\mu \nu }{q}^{\mu }{q}^{\nu }\right)g_{\alpha \delta }+q^2{\kappa }_{\alpha \delta }+{\kappa }_{\alpha \beta }{q}^{\beta }{q}^{\chi }{\kappa }_{\chi \delta }\right)D^{\delta \epsilon }={\delta }_{\alpha }^{\epsilon },$$

(7)

so that, at first order in the LV factors, it is given as follows:

$$i{D}^{\alpha \beta }=-i\frac{g^{\alpha \beta }-{\kappa }^{\alpha \beta }}{{q^2+\kappa }_{\mu \nu }{q}^{\mu }{q}^{\nu }}.$$

(8)

The photon nonbirefringent parameters are unobservable in a theory without interaction because they can be removed by a suitable coordinate transformation [47]. When the interaction is turned on, a coordinate transformation only changes the LV parameters from the gauge sector to the matter sector. In the context of this nonbirefringent electrodynamics, in the next sections, we will analyze the cross section of two well known elementary processes.

3. The Pair Annihilation ${\mathit{e}}^{+}+{\mathit{e}}^{-}\to {\mathit{\mu }}^{+}+{\mathit{\mu }}^{-}$

In this section, we calculate the cross section for the pair annihilation/production process, $e^{+}+e^{-}\to {\mu }^{+}+{\mu }^{-},$ represented diagrammatically in Figure 1. The matter sector is considered unaffected by Lorentz violation, so that the fermionic unitary spinors, vertex rules and cross section prescription remain unmodified. The process here considered will not involve photon polarization vectors and the propagator is given by Equation (8). For examining a scenario in which the fermion LV coefficients are considered, see Ref. [48].

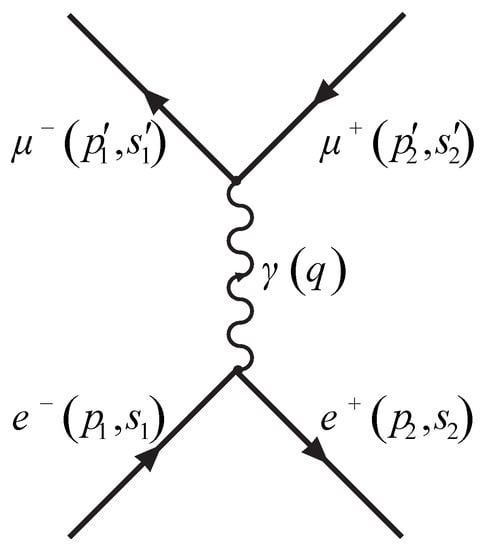
Figure 1. Anihilation process generating a muon and antimuon pair.

Using the well-known Feynman rules, the scattering amplitude for this process is:

$$-i\mathcal{M}={\overline{v}}_{s_2,p_2}ie{\gamma }^{\mu }{u}_{s_1,p_1}i{D}_{\mu \nu }\left(q\right){\overline{u}}_{s_1^{\prime },p_1^{\prime }}ie{\gamma }^{\nu }{v}_{s_2^{\prime },p_2^{\prime }},$$

(9)

where $q=p_1+p_2$ is the transferred momentum. Here, an outgoing fermion and antifermion is represented by ${\overline{u}}_{s^{\prime },p^{\prime }}=u_{s^{\prime },p^{\prime }}^{†}{\gamma }^0$ or $v_{s^{\prime },p^{\prime }},$ while an incoming fermion or antifermion is $u_{s,p}$ or ${\overline{v}}_{s,p}$. The differential cross section is given by:

$$\frac{d\sigma }{d\mathsf{\Omega }}=\frac{\left|{\mathbf{p}}^{\prime }\right|}{{\left(8\pi \right)}^2{\left(E_1+E_2\right)}^2\left|\mathbf{p}\right|}{\left|\mathcal{M}\right|}^2,$$

(10)

with $p_1=\left(E,\mathbf{p}\right),$ $p_2=\left(E,-\mathbf{p}\right)$, $p_1^{\prime }=\left(E,{\mathbf{p}}^{\prime }\right)$ and $p_2^{\prime }=\left(E,-\mathbf{p}{}^{\prime }\right),$ in the center of mass frame. For an unpolarized scattering, we work with the averaged square amplitude,

$$⟨{\left|\mathcal{M}\right|}^2⟩=\frac{1}{4}\sum _{s_1,s_2}\sum _{s_1^{\prime },s_2^{\prime }}{\left|\mathcal{M}\right|}^2,$$

(11)

given by an average on the initial spins and a sum on the final spins. The sum over polarizations are easily performed by using the Casimir’s Trick as usual, yielding the result

$$⟨{\left|\mathcal{M}\right|}^2⟩=\frac{1}{4}{e}^4{D}_{\mu \nu }\left(q\right)D_{\alpha \beta }\left(q\right)L^{\mu \alpha }{M}^{\nu \beta },$$

(12)

in which the leptonic tensors are:

$$\begin{array}{cc}\hfill L^{\mu \alpha }& =4\left[p_2^{\mu }{p}_1^{\alpha }+p_1^{\mu }{p}_2^{\alpha }-g^{\mu \alpha }\left(m_e^2+p_1·p_2\right)\right],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill M^{\mu \alpha }& =4\left[p_2^{\prime \mu }{p}_1^{\prime \alpha }+p_1^{\prime \mu }{p}_2^{\prime \alpha }-g^{\mu \alpha }\left(m_{\mu }^2+p_1^{\prime }·p_1^{\prime }\right)\right],\hfill \end{array}$$

(14)

and the unpolarized differential cross section takes the form,

$$\frac{d\sigma }{d\mathsf{\Omega }}=\frac{\left|{\mathbf{p}}^{\prime }\right|}{{\left(8\pi \right)}^2{\left(E_1+E_2\right)}^2\left|\mathbf{p}\right|}⟨{\left|\mathcal{M}\right|}^2⟩.$$

(15)

In the center of mass frame, ${\left|\mathbf{p}\right|}^2={\left|\mathbf{p}{}^{\prime }\right|}^2+m_{\mu }^2-m_e^2$ and $q=\left(2E,0\right)$. Considering the ultrarelativistic limit, ${\left|\mathbf{p}{}^{\prime }\right|}^2\gg m_{\mu }^2$, the particles energies are much larger than their resting masses. In this regime, one has $p_1=\left(\left|\mathbf{p}\right|,\mathbf{p}\right),$ $p_2=\left(\left|\mathbf{p}\right|,-\mathbf{p}\right)$, $p_1^{\prime }=\left(\left|{\mathbf{p}}^{\prime }\right|,{\mathbf{p}}^{\prime }\right)$ and $p_2^{\prime }=\left(\left|{\mathbf{p}}^{\prime }\right|,-{\mathbf{p}}^{\prime }\right),$ ${\left|\mathbf{p}\right|}^2={\left|{\mathbf{p}}^{\prime }\right|}^2,$ $q=\left(2\left|\mathbf{p}\right|,0\right)$, so that the $L^{\mu \alpha }$ and $M^{\mu \alpha }$ tensors have only pure spacial components:

$$\begin{array}{cc}\hfill L^{ij}& =8{\left|\mathbf{p}\right|}^2\left({\delta }^{ij}-{\widehat{p}}^i{\widehat{p}}^j\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill M^{ij}& =8{\left|\mathbf{p}\right|}^2\left({\delta }^{ij}-{\widehat{p}}^{\prime i}{\widehat{p}}^{\prime j}\right).\hfill \end{array}$$

(17)

The LV contribution stems from the modified propagator. At first order at LV parameters, the quadratic amplitude is:

$$⟨{\left|\mathcal{M}\right|}^2⟩=\frac{e^4}{4}\frac{\left(1-2{\kappa }^{00}\right)L^{ij}{M}^{ij}+2{\kappa }^{ij}{L}^{ki}{M}^{kj}}{{\left(2\left|\mathbf{p}\right|\right)}^4}.$$

(18)

The differential cross section takes the form,

$$\frac{d\sigma }{d\mathsf{\Omega }}=\frac{e^4}{{\left(16\pi \right)}^2}\frac{\left(1-2{\kappa }^{00}\right)L^{ij}{M}^{ij}+2{\kappa }^{ij}{L}^{ki}{M}^{kj}}{{\left(2\left|\mathbf{p}\right|\right)}^6},$$

(19)

revealing that the parity-odd coefficients have no influence on this process. Choosing the incoming beam on the z-axis, $\mathbf{p}=\left(0,0,\left|\mathbf{p}\right|\right)$, the momentum of the scattered particle is ${\mathbf{p}}^{\prime }=\left|\mathbf{p}\right|\left(sin\theta cos\varphi ,sin\theta sin\varphi ,cos\theta \right)$. In this case, the tensors (13) and (14) can be read as

$$L^{\mu \nu }=8{\left|\mathbf{p}\right|}^2\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\end{array}\right),$$

(20)

$$M^{\mu \nu }=8\left(\begin{array}{ccc}0& 0& 0\\ {p_y^{\prime }}^2+{p_z^{\prime }}^2& -p_x^{\prime }{p}_y^{\prime }& -p_x^{\prime }{p}_z^{\prime }\\ -p_x^{\prime }{p}_y^{\prime }& {p_x^{\prime }}^2+{p_z^{\prime }}^2& -p_y^{\prime }{p}_z^{\prime }\\ -p_x^{\prime }{p}_z^{\prime }& -p_y^{\prime }{p}_z^{\prime }& {p_x^{\prime }}^2+{p_y^{\prime }}^2\end{array}\right).$$

(21)

The total cross section is achieved by integrating on the solid angle element,

$${\sigma }_{total}=\int \frac{d\sigma }{d\mathsf{\Omega }}d\mathsf{\Omega }.$$

(22)

As we can see from matrix (21), the angular dependence of the differential cross section is completely contained in the M tensor, which possesses non diagonal elements. Integrating in the angle $\varphi$,

$$\int M^{ij}d\varphi =8\pi {\left|\mathbf{p}\right|}^2\left(\left(1+{cos}^2\theta \right){\delta }^{ij}+\left(1-3{cos}^2\theta \right){\widehat{p}}^i{\widehat{p}}^j\right).$$

(23)

The differential cross section now becomes

$$\frac{d\sigma }{dcos\theta }=\frac{\pi {\alpha }^2}{2s}\left(1+{cos}^2\theta \right)\left(1-2{\kappa }^{00}+{\kappa }^{ii}-{\kappa }^{ij}{\widehat{p}}^i{\widehat{p}}^j\right),$$

(24)

where $\sqrt{s}=2\left|\mathbf{p}\right|$ is the total energy at center of mass and $\alpha$ is the fine structure constant. The total cross section is:

$$\sigma ={\int }_0^{\pi }\frac{d\sigma }{dcos\theta }sin\theta d\theta .$$

(25)

From Equations (24) and (25), we attain

$$\sigma ={\sigma }_0\left(1-{\kappa }_{00}-{\widehat{p}}^i{\widehat{p}}^j{\kappa }_{ij}\right),$$

(26)

or, by making use of relations (4),

$$\sigma ={\sigma }_0\left(1-2{\kappa }_{tr}+{\left({\kappa }_{e-}\right)}_{ij}{\widehat{p}}^i{\widehat{p}}^j\right),$$

(27)

where

$${\sigma }_0=\frac{4\pi {\alpha }^2}{3s}$$

(28)

is the usual total cross section (in the absence of Lorentz violation). We thus notice that the photon LV parameters correct the usual result with two pieces: one isotropic, proportional to ${\kappa }_{tr}$; another anisotropic, depending on the components ${\kappa }_{ij}$ and its contractions (spatial angles) with the momentum components.

Sidereal Effects

The LV coefficients are considered as fixed in the Sun’s frame, but not in the Earth’s reference frame (RF), due to the rotation motions. As the experimental apparatus is located in Earth, we should be able to relate the coefficients measured in a Sun-based RF, where these coefficients are approximately constant, and in Earth’s frame. The sidereal analysis consists of translating the bounds between these RFs. We will consider, as in the literature [49], the Earth-based Lab’s RF at the colatitude $\chi$, rotating around the Earth’s axis with angular velocity $\mathsf{\Omega }=2\pi /23$ h$56\mathrm{s}$. The Earth-based RF has axes x, y and z, while the Sun-based RF has X, Y and Z as axes, so that

$$\left(\begin{array}{c}\widehat{x}\\ \widehat{y}\\ \widehat{z}\end{array}\right)={\left[{\mathcal{R}}_{ij}\right]}_{3\times 3}\left(\begin{array}{c}\widehat{X}\\ \widehat{Y}\\ \widehat{Z}\end{array}\right),$$

(29)

with ${\mathcal{R}}_{ij}$ representing merely a spatial rotation,

$${\mathcal{R}}_{ij}=\left(\begin{array}{ccc}cos\chi cos\mathsf{\Omega }t& cos\chi sin\mathsf{\Omega }t& -sin\chi \\ -sin\mathsf{\Omega }t& cos\mathsf{\Omega }t& 0\\ sin\chi cos\mathsf{\Omega }t& sin\chi sin\mathsf{\Omega }t& cos\chi \end{array}\right).$$

(30)

For experiments up to a few weeks long, the transformation law for a rank-2 tensor is $A_{ij}^{\left(\mathrm{Lab}\right)}={\mathcal{R}}_{ik}{\mathcal{R}}_{jl}{A}_{kl}^{\left(\mathrm{Sun}\right)},$ with $A_{ij}^{\left(\mathrm{Lab}\right)}\equiv A_{ij}^{(x,y,z)}$ and $A_{ij}^{\left(\mathrm{Sun}\right)}\equiv A_{ij}^{(X,Y,Z)}$. By definition, the non rotating frame has the Z-axis aligned with the direction of the Earth’s rotation axis and the other two axes are chosen to have $0^{\circ }$ declination and right ascension ($\widehat{X}$ axis) and declination $0^{\circ }$ and right ascension ${90}^{\circ }$ ($\widehat{Y}$ axis). For the rotating frame, the x-axis points from the Earth’s center to the Sun on the vernal equinox in 2000—for more details, see Refs. [5,49,50,51]. This axis scenario is illustrated in Figure 2.

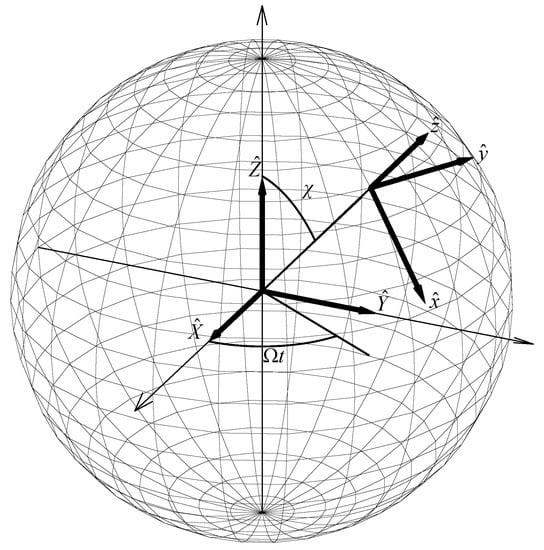
Figure 2. In the center, we have a non-rotated basis and, on the surface, we have the lab basis.

The influence of earth rotation on spatial components of $\kappa$ tensor is given as:

$${\left({\kappa }_{e-}\right)}_{LAB}^{ij}=R^{ia}{\left({\kappa }_{e-}\right)}_{SUN}^{ab}{R}^{jb}.$$

(31)

Usually, experimental data are taken at different times. Effectively is measured a time average cross section:

$${\left(\overline{\kappa }\right)}_{LAB}=\frac{\mathsf{\Omega }}{2\pi }{\int }_0^{\frac{2\pi }{\mathsf{\Omega }}}{\left(\kappa \right)}_{LAB}dt,$$

(32)

explicitly

$${\overline{\kappa }}_{e-}=\frac{{\left({\kappa }_{e-}\right)}_{ZZ}}{2}\left(\begin{array}{ccc}3{sin}^2\chi -1& 0& -\frac{3sin2\chi }{2}\\ 0& -1& 0\\ -\frac{3sin2\chi }{2}& 0& 3{cos}^2\chi -1\end{array}\right).$$

(33)

The component ${\kappa }_{tr}$ is invariant under rotations. In the lab coordinate system represented in Figure 2, the momentum of incoming particle can be considered in the x–y plane. Thus, $\widehat{p}=(cos\beta ,sin\beta ,0)$, $\widehat{\beta }=(-sin\beta ,cos\beta ,0)$, and ${\widehat{p}}^{\prime }=cos\theta \widehat{p}+sin\theta cos\varphi \widehat{\beta }+sin\theta sin\varphi \widehat{z}$. Total and differential cross sections are rewritten using Equation (33) as:

$$\frac{d\sigma }{dcos\theta }={\left(\frac{d\sigma }{dcos\theta }\right)}_0\left(1-2{\kappa }_{tr}-\frac{{\left({\kappa }_{e-}\right)}_{ZZ}}{2}\left(1-3{cos}^2\beta {sin}^2\chi \right)\right),$$

(34)

$$\sigma ={\sigma }_0\left(1-2{\kappa }_{tr}-\frac{{\left({\kappa }_{e-}\right)}_{ZZ}}{2}\left(1-3{cos}^2\beta {sin}^2\chi \right)\right).$$

(35)

The Lorentz violation effect appears as a spatial anisotropy according the experimental orientation of initial beam, represented by $\beta$ and $\chi$. The energy dependence is the same one as the standard QED.

We can now discuss the possibility of using the present results to impose upper bounds on these LV coefficients. This can be done using experimental data from Refs. [52,53,54] for the $e^{+}+e^{-}\to {\mu }^{+}+{\mu }^{-}$ scattering, which yields

$$\frac{\sigma -{\sigma }_{QED}}{{\sigma }_{QED}}=\pm \frac{2s}{{\mathsf{\Lambda }}_{\pm }^2},$$

(36)

where $\sqrt{s}=29GeV$ and ${\mathsf{\Lambda }}_{+}=170GeV$ with $95\%$ confidence level. Supposing that ${\left({\kappa }_{e-}\right)}_{ZZ}=0$ and comparing Equation (1) with the experimental uncertainty $2s/{\mathsf{\Lambda }}_{\pm }^2\simeq 0.58$, we obtain the following upper bound for the isotropic coefficient:

$${{\kappa }_{tr}<2.9\times 10}^{-2}.$$

(37)

Now, considering ${\kappa }_{tr}=0$, the bound on the parity-even coefficients is

$${\left(1-3{cos}^2\beta {sin}^2\chi \right){\left({\kappa }_{e-}\right)}_{ZZ}<1.2\times 10}^{-1}.$$

(38)

These upper bounds are not good limits. The reason is that the LV parameters are dimensionless, so that they appear alone inside the expression after the usual cross section, ${\sigma }_0$, which is not multiplying any parameter endowed with mass dimension. This is different to what is observed in similar scatterings considered in nonminimal electrodynamics [32,36], where the LV parameter appears multiplied by the center of mass energy, $s,$ implying better upper bounds by this factor. In this sense, see also Ref. [55].

4. The Scattering Process ${\mathit{e}}^{-}+{\mathit{\mu }}^{-}\to {\mathit{e}}^{-}+{\mathit{\mu }}^{+}$

In this section, we consider a process where the electron is scattered by a heavier particle, as the muon. The Feynman diagram for the process $e^{-}+{\mu }^{-}\to e^{-}+{\mu }^{+}$ is given in Figure 3: Using Feynman’s rules, we write the scattering amplitude,

$$\mathcal{M}=e^2{\overline{u}}_{s_1^{\prime },p_1^{\prime }}{\gamma }^{\mu }{u}_{s_1,p_1}{D}_{\mu \nu }\left(q\right){\overline{u}}_{s_2^{\prime },p_2^{\prime }}{\gamma }^{\nu }{u}_{s_2,p_2}.$$

(39)

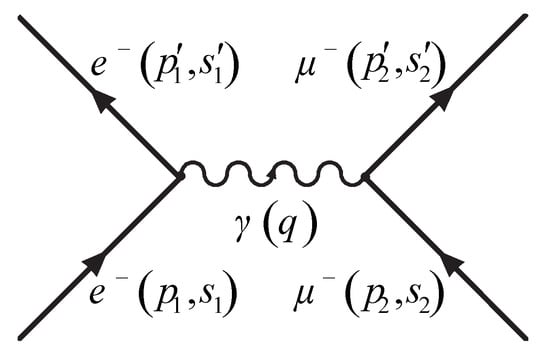
Figure 3. Feynman diagram of electron–muon scattering at tree level.

In practice, it is common to study processes where particles do not have polarization. In this case, the squared amplitude will be the same expression as Equation (12), with the $L^{\mu \alpha }$ and $M^{\mu \alpha }$ tensors now written as

$$\begin{array}{cc}\hfill L^{\mu \alpha }& =4[p_1^{\mu }{p}_1^{\prime }{}^{\alpha }+p_1^{\prime }{}^{\mu }{p}_1^{\alpha }+g^{\mu \alpha }\left(m_e^2-p_1·p_1^{\prime }\right)],\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill M^{\nu \beta }& =4[p_2^{\nu }{p}_2^{\prime }{}^{\beta }+p_2^{\prime }{}^{\nu }{p}_2^{\beta }+g^{\nu \beta }\left(m_{\mu }^2-p_2·p_2^{\prime }\right)].\hfill \end{array}$$

(41)

To calculate the cross section, we must choose a frame, adopting again the center of mass reference, where $p_1=\left(E_1,\mathbf{p}\right)$, $p_2=\left(E_2,-\mathbf{p}\right)$, $p_1^{\prime }=\left(E_1,{\mathbf{p}}^{\prime }\right)$ and $p_2^{\prime }=\left(E_2,-{\mathbf{p}}^{\prime }\right)$, which implies

$$\begin{array}{cc}\hfill L^{00}& =4\left[2m_e^2+{\left|\mathbf{p}\right|}^2+\mathbf{p}·{\mathbf{p}}^{\prime }\right],\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill L^{0i}& =4E_1{\left[p^{\prime }+p\right]}^i,\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill L^{ij}& =4\left[p^i{p^{\prime }}^j+{p^{\prime }}^i{p}^j+{\delta }^{ij}\left({\left|\mathbf{p}\right|}^2-\mathbf{p}·{\mathbf{p}}^{\prime }\right)\right],\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill M^{00}& =4\left[2m_{\mu }^2+{\left|\mathbf{p}\right|}^2+\mathbf{p}·{\mathbf{p}}^{\prime }\right],\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill M^{0i}& =-4E_2{\left[p^{\prime }+p\right]}^i,\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill M^{ij}& =4\left[p^i{p^{\prime }}^j+{p^{\prime }}^i{p}^j+{\delta }^{ij}\left({\left|\mathbf{p}\right|}^2-\mathbf{p}·{\mathbf{p}}^{\prime }\right)\right].\hfill \end{array}$$

(47)

Mott Scattering

In the Mott scattering, the target is a large mass particle. It is defined in the limit $M\gg m\gg \left|\mathbf{p}\right|$. In this situation, small relativistic effects at order $1/m$ are considered, but the recoil of the heavy particle is negligible. The tensor $M^{\mu \alpha }$ in Equation (41) becomes:

$$M^{\mu \alpha }\to 8m_{\mu }^2\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right).$$

(48)

Just as before, the rotations of the Earth induce time dependence on the $\kappa$ tensor components, which can be replaced by the temporal average:

$${\overline{\kappa }}^{00}=\frac{3}{2}{\kappa }_{tr},$$

(49)

$${\overline{\kappa }}^{0i}={\kappa }_Z(-sin\chi ,0,cos\chi ),$$

(50)

$${\overline{\kappa }}^{ij}=\frac{1}{2}{\kappa }_{tr}{\delta }^{ij}-{\left({\kappa }_{e-}\right)}^{ij}.$$

(51)

In this situation, we have the implicit form for the differential cross section:

$$\frac{d\sigma }{d\mathsf{\Omega }}=\frac{2M^2{e}^4}{{\left(8\pi \right)}^2{\left(E_1+E_2\right)}^2}\frac{L^{00}-2{\kappa }^{00}{L}^{00}+2{\overline{\kappa }}^{0i}{L}^{0i}}{{\left|\mathbf{q}\right|}^4-2{\left|\mathbf{q}\right|}^2{q}^i{\overline{\kappa }}^{ij}{q}^j},$$

(52)

which can be specialized for some particular cases.

Pure parity-odd case: when one considers only the parity-odd contribution, ${\kappa }_{tr}=0$ and ${\kappa }_{e-}=0$, the differential cross section becomes:

$$\frac{d\sigma }{d\mathsf{\Omega }}=\frac{{\alpha }^2}{8{\left({\left|\mathbf{p}\right|}^2-\mathbf{p}·{\mathbf{p}}^{\prime }\right)}^2}\left(8m_e^2+4{\left|\mathbf{p}\right|}^2+4\mathbf{p}·{\mathbf{p}}^{\prime }+8k_{Z}m\left(\left(p_z+p_z^{\prime }\right)cos\chi -\left(p_x+p_x^{\prime }\right)sin\chi \right)\right).$$

(53)

In this process, the parity-odd contribution does not vanish, which is ascribed to Equation (43). To simplify this expression, we consider the incoming beam in the x–y plane, with: $\widehat{p}=(cos\beta ,sin\beta ,0)$, $\widehat{\beta }=(-sin\beta ,cos\beta ,0)$, $\mathbf{p}=\left|\mathbf{p}\right|\widehat{p}$, and ${\widehat{p}}^{\prime }=cos\theta \widehat{p}+sin\theta cos\varphi \widehat{\beta }+sin\theta sin\varphi \widehat{z}$. By integrating over $\varphi$:

$$\frac{d\sigma }{dcos\theta }=\frac{\pi {\alpha }^2}{2{\left|\mathbf{p}\right|}^4{sin}^2\frac{\theta }{2}}\left(m^2+{\left|\mathbf{p}\right|}^2{cos}^2\frac{\theta }{2}-2k_{Z}m\left|\mathbf{p}\right|cos\beta sin\chi {cos}^2\frac{\theta }{2}\right).$$

(54)

Using the Lorentz factor $\gamma =1/\sqrt{1-{\left|\mathbf{v}\right|}^2}$, with $\mathbf{v}=\mathbf{p}/E$, the cross section is

$$\frac{d\sigma }{dcos\theta }=\frac{\pi {\alpha }^2}{2m^2{\gamma }^2{\mathbf{v}}^4{sin}^2\frac{\theta }{2}}\left(1-{\mathbf{v}}^2{sin}^2\frac{\theta }{2}-2\frac{k_Z}{\gamma }\left|\mathbf{v}\right|cos\beta sin\chi {cos}^2\frac{\theta }{2}\right).$$

(55)

The factored expression is the standard Rutherford scattering differential cross section, while the element proportional to ${\left|\mathbf{v}\right|}^2$ is the well known electron magnetic moment effect of the Mott scattering. The LV effect is similar and the angle $\beta$ represents the direction of initial beam with respect to the x-direction. If $\mathbf{p}$ is aligned with the y-direction, there will be no sign of Lorentz violation and maximum level effects correspond to the configuration in which $\mathbf{p}$ is parallel to x. This differential cross section is illustrated in Figure 4.

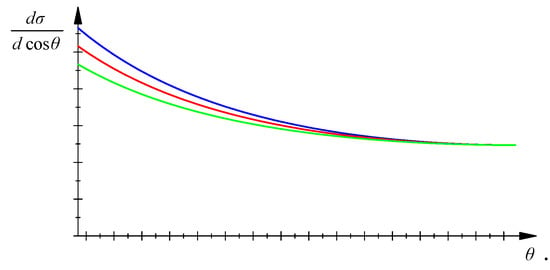
Figure 4. The differential cross section in arbitrary units. The red line corresponds to the usual case, while green and blue lines represent small Lorentz violation scenarios with $k_Z\left|\mathbf{v}\right|cos\beta sin\chi$ assuming positive and negative values. The angles $\beta$ and $\chi$ are fixed, while $\theta$ goes from $\pi /2$ to $\pi$.

Isotropic contribution: The isotropic case is defined by ${\kappa }_i=0$ and ${\kappa }_{e-}=0$, for which the differential cross section is

$$\frac{d\sigma }{d\mathsf{\Omega }}=\frac{\left(1-2{\kappa }_{tr}\right){\alpha }^2}{8{\left({\left|\mathbf{p}\right|}^2-\mathbf{p}·{\mathbf{p}}^{\prime }\right)}^2}\left(8m^2+4{\left|\mathbf{p}\right|}^2+4\mathbf{p}·{\mathbf{p}}^{\prime }\right).$$

(56)

Analogously to the previous section, the differential cross section is the same (as the Mott one), except for a multiplicative factor.

Anisotropic parity-even contribution: now we present the differential cross section for the anisotropic parity-even case, with ${\kappa }_i=0$ and ${\kappa }_{tr}=0$. After integrating over $\varphi$, the differential cross section is given by

$$\frac{d\sigma }{dcos\theta }={\left(\frac{d\sigma }{dcos\theta }\right)}^{Mott}\left(1+\frac{1}{4}{\left({\kappa }_{e-}\right)}_{ZZ}\left(1-3cos\theta \right)\left(1-3{cos}^2\beta {sin}^2\chi \right)\right),$$

(57)

which is illustrated in Figure 5. Again, the Lorentz violation effect comes with the appearance of a direction dependence (space anisotropy), without changing the behavior with the energy.

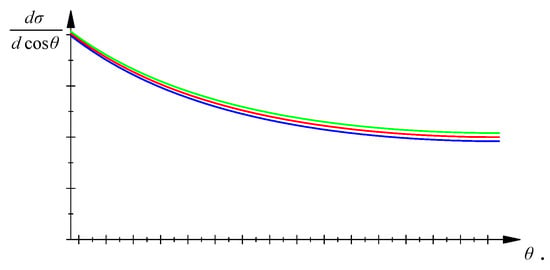
Figure 5. The differential cross section in arbitrary units. The red line corresponds to the usual case while green and blue lines represent small Lorentz violation situations with ${\left({\kappa }_{e-}\right)}_{ZZ}\left(1-3{cos}^2\beta {sin}^2\chi \right)$ assuming positive and negative values. The angles $\beta$ and $\chi$ are fixed, while $\theta$ goes from $\pi /2$ to $\pi$.

5. Conclusions

In this work, we have considered the contributions of a modified quantum electrodynamics for two known scattering processes, $e^{+}+e^{-}\to {\mu }^{+}+{\mu }^{-}$ and $e^{-}+{\mu }^{-}\to e^{-}+{\mu }^{+}$. The Feynman rules were used to evaluate the corrections to the respective cross sections, identifying the way Lorentz violation alters the usual results. The cross section for the electron–positron annihilation is modified only by the parity-even and isotropic components of the tensor ${\kappa }^{\mu \nu },$ but not by the parity-odd coefficients. The parity-even piece induces space anisotropies that are subject to sidereal variations, which were examined as well. The LV contributions represent corrections which should be comparable with experimental imprecision in the cross section measurements, as properly commented on in the final part of Section 3. As the LV coefficients are dimensionless, the upper bounds are not tight, in contrast with the analogue scenario observed in the context of nonminimal coupling models [32,36,55]. Concerning the second process, the corresponding differential cross section was carried out and particularized for three cases, in accordance with the nature of the LV coefficient: isotropic, parity-odd or parity even. The last two ones are endowed with space anisotropy and were depicted in comparative graphs. The modified cross sections have shown the same energy behavior as the usual case. Given the dimensionless nature of the LV parameters, upper bounds of similar magnitude to the ones of Equations (37) and (38) could also be attained in this case.