In the framework of the NHM, the electrons of a narrow, roughly half-filled superconducting band lower their total Coulomb energy by producing
-space magnetism. This far-reaching assertion follows from the three postulates of the NHM [
1] and from the special properties of the spin-dependent Wannier functions representing the atomic-like states in a superconducting band. In
Section 4.1, we first repeat the definition of spin-dependent Wannier functions in the special case of a metal with one atom in the unit cell (the general definition is given in Ref. [
5]), and in
Section 4.2 we show that the postulates of the NHM define an interaction producing
-space magnetism.
4.1. Spin-Dependent Wannier Functions
For the sake of simplicity, we consider a metal with only one atom in the unit cell. In this case, superconducting bands are single bands [
5]. Furthermore, we assume that this metal possesses a narrow, half-filled superconducting band in its band structure. By definition we can unitarily transform the Bloch functions of this band into optimally localized and symmetry-adapted spin-dependent Wannier functions [
5]. We do this by replacing the Bloch functions
of the superconducting band by Bloch spinors
with
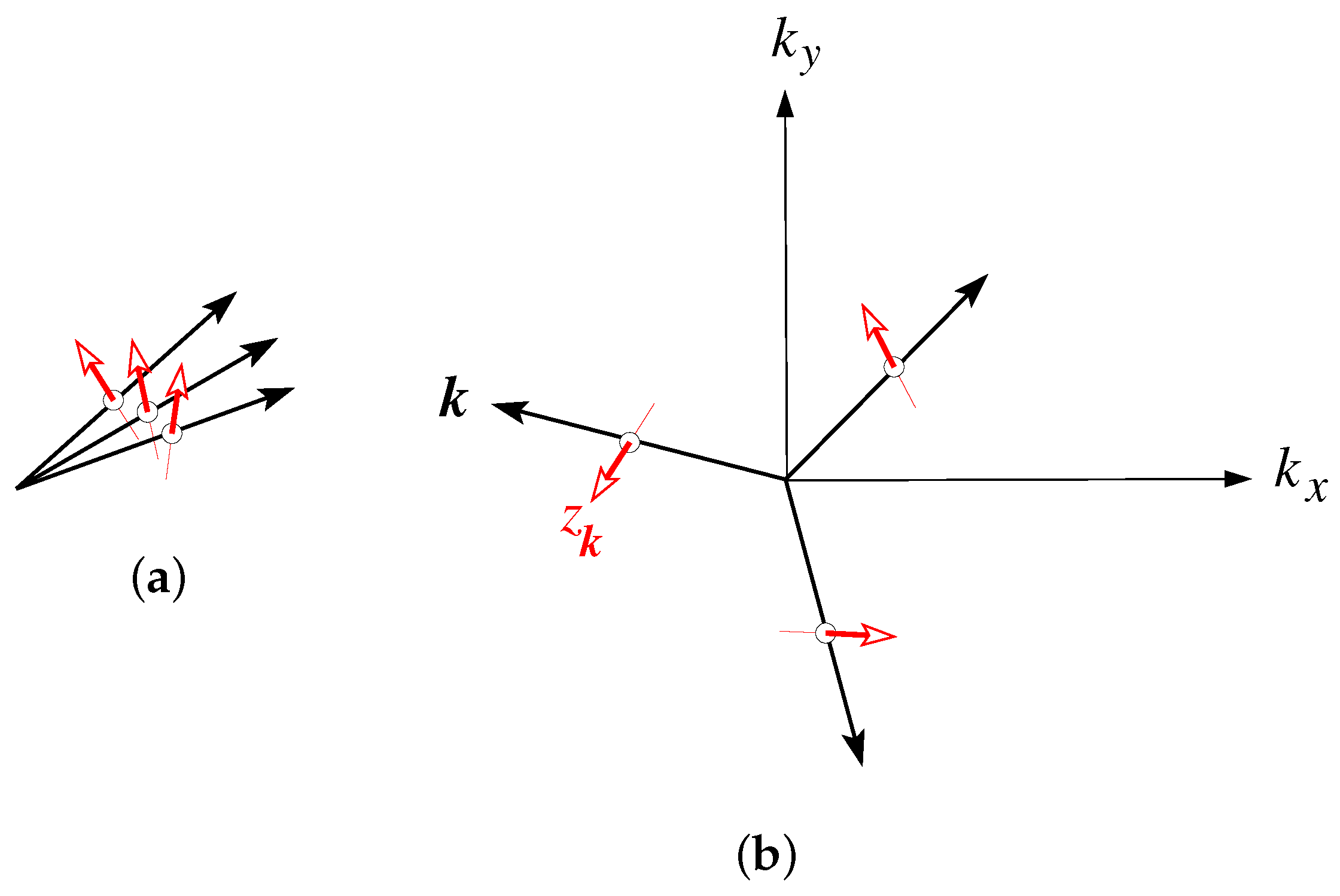
dependent spin directions. The functions
denote Pauli’s spin functions:
where
and
are the spin quantum number and the spin coordinate, respectively. (To simplify, we ignore that in some points of symmetry the Bloch spinors may not be written in the form of Equation (
7) [
5].) The coefficients
in Equation (
7) form a
dependent two-dimensional matrix
which is unitary,
in order that the spin-dependent Wannier functions in Equation (
11) form a complete orthonormal basis in the superconducting band. The Bloch spinors
are usual Bloch functions with anti-parallel spins possessing, however, a
dependent symmetry axis
defined by the matrix
.
Since still we consider a superconducting band, the coefficients
can be chosen in such a way that the spin-dependent Wannier functions
are optimally localized and symmetry-adapted to the full space group of the considered metal [
5]. The sum in Equation (
11) is over the
N vectors
of the first Brillouin zone (BZ), and
denotes a lattice vector. However, the coefficients
cannot be chosen independent of
since, as mentioned in
Section 1, we cannot unitarily transform the Bloch functions of the superconducting band into usual (i.e., spin-independent) Wannier functions that are also optimally localized and symmetry-adapted. Hence, the spin-dependent Wannier functions differ substantially from usual spin-independent Wannier functions even if we neglect spin-orbit effects.
The Bloch spinors may be calculated from the spin-dependent Wannier functions by the equation
where the sum now is over the
N lattice vectors
of the Born-von Kàrmàn volume (BvK).
4.2. Nonadiabatic Interaction Producing k-Space Magnetism
Let be the operator
the Hamiltonian in the superconducting band with
and
representing the Hartree–Fock and Coulomb energy, respectively. The fermion operators
and
create and annihilate electrons in the localized states
represented by the spin-dependent Wannier functions
in Equation (
11). We write
as
where
and
contain the matrix elements of
with
and
respectively, and
comprises the remaining (non-diagonal) matrix elements with
The operators
and
represent the Coulomb repulsion and the exchange interaction, respectively, between atomic-like electrons and, hence, do not contradict the picture of localized electron states moving as Bloch waves through the crystal.
, on the other hand, represents an interaction
destroying the atomic-like motion [
1].
Now, consider the operator
being gained from
H in Equation (
13) by putting
equal to zero, and assume the
exact ground states
and
of
H and
, respectively, to be determined. The first postulate of the NHM states that a pure atomic-like motion is energetic more favorable than an atomic-like motion disturbed by
,
if the superconducting band is one of the narrowest bands in the considered metal, see the detailed substantiation in Ref. [
1].
The second postulate of the NHM states that the electronic transitions represented by
are attributed to the adiabatic approximation and do not occur in the true nonadiabatic system,
for
if Inequality (
20) is true. At the transition to the nonadiabatic system, the electron system lowers its total Coulomb energy by the “nonadiabatic condensation energy”
Equation (
21) is suggested by the fact that the non-diagonal matrix elements of
depend very sensitively on the exact form of the localizes orbitals and, hence, only small modifications should be required to suppress the transitions represented by
. The modified localized orbitals cannot be described within the adiabatic approximation (since here Inequality (
20) is true) but require the introduction of nonadiabatic localized states
possessing the same symmetry as the spin-dependent Wannier functions, see the detailed discussion in Ref. [
1]. The new quantum number
labels the nonadiabatic motion of the atomic core following the motion of the localized electron, and
labels the special states satisfying Equation (
21).
The nonadiabatic symmetry operators (as defined in Equation (B9) of Ref. [
1]) no longer act on the electronic coordinates alone, but additionally on the coordinate describing that part of the motion of the atomic core that follows the motion of the electron. Thus, the electronic motion in the nonadiabatic localized states
is not so confined by symmetry as in the adiabatic states
. The electrons now move in a potential depending on which of the adjacent localized states are occupied and on the present positions of these electrons. Hence, the nonadiabatic localized states represent a
strongly correlated atomic-like motion.
It is essential that the NHM does not only neglect
but postulates a nonadiabatic mechanism suppressing the transitions generated by
. This has the important consequences that, first, the nonadiabatic Hamiltonian commutes with the operators of the space group if and only if the nonadiabatic localized states are adapted to the symmetry of the space group [
1], and, second, the naked electrons no longer have exact Fermi character. Now, the Fermi excitations are represented by electrons occupying the nonadiabatic states
traveling as Bloch states through the crystal.
The nonadiabatic states are postulated to interpret Inequality (
20) and to understand Equation (
21). I believe that it would be physically needless to try to determine explicitly the highly complex localized functions representing the nonadiabatic states. We may assume that the modifications of the adiabatic electronic orbitals required in Equation (
21) are so small that any calculation of expectation values (i.e., of diagonal matrix elements) still can be performed within the adiabatic approximation. That means that any expectation value in the superconducting band can be determined in close approximation by replacing the nonadiabatic localized functions by the adiabatic spin-dependent Wannier functions [
1].
This has the consequences that, first, the spin-dependent Wannier functions must be adapted to the symmetry of the space group such that the nonadiabatic Hamiltonian correctly commutes with the operators of the space group, and, second, the expectation values of the electronic spin directions are determined by the Bloch spinors in Equation (
12) because they represent the nonadiabatic Bloch states within the adiabatic approximation. Thus, the adiabatic Bloch spinors in Equation (
12) define the spin direction of the electrons in the nonadiabatic system, and, consequently, produce
-space magnetism.
In summary, the electrons in a narrow, roughly half-filled superconducting band may lower their Coulomb energy by the nonadiabatic condensation energy
in Equation (
23) by producing
-space magnetism, as described in
Section 2. The
dependent spin directions are defined by the coefficients
in Equation (
7), which in turn are determined by the demand that the spin-dependent Wannier functions must be optimally localized and symmetry-adapted to the space group of the considered metal.