A Modified Dolph-Chebyshev Type II Function Matched Filter for Retinal Vessels Segmentation
Abstract
1. Introduction
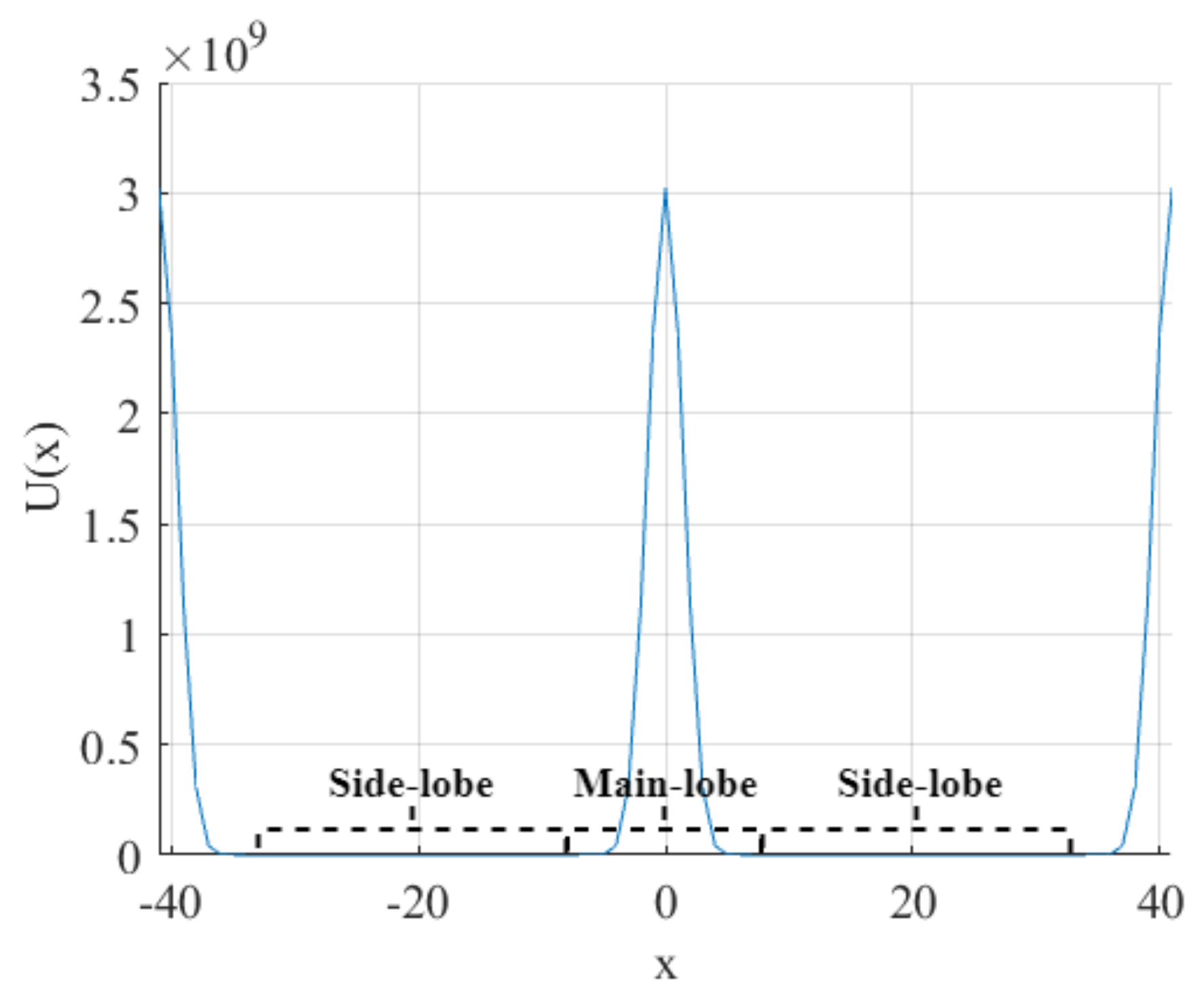
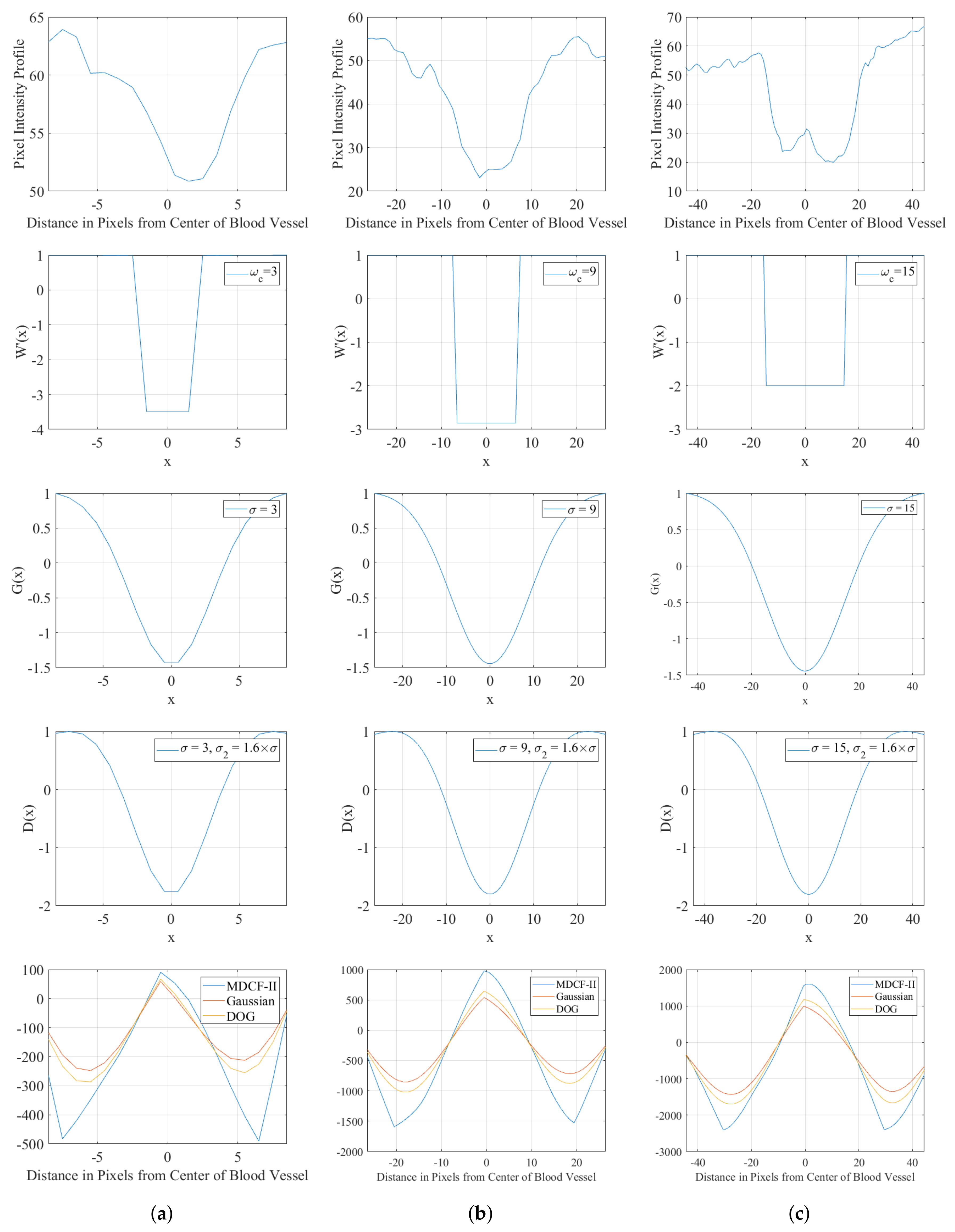
2. Design of the New Matched Filter Window
3. Retinal Vessels Segmentation Using Proposed Matched Filter
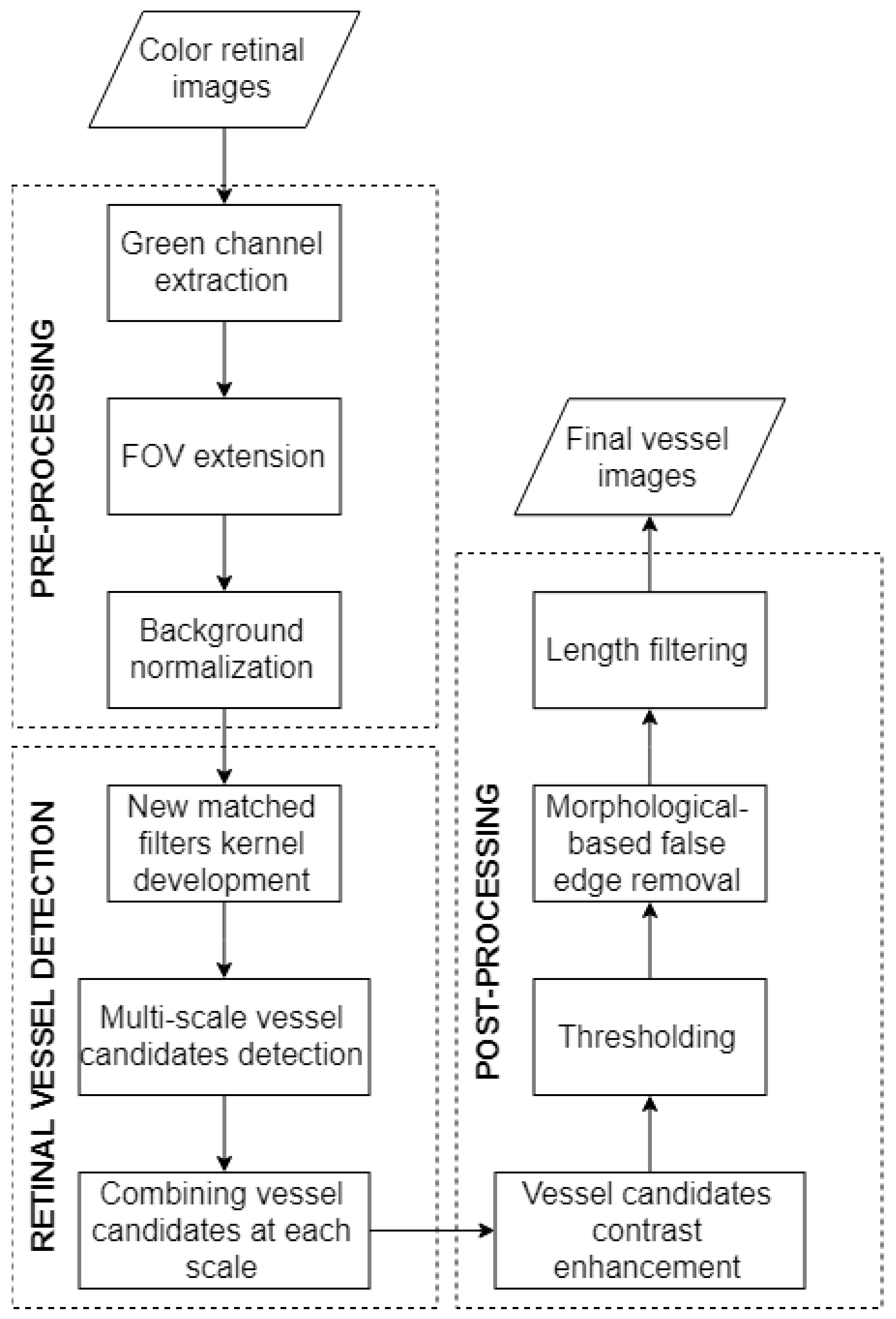
3.1. Pre-Processing and Post-Processing Phases
3.2. Retinal Vessels Detection Phase
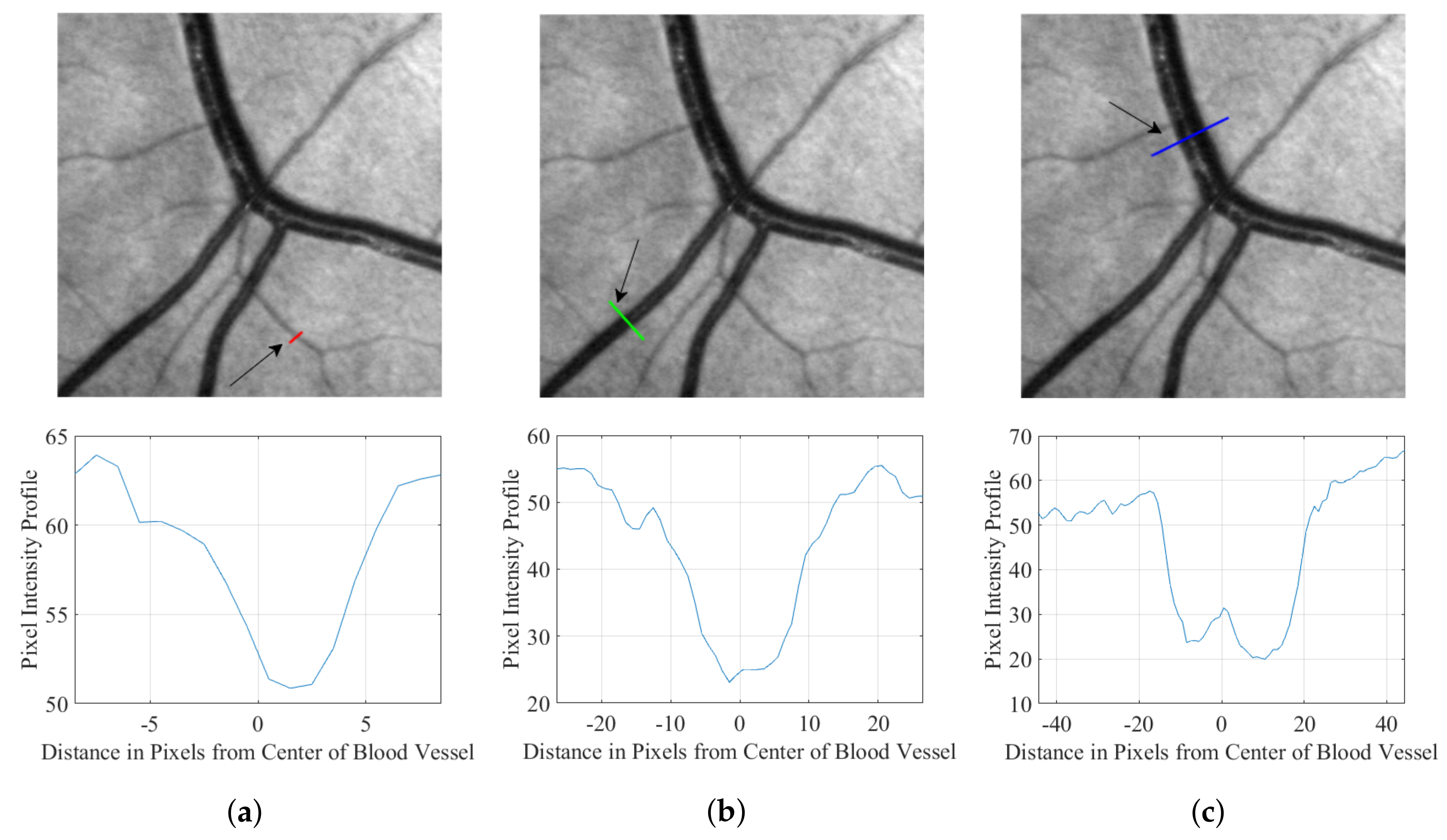
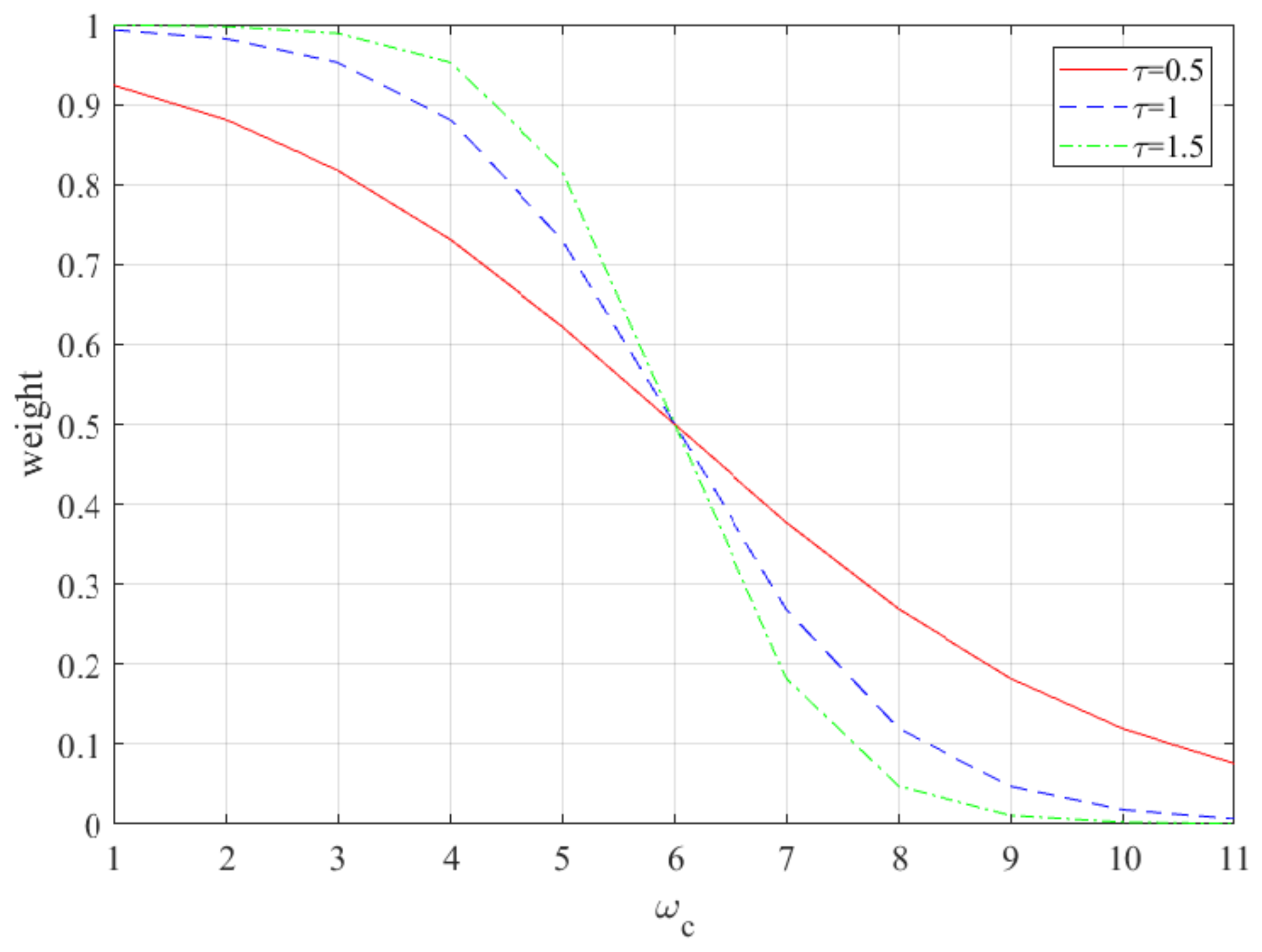
3.3. Parameter Setting
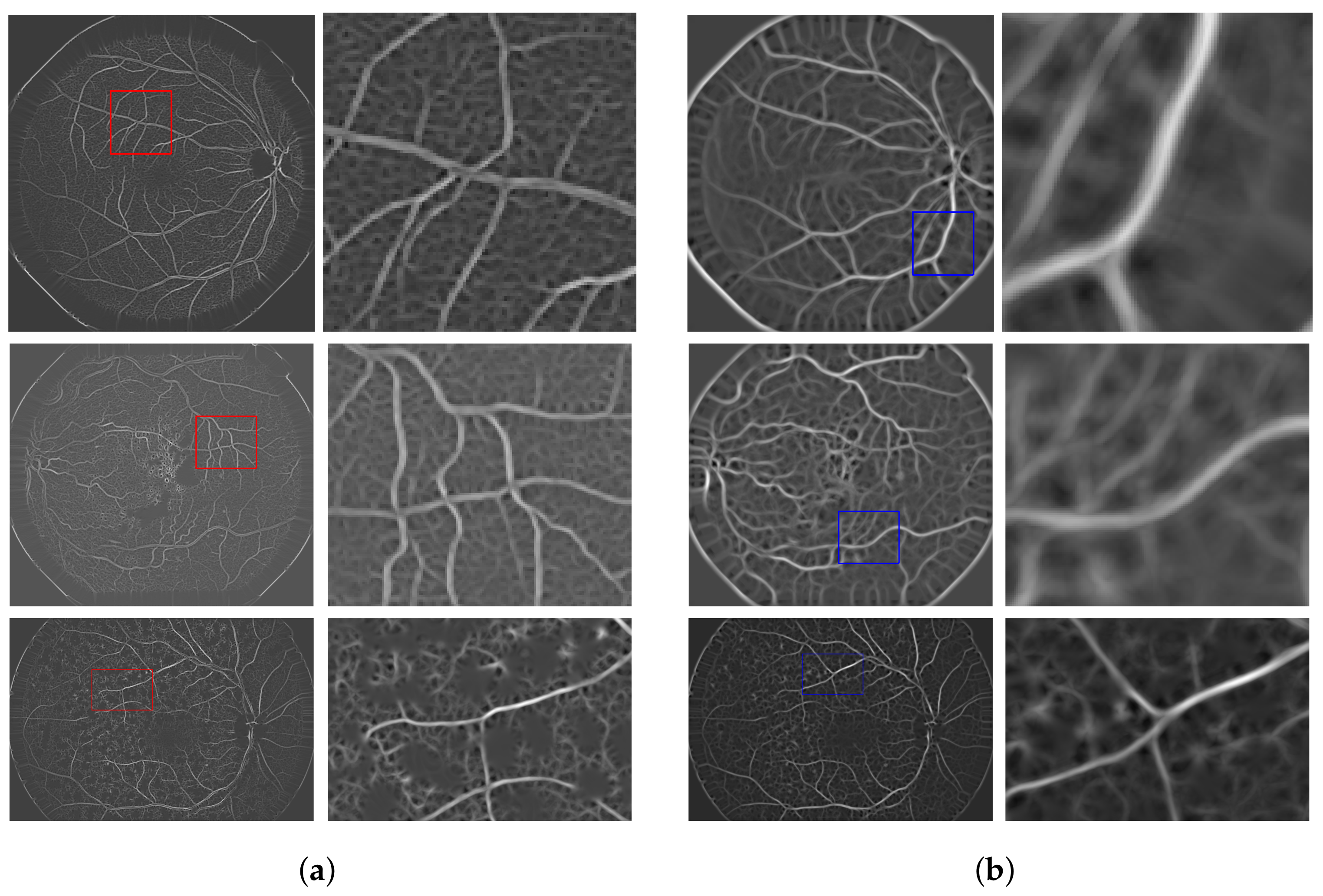
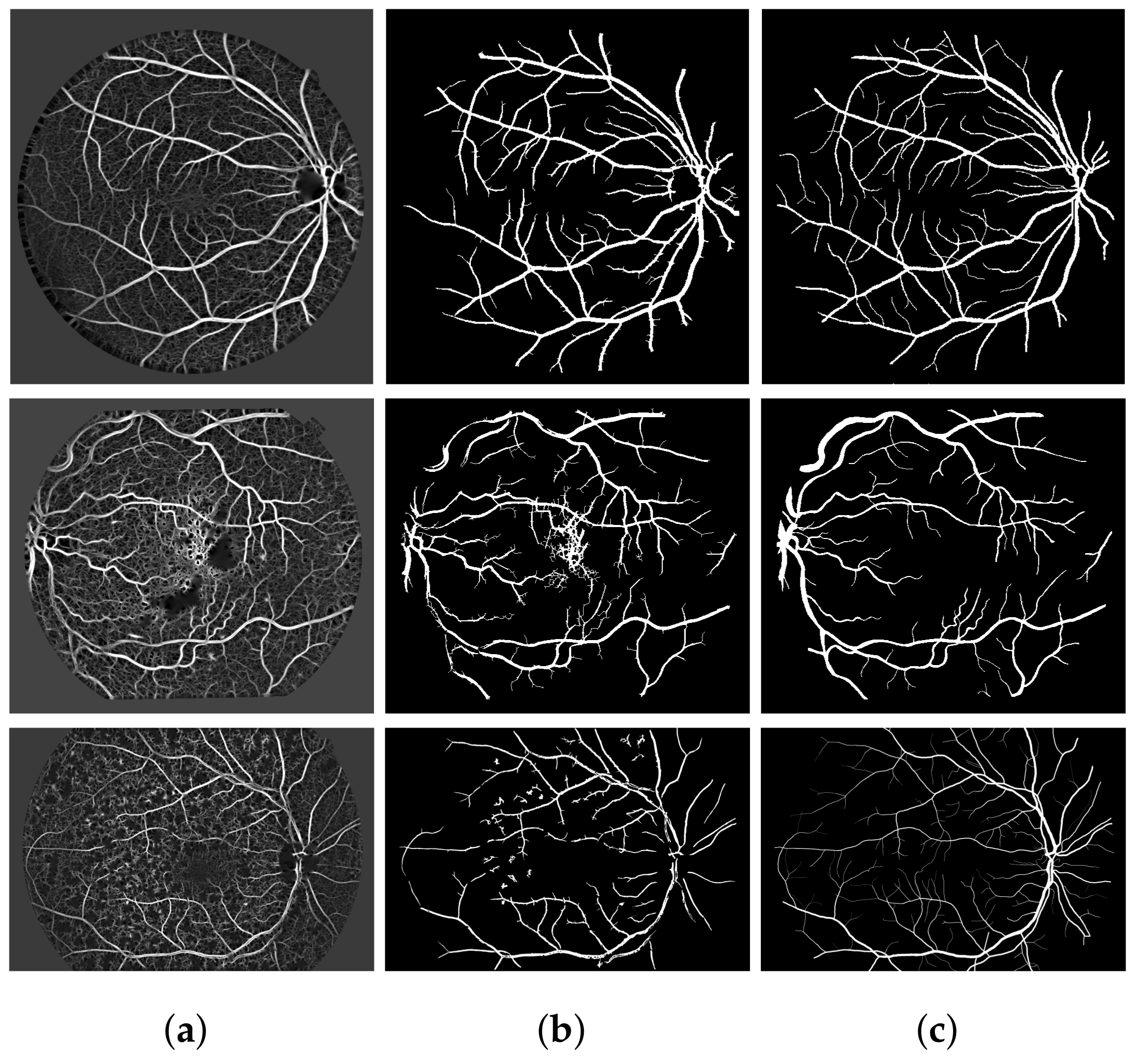
4. Experimental Results and Discussions
5. Discussion
5.1. Performance Measure of the Proposed Algorithm
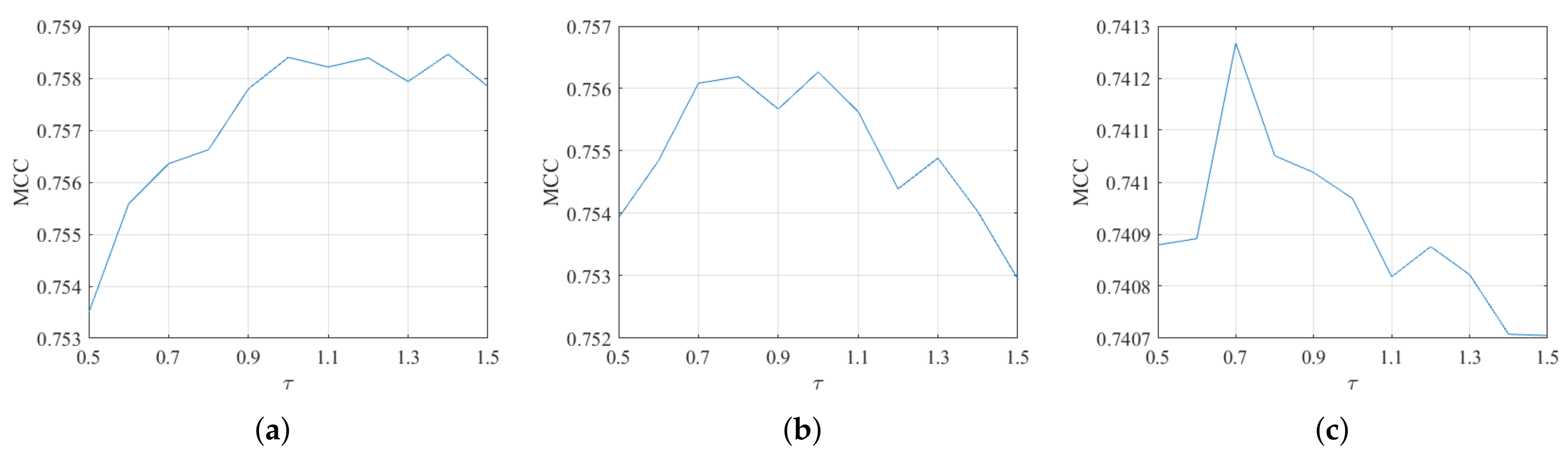
5.2. The Performance of the Proposed Algorithm with Different Values
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Salazar-Gonzalez, A.; Kaba, D.; Li, Y.; Liu, X. Segmentation of Blood Vessels and Optic Disc in Retinal Images. IEEE J. Biomed. Health Inform. 2014, 2194, 1874–1886. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, S.; Chatterjee, S.; Katz, N.; Nelson, M.; Goldbaum, M. Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Trans. Med. Imaging 1989, 8, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Odstrcilik, J.; Kolar, R.; Kubena, T.; Cernosek, P.; Budai, A.; Hornegger, J.; Gazarek, J.; Svoboda, O.; Jan, J.; Angelopoulou, E. Retinal vessel segmentation by improved matched filtering: Evaluation on a new high-resolution fundus image database. IET Image Process. 2013, 7, 373–383. [Google Scholar] [CrossRef]
- Nguyen, U.T.V.; Bhuiyan, A.; Park, L.A.F.; Ramamohanarao, K. An effective retinal blood vessel segmentation method using multi-scale line detection. Pattern Recognit. 2013, 46, 703–715. [Google Scholar] [CrossRef]
- Annunziata, R.; Garzelli, A.; Ballerini, L.; Mecocci, A.; Trucco, E. Leveraging Multiscale Hessian-Based Enhancement with a Novel Exudate Inpainting Technique for Retinal Vessel Segmentation. IEEE J. Biomed. Health Inform. 2016, 20, 1129–1138. [Google Scholar] [CrossRef] [PubMed]
- Staal, J.J.; Abramoff, M.D.; Niemeijer, M.; Viergever, M.A.; Van Ginneken, B. Ridge based vessel segmentation in color images of the retina. IEEE Trans. Med. Imaging 2005, 23, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Roychowdhury, S.; Koozekanani, D.D.; Parhi, K.K. Iterative Vessel Segmentation of Fundus Images. IEEE Trans. Biomed. Eng. 2015, 62, 1738–1749. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Rada, L.; Chen, K.; Harding, S.P.; Zheng, Y. Automated Vessel Segmentation Using Infinite Perimeter Active Contour Model with Hybrid Region Information with Application to Retinal Images. IEEE Trans. Med. Imaging 2015, 34, 1797–1807. [Google Scholar] [CrossRef] [PubMed]
- Soares, J.V.B.; Leandro, J.J.G.; Cesar, R.M.J.; Jelinek, H.F.; Cree, M.J. Retinal Vessel Segmentation Using the 2-D Gabor Wavelet and Supervised Classification. IEEE Trans. Med. Imaging 2006, 25, 1214–1222. [Google Scholar] [CrossRef] [PubMed]
- Roychowdhury, S.; Koozekanani, D.D.; Parhi, K.K. Blood vessel segmentation of fundus images by major vessel extraction and subimage classification. IEEE J. Biomed. Health Inform. 2015, 19, 1118–1128. [Google Scholar] [CrossRef] [PubMed]
- Dai, P.; Luo, H.; Sheng, H.; Zhao, Y.; Li, L.; Wu, J.; Zhao, Y.; Suzuki, K. A new approach to segment both main and peripheral retinal vessels based on gray-voting and Gaussian mixture model. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Feng, B.; Xie, L.; Liang, P.; Zhang, H.; Wang, T. A cross-modality learning approach for vessel segmentation in retinal images. IEEE Trans. Med. Imaging 2016, 35, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Orlando, J.I.; Prokofyeva, E.; Blaschko, M.B. A Discriminatively Trained Fully Connected Conditional Random Field Model for Blood Vessel Segmentation in Fundus Images. IEEE Trans. Biomed. Eng. 2017, 64, 16–27. [Google Scholar] [CrossRef] [PubMed]
- Liskowski, P.; Krawiec, K. Segmenting Retinal Blood Vessels With Deep Neural Networks. IEEE Trans. Med. Imaging 2016, 35, 2369–2380. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.; Xu, Y.; Lin, S.; Kee, D.W.; Liu, J. DeepVessel: Retinal Vessel Segmentation via Deep Learning and Conditional Random Field. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016; Ourselin, S., Joskowicz, L., Sabuncu, M.R., Unal, G., Wells, W., Eds.; Springer: Cham, Switzerland, 2016; pp. 132–139. [Google Scholar]
- Zhou, L.; Yu, Q.; Xu, X.; Gu, Y.; Yang, J. Improving dense conditional random field for retinal vessel segmentation by discriminative feature learning and thin-vessel enhancement. Comput. Methods Programs Biomed. 2017, 148, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Hoover, A.; Kouznetsova, V.; Goldbaum, M. Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response. IEEE Trans. Med. Imaging 2000, 19, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Dolph, C. A Current Distribution for Broadside Arrays Which Optimizes the Relationship between Beam Width and Side-Lobe Level. Proc. IRE 1946, 34, 335–348. [Google Scholar] [CrossRef]
- Williams, A.B.; Taylor, F.J. Electronic Filter Design Handbook, 4th ed.; The McGraw-Hill Companies, Inc.: Singapore, 2006. [Google Scholar]
- Xiao, Z.; Wang, M.; Zhang, F.; Geng, L.; Wu, J.; Su, L.; Tong, J. Retinal vessel segmentation based on adaptive difference of Gauss filter. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 15–19. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Chanwimaluang, T.; Fan, G.F.G. An efficient blood vessel detection algorithm for retinal images using local entropy thresholding. In Proceedings of the 2003 International Symposium on Circuits and Systems, Bangkok, Thailan, 25–28 May 2003; Volume 5, pp. 21–24. [Google Scholar] [CrossRef]
- Miri, M.S.; Mahloojifar, A. Retinal image analysis using curvelet transform and multistructure elements morphology by reconstruction. IEEE Trans. Biomed. Eng. 2011, 58, 1183–1192. [Google Scholar] [CrossRef] [PubMed]
- Ardizzone, E.; Pirrone, R.; Gambino, O.; Radosta, S. Blood Vessels and Feature Points Detection on Retinal Images. In Proceedings of the 30th Annual International EEE Engineering in Medicine and Biology Society Conference, Vancouver, BC, Canada, 20–25 August 2008; pp. 2246–2249. [Google Scholar] [CrossRef]
- Nergiz, M.; Akin, M. Retinal vessel segmentation via structure tensor coloring and anisotropy enhancement. Symmetry 2017, 9, 276. [Google Scholar] [CrossRef]


| Database: | DRIVE (Test Set) | STARE | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | Se | Sp | Ppv | F1 | G | MCC | Se | Sp | Ppv | F1 | G | MCC |
| Unsupervised | ||||||||||||
| Nguyen et al. [4] | 0.742 | 0.970 | 0.783 | 0.762 | 0.848 | 0.728 | 0.785 | 0.950 | 0.648 | 0.704 | 0.862 | 0.674 |
| Odstrcilik et al. [3] | 0.706 | 0.969 | − | − | 0.827 | − | 0.785 | 0.951 | − | − | 0.864 | − |
| Roychowdurry et al. [7] | 0.739 | 0.978 | − | − | 0.850 | − | 0.732 | 0.984 | − | − | 0.849 | − |
| Zhao et al. [8] | 0.742 | 0.982 | − | − | 0.854 | − | 0.780 | 0.978 | − | − | 0.873 | − |
| Annunziata et al. [5] | − | − | − | − | − | − | 0.713 | 0.984 | 0.833 | 0.768 | 0.838 | − |
| Nergiz and Akin [25] | 0.812 | 0.934 | − | − | − | − | 0.813 | 0.944 | − | − | − | − |
| Proposed Method | 0.748 | 0.978 | 0.833 | 0.786 | 0.856 | 0.758 | 0.793 | 0.973 | 0.772 | 0.780 | 0.877 | 0.756 |
| Supervised | ||||||||||||
| Dai et al. [11] | 0.736 | 0.972 | − | − | 0.846 | − | 0.777 | 0.955 | − | − | 0.861 | − |
| Roychowdurry et al. [10] | 0.725 | 0.983 | − | − | 0.844 | − | 0.772 | 0.973 | − | − | 0.867 | − |
| Li et al. [12] | 0.757 | 0.982 | − | − | 0.862 | − | 0.773 | 0.984 | − | − | 0.872 | − |
| Liskowski et al. [14] | 0.775 | 0.979 | − | − | 0.871 | − | 0.777 | 0.985 | − | − | 0.878 | − |
| Orlando et al. [13] | 0.790 | 0.968 | 0.785 | 0.786 | 0.874 | 0.756 | 0.768 | 0.974 | 0.774 | 0.764 | 0.863 | 0.742 |
| Fu et al. [15] | 0.760 | − | − | − | − | − | 0.741 | − | − | − | − | − |
| Zhou et al. [16] | 0.808 | 0.967 | 0.786 | 0.794 | 0.883 | 0.766 | 0.806 | 0.976 | 0.811 | 0.802 | 0.886 | 0.783 |
| Method | Se | Sp | Ppv | F1 | G | MCC |
|---|---|---|---|---|---|---|
| Odstrcilik et al. [3] | 0.779 | 0.965 | 0.695 | 0.732 | 0.867 | 0.707 |
| Annunziata et al. [5] | 0.713 | 0.984 | 0.809 | 0.758 | 0.838 | − |
| Orlando et al. [13] | 0.787 | 0.958 | 0.663 | 0.716 | 0.869 | 0.690 |
| Zhou et al. [16] | 0.802 | 0.970 | 0.733 | 0.763 | 0.881 | 0.740 |
| Proposed Method | 0.804 | 0.971 | 0.733 | 0.764 | 0.883 | 0.741 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dharmawan, D.A.; Ng, B.P.; Rahardja, S. A Modified Dolph-Chebyshev Type II Function Matched Filter for Retinal Vessels Segmentation. Symmetry 2018, 10, 257. https://doi.org/10.3390/sym10070257
Dharmawan DA, Ng BP, Rahardja S. A Modified Dolph-Chebyshev Type II Function Matched Filter for Retinal Vessels Segmentation. Symmetry. 2018; 10(7):257. https://doi.org/10.3390/sym10070257
Chicago/Turabian StyleDharmawan, Dhimas Arief, Boon Poh Ng, and Susanto Rahardja. 2018. "A Modified Dolph-Chebyshev Type II Function Matched Filter for Retinal Vessels Segmentation" Symmetry 10, no. 7: 257. https://doi.org/10.3390/sym10070257
APA StyleDharmawan, D. A., Ng, B. P., & Rahardja, S. (2018). A Modified Dolph-Chebyshev Type II Function Matched Filter for Retinal Vessels Segmentation. Symmetry, 10(7), 257. https://doi.org/10.3390/sym10070257





