Abstract
Bankruptcy prediction has been a popular and challenging research topic in both computer science and economics due to its importance to financial institutions, fund managers, lenders, governments, as well as economic stakeholders in recent years. In a bankruptcy dataset, the problem of class imbalance, in which the number of bankruptcy companies is smaller than the number of normal companies, leads to a standard classification algorithm that does not work well. Therefore, this study proposes a cluster-based boosting algorithm as well as a robust framework using the CBoost algorithm and Instance Hardness Threshold (RFCI) for effective bankruptcy prediction of a financial dataset. This framework first resamples the imbalance dataset by the undersampling method using Instance Hardness Threshold (IHT), which is used to remove the noise instances having large IHT value in the majority class. Then, this study proposes a Cluster-based Boosting algorithm, namely CBoost, for dealing with the class imbalance. In this algorithm, the majority class will be clustered into a number of clusters. The distance from each sample to its closest centroid will be used to initialize its weight. This algorithm will perform several iterations for finding weak classifiers and combining them to create a strong classifier. The resample set resulting from the previous module, will be used to train CBoost, which will be used to predict bankruptcy for the validation set. The proposed framework is verified by the Korean bankruptcy dataset (KBD), which has a very small balancing ratio in both the training and the testing phases. The experimental results of this research show that the proposed framework achieves 86.8% in AUC (area under the ROC curve) and outperforms several methods for dealing with the imbalanced data problem for bankruptcy prediction such as GMBoost algorithm, the oversampling-based method using SMOTEENN, and the clustering-based undersampling method for bankruptcy prediction in the experimental dataset.
1. Introduction
A huge amount of data is generated daily in the Internet Era, with many kinds of data such as image, text, sound, signal, and structured data. In order to make people’s work smarter, faster, and more effective, many strategies have been proposed to understand each kind of data and perform intelligent tasks such as stock trend prediction, bankruptcy prediction, and weather forecasting in the last two decades. For image data, many methods have been proposed to understand this kind of data, especially as deep learning has arisen in recent years [1,2]. Dang et al. [3] proposed a drone agriculture imagery system using a convolutional neural network for radish wilt disease identification. Using this system, people can easily detect disease in their vegetable farming area, which can be used widely in the agriculture sector in the near future. For text and structured data, data analysis as well as data mining with many sub-problems such as pattern mining [4,5,6], erasable pattern mining [7], high average-utility pattern mining [8], weighted closed pattern mining [9], association rules mining [10], clustering [11,12], and classification [13,14] become the most common techniques to analyze data. Using these techniques, several intelligent systems perform a number of intelligent tasks such as medical diagnosis [15], congestion control in wireless sensor networks [16], personalized facets for semantic search [17], a recommender system [18], and an interpolation-based hiding scheme [19]. Roan et al. [15] proposed a new proximity measure, namely δ-equalities, and utilized it for medical diagnosis. Next, Nguyen et al. [18] proposed a novel clustering algorithm for the neutrosophic recommender system (NRS). This algorithm was also applied for medical diagnosis. In the machine learning domain, classification is the problem of forecasting the class label a new observation belongs to. Classification is also known as supervised learning [20] and has attracted a lot of research attention; it can be applied to many practical applications in both research and industry. For example, credit card fraud detection [21] is a real-life classification problem. In this problem, a dataset has information in terms of credit card transactions. This classification aims to detect fraudulent transactions in the future.
The class imbalance problem refers to a classification for a dataset in which one or some classes have a huge number of instances compared with the rest. The most significant class is considered the majority class, while the limited one is the minority class. Class imbalance problems have been encountered in a wide variety of domains. Protein detection [22] as well as disease diagnosis [23] are the most popular issues related to this problem in the chemical and biomedical fields. For the business management domain, bankruptcy forecasting [24,25,26], a model to predict enterprises that will crash in the near future, and fraud detection [21] are the two most attractive topics. In information technology, software defect detection [27] is under imbalanced scenarios. In the class imbalance situation, standard classification algorithms such as Decision Tree and SVM mainly consider the majority class. The samples in the minority class are considered mislabeled and usually ignored by the classifier. Hence, specific techniques such as undersampling as well as oversampling or a combination of them are needed. Lin et al. [20] proposed an undersampling approach based on clustering for dealing with the imbalanced data problem and achieved promising results.
Bankruptcy prediction, the real-world application facing the class imbalance problem, has attracted many researchers in the last decade due to economic fluctuations. Due to this problem, it is necessary to design specific algorithms for effective bankruptcy prediction. There are many studies forecasting the bankruptcy using different approaches. In 2015 Kim et al. [24] proposed GMBoost, a boosting algorithm based on geometric means that modifies AdaBoost by replacing arithmetic and accuracy calculations. Instead of summing the error rates for both majority and minority cases, this algorithm will calculate the error rates of minority and majority cases separately. Next, the algorithm will take the geometric mean of those values. This geometric mean value will be used to calculate the weight of this learner and update the weight distribution of the next iteration. Based on this strategy, GMBoost has the highest performance for an experimental dataset in this study. Next, Zieba et al. [25] utilized eXtreme Gradient Boosting (XGBoost) for learning from synthetic features to predict bankruptcy. The synthetic features were generated by performing a random arithmetical operation to improve the overall performance. This method was successfully applied to predict bankruptcy for a real-life dataset of Polish companies. Then, Barboza et al. [26] surveyed and implemented several machine learning models such as Support Vector Machines, Boosting, Bagging as well as Random forest classifiers for bankruptcy prediction. A balanced training set consisting of 449 bankrupt and 449 non-bankrupt companies was used for training the experimental models. Then, the trained models were verified by the imbalanced validation set with 133 bankrupt and 13,300 normal companies. The results on this study found that bagging, boosting, and random forest classifiers are better than other models. Recently, Le et al. [28] presented a Korean bankruptcy dataset (KBD) with a highly imbalanced ratio, i.e., the number of bankrupt companies is much smaller than the number of normal companies. Moreover, the authors presented a framework for bankruptcy prediction using effective oversampling techniques. Next, the novel features extracted from the transaction dataset were added to the original features of KBD to enhance the performance. Although the proposed framework in [28] yields 84.4% in terms of AUC on KBD, it is still necessary to develop another method to improve the performance for this dataset, which is very important for the government and investors.
This study proposes a Cluster-based Boosting algorithm, namely CBoost, for dealing with the imbalanced data problem as well as a robust framework, namely the RFCI framework, for bankruptcy prediction. The first module of the proposed framework is the undersampling module, which uses the Instance Hardness Threshold (IHT) concept to remove the noise in the imbalanced class dataset. This concept is used to find a number of data samples for which it is harder to predict the class label correctly than others and remove them from the training set. This module helps the dataset increase the balancing ratio and therefore helps the classifier achieve a better performance for bankruptcy prediction. Then, the resampled set, the results of the first module, will be used to train the CBoost classifier, which is then used to predict bankruptcy for the testing set. The proposed framework will be verified by the KBD dataset introduced in [28], which has a high balancing ratio. The experimental results of this study show that the proposed framework outperforms the GMBoost algorithm [24], the oversampling-based framework [28], and the clustering-based undersampling framework [20] for KBD. The main contributions of this study are highlighted as follows: (1) We propose the CBoost algorithm, which is a boosting algorithm with initial weight based on the clustering; (2) a robust framework using the CBoost algorithm and IHT (RFCI) is then proposed for effective bankruptcy prediction; (3) several experiments were conducted to find the optimal number of clusters using the Elbow method for KBD.
The rest of this paper is structured as follows. Section 2 surveys the preliminaries including the class imbalance problem in bankruptcy prediction and the undersampling method using IHT. Section 3 first proposes the CBoost algorithm and then proposes a robust framework using the CBoost algorithm and IHT concept for bankruptcy prediction. Experiments were conducted as presented in Section 4. Finally, the conclusions of this study are given in Section 5. Moreover, we suggest several future research issues based on the limitations of this study in this section.
2. Preliminaries
2.1. Class Imbalance Problem in Bankruptcy Prediction
In financial datasets, the numbers of bankrupt enterprises are much smaller than the total number of enterprises. In this situation, most previous studies on bankruptcy prediction will divide the dataset into two classes: bankruptcy and non-bankruptcy cases. Due to the imbalance in terms of quantity between the two classes, bankruptcy prediction is a practical class imbalance problem. To understanding this issue mathematically, let χ be a dataset with χ and χ being the bankruptcy and non-bankruptcy classes, respectively. The balancing ratio, denoted by of the dataset χ, is calculated as follows:
where and are the number of samples of bankruptcy (or minority) and non-bankruptcy (or majority) classes. The balancing ratio of the dataset in the class imbalance problem will be small. The smaller the balancing ratio the more difficult the classifications will be. Therefore, many studies have been introduced to improve the performance of classification in the class imbalance scenarios.
For handling the class imbalance problem, sampling techniques used to resample the original dataset χ into the new one such that are the most widely used. Sampling work by removing majority class samples (undersampling technique) or by inflating the minority class (oversampling technique). Other methods combined undersampling and oversampling for obtaining better accuracy. For the experimental dataset in this study, i.e., KBD, Le et al. [28] conducted an experiment to compare several oversampling techniques to predict bankruptcy. Moreover, the authors analyze the relationship between bankruptcy and the income and outcome transactions of one company. After that, novel features from transaction dataset were extracted to improve the performance. The experimental results of this study [28] showed that SMOTEENN proposed in [29] combined with the Random Forest classifier is the best method for bankruptcy prediction, yielding 84.4% in terms of AUC on KBD.
2.2. Undersampling Approach Using IHT
Instance Hardness (IH) was proposed by Smith, Martinez, and Giraud-Carrier [30] in 2014 and is only used for binary classification problems. In this paper, the authors used the concept of the IH property to indicate the probability of a data point in a training set being misclassified. Data samples that are on the borderline between two or more classes or characterized by noise have high IH values due to the fact that a learning algorithm would force them to overfit correctly. For a training sample (xi, yi), p(yi|xi, h) is the conditional probability of label yi given by the weak learner h for the input feature vector xi. The smaller the value of p(yi|xi, h), the less correct h is. The IH of the training sample (xi, yi), denoted by with respect to h, is as follows:
Let be the set of weak learners and be the corresponding weight of . The IH of the training sample (xi, yi) is determined as in Equation (3):
Based on this concept, an undersampling approach using IHT has been utilized that resamples the imbalanced dataset by removing the data points in the majority class with high IH values until reaching the target balancing ratio. Figure 1 shows an example of the undersampling approach using IHT with several different balancing ratios (0.4, 0.6, and 1.0, respectively) that indicates the target balancing ratio of the resampled dataset.
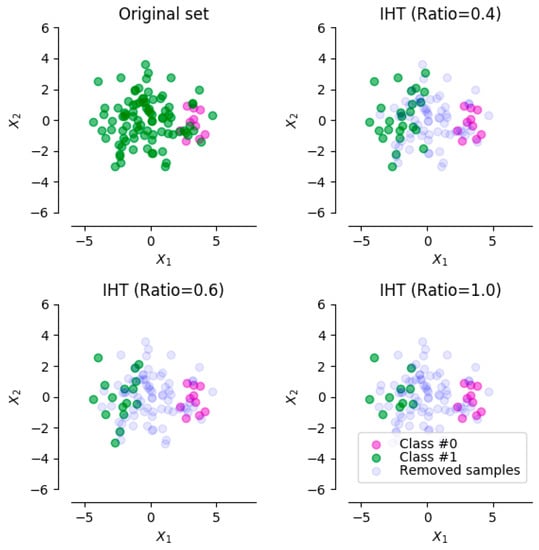
Figure 1.
An example of the undersampling approach, using Instance Hardness Threshold (IHT) with several different balancing ratios.
3. Materials and Methods
3.1. The Experimental Dataset
The Korean bankruptcy dataset (KBD) [28], which was provided by a financial company, consists of financial ratios as well as information on personnel and type of business of companies in Korea in the last two years. Each company in KBD has many financial ratios but only 19 outstanding features, including assets, liabilities, capital, profit, cost, and income, were extracted. This dataset has only 307 bankrupted enterprises and 120,048 non-bankruptcy enterprises. Therefore, the balancing ratio for this dataset is 0.0026, which is very small compared to the bankruptcy dataset in the previous study. The detailed financial features of KBD are shown in Table 1.

Table 1.
The features of Korean bankruptcy dataset (KBD).
3.2. Cluster-Based Boosting Algorithm
Figure 2 shows the pseudocode of the Cluster-based boosting (CBoost) algorithm, which was mainly based on the AdaBoost algorithm [31]. The main difference between CBoost and Adaboost is that CBoost customizes the initial weight for each data point using a k-mean clustering algorithm to effectively handle the class imbalance problem. The proposed algorithm first clusters the majority class, i.e., the non-bankruptcy class, using k-mean clustering at Line 2. Note that the k value will be determined by the first experiment for the experimental dataset. Then, for each data point in the majority class we will calculate the distance to the nearest center point (Line 3). In the next step (Line 4), the algorithm sets the distance value for each data point in the minority class equal to the maximum value of the distances of data points in the majority class. Line 5 in the CBoost algorithm will calculate the initialize weights for each data sample as follows:
where d(xi) refers to the Euclidean distance between data point xi and the nearest center point. Equation (4) makes it so that the data samples in the majority class closed the center points and the data samples in the minority class will have a higher weight values compared to the further data samples in majority class. Next, CBoost in Line 6 will normalize these values using the following equation:
where m is the total number of data points in the training set. This step will ensure that = 1. The initial weight helps the weak classifier classify more accurately the data samples in the majority class close to the center points as well as the data samples in the minority class.

Figure 2.
CBoost algorithm.
On each round t = 1, …, T, CBoost will determine the weak learner ht(x) that gives the lowest weighted classification error () in Line 8, calculates the weight for the t-th weak classifier () in Line 10, and updates the next weight Wt+1 in Line 11. The final classifier H computes the sign of a weighted combination of a weak learner as in Equation (6):
where ht(x) refers to the t-th weak learner and is the corresponding weight. In short, CBoost is a greedy algorithm that finds and adds one weak learner at an iteration and then optimizes the weights and updates the weighted distribution for the next iteration. In the final step, the algorithm combines them as in Equation (6) to create a stronger learner as the final one.
3.3. RFCI Framework
The diagram of the Robust Framework using the CBoost algorithm and IHT (RFCI) is shown in Figure 3. At the beginning of the process, the imbalanced dataset, i.e., KBD, was normalized by a Standard Scaler function. This function will remove the mean of these feature vectors and scale them to the unit variance as in the following equation:
where x, , and σ are the original feature vector of each enterprise, the mean vector for the whole dataset, and the standard deviation vector, respectively. After this step, the normalization dataset will be divided into a training set and a testing set by the k-fold cross-validation module. Note that this study uses 5-fold cross-validation for verifying the proposed framework; therefore, this framework will divide this dataset into five parts and use four parts to training and the rest for testing. Next, the training set will be passed through the undersampling module, which uses the IHT concept to remove noise as well as partially balance the training set. The result of this step, the resampled training set, will be used to train the CBoost classifier that was introduced in the previous section. In the final step, the training classifier will be used to predict bankruptcy for the testing set.
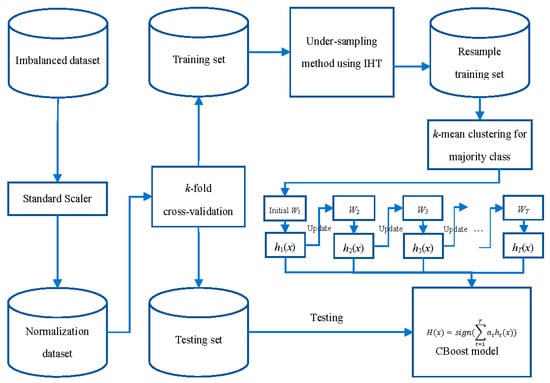
Figure 3.
Instance Hardness Threshold (RFCI) framework for bankruptcy prediction.
4. Results
4.1. Experimental Setting
All methods were executed on a desktop computer with 8 GB RAM, Intel Core i7-2600 CPU (3.40 GHz × 2 cores) running with Ubuntu 16.04 LTS. All programs were implemented in Python 2.7 environment. Multi-Layer Perceptron (MLP), Decision Tree, Random Forest and AdaBoost classifiers were implemented by Scikit-learn [13], an open-source machine learning library. In addition, SMOTEENN and the undersampling method using IHT were utilized from the imbalanced-learn package [32], an open-source Python toolbox providing several methods for handling the problem of class imbalance.
To show the effectiveness of the proposed framework, we perform the oversampling method using SMOTEENN [28] and the clustering-based undersampling method [20] combined with several classifiers such as MLP, Decision Tree, Random Forest, and AdaBoost; GMBoost [24] and the proposed framework for the experimental dataset. To evaluate these methods, the study uses 5-fold cross-validation, i.e., we used 80% of the dataset for training, leaving 20% for testing, and then repeated it five times.
4.2. Identifying k Value Experiment
We first conduct the experiment to find the optimal k to use in k-mean clustering for the experiment dataset. In this experiment, the Elbow method [33], a famous method for determining the optimal number of clusters, was used. This method was proposed to find the optimal (k) number of clusters in a specific dataset. Figure 4 shows the variation in distortion value for each value k over five repetitions and the average. The vertical axis shows the distortion, which was defined by the sum of the squared distances between each observation and its closest centroid for each k. In Figure 4A, the horizontal axis shows the k values from 1 to the number of minority data points in the training set with a jump of 10. Figure 4B shows a graph with k from 1 to 140 for better display.
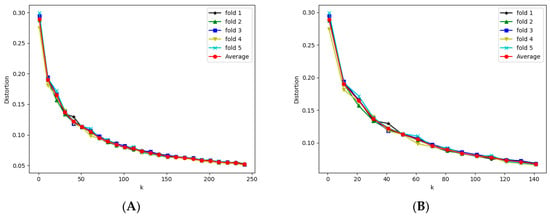
Figure 4.
The variation of distortion value for each value k. (A) shows variation k from 0 to 250. (B) shows variation k from 0 to 140 for better display.
Based on the results shown in Figure 4, k from 20 to 50 should be selected to have the best initial weights for all folds. Using these values, i.e., 20 to 50, we obtain AUCs for each fold as well as the average AUCs shown in Figure 5. Based on this experiment, we found that the performance of the proposed framework peaked at AUC = 86.8% with k = 45. Therefore, in the next experiment, we use k = 45 to get the overall AUC for the proposed framework.
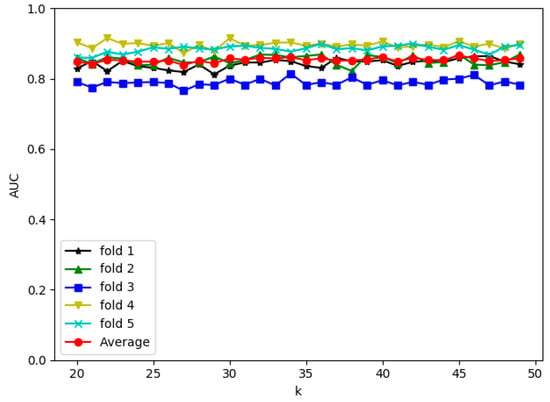
Figure 5.
The performance of RFCI framework for each fold with k from 20 to 50.
4.3. Bankruptcy Prediction Results
The results of all experimental methods for bankruptcy prediction are shown in Table 2. The clustering-based undersampling (CUS) method [20] proved ineffective for the experimental dataset. All classifiers combined with CUS have not achieved good results. MLP is even worse than random guessing when its AUC is only 46.3%. Decision Tree, Random Forest, and AdaBoost achieved 53.4%, 57.7%, and 52.7%, respectively. This is easy to explain as follows. CUS removes most of the samples in the majority class when the experimental dataset has the small number of bankruptcy cases. Consequently, the resampled dataset is not the best representative of the original dataset. Therefore, this method is not suitable for a bankruptcy dataset with small balancing ratios like the experimental dataset.

Table 2.
Experimental results for KBD.
The oversampling-based method using SMOTEENN [28] proved quite effective for KBD: all classifiers combined with this method have achieved acceptable results. Using this framework, MLP, Decision Tree, Random Forest, and AdaBoost classifier got 72.7%, 81.2%, 84.2%, and 84.8%, respectively. GMBoost [24] only obtains 75.3% for the experimental dataset. The proposed framework, which uses both undersampling method IHT and CBoost algorithm for dealing with the class imbalance problem, achieved the best performance with 86.8% for KBD.
4.4. Time Analysis
In this experiment, a time analysis of all experimental approaches for KBD was conducted. The training and testing times are shown in Table 3. The effect of the testing time of all approaches is negligible, while the training time appears to be very significant. The classifiers including MLP, Decision Tree, Random Forest, and AdaBoost, followed by the CUS method, are time-consuming in training with 134.2, 133.2, 134.0, and 135.7 s, respectively. With the oversampling method using SMOTEENN, the training times of MLP, Decision Tree, Random Forest, and AdaBoost improve: 48.3, 36.2, 36.7, and 66.4 s, respectively. Moreover, GMBoost only requires 13.7 s for training time; however, the bankruptcy prediction performance is not good. Our framework achieves a balance between time and performance: it takes 39.4 s for training. Therefore, our framework is recommended for use in bankruptcy prediction in a highly imbalanced dataset like KBD.

Table 3.
Time analysis for KBD.
5. Discussion
According to the experimental results in the previous section, the proposed framework achieved 86.8% in AUC for the KBD dataset and outperforms several methods for dealing with the imbalance data problem for bankruptcy prediction such as GMBoost algorithm [24], the oversampling-based method using SMOTEENN [28], and the clustering-based undersampling method [20] in terms of accuracy. In the bankruptcy prediction domain, our method is acceptable for predicting a normal company as well as a bankrupt company. This predicted bankruptcy prediction helps managers as well as investors to pay more attention to their company. Meanwhile, the company may show worrying signs and need correcting immediately. Therefore, the results of this study may be beneficial for those involved.
Moreover, the proposed algorithm, CBoost, applies not only to bankruptcy prediction but is also a general classifier dealing with the imbalanced data problem. This algorithm considers the minority class as well as the majority class to obtain the best performance in classification. Therefore, it can be used in imbalanced scenarios in various domains.
The limitation of this study is how time-consuming the process is. For KBD, the framework takes around 40 s in total. This will reduce the effectiveness of the system when the financial data become enormous. Therefore, an online learning approach needs to be developed to reuse the knowledge learned from previous data. Several techniques to reduce learning time such as feature selection and other effective sampling methods should also be considered in the system.
6. Conclusions
Firstly, we proposed the CBoost algorithm for dealing with the class imbalance problem effectively. Secondly, based on this algorithm, a robust framework, namely the RFCI framework with two main modules for bankruptcy prediction, was proposed. The first module is an undersampling module, which resamples the imbalanced financial dataset using the IHT concept by removing the noise instances in the majority class. Then, the CBoost algorithm was used in the second module for training and testing bankruptcy to have good performance in imbalance data. In the first experiment, we try to find the optimal k that is used in k-means clustering for our experimental dataset. Using this value, a second experiment was conducted to evaluate the proposed framework and the previous methods including GMBoost algorithm, the oversampling method using SMOTEENN, and the undersampling method based on clustering technique for KBD, which has a very small balancing ratio. The experimental results show that the RFCI framework outperforms the GMBoost algorithm, the oversampling-based methods, and the clustering-based undersampling method for KBD.
In future work, we must first investigate the best method for the normalization of feature vectors as well as the optimal feature selection method to improve the performance of the experimental dataset. Second, we will look for a cost-sensitive method of dealing with the class imbalance problem to propose an optimized model for bankruptcy prediction. In addition, other information related to the companies’ finances might be collected. We thus propose a hybrid approach for bankruptcy prediction from multiple data sources to enhance performance.
Author Contributions
S.W.B. proposed the topic and obtained funding; T.L. proposed and implemented the framework. T.L. wrote the paper. L.H.S., M.T.V., M.Y.L., and S.W.B. improved the quality of the manuscript.
Acknowledgments
This research was supported by the Korean MSIT (Ministry of Science and ICT) under the National Program for Excellence in SW (2015-0-00938), supervised by the IITP (Institute for Information & communications Technology Promotion).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cu, N.G.; Le, H.S.; Chiclana, F. Dynamic structural neural network. J. Intell. Fuzzy Syst. 2018, 34, 2479–2490. [Google Scholar]
- Dang, L.M.; Hassan, S.I.; Im, S.; Mehmood, I.; Moon, H. Utilizing text recognition for the defects extraction in sewers CCTV inspection videos. Comput. Ind. 2018, 99, 96–109. [Google Scholar] [CrossRef]
- Dang, L.M.; Syed, I.H.; Suhyeon, I.; Sangaiah, A.; Mehmood, I.; Rho, S.; Seo, S.; Moon, H. UAV based wilt detection system via convolutional neural networks. Sustain. Comput. Inform. Syst. 2018, in press. [Google Scholar] [CrossRef]
- Le, T.; Nguyen, A.; Huynh, B.; Vo, B.; Pedrycz, W. Mining constrained inter-sequence patterns: A novel approach to cope with item constraints. Appl. Intell. 2018, 48, 1327–1343. [Google Scholar] [CrossRef]
- Bui, H.; Vo, B.; Nguyen, H.; Nguyen-Hoang, T.A.; Hong, T.P. A weighted N-list-based method for mining frequent weighted itemsets. Expert Syst. Appl. 2018, 96, 388–405. [Google Scholar] [CrossRef]
- Vo, B.; Le, T.; Coenen, F.; Hong, T.P. Mining frequent itemsets using the N-list and subsume concepts. Int. J. Mach. Learn. Cybern. 2016, 7, 253–265. [Google Scholar] [CrossRef]
- Le, T.; Vo, B.; Baik, S.W. Efficient algorithms for mining top-rank-k erasable patterns using pruning strategies and the subsume concept. Eng. Appl. Artif. Intell. 2018, 68, 1–9. [Google Scholar] [CrossRef]
- Kim, D.; Yun, U. Efficient algorithm for mining high average-utility itemsets in incremental transaction databases. Appl. Intell. 2017, 47, 114–131. [Google Scholar] [CrossRef]
- Vo, B. An Efficient Method for Mining Frequent Weighted Closed Itemsets from Weighted Item Transaction Databases. J. Inf. Sci. Eng. 2017, 33, 199–216. [Google Scholar]
- Mai, T.; Vo, B.; Nguyen, L. A lattice-based approach for mining high utility association rules. Inf. Sci. 2017, 399, 81–97. [Google Scholar] [CrossRef]
- Kim, B.; Kim, J.; Yi, G. Analysis of Clustering Evaluation Considering Features of Item Response Data Using Data Mining Technique for Setting Cut-Off Scores. Symmetry 2017, 9, 62. [Google Scholar] [CrossRef]
- Soleimani, H.; Tomasin, S.; Alizadeh, T.; Shojafar, M. Cluster-head based feedback for simplified time reversal prefiltering in ultra-wideband systems. Phys. Commun. 2017, 25, 100–109. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Tajiki, M.M.; Akbari, B.; Shojafar, M.; Mokari, N. Joint QoS and Congestion Control Based on Traffic Prediction in SDN. Appl. Sci. 2017, 7, 1265. [Google Scholar] [CrossRef]
- Roan, T.N.; Ali, M.; Le, H.S. δ-equality of intuitionistic fuzzy sets: A new proximity measure and applications in medical diagnosis. Appl. Intell. 2018, 48, 499–525. [Google Scholar]
- Singh, K.; Singh, K.; Le, H.S.; Aziz, A. Congestion control in wireless sensor networks by hybrid multi-objective optimization algorithm. Comput. Netw. 2018, 138, 90–107. [Google Scholar] [CrossRef]
- Le, T.; Vo, B.; Duong, T.H. Personalized Facets for Semantic Search Using Linked Open Data with Social Networks. In Proceedings of the 2012 Third International Conference on Innovations in Bio-Inspired Computing and Applications, Kaohsiung, Taiwan, 26–28 September 2012; pp. 312–337. [Google Scholar]
- Nguyen, D.T.; Ali, M.; Le, H.S. A Novel Clustering Algorithm in a Neutrosophic Recommender System for Medical Diagnosis. Cogn. Comput. 2017, 9, 526–544. [Google Scholar]
- Lu, T.C. Interpolation-based hiding scheme using the modulus function and re-encoding strategy. Signal Process. 2018, 142, 244–259. [Google Scholar] [CrossRef]
- Lin, W.C.; Tsai, C.F.; Hu, Y.H.; Jhang, J.S. Clustering-based undersampling in class-imbalanced data. Inf. Sci. 2017, 409, 17–26. [Google Scholar] [CrossRef]
- Zakaryazad, A.; Duman, E. A profit-driven Artificial Neural Network (ANN) with applications to fraud detection and direct marketing. Neurocomputing 2016, 175, 121–131. [Google Scholar] [CrossRef]
- Herndon, N.; Caragea, D. A Study of Domain Adaptation Classifiers Derived from Logistic Regression for the Task of Splice Site Prediction. IEEE Trans. NanoBiosci. 2016, 15, 75–83. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Xiao, Q. A novel approach for predicting microRNA-disease associations by unbalanced bi-random walk on heterogeneous network. J. Biomed. Inform. 2017, 66, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.J.; Kang, D.K.; Kim, H.B. Geometric mean based boosting algorithm with over-sampling to resolve data imbalance problem for bankruptcy prediction. Expert Syst. Appl. 2015, 42, 1074–1082. [Google Scholar] [CrossRef]
- Zieba, M.; Tomczak, S.K.; Tomczak, J.M. Ensemble boosted trees with synthetic features generation in application to bankruptcy prediction. Expert Syst. Appl. 2016, 58, 93–101. [Google Scholar] [CrossRef]
- Barboza, F.; Kimura, H.; Altman, E. Machine learning models and bankruptcy prediction. Expert Syst. Appl. 2017, 83, 405–417. [Google Scholar] [CrossRef]
- Bennin, K.E.; Keung, J.; Phannachitta, P.; Monden, A.; Mensah, S. MAHAKIL: Diversity based Oversampling Approach to Alleviate the Class Imbalance Issue in Software Defect Prediction. IEEE Trans. Softw. Eng. 2018, 44, 534–550. [Google Scholar] [CrossRef]
- Le, T.; Lee, M.Y.; Park, J.R.; Baik, S.W. Oversampling Techniques for Bankruptcy Prediction: Novel Features from a Transaction Dataset. Symmetry 2018, 10, 79. [Google Scholar] [CrossRef]
- Batista, G.; Prati, R.C.; Monard, M.C. A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Smith, M.R.; Martinez, T.R.; Giraud-Carrier, C.G. An instance level analysis of data complexity. Mach. Learn. 2014, 95, 225–256. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Lemaitre, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 17:1–17:5. [Google Scholar]
- Thorndike, R.L. Who Belongs in the Family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).