Complex Fuzzy Geometric Aggregation Operators

Abstract

A complex fuzzy set is an extension of the traditional fuzzy set, where traditional [0,1]-valued membership grade is extended to the complex unit disk. The aggregation operator plays an important role in many fields, and this paper presents several complex fuzzy geometric aggregation operators. We show that these operators possess the properties of rotational invariance and reflectional invariance. These operators are also closed on the upper-right quadrant of the complex unit disk. Based on the relationship between Pythagorean membership grades and complex numbers, these operators can be applied to the Pythagorean fuzzy environment.

1. Introduction

Ramot et al. [1] introduced the innovative concept of complex fuzzy sets (CFSs), which is an extension of the traditional fuzzy sets [2] where traditional unit interval [0,1]-valued membership degrees are extended to the complex unit disk. CFSs are completely distinct from the fuzzy complex numbers discussed by Buckley [3,4,5]. The complex-valued membership grade has an amplitude term with the addition of a phase term. The phase term of complex-valued membership grade is the key feature which essentially distinguishes complex fuzzy sets from other extensions of fuzzy sets. Ramot et al. [1,6] then introduced several operators of CFSs and a novel framework for complex fuzzy reasoning. Hu et al. [7] introduced the orthogonality relation for CFSs. Bi et al. [8] proposed the parallelity of CFSs and the parallelity-preserving operators. Zhang et al. [9] proposed the $\delta$-equalities for CFSs. Alkouri and Salleh [10] and Hu et al. [11] defined several distances between CFSs. Tamir et al. [12] proposed a new interpretation of complex membership degree. They [13] then proposed complex fuzzy propositional and first-order logics. Dick [14] proposed the concept of rotational invariance for complex fuzzy operators. Recently, several scholars have developed extensions of CFSs. Greenfield et.al [15,16] introduced interval-valued complex fuzzy sets. Alkouri and Saleh [17] proposed complex intuitionistic fuzzy sets. Ali and Smarandache [18] introduced complex neutrosophic sets. Recently, CFSs and their extensions have been successfully applied in many fields, such as time series prediction [19,20,21,22], decision making [23], signal processing [1,7,9], and image restoration [24].

Yager and Abbsocv [25] discussed the relationship between CFSs and Pythagorean fuzzy sets (PFSs), which was developed by Yager [26,27] as an extension of Atanssov’s intuitionistic fuzzy sets [28]. They showed that Pythagorean fuzzy membership grades can be viewed as complex numbers on the upper-right quadrant of the complex unit disk, named $\mathsf{\Pi }-i$ numbers. Dick, Yager, and Yazdanbahksh [29] then discussed several lattice-theoretic properties of PFSs and CFSs. Quantum information processing also allows for meaningful aggregation using complex numbers. Since qubits can be represented by unit vectors in the two-dimensional complex Hilbert space, geometric information or vector aggregation are used for meaningful clustering [30,31].

The information aggregation operator plays an important role in many fields of decision making. In the past several decades, many aggregation techniques for decision making have been developed. The ordered weighted averaging (OWA) operator introduced by Yager [32] is one of the well-known aggregation operators. Many different aggregation techniques have been applied in many different fuzzy environments, such as intuitionistic [33,34,35], Pythagorean [36,37,38], neutrosophic [39,40,41], interval-valued intuitionistic [42,43,44,45], and hesitant fuzzy environments [46,47,48].

As mentioned in [19], CFSs are suitable to represent information with uncertainty and periodicity, and thus this information aggregation procedure needs to simultaneously process the uncertainty and periodicity in the data. However, comparatively few aggregation techniques have been made in the complex fuzzy environment. Ramot et al. [6] defined the complex fuzzy aggregation operations as vectors aggregation. In particular, the complex weights are used in their definition. Ma et al. [19] developed a product-sum aggregation operator for multiple periodic factor prediction problems. They proved the continuity of this operator. However, they did not focus on techniques for complex fuzzy information aggregation in these two articles.

In this paper, we study aggregation operators in the complex fuzzy environment. Dick’s [14] concept of rotational invariance is an intuitive and desirable feature for complex fuzzy operators. This feature is examined for complex fuzzy aggregation operators. This paper proposes a novel feature for complex fuzzy aggregation operators called reflectional invariance. Moreover, we study the aggregation operators of complex numbers in the upper-right quadrant of the complex unit disk.

The main contributions of the study include: (1) A concept of reflectional invariance for complex fuzzy operators. (2) Several complex fuzzy weighted geometric operators; we also show that these operators can also be used in a Pythagorean fuzzy environment. (3) A target location method which involves the complex fuzzy aggregation operators.

This paper is organized as follows. In Section 2, we review some basic and fundamental concepts of CFSs, rotational invariance, reflectional invariance, and Ramot et al.’s [6] complex fuzzy aggregation operators. In Section 3 we study the complex fuzzy weighted geometric (CFWG) operator on CFSs and its properties. In Section 4, we develop the complex fuzzy ordered weighted geometric (CFOWG) operator based on the traditional partial ordering by the modulus of a complex number, and study its properties. In Section 5, we study these operators in the domain of $\mathsf{\Pi }-i$ numbers which belong to the upper-right quadrant of the complex unit disk. In Section 6, we present an application example in a target location. Conclusions are made in Section 7.

2. Preliminaries

In this section, we present some basic material, including the concepts of CFSs [1], rotational invariance [14], reflectional invariance, and complex fuzzy aggregation operators [1].

2.1. Complex Fuzzy Sets

Ramot et al. [1] defined the concept of CFSs as follows.

Definition 1

([1]). Let X be a universe, D be the set of complex numbers whose modulus is less than or equal to 1, i.e.,

$$D=\left\{a\in \mathcal{C}\left|\right|a|\le 1\right\},$$

a complex fuzzy set A defined on X is a mapping: $X\to D$, which can be denoted as below:

$$A=\left\{<x,t_A\left(x\right)·e^{j{\nu }_A\left(x\right)}>|x\in X\right\},$$

(1)

where $j=\sqrt{-1}$, the amplitude term $t_A\left(x\right)$ and the phase term ${\nu }_A\left(x\right)$ are both real-valued, and $t_A\left(x\right)\in [0,1]$.

For convenience, we only consider the complex numbers on D, called complex fuzzy values (CFVs). Let $a=t_a·e^{j{\nu }_a}$ be a CFV, then the amplitude of a is denoted by $t_a$ and the phase of a is denoted by ${\nu }_a$. They are both real-valued, $t_a\in [0,1]$. The modulus of a is $t_a$, denoted by $\left|a\right|$.

Let $a=t_a·e^{j{\nu }_a}$ and $b=t_b·e^{j{\nu }_b}$ be two CFVs, then we have the following two commonly used binary operations.

(i)

Algebraic product:

$$a·b=t_a·t_b·e^{j({\nu }_a+{\nu }_b)}.$$

(2)

(ii)

Average:

$$\frac{a+b}{2}=\frac{t_{a}cos{\nu }_a+t_{b}cos{\nu }_b}{2}+j\frac{t_{a}sin{\nu }_a+t_{b}sin{\nu }_b}{2}.$$

(3)

The partial ordering of CFVs is the traditional partial ordering by the modulus of a complex number, that is, $a\le b$ if and only if $\left|a\right|\le \left|b\right|$, equivalently, $t_a\le t_b$.

2.2. Rotational Invariance and Reflectional Invariance

Let $a=t_a·e^{j{\nu }_a}$ be a CFV, then we have the following two commonly used unary operations:

(i)

the rotation of a by $\theta$ radians, denoted $Ro{t}_{\theta }\left(a\right)$, is defined as

$$Ro{t}_{\theta }\left(a\right)=t_a·e^{j({\nu }_a+\theta )};$$

(4)

(ii)

the reflection of a, denoted $Ref\left(a\right)$, is defined as

$$Ref\left(a\right)=t_a·e^{j-{\nu }_a}.$$

(5)

Then, based on the rotation operation, Dick [14] introduced the concept of rotational invariance for complex fuzzy operators.

Definition 2

([14]). A function $f:D^2\to D$ is rotationally invariant if and only if

$$f\left(Ro{t}_{\theta }\left(a\right),Ro{t}_{\theta }\left(b\right)\right)=Ro{t}_{\theta }\left(f(a,b)\right),$$

(6)

for any θ.

We extend the above concept to multivariate operators.

Definition 3.

Let $f:D^n\to D$ be an n-order function. f is rotationally invariant if and only if

$$f\left(Ro{t}_{\theta }\left(a_1\right),Ro{t}_{\theta }\left(a_2\right),\dots ,Ro{t}_{\theta }\left(a_n\right)\right)=Ro{t}_{\theta }\left(f(a_1,a_2,\dots ,a_n)\right),$$

(7)

for any θ.

In particular, since the periodicity of complex-valued membership grade, that is, $Ro{t}_{2\pi }\left(x\right)=x$ for any $x\in D$, we have $f\left(Ro{t}_{2\pi }\left(a_1\right),Ro{t}_{2\pi }\left(a_2\right),\dots ,Ro{t}_{2\pi }\left(a_n\right)\right)=f(a_1,a_2,\dots ,a_n)=Ro{t}_{2\pi }\left(f(a_1,a_2,\dots ,a_n)\right)$. This is a special case of rotational invariance.

Similar to the above definition, we introduce the concept of reflectional invariance for complex fuzzy operators based on the reflection operation.

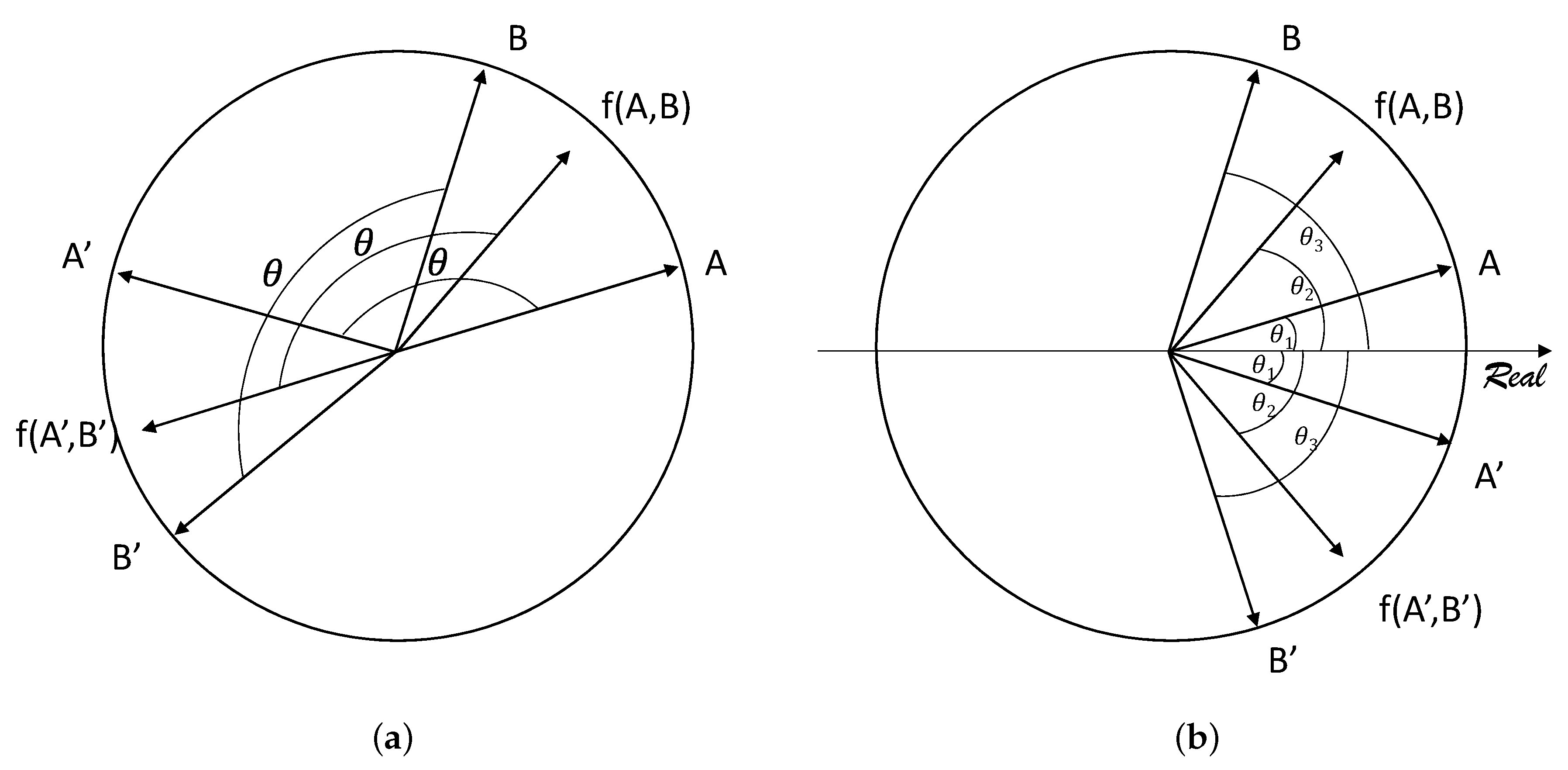
Definition 4.

Let $f:D^n\to D$ be an n-order function. f is reflectionally invariant if and only if

$$f\left(Ref\left(a_1\right),Ref\left(a_2\right),\dots ,Ref\left(a_n\right)\right)=Ref\left(f(a_1,a_2,\dots ,a_n)\right).$$

(8)

Rotational invariance and reflectional invariance are intuitive properties for complex fuzzy operators. It makes a great deal of sense that a operator is invariant under a rotation or a reflection. If we rotate two vectors by a common value, rotational invariance states that an aggregation of those vectors will be rotated by the same value, as shown in Figure 1a. If we reflect two vectors, reflectional invariance states that an aggregation of those vectors will be reflected as well, as shown in Figure 1b.

Reflectional invariance and rotational invariance are two properties which are only concerned with the phase of CFVs.

These two properties of the algebraic product and average operators were examined, and the results are given as follows.

Theorem 1

([14]). The algebraic product is not rotationally invariant.

Theorem 2.

The algebraic product is reflectionally invariant.

Proof. 

For any $a,b\in D$, we have

$$Ref\left(a\right)·Ref\left(b\right)=t_a·e^{j-{\nu }_a}·t_b·e^{j-{\nu }_b}=t_a·t_b·e^{j(-{\nu }_a-{\nu }_b)},$$

$$Ref(a·b)=Ref\left(t_a·t_b·e^{j({\nu }_a+{\nu }_b)}\right)=t_a·t_b·e^{j(-{\nu }_a-{\nu }_b)},$$

then $Ref\left(a\right)·Ref\left(b\right)=Ref(a·b)$. ☐

Theorem 3.

The average operator is reflectionally invariant and rotationally invariant.

Proof. 

(i) Let $a=r_a+j{\omega }_a,b=r_b+j{\omega }_b\in D$. We have

$$\frac{Ref\left(a\right)+Ref\left(b\right)}{2}=\frac{r_a+r_b}{2}+j\frac{-{\omega }_a-{\omega }_b}{2}=\frac{r_a+r_b}{2}-j\frac{{\omega }_a+{\omega }_b}{2}=Ref(\frac{a+b}{2}).$$

Then, the average operator is reflectionally invariant.

(ii) For any $a,b\in D$, we have

$$\frac{a·e^{j\theta }+b·e^{j\theta }}{2}=\frac{(a+b)·e^{j\theta }}{2}=\frac{(a+b)}{2}·e^{j\theta }.$$

Then, the average operator is rotationally invariant. ☐

2.3. Complex Fuzzy Aggregation Operators

Ramot et al. [6] defined the aggregation operation on CFSs as vector aggregation:

Definition 5

([6]). Let $A_1,A_2,\dots ,A_n$ be CFSs defined on X. Vector aggregation on $A_1,A_2,\dots ,A_n$ is defined by a function v.

$$v:D^n\to D.$$

(9)

The function v produces an aggregate CFS A by operating on the membership grades of $A_1,A_2,\dots ,A_n$ for each $x\in X$. For all $x\in X$, v is given by

$$\begin{array}{cc}\hfill {\mu }_A\left(x\right)& =v\left(t_{A_1}·e^{j{\nu }_{A_1}},t_{A_2}·e^{j{\nu }_{A_2}},\cdots ,t_{A_n}·e^{j{\nu }_{A_n}},\right)\hfill \\ & =\sum _{i=1}^n\left(w_i·t_{A_i}·e^{j{\nu }_{A_i}}\right),\hfill \end{array}$$

(10)

where $w_i\in D$ for all i, and ${\sum }_{i=1}^n\left|w_i\right|=1$.

The complex weights are used in Ramot et al.’s definition for the purpose of maintaining a definition that is as general as possible. In this paper, we only discuss the complex fuzzy aggregation operations with real-valued weights.

We notice that the above definition of Ramot et al’s [6] aggregation operator is a complex fuzzy weighted arithmetic (CFWA) operator. For convenience, let $a_1,a_2,\dots ,a_n$ be CFVs. The CFWA operator is given as

$$CFWA(a_1,a_2,\dots ,a_n)=\sum _{i=1}^n\left(w_i·a_i\right),$$

(11)

where $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$.

When $a_1,a_2,\dots ,a_n\in [0,1]$, the CFWA operator can reduce to a traditional fuzzy weighted arithmetic operator.

When $w_i=1/n$ for all i, then the CFWA operator is the arithmetic average of $(a_1,a_2,\dots ,a_n)$, denoted by the complex fuzzy arithmetic average (CFAA) operator. That is,

$$CFAA(a_1,a_2,\dots ,a_n)=\frac{1}{n}·\sum _{i=1}^n{a}_i.$$

(12)

When $a_1,a_2,\dots ,a_n\in [0,1]$ and $w_i=1/n$ for all i, the CFAA operator is the arithmetic mean of numbers on [0,1].

As a special case of the CFWA operator, note that the average operator on CFVs is reflectionally invariant and rotationally invariant (see Theorem 3). We show that the CFWA operator also possesses these two properties.

Theorem 4.

The CFWA operator is reflectionally invariant and rotationally invariant.

Proof. 

(i) Let $a_1=r_{a_1}+j{\omega }_{a_1},a_2=r_{a_2}+j{\omega }_{a_2},\cdots ,a_n=r_{a_n}+j{\omega }_{a_n}$ be CFVs. We have

$$\begin{array}{cc}\hfill Ref\left(CFWA(a_1,a_2,\dots ,a_n)\right)& =Ref\left(\sum _{i=1}^n\left(w_i·r_{a_i}\right)+j\sum _{i=1}^n\left(w_i·{\omega }_{a_i}\right)\right)\hfill \\ & =\sum _{i=1}^n\left(w_i·r_{a_i}\right)-j\sum _{i=1}^n\left(w_i·{\omega }_{a_i}\right)\hfill \\ & =\sum _{i=1}^n\left(w_i·(r_{a_i}-{\omega }_{a_i})\right)\hfill \\ & =\sum _{i=1}^n\left(w_i·Ref\left(a_i\right)\right).\hfill \end{array}$$

Then, the CFWA operator is reflectionally invariant.

(ii) For any CFVs $a_1,a_2,\dots ,a_n$, we have

$$\begin{array}{cc}\hfill CFWA(a_1·e^{j\theta },a_2·e^{j\theta },\dots ,a_n·e^{j\theta })& =w_1·a_1·e^{j\theta }+w_2·a_2·e^{j\theta }+\dots +w_n·a_n·e^{j\theta }\hfill \\ & =(w_1·a_1+w_2·a_2+\dots +w_n·a_n)·e^{j\theta }\hfill \\ & =CFWA(a_1,a_2,\dots ,a_n)·e^{j\theta }.\hfill \end{array}$$

Then, the CFWA operator is rotationally invariant. ☐

3. Complex Fuzzy Weighted Geometric Operators

In this section, we introduce the weighted geometric aggregation operators in a complex fuzzy environment and discuss their fundamental characteristics.

Definition 6.

Let $a_1,a_2,\dots ,a_n$ be CFVs, a complex fuzzy weighted geometric (CFWG) operator is defined as:

$$CFWG(a_1,a_2,\dots ,a_n)=\prod _{i=1}^n{a}_i^{w_i},$$

(13)

where $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$.

Denoting $CFWG(a_1,a_2,\dots ,a_n)=t·e^{j\nu }$, we have a weighted geometric aggregation (WGA) operator on [0,1], that is, $t={\prod }_{i=1}^n{t}_{a_i}^{w_i}$ and a weighted arithmetic aggregation (WAA) operator on $\mathbb{R}$, that is, $\nu ={\sum }_{i=1}^n{w}_i·{\nu }_{a_i}$.

When $a_1,a_2,\dots ,a_n\in [0,1]$, the CFWG operator can reduce to a traditional fuzzy weighted geometric operator.

When $w_i=1/n$ for all i, then $t=\sqrt[n]{t_{a_1}·t_{a_2}\cdots t_{a_n}}$ is the geometric mean of real numbers on unit interval [0,1], $\nu =\frac{1}{n}·{\sum }_{i=1}^n{\nu }_{a_i}$ is the arithmetic mean of real numbers on $\mathbb{R}$.

When $a_1,a_2,\dots ,a_n\in [0,1]$ and $w_i=1/n$ for all i, the CFWG operator is the geometric mean of real numbers on unit interval [0,1].

Theorem 5.

Let $a_1,a_2,\dots ,a_n$ be CFVs, then the aggregated value $CFWG(a_1,a_2,\dots ,a_n)$ is also a complex fuzzy value.

Proof. 

Since $|CFWG(a_1,a_2,\dots ,a_n)|={\prod }_{i=1}^n{t}_{a_i}^{w_i}$, which is a weighted arithmetic aggregation operator on unit interval [0,1], we have $\left|CFWG\right(a_1,a_2,\dots ,a_n\left)\right|\le 1$. ☐

Similar to Theorem 4, the CFWA operator is reflectionally invariant and rotationally invariant. We show that the CFWG operator also possesses these two properties.

Theorem 6.

The CFWG operator is reflectionally invariant and rotationally invariant.

Proof. 

(i) For any CFVs $a_1,a_2,\dots ,a_n$, we have

$$\begin{array}{cc}\hfill Ref\left(CFWG(a_1,a_2,\dots ,a_n)\right)& =Ref\left(\prod _{i=1}^n{t}_{a_i}^{w_i}·e^{j{\sum }_{i=1}^n{w}_i·{\nu }_{a_i}}\right)\hfill \\ & =\prod _{i=1}^n{t}_{a_i}^{w_i}·e^{j-{\sum }_{i=1}^n{w}_i·{\nu }_{a_i}}\hfill \\ & =\prod _{i=1}^n{t}_{a_i}^{w_i}·e^{j{\sum }_{i=1}^n{w}_i·(-{\nu }_{a_i})}\hfill \\ & =\prod _{i=1}^{n}Ref{\left(a_i\right)}^{w_i}\hfill \\ & =CFWG\left(Ref\left(a_1\right),Ref\left(a_2\right),\dots ,Ref\left(a_n\right)\right);\hfill \end{array}$$

(ii) and

$$\begin{array}{cc}\hfill CFWG(a_1·e^{j\theta },a_2·e^{j\theta },\dots ,a_n·e^{j\theta })& =a_1^{w_1}·e^{j{w}_1\theta }·a_2^{w_1}·e^{j{w}_2\theta }·\dots ·a_n^{w_n}·e^{j{w}_n\theta }\hfill \\ & =\left(\prod _{i=1}^n{a}_i^{w_i}\right)·e^{j(w_1·\theta +w_2·\theta +\dots +w_n·\theta )}\hfill \\ & =CFWG(a_1,a_2,\dots ,a_n)·e^{j\theta }.\hfill \end{array}$$

 ☐

Idempotency, boundedness, and monotonicity are three important properties of aggregation operators. The CFWG operator satisfies the following properties.

Theorem 7.

Let $a_1,a_2,\dots ,a_n$, $b_1,b_2,\dots ,b_n$ be CFVs, CFWG weights are real values, that is, $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$. Then, we have the following:

(1) 

(Idempotency): If $a_1=a_2=\dots =a_n$ then

$$CFWG(a_1,a_2,\dots ,a_n)=a_1.$$

(2) 

(Amplitude boundedness):

$$\left|CFWG\right(a_1,a_2,\dots ,a_n\left)\right|\le a,$$

where $a=\underset{i}{max}\left|a_i\right|$.

(3) 

(Amplitude monotonicity): If $|a_i|\le |b_i|$ $i=1,2,\dots ,n$, then

$$|CFWAA(a_1,a_2,\dots ,a_n)|\le |CFWAA(b_1,b_2,\dots ,b_n)|.$$

Proof. 

(1) Trivial form the facts that both WAA operator on [0,1] and WGA operator on $\mathbb{R}$ satisfy the property of idempotency.

(2) Trivial form the facts that $|CFWG(a_1,a_2,\dots ,a_n)|={\prod }_{i=1}^n{t}_{a_i}^{w_i}$ and WGA operator on $\mathbb{R}$ satisfy the property of boundedness.

(3) Trivial form the facts that $|CFWG(a_1,a_2,\dots ,a_n)|={\prod }_{i=1}^n{t}_{a_i}^{w_i}$ and WGA operator on $\mathbb{R}$ satisfy the property of monotonicity. ☐

In this paper, for complex fuzzy aggregation operators, boundedness and monotonicity are restricted exclusively to the amplitude of CFVs. They are two properties which are only concerned with the amplitude of CFVs. Idempotency is a property that is concerned with both the phase and amplitude of CFVs.

It is easy to prove that the CFWA operator satisfies idempotency and amplitude boundedness, but it does not satisfy the property of amplitude monotonicity.

Example 1.

Let $a_1=0.4$, $a_2=0.4·e^{j2\pi /3}$, $b_1=b_2=0.3$ and weights be $w_1=w_2=0.5$. Then,

$$\begin{array}{c}CFWA(a_1,a_2)=0.5·0.4+0.5·0.4·e^{j2\pi /3}\\ =0.2·e^{j\pi /3}\end{array}$$

and $CFWA(b_1,b_2)=0.3$. Then, $|a_1|\ge |b_1|$, $|a_2|\ge |b_2|$, but $|CFWA(a_1,a_2)|\le |CFWA(b_1,b_2)|$.

4. Complex Fuzzy Ordered Weighted Geometric Operators

Based on the partial ordering of complex numbers, we propose a complex fuzzy ordered weighted geometric (CFOWG) operator as follows:

Definition 7.

Let $a_1,a_2,\dots ,a_n$ be CFVs, a CFOWG operator is defined as

$$CFOWG(a_1,a_2,\dots ,a_n)=\prod _{i=1}^n{a}_{\sigma \left(i\right)}^{w_i},$$

(14)

where $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$, $\left(\sigma \right(1),\sigma (2),\dots ,\sigma (n\left)\right)$ is a permutation of $(1,2,\dots ,n)$ such that $|a_{\sigma (i-1)}|\ge |a_{\sigma \left(i\right)}|$ for all i.

Especially when $w_i=1/n$ for all i, then the CFOWG operator is reduced to the CFWG operator. Similar to Theorem 5, we have the following.

Theorem 8.

Let $a_1,a_2,\dots ,a_n$ be CFVs, then the aggregated value $CFOWG(a_1,a_2,\dots ,a_n)$ is also a complex fuzzy value.

Similar to Theorem 6, the CFWG operator is reflectionally invariant and rotationally invariant. The CFOWG operator also possesses these two properties.

Theorem 9.

The CFOWG operator is reflectionally invariant and rotationally invariant.

Similar to Theorem 7, the CFOWG operator satisfies idempotency, amplitude boundedness, and amplitude monotonicity.

Theorem 10.

Let $a_1,a_2,\dots ,a_n$, $b_1,b_2,\dots ,b_n$ be CFVs, CFOWAA weights are real values, that is, $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$. Then, we have the following:

(1) 

(Idempotency): If $a_1=a_2=\dots =a_n$, then

$$CFOWG(a_1,a_2,\dots ,a_n)=a_1.$$

(2) 

(Boundedness):

$$\left|CFOWG\right(a_1,a_2,\dots ,a_n\left)\right|\le a,$$

where $a=\underset{i}{max}\left|a_i\right|$.

(3) 

(Monotonicity): If $|a_i|\le |b_i|$ $i=1,2,\dots ,n$, then

$$|CFOWG(a_1,a_2,\dots ,a_n)|\le |CFWAA(b_1,b_2,\dots ,b_n)|.$$

Besides the above properties, the CFOWG operator has the following.

Theorem 11.

Let $a_1,a_2,\dots ,a_n$ be CFVs, CFOWG weights are real values, that is, $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$. Then, we have the following:

(1) 

If $w=(1,0,\dots ,0)$, then

$$|CFOWG(a_1,a_2,\dots ,a_n)|=\underset{i}{max}\left|a_i\right|;$$

(2) 

If $w=(0,0,\dots ,1)$, then

$$|CFOWG(a_1,a_2,\dots ,a_n)|=\underset{i}{min}\left|a_i\right|;$$

(3) 

If $w_i=1,w_k=0,k\ne i$, then

$$\left|CFOWG(a_1,a_2,\dots ,a_n)\right|=\left|a_{\sigma \left(i\right)}\right|,$$

where $a_{\sigma \left(i\right)}$ is the i-th (modulus-based) largest of $a_1$,$a_2$, …,$a_n$.

Now we give a brief summary of the properties of the CFWG and CFOWG operators with real-valued weights. The results are summarized in

Table 1. Properties of the complex fuzzy aggregation operators. √ and × represent that the corresponding property holds and does not hold, respectively.

	Idempotency	Amplitude Boundedness	Amplitude Monotonicity	Reflectional Invariance	Rotational Invariance
CFAA	√	√	×	√	√
CFWA	√	√	×	√	√
CFWG	√	√	√	√	√
CFOWG	√	√	√	√	√

, in which √ and × represent that the corresponding property holds and does not hold, respectively.

5. Complex Fuzzy Values and Pythagorean Fuzzy Numbers

Yager and Abbasov [25] showed that Pythagorean membership grades can be expressed using complex numbers, called $\mathsf{\Pi }-i$ numbers, which belong to the upper-right quadrant of the complex unit disk. Essentially, the CFWAA and CFOWAA operators are used to deal with special complex numbers, which belong to the complex unit disk.

In this section, we consider the CFWG and CFOWG operators in the domain of $\mathsf{\Pi }-i$ numbers.

We first recall the concepts of Pythagorean fuzzy sets (PFSs) and $\mathsf{\Pi }-i$ numbers.

Definition 8

([25]). Let X be a universe. A PFS A is defined by

$$A=\left\{<x,p_A\left(x\right),{\nu }_A\left(x\right),>|x\in X\right\},$$

(15)

where $p_A\left(x\right)\in [0,1]$ and ${\nu }_A\left(x\right)\in [0,1]$ respectively represent the membership grade and nonmembership grade of the element x to set A, such that

$$0\le {\left(p_A\left(x\right)\right)}^2+{\left({\nu }_A\left(x\right)\right)}^2\le 1$$

for all $x\in X$. The degree of indeterminacy of the element x to set A is ${\pi }_A\left(x\right)$, defined by

$${\pi }_A\left(x\right)=\sqrt{1-{\left(p_A\left(x\right)\right)}^2-{\left({\nu }_A\left(x\right)\right)}^2}.$$

For convenience, Zhang and Xu [49] referred to $\left(p_A\left(x\right),{\nu }_A\left(x\right)\right)$ as a Pythagorean fuzzy number (PFN) simply denoted by $a=(p_a,{\nu }_a)$, where $p_a\in [0,1],{\nu }_a\in [0,1]$ and ${\left(p_a\right)}^2+{\left({\nu }_a\right)}^2\le 1$.

Yager and Abbasov [25] discussed the relationship between Pythagorean membership grades and complex numbers. They showed that the complex numbers of the form $z=r·e^{j\theta }$ with conditions $r\in [0,1]$ and $\theta \in [0,\pi /2]$ can be interpretable as PFNs $(rcos\theta ,rsin\theta )$. They referred to these complex numbers as “$\mathsf{\Pi }-i$ numbers”, which are complex numbers in the upper-right quadrant of the complex unit disk.

As explained in [25], we should consider which aggregation operation is closed under $\mathsf{\Pi }-i$ numbers.

Let us consider the closeness of $\mathsf{\Pi }-i$ numbers under the CFWG and CFOWG operations. For the CFWG operator, we have the following result.

Theorem 12.

Let $z_1,z_2,\dots ,z_n$ be $\mathsf{\Pi }-i$ numbers, and the CFWG weights are real values, that is, $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$. Then, the aggregated value $CFWG(z_1,z_2,\dots ,z_n)$ is also a $\mathsf{\Pi }-i$ number.

Proof. 

Denoting $CFWG(z_1,z_2,\dots ,z_n)=t·e^{j\nu }={\prod }_{i=1}^n{t}_{z_i}^{w_i}·e^{j{\sum }_{i=1}^n{w}_i·{\nu }_{z_i}}$, from Theorem 2, we have $t=\left|CFWG\right(z_1,z_2,\dots ,z_n\left)\right|\le 1.$

Since $\nu ={\sum }_{i=1}^n{w}_i·{\nu }_{z_i}$ is a weighted geometric aggregation (WGA) operator of real numbers on $[0,\pi /2]$, then we have $\nu \in [0,\pi /2]$. Thus, $CFWG(z_1,z_2,\dots ,z_n)$ is also a $\mathsf{\Pi }-i$ number. ☐

Similar to the above Theorem, we have the following.

Theorem 13.

Let $z_1,z_2,\dots ,z_n$ be $\mathsf{\Pi }-i$ numbers, and the CFOWG weights are real values, that is, $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$. Then, the aggregated value $CFOWG(z_1,z_2,\dots ,z_n)$ is also a $\mathsf{\Pi }-i$ number.

The above theorems show us that the CFWG and the CFOWG operators are closed under $\mathsf{\Pi }-i$ numbers. When PFNs are interpreted as $\mathsf{\Pi }-i$ numbers, then we can aggregate these PFNs to a PFN by using the CFWG or CFOWG operator.

From the above theorems, the CFWG and the CFOWG operators are closed on the upper-right quadrant of complex unit disk.

Consider other quadrants of the complex unit disk. Let

$$D_k=\left\{z=r·e^{j\theta }|r\in [0,1],\theta \in [\frac{(k-1)\pi }{2},\frac{k\pi }{2}]\right\}$$

for $k=1$ to 4. $D_1$ is the set of $\mathsf{\Pi }-i$ numbers.

Now, we discuss the closeness of the CFWG and the CFOWG operators on other quadrants of the complex unit disk. Plainly, we have the following.

Theorem 14.

For any $k\in \{1,2,3,4\}$, if $z_1,z_2,\dots ,z_n\in D_k$, and the weights are real values, that is, $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$. Then, we have

$$CFWG(z_1,z_2,\dots ,z_n)\in D_k,$$

$$CFOWG(z_1,z_2,\dots ,z_n)\in D_k.$$

Proof. 

Similar to Theorem 13. ☐

Theorem 15.

For any $k\in \{1,2,3,4\}$, if $z_1,z_2,\dots ,z_n,y_1,y_2,\dots ,y_n\in D_k$, and the weights are real values, that is, $w_i\in [0,1]$ for all i, and ${\sum }_{i=1}^n{w}_i=1$. Then, we have the following:

(1) 

(Idempotency): If $z_1=z_2=\dots =z_n$, then

$$CFWG(z_1,z_2,\dots ,z_n)=z_1,$$

$$CFOWG(z_1,z_2,\dots ,z_n)=z_1.$$

(2) 

(Amplitude boundedness):

$$\left|CFWG\right(z_1,z_2,\dots ,z_n\left)\right|\le z,$$

$$\left|CFOWG\right(z_1,z_2,\dots ,z_n\left)\right|\le z,$$

where $z=\underset{i}{max}\left|z_i\right|$.

(3) 

(Amplitude monotonicity): If $|z_i|\le |y_i|$ $i=1,2,\dots ,n$, then

$$|CFWG(a_1,a_2,\dots ,a_n)|\le |CFWG(y_1,y_2,\dots ,y_n)|,$$

$$|CFOWG(a_1,a_2,\dots ,a_n)|\le |CFWG(y_1,y_2,\dots ,y_n)|.$$

Proof. 

Similar to Theorem 7. ☐

6. Example Application

In this section, we consider a target location application of the complex fuzzy aggregation operator. We do not intend to show the potential advantages of using complex fuzzy aggregation methods in comparison with existing alternative aggregation approaches in this section.

Assume the observer position is fixed. Using a position sensor and an angular sensor, the observer measures the distance and angle of the fixed target. To improve the target location accuracy, the observer repeatedly measures the same target. Then, the target position is estimated according to aggregation theory.

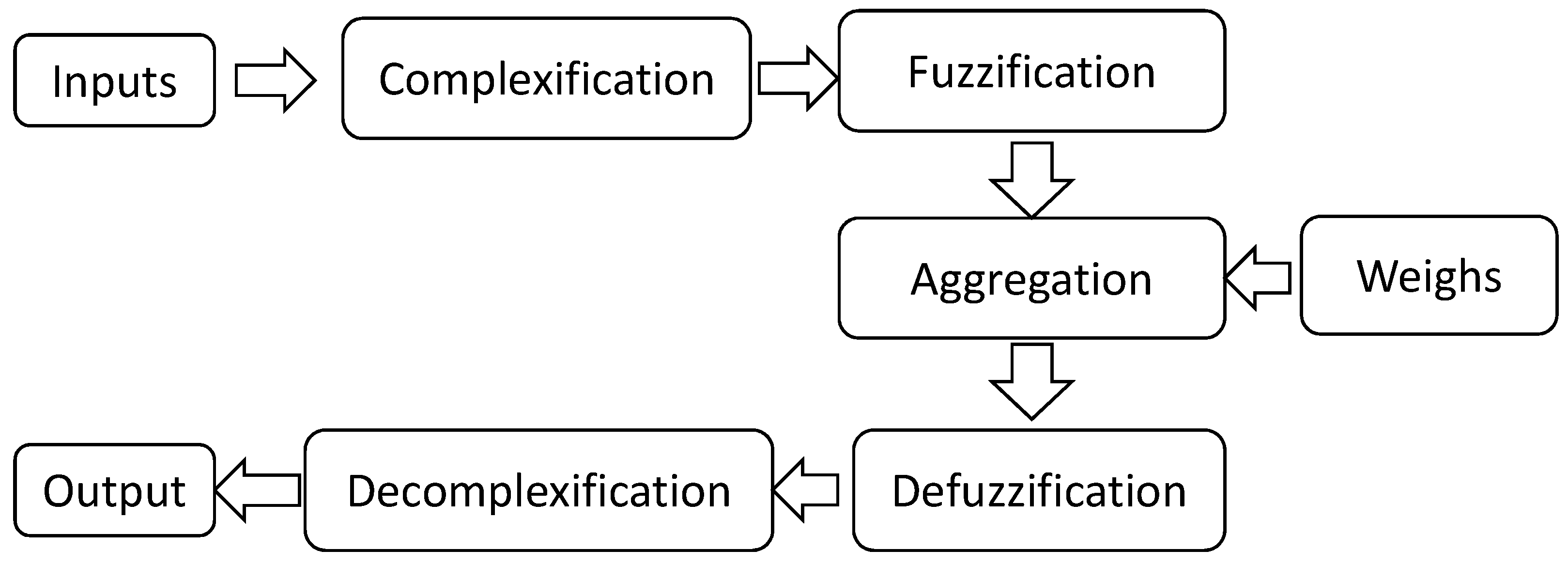
Assume n measurements $\left((d_1,{\theta }_1),(d_2,{\theta }_2),\dots ,(d_n,{\theta }_n)\right)$ have been measured by the observer. The target position is estimated in the following five stages, as illustrated in Figure 2.

Step 1

Complexification of the measured results; each measurement is represented as $c_i=d_i·e^{{\theta }_i}$.

Step 2

(Fuzzification) Normalize the amplitudes of all measurements. Let $d={max}_i{d}_i$, for each $c_i$, the normalized result is $a_i=c_i/d,$ where $t_{a_i}=d_i/d$.

Step 3

(Aggregation) Produce an aggregate result. For simplicity, using the CFWG operator with weights $(1/n,1/n,\dots ,1/n)$. We obtain

$$a=\prod _{i=1}^n{a}_i^{1/n},$$

(16)

where $t_a=\sqrt[n]{t_{a_1}·t_{a_2}\cdots t_{a_n}}$ and ${\nu }_a=\frac{1}{n}·{\sum }_{i=1}^n{\theta }_i$.

Step 4

(Defuzzification) Calculate $c=a·d$, where $t_c=t_a·d$.

Step 5

Decomplexification (or sometimes “realification”) of c. We get the target position $(p,\nu )$, where $p=t_c,\nu ={\nu }_a$.

Numerical Example:Assume that the observer obtains five measurements as follows:

$$\left((865,{24}^{°}),(867,{25}^{°}),(871,{24}^{°}),(866,{25}^{°}),(869,{23}^{°})\right),$$

where $(d,\theta )$ means that the target lies on the $\theta$ degrees east of south of the observer and d metres from the observer. Then,

Step 1

Complexifications of the measured results are calculated as

$$\left((865·e^{j2\pi 336/360}),(867·e^{j2\pi 335/360}),(871·e^{j2\pi 336/360}),(866·e^{j2\pi 335/360}),(869·e^{j2\pi 337/360})\right).$$

Step 2

Normalizations of the amplitudes of all measurements are calculated as

$$\left(0.9931·e^{j2\pi 336/360},0.9954·e^{j2\pi 335/360},1·e^{j2\pi 336/360},0.9943·e^{j2\pi 335/360},0.9977·e^{j2\pi 337/360}\right).$$

Step 3

Aggregation of CFVs is calculated as

$$0.9961·e^{j2\pi 335.8/360},$$

where the weights are $(1/5,1/5,\dots ,1/5)$.

Step 4

Defuzzification of the aggregate result is calculated as $867.6·e^{j2\pi 335.8/360}.$

Step 5

Decomplexification of the above result is calculated as $(867.6,24.2).$

Then, the target position is estimated at $(867.6,24.2)$. That is, it lies $24.2$ degrees east of south of the observer and $867.6$ m from the observer.

Note that we do not discuss how to choose complex fuzzy aggregation functions, nor their weights.

7. Conclusions

In this paper, we propose two complex fuzzy aggregation operators: the CFWG and CFOWG operators. Their main properties are summarized in Table 1. In particular, both the CFWG and the CFOWG operators are reflectionally invariant and rotationally invariant. We also showed that the CFWG and the CFOWG operators are closed under $\mathsf{\Pi }-i$ numbers.

As we know, complex data are frequently encountered in many different applications, such as engineering, management, finance, and medicine. CFSs are suitable to represent information with uncertainty and periodicity simultaneously. Complex fuzzy information aggregation techniques may be useful in these applications.