A Hybrid Fuzzy Analytic Network Process (FANP) and Data Envelopment Analysis (DEA) Approach for Supplier Evaluation and Selection in the Rice Supply Chain
Abstract
1. Introduction
2. Literature Review
2.1. Supplier Selection Methods
2.2. Criteria and Sub-Criteria for Supplier Selection
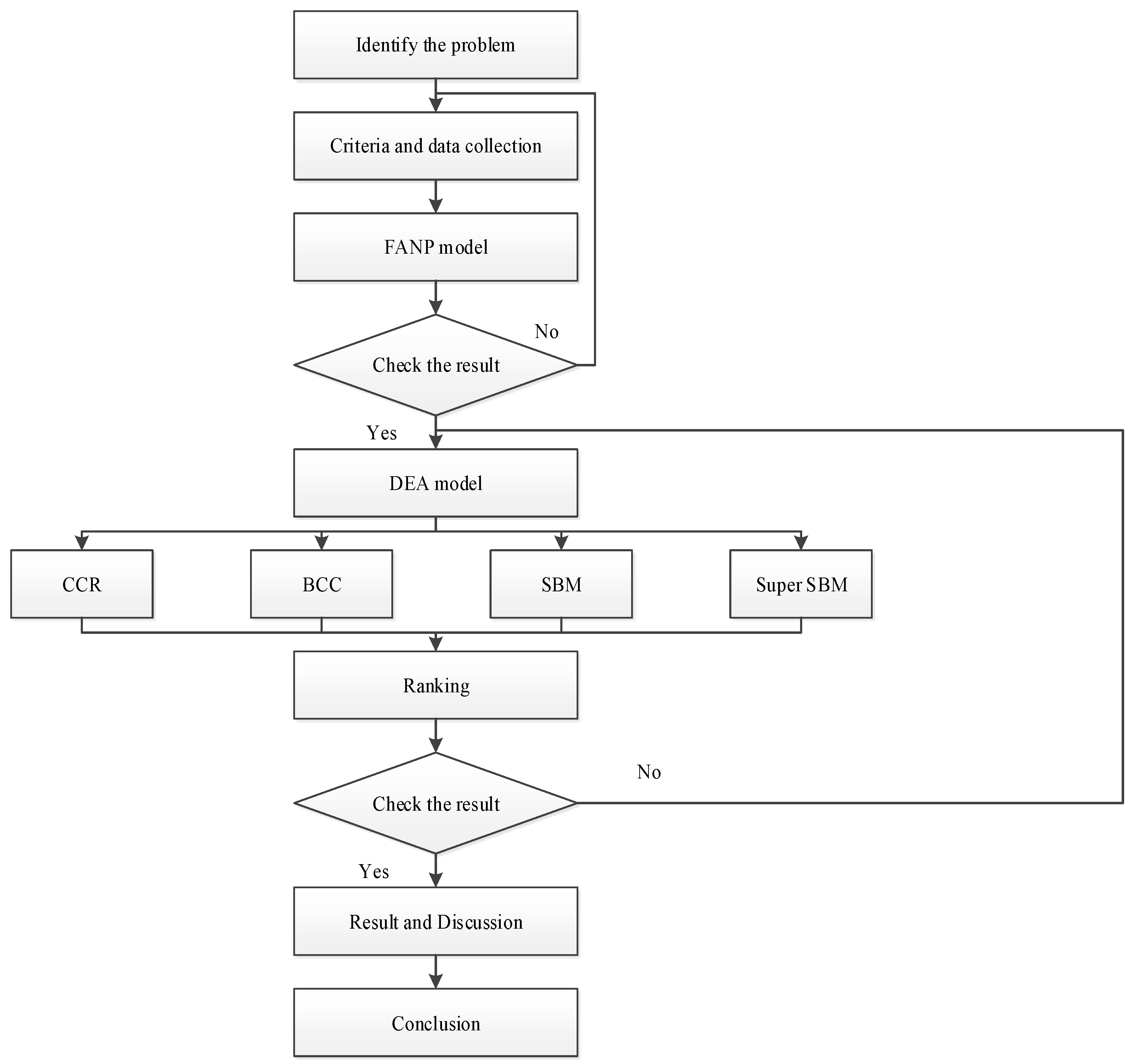
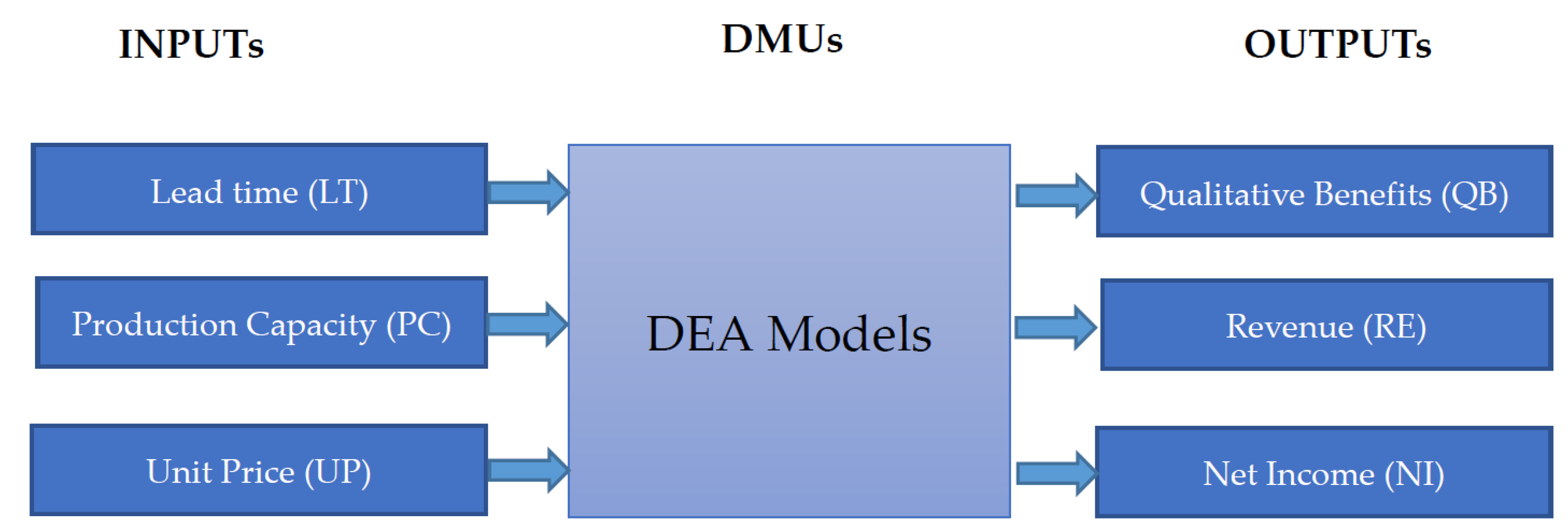
3. Material and Methodology
3.1. Research Development
3.2. Methodology
3.2.1. Fuzzy Set Theory
3.2.2. Fuzzy Analytic Network Process
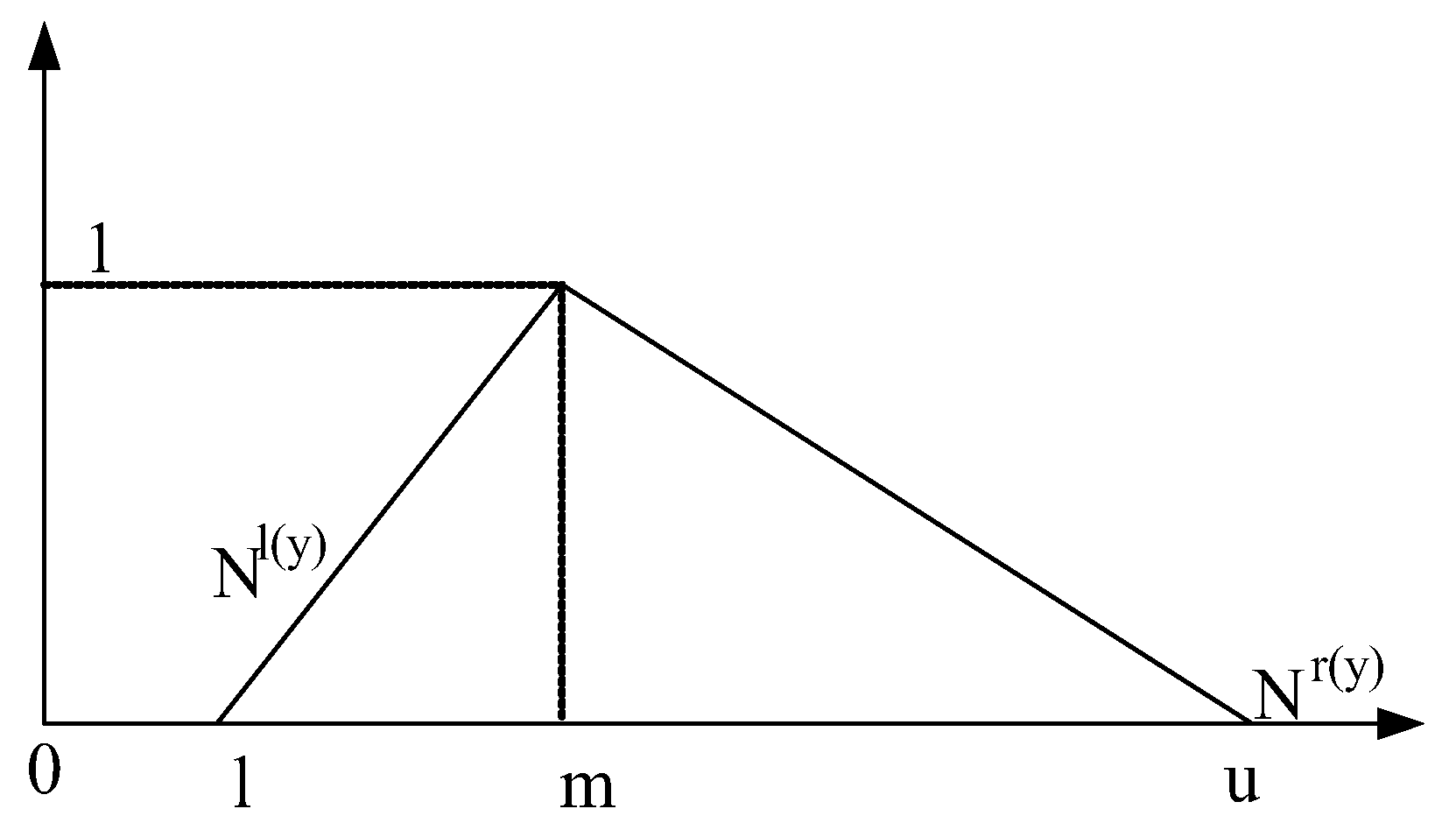
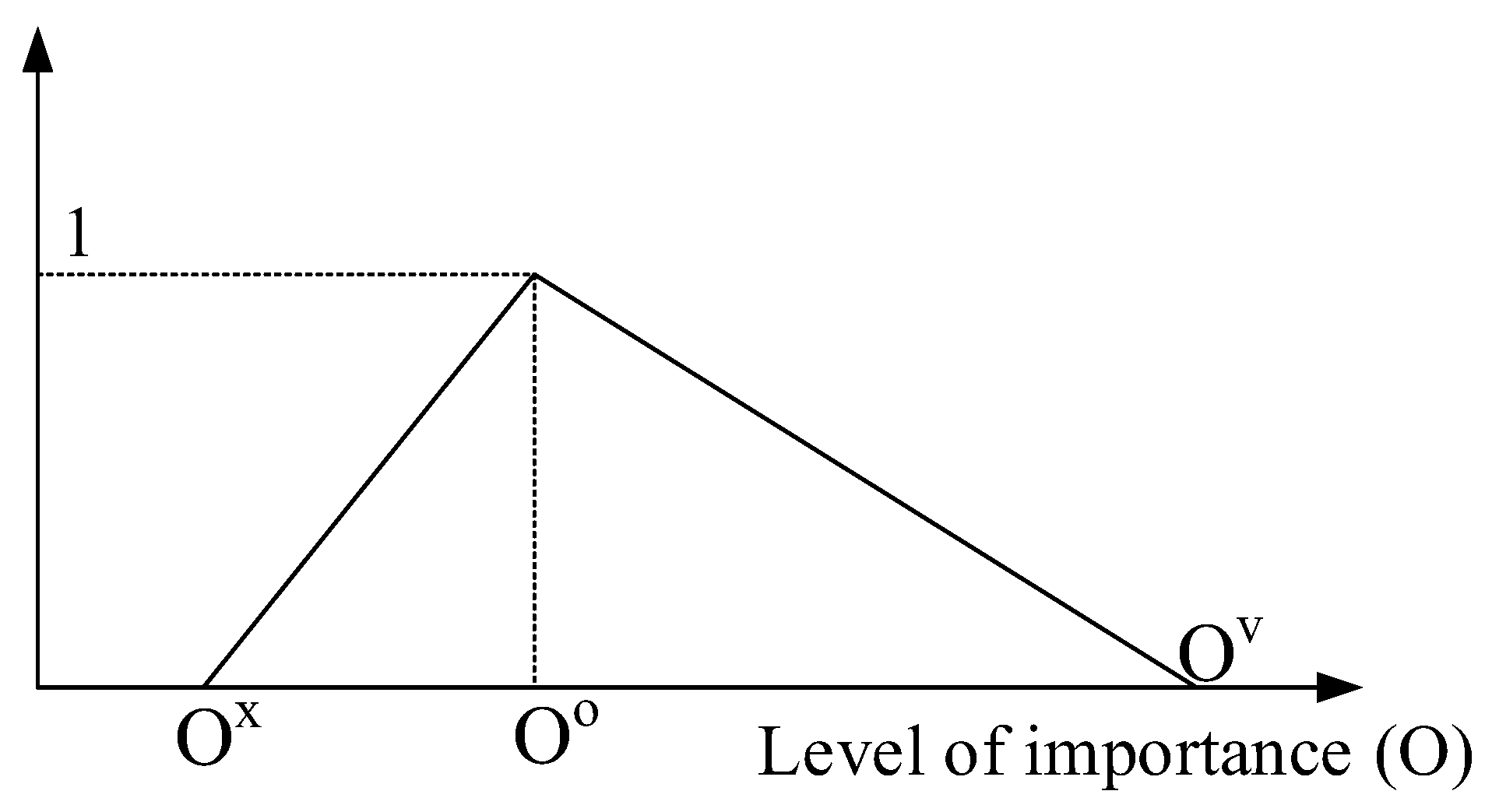
- Fuzzy synthetic extension calculation will transformed into TNT, called fuzzy synthetic extensions . using Equations (2)–(4) [74]:Assign a = 1, 2, …, n, in which a and b specifically are triangular fuzzy number (Ox, Oo, Ov) and (Nx, N0, Nv).
- Weights of criteria are addressed by using relations of the fuzzy-valued. In this step, fuzzy synthetic extensions are blurred by using the min fuzzy extension of the valued relation ≤ given by Equation (5), and weights Wi are calculated (for more detail, see [75]):For a, b = 1, 2, …., n.
- The standardization of the weights. If we expect to obtain the sum of weights within one matrix equal to 1, final weights wi are solved using Equation (7):For a, b = 1, 2, …, n.
- An assessment of a Saaty’s matrix consistency. In the line with [74], a consistency of the matrix is sufficient if inequality from Equation (8) holds:where is a symbol for the arithmetic mean of the maximum real eigenvalues of the matrices for a, b = 1, 2, ..., n is the size of the Saaty’s matrix, and RR represents a random index whose value depends on [74].
3.3. Data Envelopment Analysis
3.3.1. Charnes-Cooper-Rhodes Model (CCR Model)
3.3.2. Banker–Charnes–Cooper Model (BCC Model)
3.3.3. Slacks-Based Measure Model (SBM Model)
Input-Oriented SBM (SBM-I-C)
Output-Oriented SBM (SBM-O-C)
3.3.4. Super-Slacks-Based Measure Model (Super SBM Model)
4. Case Study
4.1. Isotonicity Test
4.2. Results and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
| DMU | Score | Rank | V (1) | V (2) | V (3) | U (1) | U (2) | U (3) |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0.312446 | 0 | 1.25 × | 4.57 × | 0 | 1.41 × |
| DMU 2 | 0.4245 | 25 | 9.96 × | 1.25 × | 2.05 × | 0 | 1.68 × | 0 |
| DMU 3 | 0.5329 | 23 | 0.121082 | 1.51 × | 2.49 × | 0 | 2.05 × | 0 |
| DMU 4 | 0.4876 | 24 | 0 | 2.12 × | 7.97 × | 0 | 0.021246 | 0 |
| DMU 5 | 1 | 1 | 7.31 × | 4.55 × | 0 | 5.74 × | 0 | 1.76 × |
| DMU 6 | 0.6428 | 22 | 0.124062 | 1.57 × | 2.79 × | 6.24 × | 2.11 × | 0 |
| DMU 7 | 0.9708 | 9 | 0 | 2.02 × | 7.59 × | 0 | 2.02 × | 0 |
| DMU 8 | 0.79 | 21 | 0.105865 | 1.37 × | 0 | 2.51 × | 1.78 × | 0 |
| DMU 9 | 0.7934 | 20 | 0.333333 | 0 | 0 | 0.10656 | 1.37 × | 0 |
| DMU 10 | 1 | 1 | 0.303641 | 0 | 2.97 × | 0.097177 | 1.41 × | 1.34 × |
| DMU 11 | 0.9529 | 11 | 0 | 0 | 3.33 × | 0.186293 | 6.31 × | 0 |
| DMU 12 | 1 | 1 | 0.136388 | 1.71 × | 0 | 0 | 2.27 × | 0 |
| DMU 13 | 0.8941 | 13 | 0.118819 | 1.54 × | 0 | 2.82 × | 2.00 × | 0 |
| DMU 14 | 0.8845 | 16 | 8.30 × | 0 | 1.67 × | 0.139719 | 4.74 × | 0 |
| DMU 15 | 0.8357 | 19 | 1.53 × | 2.29 × | 2.72 × | 2.77 × | 1.64 × | 0 |
| DMU 16 | 1 | 1 | 0.112767 | 1.49 × | 6.21 × | 0 | 2.00 × | 0 |
| DMU 17 | 0.9683 | 10 | 8.09 × | 2.11 × | 0 | 2.32 × | 1.88 × | 0 |
| DMU 18 | 0.858 | 18 | 0 | 2.33 × | 3.91 × | 2.59 × | 1.67 × | 0 |
| DMU 19 | 1 | 1 | 0 | 3.18 × | 0 | 0.134811 | 0 | 0 |
| DMU 20 | 0.8967 | 12 | 0 | 2.44 × | 4.10 × | 2.71 × | 1.75 × | 0 |
| DMU 21 | 0.8909 | 14 | 0 | 2.53 × | 4.25 × | 2.81 × | 0.018109 | 0 |
| DMU 22 | 1 | 1 | 0.25 | 0 | 0 | 0.145707 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 1.20 × | 1.92 × | 0.10872 | 4.31 × | 0 |
| DMU 24 | 0.8906 | 15 | 1.85 × | 2.69 × | 0 | 3.52 × | 4.82 × | 7.86 × |
| DMU 25 | 0.8705 | 17 | 0 | 2.36 × | 3.96 × | 2.62 × | 1.69 × | 0 |
| DMU | Score | Rank | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 2 | 0.4245 | 25 | 0 | 0 | 0 | 0.012 | 0 | 0.001 |
| DMU 3 | 0.5329 | 23 | 0 | 0 | 0 | 0.558 | 0 | 0.006 |
| DMU 4 | 0.4876 | 24 | 0.064 | 0 | 0 | 0.531 | 0 | 3.114 |
| DMU 5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 6 | 0.6428 | 22 | 0 | 0 | 0 | 0 | 0 | 0.275 |
| DMU 7 | 0.9708 | 9 | 0.995 | 0 | 0 | 2.588 | 0 | 2.98 |
| DMU 8 | 0.79 | 21 | 0 | 0 | 2.474 | 0 | 0 | 0.221 |
| DMU 9 | 0.7934 | 20 | 0 | 19.826 | 2.518 | 0 | 0 | 0.001 |
| DMU 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 11 | 0.9529 | 11 | 1.906 | 69.61 | 0 | 0 | 0 | 3.945 |
| DMU 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 13 | 0.8941 | 13 | 0 | 0 | 3.512 | 0 | 0 | 4.416 |
| DMU 14 | 0.8845 | 16 | 0 | 16.896 | 0 | 0 | 0 | 1.959 |
| DMU 15 | 0.8357 | 19 | 0 | 0 | 0 | 0 | 0 | 0.231 |
| DMU 16 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 17 | 0.9683 | 10 | 0 | 0 | 22.934 | 0 | 0 | 1.983 |
| DMU 18 | 0.858 | 18 | 0.222 | 0 | 0 | 0 | 0 | 3.722 |
| DMU 19 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 20 | 0.8967 | 12 | 0.034 | 0 | 0 | 0 | 0 | 6.509 |
| DMU 21 | 0.8909 | 14 | 0.489 | 0 | 0 | 0 | 0 | 3.554 |
| DMU 22 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 24 | 0.8906 | 15 | 0 | 0 | 13.043 | 0 | 0 | 0 |
| DMU 25 | 0.8705 | 17 | 0.116 | 0 | 0 | 0 | 0 | 2.629 |
| DMU | Score | Rank | V (1) | V (2) | V (3) | U (1) | U (2) | U (3) |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0.219376 | 9.79 × | 3.76 × | 0 | 2.27 × | 0 |
| DMU 2 | 0.4245 | 25 | 0.234678 | 2.93 × | 4.82 × | 0 | 3.97 × | 0 |
| DMU 3 | 0.5329 | 23 | 0.227195 | 2.84 × | 4.66 × | 0 | 3.84 × | 0 |
| DMU 4 | 0.4876 | 24 | 0 | 4.35 × | 1.63 × | 0 | 4.36 × | 0 |
| DMU 5 | 1 | 1 | 9.80 × | 2.85 × | 0 | 0 | 0 | 1.87 × |
| DMU 6 | 0.6428 | 22 | 0.193011 | 2.44 × | 4.34 × | 9.71 × | 3.28 × | 0 |
| DMU 7 | 0.9708 | 9 | 0 | 2.08 × | 7.82 × | 0 | 2.08 × | 0 |
| DMU 8 | 0.79 | 21 | 0.134006 | 1.74 × | 0 | 3.18 × | 2.26 × | 0 |
| DMU 9 | 0.7934 | 20 | 0.420146 | 0 | 0 | 0.134312 | 1.73 × | 0 |
| DMU 10 | 1 | 1 | 0.333333 | 0 | 0 | 0 | 0 | 1.69 × |
| DMU 11 | 0.9529 | 11 | 0 | 0 | 3.50 × | 0.195497 | 6.63 × | 0 |
| DMU 12 | 1 | 1 | 0.136388 | 1.71 × | 0 | 0 | 2.27 × | 0 |
| DMU 13 | 0.8941 | 13 | 0.132886 | 1.72 × | 0 | 3.16 × | 2.24 × | 0 |
| DMU 14 | 0.8845 | 16 | 0 | 0 | 2.83 × | 0.157959 | 5.35 × | 0 |
| DMU 15 | 0.8357 | 19 | 1.83 × | 2.74 × | 3.26 × | 0.033178 | 1.97 × | 0 |
| DMU 16 | 1 | 1 | 0.116963 | 1.52 × | 0 | 2.78 × | 1.97 × | 0 |
| DMU 17 | 0.9683 | 10 | 8.36 × | 2.18 × | 0 | 2.40 × | 1.94 × | 0 |
| DMU 18 | 0.858 | 18 | 0 | 2.72 × | 4.56 × | 3.02 × | 1.94 × | 0 |
| DMU 19 | 1 | 1 | 0 | 3.18 × | 0 | 0.134811 | 0 | 0 |
| DMU 20 | 0.8967 | 12 | 0 | 2.72 × | 4.57 × | 3.02 × | 0.019468 | 0 |
| DMU 21 | 0.8909 | 14 | 0 | 2.84 × | 4.77 × | 3.16 × | 2.03 × | 0 |
| DMU 22 | 1 | 1 | 8.23 × | 2.15 × | 0 | 2.36 × | 1.91 × | 0 |
| DMU 23 | 1 | 1 | 6.40 × | 1.37 × | 1.27 × | 0.114556 | 0 | 2.49 × |
| DMU 24 | 0.8906 | 15 | 2.08 × | 3.02 × | 0 | 3.96 × | 5.41 × | 8.82 × |
| DMU 25 | 0.8705 | 17 | 0 | 2.71 × | 4.54 × | 3.01 × | 1.94 × | 0 |
| No. | DMU | Score | Rank | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|---|---|---|
| 1 | DMU 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | DMU 2 | 0.4245 | 25 | 0 | 0 | 0 | 0.029 | 0 | 0.002 |
| 3 | DMU 3 | 0.5329 | 23 | 0 | 0 | 0 | 1.047 | 0 | 0.012 |
| 4 | DMU 4 | 0.4876 | 24 | 0.131 | 0 | 0 | 1.09 | 0 | 6.387 |
| 5 | DMU 5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | DMU 6 | 0.6428 | 22 | 0 | 0 | 0 | 0 | 0 | 0.428 |
| 7 | DMU 7 | 0.9708 | 9 | 1.025 | 0 | 0 | 2.665 | 0 | 3.07 |
| 8 | DMU 8 | 0.79 | 21 | 0 | 0 | 3.132 | 0 | 0 | 0.279 |
| 9 | DMU 9 | 0.7934 | 20 | 0 | 24.989 | 3.174 | 0 | 0 | 0.002 |
| 10 | DMU 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | DMU 11 | 0.9529 | 11 | 2 | 73.049 | 0 | 0 | 0 | 4.14 |
| 12 | DMU 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | DMU 13 | 0.8941 | 13 | 0 | 0 | 3.928 | 0 | 0 | 4.939 |
| 14 | DMU 14 | 0.8845 | 16 | 0 | 19.102 | 0 | 0 | 0 | 2.214 |
| 15 | DMU 15 | 0.8357 | 19 | 0 | 0 | 0 | 0 | 0 | 0.277 |
| 16 | DMU 16 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | DMU 17 | 0.9683 | 10 | 0 | 0 | 23.686 | 0 | 0 | 2.048 |
| 18 | DMU 18 | 0.858 | 18 | 0.259 | 0 | 0 | 0 | 0 | 4.338 |
| 19 | DMU 19 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | DMU 20 | 0.8967 | 12 | 0.037 | 0 | 0 | 0 | 0 | 7.259 |
| 21 | DMU 21 | 0.8909 | 14 | 0.549 | 0 | 0 | 0 | 0 | 3.989 |
| 22 | DMU 22 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | DMU 23 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | DMU 24 | 0.8906 | 15 | 0 | 0 | 14.645 | 0 | 0 | 0 |
| 25 | DMU 25 | 0.8705 | 17 | 0.133 | 0 | 0 | 0 | 0 | 3.019 |
| DMU | Score | Rank | V (1) | V (2) | V (3) | U (0) | U (1) | U (2) | U (3) |
|---|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0.333333 | 0 | 0 | 0 | 9.02 × | 0 | 1.13 × |
| DMU 2 | 0.7047 | 25 | 0.120608 | 9.27 × | 4.87 × | 0.7047 | 0 | 0 | 0 |
| DMU 3 | 0.8647 | 22 | 0.148001 | 1.14 × | 5.97 × | 0.8647 | 0 | 0 | 0 |
| DMU 4 | 0.9274 | 15 | 2.67 × | 1.57 × | 9.71 × | 0.9274 | 0 | 0 | 0 |
| DMU 5 | 1 | 1 | 0 | 4.68 × | 0 | 0 | 5.84 × | 0 | 1.76 × |
| DMU 6 | 0.8847 | 20 | 0.151411 | 1.16 × | 6.11 × | 0.8847 | 0 | 0 | 0 |
| DMU 7 | 0.9792 | 12 | 0 | 1.81 × | 9.41 × | 0.2364 | 0 | 1.55 × | 0 |
| DMU 8 | 0.792 | 24 | 0.106413 | 1.36 × | 0 | 0.03772 | 0 | 1.88 × | 0 |
| DMU 9 | 1 | 1 | 0.165486 | 1.47 × | 0 | 0.9636 | 1.12 × | 0 | 0 |
| DMU 10 | 1 | 1 | 0.132633 | 1.68 × | 2.98 × | 0 | 6.68 × | 2.25 × | 0 |
| DMU 11 | 1 | 1 | 0 | 0 | 3.33 × | 0.1448 | 0.179671 | 4.14 × | 0 |
| DMU 12 | 1 | 1 | 0.244753 | 7.67 × | 0 | 0 | 0 | 3.06 × | 1.47 × |
| DMU 13 | 0.9087 | 16 | 0.10788 | 1.53 × | 9.40 × | 0.297 | 1.77 × | 1.23 × | 0 |
| DMU 14 | 1 | 1 | 4.61 × | 7.35 × | 1.46 × | 0.5676 | 8.40 × | 0 | 0 |
| DMU 15 | 0.8389 | 23 | 0.017621 | 2.74 × | 0 | 0.34973 | 3.02 × | 2.44 × | 0 |
| DMU 16 | 1 | 1 | 7.04 × | 2.05 × | 0 | 0 | 0 | 0 | 1.35 × |
| DMU 17 | 0.9747 | 13 | 0.115365 | 1.68 × | 0 | 0.2037 | 1.85 × | 1.49 × | 0 |
| DMU 18 | 0.8811 | 21 | 0 | 1.76 × | 7.86 × | 0.5174 | 2.40 × | 5.68 × | 0 |
| DMU 19 | 1 | 1 | 0 | 3.18 × | 0 | 0 | 0.134811 | 0 | 0 |
| DMU 20 | 0.9679 | 14 | 1.71 × | 1.79 × | 7.96 × | 0.6404 | 0.027225 | 4.53 × | 0 |
| DMU 21 | 0.8998 | 18 | 0 | 1.87 × | 0.008356 | 0.5501 | 2.55 × | 6.04 × | 0 |
| DMU 22 | 1 | 1 | 7.72 × | 2.21 × | 0 | 0 | 0.145707 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 0 | 2.00 × | 0 | 0.117199 | 0 | 2.15 × |
| DMU 24 | 0.8989 | 19 | 2.05 × | 2.66 × | 0 | 0.6047 | 0.04485 | 0 | 0 |
| DMU 25 | 0.9038 | 17 | 1.23 × | 1.68 × | 7.35 × | 0.5734 | 2.54 × | 4.40 × | 0 |
| DMU | Score | Rank | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 2 | 0.7047 | 25 | 0 | 0 | 0 | 0.717 | 11.736 | 15.648 |
| DMU 3 | 0.8647 | 22 | 0 | 0 | 0 | 1.331 | 13.962 | 18.622 |
| DMU 4 | 0.9274 | 15 | 0 | 0 | 0 | 0.74 | 17.793 | 23.721 |
| DMU 5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 6 | 0.8847 | 20 | 0 | 0 | 0 | 0.381 | 9.551 | 12.733 |
| DMU 7 | 0.9792 | 12 | 1.076 | 0 | 0 | 2.021 | 0 | 1.311 |
| DMU 8 | 0.792 | 24 | 0 | 0 | 8.479 | 0.782 | 0 | 2.928 |
| DMU 9 | 1 | 1 | 0 | 0 | 0 | 0 | 0.001 | 0.001 |
| DMU 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 11 | 1 | 1 | 0 | 0.002 | 0 | 0 | 0 | 0 |
| DMU 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 13 | 0.9087 | 16 | 0 | 0 | 0 | 0 | 0 | 1.281 |
| DMU 14 | 1 | 1 | 0 | 0 | 0 | 0 | 0.001 | 0.001 |
| DMU 15 | 0.8389 | 23 | 0 | 0 | 1.157 | 0 | 0 | 0.626 |
| DMU 16 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 17 | 0.9747 | 13 | 0 | 0 | 19.705 | 0 | 0 | 0.379 |
| DMU 18 | 0.8811 | 21 | 0.033 | 0 | 0 | 0 | 0 | 2.897 |
| DMU 19 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 20 | 0.9679 | 14 | 0 | 0 | 0 | 0 | 0 | 2.287 |
| DMU 21 | 0.8998 | 18 | 0.424 | 0 | 0 | 0 | 0 | 3.248 |
| DMU 22 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 24 | 0.8989 | 19 | 0 | 0 | 12.923 | 0 | 0.546 | 0.724 |
| DMU 25 | 0.9038 | 17 | 0 | 0 | 0 | 0 | 0 | 1.467 |
| DMU | Score | Rank | V (0) | V (1) | V (2) | V (3) | U (1) | U (2) | U (3) |
|---|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0 | 0.333333 | 0 | 0 | 0.106578 | 2.16 × | 8.66 × |
| DMU 2 | 0.504 | 24 | 1.98413 | 0 | 0 | 0 | 0 | 3.97 × | 0 |
| DMU 3 | 0.5349 | 23 | 0.0769 | 0.216938 | 2.78 × | 0 | 0 | 3.84 × | 0 |
| DMU 4 | 0.4928 | 25 | -0.6658 | 0 | 5.08 × | 2.65 × | 0 | 4.36 × | 0 |
| DMU 5 | 1 | 1 | 0 | 0 | 2.49 × | 9.37 × | 0 | 2.50 × | 0 |
| DMU 6 | 0.6448 | 22 | 0.06573 | 0.185448 | 2.38 × | 0 | 0 | 3.28 × | 0 |
| DMU 7 | 0.9727 | 12 | -0.3183 | 0 | 2.43 × | 1.27 × | 0 | 2.08 × | 0 |
| DMU 8 | 0.8909 | 20 | 0.55846 | 0 | 1.64 × | 0 | 0 | 2.27 × | 0 |
| DMU 9 | 0.9997 | 11 | -26.435 | 4.540095 | 4.02 × | 0 | 0.308632 | 0 | 0 |
| DMU 10 | 1 | 1 | 0 | 0.133527 | 1.67 × | 2.74 × | 0 | 2.26 × | 0 |
| DMU 11 | 1 | 1 | -0.1694 | 0 | 0 | 3.90 × | 0.2101 | 4.84 × | 0 |
| DMU 12 | 1 | 1 | 0 | 0.242562 | 7.86 × | 0 | 0 | 2.27 × | 0 |
| DMU 13 | 0.8958 | 18 | 0.04537 | 0.127989 | 1.64 × | 0 | 0 | 2.27 × | 0 |
| DMU 14 | 1 | 1 | -1.3128 | 0.106691 | 1.70 × | 3.38 × | 0.194235 | 0 | 0 |
| DMU 15 | 0.8909 | 20 | 0.38995 | 0 | 2.20 × | 0 | 2.11 × | 2.10 × | 0 |
| DMU 16 | 1 | 1 | 0 | 0 | 2.81 × | 3.35 × | 3.48 × | 0 | 1.09 × |
| DMU 17 | 0.9683 | 13 | 0 | 0.083582 | 2.18 × | 0 | 2.40 × | 1.94 × | 0 |
| DMU 18 | 0.8911 | 19 | 0.38077 | 0 | 2.15 × | 0 | 2.06 × | 2.05 × | 0 |
| DMU 19 | 1 | 1 | 0 | 0 | 1.92 × | 0.018792 | 0.134811 | 0 | 0 |
| DMU 20 | 0.9106 | 16 | -1.9554 | 5.23 × | 5.47 × | 0.02431 | 8.31 × | 1.38 × | 0 |
| DMU 21 | 0.9374 | 15 | 0.55694 | 0 | 1.64 × | 0 | 0 | 2.27 × | 0 |
| DMU 22 | 1 | 1 | 0 | 7.72 × | 2.21 × | 0 | 0.145707 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 6.11 × | 1.20 × | 1.31 × | 0.10872 | 4.31 × | 0 |
| DMU 24 | 0.9456 | 14 | 1.05747 | 0 | 0 | 0 | 4.77 × | 1.59 × | 0 |
| DMU 25 | 0.8987 | 17 | 1.11266 | 0 | 0 | 0 | 5.02 × | 1.68 × | 0 |
| DMU | Score | Rank | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 2 | 0.504 | 24 | 1 | 40.546 | 30 | 2.792 | 0 | 7.633 |
| DMU 3 | 0.5349 | 23 | 0 | 0 | 8.652 | 3.321 | 0 | 6.618 |
| DMU 4 | 0.4928 | 25 | 0.219 | 0 | 0 | 0.387 | 0 | 4.289 |
| DMU 5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 6 | 0.6448 | 22 | 0 | 0 | 7.211 | 1.73 | 0 | 5.505 |
| DMU 7 | 0.9727 | 12 | 1.042 | 0 | 0 | 2.529 | 0 | 2.679 |
| DMU 8 | 0.8909 | 20 | 1 | 0 | 29.417 | 2.947 | 0 | 7.185 |
| DMU 9 | 0.9997 | 11 | 0 | 0 | 0 | 0 | 0.014 | 0.018 |
| DMU 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 11 | 1 | 1 | 0 | 0.003 | 0 | 0 | 0 | 0 |
| DMU 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 13 | 0.8958 | 18 | 0 | 0 | 9.249 | 0.641 | 0 | 7.057 |
| DMU 14 | 1 | 1 | 0 | 0 | 0 | 0 | 0.001 | 0.002 |
| DMU 15 | 0.8909 | 20 | 0.883 | 0 | 17.796 | 0 | 0 | 5.95 |
| DMU 16 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 17 | 0.9683 | 13 | 0 | 0 | 23.686 | 0 | 0 | 2.048 |
| DMU 18 | 0.8911 | 19 | 0.991 | 0 | 9.472 | 0 | 0 | 7.238 |
| DMU 19 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 20 | 0.9106 | 16 | 0 | 0 | 0 | 0 | 0 | 6.369 |
| DMU 21 | 0.9374 | 15 | 1 | 0 | 7.081 | 0.694 | 0 | 5.413 |
| DMU 22 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 24 | 0.9456 | 14 | 0.246 | 14.506 | 22.457 | 0 | 0 | 1.871 |
| DMU 25 | 0.8987 | 17 | 0.635 | 2.642 | 6.353 | 0 | 0 | 4.847 |
| DMU | Score | Rank | V (1) | V (2) | V (3) | U (1) | U (2) | U (3) |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 15.13416 | 9.60 × | 6.67 × | 0.583152 | 0 | 0.747719 |
| DMU 2 | 0.3666 | 25 | 6.67 × | 8.52 × | 4.76 × | 0 | 9.58 × | 3.73 × |
| DMU 3 | 0.4732 | 23 | 8.33 × | 1.00 × | 6.67 × | 0 | 1.82 × | 0 |
| DMU 4 | 0.4537 | 24 | 8.33 × | 1.04 × | 8.33 × | 2.58 × | 1.78 × | 0 |
| DMU 5 | 1 | 1 | 8.33 × | 6.08 × | 6.67 × | 0 | 0 | 3.68 × |
| DMU 6 | 0.569 | 22 | 8.33 × | 1.07 × | 6.67 × | 0 | 1.17 × | 5.22 × |
| DMU 7 | 0.8934 | 9 | 6.67 × | 1.88 × | 8.33 × | 0 | 2.52 × | 0 |
| DMU 8 | 0.6873 | 20 | 6.67 × | 1.43 × | 4.76 × | 0 | 1.92 × | 0 |
| DMU 9 | 0.6775 | 21 | 0.111111 | 9.70 × | 6.67 × | 3.08 × | 1.77 × | 0 |
| DMU 10 | 1 | 1 | 0.111111 | 9.41 × | 5.479046 | 10.57818 | 1.577778 | 1.061762 |
| DMU 11 | 0.7471 | 18 | 6.67 × | 1.04 × | 1.11 × | 9.77 × | 1.09 × | 0 |
| DMU 12 | 0.9036 | 8 | 17.93597 | 0.111646 | 4.76 × | 0 | 1.111111 | 0.747719 |
| DMU 13 | 0.8148 | 13 | 8.33 × | 9.79 × | 6.67 × | 2.21 × | 1.65 × | 0 |
| DMU 14 | 0.8334 | 12 | 8.33 × | 1.06 × | 8.33 × | 0.081691 | 1.18 × | 0 |
| DMU 15 | 0.7229 | 19 | 6.67 × | 1.00 × | 5.56 × | 1.30 × | 1.54 × | 0 |
| DMU 16 | 1 | 1 | 8.33 × | 9.50 × | 3.575827 | 7.933635 | 0.823944 | 0.796321 |
| DMU 17 | 0.8534 | 11 | 8.33 × | 1.04 × | 4.69 × | 5.55 × | 0.011673 | 0 |
| DMU 18 | 0.7683 | 17 | 6.67 × | 9.67 × | 6.67 × | 1.7 × | 1.56 × | 0 |
| DMU 19 | 1 | 1 | 6.67 × | 0.280893 | 6.67 × | 6.346908 | 0.946667 | 0 |
| DMU 20 | 0.8856 | 10 | 8.33 × | 9.74 × | 8.33 × | 2.73 × | 1.72 × | 0 |
| DMU 21 | 0.8027 | 15 | 6.67 × | 1.67 × | 6.67 × | 0 | 2.24 × | 0 |
| DMU 22 | 1 | 1 | 3.741093 | 1.07 × | 0.705214 | 6.346908 | 0 | 0.119497 |
| DMU 23 | 1 | 1 | 6.67 × | 9.75 × | 8.86 × | 0.683238 | 0 | 0 |
| DMU 24 | 0.789 | 16 | 6.67 × | 9.87 × | 4.76 × | 5.19 × | 0.0104 | 0 |
| DMU 25 | 0.8106 | 14 | 6.67 × | 9.80 × | 6.67 × | 6.56 × | 1.04 × | 0 |
| DMU | Score | Rank | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 2 | 0.3666 | 25 | 3.293 | 189.987 | 52.929 | 0.401 | 0 | 0 |
| DMU 3 | 0.4732 | 23 | 2.237 | 124.289 | 32.368 | 0.979 | 0 | 0.005 |
| DMU 4 | 0.4537 | 24 | 2.393 | 142.194 | 23.93 | 0 | 0 | 0.652 |
| DMU 5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 6 | 0.569 | 22 | 1.937 | 69.166 | 29.373 | 0.506 | 0 | 0 |
| DMU 7 | 0.8934 | 9 | 1.266 | 0 | 2.659 | 2.324 | 0 | 1.809 |
| DMU 8 | 0.6873 | 20 | 1.903 | 0 | 39.031 | 1.414 | 0 | 1.419 |
| DMU 9 | 0.6775 | 21 | 0.486 | 105.988 | 24.86 | 0 | 0 | 3.722 |
| DMU 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 11 | 0.7471 | 18 | 2.278 | 89.21 | 0.732 | 0 | 0 | 3.636 |
| DMU 12 | 0.9036 | 8 | 0 | 0 | 20.238 | 0.812 | 0 | 0 |
| DMU 13 | 0.8148 | 13 | 0.716 | 11.392 | 17.161 | 0 | 0 | 3.672 |
| DMU 14 | 0.8334 | 12 | 0.895 | 67.605 | 2.466 | 0 | 0 | 0.982 |
| DMU 15 | 0.7229 | 19 | 1.57 | 29.523 | 25.705 | 0 | 0 | 6.417 |
| DMU 16 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 17 | 0.8534 | 11 | 0.17 | 8.524 | 26.32 | 0 | 0 | 2.441 |
| DMU 18 | 0.7683 | 17 | 1.504 | 32.315 | 15.037 | 0 | 0 | 6.328 |
| DMU 19 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 20 | 0.8856 | 10 | 0.509 | 30.41 | 5.088 | 0 | 0 | 6.305 |
| DMU 21 | 0.8027 | 15 | 1.48 | 0 | 14.8 | 1.534 | 0 | 6.598 |
| DMU 22 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 24 | 0.789 | 16 | 1.116 | 31.378 | 22.191 | 0 | 0 | 0.565 |
| DMU 25 | 0.8106 | 14 | 1.358 | 36.497 | 9.463 | 0 | 0 | 3.803 |
| DMU | Score | Rank | V (1) | V (2) | V (3) | U (1) | U (2) | U (3) |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 272.1957 | 0 | 0 | 7.006445 | 7.57 × | 13.45895 |
| DMU 2 | 0.2795 | 24 | 0.715473 | 0 | 0 | 0.247666 | 1.32 × | 9.92 × |
| DMU 3 | 0.2564 | 25 | 0.975128 | 0 | 0 | 0.404384 | 1.28 × | 9.61 × |
| DMU 4 | 0.4089 | 23 | 0 | 4.22 × | 2.72 × | 0.189276 | 1.45 × | 1.09 × |
| DMU 5 | 1 | 1 | 0 | 2.67 × | 0 | 0.332568 | 8.32 × | 9.42 × |
| DMU 6 | 0.4189 | 22 | 0.477617 | 0 | 9.54 × | 0.207723 | 1.09 × | 8.21 × |
| DMU 7 | 0.7104 | 20 | 0 | 1.74 × | 2.01 × | 0.12946 | 6.94 × | 4.89 × |
| DMU 8 | 0.4919 | 21 | 0.087746 | 4.65 × | 0 | 0.165879 | 7.57 × | 5.68 × |
| DMU 9 | 0.7822 | 18 | 0.356897 | 6.04 × | 0 | 0.102877 | 1.02 × | 7.65 × |
| DMU 10 | 1 | 1 | 0 | 0 | 69.73439 | 134.0896 | 20 | 13.45895 |
| DMU 11 | 0.8709 | 11 | 0 | 0 | 3.94 × | 9.18 × | 1.02 × | 7.63 × |
| DMU 12 | 1 | 1 | 405.5784 | 1.320418 | 0 | 1.220084 | 20 | 13.45895 |
| DMU 13 | 0.8021 | 14 | 0.27006 | 4.89 × | 0 | 0.082931 | 7.56 × | 5.67 × |
| DMU 14 | 0.7971 | 15 | 3.51 × | 3.06 × | 3.77 × | 6.47 × | 9.56 × | 7.17 × |
| DMU 15 | 0.7845 | 17 | 3.77 × | 3.27 × | 0 | 7.15 × | 7.75 × | 5.81 × |
| DMU 16 | 1 | 1 | 0 | 0 | 60.44946 | 134.0896 | 13.71082 | 13.45895 |
| DMU 17 | 0.9518 | 9 | 0.139904 | 1.53 × | 0 | 0.054432 | 7.57 × | 5.68 × |
| DMU 18 | 0.7918 | 16 | 3.88 × | 2.32 × | 5.36 × | 7.07 × | 7.56 × | 5.67 × |
| DMU 19 | 1 | 1 | 0 | 5.980267 | 0 | 134.0896 | 20 | 5.66 × |
| DMU 20 | 0.857 | 12 | 3.88 × | 2.33 × | 5.37 × | 7.09 × | 7.57 × | 5.67 × |
| DMU 21 | 0.7152 | 19 | 0 | 9.07 × | 1.29 × | 0.102574 | 5.44 × | 5.66 × |
| DMU 22 | 1 | 1 | 79.70503 | 0 | 14.9138 | 134.0896 | 7.59 × | 2.457001 |
| DMU 23 | 1 | 1 | 0 | 5.24 × | 7.74 × | 0.453676 | 7.59 × | 5.69 × |
| DMU 24 | 0.8857 | 10 | 2.68 × | 2.95 × | 0 | 5.08 × | 7.73 × | 5.80 × |
| DMU 25 | 0.838 | 13 | 3.27 × | 2.44 × | 3.98 × | 6.01 × | 7.75 × | 5.81 × |
| DMU | Score | Rank | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 2 | 0.2795 | 24 | 0 | 0.95 | 7.5 | 7.233 | 29.712 | 39.612 |
| DMU 3 | 0.2564 | 25 | 0 | 20 | 0 | 6.039 | 17.9 | 23.87 |
| DMU 4 | 0.4089 | 23 | 0 | 0 | 0 | 3.84 | 22.72 | 35.674 |
| DMU 5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 6 | 0.4189 | 22 | 0 | 0.2 | 0 | 5.258 | 13.48 | 17.97 |
| DMU 7 | 0.7104 | 20 | 1 | 0 | 0 | 2.914 | 1.175 | 4.571 |
| DMU 8 | 0.4919 | 21 | 0 | 0 | 15.281 | 5.847 | 4.183 | 5.569 |
| DMU 9 | 0.7822 | 18 | 0 | 0 | 0.88 | 0.498 | 11.043 | 14.979 |
| DMU 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 11 | 0.8709 | 11 | 2 | 48.724 | 0 | 0 | 5.332 | 12.325 |
| DMU 12 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 13 | 0.8021 | 14 | 0 | 0 | 7.325 | 1.818 | 4.256 | 11.262 |
| DMU 14 | 0.7971 | 15 | 0 | 0 | 0 | 0.484 | 9.84 | 18.013 |
| DMU 15 | 0.7845 | 17 | 0 | 0 | 6.997 | 3.036 | 3.715 | 4.948 |
| DMU 16 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 17 | 0.9518 | 9 | 0 | 0 | 22.974 | 0.463 | 1.118 | 2.995 |
| DMU 18 | 0.7918 | 16 | 0 | 0 | 0 | 2.562 | 4.532 | 8.386 |
| DMU 19 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 20 | 0.857 | 12 | 0 | 0 | 0 | 0.799 | 4.673 | 13.202 |
| DMU 21 | 0.7152 | 19 | 0.044 | 0 | 0 | 3.877 | 0 | 0.095 |
| DMU 22 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 23 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| DMU 24 | 0.8857 | 10 | 0 | 0 | 16.147 | 1.215 | 4.357 | 5.804 |
| DMU 25 | 0.838 | 13 | 0 | 0 | 0 | 1.744 | 4.97 | 8.617 |
| No. | DMU | Score | Rank | V (1) | V (2) | V (3) | U (1) | U (2) | U (3) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | DMU 1 | 1 | 1 | 15.13416 | 9.60 x | 6.67 x | 0.583152 | 0 | 0.747719 |
| 2 | DMU 2 | 0.3666 | 25 | 6.67 × | 8.52 × | 4.76 × | 0 | 9.58 × | 3.73 × |
| 3 | DMU 3 | 0.4732 | 23 | 8.33 × | 1.00 × | 6.67 × | 0 | 1.82 × | 0 |
| 4 | DMU 4 | 0.4537 | 24 | 8.33 × | 1.04 × | 8.33 × | 2.58 × | 1.78 × | 0 |
| 5 | DMU 5 | 1 | 1 | 8.33 × | 6.08 × | 6.67 × | 0 | 0 | 3.68 × |
| 6 | DMU 6 | 0.569 | 22 | 8.33 × | 1.07 × | 6.67 × | 0 | 1.17 × | 5.22 × |
| 7 | DMU 7 | 0.8934 | 9 | 6.67 × | 1.88 × | 8.33 × | 0 | 2.52 × | 0 |
| 8 | DMU 8 | 0.6873 | 20 | 6.67 × | 1.43 × | 4.76 × | 0 | 1.92 × | 0 |
| 9 | DMU 9 | 0.6775 | 21 | 0.111111 | 9.70 × | 6.67 × | 3.08 × | 1.77 × | 0 |
| 10 | DMU 10 | 1 | 1 | 0.111111 | 9.41 × | 5.479046 | 10.57818 | 1.577778 | 1.061762 |
| 11 | DMU 11 | 0.7471 | 18 | 6.67 × | 1.04 × | 1.11 × | 9.77 × | 1.09 × | 0 |
| 12 | DMU 12 | 0.9036 | 8 | 17.93597 | 0.111646 | 4.76 × | 0 | 1.111111 | 0.747719 |
| 13 | DMU 13 | 0.8148 | 13 | 8.33 × | 9.79 × | 6.67 × | 2.21 × | 1.65 × | 0 |
| 14 | DMU 14 | 0.8334 | 12 | 8.33 × | 1.06 × | 8.33 × | 0.081691 | 1.18 × | 0 |
| 15 | DMU 15 | 0.7229 | 19 | 6.67 × | 1.00 × | 5.56 × | 1.30 × | 1.54 × | 0 |
| 16 | DMU 16 | 1 | 1 | 8.33 × | 9.50 × | 3.575827 | 7.933635 | 0.823944 | 0.796321 |
| 17 | DMU 17 | 0.8534 | 11 | 8.33 × | 1.04 × | 4.69 × | 5.55 × | 0.011673 | 0 |
| 18 | DMU 18 | 0.7683 | 17 | 6.67 × | 9.67 × | 6.67 × | 1.73 × | 1.56 × | 0 |
| 19 | DMU 19 | 1 | 1 | 6.67 × | 0.280893 | 6.67 × | 6.346908 | 0.946667 | 0 |
| 20 | DMU 20 | 0.8856 | 10 | 8.33 × | 9.74 × | 8.33 × | 2.73 × | 1.72 × | 0 |
| 21 | DMU 21 | 0.8027 | 15 | 6.67 × | 1.67 × | 6.67 × | 0 | 2.24 × | 0 |
| 22 | DMU 22 | 1 | 1 | 3.741093 | 1.07 × | 0.705214 | 6.346908 | 0 | 0.119497 |
| 23 | DMU 23 | 1 | 1 | 6.67 × | 9.75 × | 8.86 × | 0.683238 | 0 | 0 |
| 24 | DMU 24 | 0.789 | 16 | 6.67 × | 9.87 × | 4.76 × | 5.19 × | 0.0104 | 0 |
| 25 | DMU 25 | 0.8106 | 14 | 6.67 × | 9.80 × | 6.67 × | 6.56 × | 1.04 × | 0 |
| No. | DMU | Score | Rank | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|---|---|---|
| 1 | DMU 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | DMU 2 | 0.3666 | 25 | 3.293 | 189.987 | 52.929 | 0.401 | 0 | 0 |
| 3 | DMU 3 | 0.4732 | 23 | 2.237 | 124.289 | 32.368 | 0.979 | 0 | 0.005 |
| 4 | DMU 4 | 0.4537 | 24 | 2.393 | 142.194 | 23.93 | 0 | 0 | 0.652 |
| 5 | DMU 5 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | DMU 6 | 0.569 | 22 | 1.937 | 69.166 | 29.373 | 0.506 | 0 | 0 |
| 7 | DMU 7 | 0.8934 | 9 | 1.266 | 0 | 2.659 | 2.324 | 0 | 1.809 |
| 8 | DMU 8 | 0.6873 | 20 | 1.903 | 0 | 39.031 | 1.414 | 0 | 1.419 |
| 9 | DMU 9 | 0.6775 | 21 | 0.486 | 105.988 | 24.86 | 0 | 0 | 3.722 |
| 10 | DMU 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | DMU 11 | 0.7471 | 18 | 2.278 | 89.21 | 0.732 | 0 | 0 | 3.636 |
| 12 | DMU 12 | 0.9036 | 8 | 0 | 0 | 20.238 | 0.812 | 0 | 0 |
| 13 | DMU 13 | 0.8148 | 13 | 0.716 | 11.392 | 17.161 | 0 | 0 | 3.672 |
| 14 | DMU 14 | 0.8334 | 12 | 0.895 | 67.605 | 2.466 | 0 | 0 | 0.982 |
| 15 | DMU 15 | 0.7229 | 19 | 1.57 | 29.523 | 25.705 | 0 | 0 | 6.417 |
| 16 | DMU 16 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | DMU 17 | 0.8534 | 11 | 0.17 | 8.524 | 26.32 | 0 | 0 | 2.441 |
| 18 | DMU 18 | 0.7683 | 17 | 1.504 | 32.315 | 15.037 | 0 | 0 | 6.328 |
| 19 | DMU 19 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | DMU 20 | 0.8856 | 10 | 0.509 | 30.41 | 5.088 | 0 | 0 | 6.305 |
| 21 | DMU 21 | 0.8027 | 15 | 1.48 | 0 | 14.8 | 1.534 | 0 | 6.598 |
| 22 | DMU 22 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | DMU 23 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | DMU 24 | 0.789 | 16 | 1.116 | 31.378 | 22.191 | 0 | 0 | 0.565 |
| 25 | DMU 25 | 0.8106 | 14 | 1.358 | 36.497 | 9.463 | 0 | 0 | 3.803 |
| No. | DMU | Score | V (1) LT | V (2) UP | V (3) PC | U (1) QB | U (2) NI | U (3) RE |
|---|---|---|---|---|---|---|---|---|
| 1 | DMU 1 | 1 | 0.7774838 | 9.60 × | 6.67 × | 0.2139225 | 4.25 × | 5.68 × |
| 2 | DMU 2 | 0.269326 | 6.67× | 8.52 × | 4.76 × | 6.67 × | 3.56 × | 2.67 × |
| 3 | DMU 3 | 0.251235 | 8.33 × | 1.00 × | 6.67 × | 0.1015951 | 3.22 × | 2.41 × |
| 4 | DMU 4 | 0.401049 | 8.33 × | 1.04 × | 8.33 × | 7.59 × | 5.82 × | 4.37 × |
| 5 | DMU 5 | 1 | 8.33 × | 9.26 × | 6.67 × | 1.1563198 | 8.32 × | 0.3546177 |
| 6 | DMU 6 | 0.418778 | 8.33 × | 1.07 × | 6.67 × | 8.70 × | 4.58 × | 3.44 × |
| 7 | DMU 7 | 0.662241 | 6.67 × | 9.65 × | 8.33 × | 8.57 × | 4.60 × | 3.24 × |
| 8 | DMU 8 | 0.448251 | 6.67 × | 9.72 × | 4.76 × | 7.44 × | 3.39 × | 2.55 × |
| 9 | DMU 9 | 0.641302 | 0.1111111 | 9.70 × | 6.67 × | 6.60 × | 6.54 × | 4.90 × |
| 10 | DMU 10 | 1 | 1.2031017 | 9.41 × | 1.11 × | 0.3587726 | 6.42 × | 5.64 × |
| 11 | DMU 11 | 0.703643 | 6.67 × | 1.04 × | 1.11 × | 0.0585784 | 7.16 × | 5.37 × |
| 12 | DMU 12 | 1 | 66.742332 | 0.2530347 | 4.76 × | 0.1143864 | 6.5315673 | 5.68 × |
| 13 | DMU 13 | 0.753682 | 8.33 × | 9.79 × | 6.67 × | 6.25 × | 5.69 × | 4.27 × |
| 14 | DMU 14 | 0.771137 | 8.33 × | 1.90 × | 8.33 × | 0.1013309 | 7.37 × | 5.53 × |
| 15 | DMU 15 | 0.694923 | 6.67 × | 1.00 × | 5.56 × | 4.97 × | 5.38 × | 4.04 × |
| 16 | DMU 16 | 1 | 8.33 × | 9.50 × | 8.33 × | 6.10 × | 6.67 × | 4.49 × |
| 17 | DMU 17 | 0.837507 | 8.33 × | 1.55 × | 4.69 × | 7.19 × | 6.34 × | 4.76 × |
| 18 | DMU 18 | 0.73634 | 6.67 × | 9.67 × | 6.67 × | 5.21 × | 5.56 × | 4.17 × |
| 19 | DMU 19 | 1 | 6.67 × | 4.73 × | 6.67 × | 0.1230422 | 7.55 × | 1.54 × |
| 20 | DMU 20 | 0.849581 | 8.33 × | 9.74 × | 8.33 × | 6.02 × | 6.43 × | 4.82 × |
| 21 | DMU 21 | 0.669586 | 6.67 × | 1.07 × | 6.67 × | 6.87 × | 5.06 × | 3.79 × |
| 22 | DMU 22 | 1 | 8.33 × | 1.98 × | 6.67 × | 9.00 × | 7.59 × | 0.0056912 |
| 23 | DMU 23 | 1 | 0.428732 | 9.75E-04 | 7.86 × | 0.7697859 | 7.59 × | 5.69 × |
| 24 | DMU 24 | 0.769097 | 6.67 × | 1.54 × | 4.76 × | 6.75 × | 5.95 × | 4.46 × |
| 25 | DMU 25 | 0.772696 | 6.67 × | 1.55 × | 6.67 × | 8.13 × | 5.99 × | 4.49 × |
| No. | DMU | Score | Excess | Excess | Excess | Shortage | Shortage | Shortage |
|---|---|---|---|---|---|---|---|---|
| LT | UP | PC | QB | NI | RE | |||
| S−(1) | S−(2) | S−(3) | S+(1) | S+(2) | S+(3) | |||
| 1 | DMU 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | DMU 2 | 0.269326 | 0 | 0.95 | 7.5 | 7.232975 | 29.7125 | 39.6125 |
| 3 | DMU 3 | 0.251235 | 0 | 20 | 0 | 6.0388 | 17.9 | 23.87 |
| 4 | DMU 4 | 0.401049 | 0.3351382 | 0 | 3.351382 | 3.2435436 | 22.86077 | 37.47481 |
| 5 | DMU 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | DMU 6 | 0.418778 | 0 | 0.2 | 0 | 5.2584 | 13.48 | 17.97 |
| 7 | DMU 7 | 0.662241 | 1.16 | 8.436 | 1.6 | 2.669008 | 0 | 3.128 |
| 8 | DMU 8 | 0.448251 | 0.609475 | 0 | 15.11844 | 5.523653 | 4.18894 | 5.578262 |
| 9 | DMU 9 | 0.641302 | 0.384 | 114.1114 | 23.84 | 0.3322442 | 0 | 4.9922 |
| 10 | DMU 10 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | DMU 11 | 0.703643 | 2 | 56.925 | 0 | 9.27x | 4.72 | 12.025 |
| 12 | DMU 12 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | DMU 13 | 0.753682 | 0.4704 | 30.96584 | 14.704 | 0.8005335 | 0 | 6.73232 |
| 14 | DMU 14 | 0.771137 | 0.3550889 | 0 | 2.330154 | 0 | 9.940403 | 19.28401 |
| 15 | DMU 15 | 0.694923 | 1.2108863 | 0 | 22.10886 | 0.513919 | 4.343921 | 13.02279 |
| 16 | DMU 16 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | DMU 17 | 0.837507 | 0.1015444 | 0 | 26.30323 | 0 | 1.253382 | 4.748504 |
| 18 | DMU 18 | 0.73634 | 1.4704 | 34.96584 | 14.704 | 0.1084335 | 0 | 6.74232 |
| 19 | DMU 19 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | DMU 20 | 0.849581 | 9.80E-02 | 0 | 0.980336 | 0.6245277 | 4.71458 | 13.72903 |
| 21 | DMU 21 | 0.669586 | 1.4571103 | 0 | 14.5711 | 1.5883816 | 0.136121 | 6.949176 |
| 22 | DMU 22 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | DMU 23 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | DMU 24 | 0.769097 | 0.8652768 | 0 | 22.12846 | 0 | 4.613784 | 9.059744 |
| 25 | DMU 25 | 0.772696 | 1.0669574 | 0 | 9.390053 | 0 | 5.366362 | 13.68358 |
| No. | DMU | Score | V (1) LT | V (2) UP | V (3) PC | U (1) QB | U (2) NI | U (3) RE |
|---|---|---|---|---|---|---|---|---|
| 1 | DMU 1 | 1 | 2.2055847 | 2.40 × | 6.67 × | 8.96 × | 0.3318029 | 5.68E-03 |
| 2 | DMU 2 | 0.269326 | 6.67 × | 8.52 × | 4.76 × | 6.67 × | 3.56 × | 2.67 × |
| 3 | DMU 3 | 0.251235 | 8.33 × | 1.00 × | 6.67 × | 0.1015951 | 3.22 × | 2.41 × |
| 4 | DMU 4 | 0.45679 | 8.33 × | 5.91 × | 2.56 × | 8.65 × | 6.63 × | 4.98 × |
| 5 | DMU 5 | 1 | 0.1763621 | 2.58 × | 6.67 × | 0.3325684 | 7.64 × | 5.90 × |
| 6 | DMU 6 | 0.418778 | 8.33 × | 1.07 × | 6.67 × | 8.70 × | 4.58 × | 3.44 × |
| 7 | DMU 7 | 0.677494 | 6.67 × | 4.83 × | 2.28 × | 8.77 × | 4.70 × | 3.31 × |
| 8 | DMU 8 | 0.448556 | 6.67 × | 9.72 × | 4.76 × | 7.44 × | 8.89 × | 2.55 × |
| 9 | DMU 9 | 0.999453 | 9.7808186 | 7.58 × | 6.67 × | 0.1028212 | 1.02 × | 7.64 × |
| 10 | DMU 10 | 1 | 0.1111111 | 9.41 × | 8.65 × | 0.1086236 | 7.53 × | 4.40 × |
| 11 | DMU 11 | 1 | 6.67 × | 1.04 × | 9.61 × | 0.3550234 | 1.02 × | 7.63 × |
| 12 | DMU 12 | 1 | 17.038047 | 0.2170056 | 4.76 × | 0.1143864 | 2.9286539 | 5.68 × |
| 13 | DMU 13 | 0.762943 | 8.33 × | 2.10 × | 6.67 × | 6.33 × | 5.76 × | 4.32 × |
| 14 | DMU 14 | 1 | 0.2244187 | 1.37 × | 5.83 × | 0.2180815 | 9.56 × | 7.17 × |
| 15 | DMU 15 | 0.712474 | 6.67 × | 2.15 × | 5.56 × | 5.10 × | 5.52 × | 4.14 × |
| 16 | DMU 16 | 1 | 8.33 × | 9.50 × | 8.33 × | 6.10 × | 6.67 × | 4.49 × |
| 17 | DMU 17 | 0.849109 | 8.33 × | 2.52 × | 4.69 × | 4.62 × | 6.43 × | 4.82 × |
| 18 | DMU 18 | 0.744086 | 6.67 × | 2.43 × | 6.67 × | 5.26 × | 5.62 × | 4.22 × |
| 19 | DMU 19 | 1 | 6.67 × | 4.73 × | 6.67 × | 0.1230422 | 7.55 × | 1.54 × |
| 20 | DMU 20 | 0.876299 | 8.33 × | 4.66 × | 1.94 × | 6.21 × | 6.63 × | 4.97 × |
| 21 | DMU 21 | 0.693331 | 6.67 × | 5.64 × | 6.67 × | 0.0711174 | 3.10 × | 3.93 × |
| 22 | DMU 22 | 1 | 8.33 × | 1.98 × | 6.67 × | 9.00 × | 7.59 × | 0.0056912 |
| 23 | DMU 23 | 1 | 0.428732 | 9.75 × | 7.86 × | 0.7697859 | 7.59 × | 5.69 × |
| 24 | DMU 24 | 0.778043 | 6.67 × | 9.87 × | 4.76 × | 0.0835919 | 6.02 × | 4.51 × |
| 25 | DMU 25 | 0.78211 | 6.67 × | 2.83 × | 6.67 × | 4.70 × | 6.06 × | 4.55 × |
| No. | DMU | Score | Excess | Excess | Excess | Shortage | Shortage | Shortage |
|---|---|---|---|---|---|---|---|---|
| LT | UP | PC | QB | NI | RE | |||
| S−(1) | S−(2) | S−(3) | S+(1) | S+(2) | S+(3) | |||
| 1 | DMU 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | DMU 2 | 0.269326 | 1 | 79.05 | 20 | 5.5172 | 18.73 | 24.97 |
| 3 | DMU 3 | 0.251235 | 0 | 20 | 0 | 6.0388 | 17.9 | 23.87 |
| 4 | DMU 4 | 0.45679 | 0.2190489 | 0 | 0 | 2.1999675 | 23.619423 | 35.781249 |
| 5 | DMU 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | DMU 6 | 0.418778 | 0 | 0.2 | 0 | 5.2584 | 13.48 | 17.97 |
| 7 | DMU 7 | 0.677494 | 0.9193048 | 0 | 0 | 2.8828591 | 0.1189338 | 2.3581649 |
| 8 | DMU 8 | 0.448556 | 1 | 29.86573 | 20.16474 | 4.8305226 | 0 | 0.1191433 |
| 9 | DMU 9 | 0.999453 | 0 | 0 | 0 | 8.57 x | 2.24 x | 2.98 x |
| 10 | DMU 10 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | DMU 11 | 1 | 8.79 x | 0 | 0 | 0 | 0 | 5.42 x |
| 12 | DMU 12 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | DMU 13 | 0.762943 | 4.00 x | 0 | 7.325987 | 1.8174772 | 4.2561312 | 11.262405 |
| 14 | DMU 14 | 1 | 0 | 0 | 0 | 0 | 3.01 x | 4.01 x |
| 15 | DMU 15 | 0.712474 | 1.00004 | 0 | 15.19612 | 1.4748294 | 4.0633 | 9.3821192 |
| 16 | DMU 16 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 17 | DMU 17 | 0.849109 | 0 | 0 | 22.97534 | 0.4625961 | 1.118287 | 2.9958335 |
| 18 | DMU 18 | 0.744086 | 1.00004 | 0 | 8.364948 | 0.9798395 | 4.8867805 | 12.906691 |
| 19 | DMU 19 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | DMU 20 | 0.876299 | 6.41x | 0 | 0 | 0.3194245 | 4.9366059 | 13.23423 |
| 21 | DMU 21 | 0.693331 | 1.00004 | 0 | 0.621362 | 3.2900805 | 0 | 0.4775992 |
| 22 | DMU 22 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | DMU 23 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | DMU 24 | 0.778043 | 1 | 16.87501 | 22.16234 | 0 | 2.1325378 | 4.4913542 |
| 25 | DMU 25 | 0.78211 | 1.00004 | 0 | 7.196117 | 0.3049694 | 5.2773 | 12.528119 |
References
- Flórez-López, R. Strategic supplier selection in the added-value perspective: A CI approach. Inf. Sci. Int. J. 2007, 177, 1169–1179. [Google Scholar]
- Chen, C.T.; Lin, C.T.; Huang, S.F. A fuzzy approach for supplier evaluation and selection in supply chain management. Int. J. Prod. Econ. 2006, 102, 289–301. [Google Scholar] [CrossRef]
- Wu, C.; Barnes, D. A literature review of decision-making models and approaches for partner selection in agile supply chains. J. Purch. Supply Manag. 2011, 17, 256–274. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Geraghty, J.; Young, P. Supplier selection paradigm: An integrated hierarchical QFD methodology under multiple-criteria environment. Appl. Soft Comput. 2010, 10, 1013–1027. [Google Scholar] [CrossRef]
- Liu, J.; Ding, F.-Y.; Lall, V. Using data envelopment analysis to compare suppliers for supplier selection and performance improvement. Supply Chain Manag. Int. J. 2000, 5, 143–150. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Agarwal, A.; Shankar, R. Analyzing alternatives for improvement in supply chain performance. Work Study 2002, 51, 32–37. [Google Scholar] [CrossRef]
- Aissaoui, N.; Haouari, M.; Hassini, E. Supplier selection and order lot sizing modeling: A review. Comp. Oper. Res. 2007, 34, 3516–3540. [Google Scholar] [CrossRef]
- Govindan, K.; Rajendran, S.; Sarkis, J.; Murugesan, P. Multi criteria decision making approaches for green supplier evaluation and selection: A literature review. J. Clean. Prod. 2015, 98, 66–83. [Google Scholar] [CrossRef]
- Chai, J.; Liu, J.N.K.; Ngai, E. Application of decision-making techniques in supplier selection: A systematic review of literature. Expert Syst. Appl. 2013, 40, 3872–3885. [Google Scholar] [CrossRef]
- Wu, T.; Blackhurst, J. Supplier evaluation and selection: An augmented DEA approach. Int. J. Prod. Res. 2009, 47, 4593–4608. [Google Scholar] [CrossRef]
- Amirteimoori, A.; Khoshandam, L. A Data Envelopment Analysis Approach to Supply Chain Efficiency. Adv. Decis. Sci. 2011, 2011. [Google Scholar] [CrossRef]
- Lin, C.-T.; Hung, K.-P.; Hu, S.-H. A Decision-Making Model for Evaluating and Selecting Suppliers for the Sustainable Operation and Development of Enterprises in the Aerospace Industry. Sustainability 2018, 10, 735. [Google Scholar]
- Galankashi, M.R.; Helmi, S.A.; Hashemzahi, V. Supplier selection in automobile industry: A mixed balanced scorecard–fuzzy AHP approach. Alex. Eng. J. 2016, 55, 93–100. [Google Scholar] [CrossRef]
- Kilincci, O.; Onal, S.A. Fuzzy AHP approach for supplier selection in a washing machine company. Expert Syst. Appl. 2011, 38, 9656–9664. [Google Scholar] [CrossRef]
- Tyagi, M.; Kumar, P.; Kumar, D. Permutation of fuzzy AHP and AHP methods to prioritizing the alternatives of supply chain performance system. Int. J. Ind. Eng. Theory Appl. Pract. 2015, 22, 24. [Google Scholar]
- Karsak, E.E.; Dursun, M. An integrated fuzzy MCDM approach for supplier evaluation and selection. Comput. Ind. Eng. 2015, 82, 82–93. [Google Scholar] [CrossRef]
- Chen, H.M.W.; Chou, S.-Y.; Luu, Q.D.; Yu, T.H.-K. A Fuzzy MCDM Approach for Green Supplier Selection from the Economic and Environmental Aspects. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Guo, Z.G.; Liu, H.; Zhang, D.; Yang, J. Green Supplier Evaluation and Selection in Apparel Manufacturing Using a Fuzzy Multi-Criteria Decision-Making Approach. Sustainability 2017, 9, 650. [Google Scholar]
- Wu, T.-H.; Chen, C.-H.C.; Mao, N.; Lu, S.-T. Fishmeal Supplier Evaluation and Selection for Aquaculture Enterprise Sustainability with a Fuzzy MCDM Approach. Symmetry 2017, 9, 286. [Google Scholar] [CrossRef]
- Hu, C.-K.; Liu, F.-B.; Hu, C.-F. A Hybrid Fuzzy DEA/AHP Methodology for Ranking Units in a Fuzzy Environment. Symmetry 2017, 9, 273. [Google Scholar] [CrossRef]
- He, X.; Zhang, J. Supplier Selection Study under the Respective of Low-Carbon Supply Chain: A Hybrid Evaluation Model Based on FA-DEA-AHP. Sustainability 2018, 10, 564. [Google Scholar] [CrossRef]
- Parkouhi, S.V.; Ghadikolaei, A.S. A resilience approach for supplier selection: Using Fuzzy Analytic Network Process and grey VIKOR techniques. J. Clean. Prod. 2017, 161, 431–451. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, H.-K.; Liao, R.-Y. Partner Selection in Supply Chain of Vietnam’s Textile and Apparel Industry: The Application of a Hybrid DEA and GM (1,1) Approach. Math. Probl. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Wu, C.-M.; Hsieh, C.-L.; Chang, K.-L. A Hybrid Multiple Criteria Decision Making Model for Supplier Selection. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Rezaeisaray, M.; Ebrahimnejad, S.; Khalili-Damghani, K. A novel hybrid MCDM approach for outsourcing supplier selection: A case study in pipe and fittings manufacturing. J. Model. Manag. 2016, 11, 536–559. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Erol, S. The DEA—FUZZY ANP Department Ranking Model Applied in Iran Amirkabir University. Acta Polytech. Hung. 2010, 7, 103–114. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Contr. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Junior, F.R.L.; Osiro, L.; Carpinetti, L.C.R. A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Appl. Soft Comp. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Oztekin, A.O.; Ekong, J.; Dag, A. Measuring the efficiency of hospitals: A fully-ranking DEA–FAHP approach. Ann. Oper. Res. 2016. [Google Scholar] [CrossRef]
- Mohaghar, A.; Fathi, M.R.; Jafarzadeh, A.H. A Supplier Selection Method Using AR- DEA and Fuzzy VIKOR. Int. J. Ind. Eng. Theory Appl. Pract. 2013, 20, 387–400. [Google Scholar]
- Talluri, S.; Narasimhan, R.; Nair, A. Vendor performance with supply risk: A chance-constrained DEA approach. Int. J. Prod. Econ. 2006, 100, 212–222. [Google Scholar] [CrossRef]
- Saen, R.F. Restricting Weights in Supplier Selection Decisions in the presence of Dual-Role factors. Appl. Math. Model. 2010, 2, 229–243. [Google Scholar] [CrossRef]
- Saen, R.F. Supplier selection by the new AR-IDEA model. Int. J. Adv. Manuf. Tech. 2008, 39, 1061–1070. [Google Scholar] [CrossRef]
- Farzipoor, R.; Zohrehbandian, M. A Data Envelopment Analysis Approach to Supplier Selection in Volume Discount Environments. Int. J. Procure. Manag. 2008, 1, 472–488. [Google Scholar]
- Saen, R.F. Suppliers Selection in the Presence of Both Cardinal and Ordinal Data. Eur. J. Oper. Res. 2007, 183, 741–747. [Google Scholar] [CrossRef]
- Storto, C.L. A double-DEA framework to support decision-making in the choice of advanced manufacturing technologies. Manag. Decis. 2018, 56, 488–507. [Google Scholar] [CrossRef]
- Adler, N.; Friedman, L.; Sinuany-Stern, Z. Review of ranking methods in the data envelopment analysis context. Eur. J. Oper. Res. 2002, 140, 249–265. [Google Scholar] [CrossRef]
- Storto, C.L. A peeling DEA-game cross efficiency procedure to classify suppliers. In Proceedings of the 21st Innovative Manufacturing Engineering and Energy International Conference (IManE 2017), Iasi, Romania, 25–26 May 2017. [Google Scholar]
- Kuo, R.J.; Lee, L.Y.; Hu, T.-L. Developing a supplier selection system through integrating fuzzy AHP and fuzzy DEA: A case study on an auto lighting system company in Taiwan. Prod. Plan. Control 2010, 21, 468–484. [Google Scholar] [CrossRef]
- Kuo, R.J.; Lin, Y.J. Supplier selection using analytic network process and data envelopment analysis. Int. J. Prod. Res. 2011, 50, 1–12. [Google Scholar] [CrossRef]
- Taibi, A.; Atmani, B. Combining Fuzzy AHP with GIS and Decision Rules for Industrial Site Selection. Int. Interact. Multimed. Artif. Intell. 2017, 4, 60–69. [Google Scholar] [CrossRef]
- Morente-Molinera, J.; Kou, G.; González-Crespo, R.; Corchado, J.; Herrera-Viedma, E. Solving multi-criteria group decision making problems under environments with a high number of alternatives using fuzzy ontologies and multi-granular linguistic modelling methods. Knowl. Based Syst. 2017, 137, 54–64. [Google Scholar] [CrossRef]
- Adrian, C.; Abdullah, R.; Atan, R.; Jusoh, Y.Y. Conceptual Model Development of Big Data Analytics Implementation Assessment Effect on Decision-Making. Int. J. Interact. Multimed. Artif. Intell. 2018, 5, 101–106. [Google Scholar] [CrossRef]
- Staníčková, M.; Melecký, L. Assessment of efficiency in Visegrad countries and regions using DEA models. Ekonomická Revue Cent. Eur. Rev. Econ. 2012, 15, 145–156. [Google Scholar] [CrossRef]
- Schaar, D.; Sherry, L. Comparison of Data Envelopment Analysis Methods Used in Airport Benchmarking. In Proceedings of the Third International Conference on Research In Air Transportation, Fairfax, VA, USA, 1–4 June 2008. [Google Scholar]
- Kahraman, C.; Cebeci, U.; Ulukan, Z. Multi-criteria supplier selection using fuzzy AHP. Logist. Inf. Manag. 2003, 16, 382–394. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Hu, A.H. Applying hazatdous substance management to supplier selection using analytic network process. J. Clean. Prod. 2009, 17, 255–264. [Google Scholar] [CrossRef]
- Banaeian, N.; Mobli, H.; Nielsen, I.E.; Omid, M. Criteria definition and approaches in green supplier selection—A case study for raw material and packaging of food industry. Prod. Manuf. Res. 2015, 3, 149–168. [Google Scholar] [CrossRef]
- Frosch, R. Industrial Ecology: Minimising the Impact of Industrial Waste. Phys. Today 1994, 47, 63–68. [Google Scholar] [CrossRef]
- Mani, V.; Agarwal, R.; Sharma, V. Supplier selection using social sustainbility: AHP based approach in India. Int. Strateg. Manag. Rev. 2014, 2. [Google Scholar] [CrossRef]
- Grover, R.; Grover, R.; Rao, V.B.; Kejriwal, K. Supplier Selection Using Sustainable Criteria in Sustainable Supply Chain Management. Int. J. Econ. Manag. Eng. 2016, 10, 1775–1780. [Google Scholar]
- Ho, W.; Xu, X.; Dey, P.K. Multi-criteria decision making approaches for supplier evaluation and selection: A literature review. Eur. J. Oper. Res. 2010, 202, 16–24. [Google Scholar] [CrossRef]
- Dickson, G. An analysis of vendor selection systems and decisions. J. Purch. 1966, 2, 5. [Google Scholar] [CrossRef]
- Weber, C.C.J.; Weber, B.W. Vendor selection criteria and methods. Eur. J. Oper. Res. 1991, 50, 2–18. [Google Scholar] [CrossRef]
- Handfield, R.B. US Global Sourcing: Patterns of Development. Int. J. Oper. Prod. Manag. 1994, 14, 40–51. [Google Scholar] [CrossRef]
- Choi, T.Y.; Hartley, J.L. An exploration of supplier selection practices across the supply chain. J. Oper. Manag. 1996, 14, 333–343. [Google Scholar] [CrossRef]
- Verma, R.; Pullman, M.E. An Analysis of the Supplier Selection Process. Omega 1998, 26, 739–750. [Google Scholar] [CrossRef]
- Bharadwaj, N. Investigating the decision criteria used in electronic components procurement. Ind. Mark. Manag. 2004, 33, 317–323. [Google Scholar] [CrossRef]
- Kannan, D.; Khodaverdi, R.; Olfat, L.; Jafarian, A.; Diabat, A. Integrated fuzzy multi criteria decision making method and multi-objective programming approach for supplier selection and order allocation in a green supply chain. J. Clean. Prod. 2013, 47, 355–367. [Google Scholar] [CrossRef]
- Chu, T.-C.; Varma, R. Evaluating suppliers via a multiple levels multiple criteria decision making method under fuzzy environment. Comput. Ind. Eng. 2012, 62, 653–660. [Google Scholar] [CrossRef]
- Tam, M.; Tummala, V.R. An Application of the AHP in Vendor Selection of a Telecommunications System. Omega Int. J. Manag. Sci. 2001, 29, 171–182. [Google Scholar] [CrossRef]
- Shahgholian, K. A model for supplier selection based on fuzzy multi-criteria group decision making. Afr. J. Bus. Manag. 2012, 6. [Google Scholar] [CrossRef]
- Dzever, S.; Merdji, M.; Saives, A. Purchase decision making and buyer-seller relationship development in the french food processing industry. Supply Chain Manag. Int. J. 2001, 6, 216–229. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Petroni, A. From traditional purchasing to supplier management: A fuzzy logic-based approach to supplier selection. Int. J. Logist. Res. Appl. 2002, 5, 235–255. [Google Scholar] [CrossRef]
- Rezaei, J.; Ortt, R. Multi-criteria supplier segmentation using a fuzzy preference relations based ahp. Eur. J. Oper. Res. 2013, 225, 75–84. [Google Scholar] [CrossRef]
- Roshandel, J.; Miri-Nargesi, S.S.; Hatami-Shirkouhi, L. Evaluating and selecting the supplier in detergent production industry using hierarchical fuzzy topsis. Appl. Math. Model. 2013, 37, 10170–10181. [Google Scholar] [CrossRef]
- Govindaraju, R.; Akbar, M.I.; Gondodiwiryo, L.; Simatupang, T. The Application of a Decision-making Approach based on Fuzzy ANP and TOPSIS for Selecting a Strategic Supplier. J. Eng. Technol. Sci. 2015, 47, 406–425. [Google Scholar] [CrossRef]
- Nielsen, I.E.; Banaeian, N.; Golińska, P.; Mobli, H.; Omid, M. Green supplier selection criteria: From a literature review to a flexible framework for determination of suitable criteria. Logist. Oper. Supply Chain Manag. Sustain. 2014, 79–99. [Google Scholar] [CrossRef]
- Sarkis, J. A methodological framework for evaluating environmentally conscious manufacturing programs. Comput. Ind. Eng. 1999, 36, 793–810. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Services Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Zhu, K.J.; Jing, Y.; Chang, D. A discussion on extent analysis method and applications of fuzzy AHP. Eur. J. Oper. Res. 1999, 116, 450–456. [Google Scholar] [CrossRef]
- Tang, Y.C.; Lin, T. Application of the fuzzy analytic hierarchy process to the lead-free equipment selection decision. Int. J. Bus. Syst. Res. 2011, 5, 35–56. [Google Scholar] [CrossRef]
- Fiedler, M.; Nedoma, J.; Ramik, J.; Rohn, J.; Karel, Z. Linear Optimization Problems with Inexact Data, 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wen, M. Uncertain Data Envelopment Analysis. In Uncertainty and Operations Research; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. 1957, 120, 253–281. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Pastor, J.T.; Ruiz, J.L.; Sirvent, I. An enhanced DEA Russell graph efficiency measure. Eur. J. Oper. Res. 1999, 115, 596–607. [Google Scholar] [CrossRef]
- Tang, Y.-C.; Beynon, M.J. Application and Development of a Fuzzy Analytic Hierarchy Process within a Capital Investment Study. J. Econ. Manag. 2005, 1, 207–230. [Google Scholar]
- Shang, J.; Sueyoshi, T. A unified framework for the selection of a flexible manufacturing system. Eur. J. Oper. Res. 1995, 85, 297–315. [Google Scholar] [CrossRef]
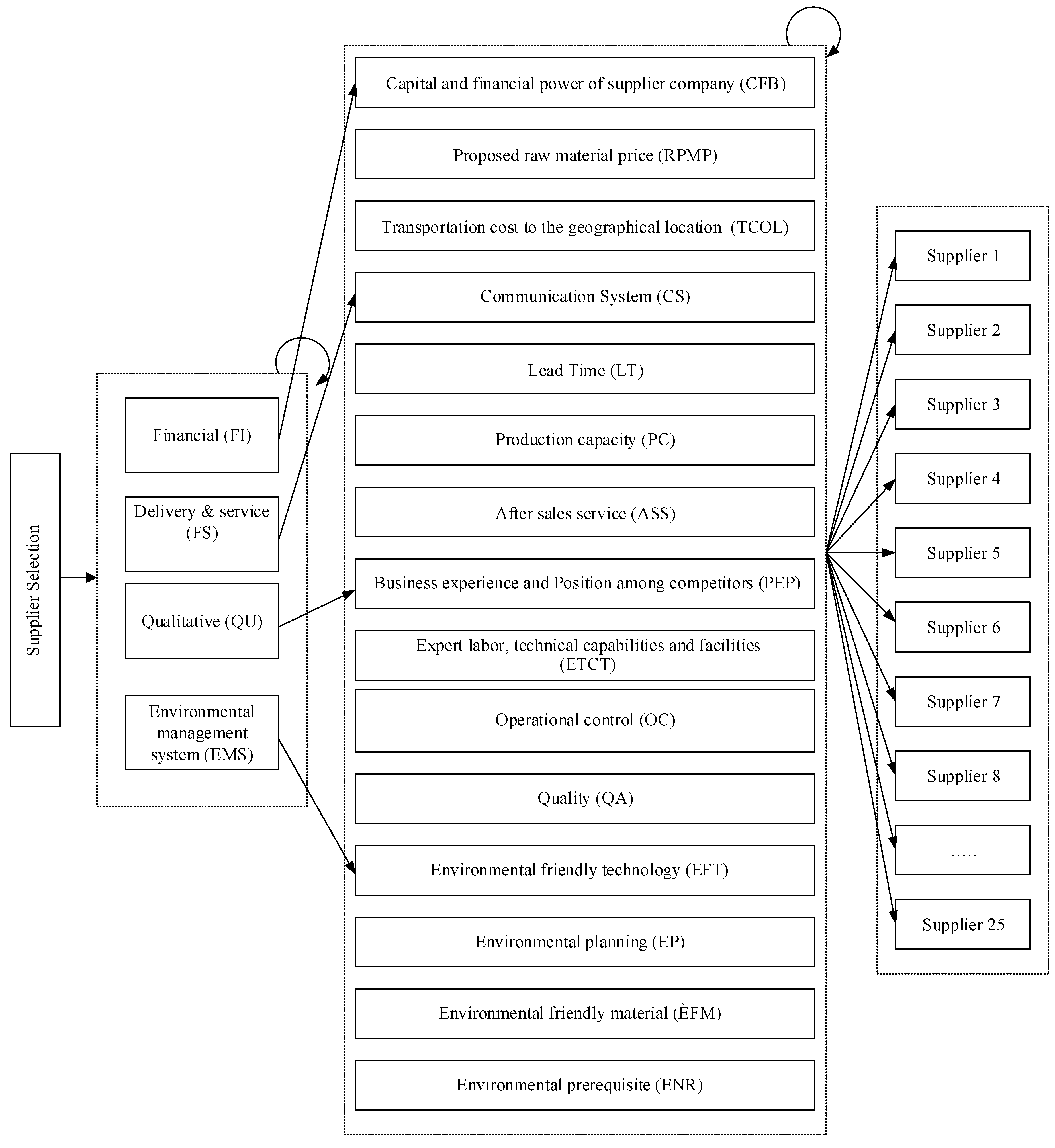
| Criteria | Sub-Criteria | Researcher |
|---|---|---|
| Financial | Capital and financial power of supplier company | Ho et al. [54], Dickson [55], Weber et al. [56] |
| Proposed raw material price | Banaeian et al. [50], Dickson [55], Weber et al. [56], Ho et al. [54] | |
| Transportation cost to the geographical location | Dickson [55], Weber et al. [56] | |
| Delivery and service | Communication system | Dickson [55], Weber et al. [56] |
| Lead time | Handfield [57], Choi & Hartley [58], Verma & Pullman [59], Bharadwa [60], Kannan et al. [61], Chu & Varma [62], Tam & Tummala [63], Shahgholian et al. [64] | |
| Production capacity | Kannan [61], Dickson [55], Weber et al. [56] | |
| After sales service | Dzever et al. [65], Choi & Hartley [58], Bevilacqua & Petroni [66], Bharadwaj [60], Rezaei & Ortt [67], Roshandel et al. [68] | |
| Qualitative | Business experience and position among competitors | Banaeian et al. [50], Dickson [55], Weber et al. [56] |
| Expert labor, technical capabilities and facilities | Banaeian et al. [50], Dickson [55], Weber et al. [56] | |
| Operational control | Dickson [55], Weber et al. [56] | |
| Quality | Grover et al. [55], Dickson [55] | |
| Environmental management system | Environmental friendly technology | Rajesri Govindaraju et al. [69], Grover et al. [53] |
| Environmental planning | Banaeian et al. [50], Nielsen et al. [70] | |
| Environmentally friendly material | Grover et al. [53] | |
| Environmental prerequisite | Banaeian et al. [50] |
| Importance Intensity | Definition |
|---|---|
| 1 | Equally importance |
| 3 | Moderate importance |
| 5 | Strongly more importance |
| 7 | Very strong more importance |
| 9 | Extremely importance |
| 2, 4, 6, 8 | Intermediate values |
| Importance Intensity | Triangular Fuzzy Scale |
|---|---|
| 1 | (1, 1, 1) |
| 2 | (1, 1, 2) |
| 3 | (1, 2, 3) |
| 4 | (2, 3, 4) |
| 5 | (3, 4, 5) |
| 6 | (4, 5, 6) |
| 7 | (5, 6, 7) |
| 8 | (7, 8, 9) |
| 9 | (9, 9, 9) |
| No | Company Name | Address | Turnover (USD) | Employees | Market Geographical Area | Symbol |
|---|---|---|---|---|---|---|
| 1 | An Gia Phu Food and Cereal Limited Liability Company | Vinh Long Province, Vietnam | 616,894 | 25 | Vietnam | DMU 1 |
| 2 | VINA Fragrant Rice Limited Liability Company | Can Tho City, Vietnam | 877,662 | 39 | Vietnam | DMU 2 |
| 3 | Thai Hung Cereal Co-operative Company | Can Tho City, Vietnam | 616,309 | 31 | Vietnam | DMU 3 |
| 4 | Sang Mai Agricultural Production Limited Liability Company | Hai Phong Provice, Vietnam | 686,350 | 39 | Vietnam | DMU 4 |
| 5 | FAS Vietnam Cereal Limited Liability Company | Vinh Long Province, Vietnam | 729,349 | 24 | Vietnam | DMU 5 |
| 6 | S1000 Food Commercial and Service Limited Liability Company | Ho Chi Minh City, Vietnam | 590,814 | 21 | Vietnam | DMU 6 |
| 7 | Khau Thien Thanh Phat Production and Commercial Export-Import Company | Ho Chi Minh City, Vietnam | 3,180,926 | 121 | Vietnam, Malaysia, Japan, Australia | DMU 7 |
| 8 | Gia Son Phat Commercial and Service Limited Liability Company | Kien Giang, Vietnam | 613,654 | 33 | Vietnam | DMU 8 |
| 9 | VILACONIC Cereal Joint Stock Company | Nghe An Province, Vietnam | 717,780 | 31 | Vietnam | DMU 9 |
| 10 | Binh Minh Cereal Joint Stock Company | Can Tho City, Vietnam | 658,272 | 26 | Vietnam | DMU 10 |
| 11 | Phu Thai Huong Joint Stock Company | Long An Province, Vietnam | 1.347,621 | 57 | Vietnam | DMU 11 |
| 12 | Long Tra Agroforestry Food Production Limited Liability Company | Ho Chi Minh City, Vietnam | 4,650,698 | 234 | Vietnam, Asia | DMU 12 |
| 13 | Huong Chien Rice Production Limited Liability Company | Long An Province, Vietnam | 674,388 | 18 | Vietnam | DMU 13 |
| 14 | Loc Troi Joint Stock Incorporated Company | An Giang Province, Vietnam | 3,077,786 | 179 | Vietnam, Lao, Cambodia | DMU 14 |
| 15 | Ngoc Oanh Rice Private Business | Ho Chi Minh City, Vietnam | 502,448 | 23 | Vietnam | DMU 15 |
| 16 | Khanh Tam Rice Private Business | Ho Chi Minh City Vietnam | 589,577 | 16 | Vietnam | DMU 16 |
| 17 | Thien Ngoc Cereal Limited Liability Company | Long An Province, Vietnam | 1,094,880 | 31 | Vietnam | DMU 17 |
| 18 | Xuyen Giang Commercial and Service Limited Liability Company | Ho Chi Minh City, Vietnam | 1,475,431 | 59 | Vietnam | DMU 18 |
| 19 | Viet Lam Commercial and Service Limited Liability Company | Vinh Long Province, Vietnam | 1,502,043 | 42 | Vietnam | DMU 19 |
| 20 | Long An Export-Production Joint Stock Company | Ha Noi City, Vietnam | 2,125,825 | 89 | Vietnam, EU | DMU 20 |
| 21 | Phat Tai Limited Liability Company | Dong Thap Province, Vietnam | 1,054,156 | 29 | Vietnam | DMU 21 |
| 22 | Thai Binh Rice Joint Stock Company | Thai Binh Province, Vietnam | 1,777,244 | 51 | Vietnam | DMU 22 |
| 23 | Angimex Kitoku Limited Liability Company | Tien Giang Province, Vietnam | 1,098,978 | 38 | Vietnam | DMU 23 |
| 24 | Hoa Lua Rice Commercial Limited Liability Company | Ho Chi Minh City, Vietnam | 1,029,622 | 59 | Vietnam | DMU 24 |
| 25 | Phuong Quan Production Limited Liability Company | Long An Province, Vietnam | 1,733,256 | 61 | Vietnam | DMU 25 |
| Criteria | FS | EMS | FI | QU |
|---|---|---|---|---|
| FS | (1, 1, 1) | (1/8, 1/7, 1/6) | (1/9, 1/8, 1/7) | (1/3, 1/2, 1) |
| EMS | (6, 7, 8) | (1, 1, 1) | (1/6, 1/5, 1/4) | (1, 2, 3) |
| FI | (7, 8, 9) | (4, 5, 6) | (1, 1, 1) | (4, 5, 6) |
| QU | (1, 2, 3) | (1/3, 1/2, 1) | (1/6, 1/5, 1/4) | (1, 1, 1) |
| Criteria | FS | EMS | FI | QU |
|---|---|---|---|---|
| FS | 1 | 1/7 | 1/8 | 1/2 |
| EMS | 7 | 1 | 1/6 | 2 |
| FI | 8 | 6 | 1 | 5 |
| QU | 2 | 1/2 | 1/5 | 1 |
| Criteria | FS | EMS | FI | QU | Weight |
|---|---|---|---|---|---|
| FS | (1, 1, 1) | (1/8, 1/7, 1/6) | (1/9, 1/8, 1/7) | (1/3, 1/2, 1) | 0.04929 |
| EMS | (6, 7, 8) | (1, 1, 1) | (1/7, 1/6, 1/5) | (1, 2, 3) | 0.20144 |
| FI | (7, 8, 9) | (5, 6, 7) | (1, 1, 1) | (4, 5, 6) | 0.64816 |
| QU | (1, 2, 3) | (1/3, 1/2, 1/1) | (1/6, 1/5, 1/4) | (1, 1, 1) | 0.10111 |
| Total | 1 | ||||
| CR = 0.09480 | |||||
| Criteria | CFB | RPMP | TCOOL | Weight |
|---|---|---|---|---|
| CFB | (1, 1, 1) | (1/5, 1/4, 1/3) | (3, 4, 5) | 0.2290 |
| RPMP | (3, 4, 5) | (1, 1, 1) | (6, 7, 8) | 0.6955 |
| TCOOL | (1/5, 1/4, 1/3) | (1/8, 1/7, 1/6) | (1, 1, 1) | 0.0754 |
| Total | 1 | |||
| CR = 0.07348 | ||||
| Criteria | CS | LT | PC | ASS | Weight |
|---|---|---|---|---|---|
| CS | (1, 1, 1) | (1/9, 1/8, 1/7) | (1/5, 1/4, 1/3) | (2, 3, 4) | 0.0924 |
| LT | (7, 8, 9) | (1, 1, 1) | (1/3, 1/2, 1) | (6, 7, 8) | 0.3956 |
| PC | (3, 4, 5) | (1, 2, 3) | (1, 1, 1) | (7, 8, 9) | 0.4672 |
| ASS | (1/4, 1/3, 1/2) | (1/8, 1/7, 1/6) | (1/9, 1/8, 1/7) | (1, 1, 1) | 0.0448 |
| Total | 1 | ||||
| CR = 0.09456 | |||||
| Criteria | PEP | ETCT | OC | QA | Weight |
|---|---|---|---|---|---|
| PEP | (1, 1, 1) | (2, 3, 4) | (4, 5, 6) | (1/5, 1/4, 1/3) | 0.2136 |
| ETCT | (1/4, 1/3, 1/2) | (1, 1, 1) | (1/4, 1/3, 1/2) | (1, 1, 1) | 0.0436 |
| OC | (1/6, 1/5, 1/4) | (2, 3, 4) | (1, 1, 1) | (1/9, 1/8, 1/7) | 0.0791 |
| QA | (3, 4, 5) | (1, 1, 1) | (7, 8, 9) | (1, 1, 1) | 0.6638 |
| Total | 1 | ||||
| CR = 0.09005 | |||||
| Criteria | EFT | EP | EFM | ENR | Weight |
|---|---|---|---|---|---|
| EFT | (1, 1, 1) | (1/9, 1/9, 1/9) | (1/6, 1/5, 1/4) | (1/6, 1/5, 1/4) | 0.0445 |
| EP | (9, 9, 9) | (1, 1, 1) | (1, 2, 3) | (5, 6, 7) | 0.5345 |
| EFM | (4, 5, 6) | (1/3, 1/2, 1) | (1, 1, 1) | (3, 4, 5) | 0.3009 |
| ENR | (4, 5, 6) | (1/7, 1/6, 1/5) | (1/5, 1/4, 1/3) | (1, 1, 1) | 0.1201 |
| Total | 1 | ||||
| CR = 0.0838 | |||||
| A Supplier (DMU) | Input | Output | ||||
|---|---|---|---|---|---|---|
| LT (Days) | UP (USD) | PC (Tons) | QB (%) | NI (USD) | RE (USD) | |
| DMU 1 | 3 | 347.3 | 50 | 3.7221 | 44.03 | 58.71 |
| DMU 2 | 5 | 391.45 | 70 | 1.3459 | 25.20 | 33.60 |
| DMU 3 | 4 | 332.4 | 50 | 0.8243 | 26.03 | 34.70 |
| DMU 4 | 4 | 321.5 | 40 | 1.7611 | 22.95 | 30.60 |
| DMU 5 | 4 | 213.5 | 50 | 1.0023 | 40.05 | 53.40 |
| DMU 6 | 4 | 312.6 | 50 | 1.6047 | 30.45 | 40.60 |
| DMU 7 | 5 | 345.3 | 40 | 2.5748 | 48.00 | 68.20 |
| DMU 8 | 5 | 342.9 | 70 | 2.0095 | 44.03 | 58.71 |
| DMU 9 | 3 | 343.6 | 50 | 3.2401 | 32.70 | 43.60 |
| DMU 10 | 3 | 354.1 | 30 | 3.0687 | 44.29 | 59.05 |
| DMU 11 | 5 | 320.10 | 30 | 4.0040 | 32.78 | 43.70 |
| DMU 12 | 3 | 346.30 | 70 | 2.9141 | 44.02 | 58.70 |
| DMU 13 | 4 | 340.60 | 50 | 4.0194 | 44.12 | 58.83 |
| DMU 14 | 4 | 315.05 | 40 | 5.1484 | 34.88 | 46.50 |
| DMU 15 | 5 | 332.40 | 60 | 4.6604 | 43.02 | 57.36 |
| DMU 16 | 4 | 350.90 | 40 | 5.4623 | 50.00 | 74.30 |
| DMU 17 | 4 | 320.00 | 71 | 6.1238 | 44.01 | 58.68 |
| DMU 18 | 5 | 344.60 | 50 | 4.7115 | 44.12 | 58.82 |
| DMU 19 | 5 | 314.03 | 50 | 7.4178 | 44.15 | 58.86 |
| DMU 20 | 4 | 342.30 | 40 | 4.7039 | 44.06 | 58.75 |
| DMU 21 | 5 | 310.80 | 50 | 3.2497 | 44.15 | 58.86 |
| DMU 22 | 4 | 312.40 | 50 | 6.8631 | 43.93 | 58.57 |
| DMU 23 | 5 | 342.00 | 50 | 7.4577 | 43.92 | 58.56 |
| DMU 24 | 5 | 337.60 | 70 | 6.5602 | 43.11 | 57.48 |
| DMU 25 | 5 | 340.10 | 50 | 5.5501 | 43.02 | 57.36 |
| Inputs/Outputs | LT | UP | PC | QB | NI | RE |
|---|---|---|---|---|---|---|
| LT | 1 | 0.02484 | 0.16149 | 0.24257 | 0.0776 | 0.07681 |
| UP | 0.02484 | 1 | 0.14105 | 0.09301 | 0.00725 | 0.03435 |
| PC | 0.16149 | 0.14105 | 1 | 0.01713 | 0.04728 | 0.00201 |
| QB | 0.24257 | 0.09301 | 0.01713 | 1 | 0.54664 | 0.51879 |
| NI | 0.0776 | 0.00725 | 0.04728 | 0.54664 | 1 | 0.98863 |
| RE | 0.07681 | 0.03435 | 0.00201 | 0.51879 | 0.98863 | 1 |
| Supplier | CCR-I | CCR-O | BCC-I | BCC-O | SBM-I-C | SBM-O-C | Super SBM-I-C | Super SBM-AR-C | Super SBM-AR-V |
|---|---|---|---|---|---|---|---|---|---|
| DMU 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DMU 2 | 25 | 25 | 25 | 24 | 25 | 24 | 25 | 24 | 24 |
| DMU 3 | 23 | 23 | 22 | 23 | 23 | 25 | 23 | 25 | 25 |
| DMU 4 | 24 | 24 | 15 | 25 | 24 | 23 | 24 | 23 | 21 |
| DMU 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DMU 6 | 22 | 22 | 20 | 22 | 22 | 22 | 22 | 22 | 23 |
| DMU 7 | 9 | 9 | 12 | 12 | 9 | 20 | 9 | 19 | 20 |
| DMU 8 | 21 | 21 | 24 | 20 | 20 | 21 | 20 | 21 | 22 |
| DMU 9 | 20 | 20 | 1 | 11 | 21 | 18 | 21 | 20 | 11 |
| DMU 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DMU 11 | 11 | 11 | 1 | 1 | 18 | 11 | 18 | 16 | 1 |
| DMU 12 | 1 | 1 | 1 | 1 | 8 | 1 | 8 | 1 | 1 |
| DMU 13 | 13 | 13 | 16 | 18 | 13 | 14 | 13 | 14 | 16 |
| DMU 14 | 16 | 16 | 1 | 1 | 12 | 15 | 12 | 12 | 1 |
| DMU 15 | 19 | 19 | 23 | 20 | 19 | 17 | 19 | 17 | 18 |
| DMU 16 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DMU 17 | 10 | 10 | 13 | 13 | 11 | 9 | 11 | 10 | 13 |
| DMU 18 | 18 | 18 | 21 | 19 | 17 | 16 | 17 | 15 | 17 |
| DMU 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DMU 20 | 12 | 12 | 14 | 16 | 10 | 12 | 10 | 9 | 12 |
| DMU 21 | 14 | 14 | 18 | 15 | 15 | 19 | 15 | 18 | 19 |
| DMU 22 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DMU 23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DMU 24 | 15 | 15 | 19 | 14 | 16 | 10 | 16 | 13 | 15 |
| DMU 25 | 17 | 17 | 17 | 17 | 14 | 13 | 14 | 11 | 14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Nguyen, V.T.; Duong, D.H.; Do, H.T. A Hybrid Fuzzy Analytic Network Process (FANP) and Data Envelopment Analysis (DEA) Approach for Supplier Evaluation and Selection in the Rice Supply Chain. Symmetry 2018, 10, 221. https://doi.org/10.3390/sym10060221
Wang C, Nguyen VT, Duong DH, Do HT. A Hybrid Fuzzy Analytic Network Process (FANP) and Data Envelopment Analysis (DEA) Approach for Supplier Evaluation and Selection in the Rice Supply Chain. Symmetry. 2018; 10(6):221. https://doi.org/10.3390/sym10060221
Chicago/Turabian StyleWang, Chia–Nan, Van Thanh Nguyen, Duy Hung Duong, and Hanh Tuong Do. 2018. "A Hybrid Fuzzy Analytic Network Process (FANP) and Data Envelopment Analysis (DEA) Approach for Supplier Evaluation and Selection in the Rice Supply Chain" Symmetry 10, no. 6: 221. https://doi.org/10.3390/sym10060221
APA StyleWang, C., Nguyen, V. T., Duong, D. H., & Do, H. T. (2018). A Hybrid Fuzzy Analytic Network Process (FANP) and Data Envelopment Analysis (DEA) Approach for Supplier Evaluation and Selection in the Rice Supply Chain. Symmetry, 10(6), 221. https://doi.org/10.3390/sym10060221







