A Novel Selection Model of Surgical Treatments for Early Gastric Cancer Patients Based on Heterogeneous Multicriteria Group Decision-Making

Abstract

Gastric cancer results in malignant tumors with high morbidity and mortality, and seriously affects the health and life quality of patients. Early detection and appropriate treatment for early-stage gastric cancer patients are very helpful to reducing the recurrence rate and improving survival rates. Hence, the selection of a suitable surgical treatment is an important part. At present, surgical treatment selection has been researched in numerous studies, but there is no study integrating fuzzy decision-making theory with quantitative analysis, considering the patient’s conditions with other relative conditions, and which can handle multisource heterogeneous information at the same time. Hence, this paper proposes a novel selection model of surgical treatments for early gastric cancer based on heterogeneous multiple-criteria group decision-making (MCGDM), which is helpful to selecting the most appropriate surgery in the case of asymmetric information between doctors and patients. Subjective and objective criteria are comprehensively taken into account in the index system of the selection model for early gastric cancer, which combines fuzzy theory with quantitative data analysis. Moreover, the evaluation information obtained from the patient’s conditions, the surgery, and the hospital’s medical status, etc., including crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic labels, is more complete and real, so the surgical treatment selection is accurate and reliable. Furthermore, the technique for order of preference by similarity to ideal solution (TOPSIS) method is employed to solve the prioritization of early gastric cancer surgical treatments. Finally, an empirical study of surgical treatment selection for early gastric cancer surgery is conducted, and the results of sensitivity analysis and comparative analysis suggest that the proposed selection model of surgical treatments for early gastric cancer patients is reliable and effective.

1. Introduction

Gastric cancer is a very common disease in the world with high morbidity and the second most frequent cause of cancer death, affecting about one million people per year [1]. As the most common gastrointestinal cancer [2], gastric cancer not only seriously threatens human health, but also severely impacts human living quality. Thus, early detection of gastric cancer is of outstanding importance for treatment [3]. Furthermore, the selection of surgical treatments, which is usually decided by medical experts, is a crucially important problem for early gastric cancer patients, but there is asymmetric information between doctors and patients [4]. Consequently, it is necessary to study and develop a proper approach to select the most appropriate surgical treatment according to the patient’s conditions. As the optimum surgical treatment is usually determined by an expert group, surgical treatment selection for early gastric cancer is a group decision-making problem affected by several conflicting factors [5] such as tumor characteristics, surgical situation, surgical outcomes, medical technology, and medical equipment.

Although some notable achievements have been made, extant studies into surgical treatment decision-making present two shortcomings. First, subjective and objective criteria which combine fuzzy theory with quantitative data analysis have not been employed comprehensively in medical treatment decision-making. Second, the evaluation information is used partially. The surgical treatment can be evaluated by hospitals, patients, and experts according to the conditions of patients, surgeries, and the hospital rather than by the case or experts. Thus, fuzziness and accuracy both exist in the evaluation information. The extant methods only considered the information of a patient’s conditions or surgical conditions [6,7,8,9], which may lead to information loss [10]. Therefore, in order to overcome the aforementioned drawbacks, a novel model of surgical treatment selection for early gastric cancer patients requires investigation.

In summary, the motivations of this paper are summarized as follows:

(1)

The evaluation of surgical treatments involves several criteria including subjective and objective criteria. Some scholars have used several objective criteria to evaluate surgical treatments quantitatively [6,11,12]. Subjective criteria such as severity of the side effects and severity of the complications were utilized in Chenabc’s study [9]. Thus, the subjective criteria combined with objective criteria are applied in the index system of the proposed model.

(2)

With regard to the partial use of information, it is appropriate to apply fuzzy logic to describe evaluation information regarding surgical treatments. The evaluation information from hospital cases mainly involves crisp numbers and interval numbers. Zhang et al. [13] presented that a neutrosophic set is an effective tool for reflecting the fuzziness in text evaluation because the evaluation information from patients is text information that represents sentiment values, and every sentiment value has not only a certain degree of truth, but also a falsity degree and an indeterminacy degree [14]. So, it needs to be transformed into neutrosophic numbers with positive, medium, and passive values. For example, when asked to assess whether medical equipment would be “good”, from the sentiment value of a patient we may deduce that the membership degree of truth is 0.6, the membership degree of indeterminacy is 0.2, and the membership degree of falsity is 0.2. Pang et al. [15] stated that probabilistic linguistic term sets (PLTS) are more convenient for the DMs to provide their preference as they may have hesitancy among several possible linguistic terms when expressing their evaluation information, so the PLTS need to be applied to express experts’ linguistic terms more accurately. For example, when asked to assess whether a surgical treatment would be appropriate for a particular patient based on the patient’s conditions, an expert may deduce that the probability of “high” is 0.7, the probability of “medium high” is 0.2, and the probability of “medium” is 0.1. Therefore, evaluation information, including crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic labels, needs to be considered in the selection model.

(3)

To deal with the priority order of surgical treatments based on heterogeneous MCGDM, a systematic approach need to be used in the proposed model. Shih et al. [16] hold that TOPSIS is a practical and useful technique for the ranking and selection of a number of externally determined alternatives through distance measures, and it has been connected to multiple-criteria decision-making (MCDM) [17]. Lourenzutti et al. [18] and Li et al. [19] presented heterogeneous TOPSIS for multicriteria group decision-making. Thus, the TOPSIS method is applied in the proposed model to solve the surgical treatment selection.

Based on the discussion above, a selection model of surgical treatments for early gastric cancer is developed in this paper, which is based on MCGDM and heterogeneous information including precise or uncertain evaluation values to help experts and the patient to select the most appropriate surgical treatments by using TOPSIS. The contributions of this paper are summarized as follows: (1) An index system of early gastric cancer surgery comprehensively considering subjective criteria and objective criteria is established. It combines fuzzy theory with quantitative data analysis; (2) Heterogeneous information including crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic labels is considered to evaluate surgical treatments. It makes evaluation results more complete and reliable; (3) The TOPSIS method for heterogeneous multicriteria group decision-making is employed to solve the priorities of surgical treatments, which can help experts and the patient to select the most appropriate surgical treatment. Finally the implementation process of the proposed selection model of surgical treatments for early gastric cancer in the paper is illustrated in detail by an empirical study of a particular patient.

The rest of the paper is organized as follows. In Section 2, previous studies about early gastric cancer surgical treatment selection are reviewed briefly. In Section 3, interval numbers, neutrosophic numbers, and the concept of probabilistic linguistic term sets are introduced. Subsequently, in Section 4, a selection model of surgical treatments based on heterogeneous MCGDM for early gastric cancer is developed. In Section 5, an experimental example and results are presented concretely, and a comparative analysis is illustrated to validate the proposed method. Finally, Section 6 summarizes the paper and provides some possible directions of future research.

2. Literature Review

At present, a large number of methods for medical treatment selection have been developed. Among them, the comparison analysis method for evaluating the performance of medical treatments is the most common approach to solving surgical treatment selection problems for early gastric cancer. A previous study analyzed various indications of different surgical treatments such as endoscopic mucosal resection (EMR), limited resection, and laparoscopic surgical resection, and provided approaches and a selection process based on the patient’s conditions [8]. Some scholars selected the most appropriate surgical management for patients by analyzing clinical features, pathological characteristics, and the feasibility of surgery [6]. Another study selected candidates with early gastric cancer for endoscopic submucosal dissection by evaluating the effectiveness of an endoscopic-ultrasonography-based treatment plan and an endoscopy-based treatment plan [7]. Furthermore, many fuzzy MCDM methods have been employed to solve the problem of the selection decision for medical treatment. It is common for decision-makers to use linguistic terms to estimate the performance of treatment methods in practical decision-making problems [9]. An interval neutrosophic linguistic multicriteria group decision-making method was developed to select medical treatments [20]. A novel TODIM (an acronym in Portuguese of interactive and multi-criteria decision making)-method-based three-way decision model was proposed to select medical treatments [21]. In conclusion, in current research, fuzzy group decision-making theory and quantitative analysis have not been applied simultaneously to solve medical problems.

Recently, numerous evaluation indices of surgical treatments have been studied. Many scholars have researched surgery performance; for instance, Kim et al. [11] evaluated the characteristics of gastric cancer, operating time, blood loss, hospital stay, and surgical outcomes, and Pisanu et al. [6] even measured surgical situations such as depth of cancer invasion, histological type, and lymph node metastasis, etc. Furthermore, a study by Chenabc [9] analyzed medical technology on the basis of considering survival rate, complication, probability of a cure, side-effect hospital stays, and efficacy, etc. Hu et al. [12] analyzed clinicopathologic features such as tumor size, differentiated degree, and lymph node metastasis, etc. Based on the indices involved in the above studies, there are no studies taking into account subjective and objective criteria simultaneously, and the conditions of medical technology in the hospital have not been considered in the evaluation of surgical treatment. However, in fact, the key factors affecting the selection of surgical treatment may be subjective, objective, or both. Thus, the conditions of patients, surgery, and hospital as well as the subjective and objective criteria should be considered comprehensively.

With respect to the method of subjective weight, many scholars have made significant contributions. Wang et al. [22] used criteria priorities to get criteria weights. The weight was calculated by using a probabilistic method in the study proposed by Zhao et al. [23]. Mangla et al. [24] computed subjective weight by using fuzzy analytic hierarchy process (AHP) or values provided by decision-makers directly. Rezaei [25,26] used the (best-worst method) BWM method to compute subjective weight with lesser comparison times and information loss compared with AHP. Tian et al. [27] stated that the BWM method can require fewer pairwise comparisons than does fuzzy AHP but obtain more highly reliable weights. Thus, the subjective weight in this paper is computed by BWM.

As studied in much medical research, extant approaches use partial information. Pisanu et al. [6] used crisp numbers and interval numbers to evaluate surgical performance. Ali et al. [28] applied neutrosophic sets in a recommender system for medical diagnosis. Zhai et al. [29] applied probabilistic linguistic labels in a personal hospital selection recommender system. None of the previous medical research considered these information types mentioned above simultaneously. Thus, in this paper, the evaluation information obtained from hospital cases, patients, and experts includes crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic labels, which need to be considered in the selection progress.

In conclusion, previous studies about surgical treatment selection for early gastric cancer should be improved in future study. In order to settle those issues based on the studies analyzed above, we (1) develop an index system selecting early gastric cancer surgery with a combination of fuzzy MCGDM theory and quantitative data analysis; (2) comprehensively consider various types of information which are obtained from the conditions of patients, surgeries, and medical technology when evaluating surgical treatments; (3) employ the BWM method to compute subjective criteria weight; and (4) manage heterogeneous information and compute the prioritization of surgical treatments by using TOPSIS.

3. Preliminaries

In this section, we present the definitions of the data types, including reals, intervals, neutrosophic sets, and probabilistic linguistic term sets, which will be useful in developing the surgical treatment selection model for early gastric cancer.

3.1. Interval Numbers

We provide some basic concepts and operational rules for interval numbers.

Definition 1.

The object a =$\left[a^L,a^U\right]$, where$a^L\le a^U$, defined on the real line, is called an interval number, as introduced in Tsaur’s study [30]. The values$a^L$and$a^U$stand for the lower and upper bounds of a, respectively.

Definition 2.

Let a =$\left[a^L,a^U\right]$and b =$\left[b^L,b^U\right]$be two interval numbers. The Euclidean distance between a and b is symmetric [31] and given as follows [32]:

$$d(\mathit{a},\mathit{b})=\sqrt{\frac{1}{2}\left[{(a^L-a^U)}^2+{(b^L-b^U)}^2\right]}.$$

(1)

3.2. Neutrosophic Set Theory

Definition 3.

[33,34] Let X be a space of points (objects), with a generic element in X denoted by x. Then a neutrosophic set (NS) A in X is characterized by three membership functions, including a truth membership function $T_A(x)$, indeterminacy membership function$I_A(x)$, and falsity membership function${\mathrm{F}}_A(x)$, and is defined as$\mathrm{A}=\left\{⟨x,T_A(x),I_A(x),{\mathrm{F}}_A(x)⟩|x\in X⟩\right\}$, where$T_A(x)$,$I_A(x)$, and${\mathrm{F}}_A(x)$are real standard or nonstandard subsets of$\left[0,1\right]$, i.e.,$T_A(x)$: X$\to$$\left[0,1\right]$,$I_A(x)$: X$\to$$\left[0,1\right]$,${\mathrm{F}}_A(x)$: X$\to$$\left[0,1\right]$. The sum of$T_A(x)$,$I_A(x)$, and${\mathrm{F}}_A(x)$is unrestricted, and$0<T_A(x)+I_A(x)+F_A(x)<3$.

Definition 4.

[35] Let X be a universal space of points (objects), with a generic element of X denoted by x. A single-valued neutrosophic set (SVNS)$\stackrel{\sim }{N}\subset X$is characterized by a truth membership function$T_{\stackrel{\sim }{N}}(x)$, an indeterminacy membership function$I_{\stackrel{\sim }{N}}(x)$, and a falsity membership function$F_{\stackrel{\sim }{N}}(x)$with$T_{\stackrel{\sim }{N}}(x)$,$I_{\stackrel{\sim }{N}}(x)$,$F_{\stackrel{\sim }{N}}(x)$$\in$ [0,1] for all $x\in X$. The sum of three membership functions of an SVNS $\stackrel{\sim }{N}$, the relation $0\le T_{\stackrel{\sim }{N}}(\mathrm{x})+I_{\stackrel{\sim }{N}}(x)+F_{\stackrel{\sim }{N}}(x)\le 3$ holds for all $x\in X$.

Definition 5.

(Euclidean distance) [36]

Let$\stackrel{\sim }{A}=\{(x_1|⟨T_{\stackrel{\sim }{A}}(x_1),I_{\stackrel{\sim }{A}}(x_1),F_{\stackrel{\sim }{A}}(x_1)⟩),\dots ,(x_n|⟨T_{\stackrel{\sim }{A}}(x_n),I_{\stackrel{\sim }{A}}(x_n),F_{\stackrel{\sim }{A}}(x_n)⟩)\}$and$\stackrel{\sim }{B}=\{(x_1|⟨T_{\stackrel{\sim }{B}}(x_1),I_{\stackrel{\sim }{B}}(x_1),F_{\stackrel{\sim }{B}}(x_1)⟩),\dots ,(x_n|⟨T_{\stackrel{\sim }{B}}(x_n),I_{\stackrel{\sim }{B}}(x_n),F_{\stackrel{\sim }{B}}(x_n)⟩)\}$be two SVNSs for$x_i\in X$$(i=1,2,\dots ,n)$. Then, the Euclidean distance between the two SVNSs$\stackrel{\sim }{A}$and$\stackrel{\sim }{B}$is symmetric [37] and can be defined as follows:

$$D(\stackrel{\sim }{A},\stackrel{\sim }{B})=\sqrt{\frac{1}{3n}{\displaystyle \sum _{i=1}^n\{{(T_{\stackrel{\sim }{A}}(x_i)-T_{\stackrel{\sim }{B}}(x_i))}^2}+{(I_{\stackrel{\sim }{A}}(x_1)-I_{\stackrel{\sim }{B}}(x_1))}^2+{(F_{\stackrel{\sim }{A}}(x_1)-F_{\stackrel{\sim }{B}}(x_1))}^2\}}.$$

(2)

Definition 6.

According to one study by Majumdar et al. [36], for single-valued neutrosophic set$\mathrm{A}=\left\{⟨x,T_A(x),I_A(x),{\mathrm{F}}_A(x)⟩|x\in X⟩\right\}$, an entropy on neutrosophic set A is computed by Equation (3):

$$E(A)=1-\frac{1}{n}{\displaystyle \sum _{x_i\in X}(T_A}(x_i)+F_A(x_i))\otimes |I_A(x_i)-I_{A^c}(x_i)|.$$

(3)

Definition 7.

The entropy weight of a neutrosophic set in the article by Tan et al. [38] is shown as follows:

$$W_j=(1-E(x_j))/{\displaystyle {\sum }_j^n(1-E(x_j))}.$$

(4)

Definition 8.

The single-valued neutrosophic weighted averaging (SVNWA) aggregation operator proposed by Ye’s research [39] is shown as follows:

$$\begin{array}{ll}{F}_{A_i}& ={\psi }_1{A}_1\oplus {\psi }_2{A}_2\oplus \dots \oplus {\psi }_n{A}_n\\ & =⟨1-{\displaystyle \prod _{i=1}^n{(1-T_{A_i})}^{{\psi }_i}},{\displaystyle \prod _{k=1}^n{(I_{A_i})}^{{\psi }_i}},{\displaystyle \prod _{i=1}^n{(F_{A_i})}^{{\psi }_i}}⟩,\end{array}$$

(5)

where $\psi ={({\psi }_1,{\psi }_2,\dots ,{\psi }_n)}^T$ is the weight vector of $A_i$.

Definition 9.

Suppose that$S=\left\{s_i|i=-t,\dots ,t\right\}$is a limited and ordered discrete label set. We construct a semantic analysis system; let$t=3$in this system, and$s_i$represent a possible linguistic term. The specific label set could be defined as a symmetric linguistic evaluation scale with the center of$s_0$: S = {s₋₃ = very bad, s₋₂ = bad, s₋₁ = slightly bad, s₀ = ok, s₁ = slightly good, s₂ = good, s₃ = very good}. The semantic values in Table 1 are computed throughout sentiment analysis by utilizing the software of ‘The R Project for Statistical Computing’. According to different sentiment words, we allocate linguistic variable$s_i$to positive, neutral, and passive values as a neutrosophic number$A_i=<T_i,I_i,F_i>$,$i=1,\dots ,n$(positive value is T value, neutral value is I, passive value is F). The T value is the average value of positive values, while the I value is 1 if s₀ exists or 0 if s₀ does not exist, and the F value is the mean of the absolute passive values. For example, for a set$S=\left\{s_{-1},s_0,s_1,s_2,s_3\right\}$, the neutrosophic value is$⟨\frac{s_1+s_2+s_3}{3},s_0,|s_{-1}|⟩$, i.e.,$⟨\frac{0.106066+0.75+0.954594}{3},1,0.10607⟩$.

Table 1. Sentiment value.

Evaluation	Very Bad	Bad	Slightly Bad	OK	Slightly Good	Good	Very Good
Sentiment degree	−0.95459	−0.75	−0.10607	0	0.106066	0.75	0.954594

3.3. Probabilistic Linguistic Term Sets and Their Basic Concepts

In fact, numerous aspects of different activities can only be evaluated in a qualitative form, not in a quantitative form in the process of settling MCGDM problems; hence, in view of the situations with uncertain or imprecise information, it is highly convenient to use linguistic term sets to evaluate alternatives with reference to concerned criteria [40,41].

Definition 10.

[42] A fixed linguistic term set (LTS) is a set$S=\{s_{\partial }|\partial =0,1,\dots ,\tau \}$, where$s_{\partial }$represents a possible value for a linguistic variable. In particular, the lower and upper limits of linguistic terms are defined as$s_0$and$s_{\tau }$, respectively, which are used by a decision-maker in practical applications.

Example 1.

In this case, when$\tau$= 4, S can be denoted as

$S=\{s_0=poor,s_1=mediumpoor,s_2=fair,s_3=mediumgood,s_4=good\}$.

Definition 11.

[15] Let$S=\{s_0,s_1,\dots ,s_{\tau })$be an LTS; a probabilistic linguistic term set (PLTS) can be defined as

$$L(p)=\{L^{(k)}(p^{(k)})|L^{(k)}\in S,p^{(k)}\ge 0,k=1,2,\dots ,\#L(p),{\displaystyle \sum _{k=1}^{\#L(p)}{p}^{(k)}\le 1}\},$$

(6)

where$L^{(k)}(p^{(k)})$is the linguistic term$L^{(k)}$associated with the probability$p^{(k)}$and$\#L(p)$is the number of all different linguistic terms in$L(p)$.

Note that if${\displaystyle \sum _{k=1}^{\#L(p)}{p}^{(k)}}$= 1, then we have complete information of the probabilistic distribution of all possible linguistic terms; if${\displaystyle \sum _{k=1}^{\#L(p)}{p}^{(k)}}$< 1, then partial ignorance exists because current knowledge is not enough to provide complete assessment information, which is not rare in practical GDM problems. In particular,${\displaystyle \sum _{k=1}^{\#L(p)}{p}^{(k)}}$= 0 means complete ignorance. Obviously, handling the ignorance of$L(p)$is a crucial application for PLTSs.

Definition 12.

Given a PLTS$L(p)$with${\displaystyle \sum _{k=1}^{\#L(p)}{p}^{(k)}}<1$, the normalization PLTS$\stackrel{.}{L}(p)$is defined by the following equation [15]:

$$\stackrel{.}{L}(p)=\{L^{(k)}({\stackrel{.}{p}}^{(k)})|k=1,2,\dots ,\#L(p)\},$$

(7)

where${\stackrel{.}{p}}^{(k)}=p^{(k)}/{\displaystyle {\sum }_{k=1}^{\#L(p)}{p}^{(k)}}$for all$k=1,2,\dots ,\#L(p)$.

Definition 13.

[15] Let$L_1(p)$and$L_2(p)$be any two PLTSs,$L_1(p)=\{L_1^{(k)}(p_1^{(k)})|k=1,2,\dots ,\#L_1(p)\}$and$L_2(p)=\{L_2^{(k)}(p_2^{(k)})|k=1,2,\dots ,\#L_2(p)\}$, and let$\#L_1(p)$and$\#L_2(p)$be the numbers of linguistic terms in$L_1(p)$and$L_2(p)$, respectively. If$\#L_1(p)>\#L_2(p)$, then we can add$\#L_1(p)-\#L_2(p)$linguistic terms to$L_2(p)$so that the numbers of linguistic terms in$L_1(p)$and$L_2(p)$are identical. The added linguistic terms are the smallest ones in$L_2(p)$, and the probabilities of all the linguistic terms are zero.

Let$L_1(p)=\{L_1^{(k)}(p_1^{(k)})|k=1,2,\dots ,\#L_1(p)\}$and$L_2(p)=\{L_2^{(k)}(p_2^{(k)})|k=1,2,\dots ,\#L_2(p)\}$; then, the normalization can be computed by the following two steps:

(1) 

If${\displaystyle \sum _{k=1}^{\#L(p)}{p_i}^{(k)}}<1$, then by Equation (3), we can compute${\stackrel{.}{L}}_i(p)$, i = 1, 2.

(2) 

If$\#L_1(p)\ne \#L_2(p)$, then we add some elements to the one with the smaller number of elements according to Definition 13.

Example 2.

Let$L_1(p)=\{s_3(0.2),s_2(0.4),s_1(0.2)\}$and$L_2(p)=\{s_2(0.6),s_3(0.4)\}$be two PLTSs, then (1) according to Definition 12,$\stackrel{.}{L_1}(p)=\{s_2(0.5),s_3(0.25),s_1(0.25)\}$; (2) since$\#L_2(p)<\#L_1(p)$, we add the linguistic term$s_2$to$L_2(p)$so that the numbers of linguistic terms in$L_1(p)$and$L_2(p)$are identical, and, hence, we have$\stackrel{.}{L_2}(p)=\{s_2(0.6),s_3(0.4),s_2(0)\}$. Therefore, we have two normalized PLTSs:$L_1(p)=\{s_2(0.5),s_3(0.25),s_1(0.25)\}$and$L_2(p)=\{s_2(0.6),s_3(0.4),s_2(0)\}$.

Definition 14.

[43] To further standardize the decision matrix when there are benefit-type and cost-type attributes, we can transform the cost type into benefit as follows:

$$\stackrel{\sim }{L}{T}_{ij}(p)=\{\begin{array}{ll}L{T}_{ij}(p),& forbenefitattribute\\ {\mathrm{C}}_j{(L{T}_{ij}(p))}^c,& forcostattribute{\mathrm{C}}_j\end{array},$$

(8)

where${(L{T}_{ij}(p))}^c$is the complement of$L{T}_{ij}(p)$, and${(L{T}_{ij}(p))}^c=\{neg(L{T_{ij}}^{(k)})(p_{ij}^{(k)})|k=1,2,\dots ,\#L{T}_{ij}(p)\}$.

Definition 15.

[15] Let$L(p)=\{L^{(k)}(p^{(k)})|k=1,2,\dots ,\#L(p)\}$be a PLTS, and$r^{(k)}$be the subscripts of linguistic terms$L^{(k)}$. Then, the score of$L(p)$is

$$E(L(p))=s_{\stackrel{-}{\partial }},$$

(9)

where$\stackrel{-}{\partial }={\displaystyle {\sum }_{k=1}^{\#L(p)}{r}^{(k)}{p}^{(k)}}/{\displaystyle {\sum }_{k=1}^{\#L(p)}{p}^{(k)}}$.

For two PLTSs$L_1(p)$and$L_2(p)$, if$E(L_1(p))>E(L_2(p))$, then$L_1(p)$is superior to$L_2(p)$, denoted by$L_1(p)>L_2(p)$; if$E(L_1(p))<E(L_2(p))$, then$L_1(p)$is inferior to$L_2(p)$, denoted by$L_1(p)<L_2(p)$.

Definition 16.

[15] Let$L_i(p)=\{L_i^{(k)}(p_i^{(k)})|k=1,2,\dots ,\#L_i(p)\}(i=1,2,\dots ,n)$be n PLTSs, where$L_i^{(k)}$and$p_i^{(k)}$are the kth linguistic term and its probability, respectively, in$L_i(p)$. Then, the probabilistic linguistic averaging (PLA) operator is defined as follows:

$$\begin{array}{l}PLA(L_1(p),L_2(p),\dots ,L_i(p))=\frac{1}{n}(L_1(p)\oplus L_2(p)\oplus \dots \oplus L_n(p))\\ =\frac{1}{n}\left({\displaystyle {\cup }_{L_1^{(k)}\in L_1(p),L_2^{(k)}\in L_2(p),\dots ,L_n^{(k)}\in L_n(p)}\{p_1^{(k)}}{L}_1^{(k)}\oplus p_2^{(k)}{L}_2^{(k)}\oplus \dots \oplus p_n^{(k)}{L}_n^{(k)}\}\right).\end{array}$$

(10)

Definition 17.

[15] Let$L_i(p)=\{L_i^{(k)}(p_i^{(k)})|k=1,2,\dots ,\#L_i(p)\}(i=1,2,\dots ,n)$be n PLTSs, where$L_i^{(k)}$and$p_i^{(k)}$are the kth linguistic term and its probability, respectively, in$L_i(p)$. Then

$$\begin{array}{l}PLWA(L_1(p),L_2(p),\dots ,L_i(p))=w_1{L}_1(p)\oplus w_2{L}_2(p)\oplus \dots \oplus w_n{L}_n(p)\\ ={\displaystyle {\cup }_{L_1^{(k)}\in L_1(p)}\left\{w_1{p}_1^{(k)}{L}_1^{(k)}\right\}}\oplus {\displaystyle {\cup }_{L_2^{(k)}\in L_2(p)}\left\{w_2{p}_2^{(k)}{L}_2^{(k)}\right\}}\oplus \dots \oplus {\displaystyle {\cup }_{L_n^{(k)}\in L_n(p)}\left\{w_n{p}_n^{(k)}{L}_n^{(k)}\right\}}\end{array}$$

(11)

is called the probabilistic linguistic weighted averaging (PLWA) operator, where$w={(w_1,w_2,\dots ,w_n}^T$is the weight vector of$L_i(p)$(i = 1, 2, …, n),$w_i\ge 0$, i = 1, 2, …, n, and${\displaystyle {\sum }_{i=1}^n{w}_i=1}$. In particular, if$w={(1/n,1/n,\dots ,1/n)}^T$, then the PLWA operator reduces to the PLA operator.

Definition 18.

[15] Let$L_i(p)=\{L_i^{(k)}(p_i^{(k)})|k=1,2,\dots ,\#L_i(p)\}(i=1,2,\dots ,n)$be n PLTSs. Then

$$\begin{array}{l}PLG(L_1(p),L_2(p),\dots ,L_i(p))={(L_1(p)\otimes L_2(p)\otimes \dots \otimes L_n(p))}^{1/n}\\ ={\left({\displaystyle {\cup }_{L_1^{(k)}\in L_1(p),L_2^{(k)}\in L_2(p),\dots ,L_n^{(k)}\in L_n(p)}\{{(L_1^{(k)})}^{P_1^{(k)}}\otimes {(L_2^{(K)})}^{P_2^{(k)}}\otimes \dots \otimes {(L_n^{(K)})}^{P_n^{(k)}}\}}\right)}^{1/n}\end{array}$$

(12)

is called the probabilistic linguistic weighted geometric (PLWG) operator, where$L_i^{(k)}$and$p_i^{(k)}$are the kth linguistic term and its probability, respectively, in$L_i(p)$.

Definition 19.

[15] Let$L_i(p)=\{L_i^{(k)}(p_i^{(k)})|k=1,2,\dots ,\#L_i(p)\}(i=1,2,\dots ,n)$be n PLTSs. Then the probabilistic linguistic weighted geometric (PLWG) operator is defined as follows:

$$\begin{array}{l}PLWG(L_1(p),L_2(p),\dots ,L_i(p))={(L_1(p))}^{w_1}\otimes {(L_2(p))}^{w_2}\otimes \dots \otimes {(L_n{(p)}^{w_n})}^{1/n}\\ ={\displaystyle {\cup }_{L_1^{(k)}\in L_1(p)}\{{(L_1^{(k)})}^{w_1{p}_1^{(k)}}\}}\otimes {\displaystyle {\cup }_{L_2^{(k)}\in L_2(p)}\{{(L_2^{(k)})}^{w_2{p}_2^{(k)}}\}}\otimes \dots \otimes {\displaystyle {\cup }_{L_n^{(k)}\in L_n(p)}\{{(L_n^{(k)})}^{w_n{p}_n^{(k)}}\}},\end{array}$$

(13)

where$L_i^{(k)}$and$p_i^{(k)}$are the kth linguistic term and its probability, respectively, in$L_i(p)$;$w={(w_1,w_2,\dots ,w_n}^T$is the weight vector of$L_i(p)$(i = 1, 2, …, n);$w_i\ge 0$; i = 1, 2, …, n; and${\displaystyle {\sum }_{i=1}^n{w}_i=1}$.

Definition 20.

[15] Let$L_1(p)=\{L_1^{(k)}(p_1^{(k)})|k=1,2,\dots ,\#L_1(p)\}$and$L_2(p)=\{L_2^{(k)}(p_2^{(k)})|k=1,2,\dots ,\#L_2(p)\}$be two PLTSs,$\#L_1(p)=\#L_2(p)$; then, the deviation degree between$L_1(p)$and$L_2(p)$is defined as follows:

$$d(L_1(p),L_2(p))=\sqrt{{\displaystyle {\sum }_{k=1}^{\#L_1(p)}(p_1^{(k)}{r}_1^{(k)}-p_2^{(k)}{r}_2^{(k)})}/\#L_1(p)},$$

(14)

where$r_1^{(k)}$and$r_2^{(k)}$are the subscripts of linguistic terms$L_1^{(k)}$and$L_2^{(k)}$, respectively.

4. The Proposed Selection Model of Surgical Treatment for Early Gastric Cancer

The optimum surgical treatment for early gastric cancer is usually determined by a consultative panel composed of various medical experts, so it is a group decision-making problem to find the best alternative from all of the feasible alternatives [44]. Actually, many issues cannot be evaluated explicitly in the selection process of surgical treatments for early gastric cancer, so accurate and imprecise data must be considered simultaneously. Therefore, the proposed model to select surgical treatments for early gastric cancer patients is established with heterogeneous information, which is helpful to solving the issue of asymmetric information between doctors and patients. The general progress of this model is depicted in Figure 1. The details of the proposed model will be described in the rest of this section.

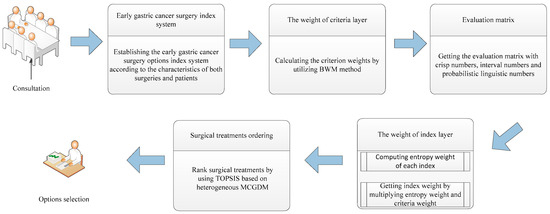
Figure 1. Summary of the process of the proposed model.

4.1. The Establishment of the Early Gastric Cancer Surgery Index System

Selecting early gastric cancer surgical treatments is complex. The surgical treatment selection for early gastric cancer is decided by a group of K experts, who consider both the disease conditions of patients and the relevant surgical situation. Based on analysis proposed in the literature review and expert opinion, the evaluation of early gastric cancer surgery’s performance can be mainly measured by five aspects, denoted by five criteria $A_i(i=1,2,\dots ,5)$: tumor characteristics, surgical situation, surgical outcomes, medical technology, and medical equipment. Moreover, under each criterion, there are several subcriteria (i.e., surgery indices) which influence the selection of surgical treatments. Particularly, the tumor characteristics indices of suitability of tumor size, suitability of differentiated degree, and suitability of depth of invasion are decided by experts, based on the extent to which surgery is appropriate for certain patient. Hence, an early gastric cancer surgery index system including the definition of the surgery index is established as shown in Table 2. Because of the complexity of surgery and the uncertainty of information, the evaluation values of surgery indices can be divided into multiple types. Therefore, there exists heterogeneous information in this proposed system, including real numbers, interval numbers, linguistic values, and probabilistic linguistic values.

Table 2. Index system of early gastric cancer surgery.

Criteria	Indices	Definition	Index Type
Tumor characteristics (A1)	Suitability of tumor size (a11)	The degree of suitability that tumor size is suitable for this surgery	Benefit
	Suitability of differentiated degree (a12)	The degree of suitability that tumor differentiation is suitable for this surgery	Benefit
	Suitability of depth of invasion (a13)	The degree of suitability that the depth of invasion is suitable for this surgery	Benefit
Surgical situation (A2)	Complexity of surgery (a21)	The more complicated the operation is, the higher the risk becomes	Cost
	Blood loss (a22)	The amount of bleeding in the surgery	Cost
	Survival rate (a23)	The survival probability in surgery	Benefit
	Operating time (a24)	The time spent in surgery	Cost
	Oncological clearance (a25)	The condition of oncological clearance	Benefit
	Operative wound (a26)	The wound size of surgery	Cost
Surgical outcomes (A3)	Wound infection (a31)	Wound infections after surgery	Cost
	Probability of a cure (a32)	The probability of curing early gastric cancer	Benefit
	Severity of the complications (a33)	The possibility of complications like wound dehiscence, fever	Cost
	Severity of the side effects (a34)	The possibility of side effects after surgery	Cost
	Probability of a recurrence (a35)	The probability of a recurrence because of unsuccessful surgery	Cost
	Hospital stays (a36)	Length of hospital stay	Cost
	Recovery time (a37)	The postoperative recovery time	Cost
	Degree of dysfunction (a38)	The function of gastric system for patients after the surgery	Cost
Medical technology (A4)	Medical technical level (a41)	The technical force and medical standards in the hospital	Benefit
	Teamwork Capacity (a42)	The teamwork capacity of medical team	Benefit
	Medical resources (a43)	Available medical resources in the hospital	Benefit
	Proficiency (a44)	Skill degree of medical professionals	Benefit
Medical equipment (A5)	Advanced equipment (a51)	The performance of medical equipment	Benefit
	Perfection level (a52)	Complete supporting facilities in medical	Benefit
	Disinfecting technical (a53)	The equipment for disinfection and sterilization	Benefit
	Emergency facilities (a54)	The perfection of emergency medical facilities	Benefit

4.2. The Estimation of Criteria Weights with BWM

In this section, we utilize a more efficient method to calculate subjective weight, which is called the BWM method. We use the BWM to compute the weight of five early gastric cancer surgery criteria with the most important criterion and the least important criterion. The detailed procedures of BWM to compute the weights of the criteria are as follows.

Step 1.

Determine a set of decision criteria.

In this step, we consider the criteria $\left\{c_1,c_2,\dots ,c_n\right\}$ that should be used to arrive at a decision.

Step 2.

Determine the best (e.g., most desirable, most important) and the worst (e.g., least desirable, least important) criterion.

Step 3.

Determine the preference of the best criterion over all the other criteria, using a number between 1 and 9. The resulting best-to-others vector would be $A_B=(a_{B1},a_{B2},\dots ,a_{Bn})$ where $a_{Bj}$ indicates the preference of the best criterion B over criterion j. It is clear that $a_{BB}$ = 1.

Step 4.

Determine the preference of all the criteria over the worst criterion, using a number between 1 and 9. The resulting others-to-worst vector would be: $A_W=(a_{1W},a_{2W},\dots ,a_{nW})$ where $a_{jW}$ indicates the preference of the criterion j over the worst criterion W. It is clear that $a_{WW}$ = 1.

Step 5.

Find the optimal weights $(w_1{}^{\ast },w_2{}^{\ast },\dots ,w_n{}^{\ast })$.

The optimal weight for the criteria is the one where, for each pair of $w_B/w_j$ and $w_j/w_W$, we have $w_B/w_j=a_{Bj}$ and $w_j/w_W=a_{jW}$. To satisfy these conditions for all j, we should find a solution where the maximum absolute differences $|\frac{w_B}{w_j}-a_{Bj}|$ and $|\frac{w_j}{w_w}-a_{jw}|$ for all j are minimized. Considering the non-negativity and condition for the weights, the following problem results:

$$\begin{array}{l}\min {\max }_j\{|\frac{w_B}{w_j}-a_{Bj}|,|\frac{w_j}{w_w}-a_{jw}|\}\\ s.t.\\ {\displaystyle \sum _j{w}_j}=1\\ w_j\ge 0,\mathrm{for}allj.\end{array}$$

(15)

Equation (15) is equivalent to the following:

$$\begin{array}{l}\min \xi \\ s.t.\\ |\frac{w_B}{w_j}-a_{Bj}|\le \xi ,forall\mathrm{j}\\ |\frac{w_j}{w_w}-a_{jw}|\le \xi ,forallj\\ {\displaystyle \sum _j{w}_j}=1\\ w_j\ge 0,\mathrm{for}allj.\end{array}$$

(16)

Solving Equation (16), the optimal weights $(w_1{}^{\ast },w_2{}^{\ast },\dots ,w_n{}^{\ast })$ and ξ^* are obtained.

Then, we calculate the consistency ratio using ξ^* and the corresponding consistency index as follows:

$$\begin{array}{l}ConsistencyRatio\hfill \end{array}=\frac{{\xi }^{＊}}{ConsistencyIndex}.$$

(17)

Table 3 shows the maximum values of ξ (consistency index) for different values of $a_{BW}$.

Table 3. Consistency Index (CI) Table.

${\mathit{a}}_{\mathit{B}\mathit{w}}$	1	2	3	4	5	6	7	8	9
Consistency Index (max ξ)	0.00	0.44	1.00	1.63	2.30	3.00	3.73	4.47	5.23

If the consistency ratio is $\le$0.1, it implies a very good consistency which is acceptable. Otherwise, we can revise $a_{Bj}$ and $a_{jW}$ to make the solution (more) consistent.

BWM introduced above is limited in deriving a unique optimum weight vector when the number of criteria is more than three. It might lead to multiple optimal solutions. The improved method presented in [45] is used to obtain optimal weights with n criteria. If we use $\{|{\mathrm{w}}_B-a_{Bj}{w}_j|,|w_j-a_{jw}{w}_w|\}$ instead of $\{|\frac{w_B}{w_j}-a_{Bj}|,|\frac{w_j}{w_w}-a_{jw}|\}$, the problem can be solved as follows:

$$\begin{array}{l}\min {\max }_j\{|{\mathrm{w}}_B-a_{Bj}{w}_j|,|w_j-a_{jw}{w}_w|\}\\ s.t.\\ {\displaystyle \sum _j{w}_j}=1\\ w_j\ge 0,for\mathrm{all}j.\end{array}$$

(18)

Equation (18) can be transferred to the following linear programming problem:

$$\begin{array}{l}\min {\xi }^L\\ s.t.\\ |w_B-a_{Bj}{w}_j|\le {\xi }^L,for\mathrm{all}j\\ |w_j-a_{jw}{w}_w|\le {\xi }^L,forallj\\ {\displaystyle \sum _j{w}_j}=1\\ w_j\ge 0,forallj.\end{array}$$

(19)

Equation (19) is a linear problem, which can calculate the only optimal weights $(w_1{}^{\ast },w_2{}^{\ast },\dots ,w_n{}^{\ast })$. Hence, we can compute the weight vector $(w_1,w_2,w_3,w_4,w_5)$ of tumor characteristics $A_1$, surgical situation $A_2$, surgical outcomes $A_3$, medical technology $A_4$, and medical equipment $A_5$.

4.3. The Evaluation Matrix of Early Gastric Cancer Surgery

The evaluation problem of early gastric cancer surgery involves hospital cases, experts, patients, and multiple evaluation indices, both qualitatively and quantitatively. Different experts may make different assessments on account of their distinct knowledge and different judgment standards, and different surgical treatments which suit different patients’ conditions. Thus, in this section, the evaluation information obtained from the early gastric cancer cases, patients, and experts is heterogeneous, including crisp numbers, interval numbers, linguistic labels, and probabilistic linguistic labels. Specifically, the crisp numbers are the evaluation values of the survival rate and probability of a recurrence; the interval numbers are the evaluation values of blood loss, operating time, number of harvested lymph nodes, hospital stays, and recovery time; the linguistic labels are the evaluation values of residual tumor cells, operative wound, medical technical level, teamwork capacity, medical resources, proficiency, advanced equipment, perfection level, disinfecting technical, and emergency facilities; the probabilistic linguistic labels are the evaluation values of the suitability of tumor size, suitability of differentiated degree, suitability of depth of invasion, complexity of surgery, wound infection, probability of a cure, severity of the complications, severity of the side effects, and degree of dysfunction. The linguistic labels provided by patients can be transformed into neutrosophic numbers because of uncertain information. Hence, we can get the evaluation matrix $R=(r_{ij})$ with real numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic numbers.

Step 1. Obtain real numbers.

The evaluation values of surgery indices such as survival rate and probability of a recurrence in the early gastric cancer surgery index system are mainly computed according to previous treatment cases in the hospital. The survival rate is the percentage of people who survived relative to total patients undergoing surgery. The probability of a recurrence is the ratio of the number of recurrences to patients that undergo surgery. In this step, we can chalk up the ratio data as the evaluation values of the two surgery indices. Because the two ratios are calculated by hospital records, every surgical treatment only has these corresponding data. Therefore, the evaluation values of these two surgery indices do not need be aggregated. Then, the evaluation matrix of $R=(r_{ij})$ based on $a_{23}$ and $a_{35}$ is completed.

Step 2. Get the interval numbers.

The evaluation information of some surgery indices, including the indicators blood loss, operating time, number of harvested lymph nodes, hospital stays, and recovery time, is derived from clinical data for patients who had surgery in the hospital. Because these data cannot be collected accurately, the index values are in the form of interval numbers. The evaluation information of these indices is aggregated by using the arithmetic mean operator. Hence, the evaluation matrix of $R=(r_{ij})$ based on $a_{22}$, $a_{24}$, $a_{36}$, and $a_{37}$ is computed.

Step 3. Calculate neutrosophic numbers.

In general, patients’ perceptions and evaluations of surgical results are the most realistic and objective over others. So, the evaluation of some indices, such as residual tumor cells, operative wound, medical technical level, teamwork capacity, medical resources, proficiency, advanced equipment, perfection level, disinfecting technical, emergency facilities, and so on, by patients who have completed the treatment can be collected to be used as the reference index for the treatment of the follow-up patients, to improve the objectivity and accuracy of the evaluation. As mentioned in the discussion in Section 1, in this step, we transform the evaluation information of these indices according to the symmetric linguistic evaluation scale into neutrosophic numbers with truth, indeterminacy, and falsity. Then, we aggregate the neutrosophic numbers by utilizing the single-valued neutrosophic weighted averaging (SVNWA) aggregation operator described by Equation (5). Therefore, the evaluation matrix of $R=(r_{ij})$ based on $a_{25}$, $a_{26}$, $a_{41}$, $a_{42}$, $a_{43}$, $a_{44}$, $a_{51}$, $a_{52}$, $a_{53}$, and $a_{54}$ is defined, where $\psi ={({\psi }_1,{\psi }_2,\dots ,{\psi }_p)}^T$ is the weight vector of patients corresponding to these indices.

Step 4. Acquire probabilistic linguistic values.

The evaluation values of some surgery indices, including the indicators suitability of tumor size, suitability of differentiated degree, suitability of depth of invasion, complexity of surgery, wound infection, probability of a cure, severity of the complications, severity of the side effects, and degree of dysfunction, etc., are probabilistic linguistic values predicted by experts according to certain specific circumstances. The three experts utilize the LTS $S=\{s_0=verylow,s_2=mediumlow,s_3=medium,s_4=mediumhigh,s_5=high,s_6=veryhigh\}$, which is defined as a symmetric linguistic evaluation scale with the center of $s_3$, to evaluate the projects $x_j(j=1,2,\dots ,n)$ by means of PLTSs. Hence, the evaluation values can be provided in the form of probabilistic linguistic values. Then, the evaluation matrix of $R=(r_{ij})$ based on $a_{11}$, $a_{12}$, $a_{13}$, $a_{21}$, $a_{31}$, $a_{32}$, $a_{33}$, $a_{34}$, and $a_{38}$ is computed.

4.4. The Calculation of Index Weight

In this section, we exploit the principle of combination between subjectivity and objectivity for the computation of the index weight. We first calculate the entropy weights of early gastric cancer surgery indices. Then, we can compute a comprehensive index weight which combines the entropy weight of early gastric cancer surgery indices with the subjective weight of criteria.

Step 1. Determine the entropy weight of data index.

Normalizing the evaluation matrix in Equation (20), the further normalization matrix $R={(r_{ij})}_{m\times n}$ is ${\left[p_{ij}\right]}_{m\times n}={\left[r_{ij}/{\displaystyle \sum _{i=1}^m{r}_{ij}}\right]}_{{}_{m\times n}}$ (m evaluated objects, n evaluation indices). The normalization equation is as follows:

$$\begin{array}{ll}{Z}_{ij}=\frac{y_{ij}-y_j^{\min }}{y_j^{\max }-y_j^{\min }}& ifjisbenefitattribute\\ Z_{ij}=\frac{y_j^{\max }-y_{ij}}{y_j^{\max }-y_j^{\min }}& ifjiscostattribute\end{array}.$$

(20)

The entropy weight can be defined as

$$\begin{array}{l}{E}_{ij}=(1-e_i)/{\displaystyle \sum _{i=1}^m(1-e_i)}\\ where{e}_i=-k{\displaystyle \sum _{j=1}^n{p}_{ij}}\ln p_{ij},k=1/\ln n,{\displaystyle \sum _{i=1}^m{E}_i}=1\end{array}.$$

(21)

Hence, the entropy weights $E_{23}$ and $E_{35}$ can be computed.

Step 2. Compute the entropy weight of the interval-valued index.

The following formula is used to normalize the interval values:

$$r_{ij}=\{\begin{array}{ll}\left[a_{ij}/b_{i\max },b_{ij}/b_{i\max }\right],& ifjisbenefitindex\\ \left[1-b_{ij}/b_{i\max },1-a_{ij}/b_{i\max }\right],& ifjis\cos tindex\end{array}.$$

(22)

The entropy weight can be computed as follows [46]:

$$\begin{array}{l}{h}_j=\lambda (-\frac{1}{\ln m}{\displaystyle \sum _{i=1}^m{H}_{ij}\ln H_{ij})+(1-\lambda )}(-\frac{1}{\ln m}{\displaystyle \sum _{i=1}^m{L}_{ij}\mathrm{In}{L}_{ij}})\\ E_{ij}=\frac{1-h_j}{{\displaystyle \sum _{j=1}^n(1-h_j)}}\end{array}$$

(23)

where $H_{ij}=\frac{\frac{1}{2}(a_{ij}+b_{ij})}{{\displaystyle \sum _{i=1}^m\frac{1}{2}(a_{ij}+b_{ij})}}$, $L_{ij}=\frac{1-(b_{ij}-a_{ij})}{m-{\displaystyle \sum _{i=1}^m(b_{ij}-a_{ij})}}$ (m evaluated objects, n evaluation indices) and $\lambda$ with $0<\lambda <1$ means the equilibrium coefficient of the median of the interval number and uncertainty for the decision-maker.

In our proposed method, we calculate the entropy weight with $\lambda =0.5$. Then, the entropy weights $E_{22}$, $E_{24}$, $E_{25}$, $E_{36}$, and $E_{37}$ can be computed.

Step 3. Manage the entropy weight of the neutrosophic-valued index.

The normalization equation for neutrosophic numbers is as follows [47]:

$$r_{ij}=\{\begin{array}{ll}{T}_{ij},I_{ij},F_{ij}& ifjisbenefitindex\\ 1-T_{ij},1-I_{ij},1-F_{ij}& ifjis\cos tindex\end{array}.$$

(24)

Equations (3) and (4) introduced in Section 3 are used to compute the entropy weight based on the evaluation matrix. As a result, the entropy weights $E_{26}$, $E_{27}$, $E_{41}$, $E_{42}$, $E_{43}$, $E_{44}$, $E_{51}$, $E_{52}$, $E_{53}$, and $E_{54}$ can be computed.

Step 4. Calculate the entropy weight of the probabilistic linguistic-valued index.

According to the proposed approach in the study by Liu et al. [43], first, transform the decision matrix $R={\left[L{T}_{ij}(p)\right]}_{m\times n}$ into $Z={\left[\overline{L{T}_{ij}}(p)\right]}_{m\times n}$, where $\overline{L{T}_{ij}}(p)={\displaystyle {\sum }_{k=1}^{\#L{T}_{ij}(p)}{r}^{(k)}{p}^{(k)}}/\#L{T}_{ij}(p)$. Next, calculate the entropy for the index: the entropy values for the jth index are

$$H_j=-\frac{1}{\ln m}{\displaystyle \sum _{i=1}^m(\overline{L{T}_{ij}}(p))}\ln (\overline{L{T}_{ij}}(p)).$$

(25)

Then, the weight of each attribute can be defined by the following:

$$E_{ij}=\frac{1-H_j}{n-{\displaystyle {\sum }_{j=1}^n{H}_j}}.$$

(26)

Therefore, the entropy weights $E_{11}$, $E_{12}$, $E_{13}$, $E_{21}$, $E_{31}$, $E_{32}$, $E_{33}$, $E_{34}$, and $E_{38}$ can be computed.

Step 5. Calculate the weight of the early gastric cancer surgery index.

The optimal weight vector of early gastric cancer surgery criteria is ${w_i}^{\ast }$ according to the explanation of BWM in Section 4.2. Based on the objective and subjective synthetic approach to determine weight [48], the synthetic weight of the early gastric cancer surgery index is calculated in the following way:

$$W_{ij}=w_i\times E_{ij}.$$

(27)

4.5. TOPSIS and Its Application in Heterogeneous MCGDM

The TOPSIS method was proposed by Hwang and Yoon [49] to deal with multicriteria decision-making problems. It provides the best alternative which is as close as possible to the best possible solution. The basic principle of the TOPSIS method is described in the following steps [18]:

Step 1.

Define and normalize the decision matrix $R=(r_{ij})$.

Step 2.

Aggregate the weights to the decision matrix by making $v_{ij}=w_j{r}_{ij}$.

Step 3.

Define the positive ideal solution (PIS), $v_j^{+}$, and the negative ideal solution (NIS), $v_j^{-}$, for each criterion. Usually, $v_j^{+}=\max \left\{v_{ij},\dots ,v_{mj}\right\}$ and $v_j^{-}=\min \left\{v_{ij},\dots ,v_{mj}\right\}$ for benefit criteria, and $v_j^{+}=\min \left\{v_{ij},\dots ,v_{mj}\right\}$ and $v_j^{-}=\max \left\{v_{ij},\dots ,v_{mj}\right\}$ for cost criteria.

Step 4.

Calculate the separation measures for each alternative.

$$S_i^{+}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_j^{+}-v_{ij})}^2}},i=1,2,\dots ,m$$

(28)

$$S_i^{-}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_j^{-}-v_{ij})}^2}},i=1,2,\dots ,m$$

(29)

Step 5.

Calculate the closeness coefficients to the ideal solution for each alternative.

$$C{C}_i=\frac{S_i^{-}}{S_i^{-}+S_i^{+}}$$

(30)

Step 6.

Rank the alternatives according to $C{C}_i$. The bigger $C{C}_i$ is, the better alternative $A_i$ will be.

The selection of early gastric cancer surgical treatment is a heterogeneous multicriteria group decision-making problem consisting of K experts $e_k(k=1,2,\dots ,K)$, denoted by $\Omega =\left\{e_1,e_2,\dots ,e_k\right\}$. Suppose that there exist $n$ surgical treatments $x_j(j=1,2,\dots ,n)$; thus, the set of surgical treatments is denoted by $X=\{x_1,x_2,\dots ,x_n\}$. In this section, we use the TOPSIS method based on heterogeneous MCGDM to solve the treatment selection. Due to the existence of heterogeneous information in terms of surgery evaluation, the criteria set $A=(A_1,A_2,A_3,A_4,A_5)$ can be divided into four subsets $O_i(i=1,2,3,4)$, where $O_i$ are sets of criteria whose values are crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic labels. The main procedure of the TOPSIS method for heterogeneous MCGDM is generalized as follows:

Step 1.

Normalize evaluation matrix R [18].

We can compute the crisp number based on Equation (20), normalized interval number based on Equation (22), normalized neutrosophic number based on Equation (24), and normalized probabilistic linguistic value based on Equation (8).

Step 2.

Construct the positive ideal solution (PIS) and the negative ideal solution (NIS) for experts.

Let the PISs of experts $e_k(k=1,2,\dots ,K)$ be $x^{k+}$; the [name], denoted by $y^{k+}$, is computed by following equation. Similarly, the NIS is denoted by $y^{k-}$, which is computed by Equation (32)

$$y_i^{k+}=\{\begin{array}{ll}{e}_i^{k+},& if{A}_i\in o_1\\ \left[a_i^{k+},b_i^{k+}\right],& if{A}_i\in o_2\\ ⟨T_i^{k+},I_i^{k+},F_i^{k+}⟩,& if{A}_i\in o_3\\ L_i{(p)}^{k+},& if{A}_i\in o_4\end{array}$$

(31)

Here, $e_i^{k+}=\max \{e_{ij}^k|j=1,\dots ,n\}$ $(A_i\in o_1^b)$ or $\min \{e_{ij}^k|j=1,\dots ,n\}$ $(A_i\in o_1^c)$; $\left[a_i^{k+},b_i^{k+}\right]=\max \{a_{ij}^k,b_{ij}^k|j=1,2,\dots ,n\}$ $(A_i\in o_2^b)$ or $\min \{a_{ij}^k,b_{ij}^k|j=1,2,\dots ,n\}$ $(A_i\in o_2^c)$; $⟨T_i^{k+},I_i^{k+},F_i^{k+}⟩=⟨\max T_{ij}^k,\min I_{ij}^k,\min F_{ij}^k⟩$ $(A_i\in o_3^b)$ or $⟨\min T_{ij}^k,\max I_{ij}^k,\max F_{ij}^k⟩$ $(A_i\in o_3^c)$; and $L{T}_i{(p)}^{k+}=\max \{L{T}_{ij}^k(p)|j=1,2,\dots ,\#L{T}_{ij}(p)\}$ $(A_i\in o_4^b)$ or $\max \left\{{(L{T}_{ij}^k(p))}^c|j=1,2,\dots ,\#L{T}_{ij}(p)\right\}$ $(A_i\in o_4^c)$, where ${(L{T}_{ij}(p))}^c=\{neg(L{T}_{ij}{}^{(k)})(p_{ij}^{(k)})|k=1,2,\dots ,\#L{T}_{ij}(p)\}$.

Similarly, the NIS $y^{k-}$ is as follows:

$$y_i^{k-}=\{\begin{array}{ll}{e}_i^{k-},& if{A}_i\in o_1\\ \left[a_i^{k-},b_i^{k-}\right],& if{A}_i\in o_2\\ ⟨T_i^{k-},I_i^{k-},F_i^{k-}⟩,& if{A}_i\in o_3\\ L_i{(p)}^{k-},& if{A}_i\in o_4\end{array}.$$

(32)

Here, $e_i^{k-}=\min \{e_{ij}^k|j=1,\dots ,n\}$ $(A_i\in o_1^b)$ or $\max \{e_{ij}^k|j=1,\dots ,n\}$ $(A_i\in o_1^c)$; $\left[a_i^{k-},b_i^{k-}\right]=\mathrm{m}in\{a_{ij}^k,b_{ij}^k|j=1,2,\dots ,n\}$ $(A_i\in o_2^b)$ or $\max \{a_{ij}^k,b_{ij}^k|j=1,2,\dots ,n\}$ $(A_i\in o_2^c)$; $⟨T_i^{k-},I_i^{k-},F_i^{k-}⟩=⟨\min T_{ij}^k,\max I_{ij}^k,\max F_{ij}^k⟩$ $(A_i\in o_3^b)$ or $⟨\max T_{ij}^k,\min I_{ij}^k,\min F_{ij}^k⟩$ $(A_i\in o_3^c)$; and $L{T}_i{(p)}^{k-}=\min \{L{T}_{ij}^k(p)|j=1,2,\dots ,\#L{T}_{ij}(p)\}$ $(A_i\in o_4^b)$ or $\min \left\{{(L{T}_{ij}^k(p))}^c|j=1,2,\dots ,\#L{T}_{ij}(p)\right\}$ $(A_i\in o_4^c)$.

Step 3.

Calculate the distances between each surgical treatment and the PIS as well as the NIS based on the symmetric [31,37,50] distance formula.

The distance between the normalized values of the surgical treatment $x_j$$(j=1,2,\dots ,n)$ and PIS $x^{k+}$ on all indices $a_i\in o_1$ is defined as follows:

$$\begin{array}{l}\rho (r_{o_{1}j}^k,r_{o_1}^{k+})={\displaystyle \sum _{a_i\in o_1}[W_i}d(r_{ij}^k,r_i^{k+}){]}^2\\ \underset{a_i\in o_1}{d(r_{ij}^k,r_i^{k+})}=|e_i^{k+}-e_{ij}^k|\end{array}$$

(33)

where $r_{o_{1}j}^k$ and $r_{o_1}^{k+}$ are the normalized value vectors of the surgical treatment $x_j$ and the PIS $x^{k+}$ on all indices in $o_1$, respectively.

The distances between the normalized values of the surgical treatment $x_j(j=1,2,\dots ,n)$ and PIS $x^{k+}$ on all indices $a_i\in o_2$ are described using Equation (1) as follows:

$$\begin{array}{l}\rho (r_{o_{2}j}^k,r_{o_2}^{k+})={\displaystyle \sum _{a_i\in o_2}[W_i}d(r_{ij}^k,r_i^{k+}){]}^2\\ \underset{a_i\in o_2}{d}(r_{ij}^k,r_i^{k+})=\sqrt{(1/2)\left[{(a_i^{k+}-a_{ij}^k)}^2+{(b_i^{k+}-b_{ij}^k)}^2\right]}\end{array}$$

(34)

where $r_{o_{2}j}^k$ and $r_{o_2}^{+}$ are the normalized value vectors of the surgical treatment $x_j$ and the PIS $x^{k+}$ on all indices in $o_2$, respectively.

The distances between the normalized values of the surgical treatment $x_j$$(j=1,2,\dots ,n)$ and PIS $x^{k+}$ on all indices $a_i\in o_3$ are described using Equation (2) as follows:

$$\begin{array}{l}\rho (r_{o_{3}j}^k,r_{o_3}^{k+})={\displaystyle \sum _{a_i\in o_3}[W_i}d(r_{ij}^k,r_i^{k+}){]}^2\\ \underset{a_i\in o_3}{d}(r_{ij}^k,r_i^{k+})=\sqrt{(1/3)\left[{(T_i^{k+}-T_{ij}^k)}^2+{(I_i^{k+}-I_{ij}^k)}^2+{(F_i^{k+}-F_{ij}^k)}^2\right]}\end{array}$$

(35)

where $r_{o_{3}j}^k$ and $r_{o_3}^{k+}$ are the normalized value vectors of the surgical treatment $x_j$ and the PIS $x^{k+}$ on all indices in $o_3$, respectively.

The distances between the normalized values of the surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and PIS $x^{k+}$ on all indices $a_i\in o_4$ are described using Equation (14) as follows:

$$\begin{array}{l}\rho (r_{o_{4}j}^k,r_{o_4}^{k+})={\displaystyle \sum _{a_i\in o_4}[W_i}d(r_{ij}^k,r_i^{+}){]}^2\\ \underset{a_i\in o_4}{d}(r_{ij}^k,r_i^{k+})=\sqrt{{\displaystyle {\sum }_{k=1}^{\#L_i{(p)}^{+}}({(p_i^{(k)}{r}_i^{(k)})}^{k+}-{(p_{ij}^{(k)}{r}_{ij}^{(k)})}^k)}/\#L_i{(p)}^{+}}\end{array}$$

(36)

where $r_{o_{4}j}^k$ and $r_{o_3}^{k+}$ are the normalized value vectors of the surgical treatment $x_j$ and the PIS $x^{k+}$ on all indices in $o_4$, respectively.

The distance between a surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and the PIS $x^{k+}$ according to Equations (33)–(36) is defined as follows:

$$\rho (r_j^k,r^{k+})=\sqrt{{\displaystyle {\sum }_{t=1}^4\rho (r_{o_{t}j}^k,r_{o_t}^{k+}})}.$$

(37)

Similarly, the distances between the normalized values of the surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and NIS $x^{k-}$ on all indices $a_i\in o_1$ are defined as follows:

$$\begin{array}{l}\rho (r_{o_{1}j}^k,r_{o_1}^{k-})={\displaystyle \sum _{a_i\in o_1}[W_i}d(r_{ij}^k,r_i^{k-}){]}^2\\ \underset{a_i\in o_1}{d(r_{ij}^k,r_i^{k-})}=|e_{ij}^k-e_i^{k-}|\end{array}$$

(38)

where $r_{o_1}^{k-}$ is the normalized value of the NIS $x^{k-}$ on all indices in $o_1$.

The distances between the normalized values of the surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and NIS $x^{k-}$ on all indices $a_i\in o_2$ are expressed as follows:

$$\begin{array}{l}\rho (r_{o_{2}j}^k,r_{o_2}^{k-})={\displaystyle \sum _{a_i\in o_2}}{[W_{i}d(r_{ij}^k,r_i^{k-})]}^2\\ \underset{a_i\in o_2}{d}(r_{ij}^k,r_i^{k-})=\sqrt{(1/2)\left[{(a_i^{k-}-a_{ij}^k)}^2+{(b_i^{k-}-b_{ij}^k)}^2\right]}\end{array}$$

(39)

where $r^k{}_{o_2}^{-}$ is the normalized value vector of the NIS $x^{k-}$ on all indices in $o_2$.

The distances between the normalized values of the surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and NIS $x^{k-}$ on all indices $a_i\in o_3$ are introduced as follows:

$$\begin{array}{l}\rho (r_{o_{3}j}^k,r_{o_3}^{k-})={\displaystyle \sum _{a_i\in o_3}}{[W_{i}d(r_{ij}^k,r_i^{k-})]}^2\\ \underset{a_i\in o_3}{d}(r_{ij}^k,r_i^{k-})=\sqrt{(1/3)\left[{(T_i^{k-}-T_{ij}^k)}^2+{(I_i^{k-}-I_{ij}^k)}^2+{(F_i^{k-}-F_{ij}^k)}^2\right]}\end{array}$$

(40)

where $r_{o_3}^{k-}$ is the normalized value vector of the NIS $x^{k-}$ on all indices in $o_3$.

The distances between the normalized values of the surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and PIS $x^{k-}$ on all indices $a_i\in o_4$ are described using Equation (14) as follows:

$$\begin{array}{l}\rho (r_{o_{4}j}^k,r_{o_4}^{k-})={\displaystyle \sum _{a_i\in o_4}[W_i}d(r_{ij}^k,r_i^{k-}){]}^2\\ \underset{a_i\in o_4}{d}(r_{ij}^k,r_i^{k-})=\sqrt{{\displaystyle {\sum }_{k=1}^{\#L_i{(p)}^{-}}|{(p_i^{(k)}{r}_i^{(k)})}^{k-}-{(p_{ij}^{(k)}{r}_{ij}^{(k)})}^k|}/\#L_i{(p)}^{-}}\end{array}$$

(41)

where $r_{o_4}^{k-}$ is the normalized value vector of the NIS $x^{k-}$ on all indices in $o_4$.

The distance between a surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and the NIS $x^{k-}$ is defined by using Equations (39)–(42) as follows:

$$\rho (r_j^k,r^{k-})=\sqrt{{\displaystyle {\sum }_{t=1}^4\rho (r_{o_{t}j}^k,r_{o_t}^{k-}})}.$$

(42)

Step 4.

Calculate relative closeness degree of surgical treatments to the PIS for experts.

The relative closeness degrees of surgical treatments $x_j$ with regard to $x^{k+}$ for the experts $e_k(k=1,2,\dots ,K)$ are defined as follows:

$$\tau (r_j^k)=\epsilon \frac{{\rho }^{-}(r^{k+})-\rho (r_j^k,r^{k+})}{{\rho }^{-}(r^{k+})-{\rho }^{+}(r^{k+})}+(1-\epsilon )\times \frac{\rho (r_j^k,r^{k-})-{\rho }^{-}(r^{k-})}{{\rho }^{+}(r^{k-})-{\rho }^{-}(r^{k-})},$$

(43)

where $\{\begin{array}{l}{\rho }^{-}(r^{k+})=\max \{\rho (r_j^k,r^{k+})|j=1,2,\dots ,n\}\\ {\rho }^{+}(r^{k+})=\min \{\rho (r_j^k,r^{k+})|j=1,2,\dots ,n\}\end{array}$, $\{\begin{array}{l}{\rho }^{+}(r^{k-})=\max \{\rho {(}_j^k,r^{k-})|j=1,2,\dots ,n\}\\ {\rho }^{-}(r^{k-})=\min \{\rho {(}_j^k,r^{k-})|j=1,2,\dots ,n\}\end{array}$, and the parameters $\epsilon \in \left[0,1\right]$ are compromise coefficients which may be identified as the weights of decision-making strategy ‘‘the majority of attributes” close to the PIS $x^{k+}$ [51]. The compromise solutions are decided by experts by consensus when $\epsilon =0.5$. Then, relative closeness degrees of surgical treatments $x_j$ $(j=1,2,\dots ,n)$ for all experts $e_k(k=1,2,\dots ,K)$ can be expressed concisely in the matrix format as follows:

$$\tau ={({\tau }_j^k)}_{K\times n},$$

(44)

where $\tau (r_j^k)$ is denoted by ${\tau }_j^k$.

Step 5.

Compute the weights of experts.

The selection of surgical treatments is decided by an expert group consisting of different experts with equal importance. Denote the weight of expert $e_k(k=1,2,\dots ,K)$ by $w^k$. Therefore, the weight vector of experts is $w^k=(1/K,1/K,\dots ,1/K)(k=1,2,\dots ,K)$.

Step 6.

Compute relative closeness degrees of surgical treatments with respect to the PIS for the group.

The PIS and the NIS for the group can be denoted as $x^{+}$ and $x^{-}$ according to the concepts of the PIS and the NIS [52], whose vectors are denoted by ${\tau }^{+}=({\tau }_1{}^{+},{\tau }_2{}^{+},\dots ,{\tau }_k{}^{+})$ and ${\tau }^{-}=({\tau }_1{}^{-},{\tau }_2{}^{-},\dots ,{\tau }_k{}^{-})$, respectively. Then, the computation is defined as follows:

$${\tau }_k{}^{+}=\max \{{\tau }_j^k|j=1,2,\dots ,n\}(k=1,2,\dots ,K)$$

(45)

and

$${\tau }_k{}^{-}=\min \{{\tau }_j^k|j=1,2,\dots ,n\}(k=1,2,\dots ,K).$$

(46)

The distances between a surgical treatment $x_j$ $(j=1,2,\dots ,n)$ and the PIS $x^{+}$ as well as the NIS $x^{k-}$ for the group are defined as follows:

$${\rho }^G(x_j,x^{+})=\sqrt{{\displaystyle {\sum }_{k=1}^K{\left[w^k({\tau }_k^{+}-{\tau }_j^k)\right]}^2}}$$

(47)

and

$${\rho }^G(x_j,x^{-})=\sqrt{{\displaystyle {\sum }_{k=1}^K{\left[w^k({\tau }_k^{-}-{\tau }_j^k)\right]}^2}}.$$

(48)

The relative closeness degrees of surgical treatment $x_j$ $(j=1,2,\dots ,n)$ with respect to the PIS $x^{+}$ for the group are similar to Equation (43) and defined as follows:

$${\tau }^G(x_j)=\epsilon \frac{{\rho }^{G-}(x^{+})-{\rho }^G(x_j,x^{+})}{{\rho }^{G-}(x^{+})-{\rho }^{G+}(x^{+})}+(1-\epsilon )\times \frac{{\rho }^G(x_j,x^{-})-{\rho }^{G-}(x^{-})}{{\rho }^{G+}(x^{-})-{\rho }^{G-}(x^{-})},$$

(49)

where $\{\begin{array}{l}{\rho }^{G-}(x^{+})=\max \{{\rho }^G(x_j,x^{+})|j=1,2,\dots ,n\}\\ {\rho }^{G+}(x^{+})=\min \{{\rho }^G(x_j,x^{+})|j=1,2,\dots ,n\}\end{array}$, $\{\begin{array}{l}{\rho }^{G+}(x^{-})=\max \{{\rho }^G(x_j,x^{-})|j=1,2,\dots ,n\}\\ {\rho }^{G-}(x^{-})=\min \{{\rho }^G(x_j,x^{-})|j=1,2,\dots ,n\}\end{array}$.

Step 7.

Rank the surgical treatments by using ${\tau }^G(x_j)$.

Clearly, $0\le {\tau }^G(x_j)\le 1$. The larger ${\tau }^G(x_j)$, the better the surgical treatment $x_j$ for the group. Thus, the asymmetry between the two ideal solutions and a surgical treatment is utilized to obtain a ranking order [53].

5. Empirical Study

The proposed selection model was applied to solve a selection problem of surgical treatments for early gastric cancer. A particular patient with early-stage gastric cancer, denoted “EGC 1”, came to Xiangya Hospital to find a surgical treatment for his disease. Several experts in the hospital diagnosed the patient’s disease and then provided four possible surgical treatments, including endoscopic mucosal resection (EMR), endoscopic submucosal dissection (ESD), laparoscopic surgery, and laparotomy, which are denoted by $x_1$, $x_2$, $x_3$, and $x_4$, respectively. These four surgical treatments were evaluated using early gastric cancer cases, patients, and experts against several evaluation indices to help the patient understand the advantages and disadvantages of the surgical treatments; the evaluation indices are listed in Table 2.

According to the selection model of surgical treatments for early gastric cancer proposed in Section 4, we first compute the early gastric cancer surgery criteria weight and get the evaluation matrix through the conditions of patient “EGC 1”, the surgery, and the hospital’s medical status. Then the synthetic weight of the early gastric cancer surgery index is calculated by multiplying the criteria weight with the entropy weight of the surgery index. Finally, the ranking order of the four early gastric cancer surgical treatments and the surgical selection for patient “EGC 1” can be calculated by using the TOPSIS method for heterogeneous MCGDM proposed in Section 4.5. Furthermore, the comparison analysis and sensitivity analysis indicate the efficiency and reliability of the proposed model.

5.1. Early Gastric Cancer Surgery Criteria Weight

According to the BWM method introduced in Section 4.2, we compute the subjective weight of early gastric cancer surgery criteria. The surgery criteria listed in Table 1 are denoted by A₁ to A₅; among them, tumor characteristics $(A_1)$ is the most important criterion and medical equipment $(A_5)$ is the least important criterion, as determined by experts. The pairwise comparison vectors of the most important and least important criteria are described in Table 4 and Table 5. Table 4 shows that the preference values of the most important criterion $(A_1)$ over criterion $(A_2)$, criterion $(A_3)$, criterion $(A_4)$, and criterion $(A_5)$ are 3, 4, 6, and 8, respectively. The preference values of criteria $(A_1)$, $(A_2)$, $(A_4)$, and $(A_5)$ over the least important criterion $(A_5)$ are 8, 7, 6, and 4, respectively, which are described in Table 5. Then, the weight vector of criteria $w^{\ast }=(w_1{}^{\ast },w_2{}^{\ast },w_3{}^{\ast },w_4{}^{\ast },w_5{}^{\ast })$ is computed.

Table 4. Pairwise comparison vector of the most important criterion.

Criteria	A1	A2	A3	A4	A5
Best criterion: A1	1	3	4	6	8

Table 5. Pairwise comparison vector of the least important criterion.

Criteria	A1	A2	A3	A4	A5
Worst criterion: A5	8	7	6	4	1

From Equations (18) and (19) defined in Rezaei’s study [45], we can get w₁^* = 0.5333, w₂^* = 0.1778, w₃^* = 0.1333, w₄^* = 0.0889, w₅^* = 0.0667, and ${\xi }^{L\ast }$ = 0. Based on the proposed method, ${\xi }^{L\ast }$ indicates the consistency of the index directly without extra computation. As ${\xi }^{L\ast }$ = 0, we can arrive at complete consistency. So, the criteria weight vector is $w^{\ast }=(0.5333,0.1778,0.1333,0.0889,0.0667)$.

5.2. Evaluation Matrix

The evaluation information is determined from medical records, patient’s sentiment, and experts. The evaluation information of tumor characteristics is obtained by experts according to the condition of the particular patient “EGC 1”; the original information is shown in Table 6.

Table 6. The information of tumor characteristics of the specific patient.

Tumor Characteristics	Tumor Size	Differentiated Degree	Depth of Invasion
Condition	6.5 × 4.5 × 2 (cm)	Middle differentiation	Invading serosa

According to the evaluation method proposed in Section 4.3, the evaluation matrix decided by the early gastric cancer cases, patients, and experts is obtained, and the information is heterogeneous, including real numbers, interval numbers, linguistic labels, and probabilistic linguistic labels. First, we evaluate numerical indices involving crisp numbers and interval numbers based on the proposed evaluation approach described in Section 4.3. Then, we transform patients’ sentiment (i.e., linguistic labels) into neutrosophic numbers by using the method introduced in Section 4.3, and aggregate the neutrosophic numbers by utilizing the single-valued neutrosophic weighted averaging (SVNWA) aggregation operator described in Equation (5) with the weight vector $\psi ={(1/n,1/n,\dots ,1/n)}^T$. Finally, we get probabilistic linguistic labels from three experts according to the description in Section 4.3. Therefore, the evaluation matrix $R=(r_{ij})$ can be determined directly, as shown in Table 7 and Table 8.

Table 7. Evaluation values of surgical treatments on quantitative indices.

Indices	Alternatives
	x1	x2	x3	x4
a22	[3.28, 5.36]	[2.58, 5.7]	[25, 80]	[80, 180]
a23	0.978	0.993	0.959	0.949
a24	[20, 30]	[60, 90]	[270, 302]	[263, 314]
a25	<0.4280, 0, 0>	<0.6036, 0, 0>	<0.3207, 0, 0>	<0.2671, 0, 0>
a26	<0.5621, 0, 0>	<0.8523, 0, 0>	<0.8182, 0, 0>	<0.1597, 0, 0>
a35	0.0835	0.004	0.0122	0.0135
a36	[5.8, 8]	[2, 10]	[9.6, 12]	[8.6, 16.2]
a37	[13.12, 17.44]	[16.29, 20.06]	[25.69, 31.39]	[41.33, 47.97]
a41	<0.8112, 0, 0>	<0.6656, 0, 0>	<0.7591, 0, 0>	<0.5927, 0, 0>
a42	<0.8129, 0, 0>	<0.7995, 0, 0>	<0.7397, 0, 0>	<0.7035, 0, 0>
a43	<0.6611, 0, 0>	<0.6784, 0, 0>	<0.7706, 0, 0>	<0.7727, 0, 0>
a44	<0.6469, 0, 0>	<0.6913, 0, 0>	<0.7851, 0, 0>	<0.8134, 0, 0>
a51	<0.7851, 0, 0>	<0.8626, 0, 0>	<0.7914, 0, 0>	<0.6776, 0, 0>
a52	<0.6157, 0, 0>	<0.6873, 0, 0>	<0.7133, 0, 0>	<0.7848, 0, 0>
a53	<0.7648, 0, 0>	<0.7897, 0, 0>	<0.8127, 0, 0>	<0.7876, 0, 0>
a54	<0.7442, 0, 0>	<0.7533, 0, 0>	<0.7194, 0, 0>	<0.8072, 0, 0>

Table 8. Evaluation values of surgical treatments given by experts.

Indices	Experts	Alternatives
		x1	x2	x3	x1
a11	e1	{s2(0.5), s3(0.4)}	{s3(0.4), s4(0.3)}	{s3(0.2), s4(0.3), s5(0.5)}	{s1(0.6), s2(0.4)}
	e2	{s2(0.3), s3(0.4)}	{s3(0.4), s4(0.6)}	{s3(0.2), s4(0.3), s5(0.4)}	{s1(0.5), s2(0.3)
	e3	{s2(0.4), s3(0.5)}	{s3(0.3), s4(0.4)}	{s3(0.3), s4(0.3), s5(0.4)}	{s1(0.6), s2(0.2)
a12	e1	{s1(0.3), s2(0.4)}	{s1(0.3), s2(0.2)}	{s3(0.2), s4(0.4), s5(0.4)}	{s4(0.4), s5(0.6)}
	e2	{s1(0.3), s2(0.4), s3(0.2)}	{s1(0.3), s2(0.4)}	{s4(0.4), s5(0.5)}	{s3(0.2), s4(0.4), s5(0.4)}
	e3	{s1(0.3), s2(0.3), s3(0.2)}	{s1(0.3), s2(0.4), s3(0.1)}	{s4(0.4), s5(0.3), s6(0.2)}	{s3(0.2), s4(0.4), s5(0.3)}
a13	e1	{s1(0.3), s2(0.5) }	{s1(0.3), s2(0.7) }	{s4(0.4), s5(0.3), s6(0.3)}	{s4(0.4), s5(0.3), s6(0.2)}
	e2	{s1(0.6), s2(0.4) }	{s1(0.5), s2(0.3) }	{s4(0.4), s5(0.6) }	{s4(0.3), s5(0.4), s6(0.3)}
	e3	{s1(0.4), s2(0.2), s3(0.1)}	{s1(0.3), s2(0.6) }	{s5(0.3), s6(0.4)}	{ s5(0.5), s6(0.2)}
a21	e1	{s2(0.1), s3(0.5), s4(0.3)}	{s2(0.1), s3(0.4), s4(0.2)}	{s2(0.1), s3(0.3), s4(0.4)}	{s2(0.2), s3(0.3), s4(0.3)}
	e2	{s2(0.2), s3(0.4), s4(0.3)}	{s4(0.2), s5(0.3), s6(0.1)}	{s3(0.2), s4(0.4), s5(0.1)}	{s4(0.4), s5(0.1)}
	e3	{s4(0.3), s5(0.2)}	{s3(0.4), s4(0.2), s5(0.3)}	{s4(0.6), s5(0.3)}	{s4(0.3), s5(0.2), s6(0.2)}
a31	e1	{s0(0.3), s1(0.3), s2(0.1)}	{s0(0.3), s1(0.3), s2(0.2)}	{s1(0.3), s2(0.3), s3(0.3)}	{s1(0.2), s2(0.3), s3(0.3)}
	e2	{s2(0.1), s3(0.2), s4(0.2)}	{s2(0.2), s3(0.3), s4(0.1)}	{s2(0.1), s3(0.3), s4(0.3)}	{s3(0.3), s4(0.3), s5(0.3)}
	e3	{s0(0.4), s1(0.3)}	{s0(0.4), s1(0.2)}	{s1(0.3), s2(0.2) }	{s2(0.4), s3(0.3)}
a32	e1	{s2(0.1), s3(0.4), s4(0.4)}	{s2(0.1), s3(0.5), s4(0.1)}	{s3(0.1), s4(0.4), s5(0.4)}	{s2(0.2), s3(0.1), s4(0.3)}
	e2	{s3(0.2), s4(0.4), s5(0.3)}	{s3(0.5), s4(0.1), s5(0.3)}	{s4(0.4), s5(0.3), s6(0.2)}	{s4(0.2), s5(0.3), s6(0.3)}
	e3	{s3(0.4), s4(0.4), s5(0.2)}	{s3(0.6), s4(0.3) }	{s4(0.5), s5(0.4)}	{s5(0.4), s6(0.3)}
a33	e1	{s1(0.5), s2(0.1), s3(0.2)}	{s1(0.5), s2(0.2), s3(0.2)}	{s1(0.2), s2(0.3), s3(0.2)}	{s1(0.3), s2(0.2), s3(0.1)}
	e2	{s2(0.1), s3(0.2), s4(0.1)}	{s1(0.5), s2(0.2)}	{s2(0.4), s3(0.2)}	{s2(0.3), s3(0.2), s4(0.4)}
	e3	{s1(0.6), s2(0.2)}	{s2(0.1), s3(0.2), s4(0.2)}	{s2(0.3), s3(0.2), s4(0.2)}	{s4(0.2), s5(0.4)}
a34	e1	{s1(0.3), s2(0.3), s3(0.4)}	{s1(0.5), s2(0.2), s3(0.3)}	{s1(0.4), s2(0.3), s3(0.2)}	{s2(0.2), s3(0.2), s4(0.6)}
	e2	{s2(0.3), s3(0.2), s4(0.4)}	{s2(0.4), s3(0.2), s4(0.1)}	{s2(0.1), s3(0.3), s4(0.4)}	{s3(0.3), s4(0.2), s5(0.2)}
	e3	{s3(0.3), s4(0.3)}	{s3(0.3), s4(0.1)}	{s3(0.4), s4(0.2)}	{s3(0.2), s4(0.4)}
a38	e1	{s0(0.2), s1(0.3), s2(0.1)}	{s1(0.3), s2(0.3)}	{s1(0.2), s2(0.3), s3(0.3)}	{s1(0.2), s2(0.2), s3(0.4)}
	e2	{s2(0.1), s3(0.2), s4(0.3)}	{s0(0.2), s1(0.2), s2(0.2)}	{s2(0.4), s3(0.4)}	{s2(0.2), s3(0.4), s4(0.2}
	e3	{s1(0.4), s2(0.2)}	{s2(0.2), s3(0.2), s4(0.2}	{s3(0.3), s4(0.2), s5(0.2)}	{s2(0.3), s3(0.6)}

5.3. Weight of Gastric Cancer Surgery Index

The weights of the indices can be computed by utilizing the entropy weight method introduced in Section 4.4. Thus, the synthetic weight of the early gastric cancer surgery index can be computed by Equation (27). First, the evaluation values of surgical treatments on the attributes in $o_1$, $o_2$, and $o_3$ are normalized by using Equations (20), (22), and (24), which is shown in Table 9. With Definition 13 and Equation (8), we can calculate the normalized and aggregated PLTSs for each surgical treatment by using the probabilistic linguistic averaging (PLA) operator with the weight vector $w^k=(1/3,1/3,1/3)$ for the three experts. Then, the aggregated PLTS values can be computed and are shown in Table 10. The weights of the attributes and indices for the group according to the description in Section 4.4 are obtained as in Table 11.

Table 9. Normalized evaluation matrix.

Indices	Alternatives
	x1	x2	x3	x4
a22	[0.9702, 0.9818]	[0.9683, 0.9857]	[0.5556, 0.8611]	[0, 0.5556]
a23	0.659090909	1	0.227272727	0
a24	[0.9045, 0.9363]	[0.7134, 0.8089]	[0.0382, 0.1401]	[0, 0.1624]
a25	<0.4280, 0, 0>	<0.6036, 0, 0>	<0.3207, 0, 0>	<0.2671, 0, 0>
a26	<0.5621, 0, 0>	<0.8523, 0, 0>	<0.8182, 0, 0>	<0.1597, 0, 0>
a35	0	1	0.896855346	0.880503145
a36	[0.5062, 0.6420]	[0.3827, 0.8765]	[0.2593, 0.4074]	[0, 0.4691]
a37	[0.6364, 0.7265]	[0.5631, 0.6604]	[0.3456, 0.4645]	[0, 0.1384]
a41	<0.8112, 0, 0>	<0.6656, 0, 0>	<0.7591, 0, 0>	<0.5927, 0, 0>
a42	<0.8129, 0, 0>	<0.7995, 0, 0>	<0.7397, 0, 0>	<0.7035, 0, 0>
a43	<0.6611, 0, 0>	<0.6784, 0, 0>	<0.7706, 0, 0>	<0.7727, 0, 0>
a44	<0.6469, 0, 0>	<0.6913, 0, 0>	<0.7851, 0, 0>	<0.8134, 0, 0>
a51	<0.7851, 0, 0>	<0.8626, 0, 0>	<0.7914, 0, 0>	<0.6776, 0, 0>
a52	<0.6157, 0, 0>	<0.6873, 0, 0>	<0.7133, 0, 0>	<0.7848, 0, 0>
a53	<0.7648, 0, 0>	<0.7897, 0, 0>	<0.8127, 0, 0>	<0.7876, 0, 0>
a54	<0.7442, 0, 0>	<0.7533, 0, 0>	<0.7194, 0, 0>	<0.8072, 0, 0>

Table 10. Aggregated evaluation values of surgical treatments given by experts.

Indices	Alternatives
	x1	x2	x3	x4
a11	{s0.95, s1.57, s0}	{s1.4, s2.13, s0}	{s0.72, s1.24, s2.25}	{s0.66, s0.68, s0}
a12	{s0.38, s0.93, s0.48}	{s0.47, s0.98, s0.13}	{s1.39, s2.02, s1.11}	{s0.95, s2.13, s1.22}
a13	{s0.51, s0.88, s0.14}	{s0.42, s1.16, s0}	{s1.78, s2.64, s0.65}	{s2.18, s1.8, s1.04}
a21	{s0.84, s1.14, s0.44}	{s0.86, s0.88, s0.33}	{s0.91, s0.86, s0.38}	{s1.17, s0.53, s0.25}
a31	{s2.27, s1.83, s0.45}	{s1.92, s1.68, s0.45}	{s1.74, s1.41, s0.63}	{s1.46, s1.25, s0.44}
a32	{s0.69, s1.57, s1.48}	{s1.32, s1.31, s0.74}	{s1.44, s1.89, s1.19}	{s1.50, s1.65, s1.43}
a33	{s2.62, s1.01, s0.42}	{s2.38, s1.08, s0.49}	{s1.94, s1.18, s0.48}	{s1.49, s0.82, s0.47}
a34	{s1.44, s0.95, s0.7}	{s2.34, s0.72, s0.39}	{s1.59, s1.03, s0.55}	{s1.02, s0.84, s0.50}
a38	{s2.00, s1.60, s0.56}	{s1.93, s1.55, s0.68}	{s1.51, s1.19, s0.47}	{s1.19, s1.50, s0.67}

Table 11. The weights of the attributes for the group.

Criteria	Weights	Indices	Weights
A1	0.5333	a11	0.263315
		a12	0.319028
		a13	0.417657
A2	0.1778	a21	0.153238
		a22	0.023316
		a23	0.270952
		a24	0.06846
		a25	0.194089
		a26	0.289945
A3	0.1333	a31	0.205559
		a32	0.228812
		a33	0.172388
		a34	0.108363
		a35	0.088117
		a36	0.003831
		a37	0.007015
		a38	0.185916
A4	0.0889	a41	0.241684
		a42	0.26108
		a43	0.246315
		a44	0.250921
A5	0.0667	a51	0.257649
		a52	0.231559
		a53	0.260798
		a54	0.249994

The eventual weights of surgery indices are computed by synthesizing subjective and objective weights, which is computed by Equation (27). The result is obtained as $E_1=(E_{11},E_{12},E_{13})$ = (0.14042594, 0.17013763, 0.222736429); $E_2=(E_{21},E_{22},E_{23},E_{24},E_{25},E_{26})$ = (0.027245754, 0.004145643, 0.04817518, 0.012172229, 0.03450895, 0.051552243); $E_3=(E_{31},E_{32},E_{33},E_{34},E_{35},E_{36},E_{37},E_{38})$ = (0.027401032, 0.030500659, 0.022979288, 0.014444737, 0.011745959, 0.000510658, 0.000935086, 0.02478258); $E_4=(E_{41},E_{42},E_{43},E_{44})$ = (0.02148573, 0.023209997, 0.021897427, 0.022306846); and $E_5=(E_{51},E_{52},E_{53},E_{54})$ = (0.017185174, 0.015444987, 0.017395253, 0.016674586).

5.4. Selecting Result of Surgical Treatments

According to Equations (31) and (32), the PIS $y^{k+}$ and the NIS $y^{k-}$ for the experts $e_k(k=1,2,3)$ are determined based on the normalized evaluation information shown in Table 9 and Table 12. Based on the method proposed in Section 4.5, the relative closeness degrees of the four surgical treatments of early gastric cancer x₁, x₂, x₃, and x₄ with respect to the PIS $x^{1+}$ for expert $e_1$ are calculated, respectively, as follows:

$$\begin{array}{cc}\hfill \tau (r_j^1)& =0.5\frac{0.096404-\rho (r_j^1,r^{1+})}{0.096404-0.006106}+0.5\frac{\rho (r_j^1,r^{1-})-0.01071}{0.101371-0.01071}\hfill \\ & =0.5\frac{0.096404-\rho (r_j^1,r^{1+})}{0.090298}+0.5\frac{\rho (r_j^1,r^{1-})-0.01071}{0.090661}\hfill \end{array}.$$

(50)

Table 12. The normalized evaluation values of surgical treatments given by experts.

Indices	Experts	Alternatives
		x1	x2	x3	x4
a11	e1	{s2(0.56), s3(0.44), s2(0)}	{s3(0.57), s4(0.43), s3(0)}	{s3(0.2), s4(0.3), s5(0.5)}	{s1(0.6), s2(0.4), s1(0)}
	e2	{s2(0.43), s3(0.57), s2(0)}	{s3(0.4), s4(0.6), s3(0)}	{s3(0.22), s4(0.33), s5(0.45)}	{s1(0.63), s2(0.37), s1(0)}
	e3	{s2(0.44), s3(0.56), s2(0)}	{s3(0.43), s4(0.57), s3(0)}	{s3(0.3), s4(0.3), s5(0.4)}	{s1(0.75), s2(0.25), s1(0)}
a12	e1	{s1(0.43), s2(0.57), s1(0)}	{s1(0.6), s2(0.4), s1(0)}	{s3(0.2), s4(0.4), s5(0.4)}	{s4(0.4), s5(0.6), s4(0)}
	e2	{s1(0.33), s2(0.45), s3(0.22)}	{s1(0.43), s2(0.57), s1(0)}	{s4(0.44), s5(0.56), s4(0)}	{s3(0.2), s4(0.4), s5(0.4)}
	e3	{s1(0.37), s2(0.37), s3(0.26)}	{s1(0.37), s2(0.5), s3(0.13)}	{s4(0.45), s5(0.33), s6(0.22)}	{s3(0.22), s4(0.45), s5(0.33)}
a13	e1	{s1(0.37), s2(0.63), s1(0)}	{s1(0.3), s2(0.7), s1(0)}	{s4(0.4), s5(0.3), s6(0.3)}	{s4(0.45), s5(0.33), s6(0.22)}
	e2	{s1(0.6), s2(0.4), s1(0)}	{s1(0.63), s2(0.37), s1(0)}	{s4(0.4), s5(0.6), s4(0)}	{s4(0.3), s5(0.4), s6(0.3)}
	e3	{s1(0.57), s2(0.29), s3(0.14)}	{s1(0.33), s2(0.67), s1(0)}	{s5(0.43), s6(0.57), s5(0)}	{s5(0.71), s6(0.29), s5(0)}
a21	e1	{s4(0.11), s3(0.56), s2(0.33)}	{s4(0.14), s3(0.57), s2(0.29)}	{s4(0.13), s3(0.37), s2(0.5)}	{s4(0.26), s3(0.37), s2(0.37)}
	e2	{s4(0.22), s3(0.45), s2(0.33)}	{s2(0.33), s1(0.5), s0(0.17)}	{s3(0.29), s2(0.57), s1(0.14)}	{s2(0.8), s1(0.2), s1(0)}
	e3	{s2(0.6), s1(0.4), s1(0)}	{s3(0.45), s2(0.22), s1(0.33)}	{s2(0.67), s1(0.33), s1(0)}	{s2(0.43), s1(0.28), s0(0.29)}
a31	e1	{s6(0.43), s5(0.43), s4(0.14)}	{s6(0.37), s5(0.38), s4(0.25)}	{s5(0.33), s4(0.33), s3(0.34)}	{s5(0.22), s4(0.45), s3(0.33)}
	e2	{s4(0.2), s3(0.4), s2(0.4)}	{s4(0.33), s3(0.5), s2(0.17)}	{s4(0.14), s3(0.43), s2(0.43)}	{s3(0.33), s2(0.33), s1(0.34)}
	e3	{s6(0.57), s5(0.43), s5(0)}	{s6(0.67), s5(0.33), s5(0)}	{s5(0.6), s4(0.4), s4(0)}	{s4(0.57), s3(0.43), s3(0)}
a32	e1	{s2(0.11), s3(0.44), s4(0.45)}	{s2(0.14), s3(0.72), s4(0.14)}	{s3(0.11), s4(0.44), s5(0.45)}	{s2(0.33), s3(0.17), s4(0.5)}
	e2	{s3(0.22), s4(0.45), s5(0.33)}	{s3(0.56), s4(0.11), s5(0.33)}	{s4(0.45), s5(0.33), s6(0.22)}	{s4(0.25), s5(0.37), s6(0.38)}
	e3	{s3(0.4), s4(0.4), s5(0.2)}	{s3(0.67), s4(0.33), s3(0)}	{s4(0.55), s5(0.45), s4(0)}	{s5(0.57), s6(0.43), s5(0)}
a33	e1	{s5(0.62), s4(0.13), s3(0.25)}	{s5(0.56), s4(0.22), s3(0.22)}	{s5(0.29), s4(0.42), s3(0.29)}	{s5(0.5), s4(0.33), s3(0.17)}
	e2	{s4(0.25), s3(0.5), s2(0.25)}	{s5(0.71), s4(0.29), s4(0)}	{s4(0.67), s3(0.33), s3(0)}	{s4(0.33), s3(0.22), s2(0.45)}
	e3	{s5(0.75), s4(0.25), s4(0)}	{s4(0.2), s3(0.4), s2(0.4)}	{s4(0.42), s3(0.29), s2(0.29)}	{s2(0.33), s1(0.47), s1(0)}
a34	e1	{s5(0.3), s4(0.3), s3(0.4)}	{s5(0.5), s4(0.2), s3(0.3)}	{s5(0.45), s4(0.33), s3(0.22)}	{s4(0.2), s3(0.2), 2(0.6)}
	e2	{s4(0.33), s3(0.22), s2(0.45)}	{s4(0.57), s3(0.29), s2(0.14)}	{s4(0.13), s3(0.37), s2(0.5)}	{s3(0.42), s2(0.29), s1(0.29)}
	e3	{s3(0.5), s2(0.5), s2(0)}	{s3(0.75), s2(0.25), s2(0)}	{s3(0.67), s2(0.33), s2(0)}	{s3(0.33), s2(0.67), s2(0)}
a38	e1	{s6(0.33), s5(0.5), s4(0.17)}	{s5(0.5), s4(0.5), s4(0)}	{s5(0.25), s4(0.37), s3(0.38)}	{s5(0.25), s4(0.25), s3(0.5)}
	e2	{s4(0.17), s3(0.33), s2(0.5)}	{s6(0.33), s5(0.33), s4(0.34)}	{s4(0.5), s3(0.5), s3(0)}	{s4(0.25), s3(0.5), s2(0.25)}
	e3	{s5(0.67), s4(0.33), s4(0)}	{s4(0.33), s3(0.33), s2(0.34)}	{s3(0.43), s2(0.29), s1(0.28)}	{s4(0.33), s3(0.67), s3(0)}

In the same way, the relative closeness degrees of the four early gastric cancer surgical treatments x₁, x₂, x₃, and x₄ with respect to the PIS $x^{k+}(k=2,3)$ for expert $e_k(k=1,2,3)$ are calculated, respectively, as follows:

$$\begin{array}{cc}\hfill \tau (r_j^2)& =0.5\frac{0.097933-\rho (r_j^2,r^{2+})}{0.097933-0.009094}+0.5\frac{\rho (r_j^2,r^{2-})-0.013081}{0.102886-0.013081}\hfill \\ & =0.5\frac{0.097933-\rho (r_j^2,r^{2+})}{0.088839}+0.5\frac{\rho (r_j^2,r^{2-})-0.013081}{0.089805}\hfill \end{array}$$

(51)

and

$$\begin{array}{cc}\hfill \tau (r_j^3)& =0.5\frac{0.105214-\rho (r_j^3,r^{3+})}{0.105214-0.00299}+0.5\frac{\rho (r_j^3,r^{3-})-0.013086}{0.17376-0.013086}\hfill \\ & =0.5\frac{0.105214-\rho (r_j^3,r^{3+})}{0.102224}+0.5\frac{\rho (r_j^3,r^{3-})-0.013086}{0.160674}\hfill \end{array}.$$

(52)

The relative closeness degrees matrix of surgical treatments $x_j$ $(j=1,2,\dots ,n)$ with respect to PISs $x^{k+}(k=1,2,3)$ for all experts $e_k$ using Equations (50)–(52) is obtained as follows:

$$\begin{array}{ccc}& & \begin{array}{cccc}{x}_1& x_2& x_3& x_4\end{array}\\ \tau ={({\tau }_j^k)}_{3\times 4}& =\begin{array}{c}{e}_1\\ e_2\\ e_3\end{array}& \left(\begin{array}{cccc}0& 0.085& 1& 0.793\\ 0& 0.060& 1& 0.795\\ 0& 0.057& 1& 0.526\end{array}\right).\end{array}$$

(53)

The PIS $x^{+}$ and the NIS $x^{-}$ for the group can be computed by utilizing Equations (47) and (48), respectively. According to Equation (49), the relative closeness degrees of the surgical treatments $x_j(j=1,2,3,4)$ with respect to $x^{+}$ for the group can be determined as follows:

$${\tau }^G(x_1)=0,{\tau }^G(x_2)=0.067281,{\tau }^G(x_3)=1,{\tau }^G(x_4)=0.70482.$$

It is clearly seen that ${\tau }^G(x_1)<{\tau }^G(x_2)<{\tau }^G(x_4)<{\tau }^G(x_3)$. Hence, the following ranking order of the four early gastric cancer surgical treatments for the group can be concluded: $x_3\succ x_4\succ x_2\succ x_1$. Therefore, the most appropriate surgical treatment is laparoscopic surgery for “EGC 1”.

5.5. Sensitivity Analysis

In order to analyze the influence of different values of compromise coefficient $\epsilon$ on the ranking results, we employ different values of $\epsilon$ and assess the obtained ranking of the surgical treatments. The specific results are shown in Table 13. Figure 2 depicts the influence on the proposed selection model with different values of $\epsilon$ based on Table 13.

Table 13. Ranking orders of surgical treatments with different $\epsilon$.

Different Values of $\mathit{\epsilon }$	The Ranking of Surgical Treatments				Ranking Orders
	x1	x2	x3	x4
$\epsilon =0$	0	0.067280513	1	0.704819514	$x_1\prec x_2\prec x_4\prec x_3$
$\epsilon =0.3$	0	0.067280513	1	0.704819514	$x_1\prec x_2\prec x_4\prec x_3$
$\epsilon =0.5$	0	0.067280513	1	0.704819514	$x_1\prec x_2\prec x_4\prec x_3$
$\epsilon =0.7$	0	0.067280513	1	0.704819514	$x_1\prec x_2\prec x_4\prec x_3$
$\epsilon =1$	0	0.067280513	1	0.704819514	$x_1\prec x_2\prec x_4\prec x_3$

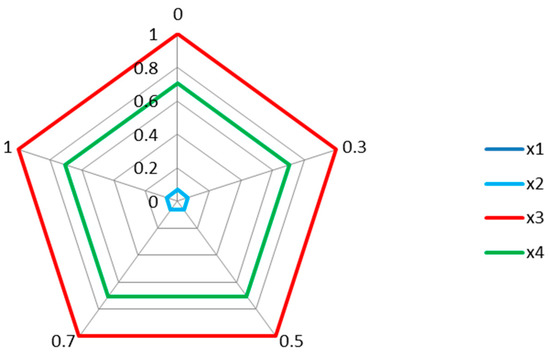
Figure 2. The radar plot displaying the result of the sensitivity analysis.

According to Table 13 and Figure 2, it is obvious that the ranking orders computed by different values of $\epsilon$ from 0 to 1 are the same as in the above experimental example. This means that the ranking results are not sensitive to the values of parameter $\epsilon$. That is to say, despite the selection process involving various values of the compromise coefficient $\epsilon$, the final ranking results are consistent.

Furthermore, it is important to point out that the above sensitivity analysis is based on the values of equilibrium coefficient $\lambda$. Therefore, we carried on the sensitivity analysis of the entropy weight of the interval-valued indices with parameter $\lambda$. The interval-valued indices include blood loss, operating time, number of harvested lymph nodes, hospital stays, and recovery time. We assume $\epsilon =0.5$, and the sensitivity analysis is carried out through modifying the weighting parameter $\lambda$ for interval-valued indices and recalculating the ranking results of surgical treatments for different values of $\lambda$. As depicted in Table 14 and Figure 3, the ranking orders of surgical treatments according to different values of $\lambda$ are slightly different. This may lead to different decisions for different patients, but the most appropriate surgical treatment for this patient is also $x_3$.

Table 14. Ranking orders of surgical treatments with different $\lambda$.

Different Values of $\mathit{\lambda }$	The Ranking of Surgical Treatments				Ranking Orders
	x1	x2	x3	x4
$\lambda =0.2$	0	0.069246088	1	0.703826118	$x_1\prec x_2\prec x_4\prec x_3$
$\lambda =0.4$	0.131619756	0	1	0.804240841	$x_2\prec x_1\prec x_4\prec x_3$
$\lambda =0.5$	0	0.067280513	1	0.704819514	$x_1\prec x_2\prec x_4\prec x_3$
$\lambda =0.6$	0	0.531275419	1	0.213842101	$x_1\prec x_4\prec x_2\prec x_3$
$\lambda =0.8$	0	0.510492538	1	0.219962121	$x_1\prec x_4\prec x_2\prec x_3$

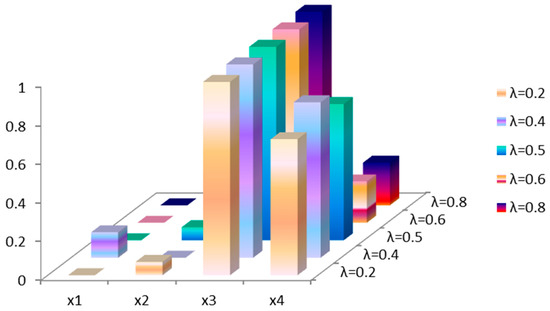
Figure 3. The result of the sensitivity analysis with different $\lambda$.

From Table 13 and Table 14, the final selection result depends on two factors: compromise coefficient $\epsilon$ and equilibrium coefficient $\lambda$. As seen in the visualized results shown in Figure 2 and Figure 3, the final selection result of the sensitivity analysis is consistent with the result in our experimental example. So, in other words, although the decision-makers consider different values of compromise coefficient $\epsilon$ and equilibrium coefficient $\lambda$, they all select $x_3$ as the most appropriate surgical treatment. The two sensitivity analysis results suggest that the ranking results of the proposed model are insensitive to the values of $\epsilon$ and $\lambda$ in this example. Thus, to an extent, the robustness of the proposed model is verified.

5.6. Comparison Analysis

As described in Section 4, the proposed model can be employed to select the surgical treatment for early gastric cancer for a specific patient considering the patient’s conditions, surgical conditions, hospital conditions, and heterogeneous information. In order to verify that the proposed model can be effectively and practically used to distinguish which surgery is most appropriate for specific patients with early gastric cancer, we use the above empirical study to analyze some comparable methods, including heterogeneous TODIM [54] and heterogeneous VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje) [55]. Table 15 shows the ranking orders of the four surgical treatments for the early gastric cancer patient as obtained using these methods. From Table 15, the ranking results computed by the proposed hybrid model are the same as those calculated by the heterogeneous TODIM and heterogeneous VIKOR methods. The validity of the proposed model is thus demonstrated. Compared with the extant approaches for the selection of surgical treatment for early gastric cancer patients, the advantages of the proposed model in this study can be summarized as the following:

Table 15. Ranking comparison.

Alternatives	Heterogeneous TODIM		Heterogeneous VIKOR
	${\epsilon }_i$	Ranking	$S_i$	$R_i$	$Q_i$	Ranking
$x_1$	0.131573	3	0.702564564	0.222736429	1	4
$x_2$	0.324262	2	0.62637026	0.216910241	0.901839	3
$x_3$	1	1	0.240544451	0.037226276	0	1
$x_4$	0	4	0.516377929	0.138206602	0.570677	2

(1)

The proposed model considers both subjective and objective criteria comprehensively in the index system for early gastric cancer, which combines fuzzy theory with quantitative data analysis. This enables the surgical treatment selection to be solved more realistically.

(2)

The evaluation information is evaluated from medical records, patient’s sentiment, and experts based on the patient’s conditions, the surgery, and the hospital’s medical status, etc., including crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic term sets; this makes the surgical treatment selection more accurate and reliable.

(3)

With the proposed model, the prioritization of alternative surgical treatment methods is determined by using TOPSIS, which is more flexible and simple in solving MGCDM problem [18]. Thus, the proposed selection model of surgical treatments for early gastric cancer patients can provide the most appropriate surgical treatment reliably.

6. Conclusions and Future Research

A selection model of surgical treatments for early gastric cancer patients has been developed in this paper, which is helpful to solving the problem of surgical treatment selection in the case of asymmetric information between doctors and patients. Subjective and objective criteria have been employed simultaneously in the early gastric cancer surgery index system combining fuzzy theory with quantitative data analysis. Moreover, heterogeneous information obtained from early gastric cancer cases, the patient’s emotional evaluation, and the experts’ estimation, such as crisp numbers, interval numbers, neutrosophic numbers, and probabilistic linguistic labels, has been utilized to decrease the information loss. In addition, TOPSIS based on heterogeneous MCGDM has been used to obtain the prioritization of early gastric cancer surgical treatments.

The proposed model has been applied to an empirical study in XiangYa for surgical treatment selection. The study illustrates the process of the model in detail. Furthermore, sensitivity analysis has been carried out and the results verify the robustness of the proposed model. In addition, the comparison results of two comparable methods by using the empirical study indicate the validity and reliability of the proposed model.

In conclusion, this paper not only contributes to the development of theory, but also contributes to practical application. First, this paper utilizes probabilistic linguistic term sets that enrich information types for heterogeneous multicriteria group decision-making. Second, the proposed model improves existing methods in the field of treatment decision-making. Third, the proposed model can be applied to provide rational support to doctors or patients in the process of surgical treatment decision-making. There are several implications for possible directions of further research. First, more information types of surgical treatment selection could be considered in the proposed model in order to adapt to the ever-changing environment in future study. Second, the presented model explores the ranking order of early gastric cancer surgical treatments by the TOPSIS method. Hence, the model can be studied by investigating MULTIMOORA (multi–objective optimization by ratio analysis plus the full multiplicative form) theory because of its simple computation to select surgical treatments for particular patients. Finally, the proposed model can be adapted for surgical treatment selection for some other diseases in future study.