1. Introduction
Mirror symmetry (hereafter ‘symmetry’) occurs when one half of the stimulus reflects the other about an axis, and it is found in both biological and man-made structures. Symmetry is a highly salient visual feature for the human visual system and plays an important role in perceptual organization, such as figure-ground segregation [
1,
2,
3,
4], object recognition [
5,
6,
7], amodal completion [
8,
9], and visual search [
10]. Brain imaging (fMRI) studies have shown that symmetry involves a wide-spread network of extra-striate visual areas, such as V3a, V4, V7 and the lateral occipital complex (LOC) [
11]. Although several recent studies have examined the contribution of visual features such as luminance polarity and colour [
12,
13,
14], stereoscopic depth [
15,
16,
17], and motion-direction [
18] to symmetry perception, little is known about how spatiotemporal characteristics of dynamic patterns affect symmetry perception. Recent studies have shown that symmetry mechanisms can integrate spatial correlations across the symmetry midline within a ~120 ms time window [
19] and that limiting the lifetime of pattern elements improves symmetry detection thresholds [
18]. Hence, here we investigate how temporal dynamics of spatial relocation and luminance contrast of pattern elements affect symmetry perception in dynamic patterns.
It is evident that any dynamic visual stimulus can be described by its temporal, as well as spatial, properties. It is important to consider dynamic stimuli because under natural viewing conditions observers must contend with continuously changing percepts. In natural scenes, objects are often partly occluded and the visible regions or parts of objects may change over time as they move through the environment. One such example is an object or animal moving behind foliage. In order to perceive that object, the visual system must integrate fragmented shape information (i.e., parts of objects/ texture elements) over time to create an accurate representation of the whole object. This is to say that the perception of such a target requires a spatiotemporal integration process. Dynamic element changes over time and space are sufficient to define boundaries and surfaces [
20,
21], occluded objects [
22], and illusory shapes [
23,
24]. That is, elements revealed at different times and locations can be assembled into unitary perceived objects [
22,
23]. The temporal integration of spatial information appears to be constrained to a temporal integration window between 80 ms [
24] and 165 ms [
21], which is in keeping with findings showing that temporal integration of symmetry occurs within ~120 ms [
19].
Several studies have shown improved performance with dynamic, compared to static, stimuli. Glass patterns have regularities which have been linked to symmetry [
25]. Improvements in Glass pattern detection thresholds have been found for dynamic compared to static patterns [
26,
27,
28]. These lower thresholds were initially attributed to the apparent motion created by presenting unique glass patterns in quick succession (i.e., temporally uncorrelated patterns) [
28]. However, more recent evidence suggests that glass patterns are subject to a temporal summation process [
27]. Improvements in performance with dynamic stimuli made of unique textural patterns (i.e., temporally uncorrelated patterns) and those in which the same textural patterns are used repeatedly (i.e., temporally correlated patterns) have also been found in stereopsis [
29] and motion in depth perception [
30].
A number of studies have compared symmetry perception with static and dynamic stimuli. Using dynamic dot-patterns refreshed at 65 Hz, Tyler et al. [
31,
32] have investigated the effect of eccentricity on symmetry perception and found that static stimuli produced superior performance compared to dynamic stimuli, with static symmetry being perceived more quickly and further into the periphery. This is in contrast to more recent studies showing better performance with dynamic than static patterns [
18,
33]. Studies have shown that using dynamic stimuli consisting of rapid successive presentations of different symmetrical patterns improves symmetry detection [
18] and orientation discrimination of the symmetry axis [
33]. It has been suggested that these improvements in performance are due to multiple weak or noisy neural responses to symmetry being integrated over time to generate a stronger response. Using dynamic patterns consisting of on-going alternation of symmetric patterns Sharman et al. [
19] found that the time window for symmetry integration is about 120 ms. On the other hand, Niimi et al. [
33] varied the stimulus onset asynchrony (SOA) between symmetric stimulus halves and reported a temporal integration window of at least 213.3 ms. Another study measured temporal thresholds for identifying the orientation of the symmetry axis in symmetric textures and found that temporal thresholds varied between 28 to 568 ms as a function of stimulus salience [
34]. All together, these studies suggest that the temporal integration window for symmetry might vary with the element lifetime duration and/or temporal frequency of dynamic stimulus presentation. Some indirect evidence for this comes from Sharman and Gheorghiu [
18] study showing that symmetry detection thresholds were lower when elements lifetime durations were shorter. Therefore, here we will examine how symmetry detection thresholds are affected by element lifetime duration.
In dynamic symmetric stimuli made of different textural patterns (i.e., temporally uncorrelated patterns) symmetrical pairs will be relocated to multiple, random, successive locations without any coherent local or global motion. Hence, a temporal cumulative process could combine the weak symmetry signals from these patterns over time, resulting in a stronger signal. If temporal integration of symmetry occurs within a fixed time period, then reducing the number of element locations (i.e., by using temporally correlated patterns) would reduce the overall strength of the symmetry signal within the integration window, thus resulting in increased symmetry detection thresholds. On the other hand, changing the elements to different locations (i.e., by using temporally uncorrelated patterns) will increase the overall symmetry strength/energy, resulting in improved performance (lower thresholds). To test this hypothesis and examine how spatial relocation of elements affects symmetry detection, we will compare thresholds obtained with dynamic stimuli in which: (a) the symmetric pairs change their positions to successive, random locations over time (i.e., multiple locations condition); (b) the symmetric pairs change position back and forth between the same two locations (i.e., two locations condition), and (c) symmetric pairs are not relocated, but their contrast is modulated over time (i.e., one location condition). We predict that symmetry detection thresholds will be lower in the multiple locations condition compared to the two locations and one location conditions.
One possible factor that might affect symmetry perception in the dynamic stimuli (i.e., multiple locations, two locations and one location) is perceived dot-density. For these dynamic stimuli, the number of different spatial locations stimulated over time will vary, with the multiple locations condition having the highest perceived density, followed by the two locations and one location (contrast modulated) conditions, which will have the lowest perceived density. If perceived density contributes to symmetry perception, then any improvement obtained with the multiple locations stimuli may not be due to the temporal properties of the stimulus. To test for this, we will compare thresholds obtained using static patterns with a range of dot densities. If perceived density mediates the differences in symmetry detection thresholds between the three dynamic stimulus conditions, then we expect symmetry detection thresholds to be lower for higher density patterns.
The one location (contrast modulated) condition differs in several ways from the multiple- and two-location conditions, but it is the closest to resembling a dynamic pattern without involving elements’ spatial relocation. Therefore, we must test whether any improvement in symmetry detection thresholds for the one location (contrast modulated) condition has the same underlying cause as that obtained in the multiple locations condition. In the one location condition, different symmetric pairs have different contrasts over time, with some symmetric pairs being of higher contrasts, others of intermediate and others of lower perceived contrast. Therefore, it is possible that symmetric pairs may also be grouped by their similar perceived contrasts and this may improve performance. To test whether perceived contrasts of elements affect symmetry detection thresholds we will use static symmetric patterns containing different contrast levels. If contrast is being used as a grouping factor we would expect symmetry detection thresholds to decrease with the number of contrast levels in the stimuli.
In sum, we will investigate how the temporal pattern of spatial relocations, luminance contrast modulation and lifetime duration of elements affect symmetry perception in order to elucidate whether different mechanisms are involved in symmetry perception various types of dynamic stimuli. This will also allow us to determine whether temporal integration of symmetry information occurs within a fixed or variable time window.
2. Materials and Methods
2.1. Participants
Six observers participated in the main experiment, the two authors and four observers who were naïve with regard to the experimental aims, and five observers (including the authors) participated in the two control experiments (i.e., density and number of contrast levels). All observers had normal or corrected-to-normal vision. Observers gave their written consent prior to participating in the study and were treated in accordance with the Declaration of Helsinki (2008, Version 6). All procedures were approved by the Psychology Ethics Committee, University of Stirling, UK.
2.2. Stimuli
Stimuli were presented on a gamma-corrected 20-in ViewSonic Professional Series PF817 cathode ray tube (CRT) monitor (ViewSonic, Brea, CA, USA) with spatial resolution 1024 × 768 and refresh rate of 85 Hz. All stimuli were presented in the centre of the monitor on a mid-grey background with average luminance of 47.2 cd/m
2. Viewing distance was 52 cm. All stimuli were generated and all data were collected using PsychoPy [
35]. Stimuli were presented in a square window of 13.77° in width, which was chosen because symmetry is easily perceived in the region close to the symmetry axis and hardly perceived at large eccentricities, in the periphery [
36]. Stimuli were comprised of 40 circular white dots (full contrast) of 0.26° diameter resulting in a dot density of 0.21 dots/degree
2. Element size and numerosity do not affect symmetry perception, however, density is inversely related to the spatial integration region for symmetry (i.e., the area over which symmetry can be processed) [
37], hence, we have chosen low dot density patterns. Symmetrical dots were randomly positioned on the left side of the square area and then mirrored about the vertical axis onto the right side. Noise dots were randomly positioned with equal numbers appearing in each stimulus half.
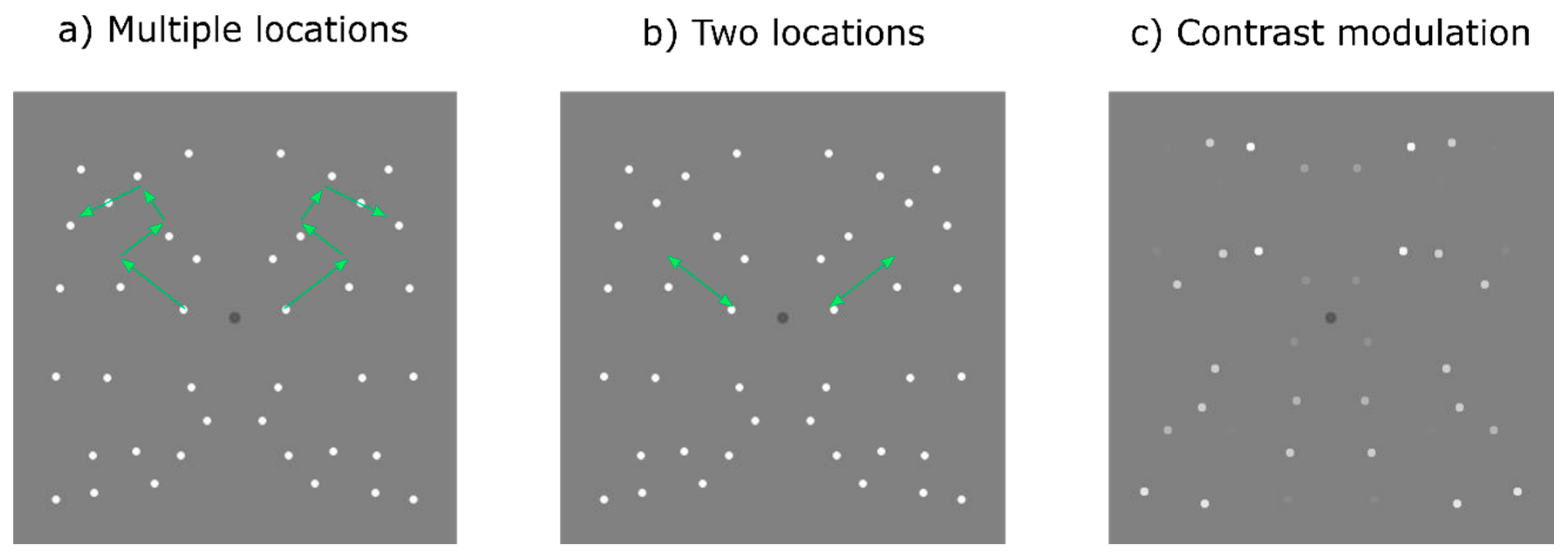
There were three dynamic stimulus conditions: (i) ‘multiple locations’ condition, in which pattern elements were relocated at different times to new random locations after a set duration; (ii) ‘two locations’ condition, in which pattern elements alternated back and forth between the same two positions; (iii) ‘one location’ condition in which the elements of a static pattern were contrast modulated over time. These dynamic stimulus conditions were compared with a ‘static’ control condition in which a single pattern was presented at full contrast for the whole stimulus duration. All dots in each pattern were positioned a minimum of 1.16° apart, except for those in the two locations condition which were 1.00°. In the two locations conditions the dots needed to be closer together because it was in effect one pattern with twice the number of dots, only half of which were visible at any point in time, thus there were fewer possible locations necessitating the dots being closer together.
For both the multiple and two locations conditions we varied elements lifetime durations. There were nine different lifetime durations: 58.8, 117.7, 176.5, 188.2, 200.0, 211.8, 223.5, 235.3, and 294.1 ms (i.e., 5, 10, 15, 16, 17, 18, 19, 20 and 25 frames at the 85 Hz refresh rate) corresponding to 17, 8.5, 5.7, 5.3, 5.0, 4.7, 4.5, 4.2 and 3.4 Hz temporal frequency. Starting ‘ages’ were randomly allocated so that different dot-pairs reached their maximum lifetime and ‘died’ at different times. In the multiple locations conditions after the maximum lifetime duration was reached the dot-pair ‘died’ and was relocated to a new random location (see
Figure 1a and
Movie S1a). Each pair of symmetrical dots was relocated simultaneously in order to maintain the same level of symmetry throughout stimulus presentation. For the two-locations condition, dots changed their position back and forth between two locations instead of being randomly relocated to a new location each time (
Figure 1b and
Movie S1b). For the one location (contrast modulated) condition, we used static pattern (i.e., dots were not relocated and remained in the same position, but their contrast was modulated by a Gaussian temporal envelope, giving the appearance of the dots fading on and off (
Figure 1c and
Movie S1c)). We varied the width of the Gaussian temporal envelope and used the same values as those employed for the lifetime durations in the multiple and two location conditions in order to allow for a direct comparison between all conditions.
We also conducted two control experiments using static patterns, in order to examine the effects of perceived dot-density and grouping by contrast on symmetry detection thresholds. In the dot-density experiment, we used static patterns with three dot densities: 20, 40, and 60 dots corresponding to 0.11, 0.21, and 0.32 dots/degree
2, respectively (
Figure 2a). These densities were chosen in order to encompass the range of perceived densities of the dynamic patterns (i.e., lower, the same and higher in density than the dot patterns used in the main experiment). For the multiple contrast-levels experiment, stimuli were again static patterns, but the different symmetric dot pairs had different contrast levels. We used static patterns containing one contrast level (i.e., all dots either 0.2 or 0.9,
Figure 2b,c), two contrast levels (i.e., half the dots were of 0.2 and half of 0.9 contrast,
Figure 2d), four levels (i.e., 25% of the dots were 0.2, 0.433, 0.666, and 0.9 contrast,
Figure 2e), five levels (i.e., 20% of the dots were 0.2, 0.375, 0.55, 0.725, 0.9 contrast,
Figure 2f) and ten levels (i.e., 10% of the dots were 0.2, 0.277, 0.355, 0.511, 0.589, 0.666, 0.744, 0.822, 0.9 contrast,
Figure 2g). These values were chosen as they allowed for equal numbers of matched-pairs at each contrast level. For comparison, we also used patterns in which all dots had the same contrast, either low (0.2) or high (0.9) contrast.
2.3. Procedure
A two-interval forced choice (2IFC) procedure was employed to measure symmetry detection thresholds. In each trial, a ‘with-symmetry’ target stimulus containing variable amounts of symmetry (between 0 and 100%) was presented in one of the two intervals, while the other interval (i.e., the foil or null interval) contained a stimulus consisting of randomly positioned (noise) dots. Each stimulus (i.e., foil and target) was presented for 400 ms with an inter-stimulus interval (ISI) of 400 ms. The presentation order of the foil and target was randomized from trial to trial. The participants were instructed to indicate, by a key press, which interval contained the symmetric stimulus.
In each trial, we varied the number of position symmetric dots and measured the minimum number of dots required for the participant to perceive the pattern as symmetrical (i.e., the symmetry detection threshold). Thresholds were measured using a one-up, three-down staircase procedure. The staircases controlled the number of position symmetric dots in the target stimulus. In each run, two staircases were interleaved: one starting with the target having 100% symmetrical dots and the other starting with 0% symmetric dots. The staircases were designed to converge at the 79.37% threshold and were terminated after 75 trials. Participants were allowed as many practice runs as required to become familiar with the task. Each participant collected a minimum of ten staircases for each condition (750 trials for each element lifetime and each dynamic stimulus condition). Given the static condition and the three dynamic stimulus (i.e., multiple, two and one location) × nine element lifetime duration (or temporal frequency) combinations, this resulted in 21,000 trials for each participant. Within a single session participants were only presented with one stimulus conditions (i.e., multiple locations, two locations or one location) and within that session the temporal frequency conditions were pseudo-randomised. The presentation order of the different stimulus conditions was also randomized across sessions and across participants.
For each participant and each experimental condition, correct responses were averaged for each amount of stimulus symmetry and a logistic function was fit to these data. Thresholds were then derived from these fits as the point at which the observer performed at 80% probability of responding correctly. These symmetry detection thresholds constitute our dependent variable and were measured for each combination of element lifetime (58.8, 117.7, 176.5, 188.2, 200.0, 211.8, 223.5, 235.3, and 294.1 ms) and dynamic stimulus (multiple locations, two locations, and one contrast modulated location) conditions.
3. Results
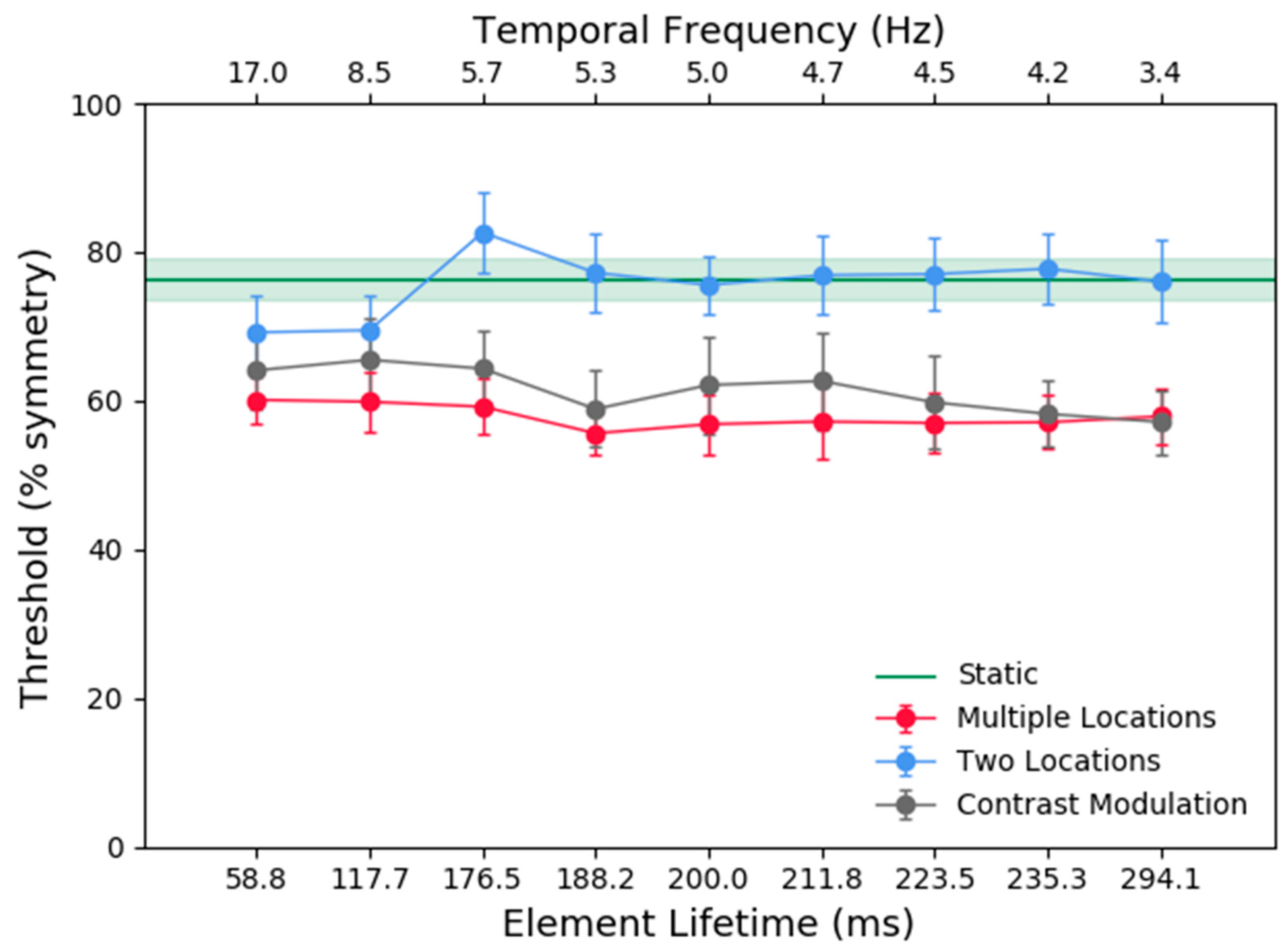
Figure 3 shows the average across participants for the symmetry detection thresholds (% symmetrical dots) in the multiple locations (red), two locations (blue), one location (black), and static (green) conditions as a function of element lifetime duration. The results show that (a) the thresholds for the multiple locations and one location (contrast modulated) conditions were comparable, irrespective of element lifetime durations (compare black and red symbols) and overall, significantly lower than those for the two locations and static conditions; (b) symmetry detection thresholds for the two locations condition were similar to the static conditions for all lifetime durations, except for very short lifetimes (<118 ms) where performance approached that for the contrast modulated condition.
A repeated-measures two-way analysis of variance (ANOVA) with factors, stimulus condition (multiple locations, two locations, one location) and element lifetime (58.8, 117.7, 176.5, 188.2, 200.0, 211.8, 223.5, 235.3, and 294.1) was conducted on the threshold data. The analysis showed a significant effect of stimulus condition (F(2, 10) = 39.413, p = 0.001, ƞ2 = 0.887). Bonferroni corrected post-hoc analysis showed that the mean symmetry detection threshold across element lifetimes for the two locations condition was higher than that for the multiple locations (p = 0.004) and one location (contrast modulated) (p ≤ 0.001) conditions, but there was no significant difference between the mean thresholds for the multiple locations and one contrast modulated location (p = 0.386) conditions. There was no significant effect of lifetime duration (F(8, 40) = 2.180, p = 0.05, ƞ2 = 0.304). However, there was a significant interaction effect between stimulus condition and lifetime duration (F(16, 80) = 2.310, p = 0.008, ƞ2 = 0.316). To further examine the interaction effect, one-way ANOVAs were performed for each stimulus condition to compare the different lifetime durations (or temporal frequency in the one location condition). For the multiple location and one location conditions, there was no effect of lifetime duration/temporal frequency (F(8, 40) = 0.523, p = 0.832, ƞ2 = 0.095 and F(8, 40) = 1.922, p = 0.083, ƞ2 = 0.278 respectively). However, the two location conditions did show an effect of lifetime duration (F(8, 40) = 5.806, p = 0.001, ƞ2 = 0.537). Bonferroni corrected post-hoc analysis showed significant differences between the 176.5ms condition and the 58.8ms condition (p = 0.021), and the 117.7 ms condition (p = 0.031). Therefore, the slightly lower thresholds in the 58.8 and 117.7 ms conditions compared lifetime durations longer than 176.5 ms seem to be driving the interaction effect.
For each stimulus condition (i.e., multiple locations, two locations, and one location) one-way ANOVAs were conducted to compare the different lifetime durations to the static condition. Thresholds in the multiple locations and one location conditions were significantly lower than those obtained with the static patterns (F(9, 45) = 6.523, p = 0.006, ƞ2 = 0.566 for the multiple locations conditions; F(9, 45) = 3.549, p = 0.0450, ƞ2 = 0.415 for the one location conditions). Thresholds in the two locations conditions were not significantly different from the static condition (p > 0.05).
3.1. Control Experiment 1: Effect of Dot Density
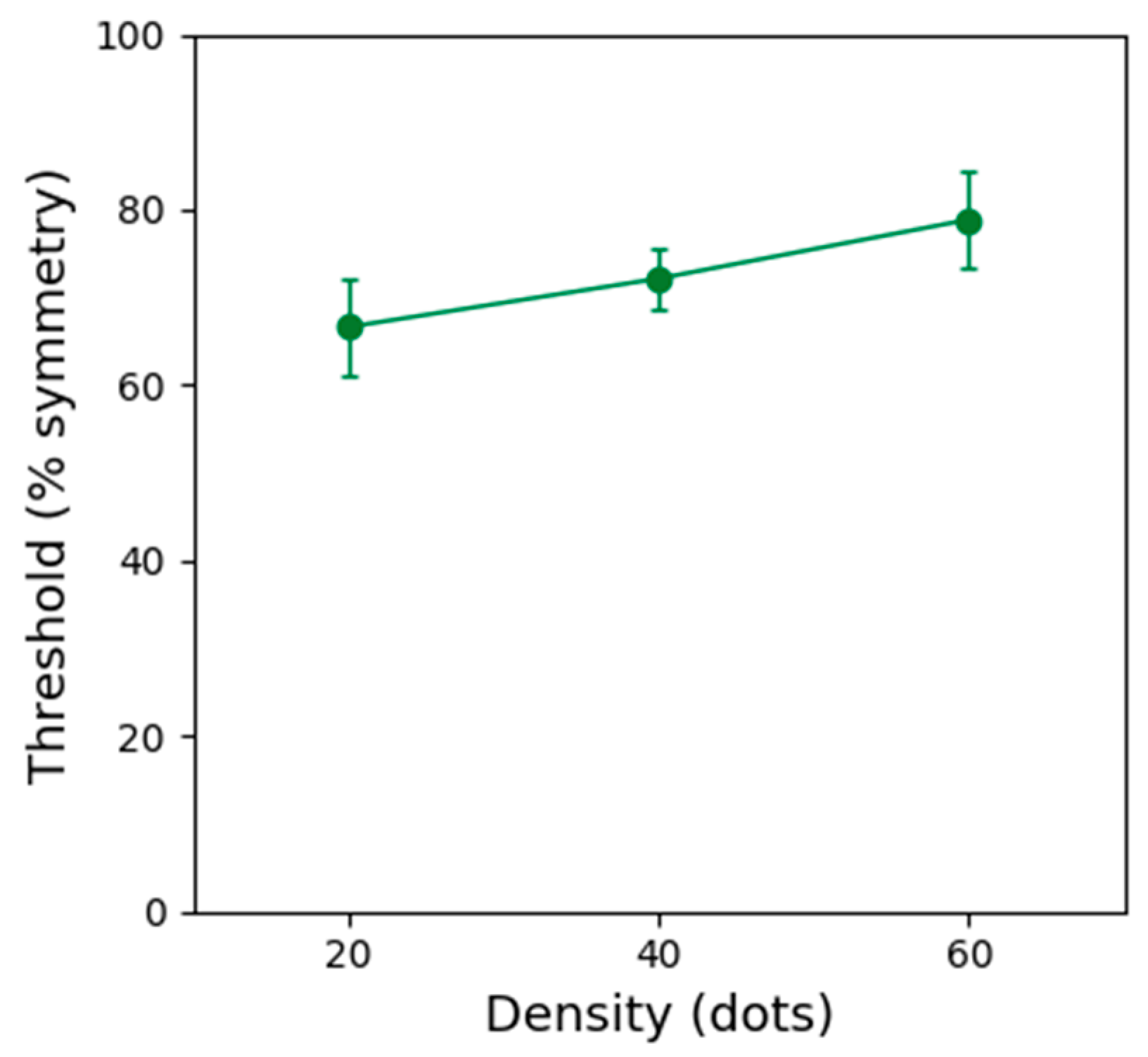
Figure 4 shows symmetry detection thresholds obtained with static stimuli of three different dot densities. These results indicate that performance improves with decreasing dot density (~10% reduction in threshold). Thus, the improved performance for low dot density patterns can explain the improved performance obtained in the one location (contrast modulated) condition. However, the higher thresholds obtained with high dot density static patterns cannot explain the improved performance obtained with the dynamic, multiple locations conditions.
A repeated-measures one-way ANOVA showed that the effect of dot density on symmetry detection thresholds was significant (F(2, 8) = 6.382, p = 0.022, ƞ2 = 0.615). Bonferroni corrected post-hoc analysis indicated a significant difference between thresholds obtained with patterns containing 20 and 60 dots (p ≤ 0.001). No other comparisons were significant (p > 0.05).
3.2. Control Experiment 2: Effect of Number of Contrast Levels
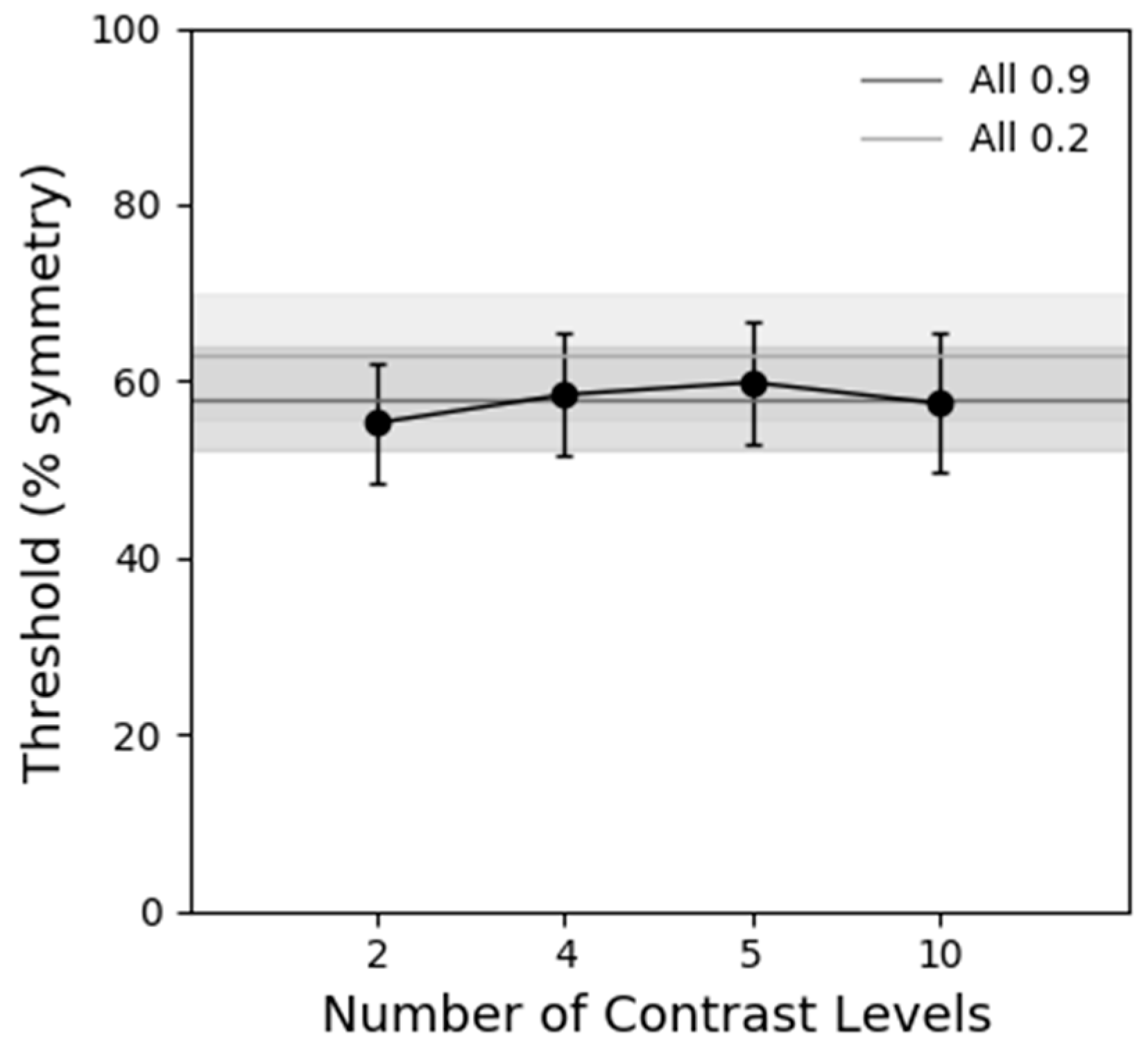
Figure 5 shows symmetry detection thresholds obtained with static stimuli containing different levels of contrast (1, 2, 4, 5 and 10 different contrast levels). The conditions where all the elements had the same contrast either low (0.2), or high (0.9) are shown by the light and dark grey lines, respectively. The results reveal that there is no significant difference in symmetry detection thresholds between the different number of levels of contrast conditions as indicated by a one-way repeated-measures ANOVA analysis (F(5, 20) = 1.565,
p = 0.275, ƞ
2 = 0.281). Thus, these results do not explain the improved performance with one location (contrast modulated) stimuli.
4. Discussion
Using dynamic dot patterns, we investigated how spatial relocation, luminance contrast modulation and lifetime duration of elements affect symmetry perception. Our results show that: (a) symmetry detection was better for the multiple locations condition compared to the two-locations and static conditions, suggesting that temporal integration of different element locations increases the strength of the symmetry energy signal; (b) performance also improved in the one location (contrast modulated) condition compared to the static condition, however, this may be due to the reduction in perceived density, and (c) increasing the number of levels of contrast in the static pattern did not affect performance, suggesting that grouping by perceived contrast does not affect symmetry detection in the one location (contrast modulated) condition.
A previous study has suggested that decreased symmetry detection thresholds for stimuli with limited lifetime pattern elements was caused by an increase in the number of element positions [
18]. In the two-locations conditions, we kept all the features of the limited-lifetime stimuli used in the previous study (i.e., elements relocated to successive new random positions), but reduced the number of different element positions. Performance in the two-location conditions was comparable to that in the static condition, suggesting that it is indeed the increased number of different spatial locations (i.e., symmetry energy) that is driving the improved performance in the multiple-locations condition. This supports our hypothesis that presenting temporally uncorrelated stimuli (i.e., increasing the number of different element locations) increases the strength of the symmetry signal and thus, improves performance.
Temporal contrast modulation of a static pattern also improved performance in comparison to the static condition, which goes against what one would predict if the reduction in thresholds in the multiple locations condition was caused by an increase in the number of locations. However, modulating the contrast of the dots over time reduces the overall perceived density of the pattern and also the perceived contrast levels in the dynamic stimuli. Thus, the improved performance with temporally contrast modulated patterns might be the result of either a reduction in perceived density or grouping by contrasts. Our control experiments showed that while varying the number of contrast levels in static patterns did not affect symmetry detection thresholds, decreasing the density of the pattern produced a modest increase (~10%) in performance. Therefore, the improved performance in the one location (contrast modulated) condition could be due to the lower perceived density. We suggest that the improved performance in the one location (contrast modulated) conditions should not be attributed to the same mechanism as the one involved in dynamic, multiple locations conditions.
Regarding the effect of element lifetime duration or temporal frequency of contrast modulation, we found no evidence for temporal tuning in any of the conditions. This is perhaps unsurprising for the one location (contrast modulated) and two-location conditions because varying the temporal frequency does not change the number of different element positions. However, it is surprising that there is no effect of element lifetime duration in the multiple-locations conditions because varying the temporal frequency does change the number of different element positions. However, it may be that when element lifetime duration is short there are many weak (or transient) symmetry signals and when element lifetime is longer there are fewer stronger (or more sustained) signals. If this is the case, both conditions would produce equivalent activation when integrated within a fixed temporal window. Previous research has shown that temporal thresholds for detecting the axis of symmetry in natural textures can range from 28 to 568 ms, depending on the salience of the features of the individual natural textures [
34]. However, we found that thresholds for the 58.8 and 117.7 ms duration in the two-location conditions were lower than those obtained with durations longer than 176.5 ms, but comparable to those obtained in the multiple-locations condition, thus, suggesting that symmetry detection in dynamic stimuli involves mechanisms that integrate symmetry signals over a relatively short, fixed time window (~120 ms). In an ecological context, a cumulative process could be useful in situations where a symmetrical object is partially occluded over time, for example a tiger moving through rushes towards a prey animal.
Previous research has shown that symmetry detection mechanisms are affected by various visual attributes, such as luminance polarity and color [
12,
13,
14], stereoscopic depth [
15,
16,
17], motion direction [
18] and speed [
38]. For example, the human visual system is sensitive to luminance polarity and color of symmetric pairs [
39,
40], but not selective for these attributes (i.e., the visual system does not have positional grouping mechanisms that are gated by luminance polarity or color) [
12]. Here, we have shown that it is not sufficient to merely consider these photometric (i.e., color and luminance polarity) or spatial (i.e., depth) parameters in symmetry perception, but that temporal factors (e.g., temporal correlation) must also be accounted for.
4.1. Relevance to Models of Symmetry Perception
Models for detecting and localising mirror-symmetry can be divided into three main categories: pixel-by-pixel correlations between the symmetric halves [
36,
41,
42], models based on complex grouping rules (based on higher-order structural correlation) from which symmetry is subsequently extracted [
5,
43,
44], and models based on early spatial mechanisms (e.g., oriented spatial filters) from which symmetrical elements are detected by the outputs of oriented receptive fields of various sizes [
34,
37,
45]. Although it is well established that receptive fields of cortical neurons are spatio-temporally oriented (i.e., they tilt along an oblique axis in the space-time domain and are space-time inseparable [
46]), none of the existing models incorporate the dynamic/temporal aspects of the stimuli.
Recently, Cohen and Zaidi [
34] proposed a symmetry energy model, whereby symmetry is detected by connecting pairs of symmetric spatial filters stimulating the receptive fields of neurons. If the two orientations were related by mirror-symmetry, then an AND-junction was activated. The AND-junctions can in principle be implemented via a variety of physiological routes and can take the form of direct multiplication or another operation equivalent to multiplication, such as Log-Exp transform, which is one of the most basic computational operations in the nervous system [
47] or the well-known Babylonian trick [
48,
49,
50]. These AND-like operations have been demonstrated to underpin several other visual processes, for example, curvature coding [
50], motion-energy model [
51], Reichardt motion-detector model [
52,
53] and stereoscopic depth processing [
54]. Thus, given Cohen and Zaidi’s [
34] symmetry model, performance improves in the multiple locations conditions because over time different and/or multiple AND-junctions will be activated in the multiple-location conditions than in the two-location conditions (in which the same AND-junctions will be repeatedly activated), thus resulting in stronger, overall symmetry energy.
In a similar way, Dakin and Watt’s [
45] model used spatial feature co-alignment in the output of oriented filters to detect and localise the symmetry axis. Given this model, we suggest that a temporal cumulative process would increase the number of activated co-aligned outputs over time in the multiple locations condition compared to the two location conditions (in which the same co-aligned outputs will be repeatedly activated), thus increasing the overall symmetry signal strength.
In sum, by studying spatiotemporal properties of symmetry perception, one can gain insight into the temporal characteristics of the mechanisms underlying symmetry perception and implicitly about their temporal limitations and flexibility. Our results are important for models of symmetry detection, which may inform computational/machine vision allowing for dynamic, real-time mirror-symmetry detection algorithms that are more representative of the human visual system. This could be used to inform navigation, traffic control and surveillance systems, and facial and man-made object recognition systems.
4.2. Relationship to Electrophysiology and Brain Imaging
One can look to measures of neural activity for insights into how a cumulative symmetry process could work. Event related potential (ERP) measurements show that symmetric patterns (and other types of regularity) elicit a sustained posterior negativity (SPN) difference wave [
55]. If a new symmetrical pattern is presented before activity has returned to baseline the responses could be combined, leading to increased amplitude of the difference wave over time. In the multiple locations conditions, new symmetrical position information is being continuously and rapidly introduced, which could theoretically generate an increase in the amplitude of the SPN over time. Future research should consider how temporal integration of symmetry signals in dynamic patterns might affect the time course of the SPN. This is of importance, considering that recent studies showed that the sustained nature of the SPN coincides with the late onset of a topographic microstate sensitive to symmetry [
14].
Symmetry perception requires pattern elements to be grouped together and as such can be seen as a form of perceptual grouping. Considering research from more general forms of perceptual grouping there is evidence that the lateral occipital complex (LOC), an area implicated in symmetry perception [
11], sub-serves grouping in figure-ground segregation [
56,
57]. Furthermore, activation in LOC persists after stimulus presentation ceases, briefly ‘storing’ the grouped elements as an object or shape (i.e., it maintains the relationship between elements) [
56]. For example, when shape-from-motion displays are used to investigate figure-ground segregation, activity has been shown to continue after motion has stopped. Future brain imaging research should consider how temporal integration of symmetry signals in dynamic patterns might differentially affect the activity of various extra-striate visual areas (V3a, V4, V7, LOC) involved in symmetry.