1. Introduction
One of the pillars of the study of chaos in dynamical systems is the search of orbits that are dense in the whole space. Typical examples of chaotic maps on the interval, where chaos can be easy visualized, are given by the tent map or by some functions of the logistic family (see, for instance, [
1,
2,
3,
4]).
The existence of orbits that spread along the whole space has been also studied in the setting of binary relations. When they are considered from one set onto itself, one can consider them from the point of view of graph theory. On the one hand, Hamilton was the first one who started to consider the analysis of graphs containing paths that visit all the nodes, named Hamiltonian paths. On the other hand, in terms of connectivity of (directed) graphs, a graph is (strongly) connected if, for every (ordered) pair of nodes, there is a path connecting them.
Roughly speaking, these two areas share the idea of the quest of orbits/paths visiting (nearly) the whole domain. But there are differences in how these problems are addressed. In the case of chaotic maps on the interval, the results usually involve computable conditions on the parameters of the function that defines the system. For instance, this is the case of how it is determined the chaos of the logistic map for . However, in the case of graphs, these results are related with the global structure of edges/arcs of the graph and/or on the quantification of the local structure at every node.
In the present work, our goal is to investigate the dynamics on graphs and on the more general frame of binary relations on topological spaces. In this setting, when a relation is composed with another one (or itself), each element of the domain does not need to be necessarily connected with a single element in the range. For this reason, we have set a connection with some recent results of the authors that were introduced to study the dynamics of multivalued continuous linear operators [
5]. We will analyze hypercyclicity, topological transitivity, and topologically mixing properties of binary relations. It is worth mentioning that the study of dynamics over finite graphs has been recently considered by Bahi et al. by setting links between Devaney chaos and strong connectivity in order to provide an algorithm for the generation of strongly connected graphs and to construct
Pseudo Random Number Generators (PRNGs) [
6]. This approach has also allowed for the obtainment of PRNGs based on the construction of Hamiltonian cycles over an
N-cube [
7,
8]. It is also worth mentioning that such results can also be considered in connection with finite state machines [
9] and explained using Turing machines [
10].
In the present work, we have also tackled the problem of the link between chaotic properties and connectivity, but analyzing more carefully the implications of using different topologies over the set of nodes. These results will allow us to stretch the connections between graph theory and dynamical systems in order to facilitate the exchange of ideas between both areas.
It is worth mentioning that there have been also recent results concerning the dynamics of continuous linear operators acting on
-spaces consisting of functions
where
, and
V is a multigraph, an infinite or a Cayley graph, a tree, or some similar structure (see, e.g., [
11,
12] and the references cited therein). We point out that our approach is different to the one of studying associations of directed graphs with finite topologies, as is taken in [
13]. It also differs from the one taken by Namayanja; she generalized the dynamics of solution
-semigroups of birth-and-death models [
14,
15,
16] to the case in which the transport equations are defined on the edges of an infinite network [
17].
2. Preliminaries
Given two nonempty sets
X and
Y, a
binary relation E is a subset of the Cartesian product
. If we consider the following relations
and
with
, then we can define the
inverse of
, denoted by
, as the relation
, and the composition of relations
by
Given , we define its set of adjacent elements by . The domain of a binary relation is given by and the range of is defined as .
We define the n-th power of as , their inverses , and the trivial relation . We also set and , for every . The definitions of the reflexive, symmetric, anti-symmetric, and transitive properties are assumed to be known, as long as the classes of equivalence and partial order relations.
When , a binary relation can be also understood as the links of a graph. If we distinguish the order in which the elements appear in each pair of the relation, then we speak of a directed graph or a digraph; if not, we will refer to it as an undirected graph or simply as a graph. Following the previous notation, a (di-)graph is given by a nonempty set X, whose elements are called nodes or vertices, and a set or (ordered) pairs of elements of X, called arcs in the directed case and edges in the undirected one. Thus, a binary relation on a graph is just the set of arcs/edges.
If , then y is not adjacent to x. In a graph, we define the degree of x as the cardinal of , . In a digraph, the outer degree of x, , is given by , and the inner degree of x, , is given by . The set X of nodes of a (di-)graph G can be considered as a topological space when endowed with certain topology over its elements. In the sequel, we will only deal with non-trivial finite simple (di-)graphs (without multiple edges connecting two nodes, and without any pair in ).
A
walk is an ordered sequence of nodes
such that
,
. In this case, we say that its length is
n. A
path is a walk that does not include any node twice, except that its first node can be the same as the last one. Such a (walk) path is called a
(walk) path. A path with
is called a
closed path or a
cycle. Given an element
, we define its set of
accessible elements by
. We say that a (di-)graph is
(strongly) connected if, forevery pair of nodes
, there is an
path. A digraph whose underlying non-directed graph, obtained by removing the direction of every arc, is connected is said to be
weakly connected. Further information on graph theory can be found in [
18,
19,
20].
Throughout the rest of the paper, we assume that X and Y are two given topological spaces. If it is not explicitly mentioned, we consider that these spaces are endowed with the discrete topology. In this case, the unique dense set of X is the whole set X itself. We will also consider the product of N copies of these spaces, and with , equipped with the usual product space topologies.
We introduce several notions of dynamical systems in the setting of binary relations:
Definition 1. Let be a sequence of binary relations between the spaces X and Y, ρ a binary relation on X, and . Then we say that
- (i)
x is a universal element for the sequence if and for each there exists an element such that the set is dense in Y. As a particular case, if , then we say x ishypercyclicfor ρ.
- (ii)
ρ is topologically transitive if, for every pair of non-empty open sets , there is some such that . If there is some such that this last condition holds for all , we say that ρ is topologically mixing.
Clearly, if x is hypercyclic for , and for some , then z is likewise hypercyclic for G. If is a binary equivalence relation and x is hypercyclic, then the underlying (di-)graph must be (strongly) connected and all the elements of X are hypercyclic for .
Let us consider
a base of non-empty open sets for the topology of
X. If we denote by
the set consisting of all hypercyclic elements of
then the following equality holds [
21]:
Remark 1. - (i)
Let be a graph with X equipped with the discrete topology. It can be simply proved that the graph G is connected if and only if ρ is topologically transitive or hypercyclic.
- (ii)
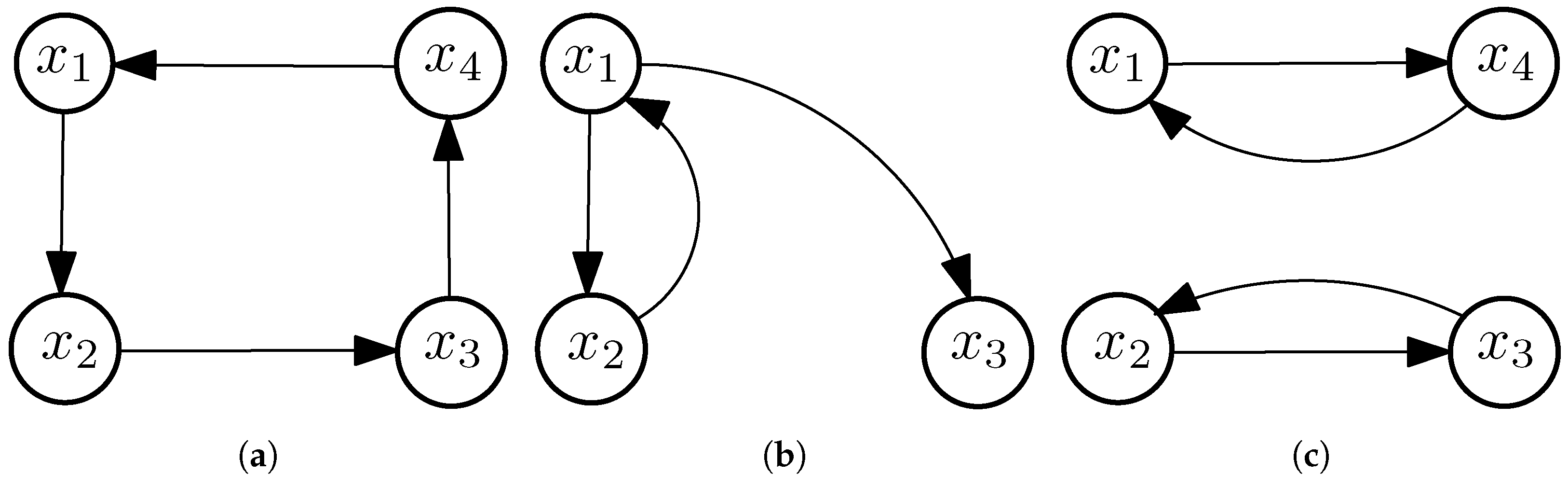
In the Definition 1 (ii), it is irrelevant whether we write or . It is also worth noting that ρ does not need to be topologically mixing whenever ρ is topologically transitive: Let us consider a graph that is isomorphic to a square, that is and , see Figure 1a. Clearly, ρ is topologically transitive, but it does not hold the topologically mixing property since there is no odd number such that . - (iii)
Unlike the linear setting, in our framework, the notion of hypercyclicity cannot be connected to that of topological transitivity in any reasonable way. It is well known that these notions are equivalent for continuous linear operators on Fréchet spaces by Baire’s category theorem (see, for instance, [21,22]). However, there exist examples of continuous linear operators on non-metrizable locally convex spaces that are topologically transitive and not hypercyclic [23]. Moreover, for any non-trivial Banach space X there exists a multivalued linear operator that is hypercyclic and not topologically transitive (cf. [24]). It is very simple to construct an example of a hypercyclic relation on a finite set that is not topologically transitive, as well: Set the digraph with and , endowing X with the discrete topology, see Figure 1b. Then is a hypercyclic element for ρ, but ρ is not topologically transitive, since for all .
By considering different topologies on the set of nodes X, the aforementioned dynamical properties can be used to generalize the notion of connectivity. The following examples illustrate these facts:
Example 1. Let be a graph without isolated nodes, and let τ be the topology on X. Let us denote by , the connected components of the graph G. Then ρ is hypercyclic if there exists a number such that is dense in , and any element of is a hypercyclic element of ρ.
We point out that the topology endowed to X is crucial in order to ensure hypercyclicity, or any other dynamical property. For example, let us take endowed with , , , , and , see Figure 1c. We now set the binary relation , then ρ is not hypercyclic in but it is hypercyclic in . Finally, observe that ρ is topologically transitive (and ρ is topologically mixing) if, for every pair of non-empty open subsets of , there exists such that and
The links between connectivity and dynamics will be thoroughly explained in the next section.
3. Hypercyclic and Chaotic Digraphs
We study the relations between different types of connectivity on digraphs and some of the aforementioned dynamical properties. This will enable us to introduce two new important classes of digraphs that are subclasses of the class of weakly connected digraphs and that extend the class of the strongly connected ones.
One of the most accepted notions of chaos is the one introduced by Devaney [
25] for continuous mappings acting on metric spaces. Three ingredients are considered in this definition: topological transitivity, density of periodic points, and sensitive dependence on the initial conditions (SDIC). Banks et al. [
26] proved that SDIC can be deduced from the other two properties. Nevertheless, since topological transitivity does not coincide with hypercyclicity in our setting, we will introduce two different notions of chaos.
Definition 2. Let ρ be a binary relation on X, and . Then we say that
- 1.
x is a periodic point of ρ if and there exists such that .
- 2.
ρ is Devaney-chaotic if it is topologically transitive and it has a dense set of periodic points.
- 3.
ρ is chaotic if it is hypercyclic and it has a dense set of periodic points.
Let us consider
, where
X is endowed with the discrete topology. It immediately follows from our definitions that
G is strongly connected if and only if
is topologically transitive. Every
is also a periodic element for
. Thus,
is also Devaney-chaotic. Besides,
is also hypercyclic and chaotic, and
for every
. Since
is hypercyclic, let us pick any
. Then, for any two different points
, an
path and an
path exists in
G. Thus, considering the underlying non-directed edges, there exists a walk connecting
y and
z, and
G is thus weakly connected. We summarize all these relations underneath.
Therefore, we are able to introduce two new classes of digraphs that are subclasses of the class of weakly connected digraphs and that extend the notion of strong connectivity. Any of these three implications is strict, as the following examples show:
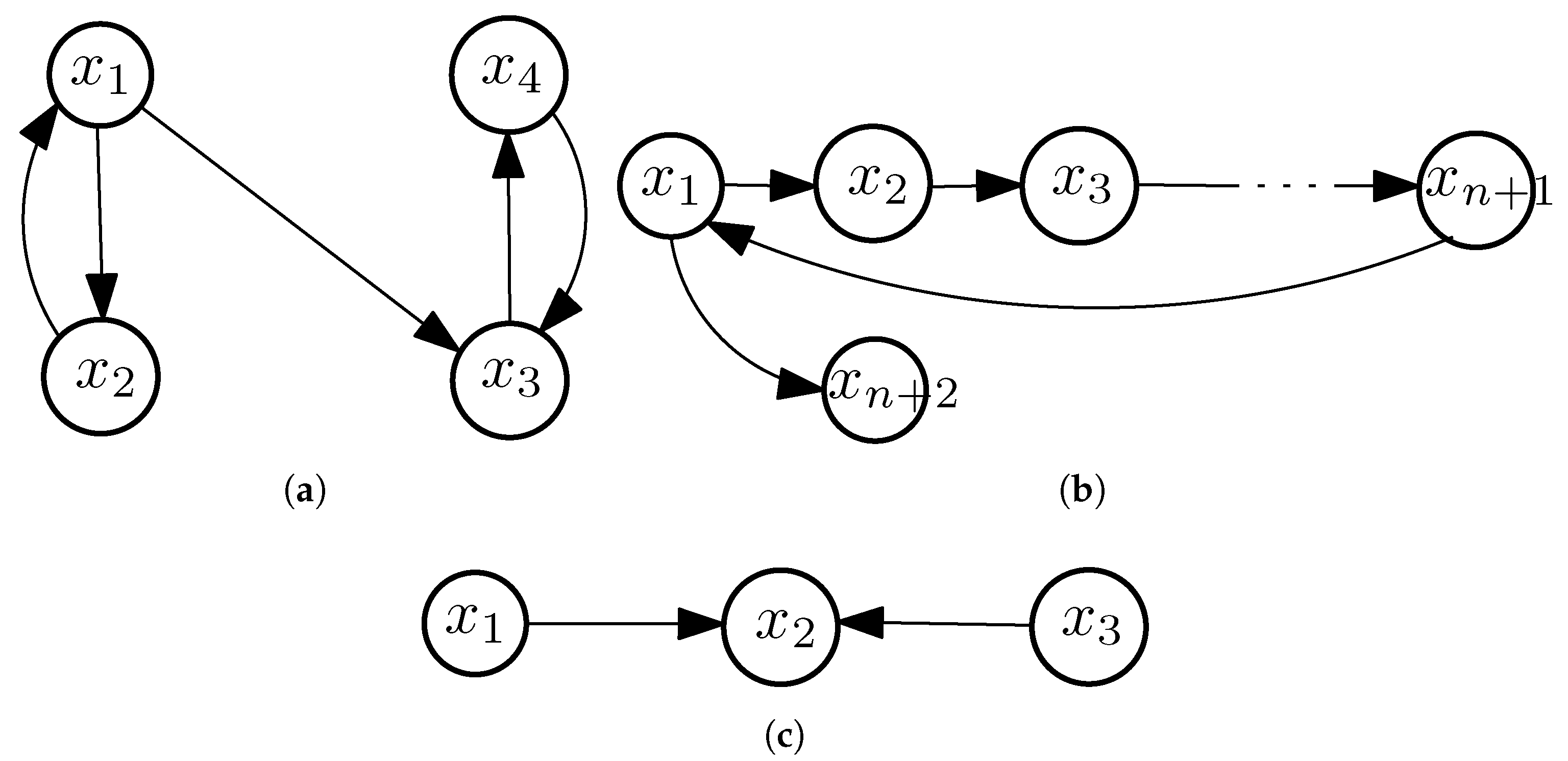
Example 2. - (i)
Let be equipped with discrete topology, and let , see Figure 2a. Then , and (), which simply yields that . It is also clear that any element of X is periodic for ρ, such that ρ is chaotic. Since there is no path connecting and in G is not strongly connected and ρ is neither topologically transitive nor Devaney-chaotic. Therefore, the first implication in Equation (2) is strict. - (ii)
Let be an oriented closed cycle of length n (with , and let where for , see Figure 2b. Then it can be easily seen that , endowed with the discrete topology, is hypercyclic, since any element lying on the cycle C is hypercyclic for ρ and that G is not chaotic, because the point cannot be a periodic element for - (iii)
Let and , see Figure 2c. Then is weakly connected but, equipped with the discrete topology, it is not hypercyclic.
A series of recent results in the theory of digraphs are devoted to the study of cyclability: Given a digraph
, a set
said to be
cyclable in
G if
G contains a cycle through all the nodes of
S. Setting
, we obtain the classical concept of a Hamiltonian (di-)graph. We refer the interested reader to [
27]. It is clear that the cyclability of
in
jointly with the denseness of
S in
X imply that
is (Devaney)-chaotic for
. However, this is far from being necessary for
to be (Devaney)-chaotic since this condition is automatically satisfied if the points in
S lie on a closed path in
G not on a circle.
It is worth noting that our conclusions from Example 1 can be reformulated for digraphs only partially; if denote the strongly connected components of a digraph , then the denseness of some in G implies that is (Devaney)-chaotic for , but the converse statement fails to be true even for discrete topology, as the next example shows:
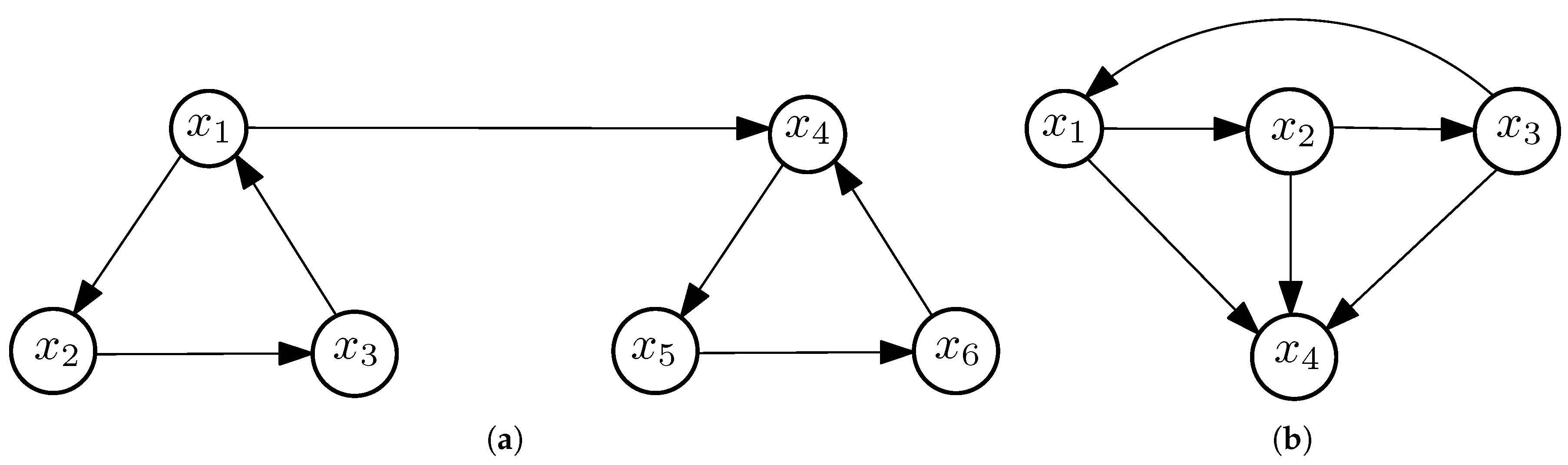
Example 3. Consider a digraph G consisting of two oriented cycles given by and joined by an arc , see Figure 3a. Then G is Devaney-chaotic but neither nor are dense in G. 5. Disjointness on Binary Relations, Graphs, and Digraphs
Disjointness was firstly introduced for dynamical systems by Furstenberg in [
30]. For linear operators, it was firstly considered in [
31,
32] (see also [
33]). Further information on the dynamics of linear operators can be found in [
34,
35,
36,
37]. We introduce analogons of disjointness of the above classes of hypercyclic and (Devaney)-chaotic graphs. Part of these results are inspired by the analogons obtained for the case of multivalued linear operators in [
5].
We first introduce the notion of disjointness for hypercyclicity, topological transitivity, and the topologically mixing property.
Definition 4. Let . Let be two topological spaces. For every , let be a sequence of binary relations between the spaces X and Y, let be a binary relation on X, and let . An element is a d-universal element for the sequences , if, for each , there exist elements such that the set is dense in . As a particular case, the binary relations are called d-hypercyclic if there exists a d-universal element x of the sequences . In this case, x is called a d-hypercyclic element of the binary relations
Definition 5. Let . Let be two topological spaces. For every , let be a sequence of binary relations between the spaces X and Y and let be a binary relation on X.
- 1.
The sequences are d-topologically transitive
if, for every non-empty open subsets and , there exists such that - 2.
The sequences are d-topologically mixing
if, for every non-empty open subsets and , there exists such that, for every we have that Equation (3) holds. - 3.
The binary relations are d-topologically transitive (d-topologically mixing) if the sequences are d-topologically transitive (d-topologically mixing).
We also introduce the notion of d-Devaney chaos and d-chaos for binary relations. For this purpose, we define the set of periodic elements
Definition 6. Given , the binary relations on X are said to be d-Devaney-chaotic if they are d-topologically transitive and the set of periodic elements is dense in . These relations are d-chaotic if they are d-hypercyclic and the set of periodic elements is dense in .
A formula similar to Equation (
1) can be given for d-hypercyclic elements of binary relations [
32], and the most important consequences of both formulae can be formulated for continuous mappings acting between topological spaces.
It is well known that two single-valued linear operators acting on a Fréchet space cannot be d-hypercyclic if one of them is a scalar multiple of the other one. This is no longer true for multivalued linear operators since there exists a multivalued linear operator
on a Banach space such that
and some arbitrary multiples of it can be d-hypercyclic [
5]. Concerning simple graphs, the notion of d-hypercyclicity is much more complicated than the notion of hypercyclicity, and it does not reduce to the connectivity of the graphs, as is described in Example 2 (ii). For the next result, we recall that a graph of
n nodes
is
complete if, for every pair of different nodes
, we have that
, i.e.,
.
Theorem 2. Let and let denote the complete graph with , equipped with discrete topology. Let us consider copies of the graphs . The following affirmations are equivalent:
- i.
The graphs are d-Devaney-chaotic.
- ii.
The graphs are d-hypercyclic.
- iii.
Each graph contains nodes.
Proof. Clearly, (i) implies (ii). To prove (ii) implies (iii), we only need to observe that, in the case we do not have the existence of a natural number such that and . Thus, any N-tuple of the containing two different components cannot be an element of the set . Hence, neither nor are d-hypercyclic elements for the N graphs . Now, let us assume and let us see that the N copies of are d-Devaney-chaotic. For any N-tuple and , we have that so that is a d-hypercyclic element for the N-tuple of graphs . Finally, the set of periodic points coincides with , even in the case . ☐
In a similar way, it can be seen the equivalence of d-chaos and d-transitivity with the condition .
Another remarkable class of graphs are bipartite graphs. A graph is said to be bipartite if with and for every , either and or and . In this case, the d-hypercyclicity can never hold. If we consider a family of bipartite graphs , sharing the partition of the set of nodes X into two sets and , then for any and every either or , depending on where is x and if k is even or odd.
Before proceeding further, we would like to observe that the notion of (d-topological transitivity) d-hypercyclicity is equivalent for simple graphs equipped with the discrete topology to the notion of d-Devaney chaos, since for any simple graph and for any we have that .
In the remaining part of this section, we will only consider digraphs.
For any digraph where we introduce the adjacency matrix of A, shortly, by if and if , for every .
Let be digraphs with, , each of which is equipped with discrete topology, and let be their corresponding adjacency matrices. Denote, for every and , the k-th power of the adjacency matrix as As is well known, the element of matrix represents the exact number of walks of length k in . Using this result and our definition of d-hypercyclic elements, we can simply clarify the following necessary and sufficient conditions for an element to be a d-hypercyclic element.
Theorem 3. Let be digraphs over , equipped with the discrete topology, with adjacency matrices . An element is d-hypercyclic for if and only if, for every , there exists such that, for all , .
By taking
,
and
in Condition
3, we obtain the following characterization of d-topological transitivity of digraphs
equipped with discrete topologies, and we can also characterize d-topologically mixing property in a similar way:
Theorem 4. Let be digraphs over , equipped with the discrete topology, with adjacency matrices . The digraphs are d-topologically transitive if and only if, for every and for every , there exists such that, for all , .
Thus, d-topological transitivity of digraphs equipped with discrete topologies immediately implies that these digraphs are d-hypercyclic with any being a d-hypercyclic element. It is clear that d-Devaney chaos of implies d-chaos, which also implies d-hypercyclicity. The converse implications do not hold in general, as can be illustrated with the following examples.
Example 5. - (i)
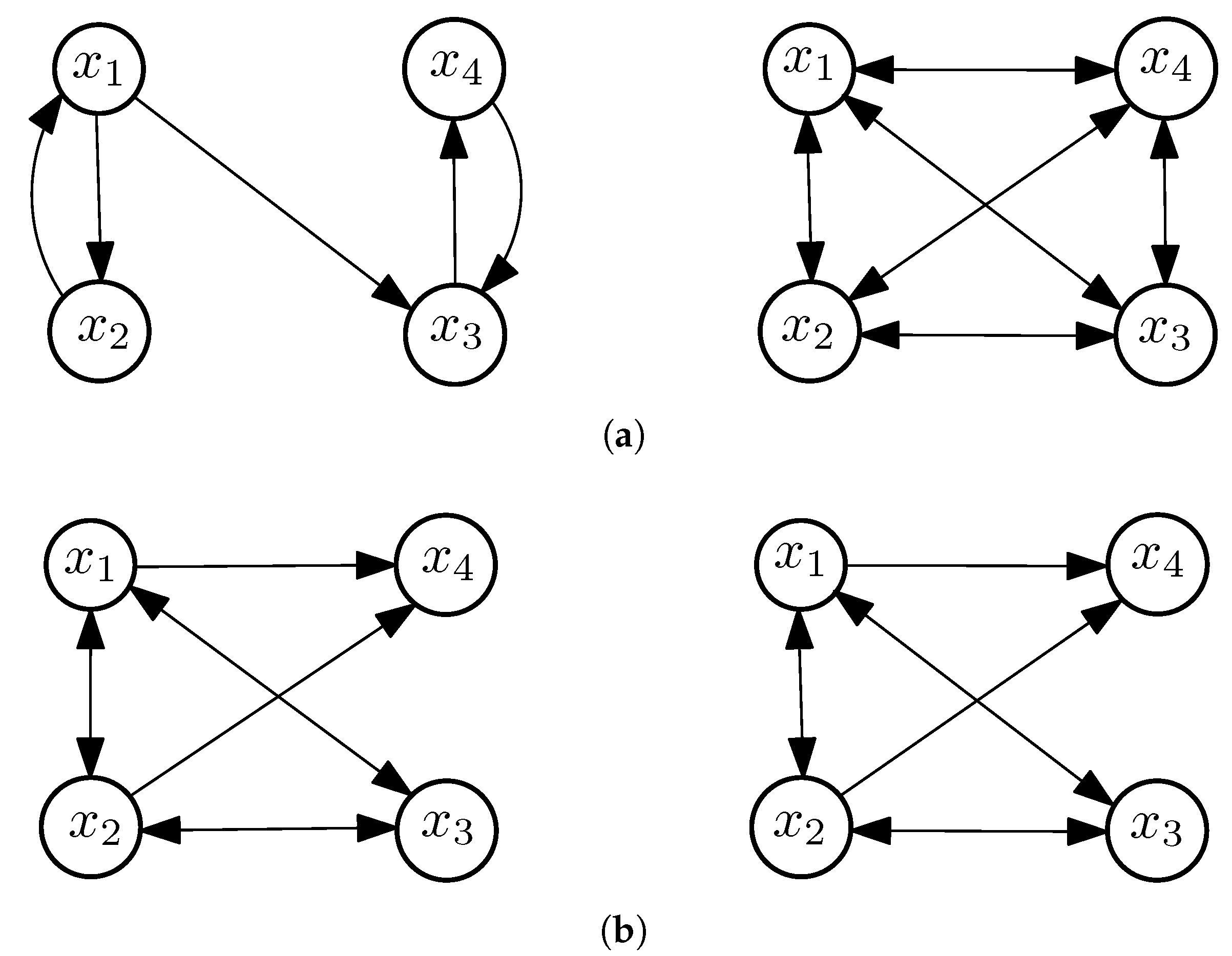
Let G be the graph appearing in Example 2 (i), and let be the complete graph of these 4 nodes, and both are equipped with discrete topologies, see Figure 4a. It can be easily seen that G and H are d-chaotic but not d-Devaney-chaotic. - (ii)
Let and let , see Figure 4b. If is equipped with the discrete topology, then the pair is d-hypercyclic, since, for any even number and for every , we have , but it is not d-chaotic since is not periodic in G.
Disjointness of tournaments depends on the size of the set of nodes.
Theorem 5. Let and let be N tournaments equipped with discrete topologies. Then cannot be d-hypercyclic nor d-topologically transitive.
Proof. Without loss of generality, we may assume that If then it can be easily seen that and must be isomorphic to an oriented segment, which is neither hypercyclic nor topologically transitive.
If , there exist only two non-isomorphic tournaments of order 3. Since and should be hypercyclic (topologically transitive), and only the Hamiltonian circles are hypercyclic (topologically transitive), it follows that and have to be a Hamiltonian circle—either or . A careful inspection of all possible cases leads us to the impossibility of satisfying any of these dynamical properties. ☐
By Theorems 2 and 5, looking at the case , we easily observe the existence of digraphs that are not d-chaotic, but whose underlying simple graphs are d-chaotic. In the case of we have the following important result.
Theorem 6. Let and let be tournaments over a set equipped with discrete topologies. The following are equivalent:
- 1.
are d-Devaney-chaotic.
- 2.
are d-topologically transitive.
- 3.
is strongly connected for all .
- 4.
is a Hamiltonian tournament for all .
Proof. Let
be d-chaotic. Then these tournaments are d-topologically transitive such that any
,
, is topologically transitive and therefore strongly connected. By Camion’s theorem (see, for instance, [
28]),
is strongly connected if and only if each
is Hamiltonian.
Therefore, it remains to be proven that the strong connectivity of all
values implies that
are d-chaotic. To see this, let us recall that the strong connectivity of any directed graph is equivalent to its irreducibility [
38]. Applying Th. 1 of [
38], we have that the adjacency matrix
of
,
, is primitive, i.e., there exists a natural number
such that
is strictly positive. In fact, Wielandt estimates that
[
39]. The result now follows from an application of Theorem 4 and from the observation that, for a given tuple
,
is a periodic point for
if and only if there exists
such that, for each
, one has
☐
Any of the above equivalencies implies that are also d-hypercyclic. However, the situation is not so simple because the strong connectivity of values for all is not equivalent to the fact that were d-hypercyclic:
Example 6. It is well known that there exist only four non-isomorphic tournaments of order four. Only two of them, and defined as follows, are hypercyclic: is the union of the Hamiltonian cycle and oriented segments , and while is the union of the Hamiltonian cycle and oriented segments and Furthermore, is hypercyclic but not topologically transitive, whereas is. It can be verified that the pair is not d-hypercyclic. Hence, the hypercyclicity of components does not imply d-hypercyclicity of a tuple. We also point out that the pair is d-hypercyclic, but is not strongly connected.
We close this work by providing one more example.
Example 7. Let and be tournaments over a set of nodes . Suppose that is a hypercyclic, non-Hamiltonian tournament and that, for , is a Hamiltonian tournament. Let x be a hypercyclic element for Then the proof of Theorem 6 shows that are d-hypercyclic, where x is their d-hypercyclic element. However, it is clear that cannot be d-topologically transitive.