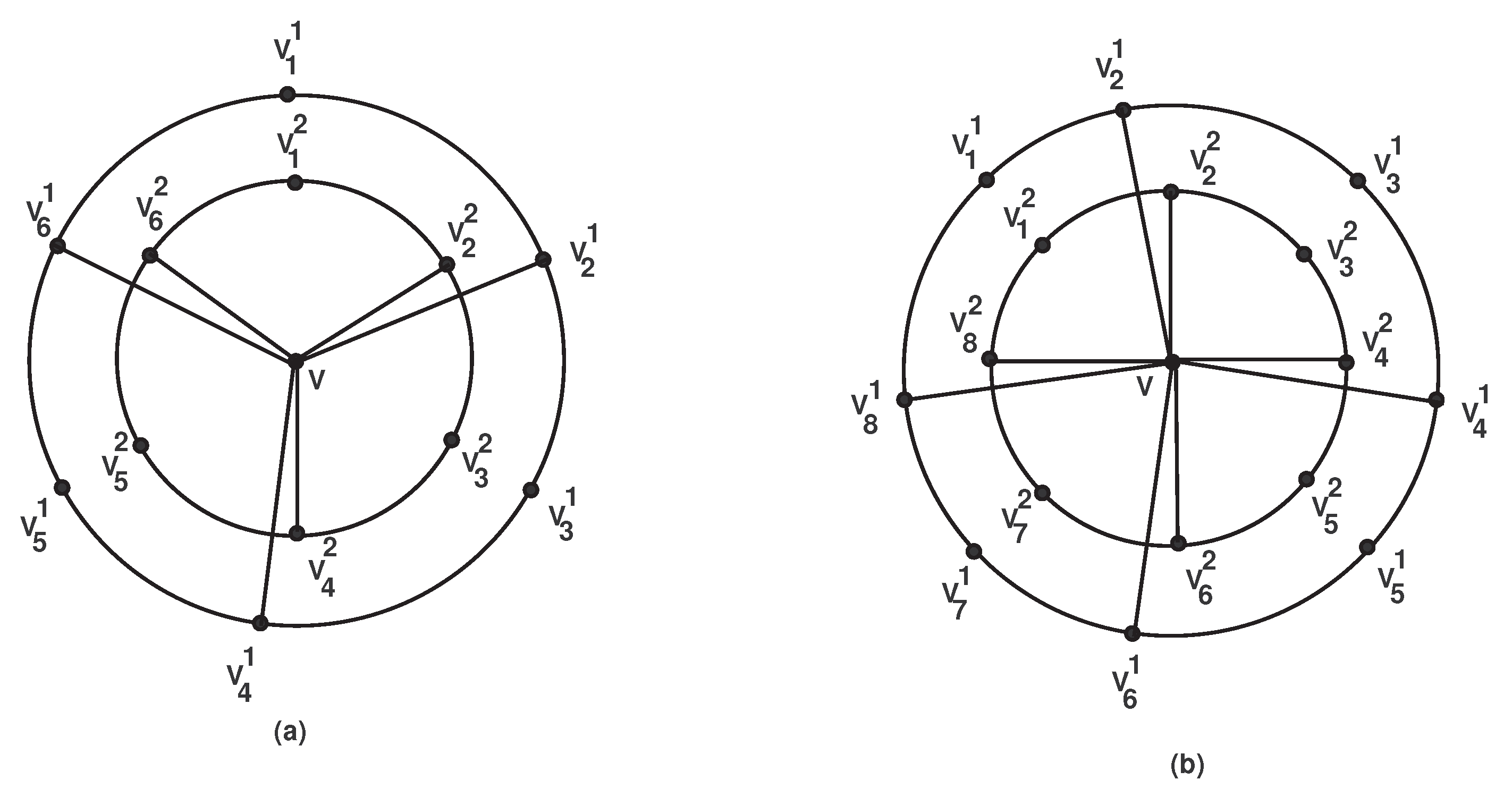
Construction and Observations
A double gear graph
(see in
Figure 1) is constructed if we consider two even cycles with
,
Now take a new vertex v adjacent to n vertices of : as well as v is also adjacent to n vertices of :. Inductively we can construct an m-level gear graph denoted by by taking m even cycles .
The vertices of , in the graph are of two kinds namely the vertices of degree 2 and the vertices of degree 3. Vertices of degree 2 and 3 will be considered as minor and major vertices respectively. One can easily check that:
When
, (central vertex v with one major and minor vertex of each form basis).
When
, (central vertex v with two minor vertices of each form basis).
When
, (two minor vertices such that of with one minor vertex and two major vertices of such that form basis).
When
, (three minor vertices satisfying , of with three minor vertices and one major vertex of satisfying , and form metric basis of ).
Consider the gear graph in which is an outer cycle of length . If B is a basis of then B contains vertices of for . Suppose then vertices of B can be ordered as such that for and are called neighboring vertices. Vertices of lying between any two neighboring vertices of B are called gaps which are denoted by for and , and their cardinalities are said to be the size of gaps. One can easily observe that every vertex of B has two neighboring vertices; gaps generated by these three vertices are called neighboring gaps following a concept already exist in and . A gap determined by neighboring vertices of basis say and will be called an with when and or when and . Hence we have three kinds of gaps namely, gap, gap and gap.
For the graph central vertex v does not belong to any basis. Since ∀, , and , if central vertex v belongs to any metric basis B then there must exists two distinct vertices and for such that . Consequently, the basis vertices of belong to the cycles induced by and . It is shown in that if B is a basis of then B consist only of the vertices of that satisfy the following properties.
If B is a basis of , then every gap, gap and gap of B contains at most 5, 4 and 3 vertices respectively.
If B is a basis of , then it contains at most one major gap.
If B is a basis of , then any two neighboring gaps contain together at most six vertices in which one gap is a major gap.
If B is a basis of , then any two minor neighboring gaps contain together at most four vertices.
Lemma 1. Let B be a basis of , , then every gap, gap and gap of B induced by and contains at most 5, 4 and 3 vertices respectively.
Proof. Suppose the result is false and there exists a gap of size 7 say , consisting of consecutive vertices of or with then which is a contradiction. If there exists a gap of size 6 then we have a path , consisting of consecutive vertices of or with and then which is again a contradiction. The existence of a gap of size 5 say induced by or with , would imply a contradiction.
The gap gap and gap containing 5, 4 and 3 vertices respectively will be referred to as major gaps and the remaining gaps are called minor gaps. In the proof of Lemmas 2–4, the major vertices will be labeled by a star (*). □
Lemma 2. Let B be a basis of , then it contains at most one major gap induced by the vertices of cycles and .
Proof. Suppose B contains two distinct major gaps induced by the vertices of cycles or .
Case-(i): When both gaps are then we have two distinct paths consisting consecutive vertices and of and respectively in this case ; a contradiction.
Case-(ii): When both gaps are then we have two distinct paths consisting of consecutive vertices and of and respectively but ; a contradiction.
Case-(iii): When both gaps are then we have two distinct paths consisting of consecutive vertices and of and respectively in this case ; a contradiction.
Case-(iv): When one gap is and other is gap then we have two distinct paths and induced by and respectively but ; a contradiction.
Case-(v): When one gap is and other is gap then we have two distinct paths consisting of consecutive vertices and of and respectively but ; a contradiction.
Case-(vi): When one gap is and other is gap then we have two distinct paths consisting of consecutive vertices and of and respectively in this case ; a contradiction.
Similarly, if both major gaps are induced by then we get a contradiction and a similar contradiction arises if induced both major gaps. □
Lemma 3. Let B be a basis of , , then any two neighboring gaps, one of which being a major gap induced by exactly one of two cycles or contain together at most six vertices.
Proof. If the major gap is then there is nothing to prove by Lemma 2. Without loss of any generality we can say that only induced a major gap by Lemma 2. If the major gap is a gap having five vertices then its neighboring minor gap contains at most one vertex. If this statement is false and gap, minor gaps having three and two vertices respectively are neighboring gaps of major gap, then we have two paths consisting of consecutive vertices of : and , where induced by major, minor gaps and major, minor gaps respectively. In this case and ; a contradiction. The existence of major gap having four vertices is not possible if its neighboring minor gap is a gap with three vertices. If this case holds then we consider the following path: , where then ; a contradiction. □
Lemma 4. Let B be a basis of , , then any two minor neighboring gaps induced by or contain together at most four vertices.
Proof. To prove the statement, it is sufficient to prove two cases.
Case-(i): minor gap with three vertices cannot be neighboring gap of minor gap having three vertices, otherwise we have a path consisting of consecutive vertices of or :, where in this case .
Case-(ii): minor gap with three vertices cannot be neighboring gap of minor gap having two vertices, otherwise we have a path consisting of consecutive vertices of or : where in this case ; a contradiction. □
Theorem 1. If be a double gear graph for , then Proof. We have seen that
,
and the central vertex
v does not belong to any basis
B of
. Moreover
and
be the outer cycles of
at level 1 and 2 respectively. First we prove that
by constructing a resolving set
W in
with
vertices.
We consider three cases according to the residue class modulo 3 to which n belongs.
Case-(i): When
, then we may write
, where
, is even and
, in this case
W can be considered as:
Case-(ii): When
, then we may write
, where
is even and
, in this case
W can be considered as:
Case-(iii): When
, then we may write
, where
is even and
, in this case
W can be considered as:
The set
W contains a unique
major gap having at most five vertices and all other gaps are
minor gaps which contain at most three vertices. The set
W is a resolving set of
since any two major or any two minor vertices respectively lying in different gaps or in the same gap are separated by at least one vertex in the set of three vertices of
W generating these neighboring gaps. When gaps are not neighboring gaps, then the set of four vertices of
W which generate two gaps make the representation unique of each vertex of these two gaps. Representation of central vertex
v is
, which is different from the representation of all other vertices of
. Hence,
Now we show that . As the central vertex v does not belong to any basis of . Let B be a basis of such that then we have r gaps. By lemma 2 B contains at most one major gap, without loss of generality we can say major gap lies on . Hence B induces gaps on and gaps on .
We denote the gaps on
by
where
and
are called neighboring gaps for
as well as
is also neighboring gap of
and the gaps on
will be denoted by
where
and
are called neighboring gaps for
as well as
is also neighboring gap of
. By Lemma 2, suppose
is a major gap. By Lemmas 3 and 4, we can write
and
We consider two cases according to the residue class modulo 2 to which r belongs.
Case-(i): When : In this case
By summing the above inequality we have
From Equations (
2) and (
3) we have,
Case-(ii): When : In this case and
By summing the above inequality we have
and
From Equations (
4) and (
5) we have
Now from Equations (
1) and (
6) we conclude that,
which complete the proof. □
Theorem 2. If be a double gear graph for , , then Proof. We will prove this result by induction on levels of gear graph denoted by .
When , then is obtained in .
When , then by Theorem 1.
Now we assume that the statement is true for , . we will show the result for , by using concept of Theorem 1 we have .
Now . . Hence the result is true for all positive integers . □