An Improved Whale Optimization Algorithm Based on Different Searching Paths and Perceptual Disturbance
Abstract
1. Introduction
2. Whale Optimization Algorithm
2.1. Inspiration
2.2. Search for Prey (Exploration Phase)
2.3. Encircling Prey
2.4. Bubble-Net Attacking Method (Exploitation Phase)
- 1.
- Shrinking encircling mechanism
- 2.
- Spiral updating position method
2.5. Idea of Improving Whale Optimization Algorithm
3. Complex Path-Perceptual Disturbance WOA
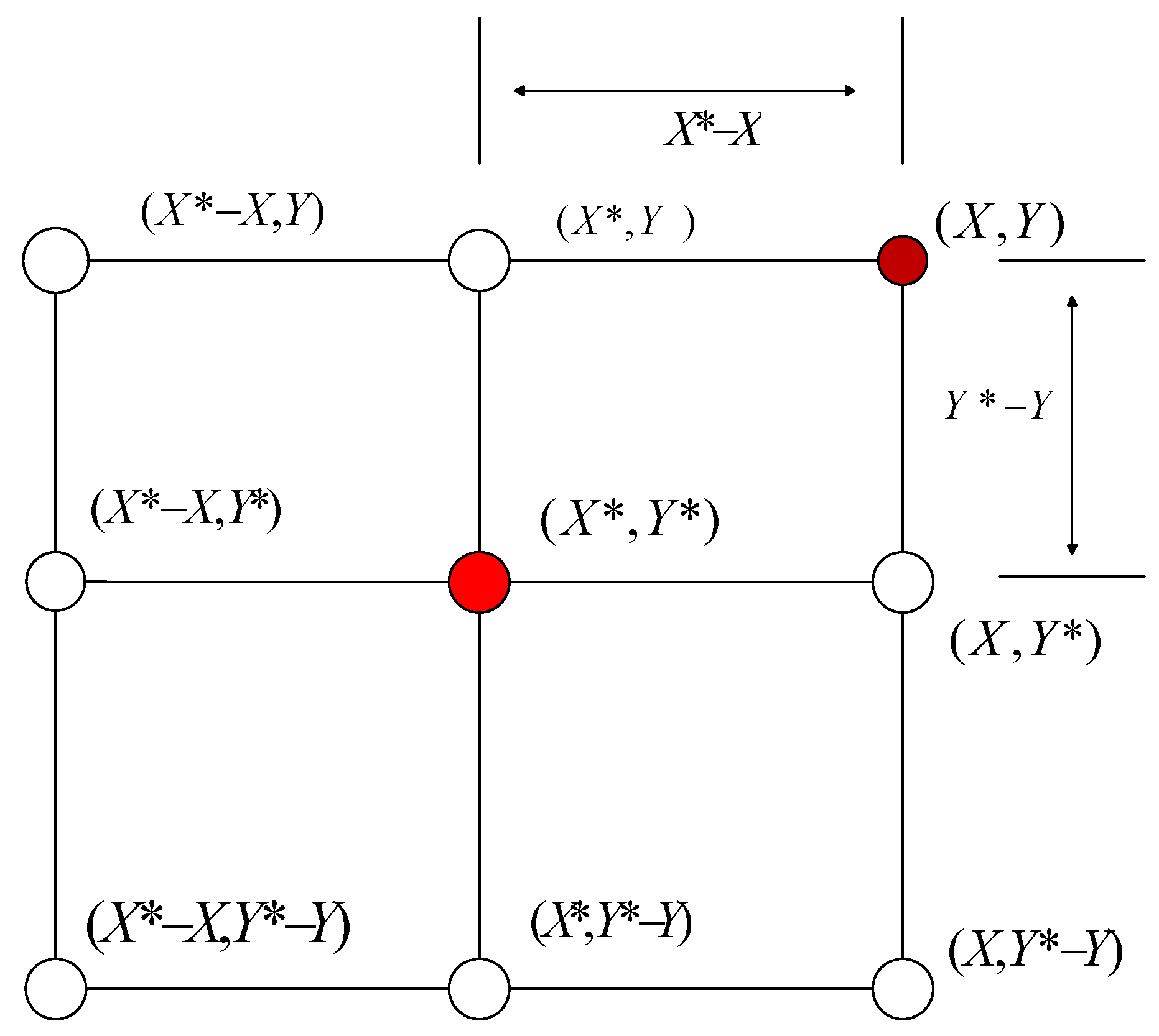
3.1. Selection of Mathematical Model of Searching Path
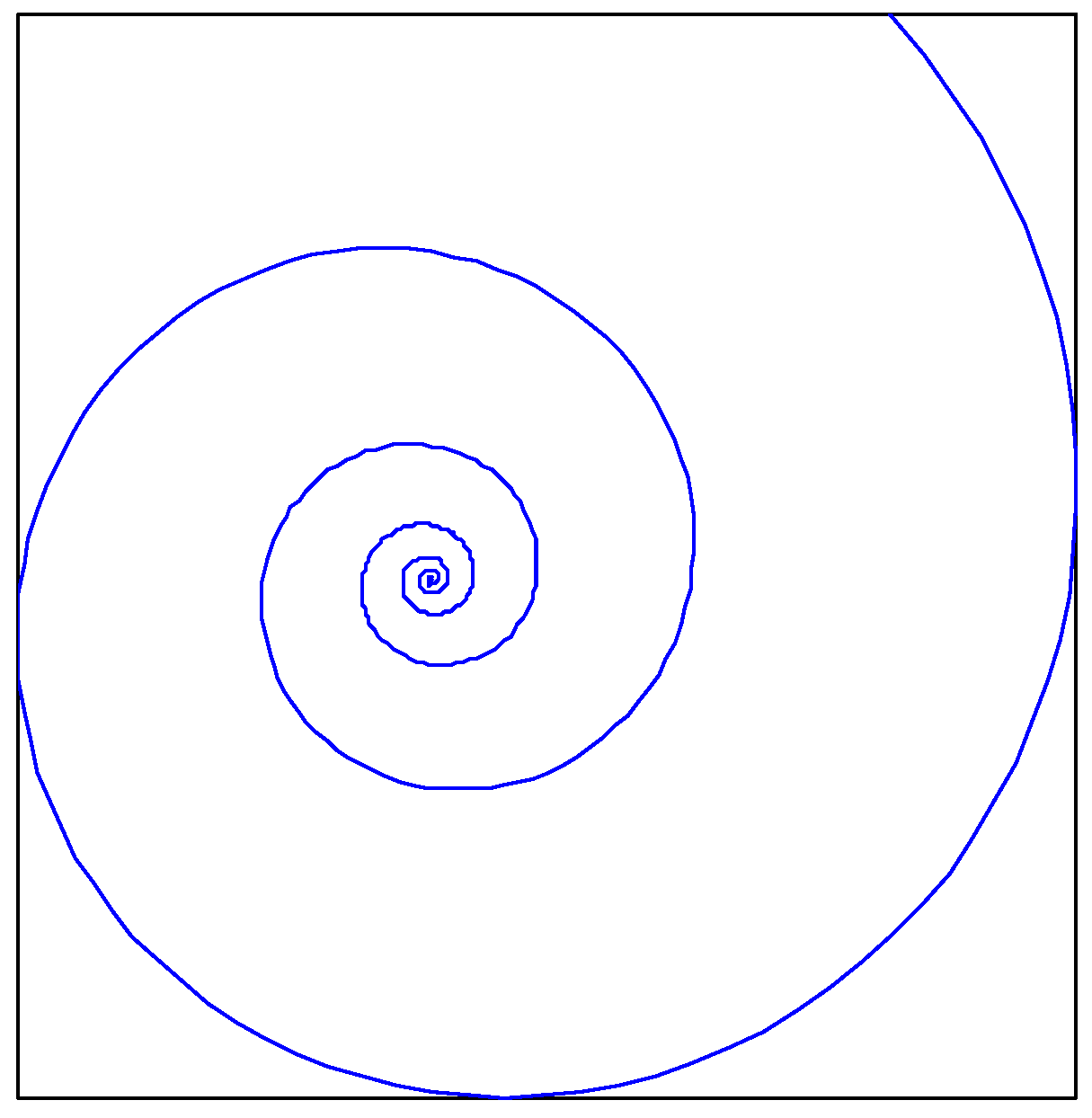
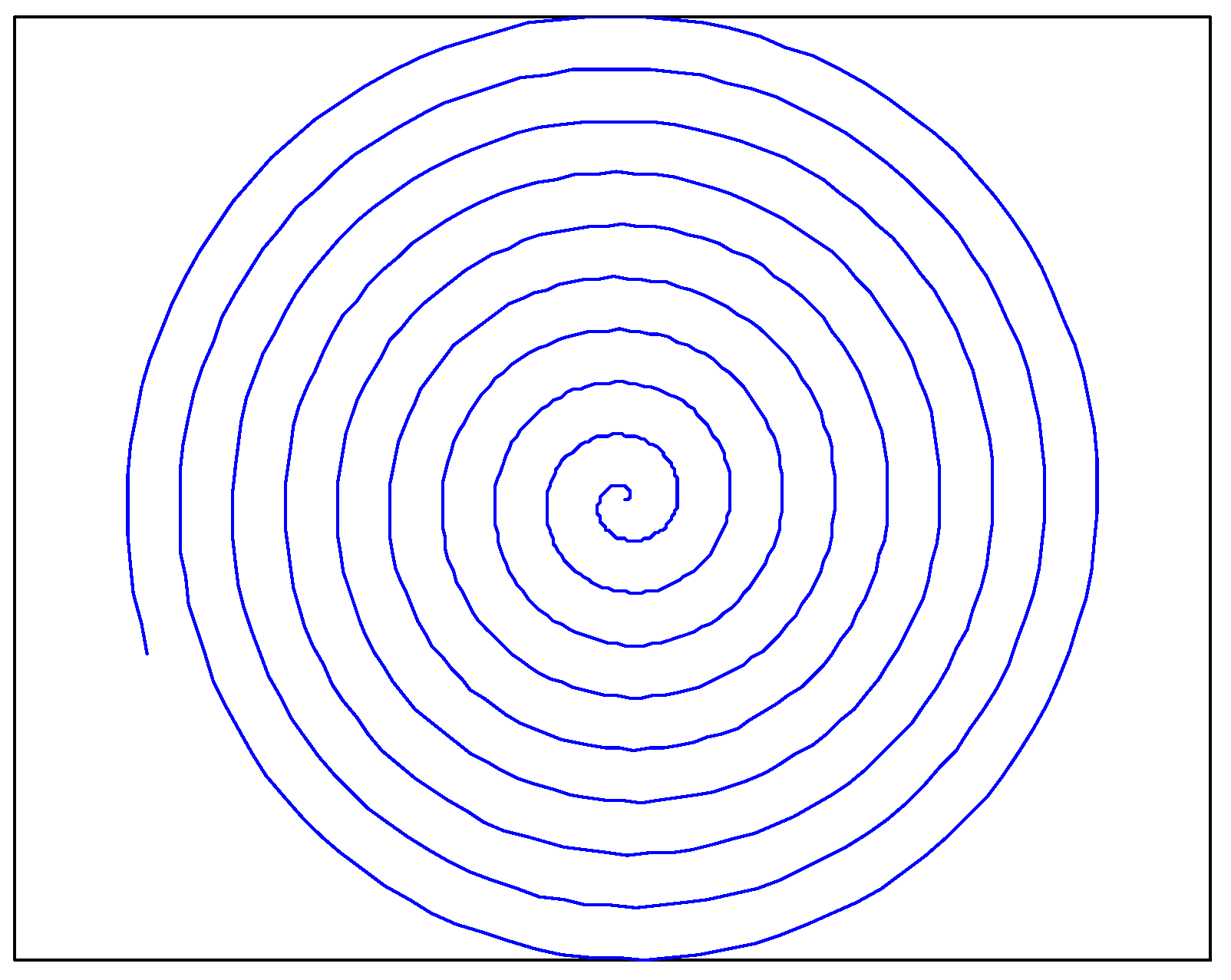
3.1.1. Logarithmic Spiral Curve (Lo)
3.1.2. Archimedes Spiral Curve (Ar)
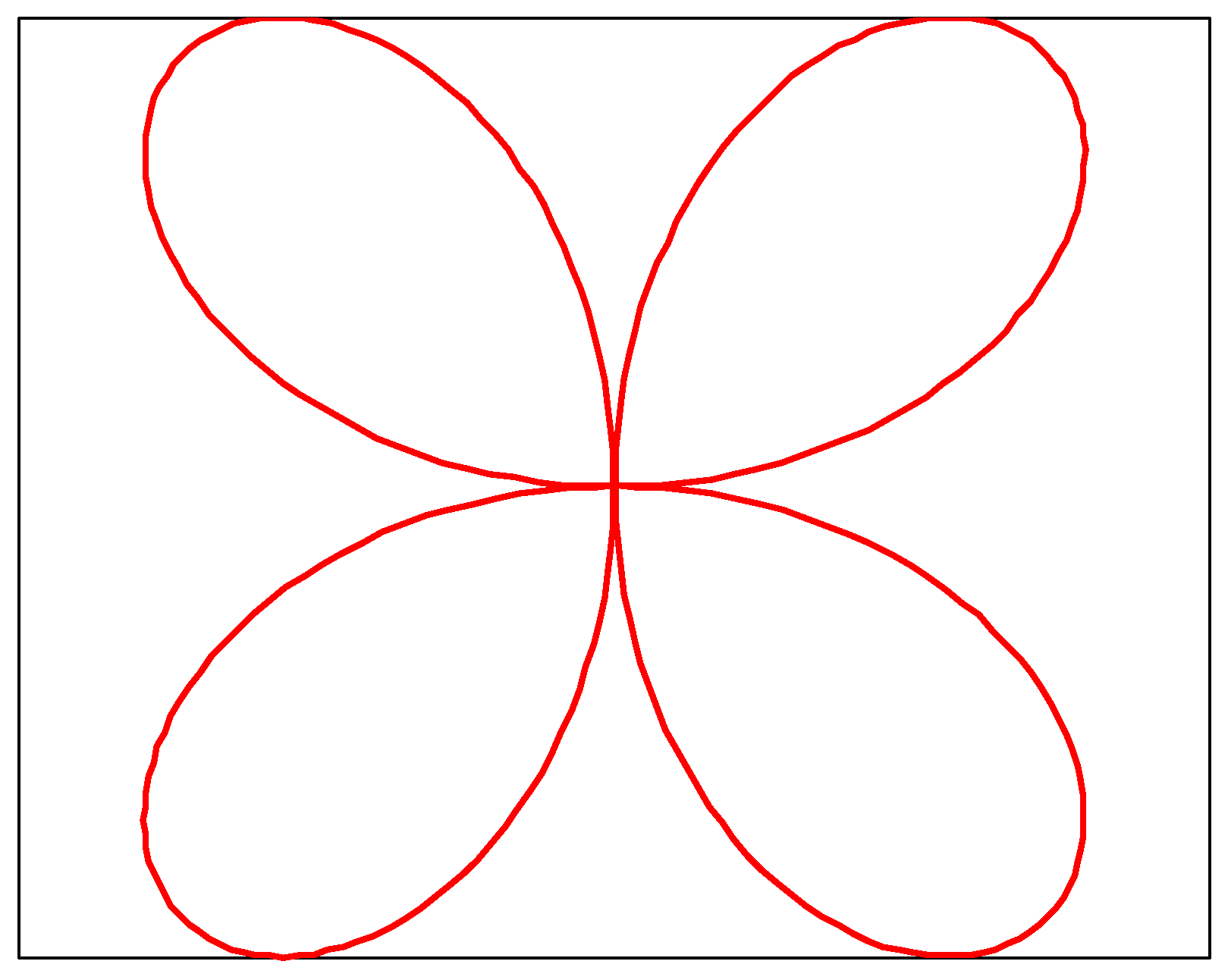
3.1.3. Rose Spiral Curve (Ro)
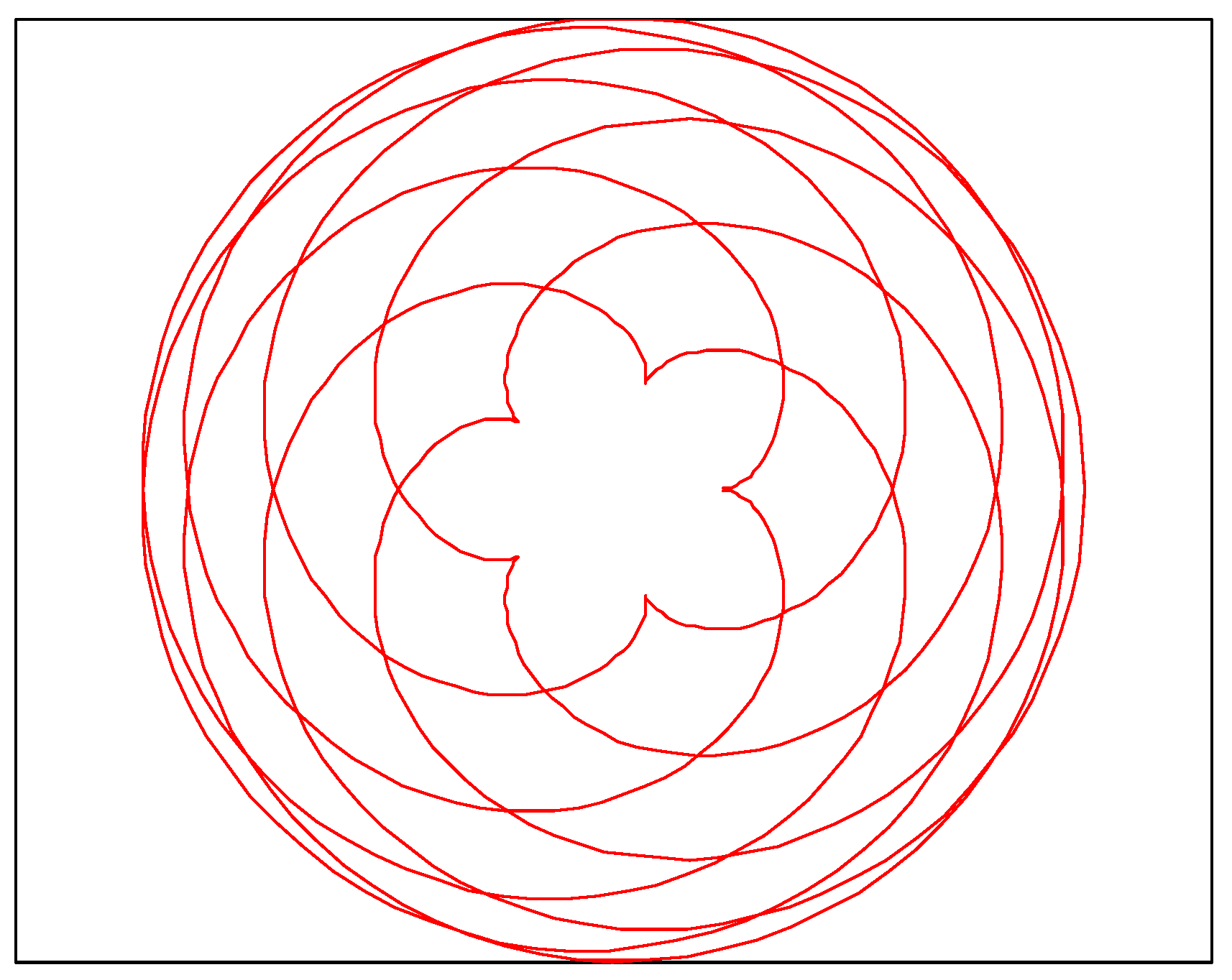
3.1.4. Epitrochoid-I (Ep-I)
3.1.5. Hypotrochoid (Hy)
3.1.6. Epitrochoid-II (Ep-II)
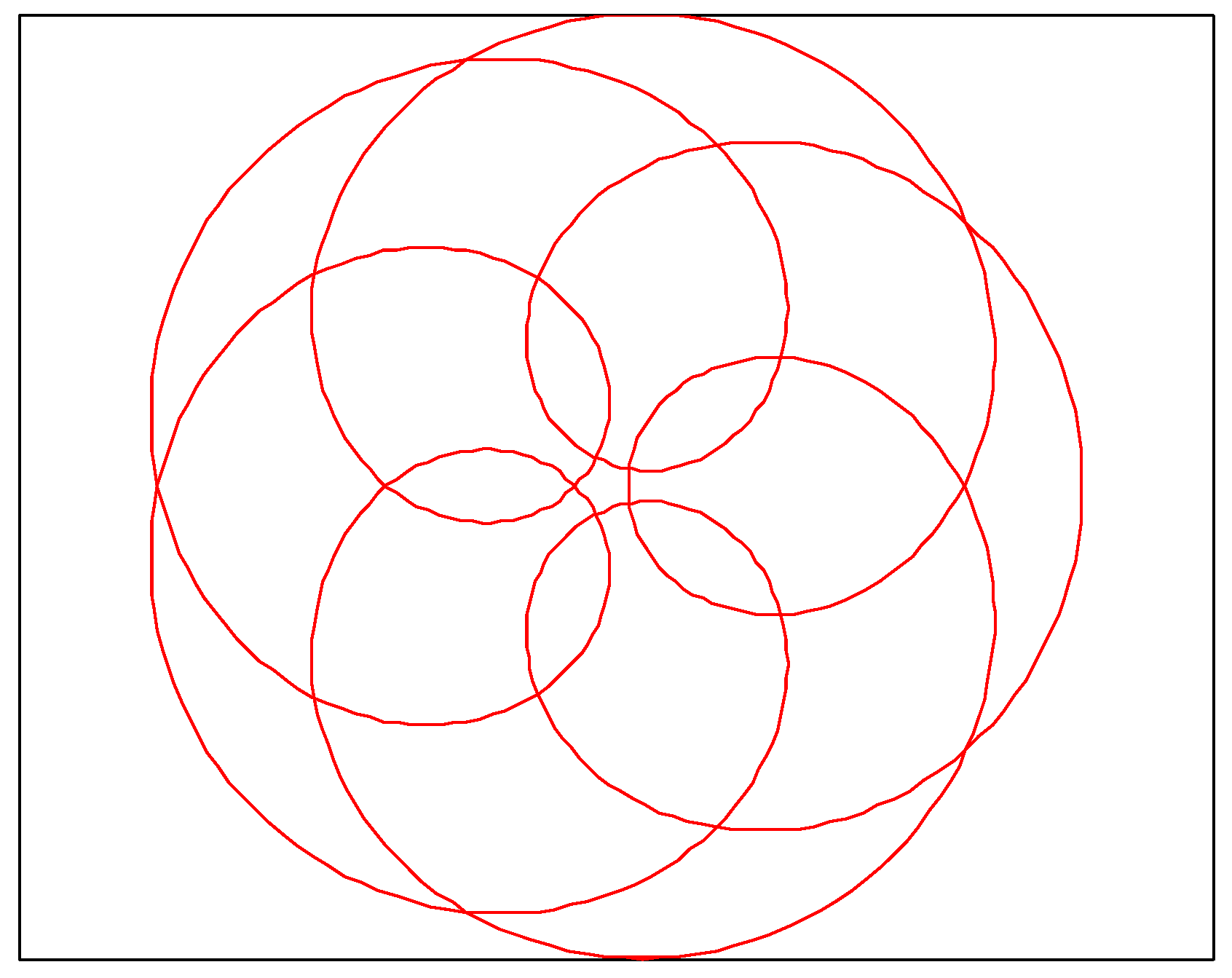
3.1.7. Fermat Spiral Curve (Fe)
3.1.8. Lituus Spiral Curve (Li)
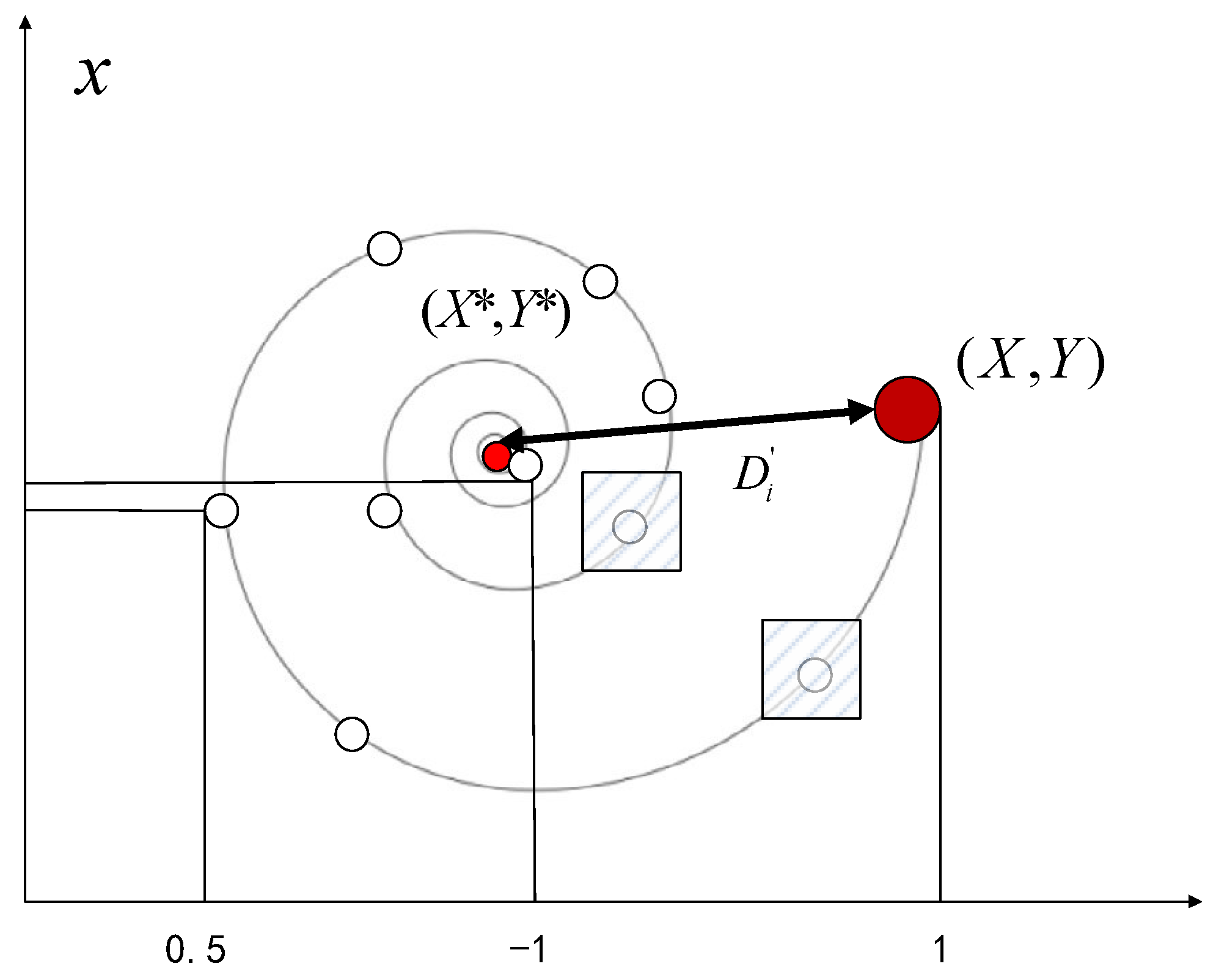
3.2. Introduction of Disturbance Factor
3.3. Improved WOA with Perceptual Disturbances and Complex Paths
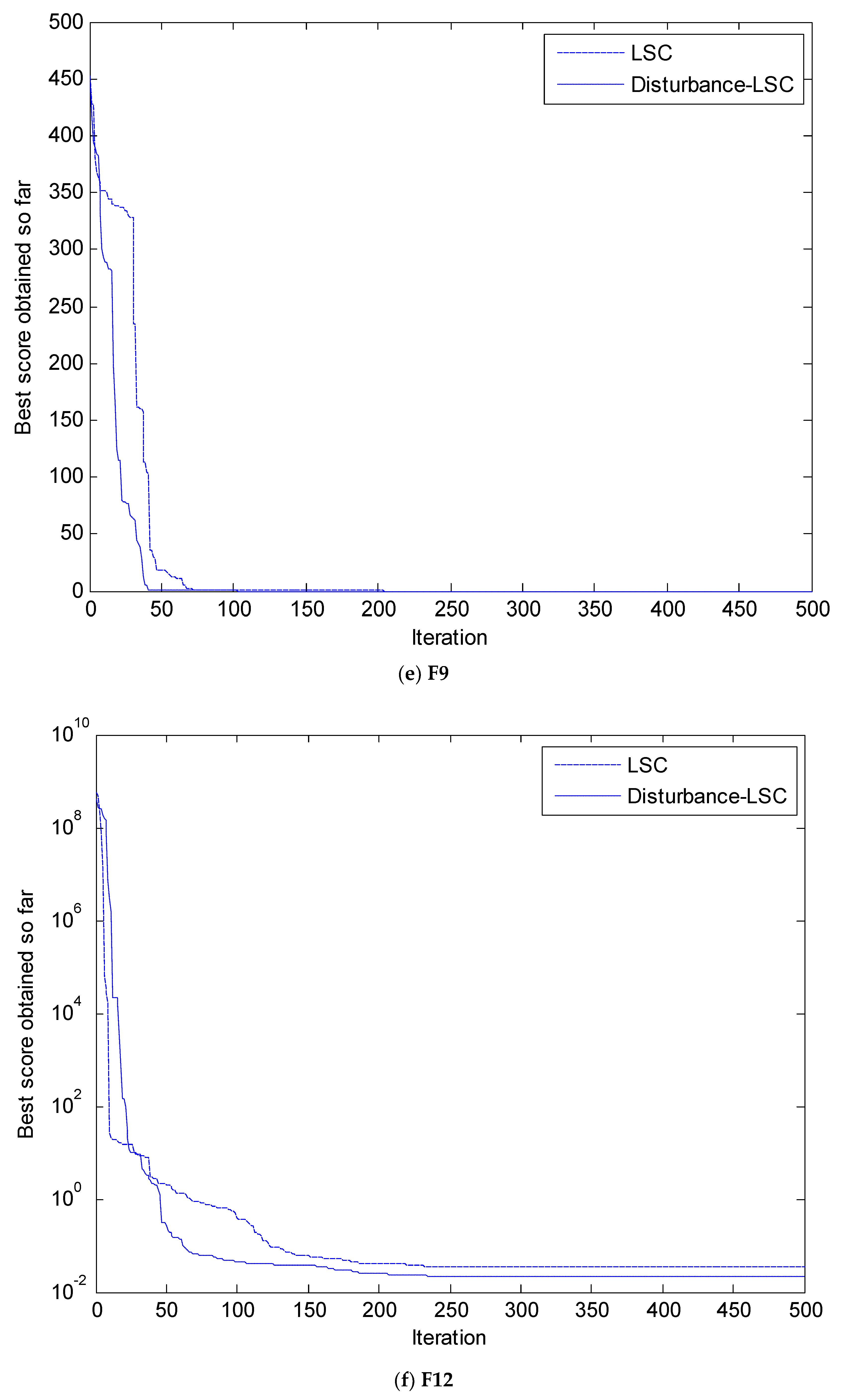
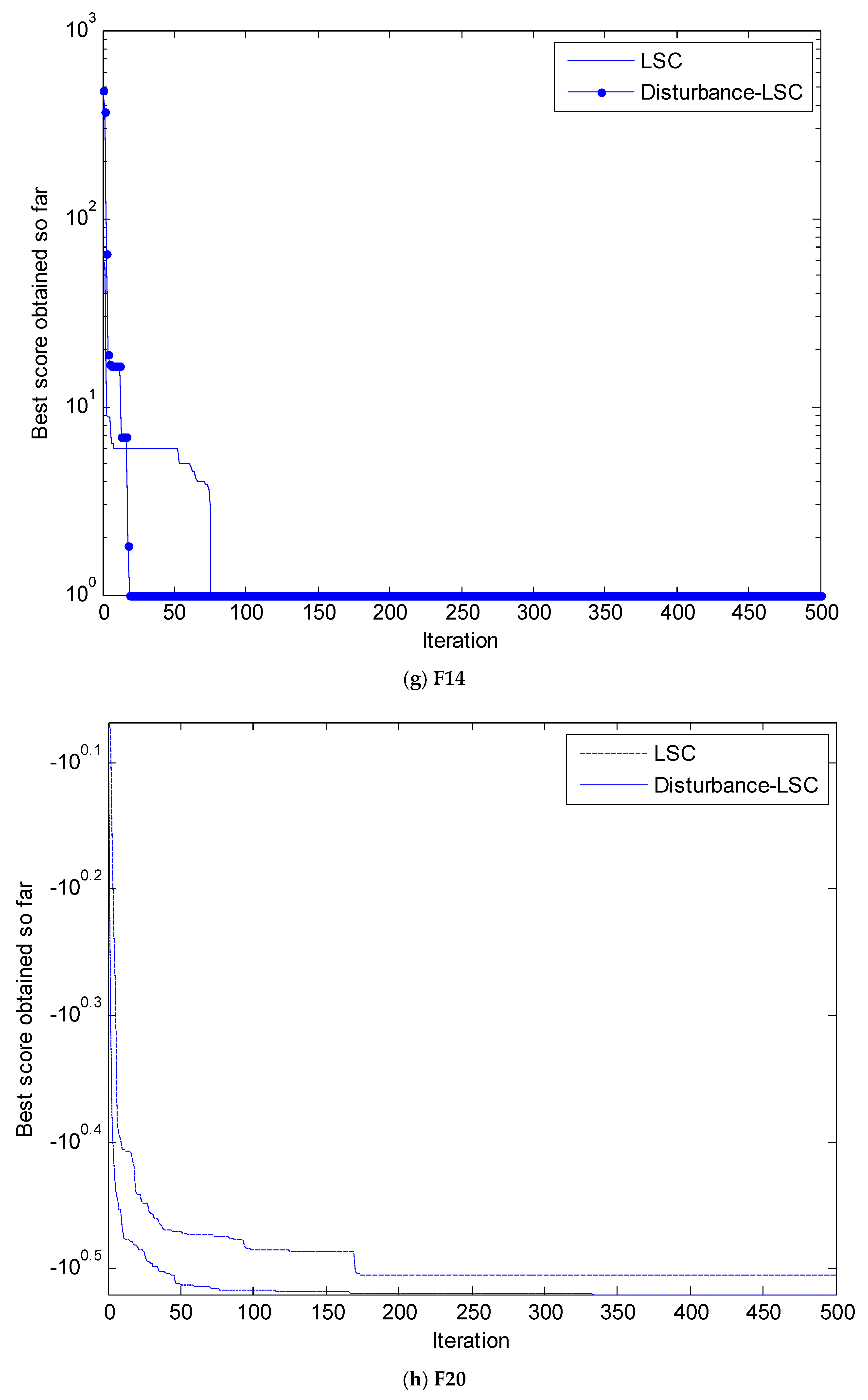
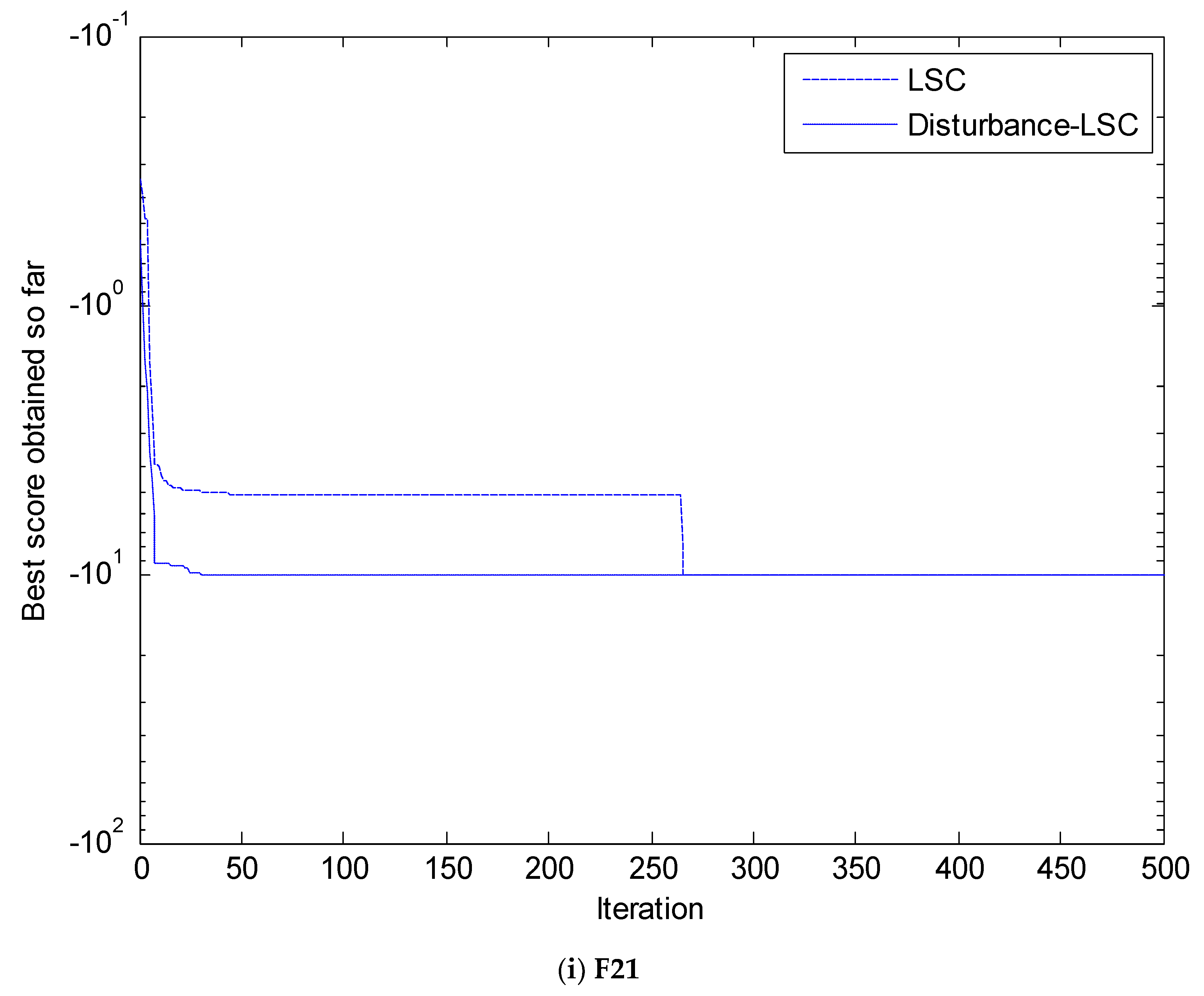
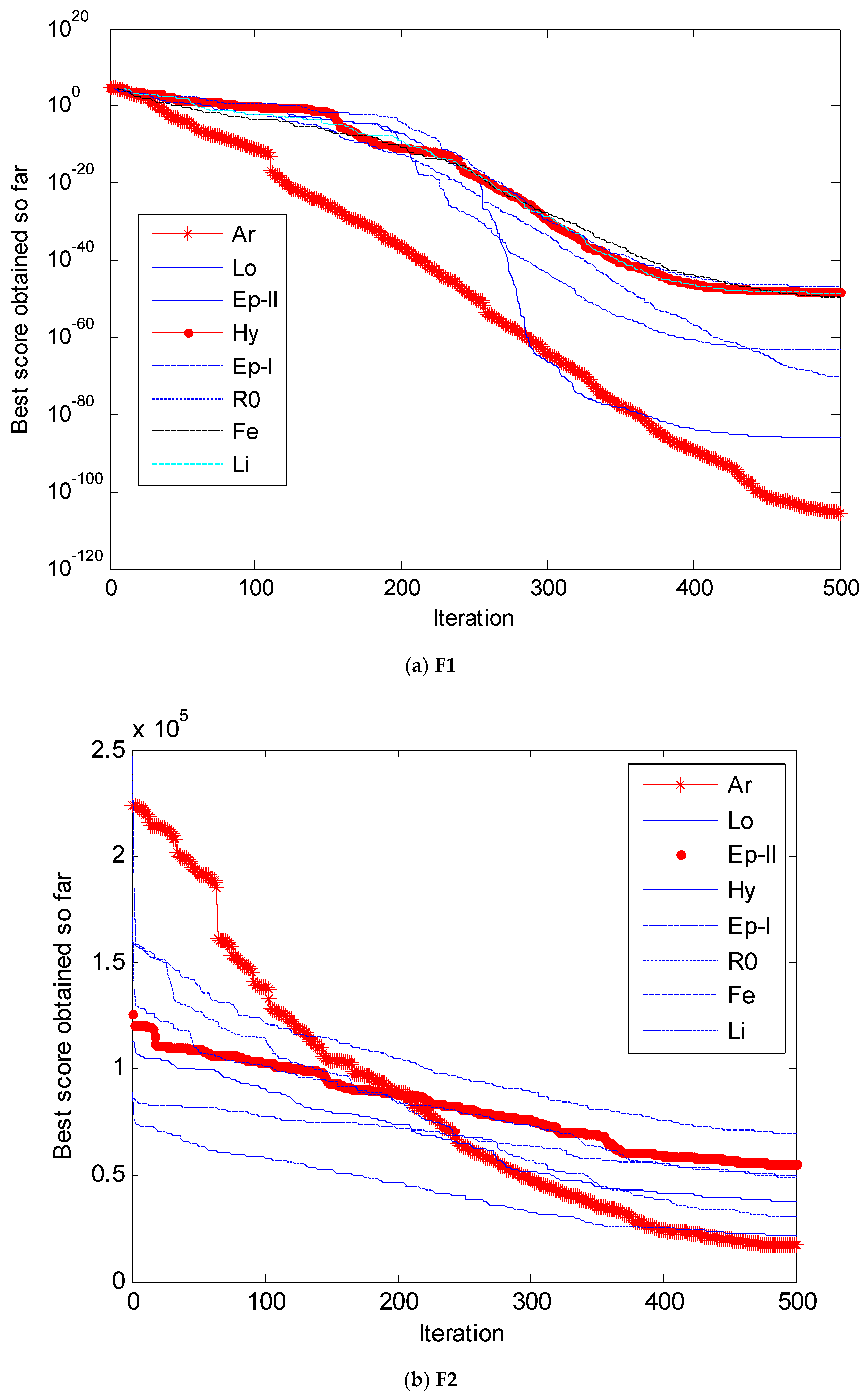
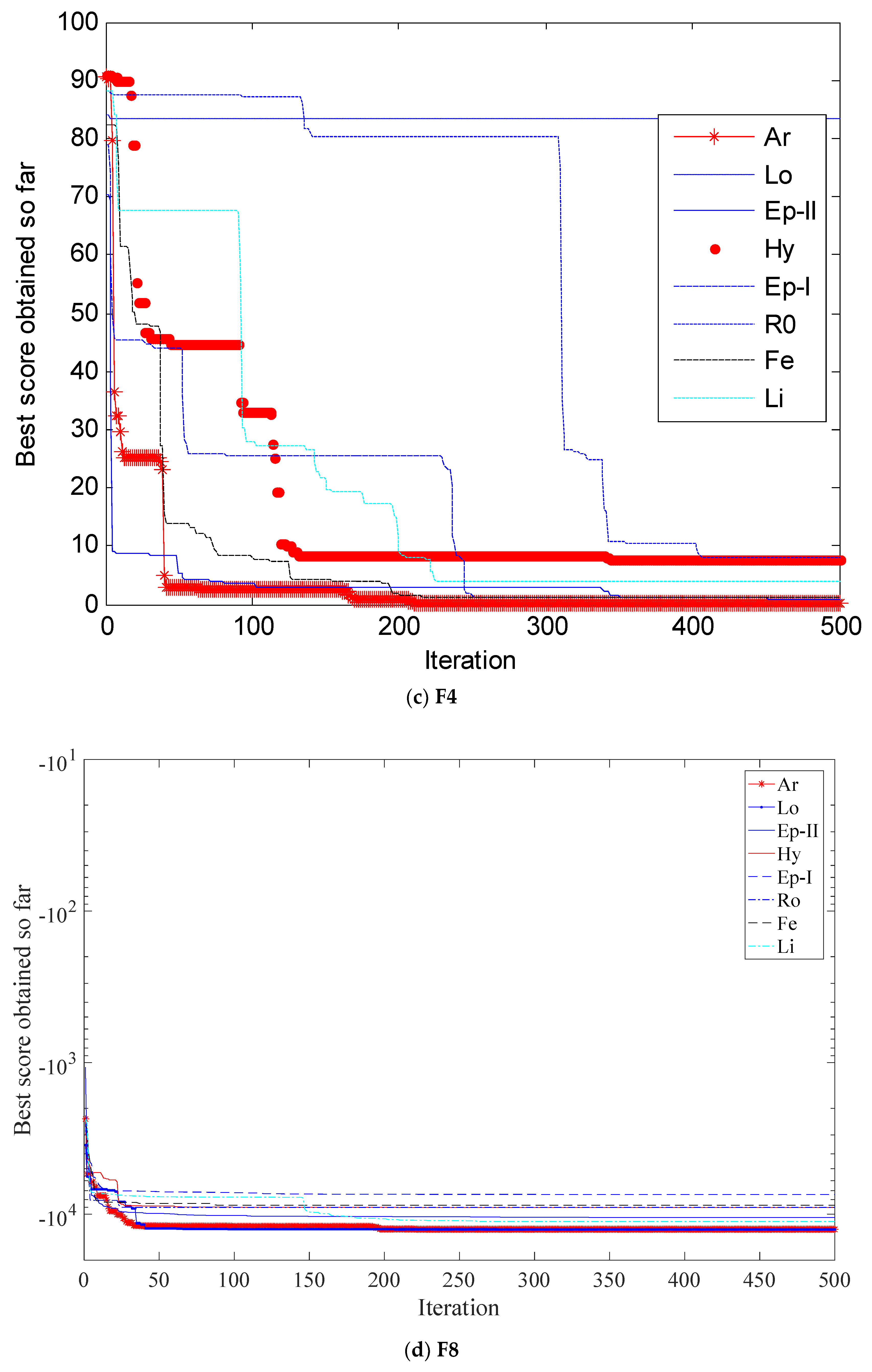
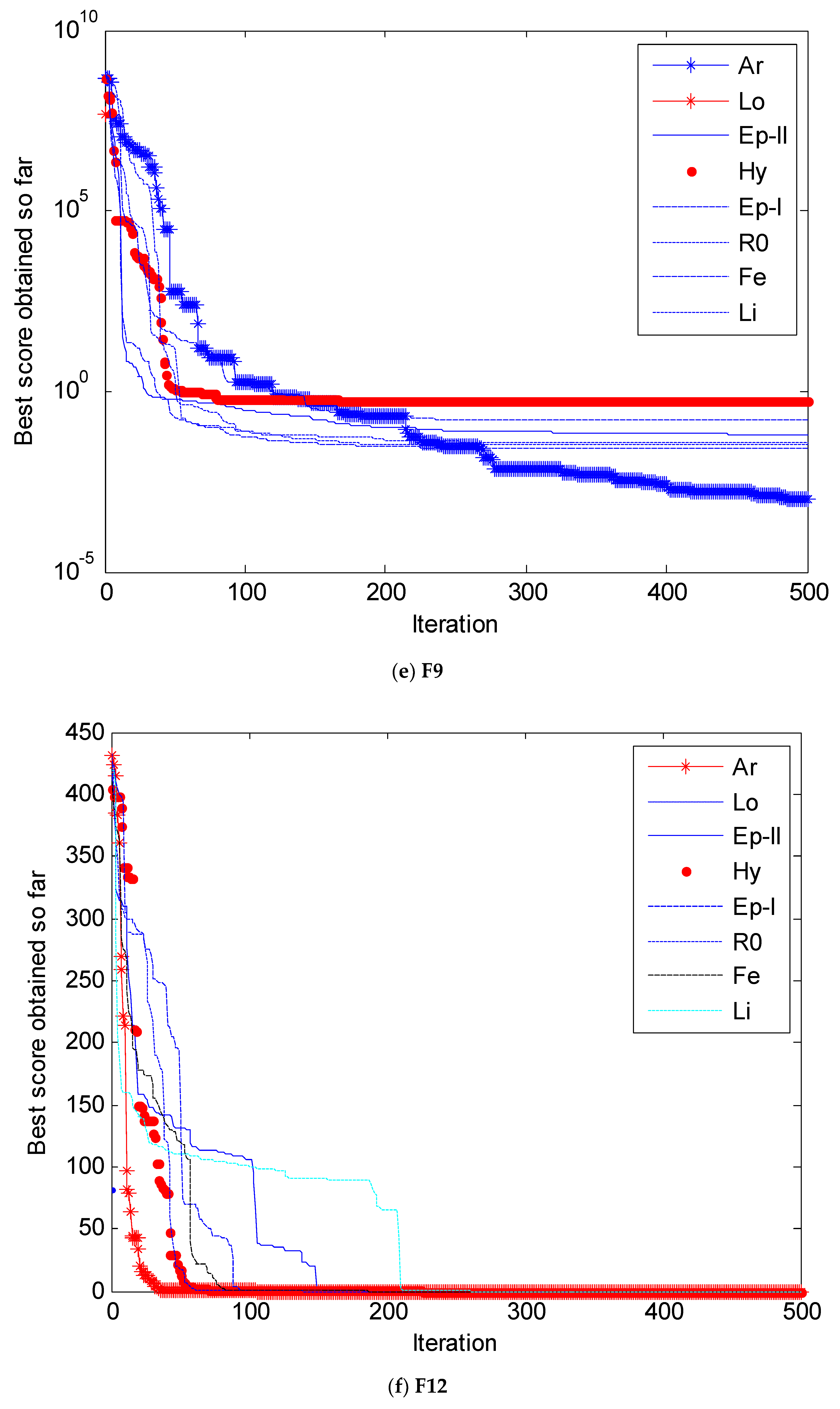
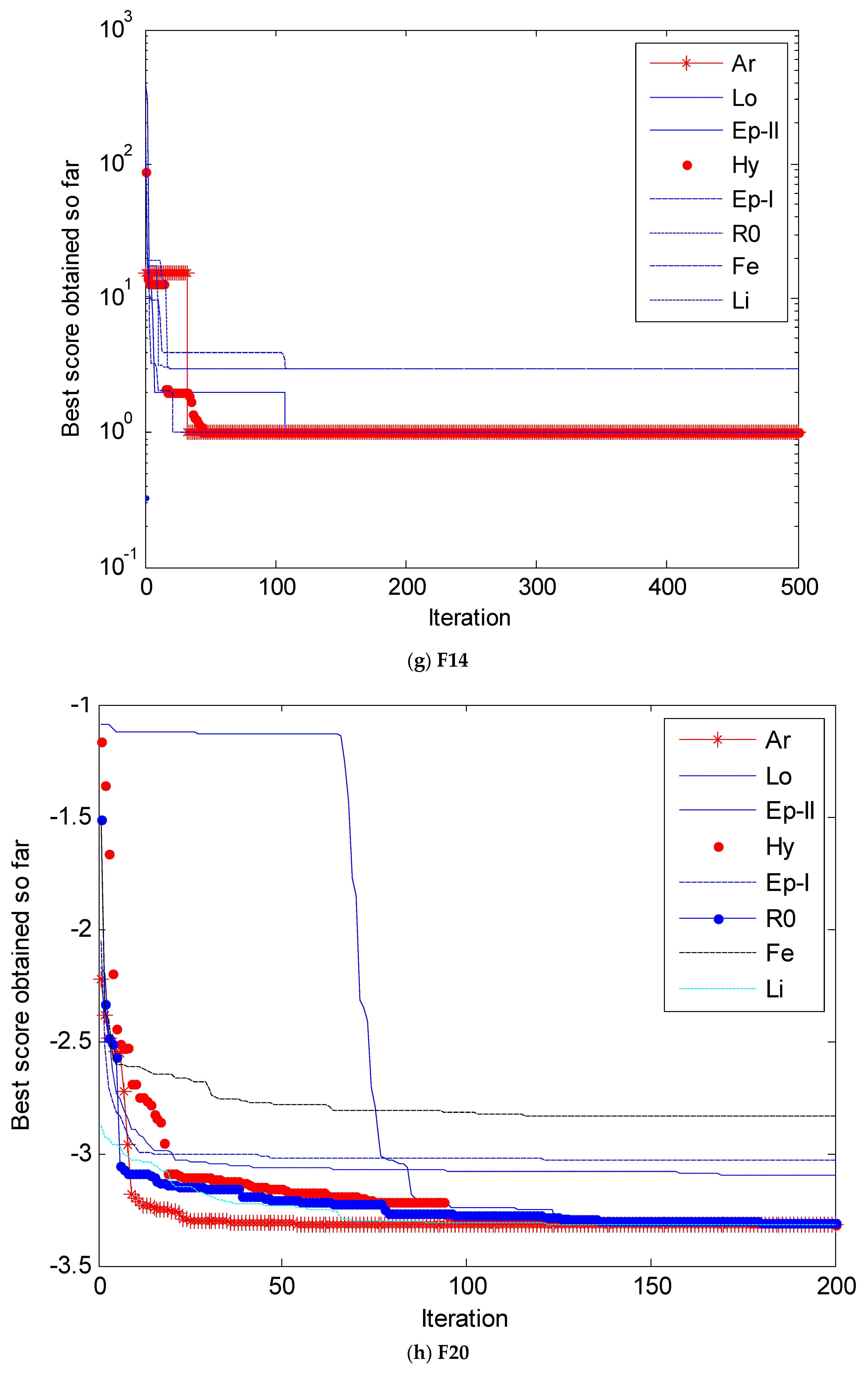
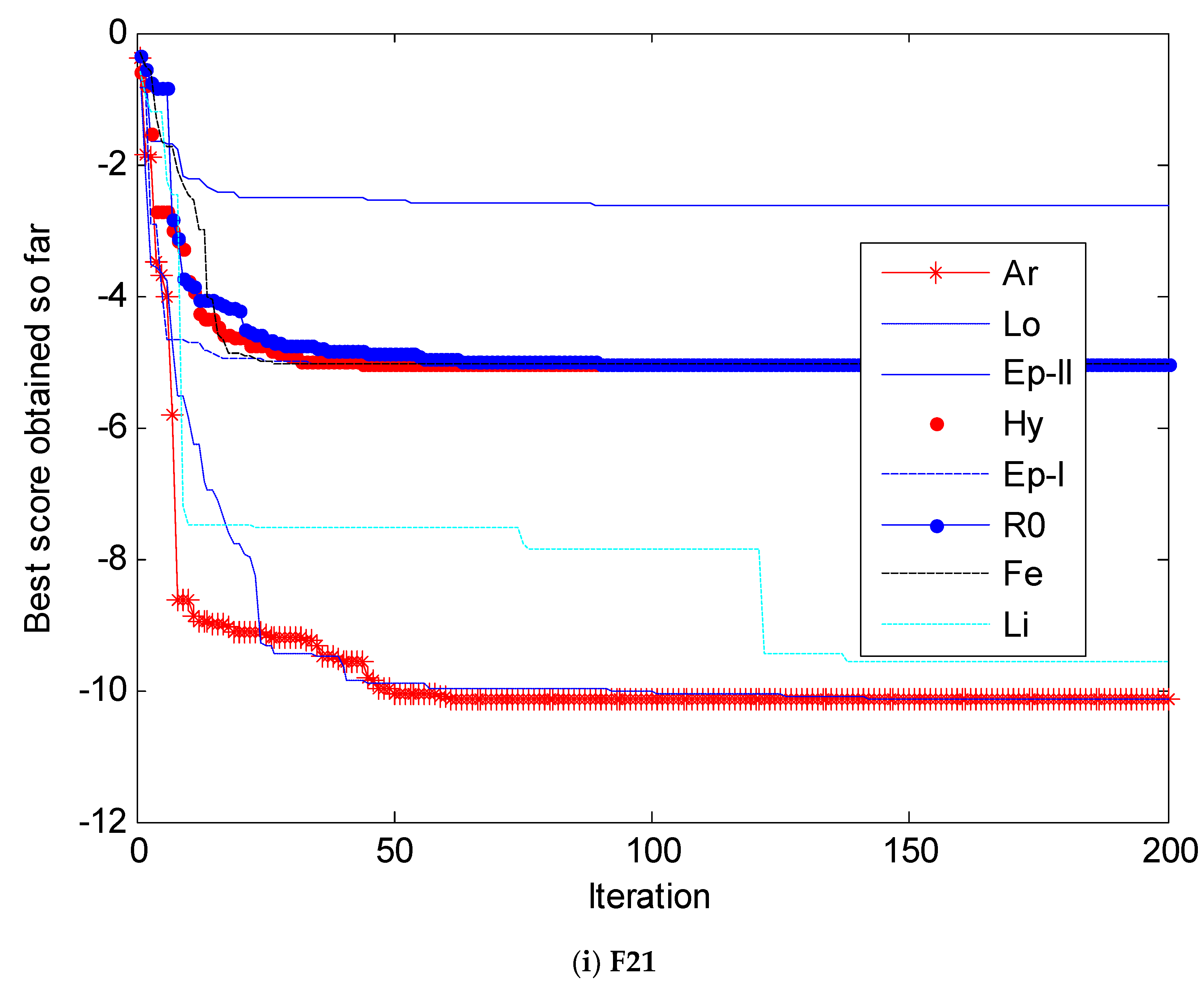
4. Simulation and Results Analysis
4.1. Selection of Testing Functions
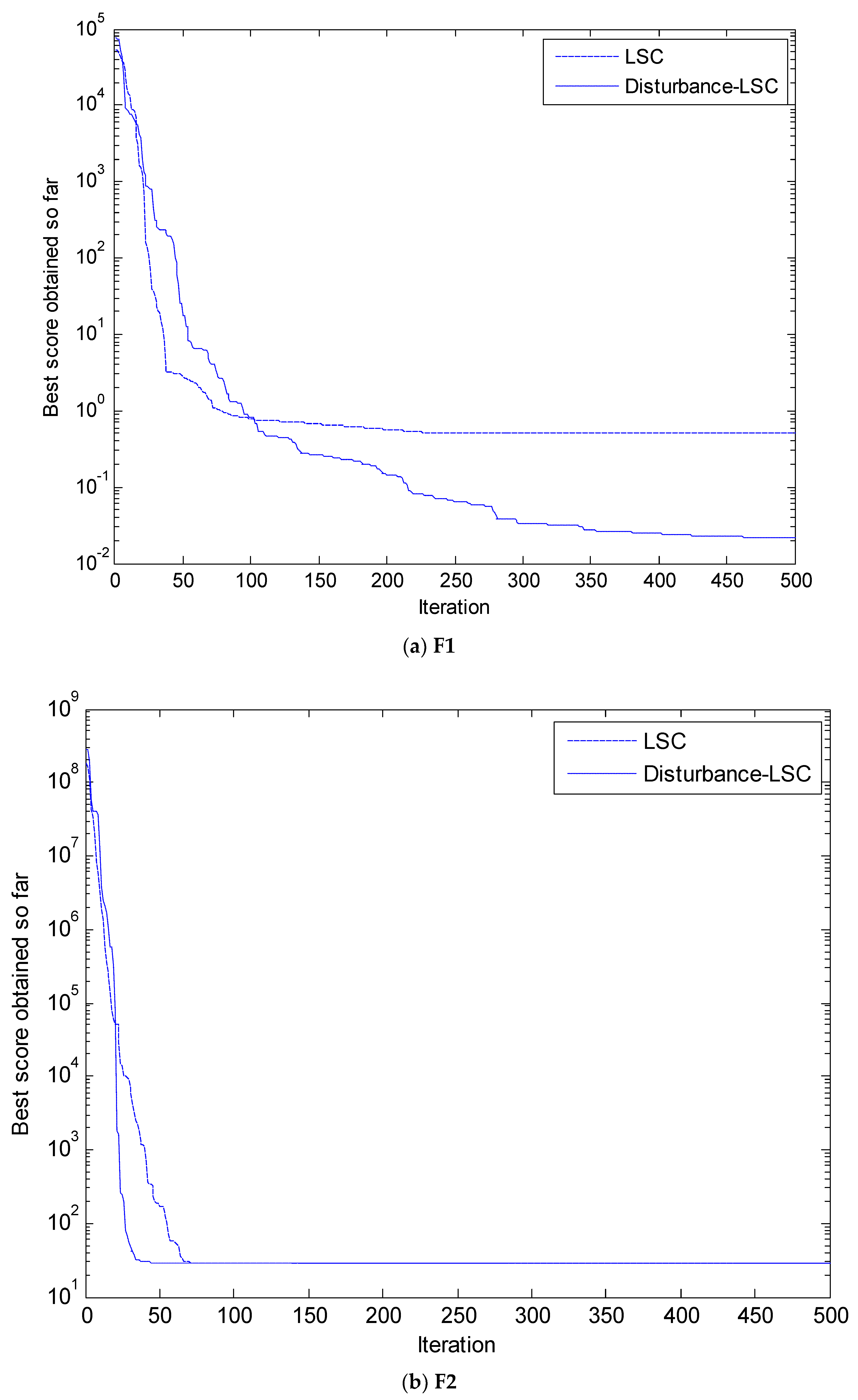
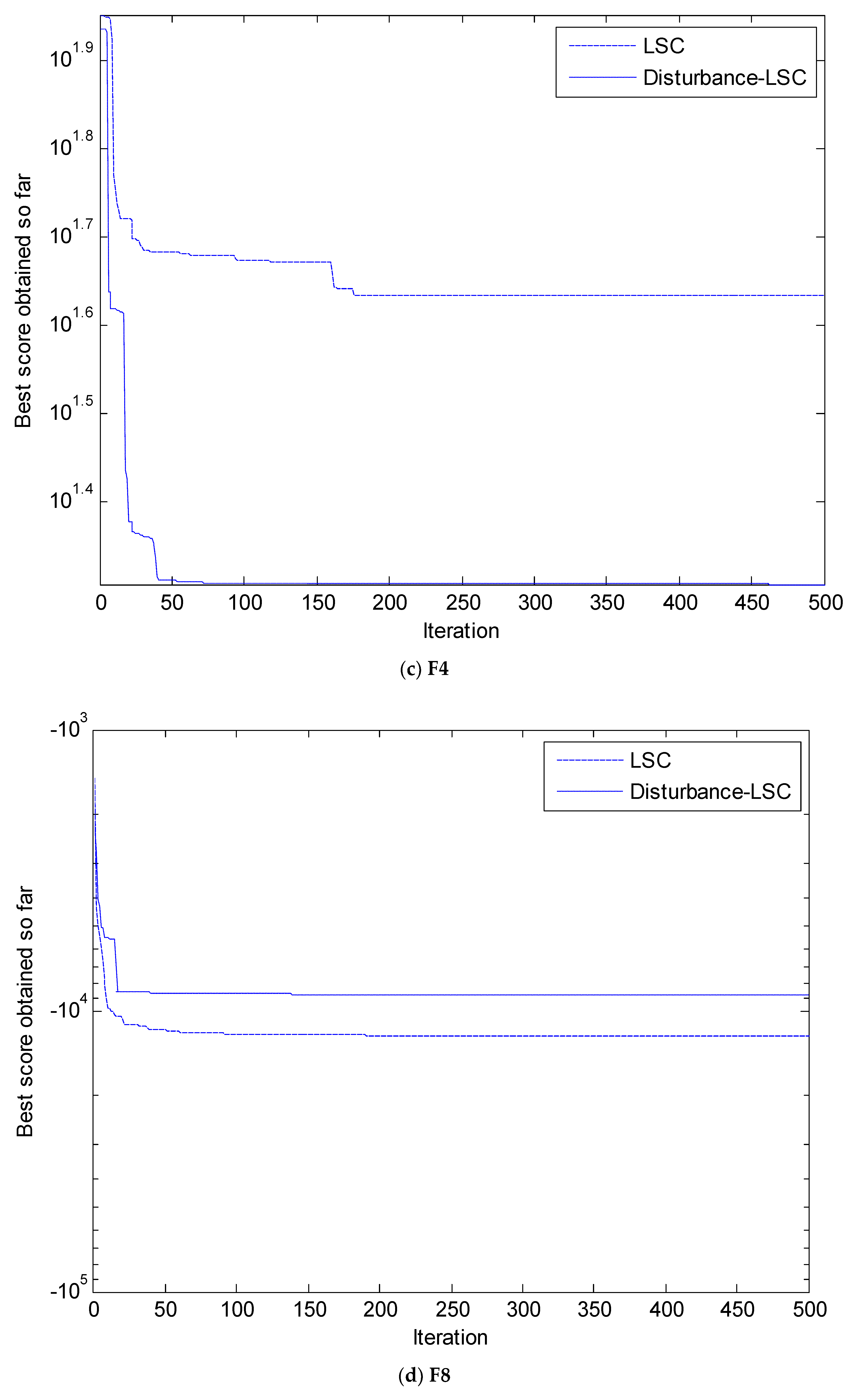
4.2. Simulation Results and Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Chandra Mohan, B.; Baskaran, R. A survey: Ant Colony Optimization based recent research and implementation on several engineering domain. Expert Syst. Appl. 2012, 39, 4618–4627. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Y.; Li, J. Nonparametric modeling of magnetorheological elastomer base isolator based on artificial neural network optimized by ant colony algorithm. J. Intell. Mater. Syst. Struct. 2015, 26, 1789–1798. [Google Scholar] [CrossRef]
- Precup, R.E.; Sabau, M.C.; Petriu, E.M. Nature-inspired optimal tuning of input membership functions of Takagi-Sugeno-Kang fuzzy models for anti-lock braking systems. Appl. Soft Comput. 2015, 27, 575–589. [Google Scholar] [CrossRef]
- Vallada, E.; Ruiz, R. A genetic algorithm for the unrelated parallel machine scheduling problem with sequence dependent setup times. Eur. J. Oper. Res. 2011, 211, 612–622. [Google Scholar] [CrossRef]
- Zăvoianu, A.-C.; Bramerdorfer, G.; Lughofer, E.; Silber, S.; Amrhein, W.; Klement, E.P. Hybridization of multi-objective evolutionary algorithms and artificial neural networks for optimizing the performance of electrical drives. Eng. Appl. Artif. Intell. 2013, 26, 1781–1794. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: New York, NY, USA, 2010; pp. 760–766. [Google Scholar]
- Yu, Y.; Li, Y.; Li, J. Parameter identification of a novel strain stiffening model for magnetorheological elastomer base isolator utilizing enhanced particle swarm optimization. J. Intell. Mater. Syst. Struct. 2015, 26, 2446–2462. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Y.; Li, J. Forecasting hysteresis behaviours of magnetorheological elastomer base isolator utilizing a hybrid model based on support vector regression and improved particle swarm optimization. Smart Mater. Struct. 2015, 24, 035025. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C.; Petriu, E.M. Grey Wolf Optimizer Algorithm-Based Tuning of Fuzzy Control Systems with Reduced Parametric Sensitivity. IEEE Trans. Ind. Electron. 2016, 64, 527–534. [Google Scholar] [CrossRef]
- Saadat, J.; Moallem, P.; Koofigar, H. Training echo state neural network using harmony search algorithm. Int. J. Artif. Intell. 2017, 15, 163–179. [Google Scholar]
- Vrkalovic, S.; Teban, T.A.; Borlea, L.D. Stable Takagi-Sugeno fuzzy control designed by optimization. Int. J. Artif. Intell. 2017, 15, 17–29. [Google Scholar]
- Reddy, P.D.P.; Reddy, V.C.V.; Manohar, T.G. Whale optimization algorithm for optimal sizing of renewable resources for loss reduction in distribution systems. Renew. Wind Water Solar 2017, 4, 3. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Bhoye, M.; Bhesdadiya, R.H.; Jangir, P.; Jangir, N.; Kumar, A. An emission constraint environment dispatch problem solution with microgrid using Whale Optimization Algorithm. In Proceedings of the Power Systems Conference, Bhubaneswar, India, 19–21 December 2016. [Google Scholar]
- Rosyadi, A.; Penangsang, O.; Soeprijanto, A. Optimal filter placement and sizing in radial distribution system using whale optimization algorithm. In Proceedings of the International Seminar on Intelligent Technology and ITS Applications, Surabaya, Indonesia, 28–29 August 2017; pp. 87–92. [Google Scholar]
- Buch, H.; Jangir, P.; Jangir, N.; Ladumor, D.; Bhesdadiya, R.H. Optimal Placement and Coordination of Static VAR Compensator with Distributed Generation using Whale Optimization Algorithm. In Proceedings of the IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016. [Google Scholar]
- Ladumor, D.P.; Trivedi, I.N.; Jangir, P.; Kumar, A. A Whale Optimization Algorithm approach for Unit Commitment Problem Solution. In Proceedings of the Conference Advancement in Electrical & Power Electronics Engineering (AEPEE 2016), Morbi, India, 14–17 December 2016. [Google Scholar]
- Prakash, D.B.; Lakshminarayana, C. Optimal siting of capacitors in radial distribution network using Whale Optimization Algorithm. Alex. Eng. J. 2016, 56, 499–509. [Google Scholar] [CrossRef]
- Yan, Z.; Sha, J.; Liu, B.; Tian, W.; Lu, J. An Ameliorative Whale Optimization Algorithm for Multi-Objective Optimal Allocation of Water Resources in Handan, China. Water 2018, 10, 87. [Google Scholar] [CrossRef]
- Medani, K.B.O.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2017. [Google Scholar] [CrossRef]
- Sun, W.Z.; Wang, J.S. Elman Neural network Soft-sensor Model of Conversion Velocity in Polymerization Process Optimized by Chaos Whale Optimization Algorithm. IEEE Access 2017, 5, 13062–13076. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2016, 22, 1–15. [Google Scholar] [CrossRef]
- Bhesdadiya, R.; Jangir, P.; Jangir, N.; Trivedi, I.N.; Ladumor, D. Training Multi-Layer Perceptron in Neural Network using Whale Optimization Algorithm. Indian J. Sci. Technol. 2016, 9, 28–36. [Google Scholar]
- Wang, J.; Du, P.; Niu, T.; Yang, W. A novel hybrid system based on a new proposed algorithm—Multi-Objective Whale Optimization Algorithm for wind speed forecasting. Appl. Energy 2017, 208, 344–360. [Google Scholar] [CrossRef]
- Niu, P.F.; Wu, Z.L.; Ma, Y.P.; Shi, C.J.; Li, J.B. Prediction of steam turbine heat consumption rate based on whale optimization algorithm. CIESC J. 2017, 68, 1049–1057. [Google Scholar]
- Aziz, M.A.E.; Ewees, A.A.; Hassanien, A.E. Whale Optimization Algorithm and Moth-Flame Optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Mostafa, A.; Hassanien, A.E.; Houseni, M.; Hefny, H. Liver segmentation in MRI images based on whale optimization algorithm. Multimed. Tools Appl. 2017, 76, 24931–24954. [Google Scholar] [CrossRef]
- Jangir, P.; Jangir, N. Non-Dominated Sorting Whale Optimization Algorithm (NSWOA): A Multi-Objective Optimization Algorithm for Solving Engineering Design Problems. Glob. J. Res. Eng. 2017, 17, 15–42. [Google Scholar]
- Oliva, D.; Aziz, M.A.E.; Hassanien, A.E. Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 2017, 200, 141–154. [Google Scholar]
- Sharawi, M.; Zawbaa, H.M.; Emary, E. Feature selection approach based on whale optimization algorithm. In Proceedings of the Ninth International Conference on Advanced Computational Intelligence, Doha, Qatar, 4–6 February 2017; pp. 163–168. [Google Scholar]
- Zhao, G.; Zhou, Y.; Ouyang, Z.; Wang, Y. A Novel Disturbance Parameters PSO Algorithm for Functions Optimization. Adv. Inf. Sci. Serv. Sci. 2012, 4, 51–57. [Google Scholar]
- Jing, Y.E. The Diversity Disturbance PSO Algorithm to Solve TSP Problem. J. Langfang Teach. Coll. 2010, 5, 2. [Google Scholar]
- Li, D.; Deng, N. An electoral quantum-behaved PSO with simulated annealing and gaussian disturbance for permutation flow shop scheduling. J. Inf. Comput. Sci. 2012, 9, 2941–2949. [Google Scholar]
- Gao, H.; Kwong, S.; Yang, J.; Cao, J. Particle swarm optimization based on intermediate disturbance strategy algorithm and its application in multi-threshold image segmentation. Inf. Sci. 2013, 250, 82–112. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid Whale Optimization Algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Ling, Y.; Zhou, Y.; Luo, Q. Lévy Flight Trajectory-Based Whale Optimization Algorithm for Global Optimization. IEEE Access 2017, 5, 6168–6186. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; El-Shahat, D.; El-Henawy, I.; Sangaiah, A.K.; Ahmed, S.H. A Novel Whale Optimization Algorithm for Cryptanalysis in Merkle-Hellman Cryptosystem. Mob. Netw. Appl. 2018, 5, 1–11. [Google Scholar] [CrossRef]
- Kaveh, A.; Ghazaan, M.I. Enhanced Whale Optimization Algorithm for Sizing Optimization of Skeletal Structures. Mech. Based Des. Struct. Mach. 2017, 45, 345–362. [Google Scholar] [CrossRef]
- Spiral Curve. Van Nostrand’s Scientific Encyclopedia; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ren, Y.; Wu, Y. An efficient algorithm for high-dimensional function optimization. Soft Comput. 2013, 17, 995–1004. [Google Scholar] [CrossRef]
- Yuan, Z.; de Oca, M.A.M.; Birattari, M.; Stützle, T. Continuous optimization algorithms for tuning real and integer parameters of swarm intelligence algorithms. Swarm Intell. 2012, 6, 49–75. [Google Scholar] [CrossRef]
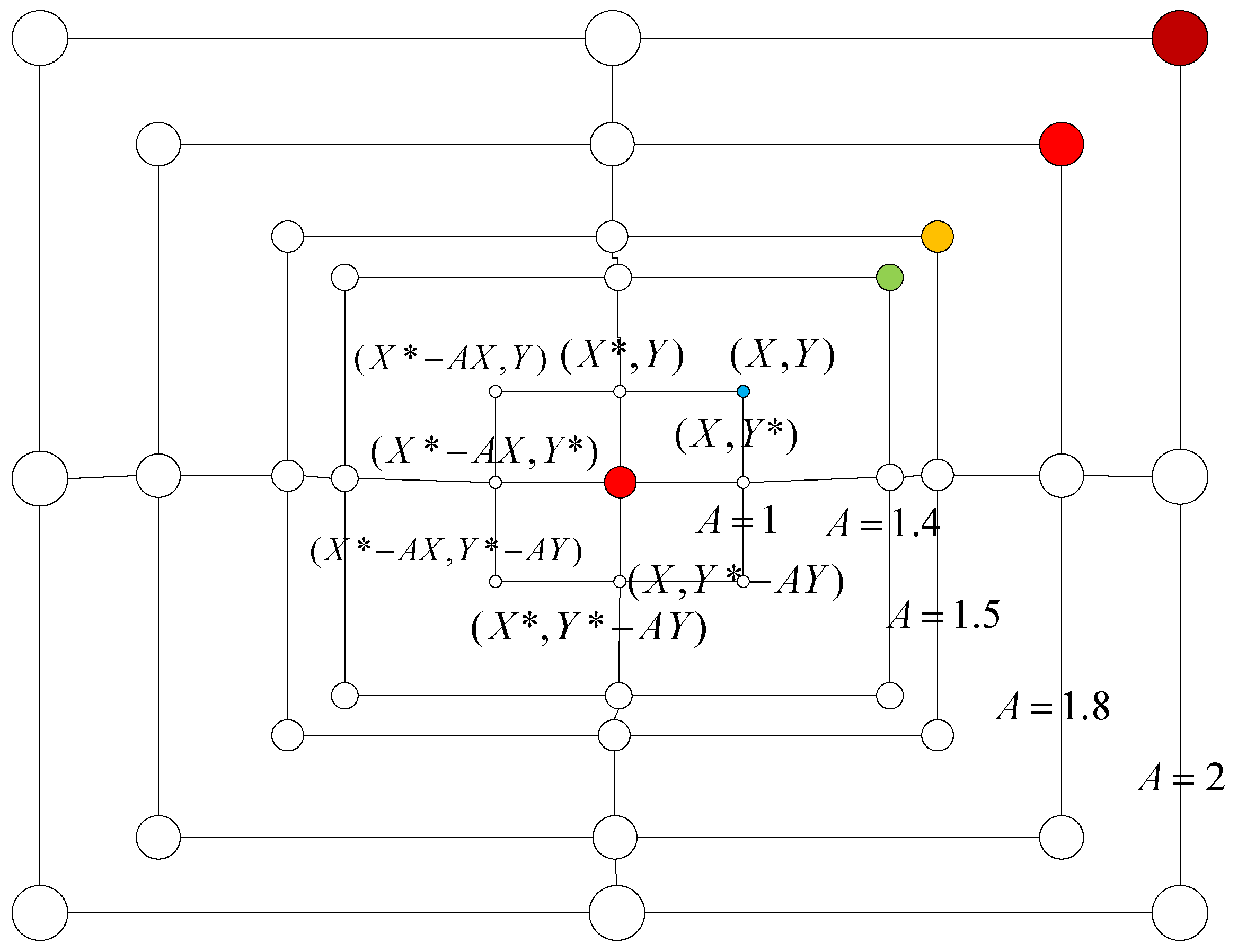

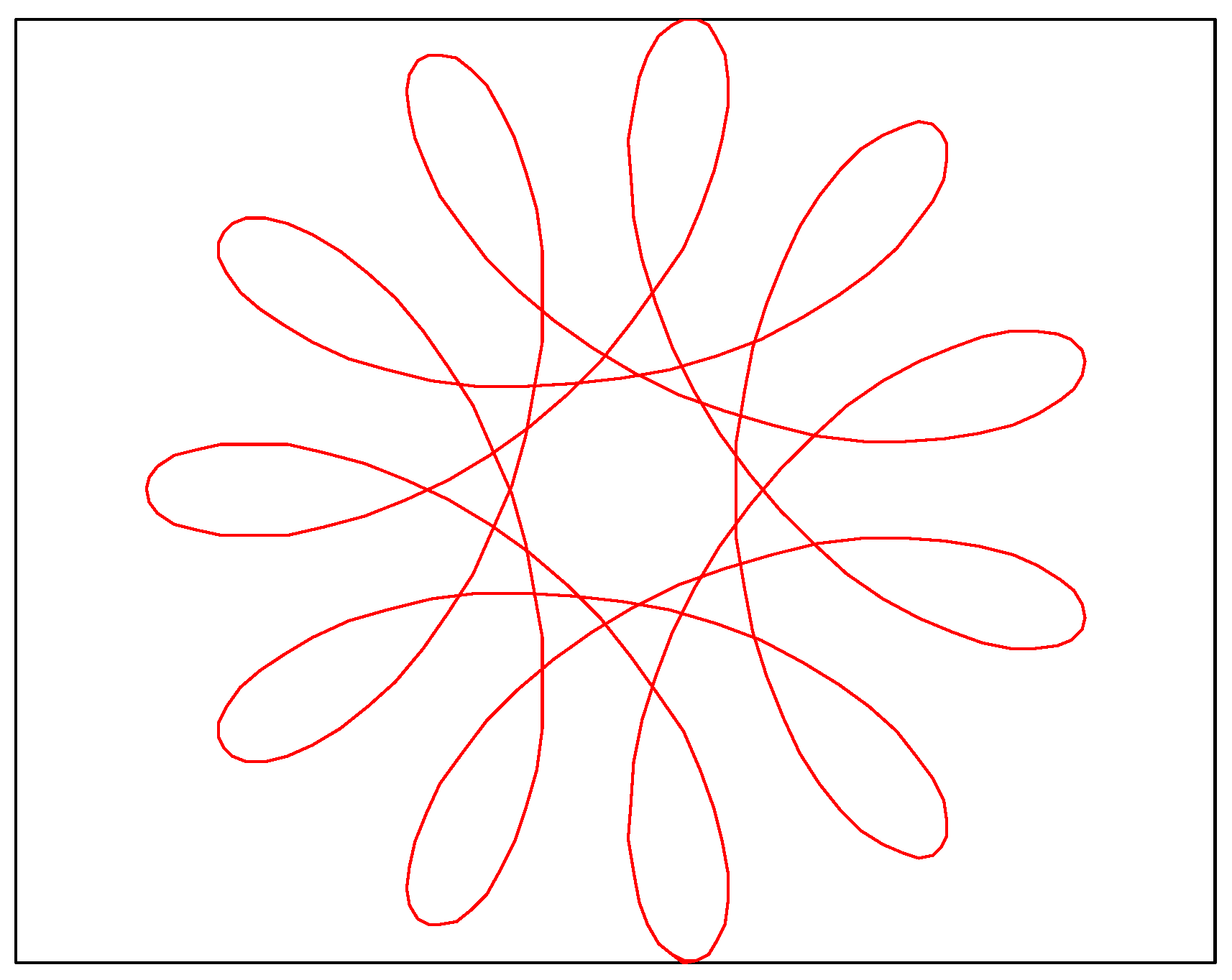

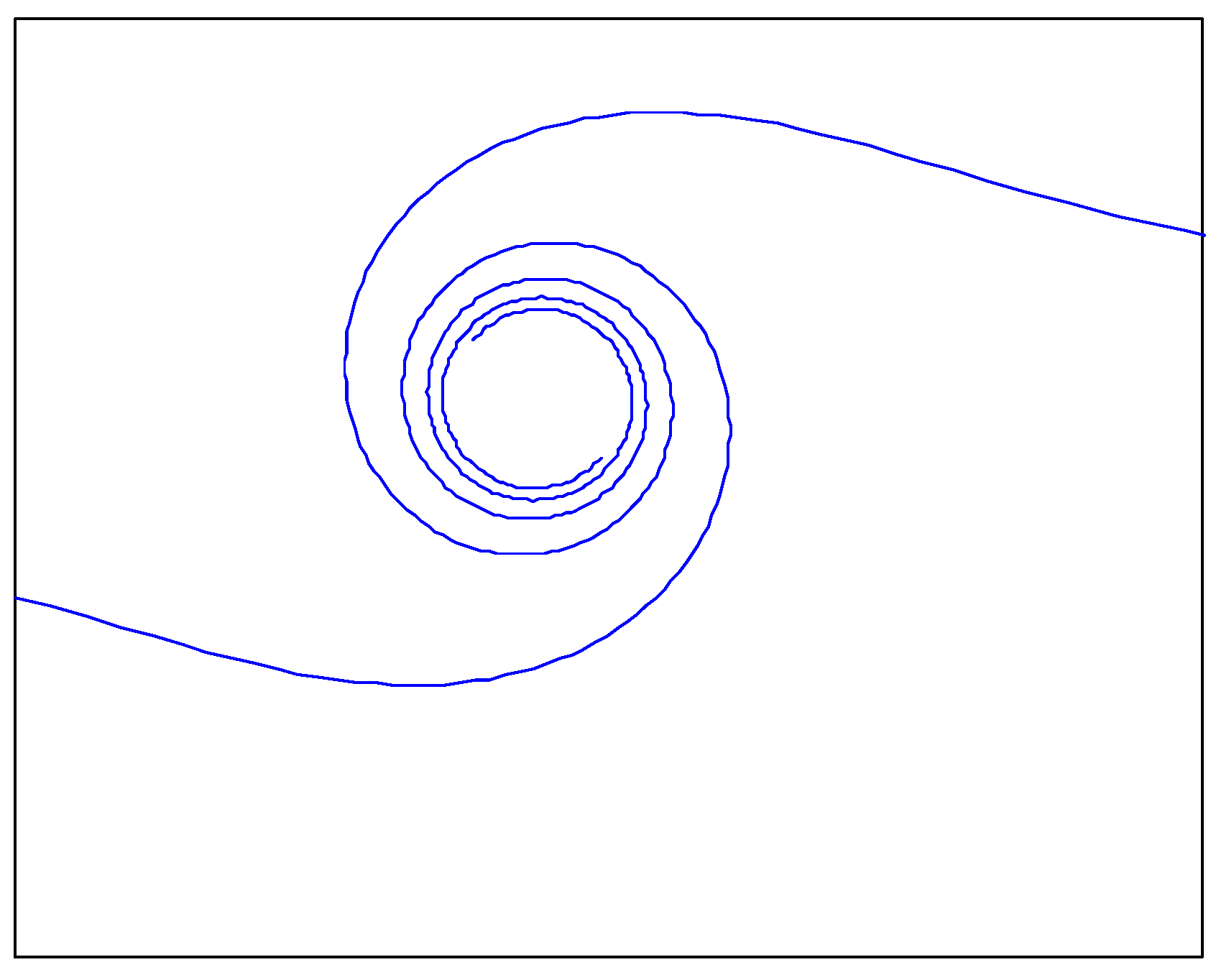
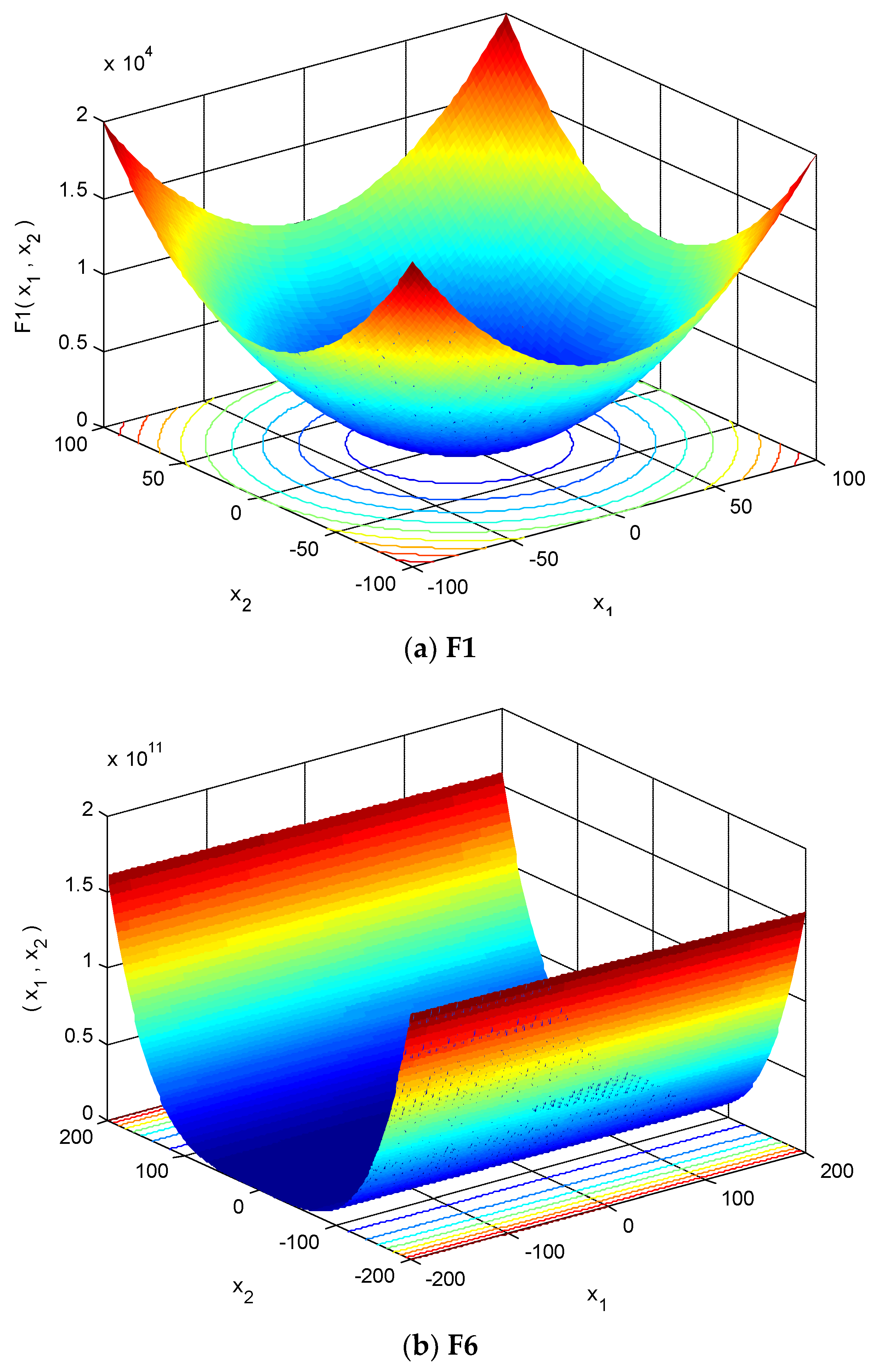
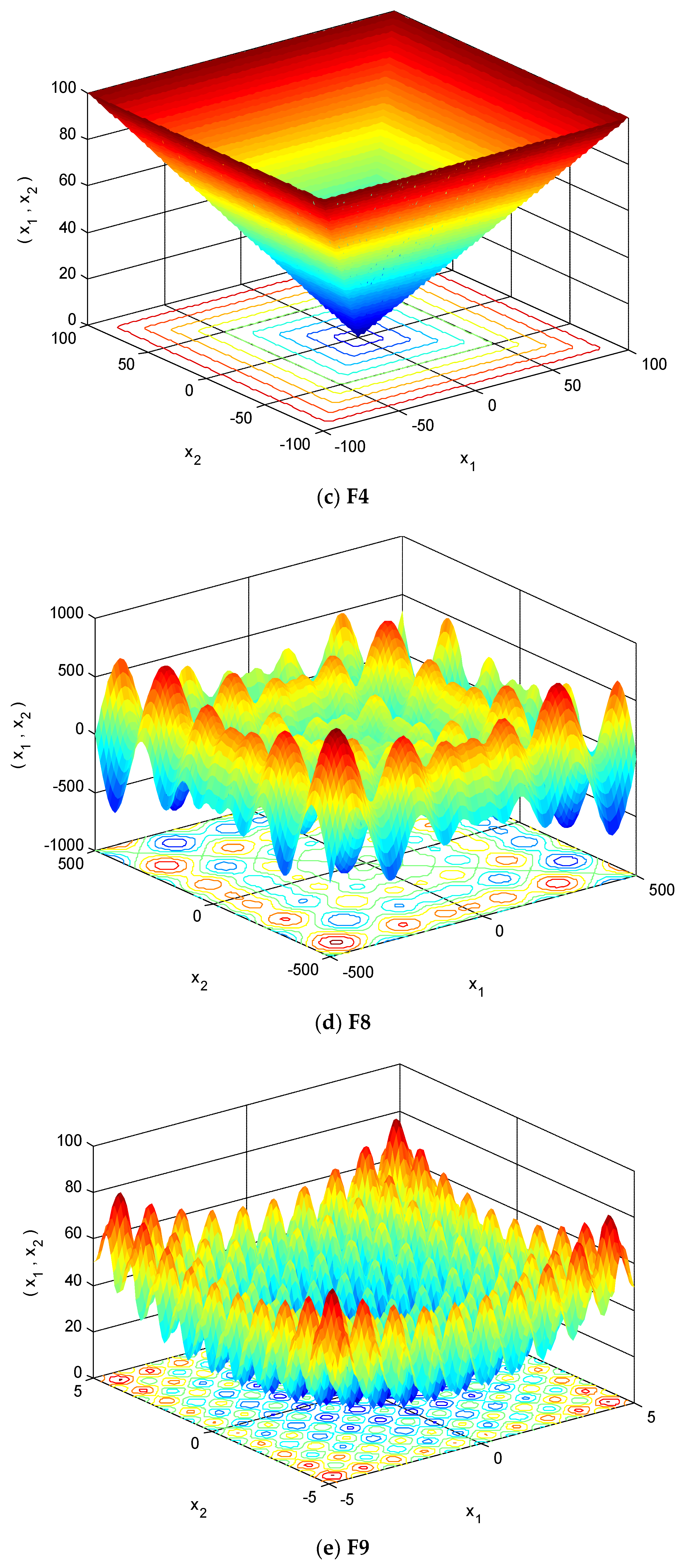
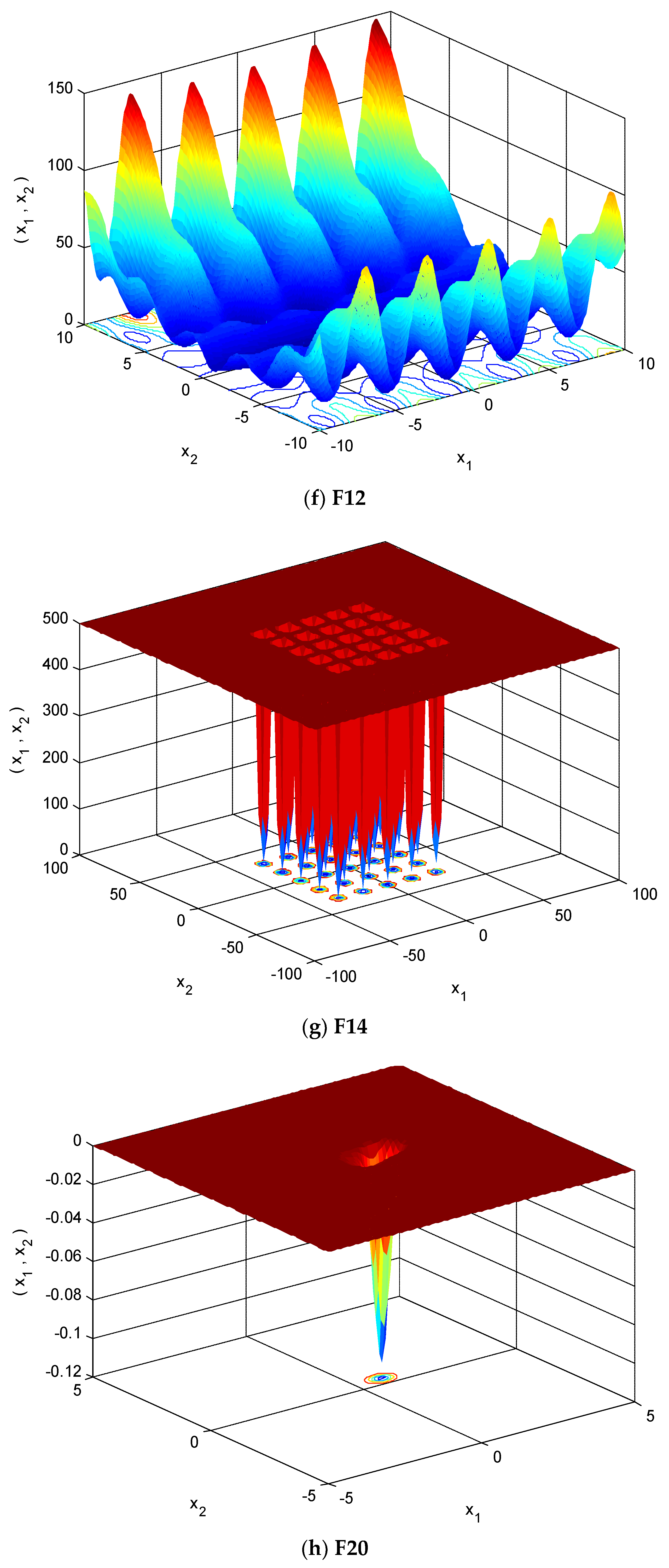
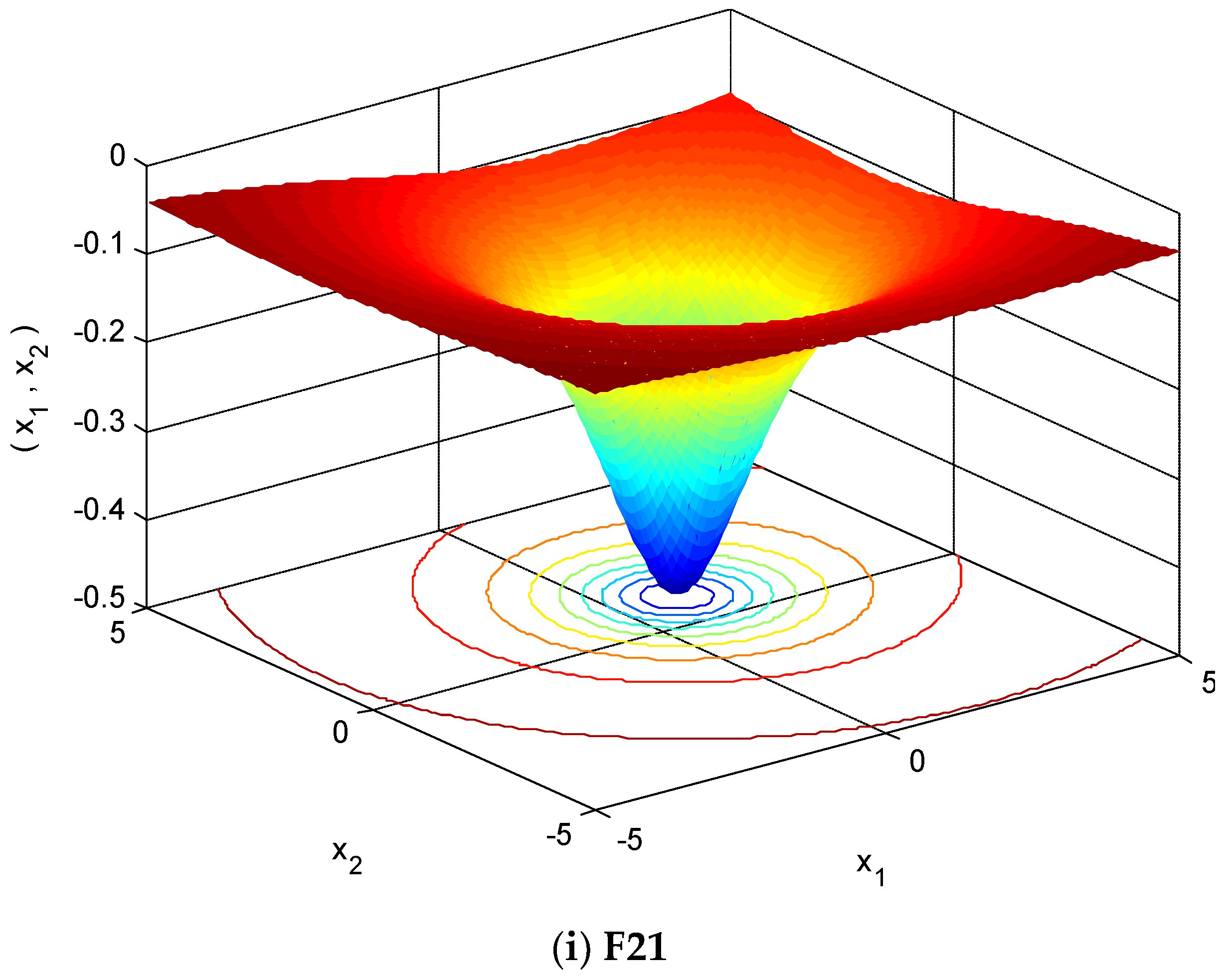
| Function | Function Expression | Range | Fmin |
|---|---|---|---|
| F1 | [−100,100] | 0 | |
| F2 | [−10,10] | 0 | |
| F3 | [−100,100] | 0 | |
| F4 | [−100,100] | 0 | |
| F5 | [−30,30] | 0 | |
| F6 | [−100,100] | 0 | |
| F7 | [−1.28,1.28] | 0 | |
| F8 | [−500,500] | −418.9 5 | |
| F9 | [−5.12,5.12] | 0 | |
| F10 | [−32,32] | 0 | |
| F11 | [−600,600] | 0 | |
| F12 | [−50,50] | 0 | |
| F13 | [−50,50] | 0 | |
| F14 | [−65,65] | 1 | |
| F15 | [−5,5] | 0.0003 | |
| F16 | [−5,5] | −1.0316 | |
| F17 | [−5,5] | 0.398 | |
| F18 | [−2,2] | 3 | |
| F19 | [1,3] | −3.80 | |
| F20 | [0,1] | −3.32 | |
| F21 | [0,10] | −10.1513 | |
| F22 | [0,10] | −10.4028 | |
| F23 | [0,10] | −10.5363 |
| Function | L0 | Ar | Ro | Hy | Pe-I | Pe-II | Fe | Li | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AVE | STD | AVE | STD | AVE | STD | AVE | STD | AVE | STD | AVE | STD | AVE | STD | AVE | STD | |
| F1 | 1.41 × 10−30 | 4.91 × 10−30 | 3.64 × 10−106 | 4992.4116 | 2.065 × 10−47 | 6816.3959 | 1.001 × 10−48 | 8014.5287 | 1.031 × 10−86 | 6343.7262 | 7.242 × 10−71 | 5094.0843 | 3.096 × 10−60 | 5251.4799 | 3.638 × 10−49 | 7360.7530 |
| F2 | 1.06 × 10−21 | 2.39 × 10−21 | 1.26 × 10−105 | 1012501 | 4.91 × 10−65 | 42530040813 | 8.33 × 10−43 | 19429812933 | 3.22 × 10−52 | 97498186729 | 3.22 × 10−52 | 5463750779 | 2.66 × 10−33 | 493771528062 | 4.66 × 10−36 | 14453630723 |
| F3 | 21,533.06 | 15,903.34 | 17,308.09 | 61,432.76 | 49,342.12 | 22,646.55 | 37,706.46 | 22,712.248 | 55,440.039 | 19,449.57 | 50,199.04 | 10,850.31 | 69,415.32 | 25,663.15 | 30,810.03 | 36,337.14 |
| F4 | 0.072581 | 0.39747 | 0.0240 | 10.750 | 8.1417 | 35.1489 | 7.8327 | 19.833 | 0.7614 | 5.7955 | 1.1439 | 15.942 | 1.0324 | 15.568 | 3.8082 | 24.589 |
| F5 | 27.86558 | 0.763626 | 0.445 | 21966964 | 28.789 | 17463450 | 27.779 | 196730 | 10.637 | 197611 | 1.651 | 209162 | 8.598 | 258619 | 5.436 | 226382 |
| F6 | 3.116266 | 0.532429 | 0.01752 | 8622.984 | 0.0001208 | 5866.599 | 0.010163 | 5806.449 | 0.01166 | 7645.330 | 0.00738 | 6855.553 | 0.01820 | 6264.7876 | 0.054570 | 4673.773 |
| F7 | 0.001425 | 0.001149 | 0.000456 | 6.0642 | 0.00617 | 8.95037 | 0.001953 | 10.1904 | 0.00352 | 10.1742 | 0.00317 | 7.3495 | 0.00564 | 7.1875 | 0.000123 | 9.778 |
| F8 | −5080.76 | 695.7968 | −12,569.062 | 882.164 | −8103.505 | 784.832 | −7574.253 | 385.518 | −7747.811 | 421.263 | −9937.307 | 625.755 | −8163.108 | 395.22 | −11,050.707 | 1125.405 |
| F9 | 0 | 0 | 0 | 49.058 | 0 | 75.368 | 0 | 69.589 | 0 | 69.735 | 0 | 87.804 | 0 | 65.9588 | 0 | 60.5413 |
| F10 | 7.4043 | 9.89757 | 8.88 × 10−16 | 2.9449 | 4.44 × 10−15 | 2.9965 | 4.44 × 10−15 | 3.5481 | 8.88 × 10−16 | 3.3239 | 8.88 × 10−16 | 3.0169 | 7.99 × 10−16 | 2.79940 | 1.39 × 10−13 | 3.05938 |
| F11 | 0.00028 | 0.00158 | 9.9767 × 10−6 | 45.548 | 0 | 50.372 | 1.5259 × 10−10 | 62.525 | 7.414 × 10−10 | 54.537 | 1.1872 × 10−13 | 55.4545 | 0.00076571 | 66.1365 | 3.4649 × 10−5 | 50.2502 |
| F12 | 0.33967 | 0.21486 | 0.00103 | 43593546 | 0.0335 | 48335777 | 0.5537 | 24074879 | 0.0631 | 46483837 | 0.1670 | 35041377 | 0.0273 | 39717531 | 0.0370 | 51384616 |
| F13 | 1.88901 | 0.26608 | 0.0052 | 57915015 | 1.6642 | 73268462 | 0.1307 | 89315333 | 0.6859 | 96698854 | 0.2089 | 96675467 | 1.0066 | 68800044 | 1.3849 | 78754257 |
| F14 | 2.11197 | 2.49859 | 0.99880 | 3.5538 | 2.9821 | 5.2941 | 0.99801 | 4.3043 | 0.9980 | 22.0250 | 0.9980 | 0.81930 | 2.9821 | 8.1928 | 2.9821 | 0.3263 |
| F15 | 0.00057 | 0.00032 | 0.00030 | 0.00055 | 0.00031 | 0.01003 | 0.00033 | 0.01561 | 0.00032 | 0.00195 | 0.00033 | 0.00550 | 0.00071 | 0.00363 | 0.00037 | 0.01032 |
| F16 | −1.0316 | 4.2 × 10−7 | −1.0316 | 4.2 × 10−7 | -1.0316 | 4.2 × 10−7 | −1.0316 | 4.2 × 10−7 | −1.0316 | 4.2 × 10−7 | −1.0316 | 4.2 × 10−7 | −1.0316 | 4.2 × 10−7 | −1.0316 | 4.2 × 10−7 |
| F17 | 0.39791 | 2.7 × 10−5 | 0.0817 | 2.7 × 10−5 | 0.39791 | 2.7 × 10−5 | 0.39791 | 2.7 × 10−5 | 0.39791 | 2.7 × 10−5 | 0.39791 | 2.7 × 10−5 | 0.39791 | 2.7 × 10−5 | 0.39791 | 2.7 × 10−5 |
| F18 | 3 | 4.22 × 10−15 | 0.3098 | 7.65 × 10−18 | 3 | 6.51 × 10−15 | 3 | 4.36 × 10−15 | 3 | 3.12 × 10−15 | 3 | 2.13 × 10−15 | 3 | 5.63 × 10−15 | 3 | 4.22 × 10−15 |
| F19 | −3.85616 | 0.002706 | −3.8621 | 0.0495 | −3.8625 | 0.1135 | −3.8627 | 0.0110 | −3.8622 | 0.00087 | −3.8599 | 0.0030 | −3.8486 | 0.0024 | −3.8612 | 0.0165 |
| F20 | −2.98105 | 0.376653 | −3.32165 | 0.1012356 | −3.31256 | 0.118835 | −3.31936 | 0.191023 | −3.31844 | 0.750346 | −3.04178 | 0.055936 | −2.83532 | 0.078376 | −3.32126 | 0.066325 |
| F21 | −7.04918 | 3.629551 | −10.152 | 0.8923 | −5.055 | 0.5159 | −5.054 | 0.4053 | −2.627 | 0.1699 | −5.0546 | 0.3044 | −5.05583 | 0.5427 | −9.629 | 1.25043 |
| F22 | −8.18178 | 3.829202 | −10.4023 | 1.2051 | −3.7242 | 0.19741 | −10.4020 | 1.4238 | −10.4014 | 2.3170 | −2.7658 | 0.2601 | −5.0876 | 0.5905 | −10.4024 | 2.6105 |
| F23 | −9.34238 | 2.414737 | −10.5361 | 1.1602 | −5.1185 | 1.3741 | −5.1241 | 1.1746 | −3.8351 | 0.3774 | −3.8354 | 0.4215 | −5.0740 | 1.16607 | −5.1166 | 1.2442 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.-z.; Wang, J.-s.; Wei, X. An Improved Whale Optimization Algorithm Based on Different Searching Paths and Perceptual Disturbance. Symmetry 2018, 10, 210. https://doi.org/10.3390/sym10060210
Sun W-z, Wang J-s, Wei X. An Improved Whale Optimization Algorithm Based on Different Searching Paths and Perceptual Disturbance. Symmetry. 2018; 10(6):210. https://doi.org/10.3390/sym10060210
Chicago/Turabian StyleSun, Wei-zhen, Jie-sheng Wang, and Xian Wei. 2018. "An Improved Whale Optimization Algorithm Based on Different Searching Paths and Perceptual Disturbance" Symmetry 10, no. 6: 210. https://doi.org/10.3390/sym10060210
APA StyleSun, W.-z., Wang, J.-s., & Wei, X. (2018). An Improved Whale Optimization Algorithm Based on Different Searching Paths and Perceptual Disturbance. Symmetry, 10(6), 210. https://doi.org/10.3390/sym10060210




