1. Introduction
The impact of the study of Laplacian spectra for graphs has increased due to its applications in different fields. Laplacian spectra have miscellaneous applications in graph theory, combinatorial optimization, mathematical biology, computer science, machine learning and in differential geometry, as well. Due to the wide range of applications, the Laplacian spectra of networks is a very interesting and attractive field of research. Computations of the Laplacian spectra of networks are involved in many results related to topological structures and dynamical processes.
Arenas et al. [
1] developed a method for understanding synchronization phenomena in networks using Laplacian spectra. Synchronization processes in populations of locally-interacting elements are the focus of intense research in physical, biological, chemical, technological and complex network topologies.
Boccaletti et al. [
2] focused on coupled biological and chemical systems, neural networks, socially-interacting species, the Internet and the World Wide Web, which are only a few examples of systems composed of a large number of highly interconnected dynamical units. The first approach to capture the global properties of such systems is to model them as graphs whose nodes represent the dynamical units and whose links stand for the interactions between them.
Liu et al. [
3] discussed and investigated the properties of the Laplacian matrices for n-prism networks. They calculated the Laplacian spectra of n-prism graphs, which are both planar and polyhedral. In particular, they derived the analytical expressions for the product and the sum of the reciprocals of all nonzero Laplacian eigenvalues. Moreover, these results were used to handle various problems that often arise in the study of networks including the Kirchhoff index, global mean-first passage time, average path length and the number of spanning trees.
Ding et al. [
4] discussed the Laplacian spectra of a three-prism graph and applied them. This graph is both planar and polyhedral and belongs to the generalized Petersen graph. Using the regular structures of this graph, they obtained the recurrent relationships for the Laplacian matrix between this graph and its initial state of a triangle and further derived the corresponding relationships for Laplacian eigenvalues between them. By these relationships, they obtained the analytical expressions for the product and the sum of the reciprocals of all nonzero Laplacian eigenvalues. Finally, they applied these expressions to calculate the number of spanning trees and mean first-passage time (MFPT) and saw the scaling of MFPT with the network size
n, which is larger than those performed on some uniformly recursive trees.
Therefore, it is of great interest to compute the Laplacian spectra of different networks. In the last decades, networks and applications of Laplacian spectra have been studied by many scientists, i.e., [
5].
Researchers have not paid much attention to applications of Laplacian spectra for networks based on different types of graph operations. Since graph products have a very significant contribution to describing very useful complex networks, we have considered networks based on a categorical product. In this paper, we study the Laplacian spectra of the complex network as a categorical product network. Categorical graph products are used to study complex networks in computer science, to understand structures in structural mechanics and to describe multilayer networks and have many applications in network topologies. Considering the structure of categorical product networks, we derive the expressions for the product and sum of reciprocals of nonzero eigenvalues of the categorical product with the help of the eigenvalues of the path and cycle. Furthermore, we compute the Kirchhoff index, global mean first passage time, average path length and number of spanning trees using the relation of nonzero eigenvalues to these applications.
The Kirchhoff index
, also simply called the resistance and denoted by R [
6], of a connected graph
G on
n nodes is defined by:
where
is the resistance distance matrix. This formula for the Kirchhoff index reduces to [
7]:
where
represents the eigenvalue of the Laplacian matrix of the graph.
The global mean-first passage time (MFPT)
has been studied with respect to transport and networks. The mean first passage time (MFPT) is very useful to estimate the speed of transport for random walks on complex networks [
8,
9]. In fact, MFPT denoted by
measures the diffusion efficiency of random walks, which is obtained by averaging
over
possible destinations and N origins of particles:
From ([
10]), let commuting time
between nodes
i and
j be exactly
, then we have:
where
denotes the number of edges in G and
is the effective resistance between two nodes
i and
j. By combining the two above relations, the MFPT can be computed by the following formula:
where
are the eigenvalues of the Laplacian matrix of the graph after t iterations.
The average path length defines the average number of steps along the shortest path
for all possible pairs of network nodes, which is the measure of the efficiency of information or mass transport on the network, then the average path length
, for G(t) (the graph after t iterations) is defined as:
Moreover, the shortest path
and effective resistance
are related by expression
, where N represents the number of nodes in the complete graph. Then, by these two relations, we have:
Spanning trees are very important in complex networks and play a key role in various networks. The exact number of spanning trees
, for
,
where
t shows the iterations in constructing a graph, discussed in the next section, can be computed by Kirchhoff’s matrix tree theorem [
11].
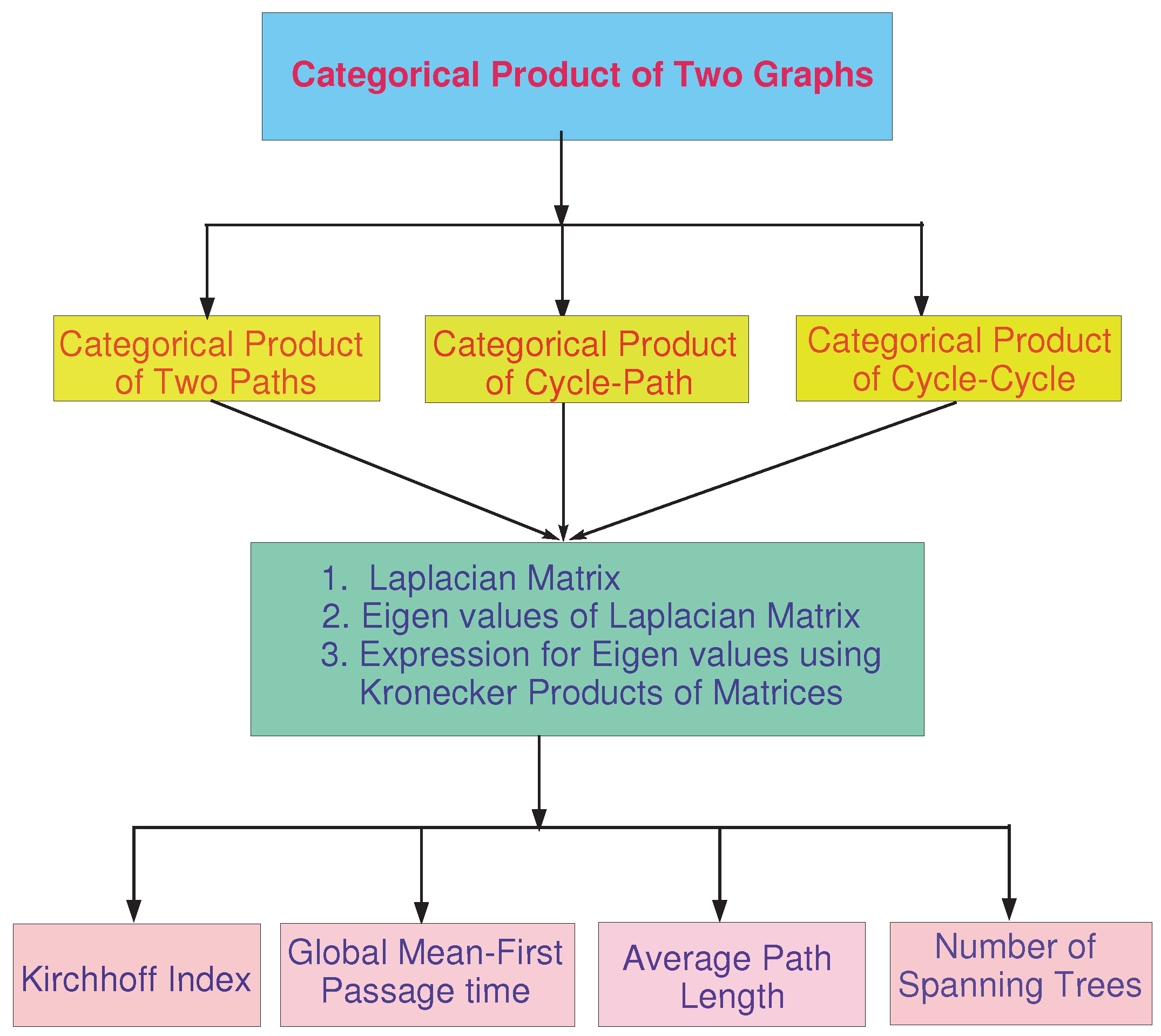
More precisely, in this paper, we have computed Laplacian spectra for categorical product networks and have discussed their applications. After the Introduction, in the second section, the materials and methods are discussed; in the main section, the categorical product network is defined in an iterative way, and then, the Laplacian spectra are computed. Finally, the applications of the Laplacian spectra are computed.
2. Materials and Methods
In this section, we state the materials and methods that are used in the main section.
In graph theory, the direct product of graphs G and H is defined as a graph such that the vertex set of is the Cartesian product and any two vertices (u, ) and (v, ) are adjacent in if and only if u is adjacent with v and is adjacent with . The direct product is also called the tensor product or categorical product.
Let G be a graph with vertices . The Laplacian matrix of G is , where A(G) is adjacency, and the matrix of G with is equal to 1 if vertices i and j are adjacent and 0 otherwise. is the diagonal matrix of vertices’ degrees.
Definition 1. Consider two matrices A and B. The Kronecker product of two matrices A and B is the matrix that is obtained by taking -th entries as for all . The Kronecker product of the matrix with the matrix is defined as (see [12,13]): The Kronecker product has the following main properties.
We have used the Kronecker product of matrices to find the Laplacian spectra for the categorical product considering the spectra for the path and cycle. Let
denote the path with n vertices. Let
be a cycle of length n. Then, their spectra can be stated as [
14]:
Lemma 1. The Laplacian eigenvalues of a path are , The Laplacian eigenvalues of a cycle are , j = 0, 1,..., n−1.
With the help of the following flowchart in
Figure 1, we will facilitate the understanding of the proposed approach in this paper clearly.
3. Main Results
3.1. Categorical Product of Two Paths and Laplacian Spectra
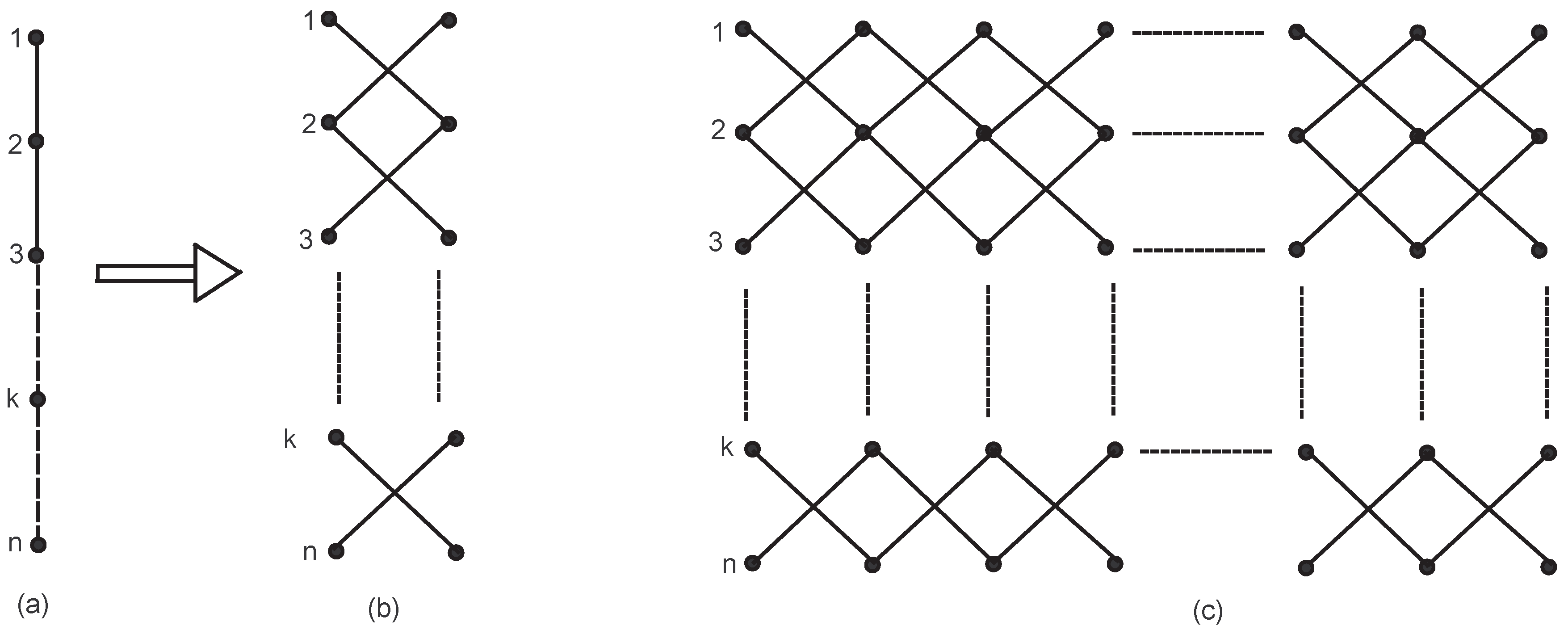
Let a categorical product network of paths be constructed in an iterative way. We take categorical product network
,
after
iterations. Initially at
is a path with n vertices. For
,
is constructed from
; from every existing vertex in
, a new vertex is created so that a new path with
n vertices is constructed; also, each new vertex in
is connected to the vertices in
, shown by
Figure 2. The number of vertices and edges in
is
and
,
.
Let and be the product of all nonzero eigenvalues of and the sum of reciprocals of these eigenvalues, respectively, i.e., and , where and , denote the nonzero eigenvalues of .
Theorem 1. The product and sum of reciprocal nonzero eigenvalues of the Laplacian matrix of G(t), are: shows the degree of vertex i. Proof. Consider a categorical product network
G as is shown in the figure. By the properties of the Kronecker product of matrices, we can write the Laplacian matrix for
G as [
15],
where
is the diagonal matrix of order
; with the diagonal elements’ degree of vertices. By using the results from linear algebra, there exists invertible matrices P and Q such that:
are the upper triangular matrices with diagonal elements,
,
and
,
, respectively. Then, using the fact that:
is the upper triangular matrix with diagonal elements, the matrix:
is upper triangular matrix with diagonal elements,
that are the eigenvalues for the categorical product network. Therefore:
Corollary 1. Let be the Laplacian matrix of , the categorical product graph with n vertices after the first iteration, , then the product and sum of the reciprocal nonzero eigenvalues of are:
☐
3.2. Categorical Product of the Cycle-Path and Laplacian Spectra
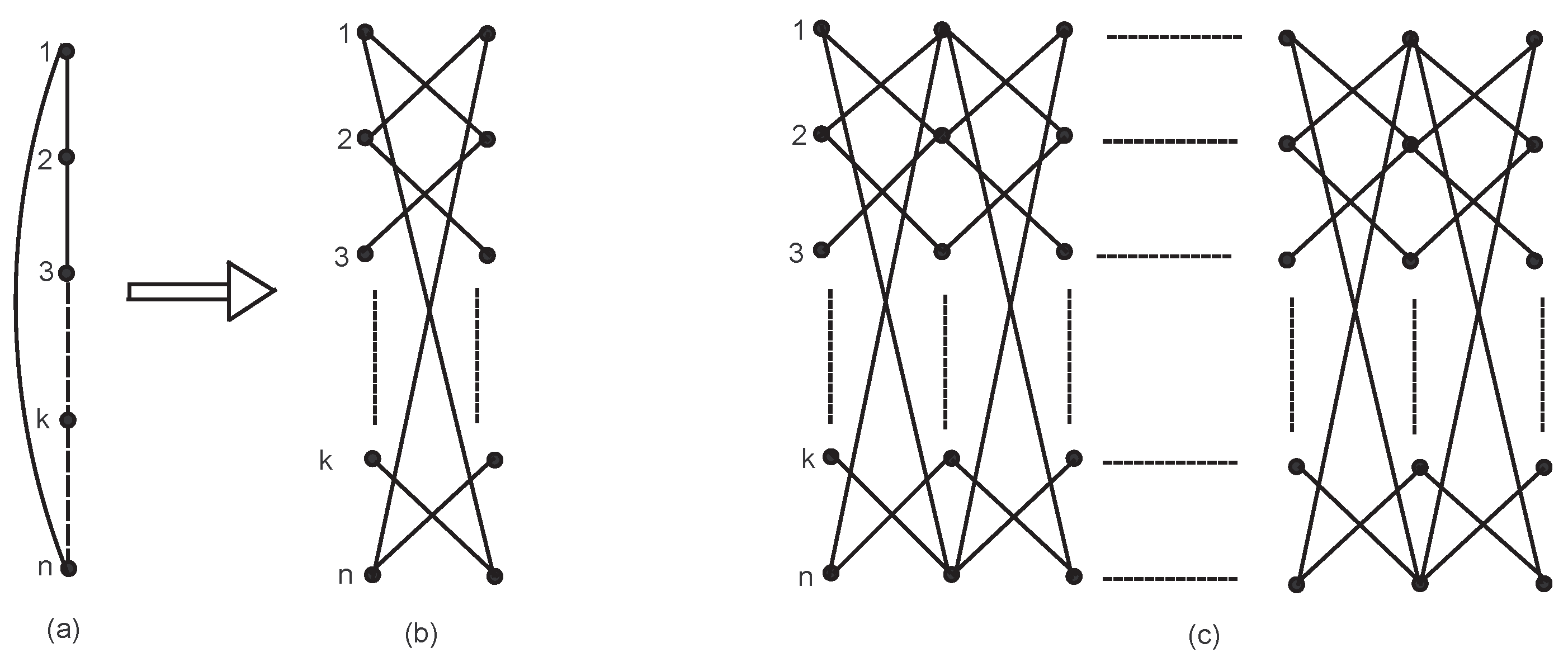
Let a categorical product network of the cycle and path be constructed in an iterative way. We take the initial categorical product network
, (
) after
iterations. Initially, at
is a cycle with
n vertices. For
,
is constructed from
, from every existing vertex in
, a new vertex is created so that a new path with
n vertices is constructed; also, each new vertex in
is connected to vertices in
, shown by
Figure 3. The number of vertices and edges in
are
and
,
.
Let and be the product of all nonzero eigenvalues of and the sum of reciprocals of these eigenvalues, respectively, i.e., and , where and , denote the nonzero eigenvalues of .
Theorem 2. The product and sum of reciprocal nonzero eigenvalues of , the Laplacian matrix of G(t), are: Proof. Consider a categorical product network
G as is shown in the figure. By the properties of the Kronecker product of matrices, we can write the Laplacian matrix for
G as:
where
is the diagonal matrix of order
; with the diagonal elements’ degree of vertices. By using the results from linear algebra, there exists invertible matrices P and Q such that:
are the upper triangular matrices with diagonal elements,
,
and
,
, respectively. Then, using the fact that:
is the upper triangular matrix with diagonal elements, the matrix:
is the upper triangular matrix with diagonal elements,
that are the eigenvalues for the categorical product network. Therefore,
☐
3.3. Categorical Product of the Cycle-Cycle and Laplacian Spectra
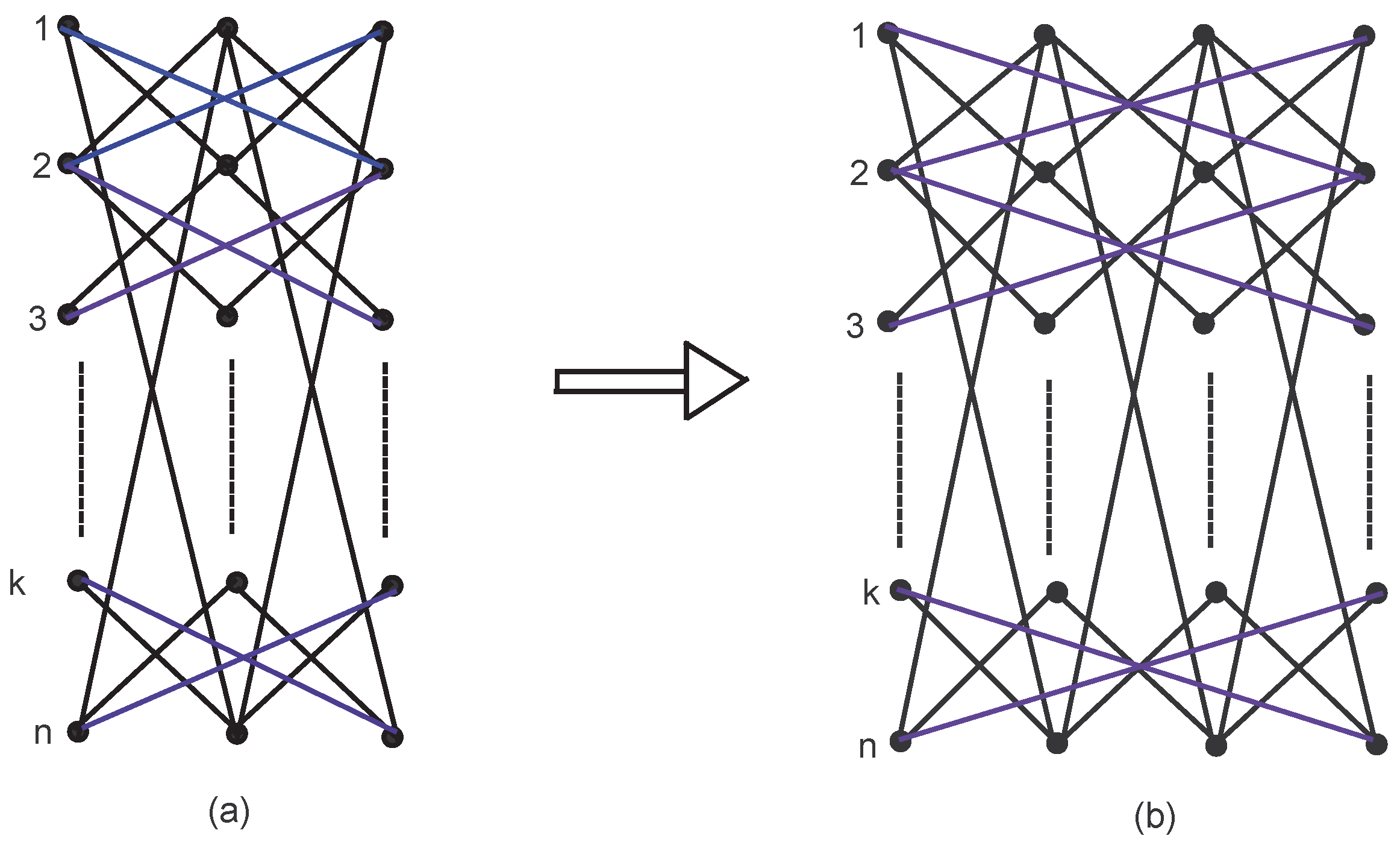
Let a categorical product network of cycles be constructed in an iterative way. We take initial categorical product network
, (
) after
iterations. Initially, at
is a categorical product network of cycle
with n vertices. For
,
is constructed from
, and from every existing vertex in
, a new vertex is created so that n vertices are constructed; also, each new vertex in
is connected to the vertices in
, shown by
Figure 4. The number of vertices and edges in
are
and
.
Let and be the product of all nonzero eigenvalues of and the sum of reciprocals of these eigenvalues, respectively, i.e., and , where and , denote the nonzero eigenvalues of .
Theorem 3. The product and sum of the reciprocal nonzero eigenvalues of , the Laplacian matrix of G(t), are: Proof. Consider a categorical product network
G as is shown in the figure. By the properties of the Kronecker product of matrices, we can write the Laplacian matrix for
G as:
where
is the diagonal matrix of order
; with the diagonal elements’ degree of vertices. By using the results from linear algebra, there exists invertible matrices P and Q such that:
are the upper triangular matrices with diagonal elements,
,
and
,
, respectively. Then, using the fact that:
is the upper triangular matrix with diagonal elements, the matrix:
is the upper triangular matrix with diagonal elements,
that are the eigenvalues for the categorical product network. Therefore:
☐