Abstract
The application of multiple criteria decision-making methods (MCDM) is aimed at choosing the best alternative out of the number of available versions in the absence of the apparently dominant alternative. One of the two major components of multiple criteria decision-making methods is represented by the weights of the criteria describing the considered process. The weights of the criteria quantitatively express their significance and influence on the evaluation result. The criterion weights can be subjective, i.e., based on the estimates assigned by the experts, and the so-called objective, i.e., those which assess the structure of the data array at the time of evaluation. Several groups of experts, representing the opinions of various interested parties may take part in the evaluation of criteria. The evaluation data on the criterion weights also depend on the mathematical methods used for calculations and the estimation scales. In determining the objective weights, several methods, assessing various properties or characteristics of the data array’s structure, are usually employed. Therefore, the use of the procedures, improving the accuracy of the evaluation of the weights’ values and the integration of the obtained data into a single value, is often required. The present paper offers a new approach to more accurate evaluation of the criteria weights obtained by using various methods based on the idea of the Bayes hypothesis. The performed investigation shows that the suggested method is symmetrical and does not depend on the fact whether a priori or posterior values of the weights are recalculated. This result is the theoretical basis for practical use of the method of combining the weights obtained by various approaches as the geometric mean of various estimates. The ideas suggested by the authors have been repeatedly used in the investigation for combining the objective weights, for recalculating the criteria weights after obtaining the estimates of other groups of experts and for combining the subjective and the objective weights. The recalculated values of the weights of the criteria are used in the work for evaluating the quality of the distant courses taught to the students.
1. Introduction
The Use of multiple criterion decision-making methods (MCDM) [1,2,3] allows a decision-maker to choose the best alternative out of a number of the considered alternatives A1, A2, ..., An or to arrange them according to their importance for the defined purpose. This may be the choice of the best technological process out of the suggested versions, the comparative evaluation of economic, social or ecological situations in particular states or their regions, as well as the performance of banks and enterprises, and the solution of many other similar problems. The MCDM methods are based on using a decision-making matrix R = ‖rij‖ of the values rij of the criteria R1, R2, ..., Rm, describing the considered process, and the vector Ω = (ωj) of the significances of these criteria, i.e., their ωj, where i = 1, 2, ..., n; j = 1, 2, ..., m; m is the number of criteria and n is the number of the considered alternatives. The values of the criteria rij can be represented by the statistical data, the estimates assigned by experts and the values of technological or technical characteristics of the considered process. The influence of the criteria on this process and their importance differ to some extent. However, the main idea of the criterion weight evaluation is that, in fact, the most important criterion is assigned the largest weight in any method used for criterion weight evaluation. The obtained weights are usually normalized as follows: .
The use of the MCDM methods is based on the integration of the criteria values rij and their weights ωj for obtaining the standard of evaluation, which is the criterion of the method. This idea is successfully realized by using the SAW (Simple Additive Weighing) method. The alternatives performance level Si is calculated by [1]:
where ωj is the weight of the j-th criteria and is the normalized value of the j-th criteria for the i-th alternative [4,5].
The actual values of the criteria weights have a great influence on determining the importance of the alternatives and choosing the best solution. Therefore, the problems associated with their estimates are widely investigated both in theory and practice of MCDM methods’ application.
As mentioned above, the weights of criteria can be subjective and objective. In practice, subjective weights determined by specialists/experts are commonly used. These weights are most commonly used for solving practical problems. A large number of methods to determine the criteria weights based on expert evaluation of their significance (weight) have been developed. These weights are most important for assessing the results because they express the opinions of highly qualified experts with extensive experience. The well-known approaches are the Delphi method [6,7], the expert evaluation method [3], the Analytic Hierarchy Process (AHP) [8,9,10], the stepwise weight assessment ratio analysis (SWARA) [6,11], the factor relationship (FARE) [12], and KEmeny Median Indicator Ranks Accordance (KEMIRA) [13].
In the process of evaluation, it is also possible to consider the structure of the data array, i.e., the criteria values, and to determine the actual degree of each criterion’s dominance, i.e., the so-called objective weights of criteria. In contrast to their subjective counterparts, the objective weights are not so commonly used in practice. They do not play an important role in this process, showing the actual influence of particular criteria at the time of evaluation. The entropy method [14,15,16,17,18], the LINMAP method [1], mathematical programming models for determining the criteria weights [19], the correlation coefficient and standard deviation (CCSD) based on the objective weight determination method [20], as well as the methods of Criterion Impact LOSs (CILOS) and Integrated Determination of Objective CRIteria Weights (IDOCRIW) [4,5,18,21,22], the projection pursuit algorithm [23], a group of correlation methods CRITIC (Criteria Importance Through Intercriteria Correlation) [24], and the least squares’ comparison [25] are the well-known practically used methods. Combination weighting is based on the integration of subjective and objective weighting [26,27,28,29].
Several groups of experts may take part in determining the weights of the criteria simultaneously. Their estimates represent the opinions of the interested parties. The assigned weights of the considered criteria also depend on the mathematical method used for calculations and the estimation scales.
A number of methods demonstrating the specific features of the data structure (a decision-making matrix) are commonly used simultaneously for determining the objective weights. Therefore, the need arises for improving the accuracy of the obtained weights’ values, as well as the integration of the estimates assigned by the experts of various groups and the objective weights obtained by using various methods into an overall estimate. Moreover, to achieve the most accurate evaluation of the criteria weights, the estimates of the objective and subjective weights should be combined.
However, the formal integration of particular weights’ estimates into a single value is not correct, because according to the Kendall’s theory, the estimates would not be in agreement. This implies that the theoretical grounds for integrating the particular estimates are required.
The authors of the present paper offer a method of weights’ recalculation, and the integration of various estimates into a single one, based on the recalculation approach offered by Bayes.
The research procedure is presented in Figure 1, including combination of criteria weights calculated by applying different methods and evaluation of courses by using four MCDM methods.
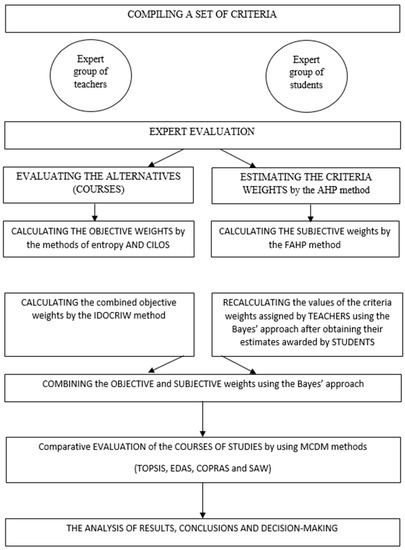
Figure 1.
The research procedure.
The ideas suggested in this paper have been repeatedly used in the investigation for combining the subjective and objective weights to evaluate the quality of the distant courses taught to the students. These cases are described to show the potential of the method suggested in the paper. In solving the particular practical problems, one of the procedures suggested in the paper may be used, depending on the type of the problem as follows: the combining of the objective weights calculated by various methods (IDOCRIW), as well as the recalculation of the objective weights assigned by one of the groups of experts after obtaining the estimates of another group or, most often, the combining of the subjective and the objective weights.
2. Integrating the Values of the Weights of the Criteria
The weights of criteria can be considered as random values. The estimates of the criteria weights may vary, depending on the variation in the number of the members in the group of experts and on its decrease or increase. Even one and the same expert can differently assess the criteria weights the day after the first evaluation. The same weights of the criteria can be determined by various groups of experts, who are more or less interested in the obtained results.
The so-called objective weights of the criteria assess the structure of the data array, i.e., the decision matrix.
The elements of the matrix are also either the estimates assigned by the experts to the criteria for the considered alternatives or the statistical data and randomly change in time. The weights of the criteria, as well as the probabilities of the random values, range from 0 to 1. The Bayes’ theorem in its application to the criteria weights may be interpreted so that these weights should be recalculated when different criteria weights obtained by another group of experts or by using other evaluation methods become available.
The criteria weights may be considered as a number of random values, making a complete set. In fact, the sum of the criteria weights’ values is equal to one: .
Besides, the criteria, describing the process evaluated by using multiple criteria methods (MCDM), were chosen in such a way that they could reflect all major aspects and characteristics of this process. Any other criteria were not used for solving the considered problem.
The Bayes’ equation [30] used for recalculating the criteria weights in this work was of the form:
where is the initial weight of the j-th criterion ; X denotes the event, when new criteria weights are obtained; denotes new weights of the criteria calculated by a different method or by another group of experts; denotes the recalculated criteria weights.
The Equation (2) applied to the weights of the criteria was of the form:
where denotes the recalculated weights of the criteria.
In using the multiple criteria evaluation (MCDM) methods, the problem of combining the weights of the criteria obtained by using various evaluation methods, or groups of experts, arises.
In these cases, the concept of the geometric mean is commonly used [16,31], though the arithmetic mean or other ideas, helping to combine weights, can also be implemented.
Equation (3) is based on the concept of the geometric mean for integrating weights. It should be noted that Equation (3) is symmetrical, which implies that the result obtained does not depend on the fact, which estimates are original and which ones are the recalculated values.
The same idea was used for calculating the aggregate objective weight by using the IDOCRIW method based on integrating the weights obtained by using the entropy and CILOS methods [18].
3. The Methods Used for Determining the Weights of the Criteria
Various methods are used for determining the subjective weights of the criteria. Experts can assess the importance (significance) of the criteria by using various evaluation techniques. They may include the method of rating the criteria according to their importance and the direct evaluation of criteria, when the sum of the obtained values is equal to one (or 100%), as well as the estimates obtained by using various estimation scales.
The present study is based on using the method of the Analytic Hierarchy Process (AHP) developed by T. Saaty and FAHP, which is an extension of this approach, taking into consideration the uncertainly of the experts’ estimates. The methods of entropy, CILOS and IDOCRIW, were used for determining the objective weights. The values of the obtained weights were recalculated using the technique suggested by the authors, which is based on the method developed by Bayes.
3.1. The Method of Fuzzy Analytic Hierarchy Process (FAHP)
The methods AHP and FAHP [8,32,33] were used to determine the weights of the criteria.
The Fuzzy AHP method is suitable for determining the weights of the qualitative criteria, when the experts evaluate the alternatives independently of the judgements of other experts. Each expert performed the evaluation procedure applying a simple AHP method of pairwise comparison. The matrix of the expert’s pairwise comparison was verified to check if the expert had not conflicted with his/her own judgment. This facilitated obtaining the weights of the qualitative criteria in a more precise way.
The weights of the criteria were determined by using the FAHP method described below:
Each expert performed pairwise comparison using the scale of the AHP method 1-3-5-7-9. The concordance [8] of the data of the filled in pairwise comparison matrix was checked.
The concordance of the estimates provided by the experts of the whole group was assessed [34].
The matrix of the pairwise comparison data obtained from the group of experts, using the FAHP method, was developed based on the particular elements of the matrix, constructed using the AHP pairwise comparison data obtained by experts, when and is the number of experts.
The fuzzy triangular numbers of the elements of the pairwise comparison matrix based on the data provided by the experts’ group were calculated by using the offered algorithm as follows [35]:
Since the matrix is inversely symmetrical, ; .
To determine the weights of the criteria based on the matrix of fuzzy numbers, the extent analysis method suggested by Chang [36] was used. The value referred to as the fuzzy synthesis extension was calculated for each criterion:
Each criterion has the value expressed by a fuzzy number of the triangle. Then, comparing the criteria (i.e., fuzzy numbers of the triangles), their probability levels (degrees) were determined. The probability level was calculated as follows:
The smallest value of the probability level was calculated as follows:
The vector of the priorities of the fuzzy matrix was calculated by the equation:
The objective weights of the criteria were calculated using the Entropy method [17] and the CILOS method [18,37]. The detailed description of these methods and their use are presented in the works of the authors [4,18,21,22].
3.2. The Method Based on Using the Aggregate Objective Weights (IDOCRIW)
Using the idea of combining different weights into an aggregate weight [16,18], it is possible to combine the entropy weights Wj and weights qj of the criterion impact loss methods as well as connecting them to the objective weights of criteria for assessing the weights ωj of the structure of the array:
These weights emphasize the separation of the particular values of criteria (entropy characteristic), but the impact of these criteria is decreased due to the higher impact loss of other criteria.
The weights calculated in the entropy and the criterion impact loss methods were combined to obtain the aggregate weights and then used in multi-criteria assessment for ranking the alternatives and for selecting the best alternative.
4. The Applied MCDM Methods
For obtaining the relative estimates of the courses and demonstrating the application of MCDM methods, such as TOPSIS (The Technique for Order of Preference by Similarity to Ideal Solution), SAW, COPRAS (Complex Proportional Assessment) and EDAS (Evaluation Based on Distance from Average Solution), which reflect the main ideas of MCDM approaches, were used in the work. They include the calculation of the optimal distance from the best and from the worst alternatives, the combination of the values and weights of the criteria for obtaining the qualitative estimate of the method, determination of the degree of influence of the maximizing and minimizing criteria and taking into consideration the optimal distance from the average estimate. The detailed description of the methods and their use are presented in the works [16,28,38] as well as in the works of the authors of the present paper [39,40,41,42,43,44].
5. Expert Evaluation of Distance Learning Courses of Studies
As mentioned above, the main constituent parts of the MCDM methods are the values of the criteria for the compared alternatives, i.e., a decision matrix, and the weights of the criteria describing their importance [16,28,33].
Relying on Belton and Stewart’s principles of the identification of quality evaluation criteria, these groups of criteria were offered for all stages of the evaluation process. The first group of criteria aims to evaluate the contents of the course of studies. The second group of criteria describes the effective use of tools. The third group or criteria refers to teaching of the course [33]. At each stage, the evaluation was made by a different group of experts. The total number of fifteen criteria was selected.
In the problem of assessing the quality of the courses of studies, the same criteria were considered for each course. The experts, who were specialists in information technologies and lecturers from the respective departments, teaching the courses in particular subjects (which had to be evaluated), as well as students, attending the respective lectures and seminars, had chosen seven criteria for evaluating the quality of the considered courses of studies.
These criteria were as follows: (1) The structure of the course; (2) The relevance of the material of the course; (3) Testing the knowledge of students; (4) Presentation of the material of the course; (5) Communication tools; (6) Readability and accessibility of the material of the course; (7) The practical use of the course of studies.
5.1. Description of the Considered Criteria
Criterion 1. The structure of the course. A general structure of the course is clear. The presentation of the material of the course is consistent. The material is presented in small amounts.
Criterion 2. The relevance of the material of the course. The presented material is relevant and not outdated.
Criterion 3. Testing the knowledge of the students. The presentation of any new topic is followed by the presentation of various tests, helping the students to learn the material. These tests are aimed at checking the knowledge acquired by the students and providing feedback, allowing students to test their knowledge at any time, whenever they wish, without the need for adapting themselves to the timetable of the teachers. A clear and consistent system of testing the knowledge of the students is presented.
Criterion 4. The comprehensiveness of the material of the course. The presented material is easily understood.
Criterion 5. Effective communication tools. Easy and fast access to the learning material is provided by the working group. Communication is secured by the availability of synchronous and asynchronous means of communication. Video conferences present the instrument, allowing all the students to connect to the system simultaneously during the examination period.
Criterion 6. Reading of the material of the course and its accessibility. Effective and fast data communication. The appropriately selected video records’ format, quick access to the material, high quality of video record and sound. The material is easily read, using well-known tools, and is accessible without any additional connection sessions.
Criterion 7. The practical use of the course of studies. Having completed the course, the students acquired knowledge, practical skills and competence required for their successful work.
The estimates of the criteria values for each course by teachers and students were used as decision matrices. The subjective weights of the criteria were calculated by using the methods AHP and FAHP, based on the estimates assigned by the teachers and students. The objective weights were determined by using the entropy, CILOS and IDOCRIW methods. Their values were recalculated using the Bayes’ method described in the present paper.
5.2. Determining the Subjective Weights
Eight teachers and ten students took part in the evaluation of the criteria weights and quality of the courses of studies. They filled in the AHP matrix of pairwise comparisons of the criteria and the matrix of estimates of the criteria values against the scale of ten points. The values of the AHP matrix filled in by one of the teachers (Table 1).

Table 1.
The AHP matrix filled in by one of the teachers.
The concordance degree of the estimates given in each filled in matrix was determined (the concordance coefficient had to be below 0.10 [34]). After evaluation of the criteria describing the course of studies, the ranking of the obtained results and determining of the concordance of the estimates assigned by the experts of each group was made [34]. The judgments of the students were in agreement: the concordance coefficient was , while the calculated criterion value was larger than the value of the table equal to 12.59 (at the significance level value α = 0.05).
The estimates assigned by the teachers were also in agreement: the concordance coefficient was , while the calculated criterion value was larger than the value of the table equal to 12.59 (at the significance level value α = 0.05).
The values of the elements of the matrices calculated by the FAHP method, using Equations (4)–(5) and based on particular AHP matrices for teachers (Table 2) are given below.

Table 2.
The matrix filled in by the teachers using the method FAHP.
The values of the parameters of fuzzy sets for teachers (Table 3) were obtained by using Equation (6). The criteria weights assigned by teachers, which were calculated by using the FAHP Methods (7)–(9), are given in Table 4.

Table 3.
The matrix of the values , for teachers.

Table 4.
The values of the subjective weights of the criteria assigned by the teachers.
In Table 1, the results, obtained using pairwise comparison of seven criteria performed by one of the teachers, are given. The scale 1-3-5-7-9 of the Saaty’s approach AHP [8] was used for comparison.
Using the algorithm for developing the matrix (5) of the FAHP method described in Section 3.1 and the estimates assigned by particular teachers, the matrix filled in by a group of teachers based on using the FAHP method was constructed (Table 2).
The values of the criteria weights assigned by the teachers (Table 3) were obtained using Equations (7)–(9) (Table 4).
According to the teachers, the important criteria, describing the preparation of the course of studies of high quality, include a clear description of the material () and the structure of the course material (), as well as the relevance of the presented material (). Table 5 provides the results of the pairwise comparison of seven criteria performed by one of the students. The scale 1-3-5-7-9 presented in the AHP method of T. Saaty was used for comparison.

Table 5.
The AHP matrix provided by a student.
Using the algorithm for developing the matrix (5) of FAHP method, which is described in Section 3.1, and the estimates assigned by individual students, the FAHP matrix of the data provided by a group of students was constructed (Table 6).

Table 6.
FAHP matrix of the group of students.
Based on the data presented in Table 6 and using Equation (6), the values of were obtained (Table 7).

Table 7.
The matrix of the values , for students.
The values of the criteria weights based on the estimates assigned by the students (Table 7) were obtained from Equations (7)–(9) (Table 8). According to the students, the important criteria, describing a high-quality course, include clear presentation of the material (), the relevance of the material for reading () and the practical use of the acquired material ().

Table 8.
The values of the subjective weights of the criteria assigned by the students.
5.3. The Calculation of the Objective Weights
The objective weights were calculated in the methods of entropy, CILOS and IDOCRIW, based on using a decision matrix, i.e., the values of the criteria obtained for the compared alternatives. In the considered case, the alternatives were the courses of various subjects, using the MOODLE system. These courses were assessed by two different groups of experts: The teachers, who are specialists in the subjects presented in the courses and the students, who learn the materials of these courses.
The objective weights of the criteria assigned by the experts of both groups, as well as their aggregate IDOCRIW weights, were calculated separately and, then, the weights awarded by the teachers were recalculated using the Bayes’ equation, when the estimates of the same criteria given by the students, were obtained. Seven criteria were assessed. Similar to the case of the objective weights’ evaluation, a group of 8 teachers and a group of 10 students took part in the process. For calculating the objective weights, the average estimates of the courses were used separately for each group. Five courses of studies were evaluated, including discrete mathematics, mathematics 2, integral calculus, operational systems and information technologies. The average estimates of the courses are given in Table 9 (teachers) and in Table 10 (students).

Table 9.
The average estimates of five courses by the teachers.

Table 10.
The average estimates of five courses by the students.
Using the data of Table 5 and Table 6, the objective weights of the criteria (in the entropy and CILOS methods) provided by the teachers and by the students were calculated. The aggregate objective weights of criteria were obtained by using the method IDOCRIW. It should be noted that using IDOCRIW is equivalent to using the Bayes’ Equation (3) for recalculating the entropy weights after the calculation of the weights by the CILOS approach. The values of the weights are presented in Table 11.

Table 11.
The objective weights of criteria calculated based on the estimates of the courses awarded by teachers and students.
The objective weights of the criteria demonstrate their actual significance at the time of evaluation. The estimates of the courses given by both the teachers and the students show good readability and accessibility of the material of the courses. Based on the judgements of the students, it can be stated that the material of the courses is relevant. According to the estimation of the courses by the teachers, the testing of the students’ knowledge of the course material is well-organized.
5.4. The Recalculation of the Values of the Subjective Weights, Assigned by the Teachers, When the Estimates of the Criteria Weights Awarded by the Students Are Obtained
The values of the subjective weights of the criteria assigned by the teachers were recalculated using the Bayes’ equation when the weights of the same criteria were obtained by the students. The results of the calculation were the aggregate subjective weights of the teachers and students. In Table 12, the subjective weights assigned by the teachers and the students, as well as the generalized subjective weights, are given. In the case, when the judgements of the groups of experts about the significance of the considered criteria coincide, the overall estimate increases (for example, the estimates of the criteria 4 and 2).

Table 12.
The recalculation of the subjective weights’ values assigned by the experts based on using the Bayes’ method.
The aggregate objective weights assigned by the teachers and students, using the method IDOCRIW (Table 11) were combined into generalized objective weights using the Bayes’ Equation (3). The recalculated values of the objective criteria weights are given in Table 13.

Table 13.
The generalized values of the objective criteria weights.
In the case of the recalculated objective weights’ values, the significance of the criterion 6, describing the accessibility and readability of the learning material, increased.
The aggregate subjective weights (Table 12) were combined with the objective weights (Table 13) using the Bayes’ approach (3). The values of the generalized weights are given in Table 14.

Table 14.
The recalculation of the values of the subjective criteria weights, taking into consideration the weights of the objective criteria, by using the Bayes’ method.
The subjective and objective weights reflect some different characteristics of the significance of the criteria. Thus, the subjective weights show ‘the desired’ significance of the criteria, assigned by the experts, while the objective weights reflect the actual weights of criteria at the time of evaluation based on the values of the criteria. The obtained estimates do not usually correlate with each other. It is natural that the most positive effect (or influence) of the criteria weights on the results of the multiple criteria evaluation can be produced in the case of the obvious correlation between these estimates. In this case, a noticeable agreement between the estimates can be observed for the criteria 6, 3 and 5.
6. Evaluating the Quality of the Course of Studies by MCDM Methods Based on the Comparative Analysis
The weights of the criteria are used in MCDM methods for evaluating the compared alternatives. In the present investigation, these methods were used for assessing the courses of studies (the quality of the teaching materials). In the first case, the suggested algorithms for assessing their quality differed because of the averaging of the initial estimates assigned to the courses by the teachers and students and combining the weights of the criteria assigned by them (method of calculation). The averaged data were used as a base for making the calculations by MCDM methods. In the second case, the estimates assigned by the teachers and students were considered separately, while the calculations by using the MCDM methods were made individually for each group, and, then, the obtained estimates were averaged (method of calculation 2).
6.1. Method of Calculation 1
In this case, a decision matrix consists of the averaged estimates of the courses of studies assigned by the students and teachers (Table 9 and Table 10). These estimates were combined into their average estimate (Table 15).

Table 15.
The average estimates of five courses of studies assigned by the students and teachers.
Five courses of studies were assessed by using the methods TOPSIS, SAW and EDAS, and the values of the aggregate objective and subjective weights were obtained (Table 14).
The calculation results and the places of courses are given in Table 16.

Table 16.
The estimates of five courses of studies obtained by using method of calculation 1 of MCDM methods.
The results obtained using the methods SAW and COPRAS were the same because all the criteria were maximizing [26].
The estimates of the courses according to method of calculation 1 were the same for all MCDM methods. The highest estimates were assigned to the course of ‘Operational systems’, while the lowest estimate was awarded to the course of ‘Discrete mathematics’. The similarity of the estimates can be attributed to the decrease in the uncertainty of the data due to the averaging of the considered data.
6.2. Method of Calculation 2
This method of calculation of MCDM methods was used to obtain separate estimates of the courses, assigned by the teachers and the students. Their average values were assumed to be the resultant estimate of the courses.
For this purpose, the subjective weights assigned by the teachers were recalculated after the calculation of the objective weights of the same criteria. The values of the recalculated weights assigned by the teachers are given in Table 17.

Table 17.
The recalculation of the values of the subjective weights of the criteria assigned by the teachers, using the Bayes’ approach, taking into consideration the values of the objective weights of criteria.
Based on the estimates of the courses assigned by the teachers (Table 9) and the recalculated weights of the criteria assigned by the teachers (Table 17), five courses of studies were evaluated, using the methods TOPSIS, SAW and EDAS. The calculation results are given in Table 18.

Table 18.
The evaluation of courses of studies by the teachers, using method of calculation 2 of the MCDM methods.
The evaluation of the courses based on the data provided by the students was performed in a similar way. For this purpose, the subjective criteria weights assigned by the students were recalculated after the calculation of the objective weights of the same criteria. The recalculated weights’ values assigned to the criteria by the students are given in Table 19.

Table 19.
The recalculation of the subjective weights of the criteria assigned by the students, using the Bayes’ equation, taking into consideration the objective criteria weights.
Based on the evaluation of courses by the students (Table 10) and their recalculated criteria weights (Table 19), as well as using the MCDM methods TOPSIS, SAW and EDAS, five courses of studies were evaluated.
The calculation results are given in Table 20.

Table 20.
The evaluation of courses of studies by the students, using the MCDM methods, and their overall estimates obtained by using method of calculation 2.
In the case of using method of calculation 2, the uncertainty of the initial data is much higher because the estimates of the teachers and students differ to some extent. Therefore, the estimates of the courses are different in these groups. However, the average estimates do not differ considerably from those obtained using method of calculation 1. The highest average estimate was awarded to the course of ‘Operational systems’, while the estimates of the courses of ‘Discrete mathematics’ and ‘Mathematics 2’ changed positions.
7. Discussion
The MCDM methods are used for selecting the best alternative or arranging the alternatives in the order of their significance under the condition of the absence of the alternative dominant over others according to all criteria. The MCDM methods take into consideration the influence of the criteria on the evaluated process or object and use scalarization of the criteria and their weights. Therefore, the weight of the criterion plays an important role in making the solution.
Solving the decision-making problems is hardly possible without taking into consideration the judgments of the highly qualified experts.
Therefore, experts in various fields of activities take part in the evaluation. Usually, these experts have different opinions about the considered problems and their interest in the result of the choice of the alternative also differs to great extent. A decision-making person may change his/her estimates, taking into consideration the judgments of other groups of experts. This also applies to the evaluation of the significance of various criteria.
There are two various approaches to determining the weights of criteria. They include the subjective approach, based on the estimates assigned by experts, and the objective approach, assessing the structure of the data array.
A great number of various methods of assessing the subjective and objective weights have been offered. Each method has its specific features because it uses various concepts, mathematical equations and approaches, as well as various estimation scales. However, none of the available methods is universal or the best. Therefore, the need for integrating the estimates obtained by using some particular methods into the overall estimate arises.
The formal integration of particular estimates into a single one is incorrect, because most probably, according to the Kendall’s theory of concordance, the results would not be in agreement. Therefore, the theoretical basis for using the method of integrating the particular estimates is required.
The experts’ estimates of the criteria weights may be considered as the random values, making a complete set of events, with the sum of values equal to one. Thus, the possibility of using the Bayes’ equation for recalculating the values of the criteria weights, when different values, yielded by other evaluation methods or assigned by the experts of another group, are obtained. This provides a theoretical basis for a wide use of the method of combining weights, obtained by employing various methods, as the geometric mean of particular values.
The described method of combining the weights according to the Bayes’ approach has been used several times in the present work for recalculating the values of the objective weights and the integration of the values of the subjective and objective weights into a single value in the process of their evaluation. The method offered in the paper may have a wide practical use in solving various decision-making problems.
In solving the particular problems, various methods of combining the weights and the recalculation of their values can be used, depending on the specific nature of the problems.
8. Conclusions
In multiple criteria decision-making methods (MCDM), the weights of the criteria, describing the considered process or object, form one of two components of the evaluation of alternatives. Therefore, in using these methods, the values of the criteria weights have a strong influence on the estimates.
The considered methods use the subjective and objective weights of criteria. The subjective weights of criteria are calculated based on the estimates of the experts, while the objective weights assess the structure of the data array. Each method has its specific features and reflects various characteristics described by the criteria. Their integration for evaluating the significance of the alternatives is of primary importance in the theory and practice of MCDM methods’ analysis and application.
In the present study, the authors offer to consider the criteria weights as random values, making a complete set. In this case, the equation offered by Bayes can be used for recalculating the criteria values, when the values of these criteria calculated by a different method are obtained. This allows for combining the weights of the criteria, yielded by various methods and used for assessing their significance, into a single estimate.
The suggested method of combining the criteria weights using the Bayes’ approach was repeatedly used in the present study for recalculating the subjective weights of criteria assigned by one of two groups of experts after the weights of these criteria assigned by the experts of the other group were obtained. It was also used for recalculating the objective weights’ values and combining the subjective and objective weights for obtaining the overall estimate.
The obtained result provides a theoretical basis for using a widely practically applied method of combining the criteria weights, obtained by using various methods, as a geometric mean of particular values.
In solving the particular decision-making problems, various methods suggested in the paper for combining and recalculating the criteria weights can be used, depending on the specific character of the problem and the available information.
The suggested method of recalculating the criteria weights based on the Bayes’ approach was used in the work for assessing the quality of various courses of studies taught to students. The MCDM methods such as SAW, TOPSIS, EDAS and COPRAS were used for evaluation.
The authors believe that the suggested new approach contributes to the solution of various decision-making problems by providing a theoretical basis for combining the weights of criteria obtained by using various MCDM methods and by demonstrating its practical application.
Author Contributions
The idea to use the Bayesian method for weights recalculation offered I.V., V.P. presented the theoretical rationality background for the IDOCRIW method, the idea to apply Bayesian method depends to E.K.Z. and V.P., E.K.Z. is the co-author of the COPRAS, EDAS methods. V.P. and E.K.Z. are authors of the CILOS and IDOCRIW methods. V.P. and I.V. are program’s developers, ran the practical calculations. V.P., I.V. and E.K.Z. finally reviewed and edited the manuscript. The discussion was a team task. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hwang, C.L.; Lin, M.J. Group Decision Making under Multiple Criteria: Methods and Applications; Springer: Berlin, Germany, 1987. [Google Scholar]
- Mardani, A.; Jusoh, A.; MD Nor, K.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res. Ekonomska Istraživanja 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Vainiūnas, P.; Turskis, Z.; Tamošaitienė, J. Multiple criteria decision support system for assessment of projects managers in construction. Int. J. Inf. Technol. Decis. Mak. 2012, 11, 501–520. [Google Scholar] [CrossRef]
- Čereška, A.; Zavadskas, E.K.; Bučinskas, V.; Podvezko, V.; Sutinys, E. Analysis of Steel Wire Rope Diagnostic Data Applying Multi-Criteria Methods. Appl. Sci. 2018, 8, 260. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Cavallaro, F.; Podvezko, V.; Ubarte, I.; Kaklauskas, A. MCDM assessment of a healthy and safe built environment according to sustainable development principles: A practical neighbourhood approach in Vilnius. Sustainability 2017, 9, 702. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Saparauskas, J. New Application of SWARA Method in Prioritizing Sustainability Assessment Indicators of Energy System. Inzinerine Ekonomika Eng. Econ. 2013, 24, 408–414. [Google Scholar] [CrossRef]
- Kurilov, J.; Vinogradova, I. Improved fuzzy AHP methodology for evaluating quality of distance learning courses. Int. J. Eng. Educ. 2016, 32, 1618–1624. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, Т. L. Decision-Making. Analytic Hierarchy Process; Radio and Communication: Moscow, Russia, 1993. [Google Scholar]
- Podvezko, V.; Sivilevicius, H. The use of AHP and rank correlation methods for determining the significance of the interaction between the elements of a transport system having a strong influence on traffic safety. Transport 2013, 28, 389–403. [Google Scholar] [CrossRef]
- Alimardani, M.; Hashemkhani Zolfani, S.; Aghdaie, M.; Tamosaitiene, J. A novel hybrid SWARA and VIKOR methodology for Supplier selection in an agile environment. Technol. Econ. Dev. Econ. 2013, 19, 533–548. [Google Scholar] [CrossRef]
- Ginevicius, R. A new determining method for the criteria weights in multi–criteria evaluation. Int. J. Inf. Technol. Decis. Mak. 2011, 10, 1067–1095. [Google Scholar] [CrossRef]
- Krylovas, A.; Zavadskas, E.K.; Kosareva, N.; Dadelo, S. New KEMIRA method for determining criteria priority and weights in solving MCDM problem. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 1119–1133. [Google Scholar] [CrossRef]
- Han, J.; Li, Y.; Kang, J.; Cai, E.; Tong, Z.; Ouyang, G.; Li, X. Global synchronization of multichannel EEG based on rényi entropy in children with autism spectrum disorder. Appl. Sci. 2017, 7, 257. [Google Scholar] [CrossRef]
- Han, Z.H.; Liu, P.D. A fuzzy multi–attribute decision–making method under risk with unknown attribute weights. Technol. Econ. Dev. Econ. 2011, 17, 246–258. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making Methods and Applications; A State of the Art Survey; Springer: Berlin, Germany, 1981. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Podvezko, V. Integrated determination of objective criteria weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 267–283. [Google Scholar] [CrossRef]
- Pekelman, D.; Sen, S.K. Mathematical programming models for the determination of attribute weights. Manag. Sci. 1974, 20, 1217–1229. [Google Scholar] [CrossRef]
- Singh, R.K.; Benyoucef, L. A consensus based group decision making methodology for strategic selection problems of supply chain coordination. Eng. Appl. Artif. Intell. 2013, 26, 122–134. [Google Scholar] [CrossRef]
- Čereška, A.; Podvezko, V.; Zavadskas, E.K. Operating characteristics analysis of rotor systems using MCDM methods. Stud. Inform. Control 2016, 25, 59–68. [Google Scholar] [CrossRef]
- Trinkuniene, E.; Podvezko, V.; Zavadskas, E.K.; Joksiene, I.; Vinogradova, I.; Trinkunas, V. Evaluation of quality assurance in contractor contracts by multi-attribute decision-making methods. Econ. Res. Ekonomska Istrazivanja 2017, 30, 1152–1180. [Google Scholar] [CrossRef]
- Su, H.; Qin, P.; Qin, Z. A Method for Evaluating Sea Dike Safety. Water Resour. Manag. 2013, 27, 5157–5170. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Wang, T.C.; Lee, H.D. Developing a fuzzy TOPSIS approach based on subjective weights and objective weights. Expert Syst. Appl. 2009, 36, 8980–8985. [Google Scholar] [CrossRef]
- Lazauskaite, D.; Burinskiene, M.; Podvezko, V. Subjectively and objectively integrated assessment of the quality indices of the suburban residential environment. Int. J. Strateg. Prop. Manag. 2015, 19, 297–308. [Google Scholar] [CrossRef]
- Md Saad, R.; Ahmad, M.Z.; Abu, M.S.; Jusoh, M.S. Hamming Distance Method with Subjective and Objective Weights for Personnel Selection. Sci. World J. Art. 2014, 2014, 865495. [Google Scholar] [CrossRef] [PubMed]
- Parfenova, L.; Pugachev, A.; Podviezko, A. Comparative analysis of tax capacity in regions of Russia. Technol. Econ. Dev. Econ. 2016, 22, 905–925. [Google Scholar] [CrossRef]
- Ustinovichius, L.; Zavadskas, E.K.; Podvezko, V. Application of a quantitative multiple criteria decision making (MCDM–1) approach to the analysis of investments in construction. Control Cybernet. 2007, 36, 251–268. [Google Scholar]
- Jeffreys, H. Scientific Inference, 3rd ed.; Cambridge University Press: Cambridge, UK, 1973; p. 31. ISBN 978-0-521-18078-8. [Google Scholar]
- Ma, J.; Fan, P.; Huang, L.H. A subjective and objective integrated approach to determine attribute weights. Eur. J. Oper. Res. 1999, 112, 397–404. [Google Scholar] [CrossRef]
- Kou, G.; Lin, C. A cosine maximization method for the priority vector derivation in AHP. Eur. J. Oper. Res. 2014, 235, 225–232. [Google Scholar] [CrossRef]
- Vinogradova, I.; Kliukas, R. Methodology for evaluating the quality of distance learning courses in consecutive stages. Procedia Soc. Behav. Sci. 2015, 191, 1583–1589. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Hafner Publishing House: New York, NY, USA, 1955. [Google Scholar]
- Kurilov, J.; Vinogradova, I.; Kubilinskienė, S. New MCEQLS fuzzy AHP methodology for evaluating learning repositories: A tool for technological development of economy. Technol. Econ. Dev. Econ. 2016, 22, 142–155. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Mirkin, B.G. Group Choice; Winston & Sons: Washington, DC, USA, 1979. [Google Scholar]
- Stefano, N.M.; Casarotto Filho, N.; Vergara, L.G.L.; Rocha, R.U.G. COPRAS (complex proportional assessment): State of the art research and its applications. IEEE Latin Am. Trans. 2015, 13, 3899–3906. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Podvezko, V. The Comparative Analysis of MCDM Methods SAW and COPRAS. Inžinerinė Ekonomika Eng. Econ. 2011, 22, 134–146. [Google Scholar]
- Podviezko, A.; Podvezko, V. Absolute and Relative Evaluation of Socio-Economic Objects Based on Multiple Criteria Decision Making Methods. Inzinerine Ekonomika Eng. Econ. 2014, 25, 522–529. [Google Scholar] [CrossRef]
- Turskis, Z.; Keršulienė, V.; Vinogradova, I. A new fuzzy hybrid multi-criteria decision-making approach to solve personnel assessment problems. Case study: Director selection for estates and economy office. Econ. Comput. Econ. Cybernet. Stud. Res. 2017, 51, 211–229. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Šarka, V. The new method of multi-criteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Mardani, A.; Turskis, Z.; Jusoh, A.; Nor, K.M.D. Development of TOPSIS method to solve complicated decision-making problems: An overview on developments from 2000 to 2015. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 645–682. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).