Laplacian Spectra for Categorical Product Networks and Its Applications

Abstract

The Kirchhoff index, global mean-first passage time, average path length and number of spanning trees are of great importance in the field of networking. The “Kirchhoff index” is known as a structure descriptor index. The “global mean-first passage time” is known as a measure for nodes that are quickly reachable from the whole network. The “average path length” is a measure of the efficiency of information or mass transport on a network, and the “number of spanning trees” is used to minimize the cost of power networks, wiring connections, etc. In this paper, we have selected a complex network based on a categorical product and have used the spectrum approach to find the Kirchhoff index, global mean-first passage time, average path length and number of spanning trees. We find the expressions for the product and sum of reciprocals of all nonzero eigenvalues of a categorical product network with the help of the eigenvalues of the path and cycles.

1. Introduction

The impact of the study of Laplacian spectra for graphs has increased due to its applications in different fields. Laplacian spectra have miscellaneous applications in graph theory, combinatorial optimization, mathematical biology, computer science, machine learning and in differential geometry, as well. Due to the wide range of applications, the Laplacian spectra of networks is a very interesting and attractive field of research. Computations of the Laplacian spectra of networks are involved in many results related to topological structures and dynamical processes.

Arenas et al. [1] developed a method for understanding synchronization phenomena in networks using Laplacian spectra. Synchronization processes in populations of locally-interacting elements are the focus of intense research in physical, biological, chemical, technological and complex network topologies.

Boccaletti et al. [2] focused on coupled biological and chemical systems, neural networks, socially-interacting species, the Internet and the World Wide Web, which are only a few examples of systems composed of a large number of highly interconnected dynamical units. The first approach to capture the global properties of such systems is to model them as graphs whose nodes represent the dynamical units and whose links stand for the interactions between them.

Liu et al. [3] discussed and investigated the properties of the Laplacian matrices for n-prism networks. They calculated the Laplacian spectra of n-prism graphs, which are both planar and polyhedral. In particular, they derived the analytical expressions for the product and the sum of the reciprocals of all nonzero Laplacian eigenvalues. Moreover, these results were used to handle various problems that often arise in the study of networks including the Kirchhoff index, global mean-first passage time, average path length and the number of spanning trees.

Ding et al. [4] discussed the Laplacian spectra of a three-prism graph and applied them. This graph is both planar and polyhedral and belongs to the generalized Petersen graph. Using the regular structures of this graph, they obtained the recurrent relationships for the Laplacian matrix between this graph and its initial state of a triangle and further derived the corresponding relationships for Laplacian eigenvalues between them. By these relationships, they obtained the analytical expressions for the product and the sum of the reciprocals of all nonzero Laplacian eigenvalues. Finally, they applied these expressions to calculate the number of spanning trees and mean first-passage time (MFPT) and saw the scaling of MFPT with the network size n, which is larger than those performed on some uniformly recursive trees.

Therefore, it is of great interest to compute the Laplacian spectra of different networks. In the last decades, networks and applications of Laplacian spectra have been studied by many scientists, i.e., [5].

Researchers have not paid much attention to applications of Laplacian spectra for networks based on different types of graph operations. Since graph products have a very significant contribution to describing very useful complex networks, we have considered networks based on a categorical product. In this paper, we study the Laplacian spectra of the complex network as a categorical product network. Categorical graph products are used to study complex networks in computer science, to understand structures in structural mechanics and to describe multilayer networks and have many applications in network topologies. Considering the structure of categorical product networks, we derive the expressions for the product and sum of reciprocals of nonzero eigenvalues of the categorical product with the help of the eigenvalues of the path and cycle. Furthermore, we compute the Kirchhoff index, global mean first passage time, average path length and number of spanning trees using the relation of nonzero eigenvalues to these applications.

The Kirchhoff index $Kf$, also simply called the resistance and denoted by R [6], of a connected graph G on n nodes is defined by:

$$Kf=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{(\mathrm{\Omega })}_{ij}$$

(1)

where ${(\mathrm{\Omega })}_{ij}$ is the resistance distance matrix. This formula for the Kirchhoff index reduces to [7]:

$$Kf(G)=N\sum _{i=2}^N\frac{1}{{\nu }_i}$$

(2)

where ${\nu }_i$ represents the eigenvalue of the Laplacian matrix of the graph.

The global mean-first passage time (MFPT) $F_{ij}$ has been studied with respect to transport and networks. The mean first passage time (MFPT) is very useful to estimate the speed of transport for random walks on complex networks [8,9]. In fact, MFPT denoted by $<F_N>$ measures the diffusion efficiency of random walks, which is obtained by averaging $F_{ij}$ over $(N-1)$ possible destinations and N origins of particles:

$$<F_N>=\frac{1}{N(N-1)}\sum _{i\ne j}{F}_{ij}(N)$$

(3)

From ([10]), let commuting time $C_{ij}$ between nodes i and j be exactly $2\mid E\mid r_{ij}$, then we have:

$$C_{ij}=F_{ij}+F_{ji}=2\mid E\mid r_{ij}$$

(4)

where $\mid E\mid$ denotes the number of edges in G and $r_{ij}$ is the effective resistance between two nodes i and j. By combining the two above relations, the MFPT can be computed by the following formula:

$$<F_N>=\frac{2E_t}{N_t(N_t-1)}\sum _{i<j}^n{r}_{ij}(G)=\frac{2E_t}{N_t-1}\sum _{k=2}^{N_t}\frac{1}{{\nu }_k}$$

(5)

where ${\nu }_k$ are the eigenvalues of the Laplacian matrix of the graph after t iterations.

The average path length defines the average number of steps along the shortest path $d_{ij}$ for all possible pairs of network nodes, which is the measure of the efficiency of information or mass transport on the network, then the average path length $D_t$, for G(t) (the graph after t iterations) is defined as:

$$D_t=\frac{2}{N_t-1}\sum _{j>i}{d}_{ij}$$

(6)

Moreover, the shortest path $d_{ij}$ and effective resistance $r_{ij}$ are related by expression $r_{ij}=\frac{2d_{ij}}{\left|N\right|}$, where N represents the number of nodes in the complete graph. Then, by these two relations, we have:

$$\begin{array}{c}\hfill D_t=\frac{2}{N_t(N_t-1)}\frac{N_t}{2}\sum _{j>i}{r}_{ij}=\frac{N_t}{N_t-1}\frac{N_t}{2}{N}_t\sum _{k=2}^{N_t}\frac{1}{{\nu }_k}\end{array}$$

(7)

Spanning trees are very important in complex networks and play a key role in various networks. The exact number of spanning trees $N_{st}(G_t)$, for $G(t)$, $(t\ge 1),$ where t shows the iterations in constructing a graph, discussed in the next section, can be computed by Kirchhoff’s matrix tree theorem [11].

More precisely, in this paper, we have computed Laplacian spectra for categorical product networks and have discussed their applications. After the Introduction, in the second section, the materials and methods are discussed; in the main section, the categorical product network is defined in an iterative way, and then, the Laplacian spectra are computed. Finally, the applications of the Laplacian spectra are computed.

2. Materials and Methods

In this section, we state the materials and methods that are used in the main section.

In graph theory, the direct product $G\times H$ of graphs G and H is defined as a graph such that the vertex set of $G\times H$ is the Cartesian product $V(G)\times V(H)$ and any two vertices (u, $u_1$) and (v, $v_1$) are adjacent in $G\times H$ if and only if u is adjacent with v and $u_1$ is adjacent with $v_1$. The direct product is also called the tensor product or categorical product.

Let G be a graph with vertices $1,2,\cdots ,n$. The Laplacian matrix of G is $L(G)=D(G)-A(G)$, where A(G) is $n\times n$ adjacency, and the matrix of G with $(i,j)-entry$ is equal to 1 if vertices i and j are adjacent and 0 otherwise. $D(G)$ is the diagonal matrix of vertices’ degrees.

Definition 1.

Consider two matrices A and B. The Kronecker product $A\otimes B$ of two matrices A and B is the matrix that is obtained by taking $(i,j)$-th entries as $a_{ij}B$ for all $i,j$. The Kronecker product of the matrix $A\in M^{(p,q)}$ with the matrix $B\in M^{(r,s)}$ is defined as (see [12,13]):

$$\left(\begin{array}{ccc}{a}_{11}B& \cdots & a_{1q}B\\ ..& .& .\\ a_{p1}B& \cdots & a_{pq}B\end{array}\right)$$

The Kronecker product has the following main properties.

$$\begin{array}{ccc}\hfill (\alpha A)\otimes B& =& A\otimes (\alpha B)=\alpha (A\otimes B),\forall ,A\in M^{(p,q)},B\in M^{(r,s)}\mathit{and} \mathit{scalar}\alpha \hfill \\ \hfill {(A\otimes B)}^T& =& A^T\otimes B^T,\forall A\in M^{p,q},B\in M^{r,s}\hfill \\ \hfill (A\otimes B)\otimes C& =& A\otimes (B\otimes C),\forall A\in M^{(m,n)},B\in M^{(p,q)},C\in M^{(r,s)}\hfill \\ \hfill (A\otimes B)(C\otimes D)& =& AC\otimes BD,\forall A\in M^{(p,q)},B\in M^{(r,s)},C\in M^{(q,k)},D\in M^{(s,l)}\hfill \\ \hfill trace(A\otimes B)& =& trace(B\otimes A)=trace(A)trace(B),\forall A\in M^m,B\in M^n.\hfill \end{array}$$

We have used the Kronecker product of matrices to find the Laplacian spectra for the categorical product considering the spectra for the path and cycle. Let $P_n$ denote the path with n vertices. Let $C_n$ be a cycle of length n. Then, their spectra can be stated as [14]:

Lemma 1.

The Laplacian eigenvalues of a path $P_n$ are $2-2cos\frac{i\pi }{n}$, $(i=0,1,\cdots ,n-1).$ The Laplacian eigenvalues of a cycle $C_n$ are $2-2cos\frac{2j\pi }{n}$, j = 0, 1,..., n−1.

With the help of the following flowchart in Figure 1, we will facilitate the understanding of the proposed approach in this paper clearly.

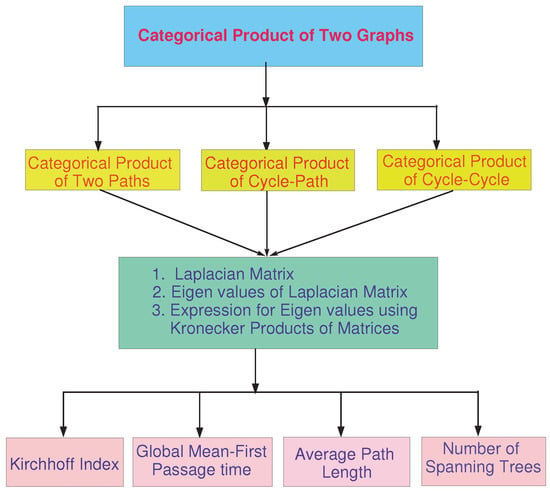
Figure 1. Flowchart for the methods.

3. Main Results

3.1. Categorical Product of Two Paths and Laplacian Spectra

Let a categorical product network of paths be constructed in an iterative way. We take categorical product network $G(t)$, $(t\ge 1)$ after $t-1$ iterations. Initially at $t=1,G(1)$ is a path with n vertices. For $t\ge 2$, $G(t)$ is constructed from $G(t-1)$; from every existing vertex in $G(t-1)$, a new vertex is created so that a new path with n vertices is constructed; also, each new vertex in $G(t)$ is connected to the vertices in $G(t-1)$, shown by Figure 2. The number of vertices and edges in $G(t)$ is $N_t=nt$ and $E_t=(2t-2)n-(2t-2)$, $n\ge 2$.

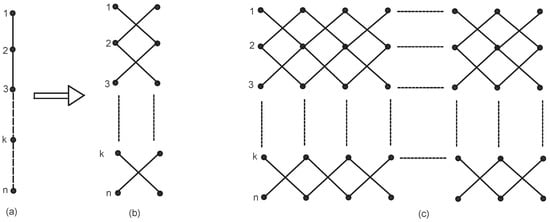
Figure 2. (a) Path $P_n$. (b) Grid $P_n\times P_2$ after the first iteration for $t=2$. (c) General grid $P_n\times P_t$ structure.

Let ${\lambda }_t$ and ${\mu }_t$ be the product of all nonzero eigenvalues of $G_t$ and the sum of reciprocals of these eigenvalues, respectively, i.e., ${\lambda }_t={\prod }_{i=2}^{N_t}{\nu }_i$ and ${\mu }_t={\sum }_{i=2}^{N_t}\frac{1}{{\nu }_i}$, where ${\nu }_1=0$ and ${\nu }_i$, $i=2,3,\cdots ,N_t$ denote the $N_t-1$ nonzero eigenvalues of $L(G_t)$.

Theorem 1.

The product and sum of reciprocal nonzero eigenvalues of $L(G_t),$ the Laplacian matrix of G(t), are:

$$\begin{array}{c}\hfill {\lambda }_t=\prod _{i=0}^{t-1}\prod _{j=0}^{n-1}\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)\\ \hfill {\mu }_t=\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\end{array}$$

$d_i$ shows the degree of vertex i.

Proof. 

Consider a categorical product network G as is shown in the figure. By the properties of the Kronecker product of matrices, we can write the Laplacian matrix for G as [15],

$$\begin{array}{c}\hfill L(G_t)=L(P_n)\otimes D(P_t)+D(P_n)\otimes L(P_t)-L(P_n)\otimes L(P_t)\end{array}$$

where $D(P_n)$ is the diagonal matrix of order $n\times n$; with the diagonal elements’ degree of vertices. By using the results from linear algebra, there exists invertible matrices P and Q such that:

$${(L(P_n))}^{{}^{\prime }}=P^{-1}L(P_n)P,{(L(P_t))}^{{}^{\prime }}=Q^{-1}L(P_t)Q$$

are the upper triangular matrices with diagonal elements, $2-2cos\frac{\pi j}{n}$, $j=0,1,\cdots ,n-1$ and $2-2cos\frac{\pi i}{t}$, $i=0,1,\cdots ,t-1$, respectively. Then, using the fact that:

$${(P\otimes Q)}^{-1}·\left(L(P_n)\otimes L(P_t)\right)·(P\otimes Q)=(P^{-1}\otimes Q^{-1})·\left(L(P_n)P\otimes L(P_t)Q\right)=P^{-1}L(P_n)P\otimes Q^{-1}L(P_t)Q$$

is the upper triangular matrix with diagonal elements, the matrix:

$${(P\otimes Q)}^{-1}·\left(L(P_n)\otimes D(P_t)+D(P_n)\otimes L(P_t)-L(P_n)\otimes L(P_t)\right)·(P\otimes Q)$$

is upper triangular matrix with diagonal elements,

$$\begin{array}{c}\hfill (2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t});\\ \hfill i=0,1,\cdots ,t-1,j=0,1,\cdots ,n-1,\\ \hfill d_1=d_t=d_n=d_{nt}=1,\\ \hfill d_{k+1}=d_{nt-k}=2,k=1,\cdots ,n-2,d_{1+nq}=d_{n+nq}=2,q=1,\cdots ,t-2,\\ \hfill \mathrm{all}\mathrm{other}{d}_i\mathrm{have}\mathrm{a}\mathrm{value}\mathrm{of}\mathrm{four}.\end{array}$$

(8)

that are the eigenvalues for the categorical product network. Therefore:

$$\begin{array}{ccc}\hfill {\lambda }_t& =& \prod _{i=0}^{t-1}\prod _{j=0}^{n-1}{\nu }_{i,j}\hfill \\ & =& \prod _{i=0}^{t-1}\prod _{j=0}^{n-1}\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\mu }_t& =& \sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{{\nu }_{i,j}}\hfill \\ & =& \sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\hfill \end{array}$$

(10)

Corollary 1.

Let $L(G_2)$ be the Laplacian matrix of $P_n\times P_2$, the categorical product graph with n vertices after the first iteration, $t=2$, then the product and sum of the reciprocal nonzero eigenvalues of $L(G_2)$ are:

$$\begin{array}{ccc}{\lambda }_2& =& \prod _{i=0}^1\prod _{j=0}^{n-1}{\nu }_{i,j}=\prod _{i=0}^1\prod _{j=0}^{n-1}\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)\hfill \\ {\mu }_2& =& \sum _{i=0}^1\sum _{j=0}^{n-1}\frac{1}{{\nu }_{i,j}}=\sum _{i=0}^1\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\hfill \end{array}$$

☐

3.2. Categorical Product of the Cycle-Path and Laplacian Spectra

Let a categorical product network of the cycle and path be constructed in an iterative way. We take the initial categorical product network $G(t)$, ($t\ge 1$) after $t-1$ iterations. Initially, at $t=1,G(1)$ is a cycle with n vertices. For $t\ge 2$, $G(t)$ is constructed from $G(t-1)$, from every existing vertex in $G(t-1)$, a new vertex is created so that a new path with n vertices is constructed; also, each new vertex in $G(t)$ is connected to vertices in $G(t-1)$, shown by Figure 3. The number of vertices and edges in $G(t)$ are $N_t=nt$ and $E_t=2n(t-1)$, $n\ge 2$.

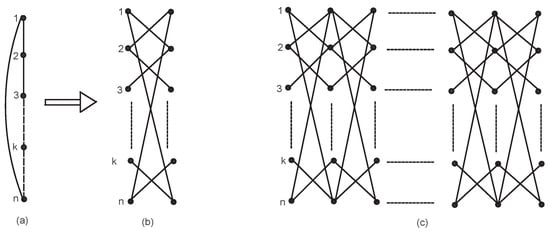
Figure 3. (a) Cycle $C_n$. (b) Grid $C_n\times P_2$ after the first iteration for $t=2$. (c) General grid $C_n\times P_t$ structure.

Let ${\lambda }_t$ and ${\mu }_t$ be the product of all nonzero eigenvalues of $G_t$ and the sum of reciprocals of these eigenvalues, respectively, i.e., ${\lambda }_t={\prod }_{i=2}^{N_t}{\nu }_i$ and ${\mu }_t={\sum }_{i=2}^{N_t}\frac{1}{{\nu }_i}$, where ${\nu }_1=0$ and ${\nu }_i$, $i=2,3,\cdots ,N_t$ denote the $N_t-1$ nonzero eigenvalues of $L(G_t)$.

Theorem 2.

The product and sum of reciprocal nonzero eigenvalues of $L(G_t)$, the Laplacian matrix of G(t), are:

$$\begin{array}{c}\hfill {\lambda }_t=\prod _{i=0}^{t-1}\prod _{j=0}^{n-1}\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t})\right)\\ \hfill {\mu }_t=\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\end{array}$$

Proof. 

Consider a categorical product network G as is shown in the figure. By the properties of the Kronecker product of matrices, we can write the Laplacian matrix for G as:

$$\begin{array}{c}\hfill L(G_t)=L(C_n)\otimes D(P_t)+D(C_n)\otimes L(P_t)-L(C_n)\otimes L(P_t)\end{array}$$

where $D(C_n)$ is the diagonal matrix of order $n\times n$; with the diagonal elements’ degree of vertices. By using the results from linear algebra, there exists invertible matrices P and Q such that:

$${(L(C_n))}^{{}^{\prime }}=P^{-1}L(C_n)P,{(L(P_t))}^{{}^{\prime }}=Q^{-1}L(P_t)Q$$

are the upper triangular matrices with diagonal elements, $2-2cos\frac{2\pi j}{n}$, $j=0,1,\cdots ,n-1$ and $2-2cos\frac{\pi i}{t}$, $i=0,1,\cdots ,t-1$, respectively. Then, using the fact that:

$$\begin{gathered} {(P\otimes Q)}^{-1}·\left(L(C_n)\otimes L(P_t)\right)·(P\otimes Q)=(P^{-1}\otimes Q^{-1})·\left(L(C_n)P\otimes L(P_t)Q\right) \\ =P^{-1}L(C_n)P\otimes Q^{-1}L(P_t)Q \end{gathered}$$

is the upper triangular matrix with diagonal elements, the matrix:

$${(P\otimes Q)}^{-1}·\left(L(C_n)\otimes D(P_t)+D(C_n)\otimes L(P_t)-L(C_n)\otimes L(P_t)\right)·(P\otimes Q)$$

is the upper triangular matrix with diagonal elements,

$$\begin{array}{c}\hfill (2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t});\\ \hfill i=0,1,\cdots ,t-1,j=0,1,\cdots ,n-1,\\ \hfill \mathrm{all}{d}_i\mathrm{have}\mathrm{a}\mathrm{value}\mathrm{of}\mathrm{two}.\end{array}$$

(11)

that are the eigenvalues for the categorical product network. Therefore,

$$\begin{array}{c}\hfill \begin{array}{ccc}{\lambda }_t& =& \prod _{i=0}^{t-1}\prod _{j=0}^{n-1}{\nu }_{i,j}\hfill \\ & =& \prod _{i=0}^{t-1}\prod _{j=0}^{n-1}\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t})\right)\hfill \end{array}\end{array}$$

(12)

$$\begin{array}{c}\hfill \begin{array}{ccc}{\mu }_t\hfill & =& \sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{{\nu }_{i,j}}\hfill \\ & =& \sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\hfill \end{array}\end{array}$$

(13)

 ☐

3.3. Categorical Product of the Cycle-Cycle and Laplacian Spectra

Let a categorical product network of cycles be constructed in an iterative way. We take initial categorical product network $G(t)$, ($t\ge 1$) after $t-1$ iterations. Initially, at $t=1,G(1)$ is a categorical product network of cycle $C_n\times C_3$ with n vertices. For $t\ge 2$, $G(t)$ is constructed from $G(t-1)$, and from every existing vertex in $G(t-1)$, a new vertex is created so that n vertices are constructed; also, each new vertex in $G(t)$ is connected to the vertices in $G(t-1)$, shown by Figure 4. The number of vertices and edges in $G(t)$ are $N_t=n(t+2)$ and $E_t=2n(t+2)-2$.

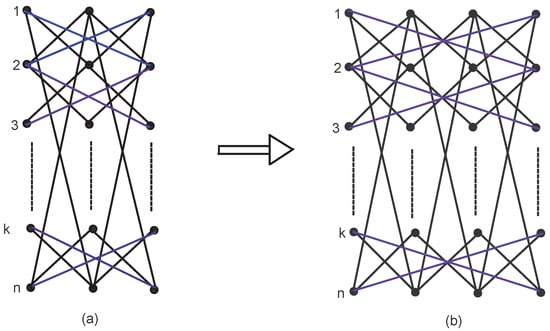
Figure 4. (a) Initial product $C_n\times C_3$ for $t=1$. (b) Grid $C_n\times C_4$ after the first iteration for $t=2$.

Let ${\lambda }_t$ and ${\mu }_t$ be the product of all nonzero eigenvalues of $G_t$ and the sum of reciprocals of these eigenvalues, respectively, i.e., ${\lambda }_t={\prod }_{i=2}^{N_t}{\nu }_i$ and ${\mu }_t={\sum }_{i=2}^{N_t}\frac{1}{{\nu }_i}$, where ${\nu }_1=0$ and ${\nu }_i$, $i=2,3,\cdots ,N_t$ denote the $N_t-1$ nonzero eigenvalues of $L(G_t)$.

Theorem 3.

The product and sum of the reciprocal nonzero eigenvalues of $L(G_t)$, the Laplacian matrix of G(t), are:

$$\begin{array}{ccc}\hfill {\lambda }_t& =& \prod _{i=0}^{t+1}\prod _{j=0}^{n-1}\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2})\right)\hfill \\ \hfill {\mu }_t& =& \sum _{i=0}^{t+1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2})\right)}\hfill \end{array}$$

Proof. 

Consider a categorical product network G as is shown in the figure. By the properties of the Kronecker product of matrices, we can write the Laplacian matrix for G as:

$$\begin{array}{c}\hfill L(G_t)=L(C_n)\otimes D(C_t)+D(C_n)\otimes L(C_t)-L(C_n)\otimes L(C_t)\end{array}$$

where $D(C_n)$ is the diagonal matrix of order $n\times n$; with the diagonal elements’ degree of vertices. By using the results from linear algebra, there exists invertible matrices P and Q such that:

$${(L(C_n))}^{{}^{\prime }}=P^{-1}L(C_n)P,{(L(C_t))}^{{}^{\prime }}=Q^{-1}L(C_t)Q$$

are the upper triangular matrices with diagonal elements, $2-2cos\frac{2\pi j}{n}$, $j=0,1,\cdots ,n-1$ and $2-2cos\frac{2\pi i}{t+2}$, $i=0,1,\cdots ,t+1$, respectively. Then, using the fact that:

$$\begin{gathered} {(P\otimes Q)}^{-1}·\left(L(C_n)\otimes L(C_t)\right)·(P\otimes Q)= \\ (P^{-1}\otimes Q^{-1})·\left(L(C_n)P\otimes L(C_t)Q\right)=P^{-1}L(C_n)P\otimes Q^{-1}L(C_t)Q \end{gathered}$$

is the upper triangular matrix with diagonal elements, the matrix:

$${(P\otimes Q)}^{-1}·\left(L(C_n)\otimes D(C_t)+D(C_n)\otimes L(C_t)-L(C_n)\otimes L(C_t)\right)·(P\otimes Q)$$

is the upper triangular matrix with diagonal elements,

$$\begin{array}{c}\hfill \begin{array}{c}(2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2});\hfill \\ i=0,1,\cdots ,t+1,j=0,1,\cdots ,n-1,\hfill \\ d_1=d_t=d_n=d_{nt}=3,\mathrm{all}\mathrm{other}{d}_i\mathrm{have}\mathrm{a}\mathrm{value}\mathrm{of}\mathrm{four}.\hfill \end{array}\end{array}$$

(14)

that are the eigenvalues for the categorical product network. Therefore:

$$\begin{array}{ccc}{\lambda }_t\hfill & =\hfill & \prod _{i=0}^{t+1}\prod _{j=0}^{n-1}{\nu }_{i,j}\hfill \\ & =& \prod _{i=0}^{t+1}\prod _{j=0}^{n-1}\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2})\right)\hfill \end{array}$$

(15)

$$\begin{array}{ccc}{\mu }_t\hfill & =\hfill & \sum _{i=0}^{t+1}\sum _{j=0}^{n-1}\frac{1}{{\nu }_{i,j}}\hfill \\ & =& \sum _{i=0}^{t+1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2})\right)}\hfill \end{array}$$

(16)

 ☐

4. Applications of Laplacian Spectra

In this section, by the use of Expressions (15) and (16), we will find the Kirchhoff index, global mean-first passage time, average path length and the number of spanning trees.

4.1. Kirchhoff Index

The Kirchhoff index of a connected graph G is defined as the sum of resistance distances between all pairs of vertices, mathematically:

$$\begin{array}{ccc}\hfill Kf(G(t))& =& \sum _{i<j}{r}_{ij}(G)\hfill \end{array}$$

where $r_{ij}(G)$ represents the resistance distance between a pair of vertices. In terms of eigenvalues for a connected network G of order N with all its nonzero eigenvalues represented by ${\nu }_i;$ $i=2,\cdots ,N$, a well-known identity Kirchhoff index is defined as:

$$\begin{array}{ccc}\hfill Kf(G(t))& =& N_t\sum _{k=2}^{N_t}\frac{1}{{\nu }_k}=N_t\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{{\nu }_{i,j}},(i,j)\ne (0,0)\hfill \end{array}$$

The Kirchhoff index for the categorical path-path product network:

$$\begin{array}{ccc}\hfill Kf(G(t))& =& nt\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\hfill \\ \hfill (i,j)& \ne & (0,0)\hfill \end{array}$$

The Kirchhoff index for the categorical cycle-path product network:

$$\begin{array}{ccc}\hfill Kf(G(t))& =& nt\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{(2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t})}\hfill \end{array}$$

The Kirchhoff index for the categorical cycle-cycle network:

$$\begin{array}{ccc}Kf(G(t))\hfill & =\hfill & n(t+2)\sum _{i=0}^{t+1}\sum _{j=0}^{n-1}\frac{1}{(2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2})}\hfill \end{array}$$

4.2. Global Mean-First Passage Time

The global mean first-passage time (MFPT) is defined as the average of the first-passage time (FPT) between two nodes of a network. Mathematically, the global mean-first passage time (MFPT) for $G(t)$ is:

$$\begin{array}{ccc}\hfill <F_N>& =& \frac{2E_t}{(N_t-1)}\sum _{k=2}^{N_t}\frac{1}{{\nu }_k}=\frac{2E_t}{(N_t-1)}\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{{\nu }_k},(i,j)\ne (0,0)\hfill \end{array}$$

The global mean-first passage time for the categorical path-path product network:

Since $E_t=(2t-2)n-(2t-2)$ and $N_t=nt$:

$$\begin{array}{ccc}\hfill <F_N>& =& \frac{2((2t-2)n-(2t-2))}{(nt-1)}\hfill \\ & \times & \sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\hfill \\ \hfill (i,j)& \ne & (0,0)\hfill \end{array}$$

The global mean-first passage time for the categorical cycle-path product network:

Since $E_t=2n(t-1)$ and $N_t=nt$:

$$\begin{array}{ccc}\hfill <F_N>& =& \frac{2(2n(t-1))}{(nt-1)}\hfill \\ & \times & \sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\hfill \end{array}$$

The global mean-first passage time for the categorical cycle-cycle product network:

Since $E_t=2n(t+2)-2$ and $N_t=n(t+2)$:

$$\begin{array}{ccc}\hfill <F_N>& =& \frac{2(2n(t+2)-2)}{n(t+2)-1}\hfill \\ & \times & \sum _{i=0}^{t+1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2})\right)}\hfill \end{array}$$

4.3. Average Path Length

The average path length is an idea in network topology that can be defined as the average number of steps along with the shortest paths for all possible pairs of vertices of a network. The average path length in terms of the Laplacian eigenvalues is defined as:

$$\begin{array}{c}\hfill D_t=\frac{N_t}{N_t-1}\sum _{k=2}^{N_t}\frac{1}{{\nu }_k},(i,j)\ne (0,0)\end{array}$$

The average path length for the categorical path-path product network:

$$\begin{array}{ccc}\hfill D_t& =& \frac{nt}{nt-1}\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}\hfill \end{array}$$

The average path length for the categorical cycle-path product network:

$$\begin{array}{ccc}\hfill D_t& =& \frac{nt}{nt-1}\sum _{i=0}^{t-1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t}))\right)}\hfill \end{array}$$

The average path length for the categorical cycle-cycle product network:

$$\begin{array}{ccc}\hfill D_t& =& \frac{n(t+2)}{n(t+2)-1}\hfill \\ & \times & \sum _{i=0}^{t+1}\sum _{j=0}^{n-1}\frac{1}{\left((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2})\right)}\hfill \end{array}$$

4.4. The Number of Spanning Trees

The number of spanning trees has a very important role in various networks, and it can be computed using the product of nonzero eigenvalues of the Laplacian matrix [16];

$$\begin{array}{ccc}\hfill N_{ST}(G_t)& =& \frac{{\prod }_{k=2}^{N_t}{\nu }_i}{N_t}=\frac{A_t}{N_t}=\frac{{\prod }_{i=0}^{t-1}{\prod }_{j=0}^{n-1}{\nu }_{i,j}}{N_t},(i,j)\ne (0,0)\hfill \end{array}$$

The number of spanning trees for the categorical path-path product network:

$$\begin{array}{ccc}\hfill N_{ST}(G_t)& =& \frac{{\prod }_{i=0}^{t-1}{\prod }_{j=0}^{n-1}\left((2-2cos\frac{j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{j\pi }{n})(2-2cos\frac{i\pi }{t})\right)}{nt}\hfill \end{array}$$

The number of spanning trees for the categorical cycle-path product network:

$$\begin{array}{ccc}\hfill N_{ST}(G_t)& =& \frac{{\prod }_{i=0}^{t-1}{\prod }_{j=0}^{n-1}((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{i\pi }{t})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{i\pi }{t}))}{nt}\hfill \end{array}$$

The number of spanning trees for the categorical cycle-cycle product network:

$$\begin{array}{ccc}\hfill N_{ST}(G_t)& =& \frac{{\prod }_{i=0}^{t+1}{\prod }_{j=0}^{n-1}((2-2cos\frac{2j\pi }{n})d_{i+1}+d_{j+1}(2-2cos\frac{2i\pi }{t+2})-(2-2cos\frac{2j\pi }{n})(2-2cos\frac{2i\pi }{t+2}))}{n(t+2)}\hfill \end{array}$$

5. Discussion

Laplacian spectra and their applications for different networks have been studied for many years, but the Laplacian spectra and their applications for networks based on graph operations are very rare. Laplacian spectra are used as a tool to analyze the structure of a network, and the importance of graph products cannot be denied in multilayer networking. Therefore, we have considered all cases of categorical product networks to compute Laplacian spectra and further to find their applications. The Laplacian spectra of a family of recursive trees and their applications in network coherence were discussed in [17]. Furthermore, we have computed the Laplacian spectra of the categorical product network and have established the expressions for the product of the nonzero Laplacian eigenvalues and the sum of the reciprocals of all nonzero Laplacian eigenvalues. Using these expressions, we have computed the Kirchhoff index, also called the “network criticality”, for the categorical product network. The enumeration of spanning trees on generalized pseudofractal networks is discussed in [18].

6. Conclusions

In this paper, we discuss a complex network based on the categorical product and have used the spectrum approach to find the Kirchhoff index. The global mean first-passage time (MFPT) is computed for a complex network based on the categorical product. Moreover, using the Laplacian spectra for the categorical product network, we compute the average path length, which is the basic idea in network topologies. It describes the measure of the efficiency of transport (mass or information) on a network. The last application of Laplacian spectra for the categorical product network that we have computed was for spanning trees, which is the direct application in designing a network. We can extend our work to different networks based on graph operations other than the categorical product.

These results are indirectly related to entropy. Using the same spectra, we have future plans to compute the global first-passage time for maximal-entropy random walks in categorical product networks, and the categorical product network entropy is also in our future plans using the idea given in [19,20].