1. Introduction
Because human preferences are inherently vague, it is more suitable to deal with uncertainty and imprecise information by linguistic terms (LTs). For example, when evaluating customer satisfaction of a service or product, experts are inclined to select some LTs such as “poor”, “good” or “excellent”, etc., to give their evaluation of the criteria. Since Zadeh [
1] presented the fuzzy linguistic technique in 1975, which utilized linguistic variables (LVs) to describe qualitative information, some methods based on LVs have been utilized in a number of areas, such as supply chain management [
2], qualify function deploy [
3], health care system [
4], housing marker [
5], risk evaluation [
6], etc.
Generally, if the qualitative information is only represented by a single LT, it might sometimes not accurately reflect what it means. When the decision-making problems become more ambiguous, the experts might be hesitant among several LTs and need two or more LTs to express their preference. Based on hesitant fuzzy set (HFS), Rodríguez et al. [
7,
8] defined a hesitant fuzzy LT set (HFLTS), which is a set with ordered consecutive LTs. In real applications, experts can give several possible LTs instead of a single LT to evaluate the criteria. Although HFLTS improves the previous linguistic approaches, it is still difficult to express the hesitance preference of experts only by consecutive LTs. In addition, there are some limitations in the calculation of HFLTS and this will be illustrated in
Section 2 of this paper. Thus, hesitant fuzzy linguistic sets (HFLSs), as an extension of HFLTS, were produced, which allow for inconsecutive LTs. However, in practice, when multi-persons give the same LT in assessment information, this LT is handled as one time by default and the significance of repeated LTs is neglected. Since the evaluation values
,
and
are not equivalent to each other, the repeated occurrence of
can convey importance or a certain special meaning. In addition, the LVs provided by experts generally fluctuate in evaluation period [
9]. So, MHFLTS [
10] was proposed based on multi-HFSs to solve the mentioned problems, and each multi-hesitant LT element (MHFLTE) can contain inconsecutive and repeated LTs. Based on the MHFLTS, one expert can assess an alternative under specific criteria by one or several arbitrary LTs, and the assessment values from the different experts, can be collected, and the frequency of a LT can be expressed in the assessment information [
11]. In a word, MHFLTS is more energetic than the HFLTS and HFLS, and it can be applied to present the hesitance linguistic information by multi-repeated LTs in primary assessment information.
To date, many contributions have concentrated on the decision-making techniques based on HFLTSs, which are from three domains: (1) the theory of foundations, for instance, operational laws [
7,
8], comparative methods [
12,
13], distance and similarity measures [
14], likelihood [
15], outranking degree [
16], consistency [
17] or multiplicative consistency [
18],correlation coefficient [
19] and so on; (2) the extended multicriteria decision making (MCDM) approaches for HFLTS, such as TOPSIS [
20], ELECTRE [
21], VIKOR [
22], TODIM [
23], Entropy [
24], GRA [
25] and other methods, such as MACBETH [
26], linear programming technique [
27],Shapely [
28], EDAS [
29], Fuzzy Petri Net [
30] and so on; (3) the MCDM techniques based on aggregation operators of HFLS. The MCDM methods based on aggregation operators can acquire the comprehensive values of alternatives by aggregating all attribute values, and then rank the alternatives. Obviously, they have more superiority than the traditional MCDM methods, and it is meaningful to research the aggregation operators and then to solve the MCDM problems.
As an important tool for information fusion, a great number of research achievements about aggregation operators of HFLS have been produced. Wang et al. [
31] presented a 2-tuple linguistic aggregation operator for MHFLTEs; Wu [
32] applied possibility distribution to develop the weighted average (WA) operator for HFLSs (HFLWA) and the ordered WA operator (OWA) for HFLSs (HFLOWA). Gou et al. [
33] developed the hesitant fuzzy linguistic BM operator for HFLSs (HFLBM) and the weighted HFLBM operator (WHFLBM). Zhu et al. [
34] investigated some linguistic hesitant fuzzy power aggregation (LHFPA) operators. Wang et al. [
35] proposed the cloud WA (CWA) operator, cloud OWA (COWA) operator, and cloud hybrid arithmetic (CHA) operator for LVs. Liu et al. [
36] investigated prioritized WA operator for HIFLSs (HIFLPWA) and prioritized weighted geometric operator for HIFLSs (HIFLPWG). However, these operators for HFLTSs do not pay attention to the interrelation among input arguments.
MSM was proposed by Maclaurin [
37] and was further developed by Detemple and Robertson [
38], which has distinct advantage, i.e., it can deal with the interrelationship among multi-inputs, however Bonferroni mean (BM) operator and Heronian mean (HM) operator can only consider the correlation between two arguments. Consequently, based on its main advantage of more flexible and robust in information fusion, the related research achievements of MSM operator have been quite fruitful. Liu and Zhang [
39] introduced some MSM operator for single-valued trapezoidal neutrosophic numbers. Yu et al. [
33] developed the MSM operator for HFLSs and the weighted MSM operator for HFLSs. Liu and Qin [
40] extended the MSM operator for linguistic intuitionistic fuzzy numbers (LIFNs). Qin and Liu [
41] investigated the dual MSM (DMSM) operator and extended the DMSM operator to uncertain LVs. Moreover, the MSM operators were also applied to handle the 2-tuple linguistic information [
42] and single-valued neutrosophic linguistic information [
43] and so on.
However, research about MHFLTSs and their application in MCDM is limited. Wang et al. [
31] presented a generalized 2-tuple linguistic WA operator and a generalized 2-tuple linguistic OWA to deal with MHFLTSs. Afterwards, a likelihood-based TODIM method based on the MHFLTSs for evaluation in logistics outsourcing was also proposed [
11]. Then, Wang et al. [
10] further developed the HM and prioritized operators to solve the MCDM problem with the MHFLTSs. Liu and Teng [
44] proposed some normal neutrosophic number Heronian Mean operators for solving multiple attribute group decision making problems. However, because MHFLTSs can describe inconsecutive and repeated LTs and MSM aggregation operator can process the correlations among multi-inputs, to develop some MSM operators to deal with MHFLTSs is an important work. So, the aim of this paper is to establish some MSM operators for MHFLTSs and use them to solve the MCDM problem in which the attributes take the form of MHFLTSs.
This paper is organized as follows.
Section 2 reviews and discusses some basic concepts and theories.
Section 3 proposes some multi-hesitant fuzzy linguistic generalized MSM operators, including the generalized MSM operator for MHFLTSs (MHFLGMSM), the generalized geometric MSM operator for MHFLTSs (MHFLGGMSM), the weighted generalized MSM operator for MHFLTSs (WMHFLGMSM) and the weighted generalized geometric MSM operator for MHFLTSs (WMHFLGGMSM), and studies some properties and some particular examples of these operators.
Section 4, outlines an MCDM approach based on the proposed aggregation operators.
Section 5 gives a case to verify the availability of the presented methods.
Section 6 presents a few conclusions.
2. Preliminaries
In this part, the definitions of HFLTSs, HFLSs and MHFLTEs are briefly reviewed and their corresponding operations are given. Subsequently, the linguistic scale function (LSF) and score function of MHFLTS were given.
2.1. HFLTSs
Assume that
is a LT set (LTs) with odd cardinality, where
si is called a LV. Then the following requirements must be satisfied [
2]:
- (1)
The set is ordered: ;
- (2)
There is a negation operator: .
Definition 1. Let , then a HFLTS is an ordered finite consecutive LTs of S [31]. Definition 2. Let , and be any three HFLTSs on S [31]. Then we have - (1)
The upper bound ; and the lower bound of Hs: and ;
- (2)
The intersection between and : ;
- (3)
The union of and : .
Example 1. Assume that , , and are three HFLTSs on S. Then, we get:
- (1)
and ;
- (2)
and .
Obviously, the union of and is not a HFLTS because the HFLTS must be consecutive LTs. So, the HFLTSs were extended to HFLSs.
2.2. HFLSs
In order to preserve the provided information, the LTs S is developed to a successive LTs . If , then is named the original LT; if not so, is named the virtual LT which has no practical meaning and only it is used to operational process.
Definition 3. Let X be a reference set and . Then a HFLS on X can be defined in terms of a function that returns a subset of [32]. For simple and convenient, is called a HFLE.
Definition 4. Let be a LTs, , and be three HFLEs on and , [32]. Thus, the operations can be defined as follows: Example 2. Suppose that and , , are three HFLEs on . , and . Then, , .
The results obtained by Definition 4 have exceed the domain of . Many elements based on the subscript of LTs in and do not exist in .
Definition 5. Let be a LTs and be a HFLE on [33]. The score function of iswhere indicates the count of elements in . , are two arbitrary HFLEs, if then , and if then . Example 3. Assume that and , are two HFLEs on . , , , then . However, this comparison result is insufficient due to the existence of . Therefore, it is essential to give some revisions.
2.3. MHFLTS
Although the definitions of HFLTS and HFLS have been widely and consistently used, the frequency of one repeated LT is assigned to be one time and the operations are contradictory to the definitions. Thus, a further extended definition of them is proposed in this section.
Definition 6. Suppose X is a reference set, a multi-HFS on X can be defined about a function that returns a multi-subset of values in [31]. Definition 7. Suppose X is a reference set and is a LTs. Then a MHFLTS H on X is defined about a function h that returns an ordered finite multi-subset of , denoted by [31]:where h(x) indicates the possible membership degrees of the element to the set X. For simple and convenient, h(x) = h is a MHFLTE and is the set of all MHFLTEs. There is the strong possibility that the virtual LTs of h exist in but not in S. Essentially, MHFLTSs are a development of HFLTSs and HFLSs. If h is a set of successive LTs and no duplicate LT, then h is a HFLTSs. If h is a set of discrete LTs with no duplicate LT, then h is a HFLS. Therefore, all the operations and approaches on MHFLTSs can be applied to HFLTSs and HFLSs because they are both special cases of MHFLTSs.
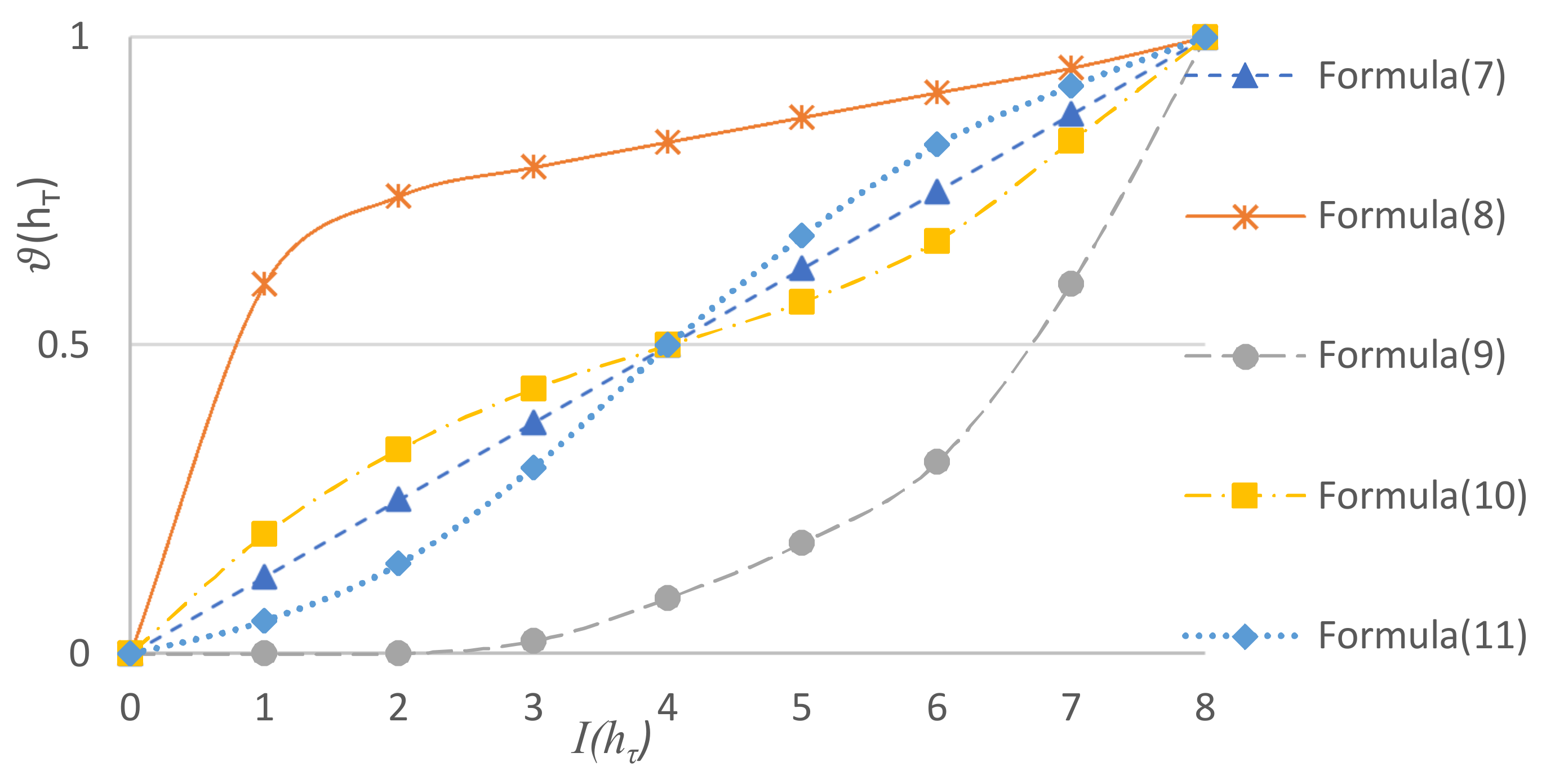
Definition 8. Let be a LTs. The LSF is a strictly monotone increasing and continuous function satisfying and . The inverse function of exists and is denoted by . Then , where and [41,42]. There are five normal LSFs which are shown as below.
A great quantity of experiment research has proven the value of
a in Equation (10) lies in the interval [1.36, 1.4]. Suppose
,
and
, the character of Equations (7)–(11) can be shown in
Figure 1.
The Equation (10) is regarded as one representative among all Equations for , thus we choose it to deal with the MHFLTEs in this paper.
2.4. Basic Operations of MHFLTS
Definition 9. Let h1 and h2 be any two MHFLTEs on . Then, we can give the following operations.
Definition 10. Let h, h1, h2 be arbitrary MHFLTEs on . Then we give the score function of h as follows [31]:and the variance function of h as follows:where #h denotes the count of elements in h. Then the comparison rules for MHFLTEs can be re-defined as follows: - (1)
If , then is strictly greater than , denoted by ;
- (2)
If , then is greater than , denoted by ; If , and , then ; If , and , then .
2.5. MSM Operator
Definition 11. Let be a group of positive real values and [43]. If Then is called the MSM operator where traversal all the combination of , is the binominal coefficient.
It is clear that the has the following properties:
- (1)
Idempotency. ;
- (2)
Monotonicity. , if for all i;
- (3)
Boundedness. .
Especially, if
m = 1, then the
reduces to the WA operator as follows:
If
m = 2, then the
reduces to a BM operator (
), as follows:
If
m = 3, then the
reduces to a generalized BM operator (
) as follows:
Definition 12. Let be a set of positive real values and [43]. If Then is called the generalized MSM (GMSM) operator, where , traversal all the combination of , is the binominal coefficient.
The has the following properties:
Property 1. - (1)
Idempotency. ;
- (2)
Monotonicity. , if for all i;
- (3)
Boundedness. .
Proof. - (1)
- (2)
Assume that
m-tuple
is given randomly, and
. if
for all
, then
and
, therefore,
- (3)
Let and . According to the property of idempotency, . According to the property of monotonicity, when for all i, we have . Similarly, we also have .
Finally, . □
Especially, if
m = 1, then the
reduces to the generalized WA operator.
If
m = 2, then the
reduces to the BM operator as follows:
If
m = 3, then the
reduces to the GBM operator as follows:
Definition 13. Let be a group of positive real values and [43]. If Then is called the generalized geometric MSM (GGMSM), where , traversal all the combination of , is the binominal coefficient.
The has the following properties:
Property 2. - (1)
Idempotency. ;
- (2)
Monotonicity. , if for all ;
- (3)
Boundedness. .
Property 2 is similar to the Property 1, the proof is omitted here.
Especially, if
m = 1, then the
reduces to the generalized geometric operator
If
m = 2, then the
reduces to the geometric BM operator as follows:
If
m = 3, then the
reduces to the generalized geometric BM operator as follows:
3. Some Multi-Hesitant Fuzzy Linguistic MSM Operators
In this section, we will extend GMSM operator and GGMSM operator to process MHFLTSs and develop the MHFLGMSM operator, MHFLGGMSM operator, WMHFLGMSM operator and WMHFLGGMSM operator.
3.1. MHFLGMSM Operator
Definition 14. Let be a group of MHFLTESs on . A MHFLGMSM operator is a mapping defined as follows:where and is the set of all MHFLTESs. Based on the operations of the MHFLTESs described in
Section 2, we can get the following theorem.
Theorem 1. Let be a set of MHFLTESs on , the value aggregated by the MHFLGMSM operator from (30) is still a MHFLTSs andwhere and . represents the th element in th union of each permutation which consists of one element from each . Because the form of involves selecting an element from each , each must mutual calculation and obviously the MHFLGMSM operator will be used times, where denotes the number of elements in . The final aggregated result consists of elements because of each aggregated result becomes an element which based on the operational laws of MHFLTSs. Property 3. Let be a set of MHFLTESs on . The value aggregated by operator has the following desirable properties:
- (1)
Idempotency. If the , then - (2)
Monotonicity. If and are two sets of MHFLTESs on and , then for , - (3)
Boundedness. If is obtained by replacing the minimum of for each element of , is obtained by replacing the maximum of for each element of , then - (4)
Commutativity. Let be any permutation of , then
Proof - (1)
Since the MHFLTSs
, then
- (2)
If
and
are two sets of MHFLTESs on
and
, then for
The
, and for
states the minimum element of
is more than the maximum element of
, then
. In addition, MHFLGMSM operator can satisfy the property of monotonicity, so
- (3)
If
is obtained by replacing the minimum of
for each element of
and
is obtained by replacing the maximum of
for each element of
, then
and
for
. In addition, the MHFLGMSM operator can satisfy the property of monotonicity, so
- (4)
Because
is a permutation of
, so
. Therefore
where
for
. So
The proof of Theorem 2 is completed now. □
Next, by taking into account diverse values of the parameter m, some particular cases of the can be discussed as follows:
3.2. MHFLGGMSM Operator
Definition 15. Suppose is a set of MHFLTESs on . A MHFLGGMSM operator is a mapping defined as follows:where and is the set including all MHFLTSs. Based on the operations of MHFLTSs described in Section 2, we can get the following theorem. Theorem 2. Suppose is a set of MHFLTESs on , the value aggregated by MHFLGGMSM operator from (35) is still a MHFLTSs andwhere and . represents the ijth element in kth union of each permutation which consists of one element from every . Because the form of MHFLGGMSM operator involves selecting an element from every , each hi must mutual calculation, and obviously the MHFLGGMSM operator will be used times, where indicates the count of elements in hi. The final aggregated result consists of elements because of each aggregated result becomes an element which is based on the operation law of MHFLTSs. Property 4. Suppose is a group of the MHFLTESs on . The value aggregated by MHFLGGMSM operator has the following desirable properties:
- (1)
Idempotency. If the , then - (2)
Monotonicity. If and are two collections of MHFLTSs on and , then for . - (3)
Boundedness. If is obtained by replacing the minimum of for each element of , is obtained by replacing the maximum of for each element of , then - (4)
Commutativity. Let be any permutation of , then .
The proof of property 4 is similar to Property 3, therefore, it is omitted here.
Next, by taking into account diverse values of the parameter m, some particular cases of the MHFLGGMSM operator can be discussed as below:
3.3. WMHFLGMSM Operator
Under many practical situations, each attribute has different importance. In this section, taking the weight of the attributes into account, we propose WMHFLGMSM operator which can be defined as below:
Definition 16. Suppose is a set of MHFLTESs on , and is the weight vector, which satisfies and . Each denotes the importance degree of . The WMHFLGMSM operator: is:where and is the set containing all MHFLTSs. By the calculation laws for MHFLTSs depicted earlier, we can get the following theorem.
Theorem 3. Suppose is a set of MHFLTESs on , and is the weight vector, which satisfies and . Each denotes the importance degree of . Then, the overall value aggregated by WMHFLGMSM operator from (40) is still a MHFLTSs andwhere and . represents the th element in th union of each permutation which consist of one element from each . Property 5. (Reducibility). Let . Then = .
3.4. WMHFLGGMSM Operator
In this section, taking the weight into account, we propose WMHFLGGMSM operator which can be defined as follows:
Definition 17. Suppose is a set of MHFLTESs on , and is the weight vector, which satisfies and . indicates the weight of . The WMHFLGGMSM operator: is:where and is the set including all MHFLTSs. By the operations of MHFLTSs depicted in
Section 2, we can get the theorem as follows.
Theorem 4. Suppose is a set of MHFLTESs on , and is the weight vector, which satisfies and . indicates the weight of . Then, the overall value aggregated by WMHFLGGMSM operator from (42) is still a MHFLTSs andwhere and . represents the th element in th union of each permutation which consist of one element from each . Property 6. (Reducibility)
Let .
Then The proof of property 6 is similar to Property 5, therefore, it is omitted here.
4. A MCDM Approach with MHFLTs
In this section, based on the defined aggregation operators, a MCDM approach is developed to process the criteria information with the MHFLTs, which is also valid and feasible for the HFLTS or HFLEs.
Considering a MCDM problem as follows. There are d alternatives, denoted by and n criteria, denoted by , which weight vector is satisfying , . The assessments are performed by l experts and the result of alternative ti given by ek under rj is denoted by based on the LTs . bij is a MHFLTE that contains inconsecutive and repetitive LTs by combing with the result from l experts, then we obtain the decision matrix , and the goal is to rank the alternatives.
The presented method for this MCDM problem is shown as follows:
- Step 1.
Normalize the MHFLTE matrix . Only for the cost criterion rj, bij is normalized by using the negation operator.
- Step 2.
Integrate the assessment value of every alternative under n criteria and obtain the comprehensive assessment results bi for .
- Step 3.
Calculate S(bi) and V(bi) for alternative ti.
- Step 4.
Ranking all alternatives based on S(bi) and V(bi).
5. An Illustrative Example
In this part, we cited an example (adapted from [
10]) to display the flexibility of the proposed methods. In order to get a fast development, the car manufacturer company will select a logistics service provider to concentrate on core competencies. After thorough investigation, five possible logistic providers will take into account, denoted by
. The criteria, denoted by
, are shown as follows:
r1: cost (such as the total cost of logistics operation);
r2: relationship (such as shared risks and cooperation rewards);
r3: service (such as breadth, specialization, variety);
r4: quality (such as management and improvement). The weight vector of the criteria is
. The evaluation is carry out by three experts, denoted by
.
S = {
s0 = Extremely Poor (
EP),
s1 =
Very Poor (
VP),
s2 =
Poor (
P),
s3 =
Slightly Poor (
SP),
s4 =
Fair (
F),
s5 =
Slightly Good (
SG),
s6 =
Good (
G),
s7 =
Very Good (
VG),
s8 =
Extremely Good (
EG)} be a LTs. The evaluation value of each criteria
bij from three experts are represented in the form of MHFLTEs as demonstrated in
Table 1.
The evaluation value in the form of MHFLTSs are transformed into numerical data using Equation (6). If g = 4 and a = 1.4, then , , , , , , , , .
In order to obtain the best alternative, we adopt the approach described in
Section 4 to solve the MCDM problems.
5.1. Procedure of Decision Making Based on WMHFLGMSM Operator
- Step 1.
Get the normalized decision matrix .
Because the four criteria
are all benefit type in this example, thus, this step can be omitted. The decision matrix is shown below:
- Step 2.
Integrate the evaluation value of every alternative for four criteria and obtain the comprehensive assessment results for by the WMHFGMSM operator (suppose , ).
- Step 3.
Calculate
for alternative
, and get
- Step 4.
Rank alternatives based on
, and get
5.2. Procedure of Decision Making Based on WMHFLGGMSM Operator
- Step 1.
Same as the above step 1.
- Step 2.
Integrate the evaluation value of every alternative for four criteria and obtain the comprehensive assessment results for by the WMHFLGGMSM operator (suppose , ).
- Step 3.
Calculate
for alternative
.
- Step 4.
Rank alternatives based on
, and get
From the above two cases, we can find that the methods based on WMHFLGMSM operator and based on WMHFLGGMSM operator get the same ranking result, and the optimal alternative is all t4. The WMHFLGMSM operator has the dominant advantage of stressing on the influence of the entire and general data, which permits forceful supplementary among the attribute values, while the WMHFLGGMSM operator has the dominant advantage of stressing on the counterpoise and the coordination among the attribute values.
5.3. Analysis the Effect of the Parameters m, p1, p2, …, pm
In order to observe the effects of the parameters
on this illustrate example, we assign distinct parameter values
to obtain the ranking results, and the results are demonstrated in
Table 2,
Table 3,
Table 4 and
Table 5.
- (1)
If we keep the balance of parameter assignment (i.e., ), the ranking results of alternatives are identical in the condition of distinct parameter values. If the balance of parameter assignment is broken, the ranking results of alternatives will start to be changed, but as the value of parameter gap becomes lager and lager or the value of one parameter is much larger than other parameters, the ranking results will not be changed. So, the risk preference of experts plays an important role in real MCDM.
- (2)
In
Table 2 and
Table 3, if
p1 = 0 or
p2 = 0, the WMHFLGMSM operator and WMHFLGGMSM operator cannot consider the interrelation of the criteria. Moreover, the similar situation exists in
Table 4 and
Table 5.
- (3)
For the WMHFLGMSM operator, the greater value of m becomes, in other words, the more interrelationships of criteria we take into account, the smaller value of score function will get. Nevertheless, for the WMHFLGGMSM operator, the results are the opposite, the greater value of m becomes, in other words, the more interrelationships of criteria we take into account, the greater value of score function will get.
Therefore, experts should select the suitable parameter values in order to keep their risk preference at real MCDM environment. If expert has risk preference, he/she should assign the parameter as large as possible; if expert has risk aversion, he/she should assign the parameter as small as possible. Generally, we propose that experts assign the values of the parameters as m = 2, p1 = p2 = 1 in practical problems, which are not only simple for operations, but also take into account the interrelations for two parameters.
5.4. Comparison with the Other Methods
To verify the validity of the proposed approaches, we use the existing generalized weighted average operator for HFLSs (GHFLWA) [
45], weighted BM operator for HFLSs (WHFLBM) [
33] and multi-HFLS weighted generalized HM (MHFL-WGHM) operator [
10] respectively to solve an illustrative example from [
40] which is listed as follows:
For the sake of further optimizing healthcare resource allocation, we need to select a general hospital to improve the traditional healthcare system and build a new comprehensive healthcare system. After thorough investigation, four general hospitals will take into account, denoted by
, namely SU hospital (
t1), FU hospital (
t2), UMC hospital (
t3), PLA hospital (
t4). Three main criteria, denoted by
, are shown as follows: service environment (
r1), diagnosis and treatment (
r2) and social resource allocation (
r3); The weight vector of the criteria is
. The linguistic evaluation result is listed in
Table 6 and the ranking results of different methods are shown in
Table 7.
From
Table 7, we can find that the approach based on the
operator in this paper and the approach based on GHFLWA operator [
45] have the same ranking result, i.e.,
, and the method based on
operator proposed in this paper and the method based on WHFLBM operator and MHFL-WGHM operator have also the same ranking result, i.e.,
. Obviously, we can easily explain these results (1) because both of the proposed approaches based on the
operator in this paper and the approach based on GHFLWA operator [
45] don’t consider the interrelationship of criteria, they produce the same ranking result; (2) while all of the proposed methods based on the
operator and the approach based on WHFLBM operator [
33] and MHFL-WGHM operator [
10] can consider the interrelationship between two criteria, they get the same ranking result. So, these results can demonstrate that the presented approaches are rational and valid in HFLS.
In order to show the advantage of the novel method based on WMHFLGMSM operator in this paper, we continue to calculate the same example from [
10] by comparing with some existing methods. We can get the final result demonstrated in
Table 8.
From
Table 8, we can find that the final result by the approach based on the MHFL-WGHM operator [
10] is the same with using the WMHFLGMSM operator proposed in this paper, whereas the methods using GHFLWA operator [
45] and WHFLBM operator [
33] and the method using the WMHFLGMSM operator get different ranking results.
In the following, we analyze the reason of producing these results as follows.
- (1)
The final overall results from the GHFLWA operator [
45] and the WHFLBM operator [
33] are achieved under the condition that the repeated assessment values in
Table 1 are eliminated. Obviously, this can lead to information loss, and make the ranking results unreasonable. From
Table 8, we can also get this conclusion because they produced the different ranking results.
- (2)
The approaches based on the MHFL-WGHM operator [
10] and the WMHFLGMSM operator proposed in this paper produced the same ranking results because they can fully express the evaluation information, and all considered the interrelationship between two criteria. However, the proposed method based on the WMHFLGMSM operator in this paper can consider the interrelationship among any number of attributes by some parameters.
Obviously, the presented approach based on the WMHFLGMSM operator in this paper can get over the weakness of the approaches based on the GHFLWA operator [
45] and the WHFLBM operator [
33] because the HFLTSs cannot sufficiently convey the hesitance of experts, and WMHFLGMSM operator in this paper can take into the interrelation among any number of the criteria, which is more general than some existing methods. In summary, the presented approach based on the WMHFLGMSM operator not only considers the significance of repeated assessment values, but also takes into account the interrelationships among any criteria.
In the following, we give a detailed contrastive analysis for the different methods, and state these clearly in
Table 9.
From
Table 9, we obtain the conclusion as follows:
- (1)
Compared with the approach based on GHFLWA operator proposed by [
45], we can note the weakness of the GHFLWA operator is that the input assessment values are independent and does not think about the interrelationships among input arguments. Under these circumstances, the GHFLWA operator proposed by [
45] is a particular example of WMHFLGMSM operator when
m = 1,
p = 1. Our novel method takes into account the real decision environment in which there are some relationships among some criteria. In above illustrative example, the level of management and improvement will have an effect on the breadth, specialization, variety of logistic company, that is to say we should consider the interrelationships between
r3 and
r4. Therefore, our presented approach is more suitable for dealing with actual decision problems than the presented approach based on GHFLWA operator proposed by [
45]. Another weakness of the presented approach based on GHFLWA operator [
45] is that it adopts HFLTSs which cannot sufficiently convey the hesitance of experts. At the same time, our presented approach can completely express the evaluation information.
- (2)
Compared with the approach based on the WHFLBM operator presented by [
33], our new method can preserve the repetition of linguistic evaluation information and considers the interrelationship among more than two input arguments. However, the approach based on the WHFLBM operator only considers the interrelationship between two input arguments and the frequencies of repeated values are neglected. Therefore, as an extension of HFLSs and HFLTSs, the presented approach based on the WMHFLGMSM operator is more reasonable to aggregate the repeated linguistic information in practice. Moreover, we also noticed that the WMHFLGMSM operator with parameters will degrade into the WHFLBM operator proposed by [
33] if
m = 2,
p1 = 1,
p2 = 1. Therefore, the WMHFLGMSM operators have more generality and are more robust.
- (3)
Compared with the approach based on the MHFL-WGHM operator presented by [
10], our presented novel method can take into account the correlation among multi-inputs. However, the MHFL-WGHM operator can only consider correlation between two inputs. In many real decision-making problems, the interrelationships among multi-input arguments must be considered. Thus, the presented approach is more general and wider, and it is more adequate to deal with MCDM problems.
By the contrast analysis above, we can show that the WMHFLGMSM operator we prosed in this paper is better than the WHFLBM operator proposed by [
33], the MHFL-WGHM operator proposed by [
10], and the GHFLWA operator proposed by [
45] for aggregating the multi-hesitant fuzzy linguistic information.
6. Conclusions
A MHFLTS is an extension of HFLS and HFLTS, which can preserve the frequencies of repeated LTs. In addition, the MSM operator can take into account the correlativity among multi-inputs. In this paper, we investigate the MCDM problems with the information of the MHFLTSs. Firstly, we developed the MHFLGMSM operator, MHFLGGMSM operator, WMHFLGMSM operator, and WMHFLGGMSM operator, respectively. Then, their properties and particular cases of these operators are further studied. Based on these operators, we proposed a method to solve the MCDM problem with MHFLTEs. Finally, some examples are provided to contrast the presented approaches with the existing approaches, such the methods based on the WHFLBM operator [
33], the MHFL-WGHM operator [
10], the GHFLWA operator [
45]. The comparison results demonstrate that the presented approaches outperform some existing approaches [
10,
33,
45].
Fortunately, we maybe use these novel operators to solve new MCDM problems in practice, such as industrial site selection [
46], intrusion detection [
47], EEG signals analysis [
48], consensus model [
49], temporary disaster debris Management [
50], etc. The limitation of proposed operators is that if we consider interrelationships among more than three criteria, more parameters will be given, which may bewilder experts, such that they perhaps cannot decide how to choose the values of parameters. In further research, it is necessary to apply these operators to real decision-making problems, such as evaluations on population resources and environment [
51,
52,
53,
54] or Chinese culture [
55].