A Novel Skin Lesion Detection Approach Using Neutrosophic Clustering and Adaptive Region Growing in Dermoscopy Images
Abstract
1. Introduction
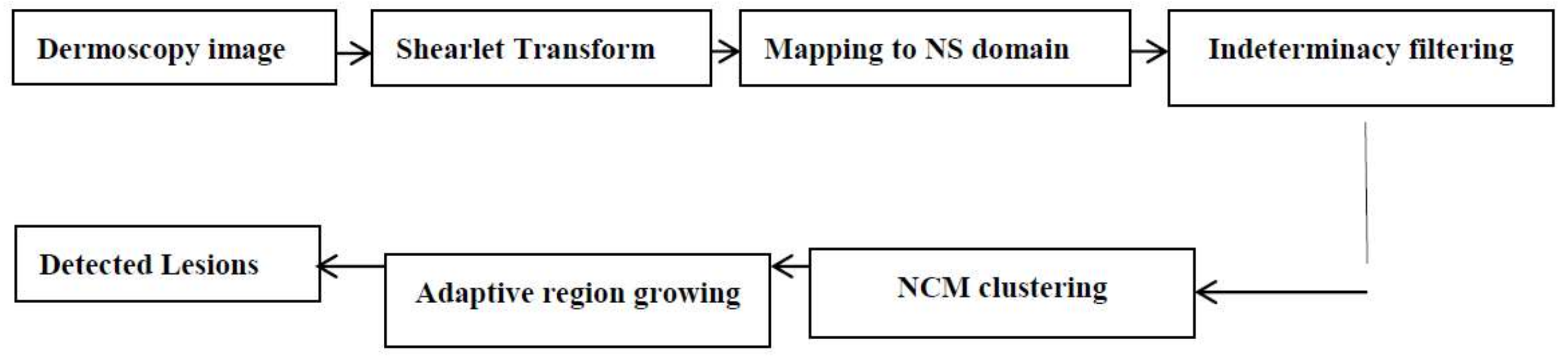
2. Methodology
2.1. Shearlet Transform
2.2. Neutrosophic Images
2.3. Neutrosophic Indeterminacy Filtering
2.4. Neutrosophic C-Means (NCM)
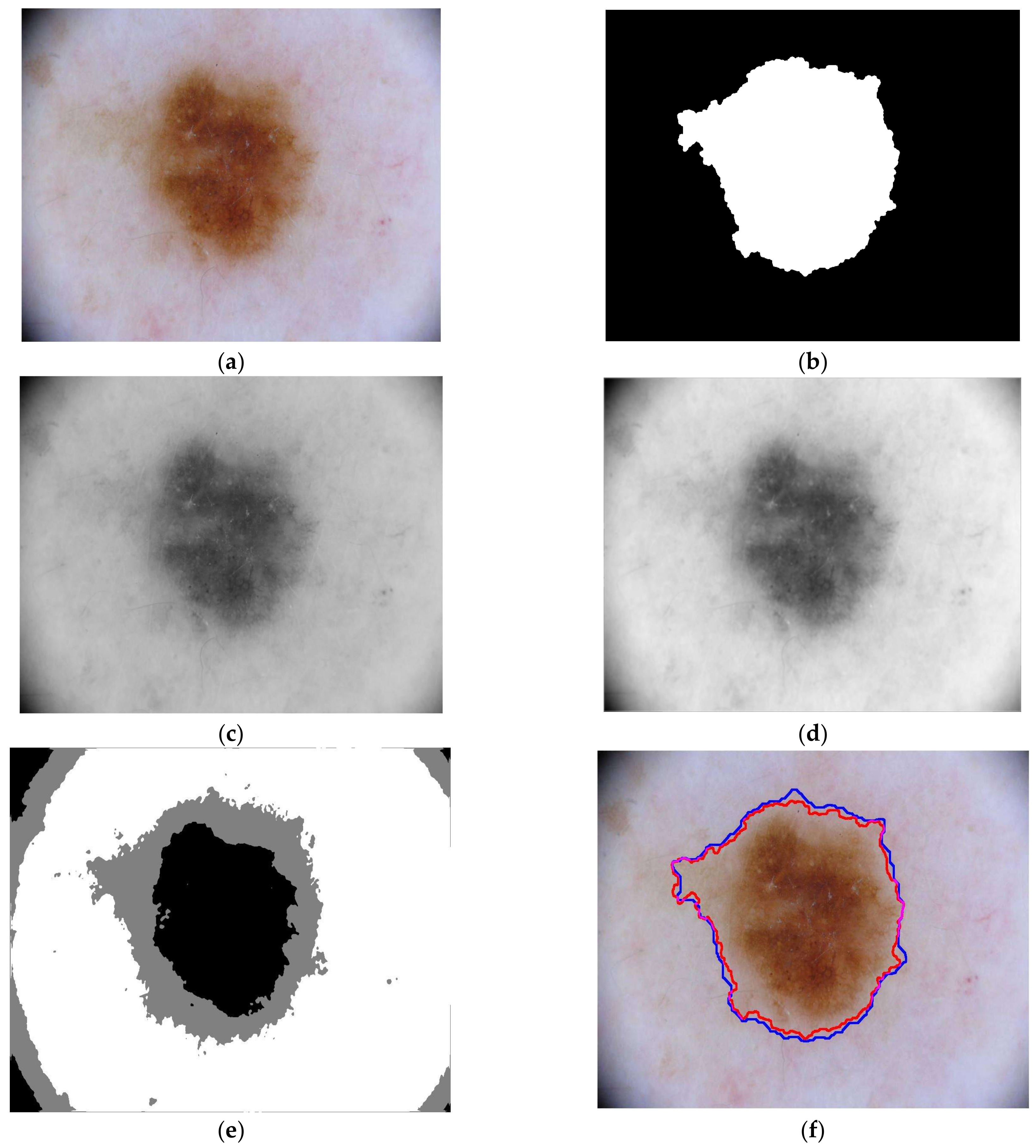
2.5. Lesion Detection
2.6. Evaluation Metrics
3. Experimental Results and Discussion
3.1. Dataset
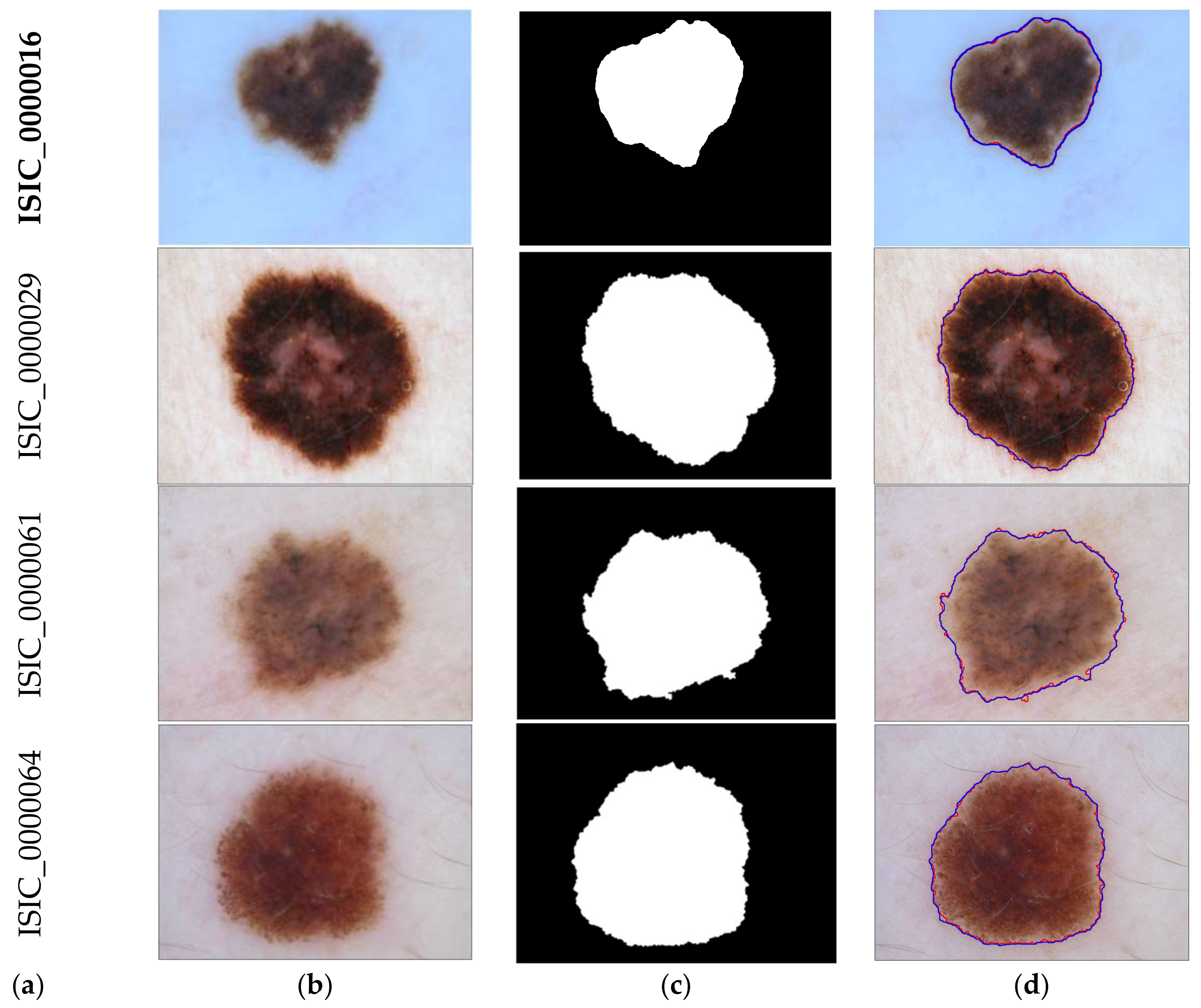
3.2. Detection Results
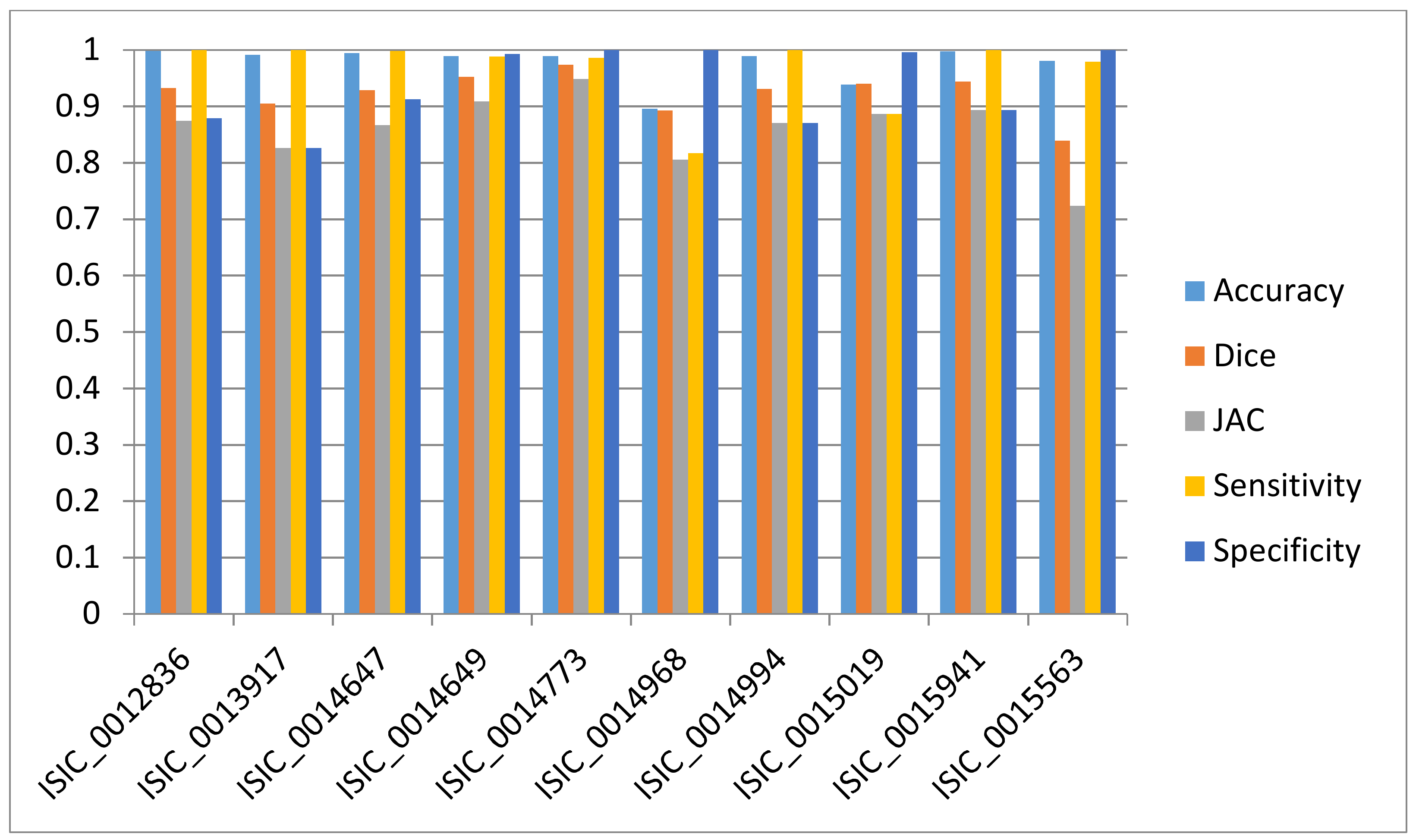
3.3. Evaluation
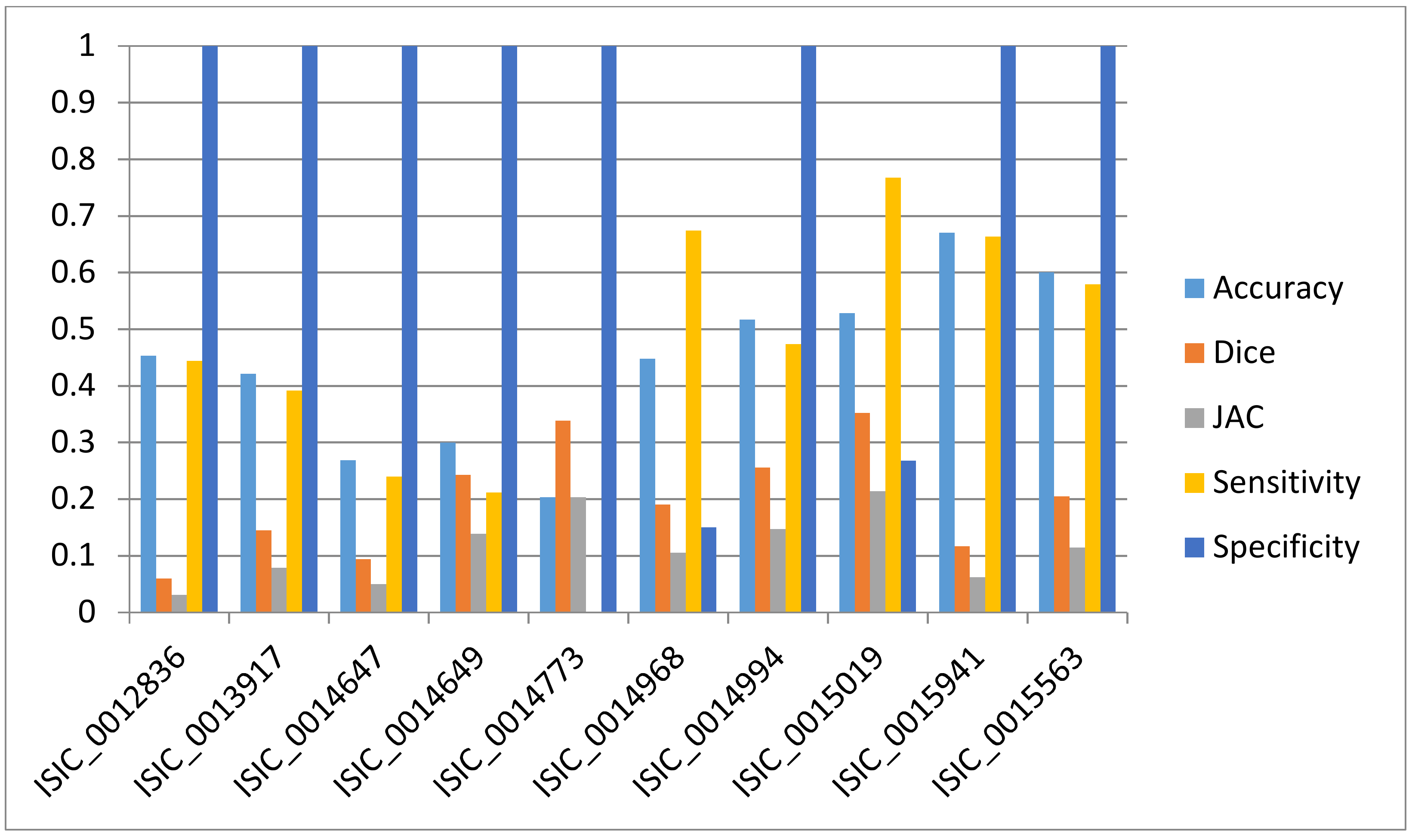
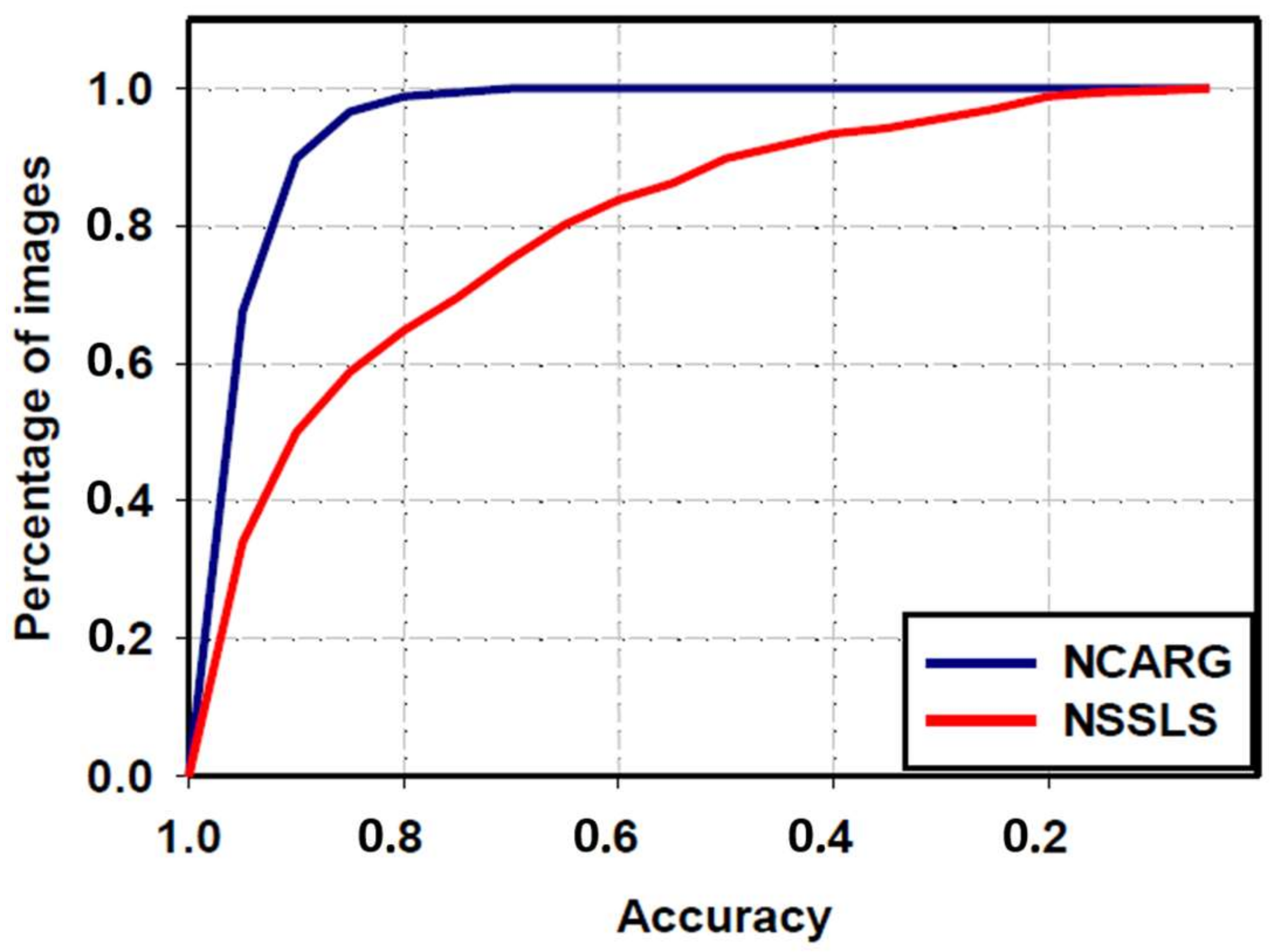
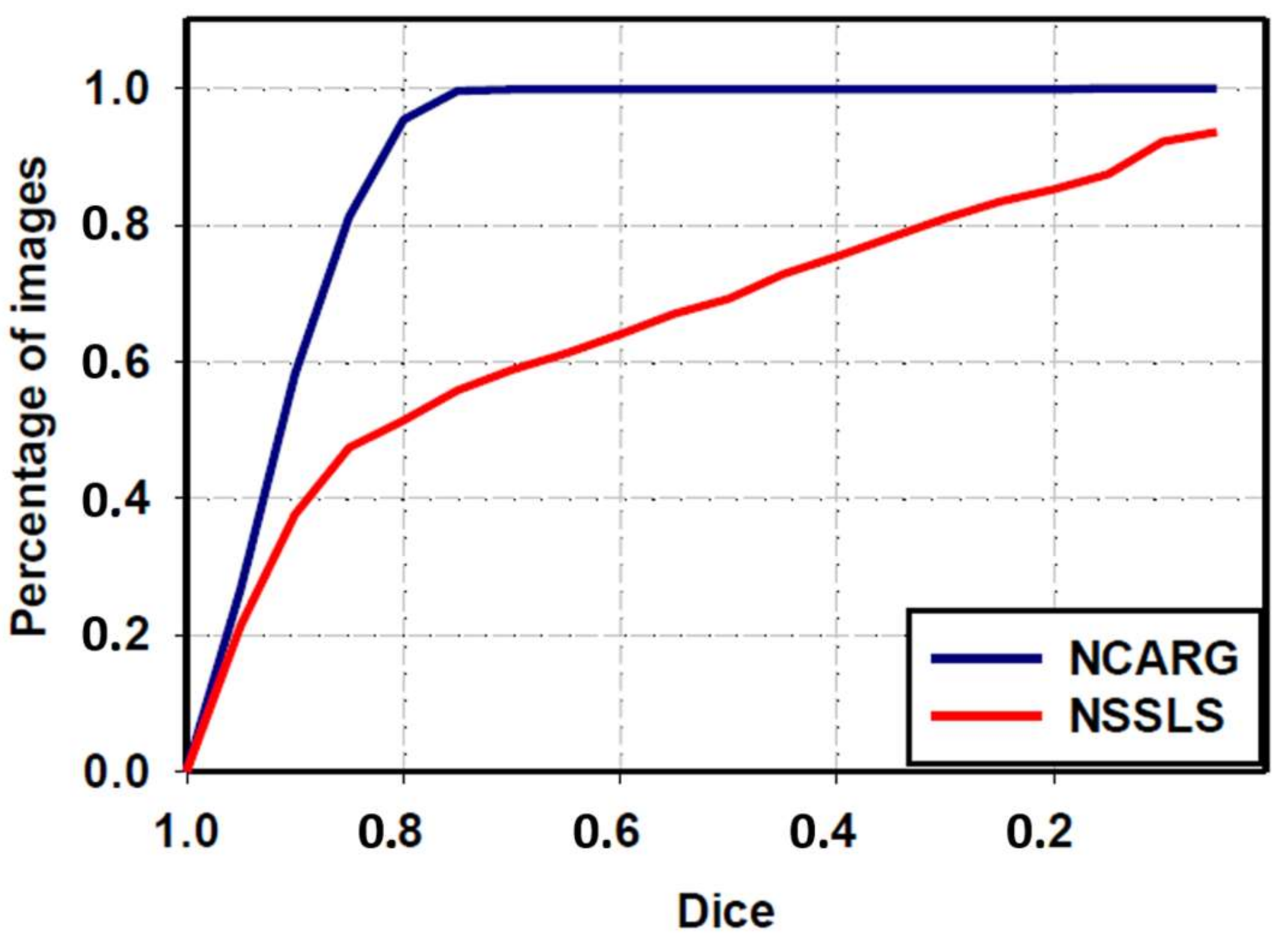
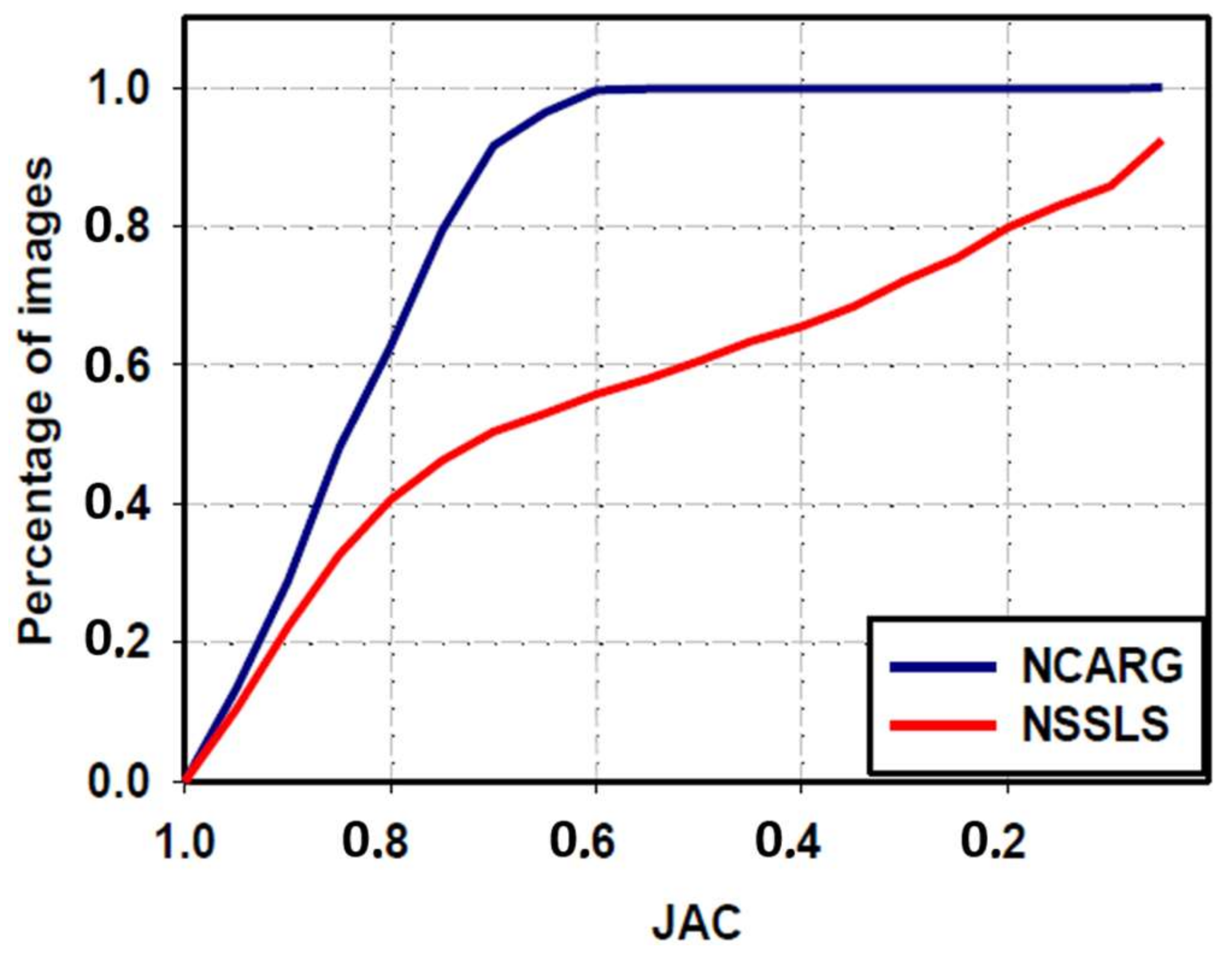
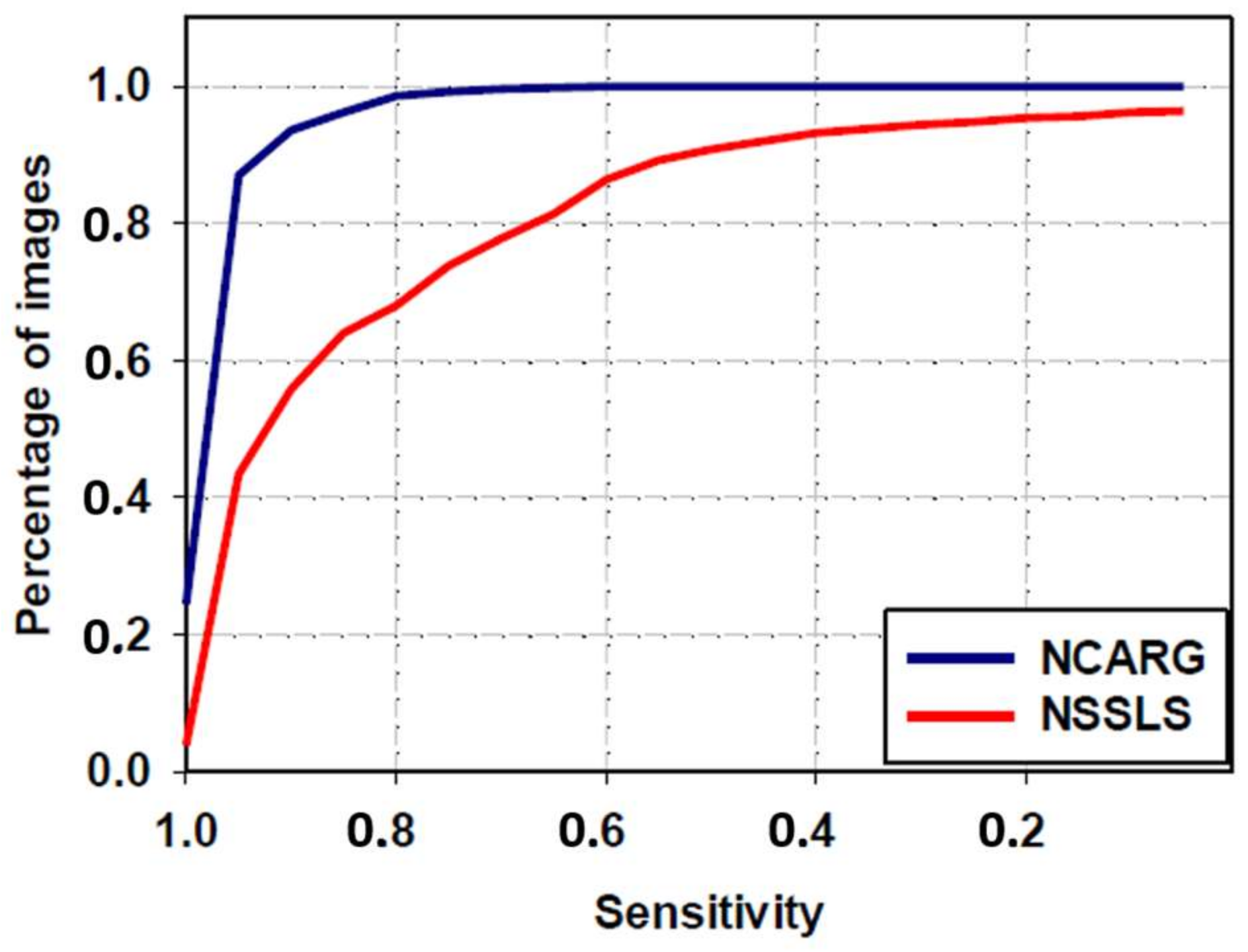
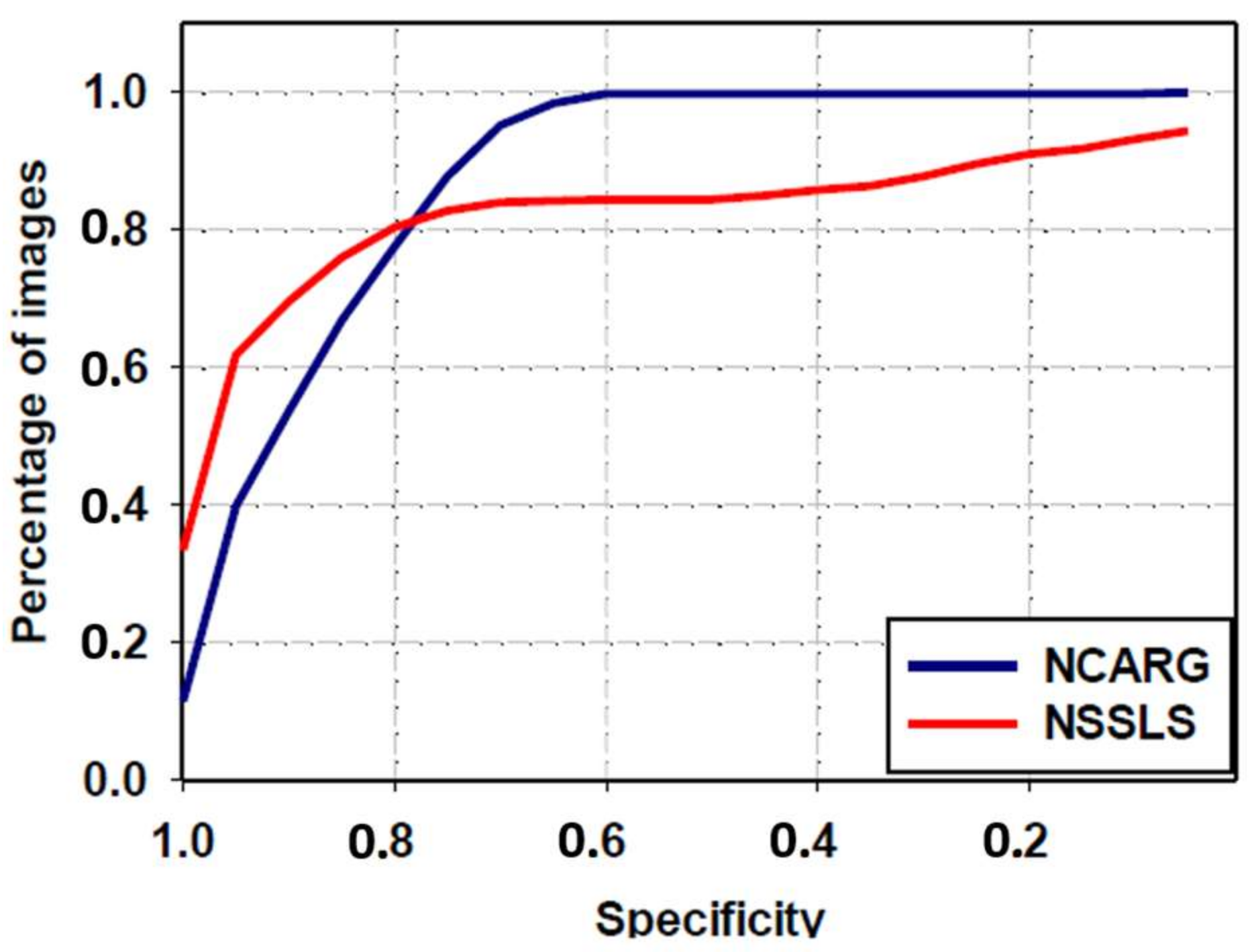
3.4. Comparative Study with NSSLS Method
3.5. Comparison with Other Segmentation Methods Using the ISIC Archive
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Marghoob, A.A.; Swindle, L.D.; Moricz, C.Z.; Sanchez, F.A.; Slue, B.; Halpern, A.C.; Kopf, A.W. Instruments and new technologies for the in vivo diagnosis of melanoma. J. Am. Acad. Dermatol. 2003, 49, 777–797. [Google Scholar] [CrossRef]
- Wolfe, J.M.; Butcher, S.J.; Lee, C.; Hyle, M. Changing your mind: On the contributions of top-down and bottom-up guidance in visual search for feature singletons. J. Exp. Psychol. Hum. Percept. Perform. 2003, 29, 483–502. [Google Scholar] [CrossRef] [PubMed]
- Binder, M.; Schwarz, M.; Winkler, A.; Steiner, A.; Kaider, A.; Wolff, K.; Pehamberger, M. Epiluminescence microscopy. A useful tool for the diagnosis of pigmented skin lesions for formally trained dermatologists. Arch. Dermatol. 1995, 131, 286–291. [Google Scholar] [CrossRef] [PubMed]
- Celebi, M.E.; Wen, Q.; Iyatomi, H.; Shimizu, K.; Zhou, H.; Schaefer, G. A State-of-the-Art Survey on Lesion Border Detection in Dermoscopy Images. In Dermoscopy Image Analysis; Celebi, M.E., Mendonca, T., Marques, J.S., Eds.; CRC Press: Boca Raton, FL, USA, 2015; pp. 97–129. [Google Scholar]
- Celebi, M.E.; Iyatomi, H.; Schaefer, G.; Stoecker, W.V. Lesion Border Detection in Dermoscopy Images. Comput. Med. Imaging Graph. 2009, 33, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Garnavi, R.; Aldeen, M.; Celebi, M.E.; Varigos, G.; Finch, S. Border detection in dermoscopy images using hybrid thresholding on optimized color channels. Comput. Med. Imaging Graph. 2011, 35, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Silveira, M.; Nascimento, J.C.; Marques, J.S.; Marçal, A.R.; Mendonça, T.; Yamauchi, S.; Maeda, J.; Rozeira, J. Comparison of segmentation methods for melanoma diagnosis in dermoscopy images. IEEE J. Sel. Top. Signal Process. 2009, 3, 35–45. [Google Scholar] [CrossRef]
- Celebi, M.E.; Aslandogan, Y.A.; Stoecker, W.V.; Iyatomi, H.; Oka, H.; Chen, X. Unsupervised border detection in dermoscopy images. Skin Res. Technol. 2007, 13, 454–462. [Google Scholar] [CrossRef] [PubMed]
- Argenziano, G.; Kittler, H.; Ferrara, G.; Rubegni, P.; Malvehy, J.; Puig, S.; Cowell, L.; Stanganelli, I.; de Giorgi, V.; Thomas, L.; et al. Slow-growing melanoma: A dermoscopy follow-up study. Br. J. Dermatol. 2010, 162, 267–273. [Google Scholar] [CrossRef] [PubMed]
- Xie, F.; Bovik, A.C. Automatic segmentation of dermoscopy images using self-generating neural networks seeded by genetic algorithm. Pattern Recognit. 2013, 46, 1012–1019. [Google Scholar] [CrossRef]
- Barata, C.; Celebi, M.E.; Marques, J.S. Development of a clinically oriented system for melanoma diagnosis. Pattern Recognit. 2017, 69, 270–285. [Google Scholar] [CrossRef]
- Lee, H.; Chen, Y.P.P. Skin cancer extraction with optimum fuzzy thresholding technique. Appl. Intell. 2014, 40, 415–426. [Google Scholar] [CrossRef]
- Jaisakthi, S.M.; Chandrabose, A.; Mirunalini, P. Automatic Skin Lesion Segmentation using Semi-supervised Learning Technique. arXiv, 2017; arXiv:1703.04301. [Google Scholar]
- Zhou, H.; Schaefer, G.; Sadka, A.H.; Celebi, M.E. Anisotropic mean shift based fuzzy c-means segmentation of dermoscopy images. IEEE J. Sel. Top. Signal Process. 2009, 3, 26–34. [Google Scholar] [CrossRef]
- Guo, Y.; Sengur, A. NCM: Neutrosophic c-means clustering algorithm. Pattern Recognit. 2015, 48, 2710–2724. [Google Scholar] [CrossRef]
- Mohan, J.; Krishnaveni, V.; Guo, Y. Automated Brain Tumor Segmentation on MR Images Based on Neutrosophic Set Approach. In Proceedings of the 2015 2nd International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; pp. 1078–1083. [Google Scholar]
- Sengur, A.; Guo, Y. Color texture image segmentation based on neutrosophic set and wavelet transformation. Comput. Vis. Image Underst. 2011, 115, 1134–1144. [Google Scholar] [CrossRef]
- Khalid, S.; Jamil, U.; Saleem, K.; Akram, M.U.; Manzoor, W.; Ahmed, W.; Sohail, A. Segmentation of skin lesion using Cohen–Daubechies–Feauveau biorthogonal wavelet. SpringerPlus 2016, 5, 1603. [Google Scholar] [CrossRef] [PubMed]
- Guo, K.; Labate, D. Optimally Sparse Multidimensional Representation using Shearlets. SIAM J. Math. Anal. 2007, 39, 298–318. [Google Scholar] [CrossRef]
- Guo, K.; Labate, D. Characterization and analysis of edges using the continuous shearlet transform. SIAM J. Imaging Sci. 2009, 2, 959–986. [Google Scholar] [CrossRef]
- Cavalcanti, P.G.; Scharcanski, J. Automated prescreening of pigmented skin lesions using standard cameras. Comput. Med. Imaging Graph. 2011, 35, 481–491. [Google Scholar] [CrossRef] [PubMed]
- Labate, D.; Lim, W.; Kutyniok, G.; Weiss, G. Sparse Multidimensional Representation Using Shearlets. In Proceedings of the Wavelets XI, San Diego, CA, USA, 31 July–4 August 2005; SPIE: Bellingham, WA, USA, 2005; Volume 5914, pp. 254–262. [Google Scholar]
- Zhou, H.; Niu, X.; Qin, H.; Zhou, J.; Lai, R.; Wang, B. Shearlet Transform Based Anomaly Detection for Hyperspectral Image. In Proceedings of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Optoelectronic Materials and Devices for Sensing, Imaging, and Solar Energy, Xiamen, China, 26–29 April 2012; Volume 8419. [Google Scholar]
- Theresa, M.M. Computer aided diagnostic (CAD) for feature extraction of lungs in chest radiograph using different transform features. Biomed. Res. 2017, S208–S213. Available online: http://www.biomedres.info/biomedical-research/computer-aided-diagnostic-cad-for-feature-extraction-of-lungs-in-chest-radiograph-using-different-transform-features.html (accessed on 26 March 2018).
- Liu, X.; Zhou, Y.; Wang, Y.J. Image fusion based on shearlet transform and regional features. AEU Int. J. Electron. Commun. 2014, 68, 471–477. [Google Scholar] [CrossRef]
- Mohan, J.; Krishnaveni, V.; Guo, Y. A new neutrosophic approach of Wiener filtering for MRI denoising. Meas. Sci. Rev. 2013, 13, 177–186. [Google Scholar] [CrossRef]
- Mohan, J.; Guo, Y.; Krishnaveni, V.; Jeganathan, K. MRI Denoising Based on Neutrosophic Wiener Filtering. In Proceedings of the 2012 IEEE International Conference on Imaging Systems and Techniques, Manchester, UK, 16–17 July 2012; pp. 327–331. [Google Scholar]
- Cheng, H.; Guo, Y.; Zhang, Y. A novel image segmentation approach based on neutrosophic set and improved fuzzy c-means algorithm. New Math. Nat. Comput. 2011, 7, 155–171. [Google Scholar] [CrossRef]
- Guo, Y.; Xia, R.; Şengür, A.; Polat, K. A novel image segmentation approach based on neutrosophic c-means clustering and indeterminacy filtering. Neural Comput. Appl. 2017, 28, 3009–3019. [Google Scholar] [CrossRef]
- Guo, Y.; Zhou, C.; Chan, H.P.; Chughtai, A.; Wei, J.; Hadjiiski, L.M.; Kazerooni, E.A. Automated iterative neutrosophic lung segmentation for image analysis in thoracic computed tomography. Med. Phys. 2013, 40. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Şengür, A.; Tian, J.W. A novel breast ultrasound image segmentation algorithm based on neutrosophic similarity score and level set. Comput. Methods Programs Biomed. 2016, 123, 43–53. [Google Scholar]
- ISIC. Available online: http://www.isdis.net/index.php/isic-project (accessed on 26 March 2018).
- Gutman, D.; Codella, N.C.; Celebi, E.; Helba, B.; Marchetti, M.; Mishra, N.; Halpern, A. Skin lesion analysis toward melanoma detection: A challenge at the international symposium on biomedical imaging (ISBI) 2016, hosted by the international skin imaging collaboration (ISIC). arXiv, 2016; arXiv:1605.01397. [Google Scholar]
- Yu, L.; Chen, H.; Dou, Q.; Qin, J.; Heng, P.A. Automated melanoma recognition in dermoscopy images via very deep residual networks. IEEE Trans. Med. Imaging 2017, 36, 994–1004. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Ma, Z.; Tavares, J.M.R. A novel approach to segment skin lesions in dermoscopic images based on a deformable model. IEEE J. Biomed. Health Inform. 2016, 20, 615–623. [Google Scholar]
- Codella, N.C.; Gutman, D.; Celebi, M.E.; Helba, B.; Marchetti, M.A.; Dusza, S.W.; Kalloo, A.; Liopyris, K.; Mishra, N.; Kittler, H.; et al. Skin lesion analysis toward melanoma detection: A challenge at the 2017 international symposium on biomedical imaging (ISBI), 2017, hosted by the international skin imaging collaboration (ISIC). arXiv, 2017; arXiv:1710.05006. [Google Scholar]

| Metric Value | Accuracy (%) | Dice (%) | JAC (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|
| Average | 95.3 | 90.38 | 83.2 | 97.5 | 88.8 |
| Standard deviation | 6 | 7.6 | 10.5 | 3.5 | 11.4 |
| Image ID | Accuracy (%) | Dice (%) | JAC (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|
| ISIC_0012836 | 99.7819 | 93.2747 | 87.397 | 99.9909 | 87.851 |
| ISIC_0013917 | 99.1485 | 90.4852 | 82.6237 | 1 | 82.6237 |
| ISIC_0014647 | 99.4684 | 92.8643 | 86.6791 | 99.7929 | 91.2339 |
| ISIC_0014649 | 98.8823 | 95.2268 | 90.8886 | 98.8313 | 99.2854 |
| ISIC_0014773 | 98.9017 | 97.3678 | 94.8707 | 98.6294 | 99.9692 |
| ISIC_0014968 | 89.5888 | 89.2267 | 80.5489 | 81.7035 | 99.9913 |
| ISIC_0014994 | 98.9242 | 93.0613 | 87.023 | 1 | 87.023 |
| ISIC_0015019 | 93.8788 | 93.9689 | 88.6239 | 88.6218 | 99.602 |
| ISIC_0015941 | 99.7687 | 94.3589 | 89.3203 | 1 | 89.3203 |
| ISIC_0015563 | 98.0344 | 83.939 | 72.3232 | 97.928 | 1 |
| Average (%) | 97.63777 | 92.3774 | 86.0298 | 96.54978 | 93.68998 |
| SD (%) | 3.31069 | 3.7373 | 6.2549 | 6.26068 | 6.76053 |
| Method | Accuracy (%) | Dice (%) | JAC (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|
| NSSLS method | 80.6 ± 22.1 | 66.4 ± 32.6 | 57.9 ± 33.7 | 82.1 ± 24 | 83.1 ± 30.4 |
| Proposed NCARG method | 95.3 ± 6 | 90.4 ± 7.6 | 83.2 ± 10.5 | 97.5 ± 6.3 | 88.8 ± 11.4 |
| p-value | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| Method | Accuracy (%) | Dice (%) | JAC (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|
| FCRNs of 38 layers [34] | 92.9 | 85.6 | 78.5 | 88.2 | 93.2 |
| FCRNs of 101 layers [34] | 93.7 | 87.2 | 80.3 | 90.3 | 93.5 |
| VGG-16 [34,35] | 90.3 | 79.4 | 70.7 | 79.6 | 94.5 |
| GoogleNet [34,36] | 91.6 | 84.8 | 77.6 | 90.1 | 91.6 |
| Proposed NCARG method | 95.3 | 90.4 | 83.2 | 97.5 | 88.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Ashour, A.S.; Smarandache, F. A Novel Skin Lesion Detection Approach Using Neutrosophic Clustering and Adaptive Region Growing in Dermoscopy Images. Symmetry 2018, 10, 119. https://doi.org/10.3390/sym10040119
Guo Y, Ashour AS, Smarandache F. A Novel Skin Lesion Detection Approach Using Neutrosophic Clustering and Adaptive Region Growing in Dermoscopy Images. Symmetry. 2018; 10(4):119. https://doi.org/10.3390/sym10040119
Chicago/Turabian StyleGuo, Yanhui, Amira S. Ashour, and Florentin Smarandache. 2018. "A Novel Skin Lesion Detection Approach Using Neutrosophic Clustering and Adaptive Region Growing in Dermoscopy Images" Symmetry 10, no. 4: 119. https://doi.org/10.3390/sym10040119
APA StyleGuo, Y., Ashour, A. S., & Smarandache, F. (2018). A Novel Skin Lesion Detection Approach Using Neutrosophic Clustering and Adaptive Region Growing in Dermoscopy Images. Symmetry, 10(4), 119. https://doi.org/10.3390/sym10040119







