Pre-Rationalized Parametric Designing of Roof Shells Formed by Repetitive Modules of Catalan Surfaces
Abstract
:1. Introduction
2. Early Stage of Rationalized Design
3. Geometric Properties of Catalan Surfaces
- oblique ruled surfaces of second order—hyperbolic paraboloid
4. Parametric Pre-Designing of Roof Shells—Results
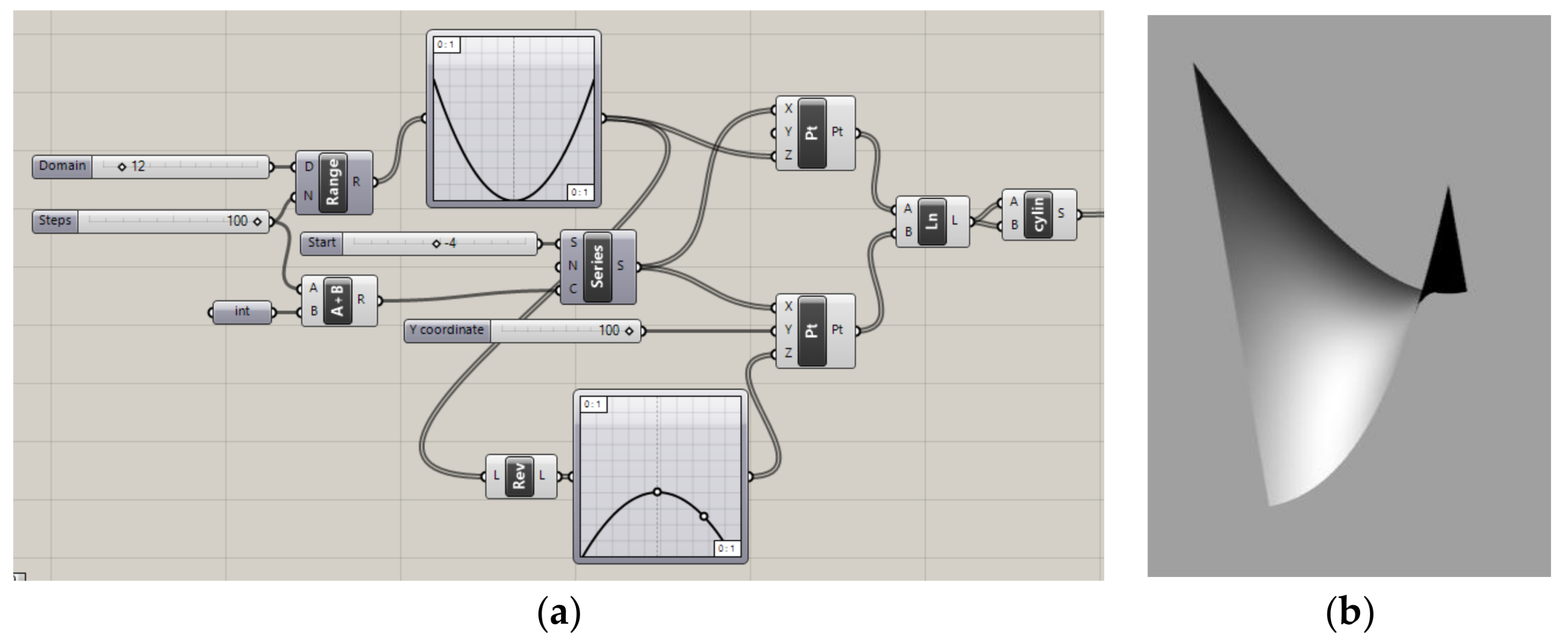
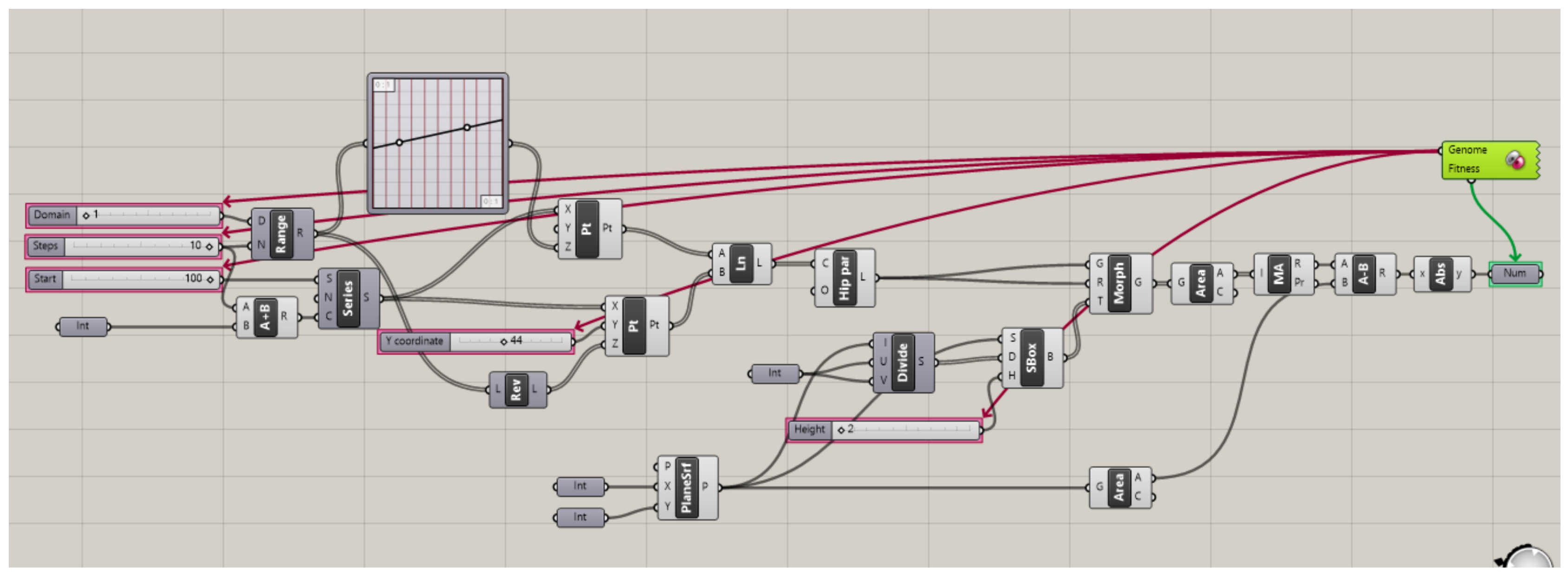
4.1. Geometric Modeling by Means of Grasshopper Scripts
4.1.1. Hyperbolic Paraboloid
4.1.2. Cylindroid and Conoid
4.2. Form Optimisation by Means of Galapagos
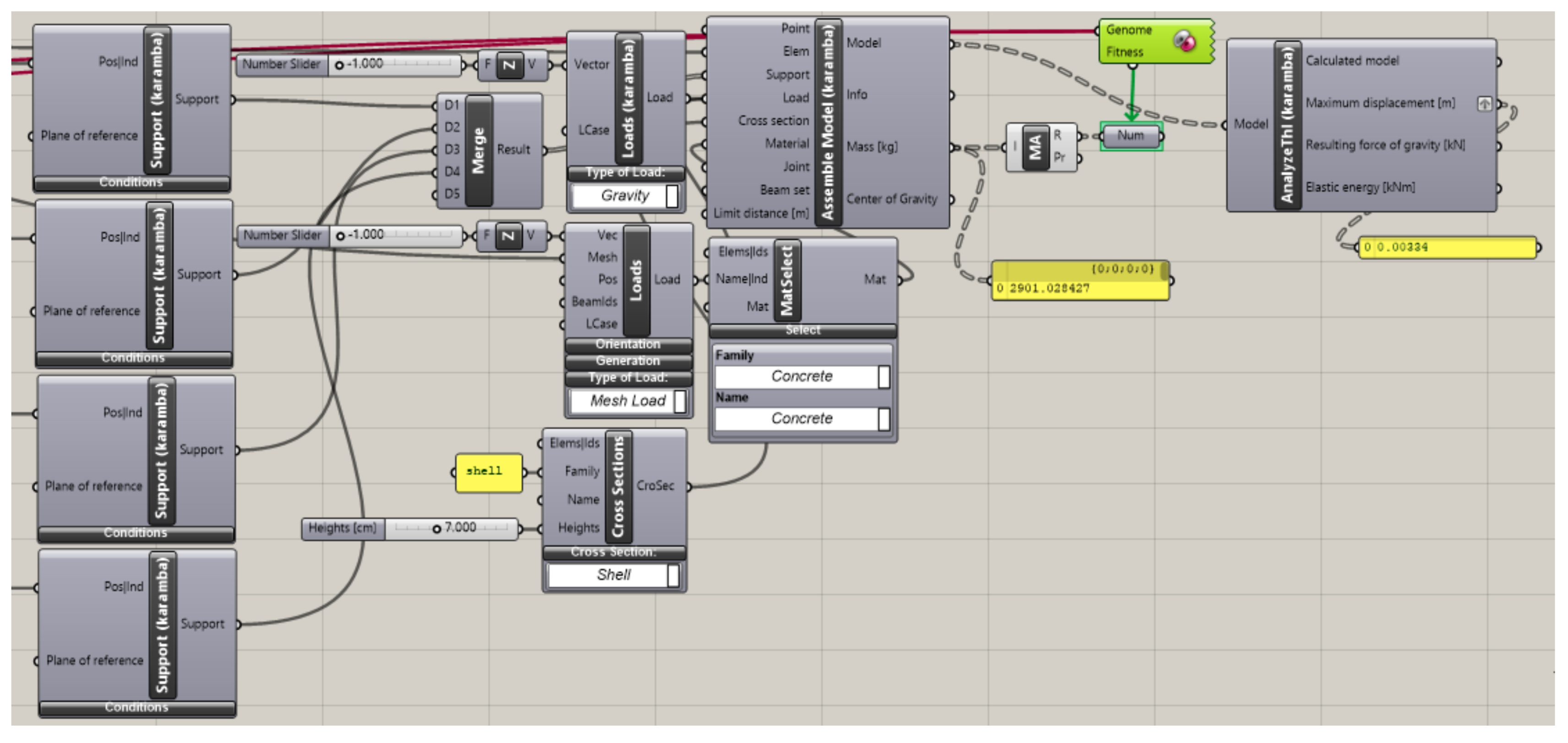
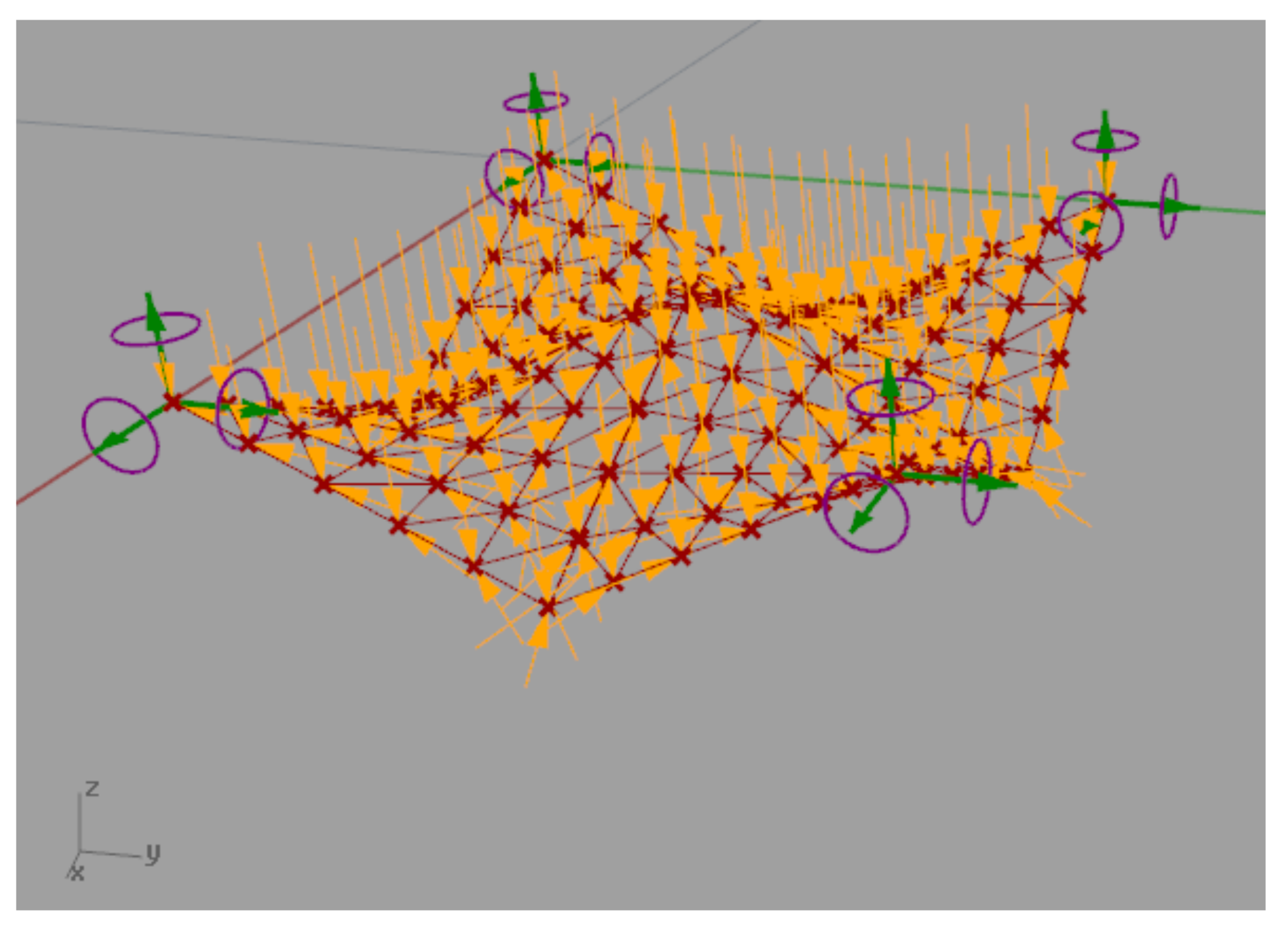
4.3. Optimization Based on Structural Analysis
4.4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Vitruvius, P. Vitruvius: The Ten Books on Architecture, 1st ed.; Harvard University Press: Cambridge, UK, 1914; pp. 13–31. [Google Scholar]
- Biermann, V.; Borngasser, B. Architectural Theory from the Renaissance to the Present, 1st ed.; Taschen: Koln, Germany, 2003; pp. 6–20. [Google Scholar]
- Oxman, R. Theory and design in the first digital age. Des. Stud. 2006, 27, 229–265. [Google Scholar] [CrossRef]
- Unwin, S. Nalyzing architecture through drawing. Build. Res. Inf. 2007, 35, 101–110. [Google Scholar] [CrossRef]
- Hewitt, M. Representational Forms and Modes of Conception; an Approach to the History of Architectural Drawing. J. Archit. Educ. 2014, 39, 2–9. [Google Scholar]
- Biagini, C.; Donato, V. Behind the complexity of a folded paper. In Proceedings of the Mo. Di. Phy. Modeling from Digital to Physical. Innovation in design languages and project procedures, Milano, Italy, 11–12 November 2013; pp. 160–169. [Google Scholar]
- Kim, D.-Y.; Lee, S.; Kim, S.-A. Interactive decision Making Environment for the Design optimization of climate Adaptive building Shells. In Proceedings of the International Conference on Cooperative Design, Visualization and Engineering (CDVE 2013), Mallorca, Spain, 22–25 September 2013; Springer: Berlin/Heindelberg, Germany, 2013. [Google Scholar]
- Luo, Y.; Dias, J.M. Development of a Cooperative Integration System for AEC Design. In Proceedings of the International Conference on Cooperative Design, Visualization and Engineering (CDVE 2004), Palma de Mallorca, Spain, 19–22 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3190. [Google Scholar]
- Wang, J.; Chong, H.-Y.; Shou, W.; Wang, X.; Guo, J. BIM- Enabled design Collaboration for Complex Building. In Proceedings of the International Conference on Cooperative Design, Visualization and Engineering (CDVE 2013), Mallorca, Spain, 22–25 September 2013; Springer: Berlin/Heindelberg, Germany, 2013. [Google Scholar]
- Barlish, K.; Sullivan, K. How to measure the benefits of BIM- A case study approach. Autom. Constr. 2012, 24, 149–159. [Google Scholar] [CrossRef]
- Kolarevic, B. Architecture in the Digital Age: Design and Manufacturing, 1st ed.; Spon Press: London, UK, 2003; pp. 20–98. [Google Scholar]
- Stravic, M.; Marina, O. Parametric Modeling for Advanced Architecture. Int. J. Appl. Math. Inform. 2011, 5, 9–16. [Google Scholar]
- Elango, M.; Devadas, M.D. Multi-Criteria Analysis of the Design Decisions In architectural Design Process during the Pre-Design Stage. Int. J. Eng. Technol. 2014, 6, 1033–1046. [Google Scholar]
- Bhooshan, S. Parametric design thinking: A case study of practice-embedded architectural research. Des. Stud. 2017, 52, 115–143. [Google Scholar] [CrossRef]
- Wortmann, T.; Tuncer, B. Differentiating parametric design: Digital Workflows in Contemporary Architecture and Construction. Des. Stud. 2017, 52, 173–197. [Google Scholar] [CrossRef]
- Oxman, R. Thinking difference: Theories and models of parametric design thinking. Des. Stud. 2017, 52, 4–39. [Google Scholar] [CrossRef]
- Woodburg, R.; Arish, R.; Kilian, A. Some Patterns for Parametric Modeling. In Proceedings of the 27th Annual Conference of the Association for Computer Aided Design in Architecture, Halifax, NS, Canada, 1–7 October 2007; pp. 222–229. [Google Scholar]
- Turrin, M.; von Buelow, P.; Stouffs, R. Design explorations of performance driven geometry in architectural design using parametric modeling and genetic algorithms. Adv. Eng. Inform. 2011, 25, 656–675. [Google Scholar] [CrossRef]
- Moussavi, F. Parametric software is not substitute for parametric thinking. Archit. Rev. 2011, 230, 39–40. [Google Scholar]
- Hardling, J.E. Meta-parametric Design. Des. Stud. 2017, 52, 73–95. [Google Scholar] [CrossRef]
- Tofli, J. Application of Catalan surface in designing roof structures—An important issue in the education of the future architect engineer. In Proceedings of the International Conference on Engineering Education (ICEE 2007), Coimbra, Portugal, 3–7 September 2007. [Google Scholar]
- Przewlocki, S. Descriptive Geometry in Construction, 1st ed.; Arkady: Warsaw, Poland, 1982; pp. 57–209. [Google Scholar]
- Abramczyk, J. Shaping Free Forms of Buildings Roofted with Transformed Corrugated Sheeting; Publishing House of Rzeszow University of Technology: Rzeszow, Poland, 2017. [Google Scholar]
- Abramczyk, J. Shaping Innovative Forms of Buildings Roofted with Corrugated Hyperbolic Paraboloid Sheeting. Procedia Eng. 2016, 161, 60–66. [Google Scholar] [CrossRef]
- Abramczyk, J. Building Structures Roofted with Multi-Segment Corrugated Hyperbolic Paraboloid Steel Shells. Procedia Eng. 2016, 161, 1545–1550. [Google Scholar] [CrossRef]
- Zboinska, M.A.; Cudzik, J.; Juchnevic, R.; Radziszewski, K. A Design Framework and Digital Toolset Supporting the Early-Stage Explorations of Responsive Kinetic Building Skin Concepts. In Proceedings of the 33rd Annual eCAADe Conference, Real Time: Extending the Reach of Computation, Vienna, Austria, 16–18 September 2015; Volume 2, pp. 715–724. [Google Scholar]
- Prokopska, A. Methodology of Architectural Design, Preliminary Phases of the Architectural Process; Publishing House of Rzeszow University of Technology: Rzeszow, Poland, 2015; pp. 39–121. (In Polish) [Google Scholar]
- Prokopska, A. Morphology of the Architectural Achievement. A Methodological Analysis of Selected Morphological Systems of the Natural and Architectural Environments. Syst. J. Transdiscipl. Syst. Sci. 2002, 7, 1–116. [Google Scholar]
- Woodburg, R.; Mohiuddin, A. Interactive design galleries: A general approach to interacting with design alternatives. Des. Stud. 2017, 52, 40–72. [Google Scholar] [CrossRef]
- Dzwierzynska, J.; Abramczyk, J. Engineering Descriptive Geometry; Publishing House of Rzeszow University of Technology: Rzeszow, Poland, 2015. [Google Scholar]
- Pottman, H.; Asperl, A.; Hofer, M.; Kilian, A. Architectural Geometry, 1st ed.; Bentley Institute Press: Exton, PA, USA, 2007; pp. 35–194. [Google Scholar]
- Krivoshapko, S.; Ivanov, V.N. Encyclopedia of Analytical Surfaces; Springer International Publishing: Cham, Switzerland, 2015; pp. 60–77. [Google Scholar]
- Chudley, R.; Greeno, R. Advanced Construction Technology, 4th ed.; Dorset Press: Dorchester, UK, 2006; pp. 528–529. [Google Scholar]
- Min, C.S.; Gupta, A.K. Inelastic behavior of reinforced concrete hyperbolic paraboloid saddle shell. Eng. Struct. 1994, 16, 227–237. [Google Scholar] [CrossRef]



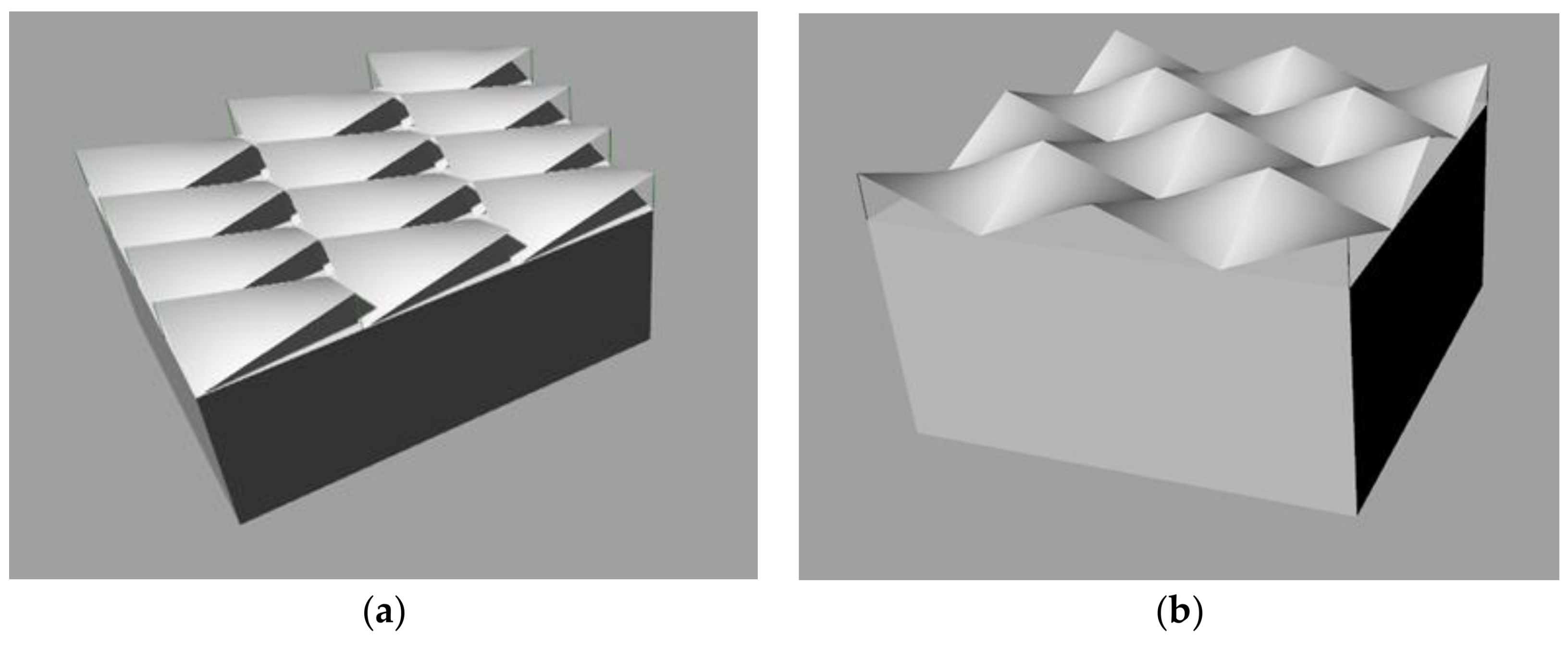
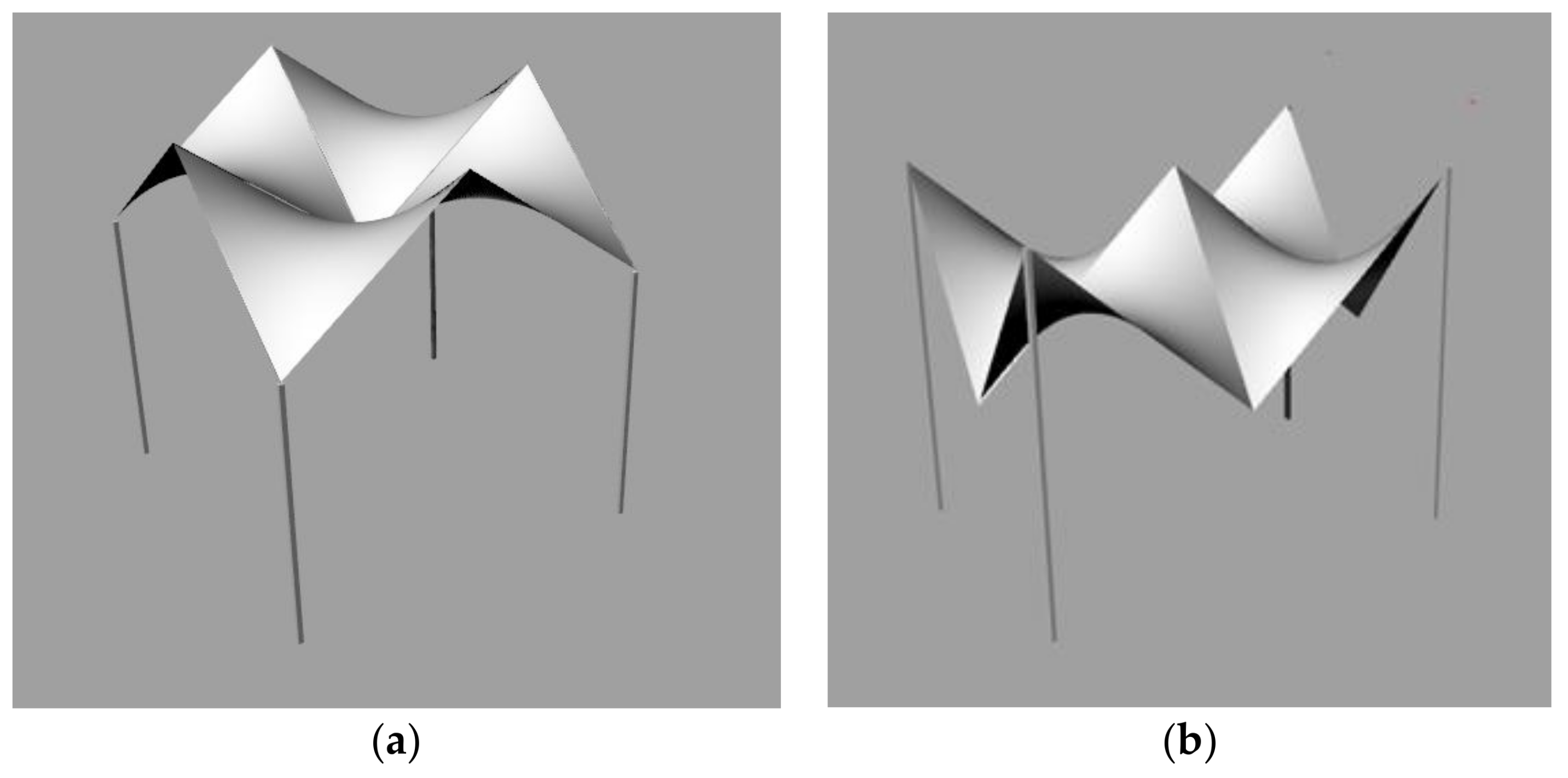


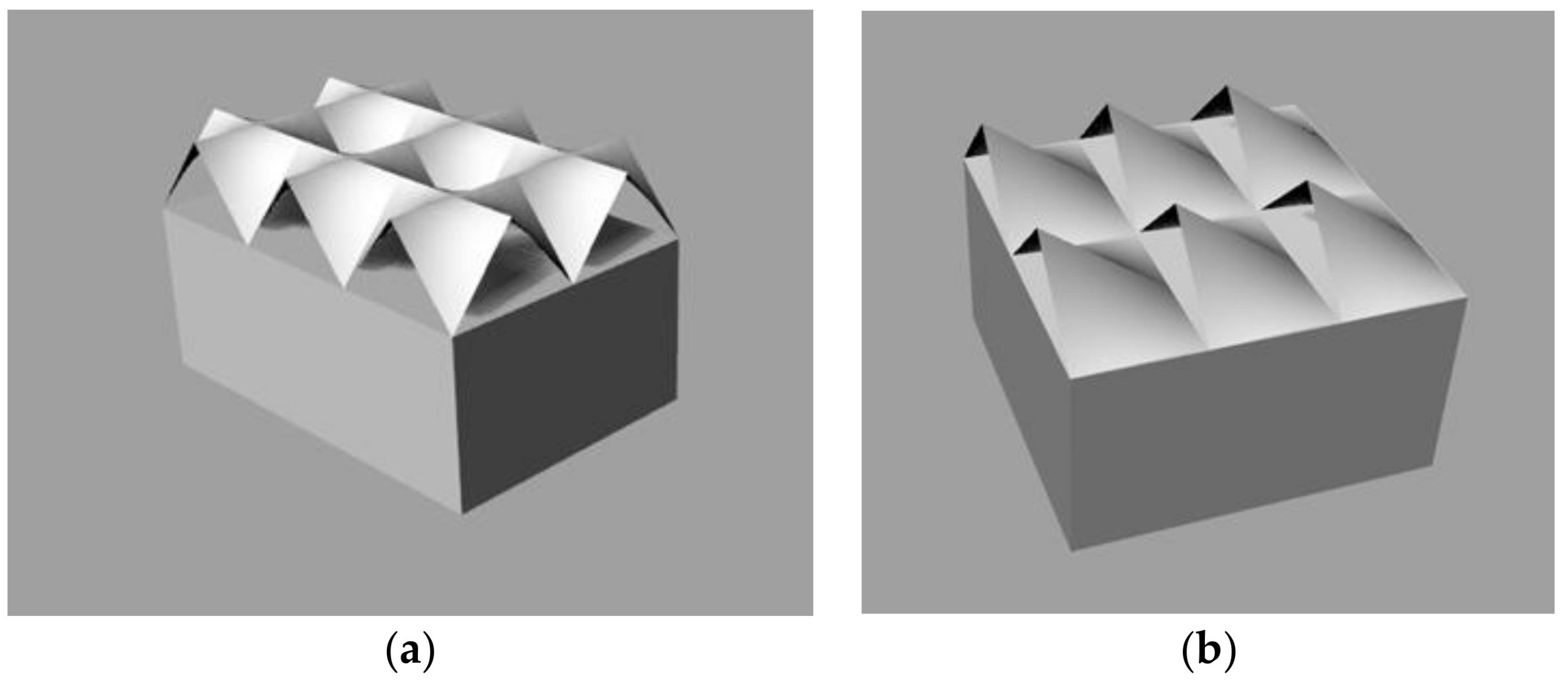

| Kind of Thse Urface | Type of the Compoud Roof Shell | |
|---|---|---|
| Hyperbolic paraboloid |  | 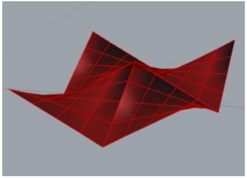 |
| 1 | 2 | |
| Conoid |  |  |
| 3 | 4 | |
| Cylindroid | 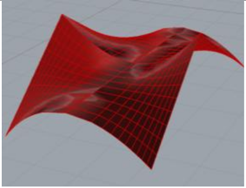 |  |
| 5 | 6 | |
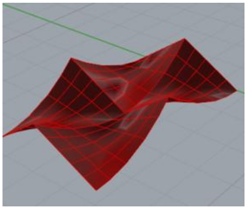 | ||
| 7 | ||
| Kind of the Surface | The Scheme of the Mesh and Supports’ Location | Dimmentions (m) | Mass (kg) | Displacement (m) |
|---|---|---|---|---|
| Hyperbolic paraboloid 1 |  | a = b = 4.00 | 3021.93 | 0.0004 |
| h = 1 | ||||
| Hyperbolic paraboloid 2 | 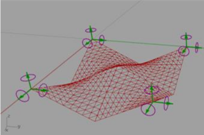 | a = b = 4.00 | 3021.93 | 0.0000 |
| h = 1 | ||||
| Conoid 3 |  | a = 4.75 | 2993.24 | 0.0042 |
| b = 3.35 | ||||
| h = 1 | ||||
| Conoid 4 |  | a = 4.75 | 3993.52 | 0.0035 |
| b = 3.35 | ||||
| h = 1 | ||||
| Cylindroid 5 |  | a = 3.47 | 2901.03 | 0.0033 |
| b = 4.61 | ||||
| h = 1 | ||||
| Cylindroid 6 | 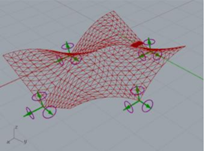 | a = 4.69 | 3113.00 | 0.0033 |
| b = 3.41 | ||||
| h = 1 | ||||
| Cylindroid 7 | 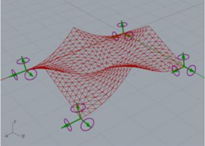 | a = 4.67 | 3107.00 | 0.0008 |
| b = 3.47 | ||||
| h = 1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzwierzynska, J.; Prokopska, A. Pre-Rationalized Parametric Designing of Roof Shells Formed by Repetitive Modules of Catalan Surfaces. Symmetry 2018, 10, 105. https://doi.org/10.3390/sym10040105
Dzwierzynska J, Prokopska A. Pre-Rationalized Parametric Designing of Roof Shells Formed by Repetitive Modules of Catalan Surfaces. Symmetry. 2018; 10(4):105. https://doi.org/10.3390/sym10040105
Chicago/Turabian StyleDzwierzynska, Jolanta, and Aleksandra Prokopska. 2018. "Pre-Rationalized Parametric Designing of Roof Shells Formed by Repetitive Modules of Catalan Surfaces" Symmetry 10, no. 4: 105. https://doi.org/10.3390/sym10040105
APA StyleDzwierzynska, J., & Prokopska, A. (2018). Pre-Rationalized Parametric Designing of Roof Shells Formed by Repetitive Modules of Catalan Surfaces. Symmetry, 10(4), 105. https://doi.org/10.3390/sym10040105






