A Robust Image Watermarking Technique Based on DWT, APDCBT, and SVD

Abstract

Copyright protection for digital multimedia has become a research hotspot in recent years. As an efficient solution, the digital watermarking scheme has emerged at the right moment. In this article, a highly robust and hybrid watermarking method is proposed. The discrete wavelet transform (DWT) and all phase discrete cosine biorthogonal transform (APDCBT) presented in recent years as well as the singular value decomposition (SVD) are adopted in this method to insert and recover the watermark. To enhance the watermark imperceptibility, the direct current (DC) coefficients after block-based APDCBT in high frequency sub-bands (LH and HL) are modified by using the watermark. Compared with the conventional SVD-based watermarking method and another watermarking technique, the watermarked images obtained by the proposed method have higher image quality. In addition, the proposed method achieves high robustness in resisting various image processing attacks.

1. Introduction

With the widespread use of image processing tools, it becomes increasingly easy for ordinary people to obtain images and modify their contents. Copyright authentication for digital images has therefore become a challenging problem. To address this issue, digital watermarking theory has been proposed in recent decades. Generally speaking, digital watermarking schemes can fall into two broad categories according to different application scenarios: robust watermarking and fragile watermarking [1]. Robust watermarking techniques can resist most common attacks and consequently are widely used in copyright protection. By contrast, fragile watermarking methods are usually susceptible to any modification and thus are often employed in image tamper detection and restoration. For copyright protection, a robust watermarking scheme should satisfy two basic conditions, namely, robustness and imperceptibility [2]. Here, robustness means that the watermark in a watermarked image can be integrally extracted even when the watermarked image has been distorted by attacks. Imperceptibility means that the quality of the watermarked image cannot be strongly influenced. In other words, no traces of watermark embedding are visible to the naked eyes.

According to the working domain, the watermarking techniques can be further split into two categories. One is the watermarking methods performed in the spatial domain, in which the watermarking bits are inserted into carrier image by modifying its pixel values [3]. The second kind of watermarking methods are based on the transform domain [4,5,6,7]. Compared with the former, the watermarking schemes in the transform domain are more robust because the watermark is embedded by modulating the transform coefficients. Because of this property, many robust watermarking methods performed in the transform domain have been proposed for copyright protection. The most widely used transforms are the discrete cosine transform (DCT) [4], the discrete wavelet transform (DWT) [5], and the discrete Fourier transform (DFT) [6]. In recent years, singular value decomposition (SVD) has received considerable attention in watermarking theory due to its good stability in signal processing. In [7], Liu and Tan introduced a classical SVD-based robust watermarking method. In their method, the watermark is inserted into the carrier image by directly modulating the singular values of the image. However, this method is not secure enough, and the watermark has much influence on the image quality. To resolve this issue, many robust watermarking methods based on hybrid transforms have been proposed, which combine SVD with other transforms, such as DWT and DCT. Lai and Tsai [8] introduced a DWT-SVD-based watermarking algorithm, in which the watermark is inserted by modifying the singular values of high-frequency sub-bands. In [9], another DWT-SVD-based robust watermarking method was proposed by Gupta and Raval. In this scheme, the original image is first decomposed by DWT, and the principal component of the watermark is then superimposed on the singular values of the diagonal high-frequency sub-band (HH). However, experimental results indicate that the extracted watermark has poor image quality when the watermarked image has been attacked. In [10], Singh et al. proposed a hybrid dual watermarking scheme for telemedicine applications. Two watermarks (image and text) are embedded into a radiological image using a DWT-SVD-based watermarking method. During the embedding and extraction processes of the text watermark, four error correction codes (ECCs) are applied to improve the robustness of the watermark. Based on [10], Singh [11] designed an improved hybrid watermarking method. Unlike reference [10], the carrier image and the watermark image are both decomposed using the DWT, DCT, and SVD. Then, the singular value matrix of the watermark information is embedded into the carrier image using an SVD-based method. However, the quality of the watermarked images is greatly affected in these two methods because two watermarks are embedded in each image. In [12], Singh et al. designed another hybrid watermarking method performed in DWT-DCT-SVD domain. The carrier image is firstly decomposed by DWT transform, then the low frequency sub-band (LL) and the watermark image are both transformed by DCT transform. The singular values of the DCT coefficients in watermark image are embedded into the singular values of the DCT coefficients in LL sub-band. To select an appropriate wavelet basis for DWT-DCT-SVD-based robust watermarking, Singh and Tayal [13] studied different wavelet families in DWT transform and analyzed their effects on the performance of hybrid watermarking. The comparison experiments indicate that different wavelets have different impacts on the watermarking scheme, and “the best wavelet” choice is dependent on several factors. To protect the copyright of color images, Roy and Pal [14] proposed a hybrid robust watermarking scheme that combines SVD with the redundant discrete wavelet transform (RDWT). In [15], Laur et al. proposed a robust color image watermarking based on entropy and QR decomposition. The entropy is used to select the image blocks for watermark embedding. After chirp Z-transform, DWT transform, QR decomposition, and SVD transform, the watermark information is finally embedded into the singular values of carrier image.

It is generally known that the scaling factor has a significant effect on SVD-based watermarking algorithms. To select an optimal scaling factor for SVD-based watermarking, Mishra et al. [16] analyzed the effect of different scaling factors on watermark imperceptibility and robustness. Based on the analysis, they proposed an optimized SVD-based watermarking method, in which an optimal scaling factor is identified using an optimization algorithm called the firefly algorithm (FA) [17]. Although this scheme achieves a good balance between robustness and imperceptibility, it can also lead to false-positive problem during the watermark extraction process [18]. To solve this problem, Makbol and Khoo [19] presented a false-positive-free watermarking scheme that combines SVD with the integer wavelet transform (IWT). To prevent false-positive problem, a signature generated from two orthogonal matrices $\mathit{U}$ and $\mathit{V}$ is inserted into the carrier image along with the watermark. During watermark detection, this signature is firstly extracted, and a certification process is then performed before watermark extraction. To further improve watermark robustness and imperceptibility, Ansari et al. [20] presented an improved robust watermarking algorithm based on [19], in which an optimal scaling factor is selected through artificial bee colony (ABC) optimization. Compared with the previous method, this method achieves promising performance. A blind and robust watermarking method executed in the DWT, SVD, and DCT domains has been proposed in [21]. Two matrices generated from the four most significant bit-planes and the four least significant bit-planes of the watermark are transformed by DCT and inserted into the singular values of the carrier image using a DWT-SVD-based method. Fazli and Moeini [22] also proposed a hybrid DWT-DCT-SVD-based watermarking algorithm. In this method, the original carrier image is average split into four parts. For each part, the DWT and DCT transforms are successively applied, and the first two alternating current (AC) coefficients are used to form a new matrix. Finally, the watermark is embedded into this new matrix using an SVD-based watermarking method. Since these four parts are all embedded by the same watermark, this method has a high robustness to cropping operations.

In this article, a robust watermarking algorithm with high imperceptibility and robustness is proposed, which combines SVD with DWT and all phase discrete cosine biorthogonal transform (APDCBT). The carrier image is first decomposed by DWT, and the vertical and horizontal frequency sub-bands (LH and HL) are selected respectively to embed two identical watermarks. On each sub-band, the block-based APDCBT is performed. Compared with the DCT transform, the APDCBT transform has better energy concentration characteristic, which can provide better protection for the watermark. Because the direct current (DC) coefficients have much larger perceptual capacity than AC coefficients, the DC coefficient of each sub-block is extracted to form a new matrix. Finally, the watermark is embedded into the coefficient matrix by singular value modification in the SVD domain. On the receiving end, the two identical watermarks are extracted from LH and HL sub-bands respectively, and a watermark correction process is applied to further improve the quality of the extracted watermark.

The remainder of this article is organized as follows. In Section 2, APDCBT and SVD transforms are briefly described. The proposed method, including watermark insertion and watermark extraction, is developed in Section 3. Section 4 presents the experimental results and performance analysis. The conclusions and an outlook on possible future work are presented in Section 5.

2. APDCBT and SVD

2.1. APDCBT

It is widely shared that the DCT has good properties of energy concentration. For this reason, it has been broadly applied in image compression and watermarking techniques. However, as research continues, some negative effects have been revealed that the image compressed by DCT has serious block artifacts at low bit rates. To solve this problem, a new transform called APDCBT was presented in [23]. Compared with the conventional DCT transform, the APDCBT transform shows outstanding performance in high-frequency attenuation and low-frequency aggregation. Thanks to these features, the APDCBT gets extensive usage in image processing and watermarking techniques [24,25]. In [25], the APDCBT was first introduced into the field of information hiding, in which the APDCBT was just adopted to replace the DCT in conventional DCT-based robust watermarking method. To make better use of APDCBT, in this article, we introduce a hybrid watermarking method by combining APDCBT with DWT and SVD. In APDCBT transform, a transformation matrix $\mathit{B}$ with dimensions of $N\times N$ is defined as:

$$\mathit{B}(m,n)=\{\begin{array}{ll}\frac{N-m}{N^2},& m=0,1,\cdots ,N-1,n=0,\\ \frac{1}{N^2}\left[(N-m)\cos \frac{mn\mathsf{\pi }}{N}-\csc \frac{n\mathsf{\pi }}{N}\sin \frac{mn\mathsf{\pi }}{N}\right],& m=0,1,\cdots ,N-1,n=1,2,\cdots ,N-1.\end{array}$$

(1)

For an image block $\mathit{X}$ with dimensions of $N\times N$, the APDCBT can be expressed as follows:

$$\mathit{Y}=\mathit{B}\mathit{X}{\mathit{B}}^{\mathrm{T}},$$

(2)

where $\mathit{Y}$ denotes the transform coefficient matrix after APDCBT.

2.2. SVD

SVD is a common transform that is often used in numerical analysis and principal component analysis (PCA). Through SVD, a matrix $\mathit{M}$ can be decomposed into three parts denoted by $\mathit{U}$, $\mathit{S}$, and $\mathit{V}$:

$$\mathit{M}=\mathit{U}\mathit{S}{\mathit{V}}^{\mathrm{T}},$$

(3)

where $\mathit{U}$ and $\mathit{V}$ are two orthogonal matrices and $\mathit{S}$ is a diagonal matrix. The elements in matrix $\mathit{S}$, which are also called singular values, have good stability in signal processing and can resist common attacks to a certain extent. In addition, SVD can be performed on any matrices with no limitation. The top few singular values contain the majority of the image information. Because of these properties, SVD has been widely used in watermarking schemes for copyright authentication.

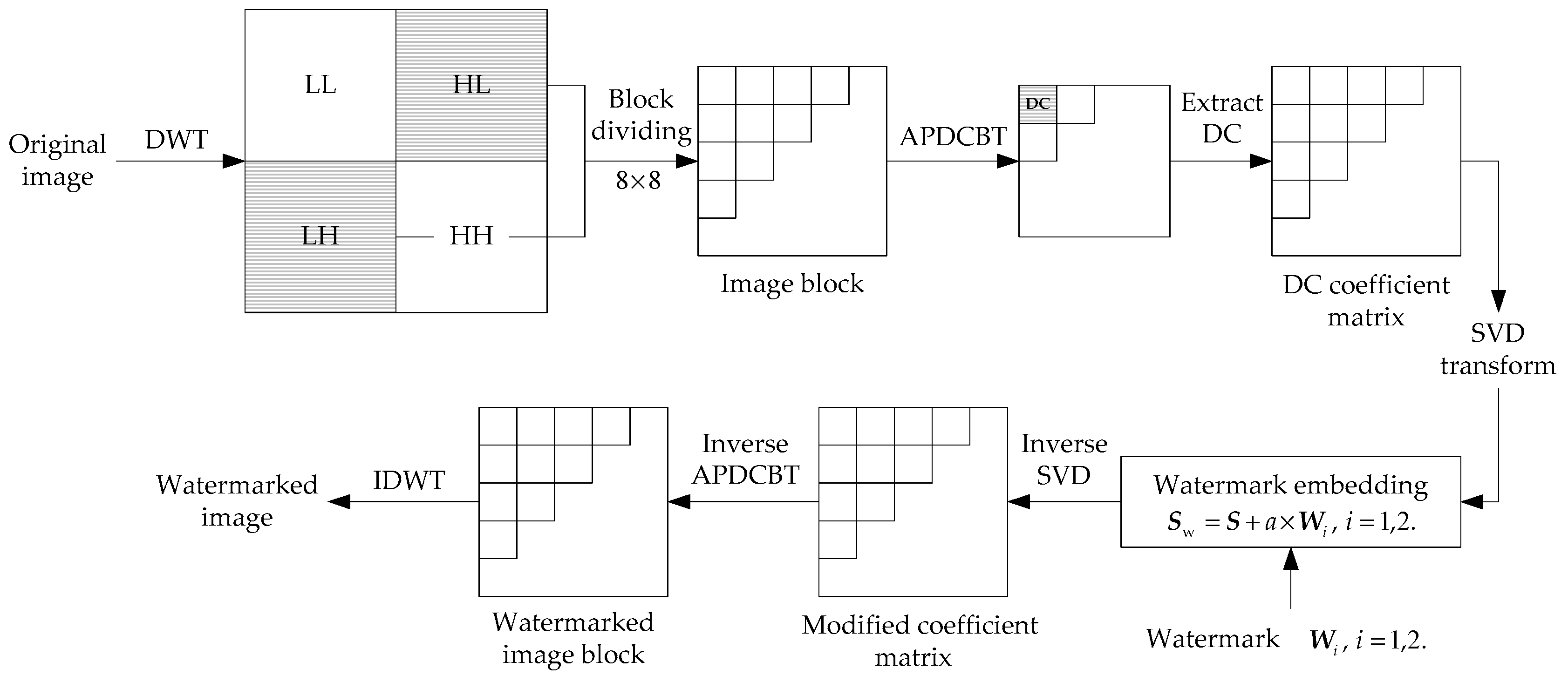
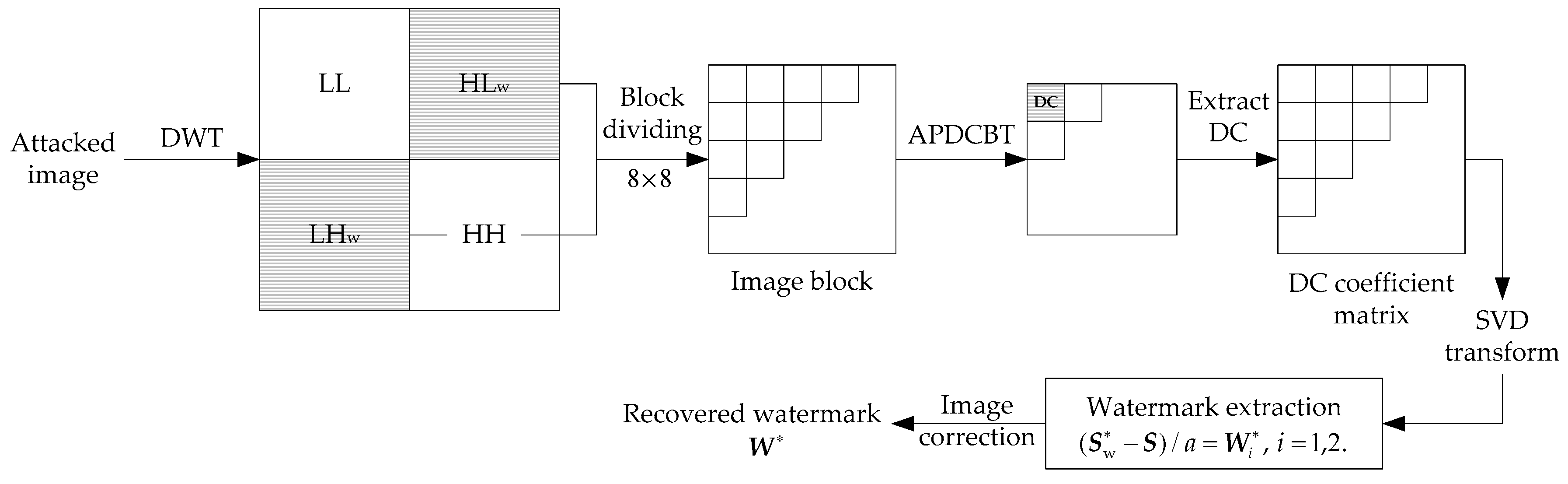
3. The Proposed Scheme

We present the proposed method based on DWT, APDCBT, and SVD in this section. It involves two stages: watermark insertion and watermark extraction. The concrete steps are introduced in the following subsections.

3.1. Watermark Insertion

Figure 1 depicts the process of watermark insertion, and the detailed steps are presented below:

Step 1. One-level DWT decomposition with “Haar” wavelet is first performed on the carrier image, yielding four sub-bands: three high-frequency sub-bands (LH, HL, and HH) and a low-frequency sub-band (LL).

Step 2. To reduce the influence of watermark insertion, two high-frequency sub-bands, LH and HL, are selected for the insertion of two identical watermarks. Using the HL sub-band as an example, the block-based APDCBT is applied to each sub-block obtained by dividing the image into 8 × 8 blocks.

Step 3. The DC coefficient of each sub-block is used to generate a new coefficient matrix, denoted by $\mathit{M}$. Then, the SVD is applied to this coefficient matrix, and the singular value matrix $\mathit{S}$ of the matrix $\mathit{M}$ is computed according to Equation (3).

Step 4. The first watermark ${\mathit{W}}_1$ is inserted into the coefficient matrix, which is shown as follows:

$${\mathit{S}}_{\mathrm{w}}=\mathit{S}+a\times {\mathit{W}}_1, {\mathit{S}}_{\mathrm{w}}={\mathit{U}}_{\mathrm{w}}{\mathit{S}}_{\mathrm{w}1}{\mathit{V}}_{\mathrm{w}}^{\mathrm{T}},$$

(4)

where $a$ is the watermark embedding intensity, S_w is a matrix containing the watermark information, ${\mathit{U}}_{\mathrm{w}}$ and ${\mathit{V}}_{\mathrm{w}}$ are newly generated orthogonal matrices, and ${\mathit{S}}_{\mathrm{w}1}$ is the modified singular value matrix after watermark insertion.

Step 5. The inverse SVD is applied to ${\mathit{S}}_{\mathrm{w}1}$, then we get a modified coefficient matrix ${\mathit{M}}^{\prime }$. After the inverse APDCBT, the HL sub-band embedded by watermark ${\mathit{W}}_1$ is obtained.

Step 6. To embed the second watermark ${\mathit{W}}_2$, the same process is performed on the LH sub-band.

Step 7. The inverse DWT (IDWT) is applied to obtain the watermarked carrier image.

3.2. Watermark Extraction

The flow diagram of watermark extraction is shown in Figure 2. The extraction process consists of the following steps:

Step 1. The received image, which might have been distorted by various attacks, is transformed by one-level DWT with “Haar” wavelet. Then, the high-frequency sub-bands, LH_w and HL_w, are obtained.

Step 2. To extract the watermark ${\mathit{W}}_1^{\ast }$ in HL_w sub-band, the sub-band image is first divided into 8 × 8 non-overlapping sub-blocks. Then, the APDCBT is performed on each sub-block. Subsequently, the DC coefficients in the APDCBT coefficient matrices are used to produce a new matrix ${\mathit{M}}^{\ast }$.

Step 3. The newly generated matrix ${\mathit{M}}^{\ast }$ is transformed by SVD to obtain three new matrices, ${\mathit{U}}^{\ast }$, ${\mathit{S}}^{\ast }$, and ${\mathit{V}}^{\ast }$, as given in Equation (5):

$${\mathit{M}}^{\ast }={\mathit{U}}^{\ast }{\mathit{S}}^{\ast }{({\mathit{V}}^{\ast })}^{\mathrm{T}}.$$

(5)

Step 4. The watermark ${\mathit{W}}_1^{\ast }$ is computed by applying the inverse process of Step 4 in watermark embedding procedure, which can be expressed as follows:

$${\mathit{S}}_{\mathrm{w}}^{\ast }={\mathit{U}}_{\mathrm{w}}{\mathit{S}}^{\ast }{\mathit{V}}_{\mathrm{w}}^{\mathrm{T}}, {\mathit{W}}_1^{\ast }=({\mathit{S}}_{\mathrm{w}}^{\ast }-\mathit{S})/a.$$

(6)

To obtain another watermark, ${\mathit{W}}_2^{\ast }$, the same process is applied to the LH_w sub-band. Finally, the watermark $\mathit{W}$ is computed by averaging these two watermarks, i.e., $\mathit{W}=({\mathit{W}}_1^{\ast }+{\mathit{W}}_2^{\ast })/2$. To further improve the quality of the extracted watermark, a sign function used in [22] is employed to correct the watermark:

$${\mathit{W}}^{\ast }(i,j)=\{\begin{array}{l}1,\mathit{W}(i,j)\ge T,\\ 0,\mathit{W}(i,j)<T,\end{array}$$

(7)

where $T$ is a threshold between 0 and 1, ${\mathit{W}}^{\ast }$ is the extracted watermark after correction, and $(i,j)$ represents the coordinates of a pixel in watermark image. In the experiments reported below, $T$ is set to 0.5.

To better understand the proposed watermarking scheme, the pseudocode forms of the watermark insertion and extraction processes are presented in Algorithms 1 and 2, respectively:

Algorithm 1 Watermark Insertion

Variable Declaration:   Lena: carrier image   SDUW: watermark image   I: read the carrier image   ${\mathit{W}}_i(i=1,2)$: read the watermark images   $a$: scaling factor   DWT, APDCBT, and SVD: transforms used in the algorithm   Wavelet filter: Haar   LL, LH, HL, and HH: sub-bands after the first-level DWT decomposition   $\mathit{M}$: coefficient matrix formed by DC coefficients in LH or HL sub-band   $\mathit{S}$: diagonal matrix for $\mathit{M}$   $\mathit{U}$ and $\mathit{V}$: orthogonal matrices for $\mathit{M}$   ${\mathit{S}}_{\mathrm{w}}$: watermarked diagonal matrix   ${\mathit{S}}_{\mathrm{w}1}$: diagonal matrix for ${\mathit{S}}_{\mathrm{w}}$   ${\mathit{U}}_{\mathrm{w}}$ and ${\mathit{V}}_{\mathrm{w}}$: orthogonal matrices for ${\mathit{S}}_{\mathrm{w}}$   ${\mathit{M}}^{\prime }$: watermarked DC coefficient matrix   LHw and HLw: the watermarked LH and HL sub-bands   ${\mathit{I}}_{\mathrm{w}}$: watermarked image Watermark Embedding Procedure: 1. Read the Images and Perform DWT on Carrier Image   I$\leftarrow$Lena.bmp (carrier image with size of 512 × 512)   ${\mathit{W}}_1$$\leftarrow$SDUW.bmp (watermark image with size of 32 × 32)   [LL, LH, HL, HH]$\leftarrow$DWT (I, ‘Haar’) 2. Perform Block-based APDCBT on HL Sub-band   DC coefficients$\leftarrow$APDCBT (HL) 3. Get DC Coefficient Matrix $\mathit{M}$ and Perform SVD on $\mathit{M}$   // Form a new coefficient matrix $\mathit{M}$ using the DC coefficients obtained in Step 2, and perform SVD on coefficient matrix $\mathit{M}$   $\mathit{M}$$\leftarrow$DC coefficients   $[\mathit{U},\mathit{S},\mathit{V}]$$\leftarrow$SVD ($\mathit{M}$) 4. Watermark Insertion   ${\mathit{S}}_{\mathrm{w}}=\mathit{S}+a\times {\mathit{W}}_1$   $[{\mathit{U}}_{\mathrm{w}},{\mathit{S}}_{\mathrm{w}1},{\mathit{V}}_{\mathrm{w}}]$$\leftarrow$SVD (${\mathit{S}}_{\mathrm{w}}$)   ${\mathit{M}}^{\prime }$$\leftarrow$$\mathit{U}{\mathit{S}}_{\mathrm{w}1}{\mathit{V}}^{\mathrm{T}}$   Watermarked DC coefficients$\leftarrow$${\mathit{M}}^{\prime }$   HLw$\leftarrow$inverse $\mathrm{APDCBT}$ (Watermarked DC coefficients)   // Apply Steps 1–4 to LH sub-band to embed the same watermark ${\mathit{W}}_2$ and obtain the watermarked LHw sub-band   5. Perform IDWT to Get the Watermarked Image   ${\mathit{I}}_{\mathrm{w}}$$\leftarrow$inverse DWT (LL, LHw, HLw, HH)

Algorithm 2 Watermark Extraction

Variable Declaration:   ${\mathit{I}}_{\mathrm{a}}$: attacked image obtained on the receiving end   DWT, APDCBT, and SVD: transforms used in the algorithm   Wavelet filter: Haar   LL, LHw, HLw, and HH: new sub-bands after the first-level DWT decomposition   ${\mathit{M}}^{\ast }$: coefficient matrix formed by DC coefficients in LHw or HLw sub-band   $a$: scaling factor   ${\mathit{S}}^{\ast }$: diagonal matrix for ${\mathit{M}}^{\ast }$   ${\mathit{U}}^{\ast }$ and ${\mathit{V}}^{\ast }$: orthogonal matrices for ${\mathit{M}}^{\ast }$   ${\mathit{S}}_{\mathrm{w}}^{\ast }$: watermarked diagonal matrix   ${\mathit{U}}_{\mathrm{w}}$ and ${\mathit{V}}_{\mathrm{w}}$: orthogonal matrices for ${\mathit{S}}_{\mathrm{w}}$   T: threshold for watermark correction   ${\mathit{W}}_i^{\ast }(i=1,2)$: extracted watermark images   $\mathit{W}$: extracted watermark without correction   ${\mathit{W}}^{\ast }$: extracted watermark after correction Watermark Extraction Procedure: 1. Read the Attacked Image and Perform DWT on It   ${\mathit{I}}_{\mathrm{a}}$$\leftarrow$Received image.bmp   [LL, LHw, HLw, HH]$\leftarrow$DWT (${\mathit{I}}_{\mathrm{a}}$, ‘Haar’) 2. Perform Block-based APDCBT on HLw Sub-band and Get DC Coefficient Matrix ${\mathit{M}}^{\ast }$   Watermarked DC coefficients$\leftarrow$APDCBT (HLw)   ${\mathit{M}}^{\ast }$$\leftarrow$Watermarked DC coefficients 3. Perform SVD on ${\mathit{M}}^{\ast }$   $[{\mathit{U}}^{\ast },{\mathit{S}}^{\ast },{\mathit{V}}^{\ast }]$$\leftarrow$SVD (${\mathit{M}}^{\ast }$) 4. Watermark Extraction   ${\mathit{S}}_{\mathrm{w}}^{\ast }\leftarrow {\mathit{U}}_{\mathrm{w}}{\mathit{S}}^{\ast }{\mathit{V}}_{\mathrm{w}}^{\mathrm{T}}$   ${\mathit{W}}_1^{\ast }\leftarrow ({\mathit{S}}_{\mathrm{w}}^{\ast }-\mathit{S})/a$   // Apply Steps 1-4 to LHw sub-band to extract the second watermark ${\mathit{W}}_2^{\ast }$ 5. Watermark Correction   $\mathit{W}\leftarrow \frac{{\mathit{W}}_1^{\ast }+{\mathit{W}}_2^{\ast }}{2}$   for i = 1:32 and j = 1:32     if $\mathit{W}(i,j)\ge T$ then     ${\mathit{W}}^{\ast }(i,j)\leftarrow 1$     else ${\mathit{W}}^{\ast }(i,j)\leftarrow 0$     end if   end for   // The extracted watermark after correction ${\mathit{W}}^{\ast }$ is obtained

4. Performance Analysis

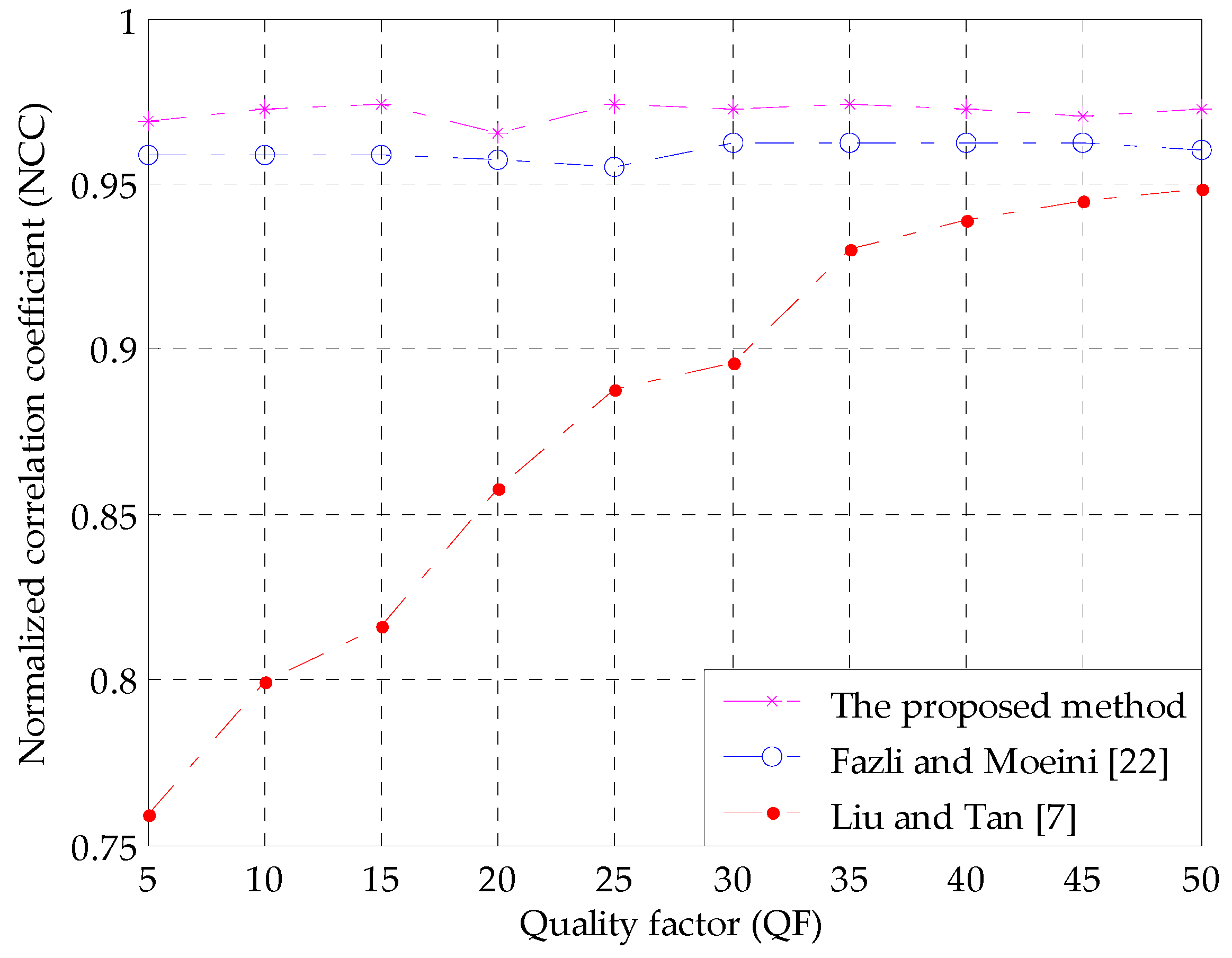
In this section, several experiments are conducted to evaluate the imperceptibility and robustness of the proposed watermarking method. Since the proposed method is implemented in the frequency domain, the watermark information is distributed on the whole image. In this paper, we use the standard test images with size of 512 × 512 as the example to show the algorithm performance. The gray-scale image Lena with dimensions of 512 × 512 is adopted as the carrier image. A binary logo image (SDUW, the abbreviation for Shandong University at Weihai) with dimensions of 32 × 32 is used as the watermark. In watermarking schemes based on SVD, the watermarking intensity plays an important role for the performance of the algorithm. To make better experimental comparisons, the embedding intensity used in these experiments is the same as that used in reference [22], which is equal to 0.05.

4.1. Imperceptibility

The peak signal-to-noise ratio (PSNR) is a common image quality evaluation index used in the field of image processing [26]. For an image with dimensions of 512 × 512, the PSNR is defined as:

$$\mathrm{PSNR}=10\lg \left[\frac{512\times 512\times \max {\left[\mathit{I}(i,j)\right]}^2}{{\displaystyle \sum _{i=1}^{512}{\displaystyle \sum _{j=1}^{512}{\left[\mathit{I}(i,j)-{\mathit{I}}_{\mathrm{w}}(i,j)\right]}^2}}}\right],$$

(8)

where $\mathit{I}$ and ${\mathit{I}}_{\mathrm{w}}$ are the original carrier image and the watermarked image, respectively.

Generally, a higher PSNR implies that the watermark in the watermarked image has better imperceptibility. To evaluate the quality of an extracted watermark, the similarity between the original watermark ${\mathit{W}}_1$ and the extracted watermark ${\mathit{W}}^{\ast }$ is calculated as the normalized correlation coefficient (NCC). For the experiments reported in this paper, the NCC can be represented as follows:

$$\mathrm{NCC}=\frac{{\displaystyle \sum _{i=1}^{32}{\displaystyle \sum _{j=1}^{32}{\mathit{W}}_1(i,j)\times {\mathit{W}}^{\ast }(i,j)}}}{{\displaystyle \sum _{i=1}^{32}{\displaystyle \sum _{j=1}^{32}{\mathit{W}}_1(i,j)\times {\mathit{W}}_1(i,j)}}}.$$

(9)

Figure 3 shows the carrier images and watermarks without performing any attack. It can be observed that there is no subjective visual difference between the original image and its watermarked counterpart. To compare with other watermarking algorithms,

Table 1. Comparisons among different robust watermarking methods in terms of watermark capacity, peak signal-to-noise ratio (PSNR), and normalized correlation coefficient (NCC).

Items	Liu and Tan [7]	Fazli and Moeini [22]	Proposed
Watermark image	gray	binary	binary
Capacity	32 × 32	32 × 32 × 4	32 × 32 × 2
PSNR (dB)	53.83	101.97	101.97
NCC	1	0.9603	0.9724

lists the watermark capacity, PSNR, and NCC of two robust watermarking methods. It should be noted that for comparison, the watermark in [7] is embedded into the top left corner of carrier image. From Table 1, it can be observed that the proposed scheme and the method in reference [22] have higher PSNR values than the method proposed by Liu and Tan [7]. The NCC value of the proposed scheme is slightly lower than reference [7], but it is higher than the recently proposed method in reference [22]. Though there are not too many advantages for the proposed scheme in watermark imperceptibility, the proposed scheme achieves better robustness than references [7] and [22], which could be confirmed by the experiments in next subsection.

4.2. Robustness

To test the robustness of the proposed algorithm, various common signal processing attacks are applied to the watermarked images, such as salt and pepper noise, Gaussian noise, and JPEG compression. Figure 4 shows the attacked images and their corresponding watermarks extracted from them. The results demonstrate that the extracted watermarks obtained using the presented method show good robustness to various attacks. To objectively evaluate the robustness of the proposed method,

Table 2. NCC values of the extracted watermarks under different attacks.

Attack	Liu and Tan [7]	Fazli and Moeini [22]	Proposed
Embedding intensity	0.05	0.05	0.05
Salt and pepper noise (0.005)	09628	0.9993	0.9988
Salt and pepper noise (0.01)	0.9158	1	0.9985
Gaussian noise (0, 0.005)	0.8606	1	0.9986
Gaussian noise (0, 0.01)	0.8235	1	0.9993
Scaling (2, 0.5)	0.9838	0.9621	0.9638
Scaling (0.5, 2)	0.9123	0.9603	0.9672
Median filtering (3 × 3)	0.9321	0.9638	0.9793
Median filtering (5 × 5)	0.8510	0.9621	0.9724
Average filtering (3 × 3)	0.8987	0.9793	0.9741
Average filtering (5 × 5)	0.8153	0.9586	0.9690
Rotation (5°)	0.8223	1	0.9897
Rotation (15°)	--	0.9948	1
Contrast enhancement (1.2)	0.9889	1	1
Contrast enhancement (1.5)	0.9844	1	1
Brightness adjustment (+50)	1	0.9672	0.9741
Brightness adjustment (+100)	0.7598	0.9603	0.9707

lists the NCC values of the extracted watermarks under different attacks. In addition, we compare the proposed method with a conventional SVD-based watermarking method [7] and a hybrid watermarking method presented in [22]. Considering the randomness of the noise, the NCC values of the extracted watermarks after noise attacks are the average values from multiple experiments. From Table 2, we can see that the NCC values obtained using the proposed method are approximately equal to or even greater than those achieved by other methods under the same attacks. Furthermore, the NCC results are extremely stable under different attack intensities. These results suggest that the proposed method is highly robust compared with the scheme proposed in reference [22].

JPEG compression is widely adopted in image transmission and storage. To test the properties of the proposed algorithm under JPEG compression, the watermarked images are compressed by JPEG compression with different QFs. Figure 5 presents the curves of the NCC values under JPEG compression with different QFs. The experimental results show that the proposed scheme has higher NCC values than the other two methods. Besides, it can also be noticed from the figure that the NCC values obtained by the proposed scheme and reference [22] are more stable than those of Liu and Tan’s method [7]. The reason is that the reference [7] is a pure SVD-based watermarking scheme, while the proposed scheme and reference [22] are based on hybrid transforms. Compared to the former, the hybrid transform based watermarking schemes have better robustness for JPEG compression with different QFs. When the watermarked images in [7] are highly compressed by JPEG compression (with low QFs), the watermark information will be destroyed more easily than the other two methods. In conclusion, the data in Figure 5 prove that our proposed algorithm exhibits better robustness against JPEG compression than the other methods.

However, in practical applications, images are always vulnerable to more than one kind of attack. Moreover, digital images need to be preprocessed to reduce the bandwidth and memory required for the transmission and storage. To test the robustness of the proposed method under hybrid attacks, Figure 6 shows watermarked images subjected to hybrid signal processing attacks and their corresponding extracted watermarks.

Table 3. NCC values of the watermarks extracted after hybrid attacks.

Attack	Liu and Tan [7]	Fazli and Moeini [22]	Proposed
Gaussian noise (0, 0.01) + median filtering (3 × 3)	0.9401	0.9995	0.9971
Gaussian noise (0, 0.01) + average filtering (3 × 3)	0.9716	1	0.9964
Salt and pepper noise (0.01) + median filtering (3 × 3)	0.9332	0.9631	0.9793
Salt and pepper noise (0.01) + average filtering (3 × 3)	0.9647	0.9993	0.9867
Scaling (2, 0.5) + JPEG compression (QF = 50)	0.9462	0.9621	0.9707
Scaling (0.5, 2) + JPEG compression (QF = 50)	0.8942	0.9621	0.9724
JPEG compression (QF=50) + cropping (25%)	0.9485	0.8086	0.8569
Median filtering (3 × 3) + JPEG compression (QF = 50)	0.9455	0.9569	0.9707
Average filtering (3 × 3) + JPEG compression (QF = 50)	0.8885	0.9707	0.9759

gives the NCC values of the watermarks extracted under different conditions. It is observed that our proposed scheme achieves promising results compared with those of Fazli and Moeini’s method [22]. The watermarks could be extracted without much degradation. Based on the above comparisons and analysis, we conclude that the proposed watermarking algorithm shows superior robustness in resisting various signal processing attacks.

5. Conclusions

In this article, we have presented a highly robust watermarking algorithm, in which the APDCBT is introduced into the hybrid watermarking technique by combining with DWT and SVD. To make a good use of the low-frequency aggregation property of APDCBT and reduce the influence of watermark embedding, the DC coefficients of each sub-block in HL and LH sub-bands are used as the embedding locations. Experimental comparisons suggest that the proposed scheme has little perceptible effect on the original image, and it exhibits better robustness against typical signal processing attacks than other algorithms. However, the proposed scheme is subjected to the false-positive problem, which remains unsolved in this paper. In the future work, we will address this issue and apply the proposed method to color images.