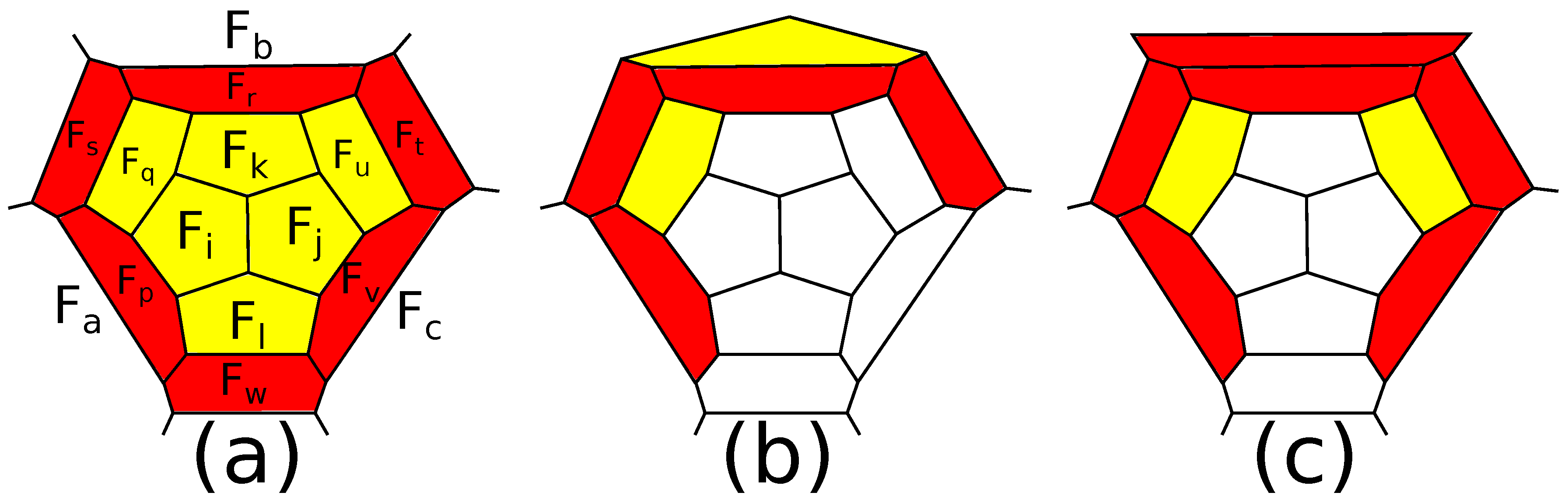1. Introduction
By an
n-polytope, we mean a combinatorial convex
n-dimensional polytope, that is a class of combinatorial equivalence of convex
n-dimensional polytopes. For details on the theory of polytopes, we recommend the books [
1,
2]. A 3-polytope
P is called a Pogorelov polytope (
-polytope; see [
3,
4]), if it can be realized in the Lobachevsky (hyperbolic) space
as a bounded polytope with right dihedral angles (see [
5]). An
n-polytope is called simple if any of its vertex is contained in exactly
n facets. A flag polytope is a simple polytope such that any of its set of pairwise intersecting facets has a non-empty intersection. A
k-belt is a cyclic sequence of facets with empty common intersection such that two facets are adjacent if and only if they follow each other (in [
6], it is called a
k-gonal prismatic element, in [
7] a ring, and in [
8,
9] the corresponding object in the dual polytope is called a separating
k-circuit). It can be shown that a 3-polytope
P is flag if and only if it is different from the simplex
and has no 3-belts. Results by A.V. Pogorelov [
10] and E.M. Andreev [
6] imply that a 3-polytope
P is a
-polytope if and only if it is flag and has no 4-belts. Moreover, a right-angled realization in the Lobachevsky space is unique up to isometries.
Recently,
-polytopes attracted the attention of specialists in toric topology [
11] and hyperbolic geometry. To each simple 3-polytope
P with
m faces, the toric topology assigns an
-dimensional manifold
with an action of the compact torus
. If was proven in [
12] (see also [
13]) that if the cohomology rings of
and
are isomorphic as graded rings and
P is a
-polytope, then
P and
Q are equal as combinatorial polytopes. For given mappings
and
from the set of faces of
P to
and
, respectively (where by
, we mean
), such that the images of any three faces intersecting in a vertex form a basis, the toric topology assigns a 6-dimensional manifold
with an action of
and a 3-dimensional manifold
with an action of
. For a
-polytope
P, the mapping
defines a subgroup in the right-angled Coxeter group of the polytope
P such that the factor-space of the action of this subgroup on the Lobachevsky space can be identified with
. Such hyperbolic manifolds were introduced in [
14]. An example of mappings
and
can be constructed from any regular coloring of faces of a polytope in four colors. In [
3], it was proven that an isomorphism of graded cohomology rings of
and
(respectively of graded
-cohomology rings of
and
), where
P is a
-polytope, implies that
P and
Q are equal as combinatorial polytopes, and the mappings are equivalent in a natural sense.
The notions of flag and
-polytopes are closely related to the notion of cyclic
k-edge connectivity in graph theory. A graph
G is called cyclically
k-edge connected (
-connected) if
G cannot be separated into two components, each containing a cycle, by deletion of fewer than
k edges (see [
2,
15]). Following [
8,
9,
16,
17], we additionally assume that for
, the complete graph on four vertices is not
-connected. Then, a simple 3-polytope
P is flag if and only if its graph is
-connected. A simple 3-polytope
P is a
-polytope if and only if its graph is
-connected. The notion of a
-connectivity arose during attempts to prove the four color problem (now the four color theorem due to K. Appel and W. Haken [
18,
19,
20]) for planar graphs, which states that any planar graph can be colored in four colors in such a way that any two faces with common edge have different colors. In particular, results by G.D. Birkhoff [
7] imply that the four color problem can be reduced to the graphs of
-polytopes with any 5-belt surrounding a face. We will call such polytopes
-polytopes. Graphs of these polytopes are strongly cyclically 5-edge connected (abbreviated
-connected), that is they are
-connected, and any separation of the graph by cutting five edges leaves one component that is a simple circuit of five edges [
9].
An example of
-polytopes is given by fullerenes, simple 3-polytopes with only 5- and 6-gonal faces. It follows from the results by T. Dǒslić that fullerenes are flag [
21] (see also [
22,
23]) and have no 4-belts [
24] (see also [
4,
25,
26]). They are mathematical models for spherical-shaped carbon molecules discovered in 1985 by R.F. Curl [
27], H.W. Kroto [
28] and R.E. Smalley [
29] (Nobel Prize 1996 in Chemistry). For surveys on the mathematical theory of fullerenes, see [
30,
31,
32]. For mathematical, physical and chemical aspects of fullerenes, see [
33,
34,
35]. We also recommend a remarkable paper by W.P. Thurson [
36], who gives a parametrization for the set of all fullerenes. In particular, the results of [
36] imply that the number of fullerenes with given number
m faces grows like
. Another example of
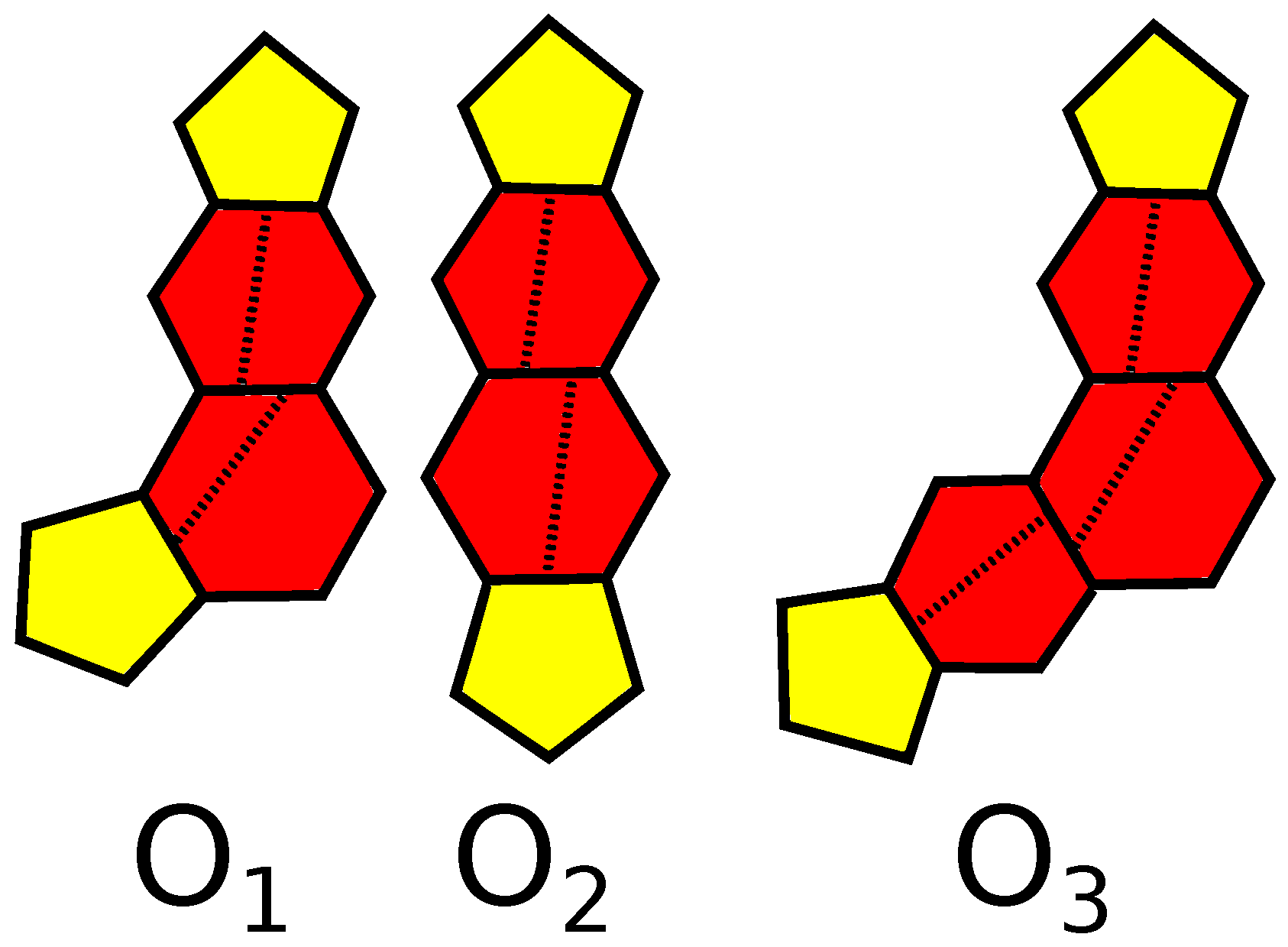
-polytopes is given by
k-barrels,
(or Löbel polytopes [
5,
14,
37]; see
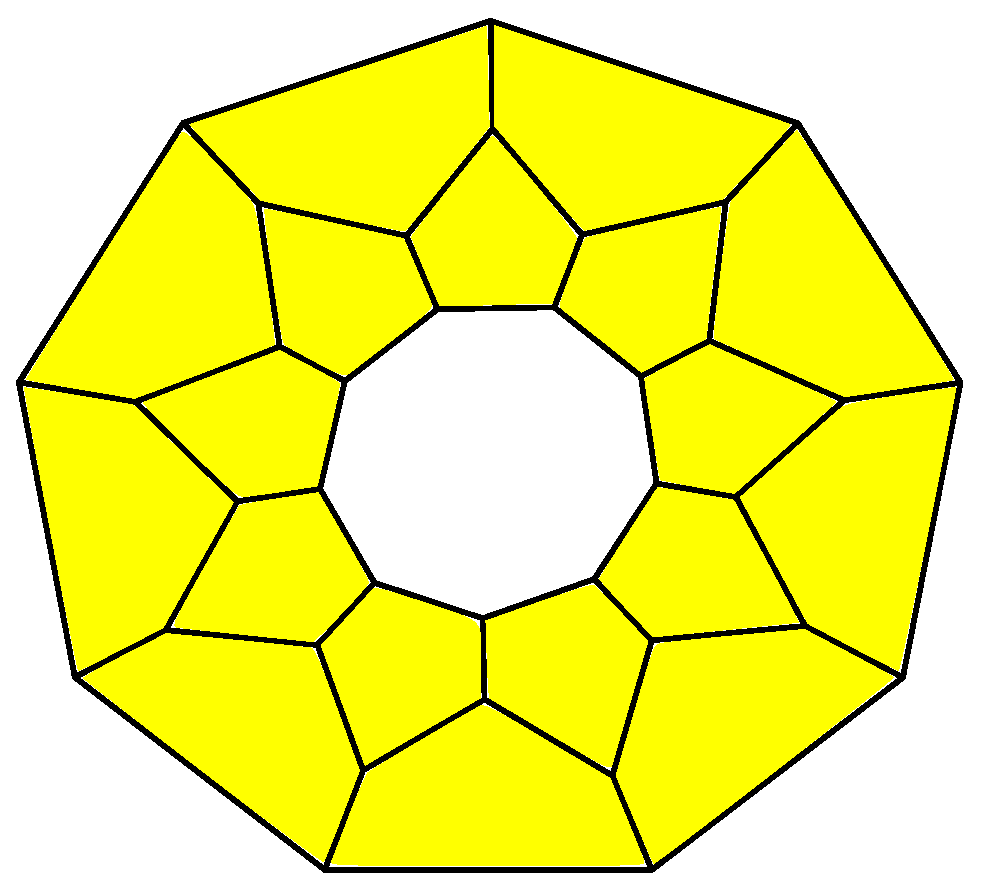
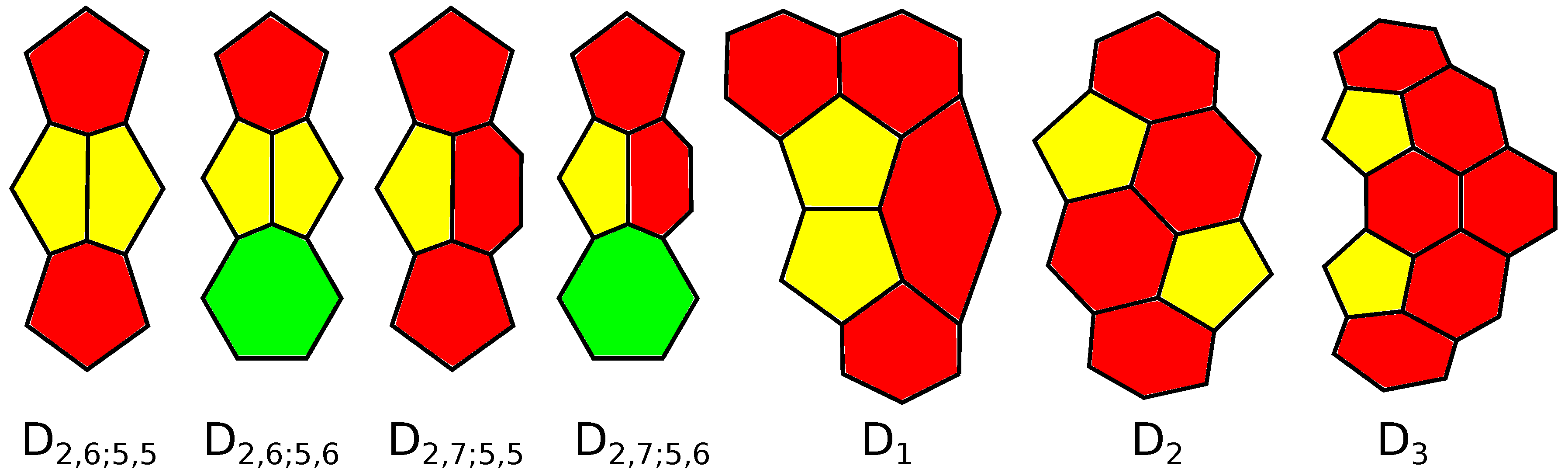
Figure 1 for
), simple 3-polytopes with the boundary glued from two equal parts consisting of a
k-gon surrounded by 5-gons. In [
17], the graphs of these polytopes are called biladders on
vertices.
A nice characterization of flag and
-polytopes is given by the following result. For flag and
-polytopes it was noted in [
3,
4], and for
-polytopes – in [
7].
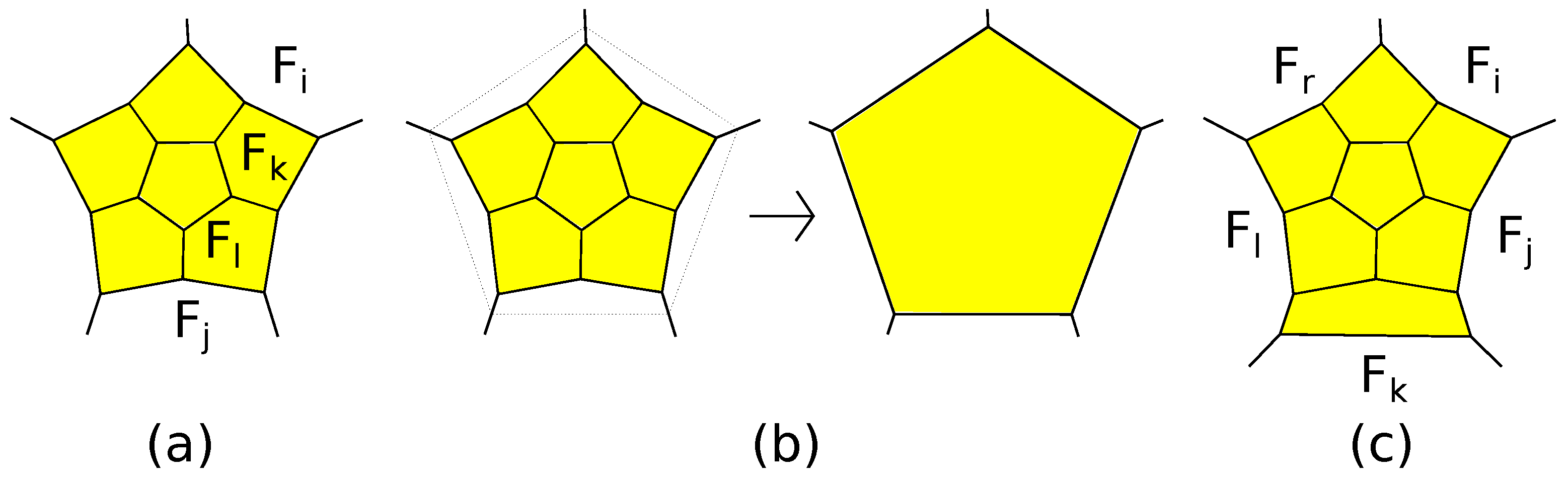
Proposition 1. A simple 3-polytope is flag if and only if any its face is surrounded by a belt.
A simple 3-polytope is a -polytope if and only if any pair of its adjacent faces is surrounded by a belt.
A simple 3-polytope is a -polytope if and only if any its face is surrounded by two belts.
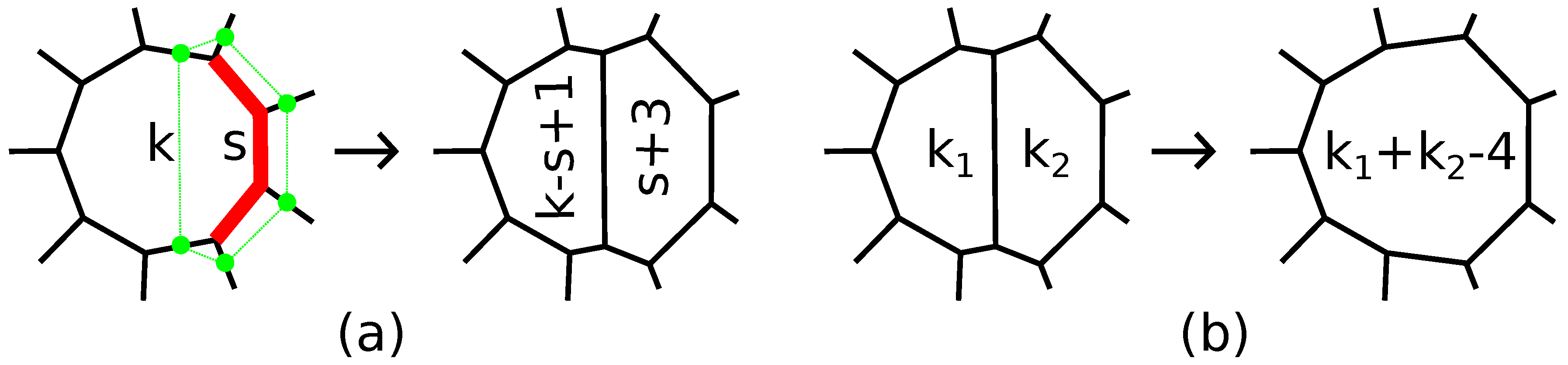
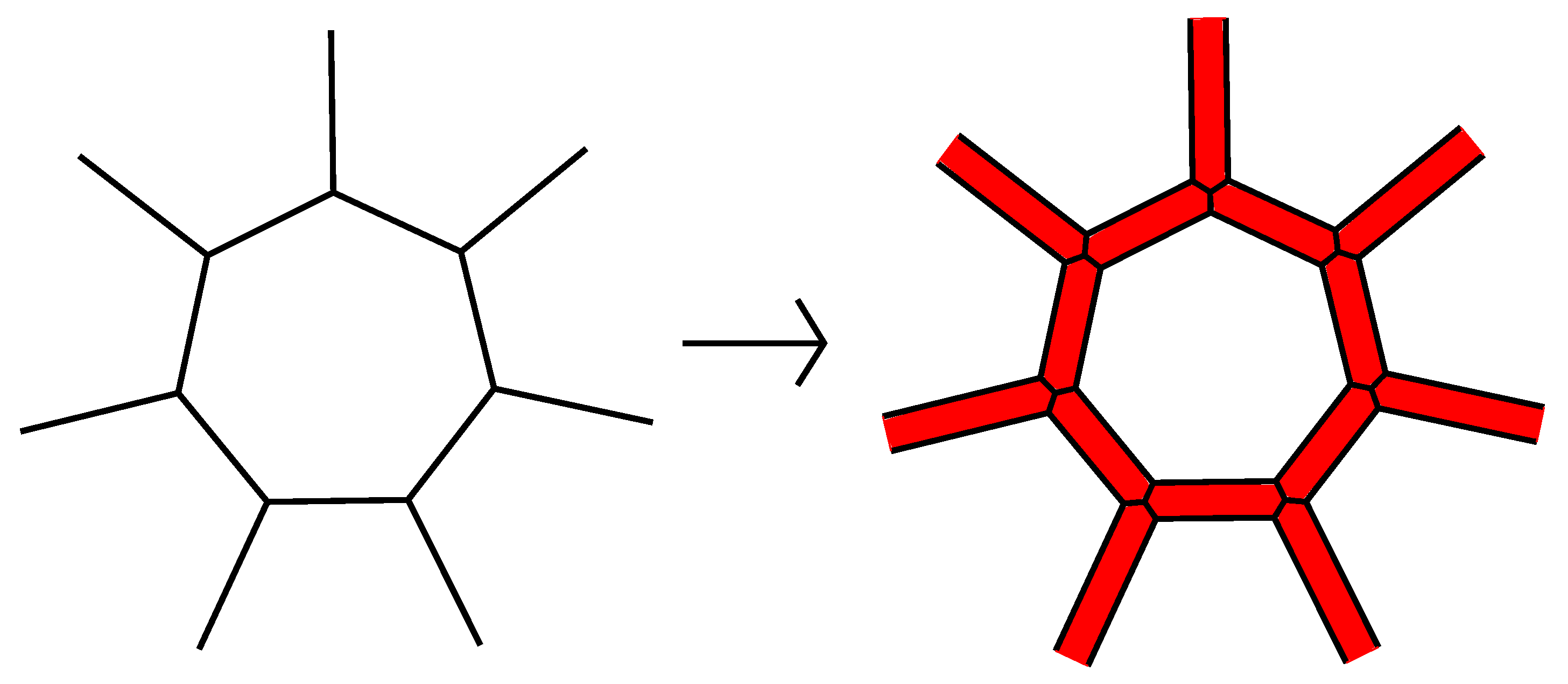
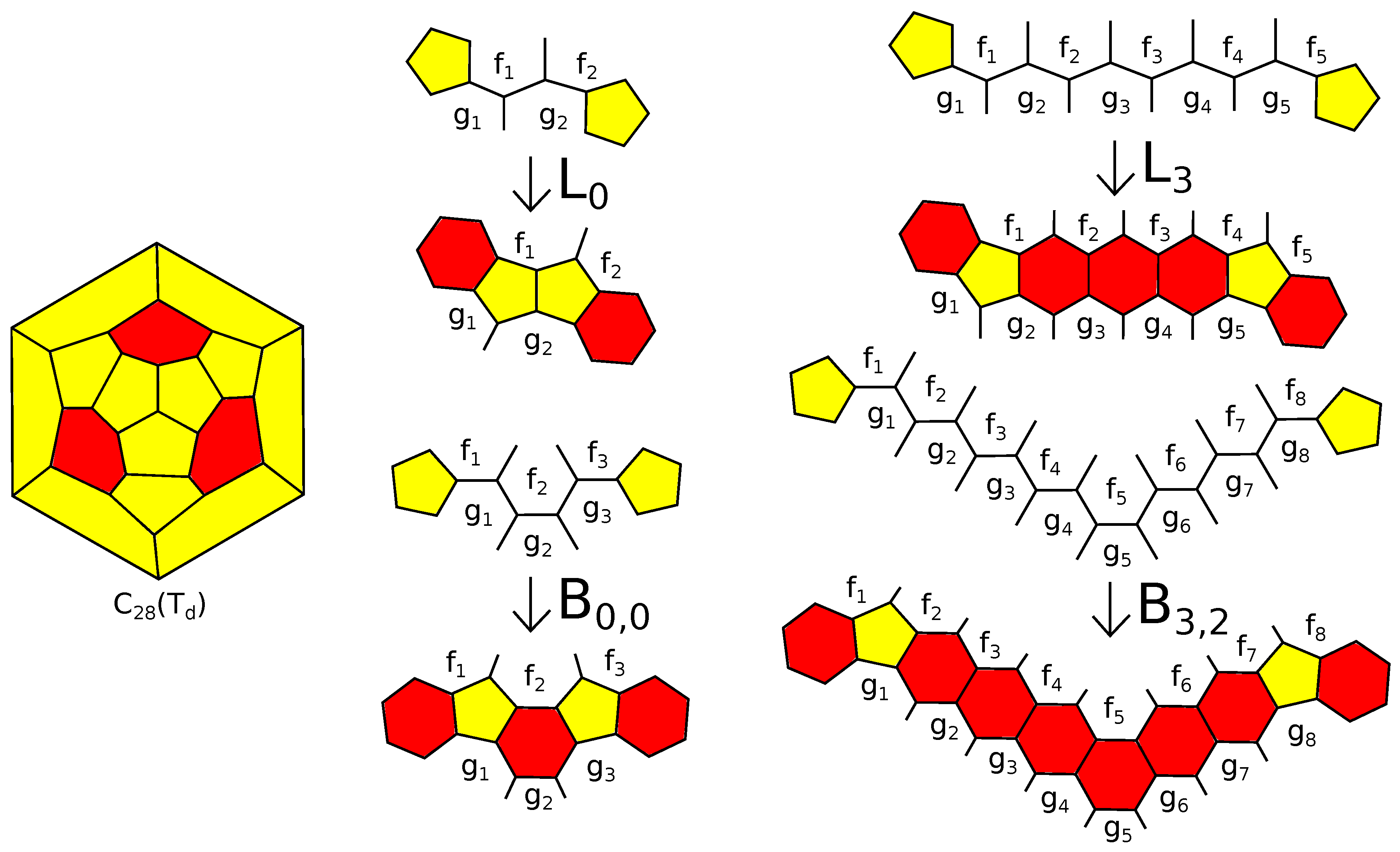
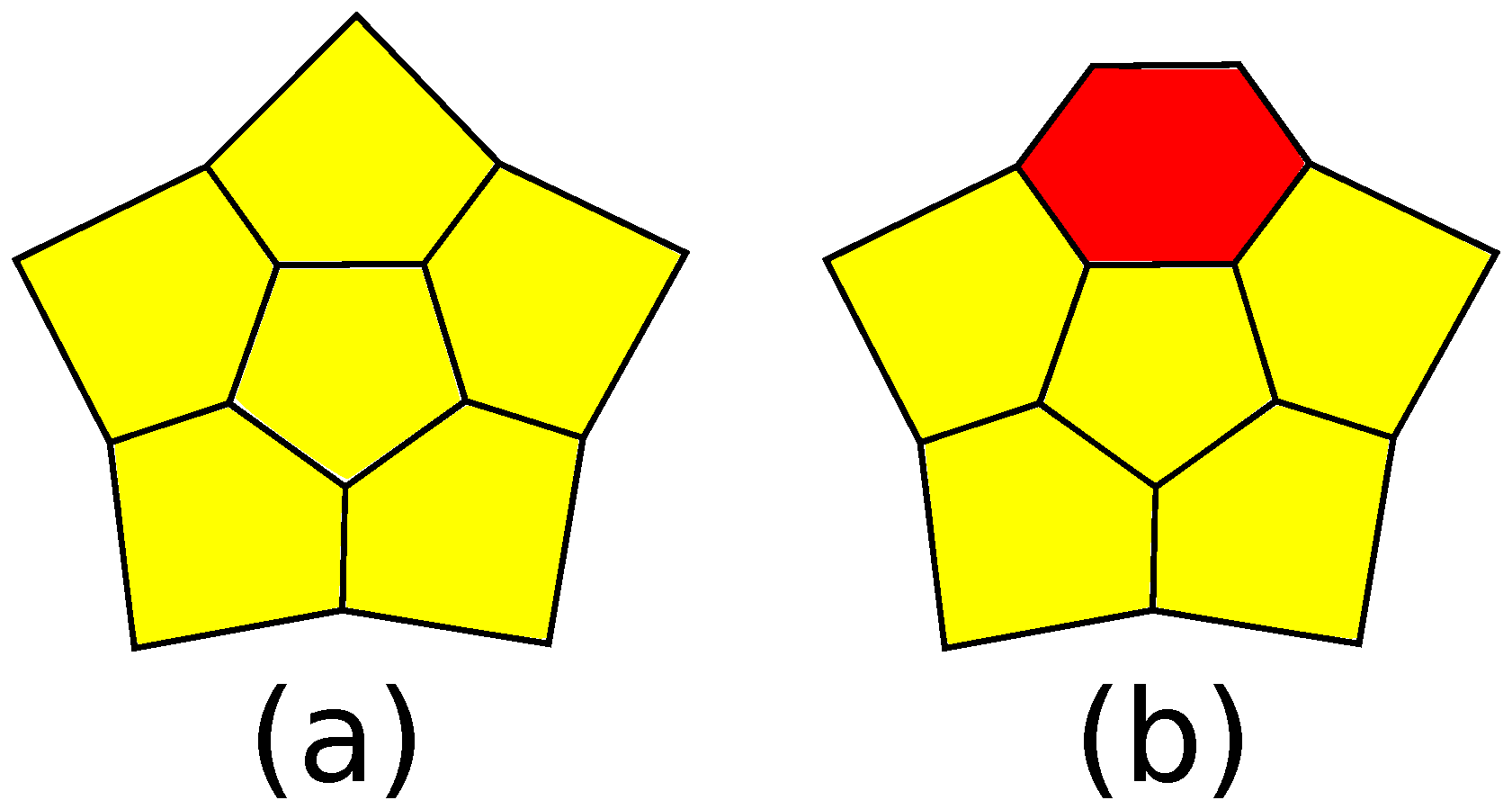
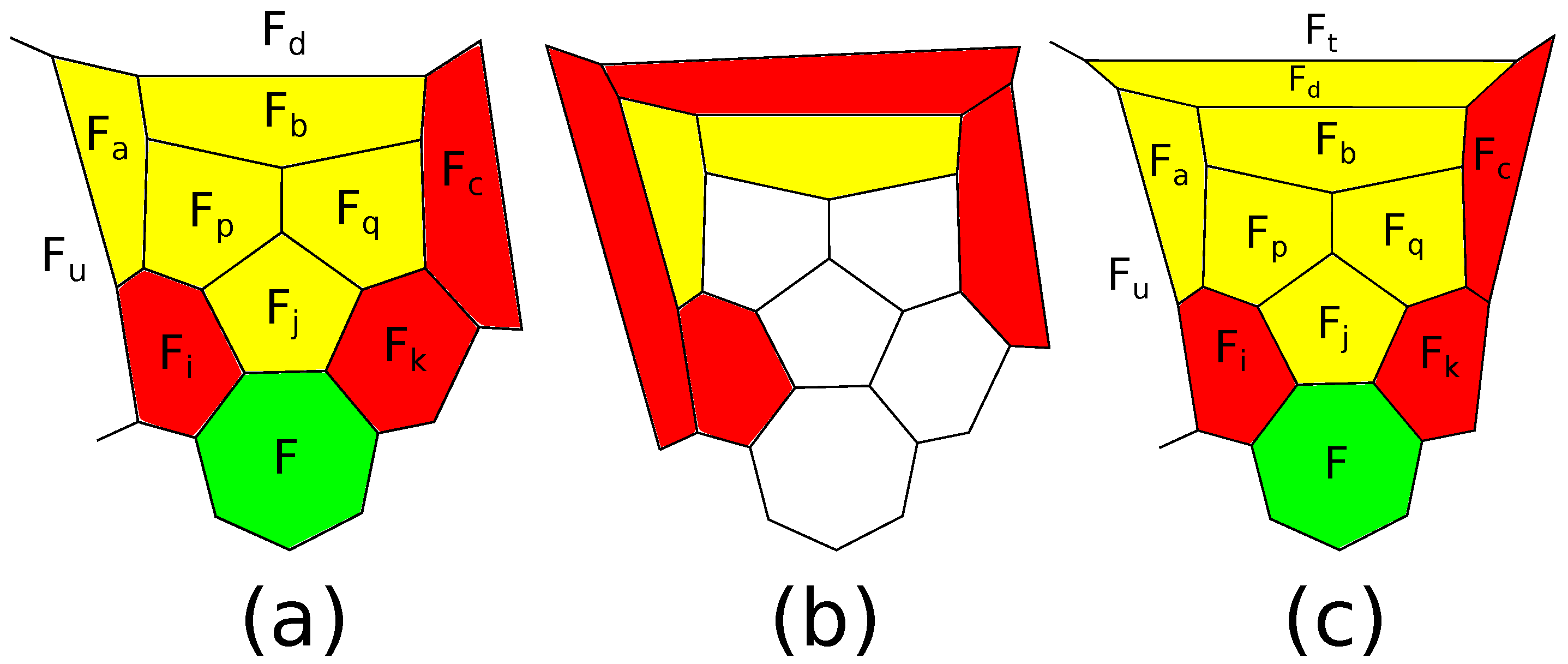
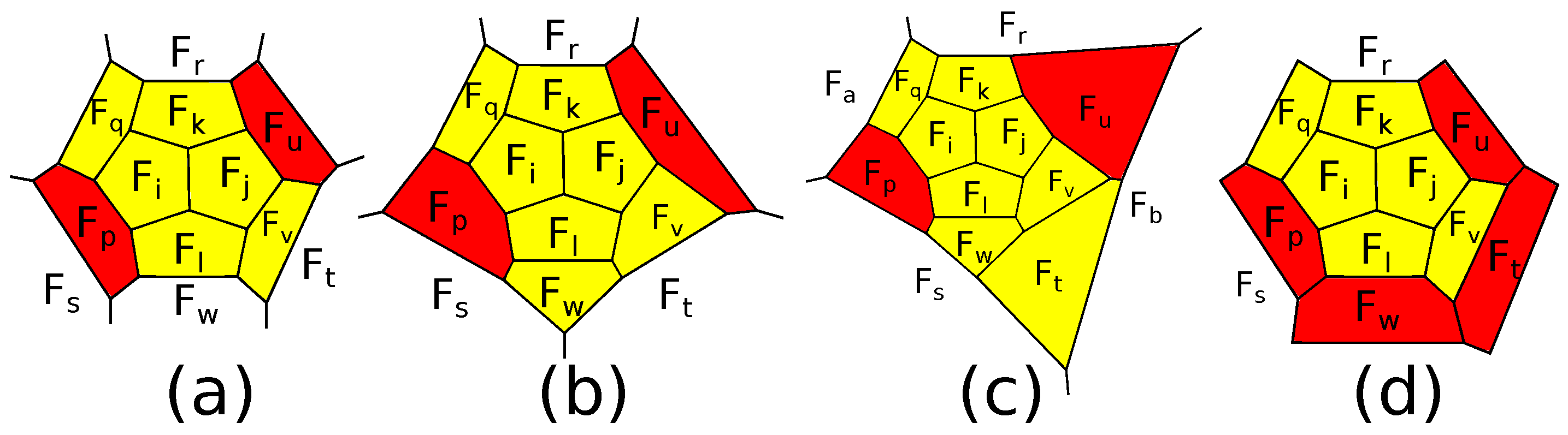
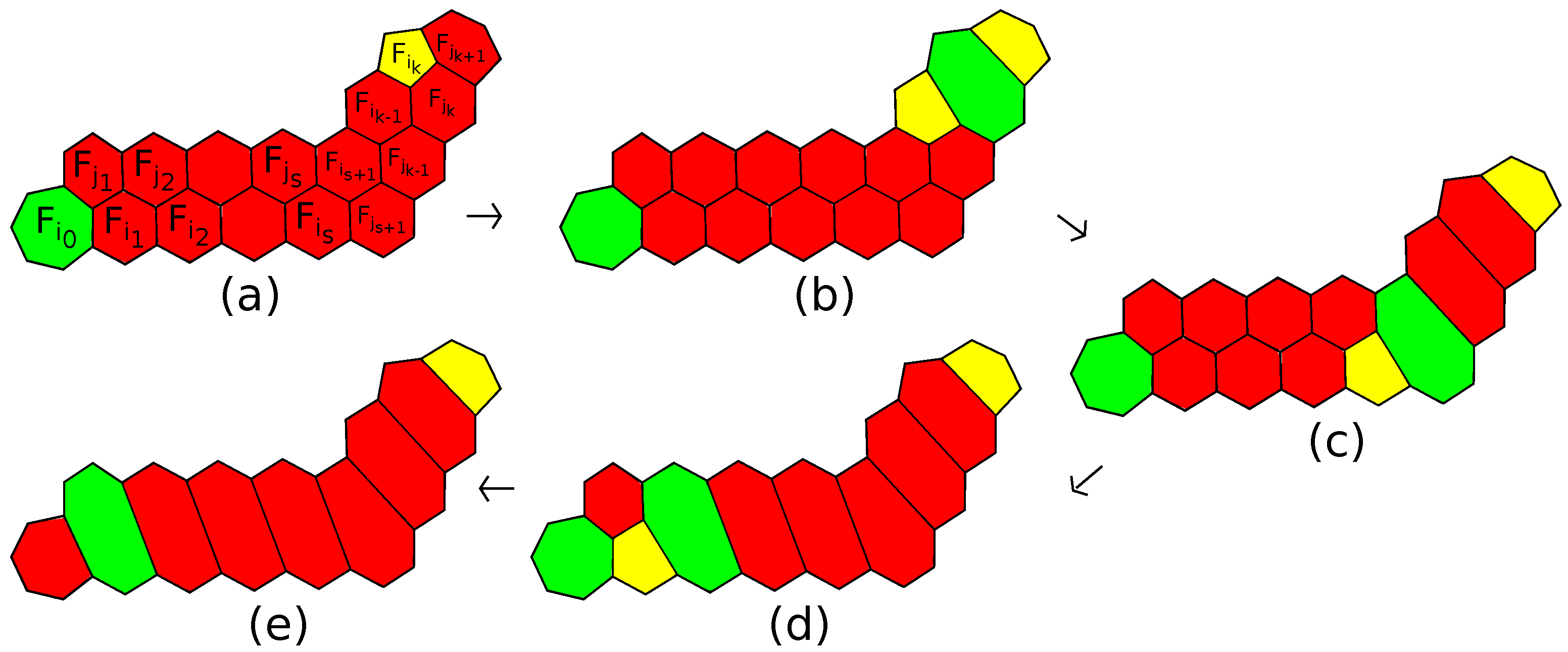
There are two operations transforming
-polytopes into
-polytopes. The first of them is a cutting off of
s subsequent edges of a
k-gonal face,
, of a simple 3-polytope by a single plane and is called an
-truncation; see
Figure 2a. If the inverse operation is defined, we call it a straightening along an edge; see
Figure 2b. The operation of an
-truncation also appears in the literature as an addition of an edge [
8,
9], a simple face splitting [
16], an edge surgery [
38] or a handle expansion [
17]. It is proven in [
9] that also an
-truncation of a
-polytope is a
-polytope, provided
.
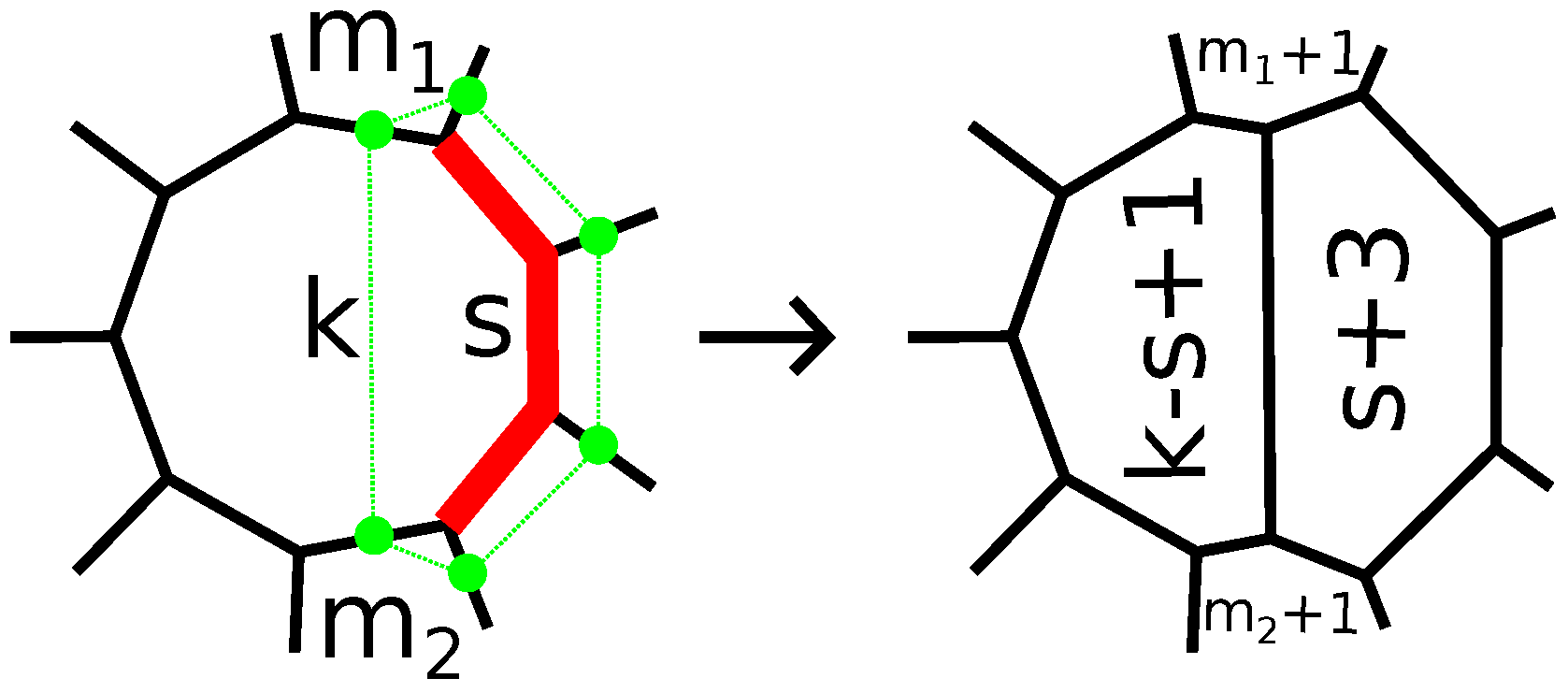
If the
k-gon is adjacent to an
- and an
-gon by edges next to cut edges, then we call the operation an
-truncation (see
Figure 3). We do not take into account the orientation of the surface of the polytope; hence, we do not distinguish between
- and
-truncations. As we will see later, the parameters
s,
k,
and
are important to prove finer results.
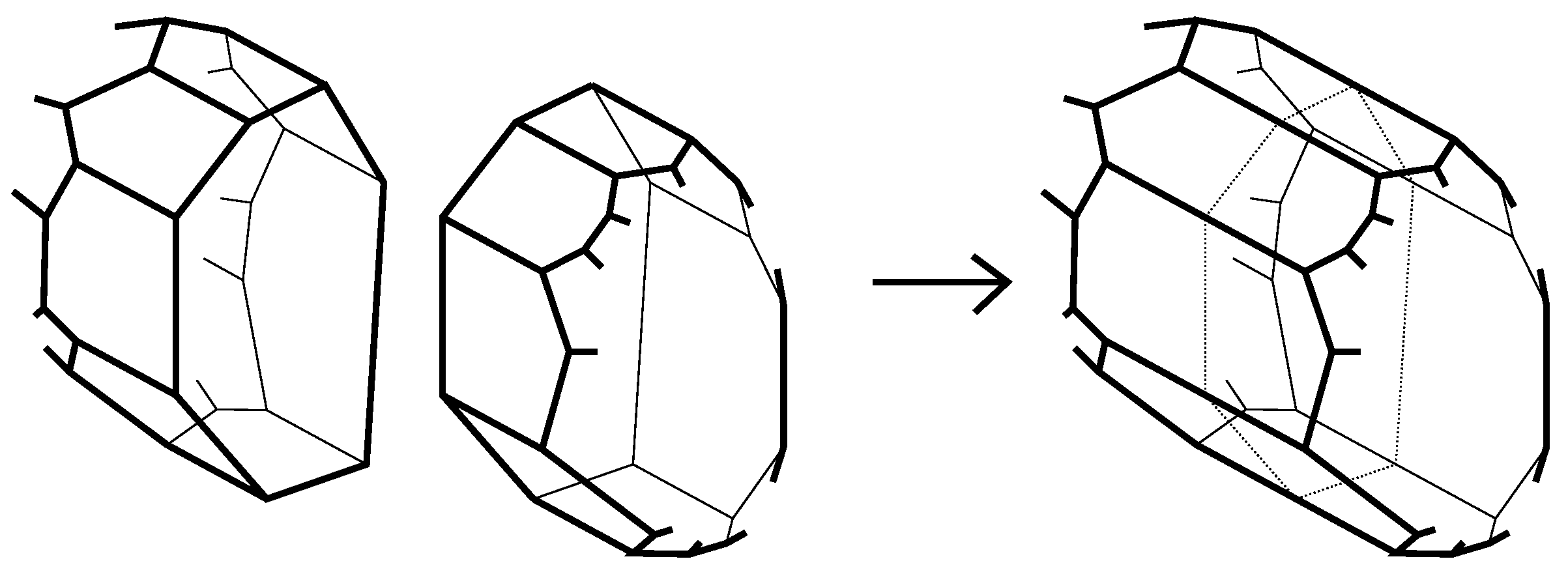
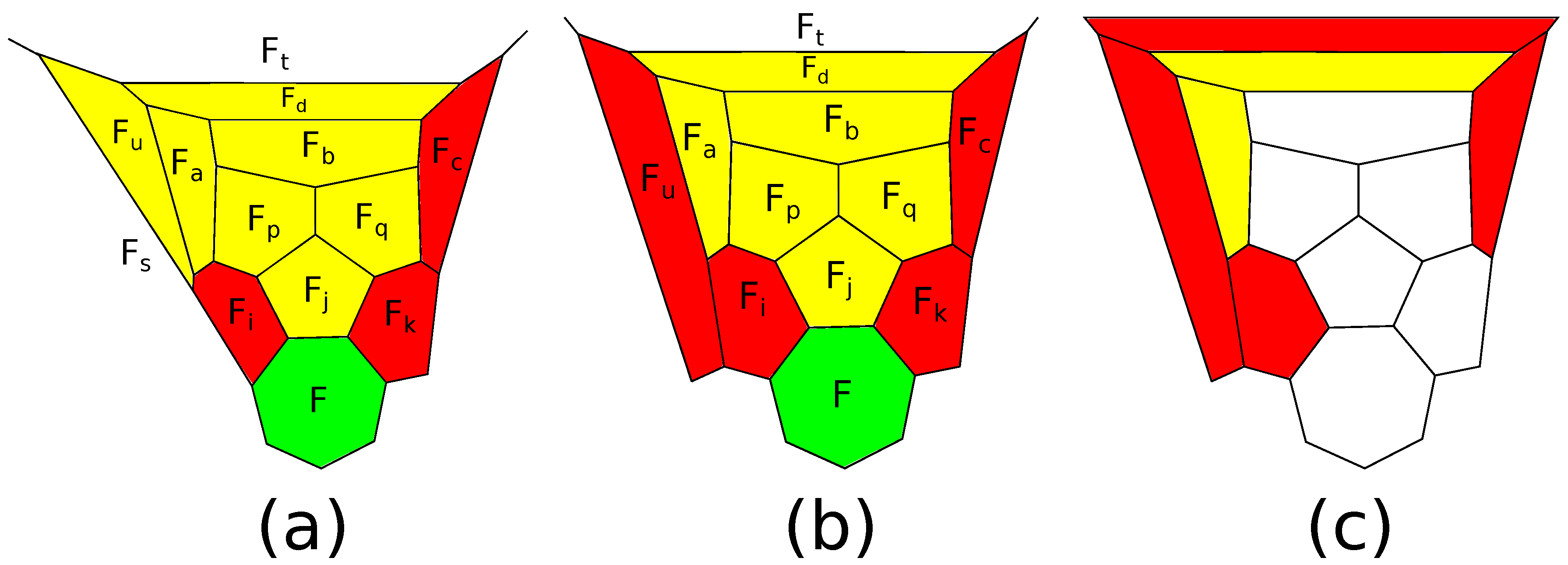
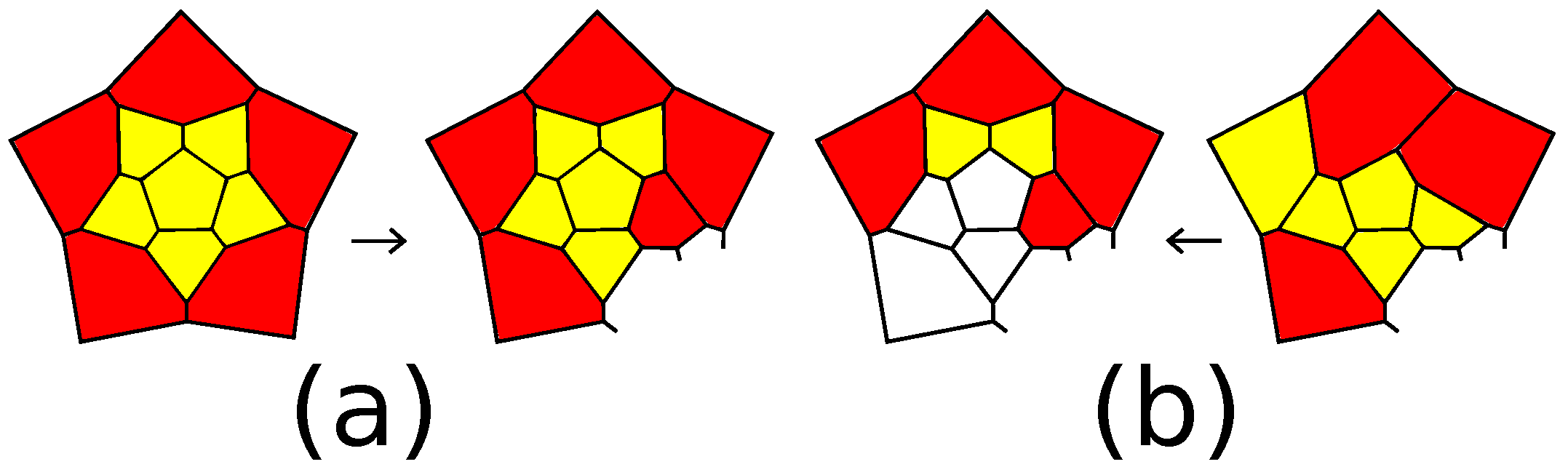
The second operation we need is a connected sum of 3-polytopes along
k-gons surrounded by
k-belts (see
Figure 4). It is the combinatorial analog of the gluing of two polytopes along
k-gonal faces orthogonal to adjacent faces. The most important case will be the connected sum with the 5-barrel. This operation appears in [
8,
9] as a replacing a pentagon, in [
16] as a face splitting of Type 3 and in [
17] as a circuit expansion.
The existence of certain combinatorial types of 3-polytopes we usually verify using the Steinitz theorem (see [
1,
2]). We formulate it in the form (see, for example, [
13,
30]) convenient for our arguments.
Theorem 1 (Steinitz)
. A simple connected plane graph G is the graph of some convex three-dimensional polytope if and only if any of its faces is bounded by a simple edge cycle and boundary cycles of any two faces either do not intersect, or intersect by a vertex, or intersect by an edge.
Moreover, there is Whitney’s theorem (see [
1]), which states that a plane realization of the graph of a 3-polytope is combinatorially unique. Using the Steinitz theorem, the following fact may be proven ([
30], see also [
4]).
Theorem 2. Let P be a connected 3-valent plane graph with each face bounded by a cycle with at least five and at most seven edges, where the number of boundary cycles with seven edges is at most one. Then, this graph is a graph of a simple 3-polytope.
In [
30], simple 3-polytopes with 5-, 6- and one
n-gon are called
n-disk-fullerenes. Denote by
the family of fullerenes, by
the family of 7-disk-fullerenes, by
its subfamily consisting of polytopes with the 7-gon adjacent to a 5-gon, by
the family
and by
the family
. For a family
, we denote by
the subfamily consisting of all
-polytopes in
A. In [
4,
26], the following generalization of Theorem 2 was proven.
Theorem 3 ([
4,
26])
. Let . Then P is a -polytope.
This result leads to a natural question. Let
be the number of
k-gonal faces of a simple 3-polytope
P. The collection
is called a
p-vector. The Euler formula in the case of simple 3-polytopes implies the following formula (see [
2]), which can be proven by a direct calculation:
V. Eberhard proved ([
39], see also [
2]) that for any finite collection of non-negative integers
satisfying the Equation (
1), there exists a simple 3-polytope
P with
for all
. A flag polytope has no 3-gons. On the basis of Eberhard’s result, it was proven in [
23] that for any finite collection of non-negative integers
satisfying Equation (
1), there exists a flag polytope
P with
,
. The proof used the construction of a simultaneous cutting off of all the edges of a simple 3-polytope by different planes; see
Figure 5. It corresponds to the Goldberg–Coxeter or Caspar–Klug construction (see [
40]) with parameters
. This operation does not change the numbers
,
and increases the number
by the number of edges.
It turns out that for a polytope with no 3-gons, the cut polytope is flag. A
-polytope has no 3- and 4-gons, since any face of a flag polytope is surrounded by a belt. In [
3,
4], it is was proven that for any finite collection of non-negative integers
, there exists a
-polytope with
,
. Moreover,
. The proof is similar to the case of flag polytopes. Namely, for a polytope without 3- and 4-gons, the cut polytope is a
-polytope.
Question: Which restrictions on the numbers imply that a polytope without 3- and 4-gons is a -polytope?
We have seen that the example is given by the restriction , , .
Example 1. In Figure 6, we present the graph of a simple 3-polytope (this can be easily checked using the Steinitz theorem) with 5-, 6- and two 7-gonal faces. This polytope has a 3-belt containing both 7-gons; hence, it is not a -polytope.
The first main result of our paper is the answer to this question.
Theorem 4 (The first main result)
. For any finite collection of non-negative integers with or and , there exists a non-flag simple polytope P with , .
Remark 1. We will also give a slight modification of this construction producing a -polytope with prescribed numbers , , not using Eberhard’s result.
Hence, is a natural subclass in the class of -polytopes.
It can be shown that an
-truncation transforms a
-polytope into a
-polytope if and only if
, and a connected sum of any two
-polytopes along faces is a
-polytope (see [
4,
8,
16,
38]).
It is easy to see that
k-barrels,
, are irreducible polytopes with respect to
-truncations and connected sums along faces in the class of
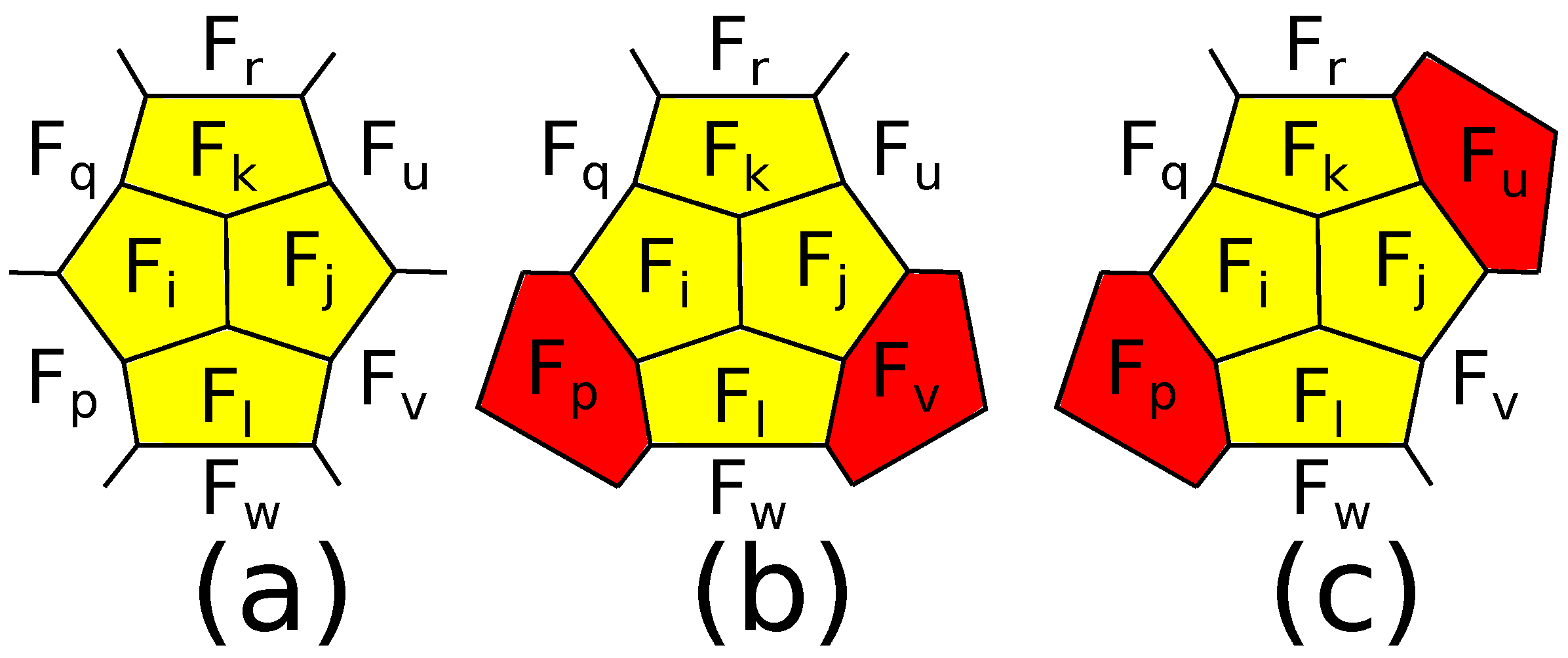
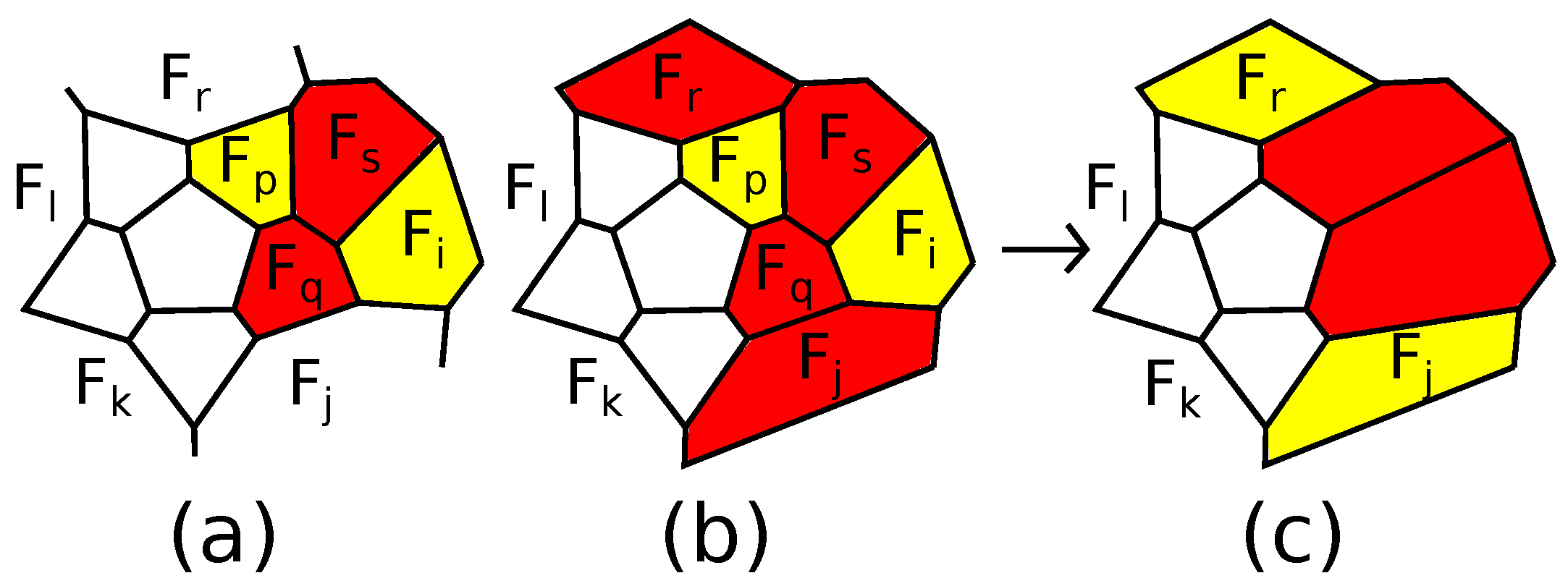
-polytopes. There is an additional operation transforming
-polytopes into
-polytopes ([
8,
16]; see
Figure 7). It splits a pair of adjacent 5-gons into four 5-gons and is called in [
8] adding a pair of edges. In [
8,
16], it was independently proven that any
-polytope can be obtained from the 5-barrel by a sequence of
-truncations,
, additions of pairs of edges and connected sums with the 5-barrel.
It is easy to see that the
-barrel is obtained from the
n-barrel by adding a pair of edges. It turns out that this is the only essential case for this operation. Namely, in [
9], it was proven that any
-polytope can be obtained from a
q-barrel,
, by a sequence of
-truncations,
, and it was remarked that a similar reasoning proves that any
-polytope can be obtained from a
q-barrel,
, by a sequence of
-truncations,
, and connected sums with the 5-barrel. In [
4], the latter fact was rediscovered in a stronger form. Namely, for
-polytopes, it is sufficient to use only
-truncations,
, and connected sums with the 5-barrel, and for polytopes different from
q-barrels, the initial set can be reduced only to the 5- and the 6-barrel. A careful study of arguments in [
9] shows that they also allow one to leave only
-truncations,
, for
-polytopes and
-truncations,
, and connected sums with the 5-barrel for
-polytopes. Combining this reasoning with arguments in [
4], it is possible to leave only the 5- and the 6-barrel in the initial set.
Theorem 5 ([
4,
9])
. A simple 3-polytope P is a -polytope if and only if either P is a q-barrel, , or it can be constructed from the 5- or the 6-barrel by a sequence of -truncations (Figure 8a), , and connected sums with the 5-barrel (Figure 8b).
A simple 3-polytope P is a -polytope if and only if either P is a q-barrel, , or it can be constructed from the 6-barrel by a sequence of -truncations, .
In [
38], this result was rediscovered in a slighter form for
-polytopes in the context of hyperbolic geometry. Namely, T. Inoue proved that any
-polytope can be obtained from
q-barrels,
, by
-truncations,
, and connected sums along
p-gons,
(more precisely, the reasoning in [
38] leaves only the case
). He also proved that any
-truncation,
, increases the hyperbolic volume of the right-angled realization, and the volume of the right-angle realization of a connected sum of polytopes along faces is greater than or equal to the sum of the volumes of their realizations. He concluded that the 5-barrel has the smallest, while the 6-barrel has the second value of the hyperbolic volume. In [
41], using this method, the first 825
-polytopes according to hyperbolic volumes were found (and the first 100 of them are explicitly drawn in this paper).
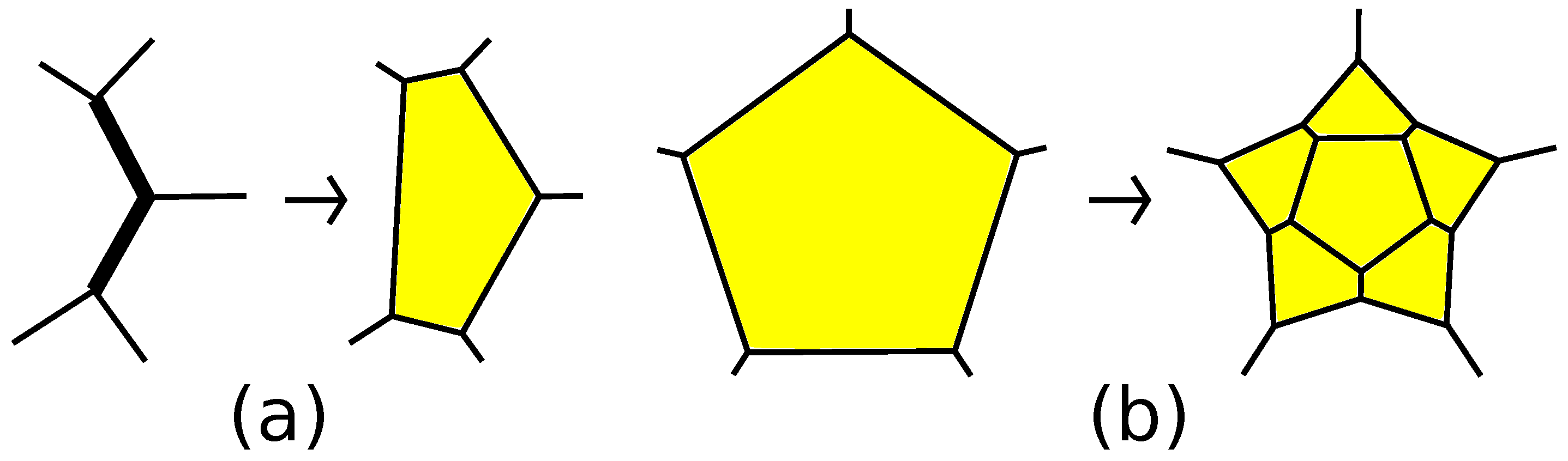
Theorem 5 is related to the classical results in polytope theory. It was proven by V. Eberhard [
39] and by M. Bruckner [
42] (see also [
2,
43]) that a 3-polytope is simple if and only if it can be constructed from the 3-simplex by a sequence of operations each being a cutting off a vertex, an edge or a pair of two adjacent edges by a single plane. This result was used by a famous crystallographer, E.S. Fedorov [
44]. From the result by A. Kotzig [
45] (later proven also by G.B. Faulkner and D.H. Younger [
46] and V. Volodin [
47]), it follows that a simple 3-polytope is flag if and only if it can be constructed from the 3-cube by a sequence of
-truncations,
. In [
23] this result was improved. Namely, a simple 3-polytope
P is flag if and only if
P can be constructed from the 3-cube by a sequence of operations of cutting off an edge and a
-truncation,
. For fullerenes, there are analogs of this result (see [
4,
13,
26,
48,
49]). The starting point can be taken to be the 5- or the 6-barrel, but the difficulty is that the only
-truncation transforming fullerenes to fullerenes is a
-truncation, also called an Endo–Kroto operation [
50]. This is a growth operation, that is it transforms a simple 3-polytope into a simple 3-polytope substituting a new patch (disk partitioned into polygons bounded by a simple edge-cycle on the surface of a simple polytope) with more faces and the same boundary for a patch of a polytope. It was proven in [
51] that there is no finite sets of growth operations transforming fullerenes to fullerenes sufficient to construct any fullerene from a finite set of initial fullerenes (seeds). In [
49], an infinite family of operations sufficient to construct any fullerene except for
from the 5-barrel was found (here,
means tetrahedral symmetry). This family consists of operations
,
,
,
(see
Figure 9 for
,
,
and
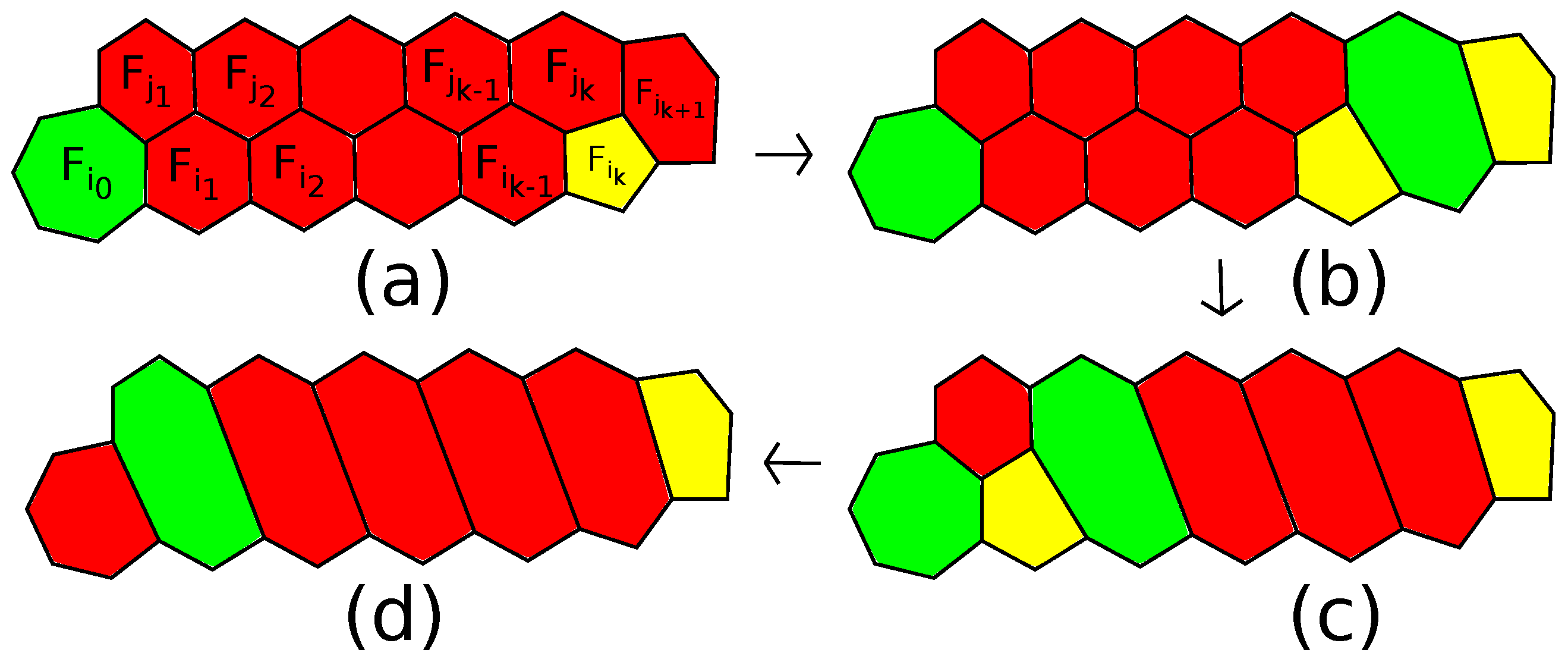
) and a connected sum with the 5-barrel along a 5-gon surrounded by 5-gons.
The faces are completely included in the figure, and all the faces
and
should be pairwise distinct. Each of the faces
and
may be either a 5- or a 6-gon. Using the fact that in the fullerenes without adjacent pentagons (
-fullerenes), any 5- or 6-belt surrounds a face (it follows from [
52]; see also [
4]), it can be shown that it is sufficient to consider only transformations
such that the two 5-gons and the faces
in the initial fullerene form a patch, and only transformations
such that the two 5-gons and the faces
in the initial fullerene form a patch. This gives an infinite family of growth operations sufficient to construct any fullerene from the 5-barrel and the fullerene
.
In [
4,
13,
26,
48], finite sets of growth operations sufficient to build any fullerene from a finite set of seeds was found on account of allowing, at intermediate steps, simple 3-polytopes with 5-, 6- and one 7-gon adjacent to some 5-gon. By Theorem 3, any such polytope is a
-polytope.
Let us formulate the strongest result in this direction improving Theorem 5 for a special class of polytopes. Let us introduce a special subfamily of fullerenes. The first polytope
is the dodecahedron (the 5-barrel).
is a connected sum of two copies of
.
is a connected sum of
with
along a 5-gon surrounded by 5-gons (see
Figure 10). The polytopes
,
, are called
-nanotubes. Denote the family of polytopes
by
. It was proven in [
4,
13,
26] that a fullerene
P belongs to
if and only if
P contains a patch
consisting of a 5-gon surrounded by 5-gons. It follows from [
52,
53] that a fullerene
P belongs to
if and only if either
P is the 5-barrel or
.
Theorem 6 ([
4])
. Any fullerene can be constructed from the 5-barrel by operations of a connected sum with a copy of the 5-barrel along the center of a patch . It cannot be obtained from a simple 3-polytope without 4-gons by a -truncation, .
Any fullerene is either the 5-barrel or can be constructed from the 6-barrel by a sequence of -, -, - and -truncations in such a way that any intermediate polytope is either a fullerene in or a polytope in .
Nevertheless, not any polytope in
can be obtained by a connected sum with the 5-barrel or by a
-truncation from a polytope in
. The example is given by the polytope with the graph drawn in
Figure 11. Indeed, a connected sum with the 5-barrel produces a 5-gon surrounded by 5-gons, and a
-truncation produces a 5-gon with one edge lying in an
r-gon,
or 6, and intersecting by vertices a
p- and a
q-gon with
. In the presented polytope
P, any such edge belongs to a 6-gon and intersects two 6-gons, which means that the polytope
Q transforming to
P contains two 7-gons.
Let us mention that a connected sum with the 5-barrel is evidently a growth operation. Furthermore, an -truncation, , is a growth operation on the class of flag polytopes, since it substitutes the patch consisting of the new 5-gon, and the -, - and -gons for the patch consisting of the corresponding k-, - and -gons.
Our second main result gives the method to construct any polytope in from the 6-barrel by a sequence of growth operations from the finite list in such a way that intermediate polytopes belong to the same family.
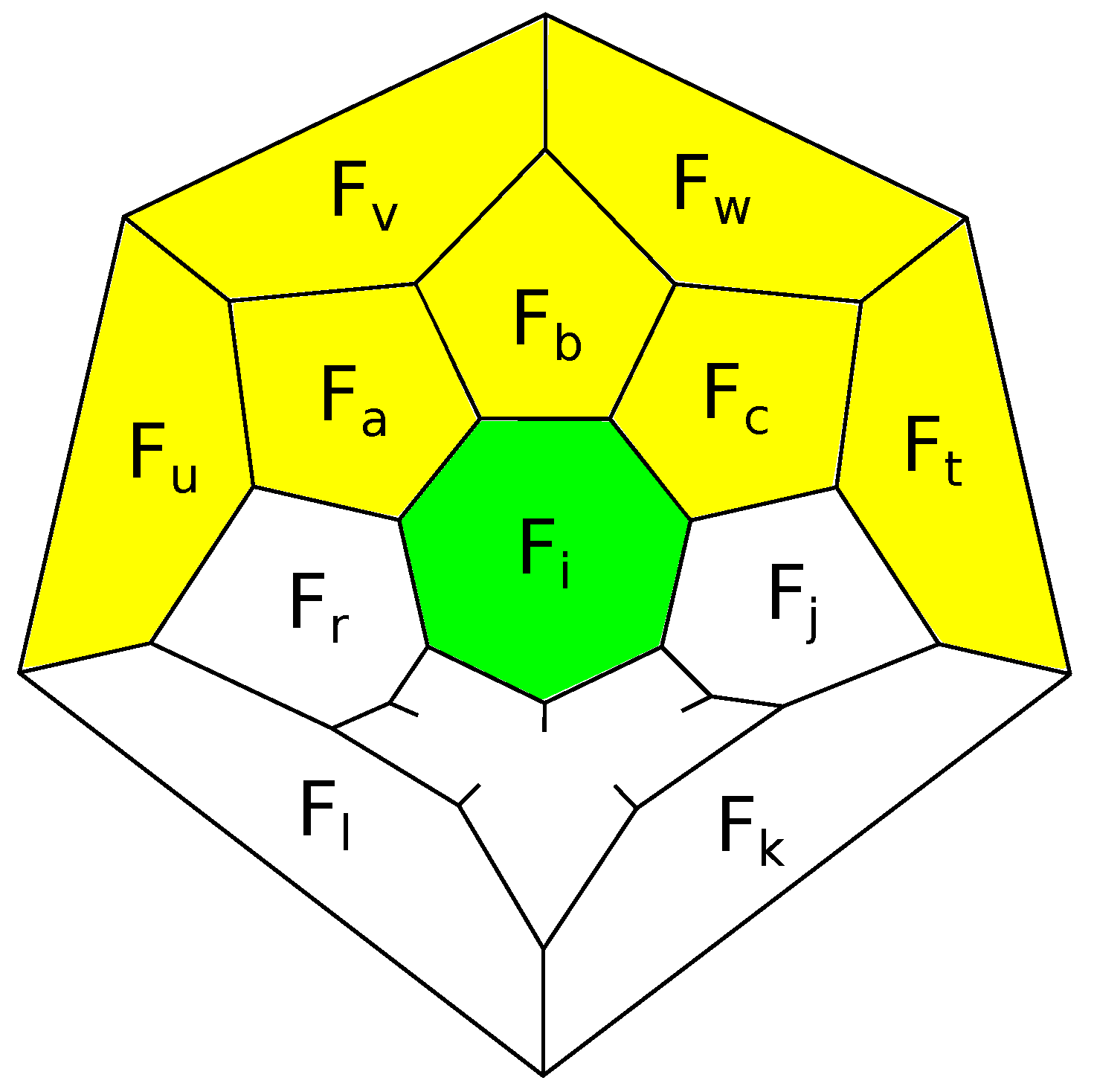
Since any face of a flag 3-polytope is surrounded by a belt, if a
-polytope contains a 5-gon surrounded by 5-gons, these six faces together form a patch, which we denote
; see
Figure 12a. Similarly, denote by
a patch consisting of a 5-gon surrounded by four 5-gons and a 6-gon; see
Figure 12b.
Proposition 2. A polytope is not a -polytope if and only if it contains a patch and is different from the 5-barrel. In this case, P is obtained from a polytope in by a connected sum with the 5-barrel producing this patch.
The proof of this proposition and the following theorem will be given below.
Theorem 7 (The second main result)
. Any polytope in either belongs to and is constructed from the 5-barrel by a sequence of connected sums with a copy of the 5-barrel along the center of a patch or can be constructed from a fullerene in by a connected sum with the 5-barrel along the center of a patch followed by a sequence of connected sums with the 5-barrel along the center of arising patch .
Any polytope in is either the 5-barrel or can be constructed from the 6-barrel by a sequence of growth operations, each being either a -,-, - or -truncation or one of the operations , , drawn in Figure 13 in such a way that the intermediate polytopes also belong to . Any of the operations , , is a composition of -, -, -truncations, such that the intermediate polytopes are -polytopes with 5-, 6- and at most two 7-gonal faces.
The third main result concerns all the polytopes in . There are polytopes , which cannot be obtained by any of the operations used in Theorem 7 from any polytope . To obtain an example, we can cut off all the edges of any polytope in several times. The resulting polytope still belongs to , but it has the non-hexagonal faces far from each other. Then, it can be obtained from some polytope only by a -truncation. However, Q should have two 7-gons; a contradiction. To generalize Theorem 8 to the class and a finite set of growth operations, we add a -truncation and allow intermediate polytopes to have two 7-gons.
Theorem 8 (The third main result)
. Any polytope in can be constructed from the 6-barrel by a sequence of growth operations each being either a -,-, -, - or -truncation or one of the operations , , in such a way that the intermediate polytopes are -polytopes with 5-, 6- and at most two 7-gonal faces.
2. Proof of the Main Results
Proof of the first main result (Theorem 4). We will develop the idea of Example 1 corresponding to the case
,
,
. First let us take the disk drawn in
Figure 14a. Let
be its boundary circle. If
,
, and
,
, then add to
two 2-valent vertices on
to become a 8-gon, and to
and
one 2-valent vertex to become 6-gons. Then, glue to the boundary of the disk a copy of the disk lying inside the 3-belt
to obtain a graph of a polytope due to the Steinitz theorem. This graph can be also obtained by adding to the figure the image of the graph inside the belt under the circle inversion interchanging the boundary circles of
.
Now, let either
or
and
. For each
with
, take
k-gons and arrange all the polygons in the descending order of the numbers of edges. Add to
vertices of valency two on
to become the first polygon. If
, do the same for
,
and the second and the third polygons. Otherwise take 6-gons instead of lacking polygons. Let
,
,
be the numbers of edges of
,
and
. The number
of 2-valent vertices on
is equal to
. Then,
, since either
,
, or
,
,
, or
. Furthermore, any face has at least one 2-valent vertex on
. If there are still polygons not in use, we form from them a
-belt of faces around
, taking 6-gons for lacking polygons intersecting two edges on the boundary of
and 5-gons for lacking polygons intersecting one edge, if necessary. Each face of the new belt
has at least one 2-valent vertex on the outer boundary circle
; hence, the number
of 2-valent vertices on
is not smaller than
. Repeat this argument until all the polygons are in use. Now, add one new belt consisting only of 5- and 6-gons, where each 5-gon intersects the boundary of the previous disk by one edge and each 6-gon by two edges. We obtain a new disk with the boundary faces having two edges on the boundary circle, where the number
b of boundary faces is at least 5 (see
Figure 14b for the case
,
,
.).
Let us build another disk with the identical boundary neighborhood. First, take a 5-gon. Add a 5-belt of faces around it consisting of c pentagons and d hexagons, . This belt has vertices of valency two on the outer boundary circle, and each face has at least one 2-valent vertex. If , then take , . Otherwise, take , and add a new belt of faces around the obtained disk, where 3-valent vertices on the boundary circle of the disk correspond to 6-gons of the belt (we say that they are of the first type), and edges of connecting 2-valent vertices correspond to 5-gons and 6-gons (of the second type). In the new belt, any face has at least one 2-valent vertex on the outer boundary circle , and the total number of the 2-valent vertices on is equal to plus the number of 6-gons of the second type. If the value of cannot reach the number b by varying the number of 6-gons of the second type, then make this value the maximal possible and add new belts in the same manner. In the end, we add the last belt without 6-gons of the second type to obtain the desired disk.
Now, glue both disks together to obtain a 2-sphere with a 3-valent graph on it. We claim that this graph is a graph of a simple 3-polytope. Indeed, any face by construction is a disk bounded by a simple edge-cycle. Two faces intersect if and only if either one of them is the center of one of the disks and the other belongs to the belt surrounding it, or they are subsequent faces of the same belt, or they belong to subsequent belts. In the first two cases, it is evident that the faces intersect by an edge. In the last case, this is also true, since by construction, any face of a new belt in each disk intersects any face of the previous belt either by the empty set or by an edge, and the same is true for faces of the boundary belts of disks. This finishes the proof of the theorem. ☐
Corollary 1. A slight modification of the proof of Theorem 4 gives a new explicit construction of a -polytope with given numbers different from constructions based on Eberhard’s [39] and Grünbaum’s [54] constructions of polytopes with given p-vectors and an operation of a cutting off of all the edges.
Construction 1: For , take any fullerene. Let . For each , , take k-gons, and arrange all the polygons in a linear order. If there is more than one polygon, add around the first polygon a belt of polygons from the remaining list, taking 5-gons for missing faces, if necessary. If not all polygons are in use, add new belts by the same manner, taking 6-gons for lacking polygons intersecting two edges on the boundary of the previous belt and 5-gons for lacking polygons intersecting one edge. In the end, add around the disk the last belt of 5- and 6-gons with 3-valent vertices on the boundary of the disk corresponding to 6-gons and the edges on the boundary of the disk connecting 2-valent vertices corresponding to 5-gons. We have the disk with boundary faces each having two edges on the boundary circle. The number of faces in added belts does not decrease; in particular, each belt has at least seven faces. Take the second disk with the same boundary neighborhood constructed above. In this disk, the number of faces in added belts also does not decrease; in particular, each belt has at least five faces. Glue the two disks along the boundaries to obtain a 2-sphere with a plane graph corresponding to a simple 3-polytope with prescribed numbers , . We claim that this polytope is a -polytope.
Proof. We will prove that P has no 3- and 4-belts. First, observe that a 3- or a 4-belt cannot contain the center of one of the two disks in construction, since any two non-subsequent faces of the belt surrounding the center are not adjacent in the polytope and do not intersect the same face outside this belt by construction. The polytope P outside the centers of the disks consists of the belts added in construction. Let us call them levels. In each disk, arrange levels in the order they were added. Let us call the top level of a disk a boundary level.
Let be a 3-belt. Since adjacent faces should belong to the same or adjacent levels and a 3-belt cannot belong to one level, two faces, say and , lie on one level and on another level . If is next to in one disk or both levels are boundary levels, then intersects at most two faces, which should intersect it by a common vertex; a contradiction. If is next to , then and are subsequent faces of the level. By construction, there are at least five faces on , each having a 2-valent vertex on the circle between and , whence the edge intersects ; a contradiction. Thus, P has no 3-belts.
Let be a 4-belt. Since it cannot belong to one level, assume that and lie on adjacent levels and . Without loss of generality, assume that either both levels are boundary levels or is next to in one disk. Then, intersects at most two faces on , which should intersect it by a common vertex. Since , and , lies either on or on the third level . In the first case, and are subsequent in , and is one of the two faces intersecting on . The second face intersects . The face should intersect both and ; hence, it lies on or . If it lies on , it is a subsequent to and can not intersect . If it lies on , it is one of the two faces intersecting on and it does not intersect . Then, it does not intersect ; a contradiction. Now, let lie on . Since intersects both and , it lies on . If and belong to the same disk, then is either next to or both and are boundary levels. Then, and should be adjacent, since they both intersect on ; a contradiction. If and are boundary levels, then and should be adjacent, since they both intersect on ; a contradiction. Hence, P has no 4-belts, and it is a -polytope. ☐
Example 2. For the case, , , , the first disk is drawn in Figure 15. The second disk is drawn in Figure 14c.
Remark 2. Construction 1 of -polytopes with given numbers can be generalized by taking two disks of the first type and substituting several belts of 5- and 6-gons for the last belt of the disk with a shorter boundary circle to make the lengths of the boundary circles equal. Then, for the case , , , the modified construction can produce the 7-barrel.
Now, we proceed to prove the second and the third main results. We call by a
k-loop a cyclic sequence of faces with adjacent subsequent faces. For a
k-belt
, the set
is homeomorphic to a cylinder. Each of its boundary components has a boundary code
corresponding to the number of edges of faces lying on this component. We will need the following result. For fullerenes, it follows from the results in [
52,
53] (see also [
13,
26] and [
4] (Theorem 2.12.1)). For polytopes in
, it was proven in [
4] (Theorem 3.2.6).
Theorem 9. Let . Then, any 5-belt either surrounds a face and has on this side the boundary code or surrounds a patch obtained by the addition of 5-belts of 6-gons around the patch and has on this side the boundary code .
Proof of the second main result (Theorem 7). The first part of Theorem 7 follows from Proposition 2, since polytopes in do not contain a patch .
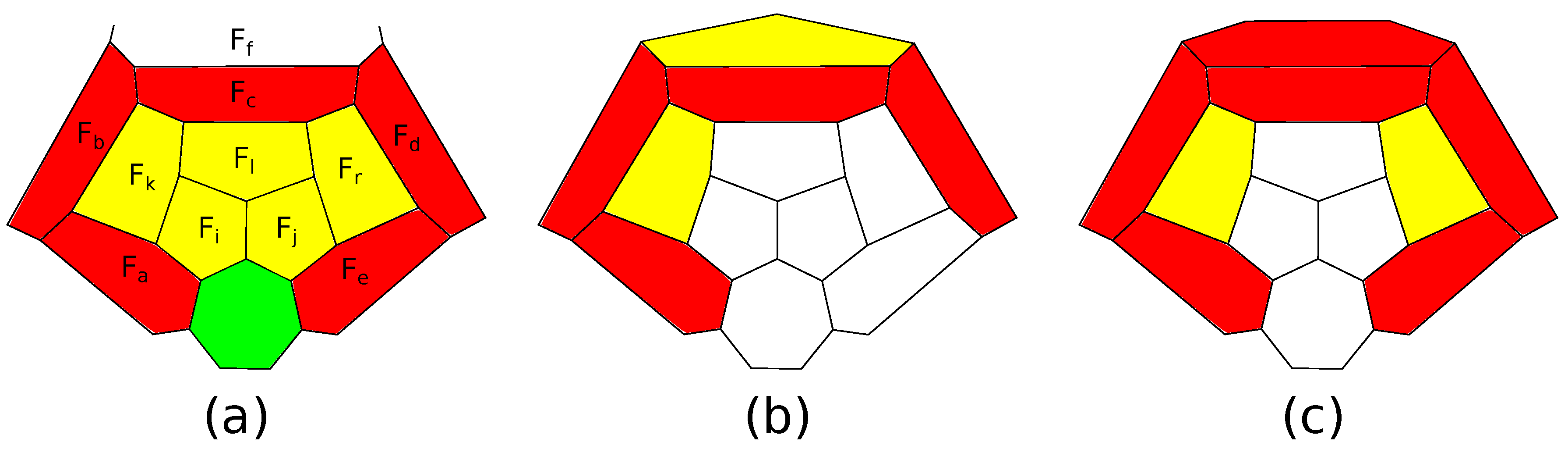
Proof of Proposition 2. First note that the patch
is surrounded by a 5-belt on a
-polytope. Indeed, it is surrounded by a 5-loop. If two non-subsequent faces intersect, without loss of generality, these are
and
drawn in
Figure 16a. However, they are non-subsequent faces of the 6-belt surrounding the adjacent 5-gons
and
; a contradiction. Thus,
is surrounded by a 5-belt. If this belt contains no 5-gons, then we can apply an operation inverse to a connected sum with the 5-barrel; see
Figure 16b. It is well defined by the Steinitz theorem and produces a polytope in
. Let one of the faces of the belt be a 5-gon; see
Figure 16c. We claim that for
, the patch consisting of
and an additional 5-gon is surrounded by a 5-belt
. Indeed, faces
belong to the 5-belt surrounding
, whence they are distinct and
. Faces
and
belong to the belt surrounding
. They are distinct, since
has at least five edges. They are adjacent if and only if
has exactly five edges. In this case, the 4-loop
can not be a 4-belt, whence
, since
. Then,
.
Thus, for , we have and by a similar argument, and is a 5-belt. By Theorem 9, either this belt surrounds a 5-gon or each face of the belt has two edges on the outer part of the boundary of P. In the first case, is a 4-gon, and in the second case, both and are 7-gons; a contradiction. ☐
Corollary 2. Let . If P contains a patch , then this patch is surrounded by a 5-belt of 6- or 7-gons, and P has no other patches of the form .
Proof. Since , it is not a fullerene. Proposition 2 implies that P is obtained from a fullerene Q containing a patch by a sequence of connected sums with the 5-barrel, where the first connected sum is along the center of , and all the other connected sums are along the center of the arising patch . If P contains another patch , then Q should also contain the same patch. Then, . However, any fullerene in does not contain the patch ; a contradiction. ☐
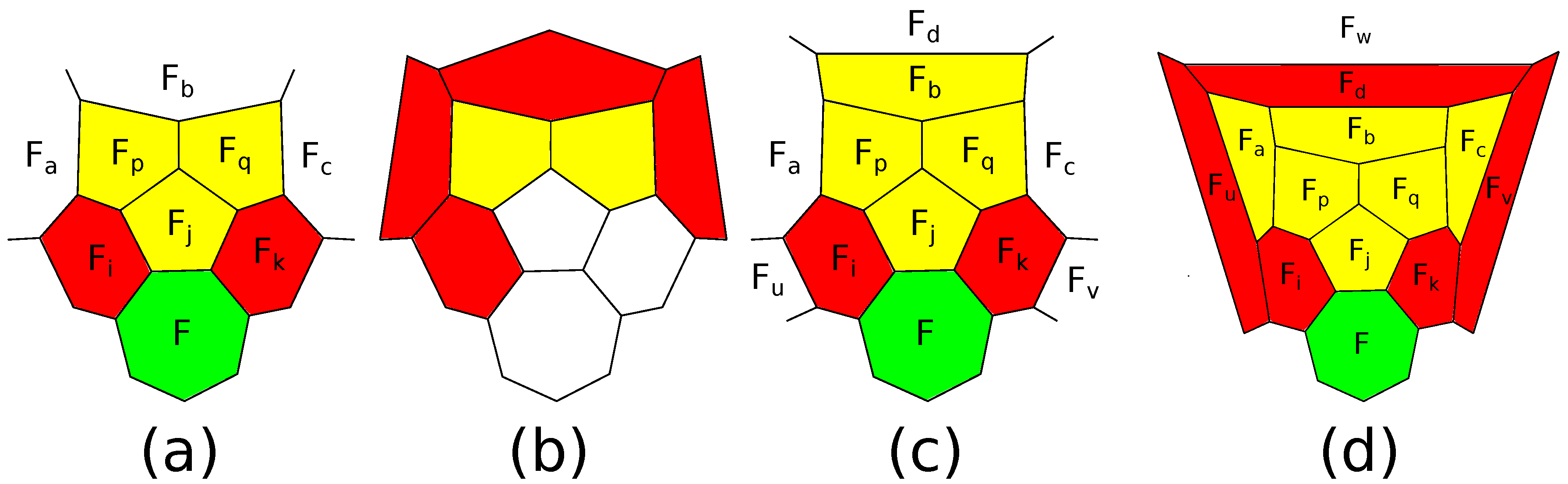
Denote the patches arising after operations of a
-,
-,
- or
- truncation or operations
,
, or
, by
,
,
,
,
,
,
, respectively (see
Figure 17). We do not take into account the orientation. Therefore, we do not distinguish between a patch and its mirror image.
By Theorem 2 and Proposition 2, a polytope P in the class can be obtained from a polytope Q in the class B by an operation of a connected sum with the 5-barrel, or of a -, -, - or - truncation, or , , , if and only if P contains respectively a patch , , , , , , , , where for a connected sum, a - truncation and operations , , ; for a -truncation; for a -truncation; and for a -truncation. Let us call a polytope irreducible, if it cannot be obtained from a polytope in by these operations. Otherwise, let us call P reducible. First, we will prove that only the 5- and the 6-barrel are irreducible, and then, we will explain how to avoid non--polytopes.
It can be proven that a collection of faces of a polytope
with the same combinatorics as in any of these patches indeed forms the corresponding patch. For the first six patches, this follows from the fact that the collection of faces consists of two adjacent faces and some faces of the belt surrounding them. For the patch
, this argument works for the collection without the top face and the collection without the bottom face. These faces should be distinct, for otherwise, a 4-belt arises, and they should be non-adjacent, for otherwise, a 5-belt with both boundary codes different from
and
arises (see more details in [
4] (Lemma 4.0.1)).
Lemma 1. Let be irreducible. Then, the 7-gon cannot be adjacent to 5-gons by three subsequent edges.
Proof. The 7-gon is surrounded by a 7-belt. If three of its subsequent faces
,
,
are 5-gons, then the four faces
,
,
,
adjacent to them and lying in the outer part of
are 5-gons (see
Figure 18), for otherwise,
P contains one of the patches
or
. All seven 5-gons are distinct, since they belong to the patch formed by two adjacent 5-gons
and
and the 6-belt
surrounding them. Consider the sixth face of
. It is different from the 7-gon, since these two faces are non-subsequent in the 6-belt surrounding the 5-gons
. It cannot be a 5-gon, for otherwise, the patch
appears. Therefore, it is a 6-gon. Consider the 5-loop
arising on the boundary of
, where
is the 7-gon. Any two non-subsequent faces of this loop do not intersect, since they are adjacent to the same face of this loop by non-adjacent edges. Then,
is a 5-belt. Since on the side of the belt
, it has the boundary code
and
has on the other side two edges, by Theorem 9 the other boundary code is
, and
P contains the patch
and is obtained by a connected sum with the 5-barrel by Proposition 2. The lemma is proven. ☐
Lemma 2. Let be irreducible. Then, the 7-gon cannot be adjacent to 5-gons by two subsequent edges.
Proof. The 7-gon is surrounded by a 7-belt. If two of its subsequent faces
and
are 5-gons, then the three faces
,
,
adjacent to them and lying in the outer part of
are 5-gons (see
Figure 19a), for otherwise,
P contains one of the patches
or
. All five 5-gons are distinct since they belong to the patch formed by the 5-gon
and the 5-belt
surrounding it. Consider the fifth face
of
. It does not intersect the 7-gon, since these two faces are non-subsequent faces of the 6-belt surrounding the 5-gons
. It cannot be a 5-gon, for otherwise, the patch
appears. Therefore, it is a 6-gon. The faces
and
are 6-gons by Lemma 1. Furthermore,
and
are 6-gons, for otherwise, the patch
appears. The face
is not the 7-gon, since the 7-gon and
are not adjacent. If
is a 5-gon, we obtain the patch
(see
Figure 19b). If
is a 6-gon, we obtain the patch
(see
Figure 19c). The lemma is proven. ☐
Lemma 3. Any polytope is reducible.
Proof. Let a polytope
be irreducible. By definition, the 7-gon
F is adjacent to at least one 5-gon, say
. By Lemma 2, the faces
and
adjacent to
F by the edges next to
are 6-gons. The remaining two faces adjacent to
are 5-gons, for otherwise, the patch
appears. We obtain the picture drawn in
Figure 20a. The faces
and
F do not intersect, since they are non-subsequent in the belt surrounding
and
. If
is a 6-gon, then
and
are also 6-gons, for otherwise, the patch
appears. Then,
P contains the patch
(see
Figure 20b). Thus,
is a 5-gon (see
Figure 20c). The faces
are different from
F, since
. If both
and
are 6-gons, then either
is a 5-gon, and we obtain the patch
, or
is a 6-gon, and we obtain the patch
. If both
and
are 5-gons, then
is a 6-gon, for otherwise, we obtain the patch
. Furthermore,
and
are 6-gons, for otherwise, the patch
appears. Thus, we obtain the scheme drawn in
Figure 20d. The face
is different from
F, for otherwise,
is a 5-belt, since any two non-subsequent faces of this 5-loop are adjacent to some face of this loop by non-subsequent edges. However, this belt has both boundary codes different from
and
, which contradicts Theorem 9. Like in the proof of Lemma 2, we see that either
is a 5-gon, and we obtain the patch
, or
is a 6-gon, and we obtain the patch
.
Now, we can assume that one of the faces
and
is a 5-gon and the other is a 6-gon. Since we do not take into account the orientation, without loss of generality, assume that
is a 5-gon and
is a 6-gon (
Figure 21a). If
is a 6-gon, then
is also a 6-gon, for otherwise, we obtain the patch
. Then, we have the patch
(
Figure 21b). Thus,
is a 5-gon, and we obtain
Figure 21c. The face
is different from
F, for otherwise,
is a 5-belt, since any two non-subsequent faces of this 5-loop are adjacent to some face of this loop by non-subsequent edges. However, this belt has both boundary codes different from
and
.
If
is a 5-gon, we obtain
Figure 22a. All the 5-gons are distinct, since they consist of adjacent faces
and some faces of the 6-belt surrounding them. We have a 5-loop
, which is a 5-belt, since any two non-subsequent faces of this 5-loop are adjacent to some face of this loop by non-subsequent edges. However, this belt has both boundary codes different from
and
, which contradicts Theorem 9. Hence,
is a 6-gon, and we obtain
Figure 22b. Then, if
is a 5-gon, we obtain the patch
, and if
is a 6-gon, we obtain the patch
(or, more precisely, its mirror image, which we do not distinguish from it); see
Figure 22c. ☐
Thus, any irreducible polytope in
is a fullerene. Now, we will prove the result, which will be useful also for
. For fullerenes, it was proven in [
4] (Theorem 4.0.2 1).
Lemma 4. Let P be a fullerene or a polytope in with the 7-gon surrounded by 6-gons. If P has two adjacent 5-gons, then either P is the 5- or the 6-barrel, or it can be obtained from a fullerene or a polytope in , respectively, by one of the operations: a connected sum with the 5-barrel, a -truncation, , , .
Proof. We need to prove that
P contains one of the corresponding patches. Assume that this is not true. Consider two adjacent 5-gons
and
. Then, the edge
intersects by one of its edges some 5-gon
, for otherwise, the patch
appears. If this patch consisting of three 5-gons with a common vertex is surrounded by 6-gons, then
P contains the patch
. Hence, one of the faces around the patch is a 5-gon. If it intersects only one of the three 5-gons, then the edge of intersection should intersect by a vertex a new 5-gon adjacent to two 5-gons of the patch, for otherwise, the patch
appears. Therefore, without loss of generality, assume that the edge
intersects two 5-gons
and
by vertices (see
Figure 23a). Then, each pair of faces
and
contains at least one 6-gon, for otherwise, the patch
appears. Up to a mirror symmetry corresponding to the change of an orientation of the polytope, we have two possibilities:
,
are 6-gons (
Figure 23b), or
,
are 6-gons (
Figure 23c).
In the first case,
is a 6-gon, for otherwise, the patch
appears. Then,
and
are 5-gons, for otherwise, the patch
appears. Then,
and
are 5-gons, for otherwise, the patch
appears.
is a 6-gon, for otherwise, the patch
appears (see
Figure 24a). Furthermore, faces
and
are 6-gons, for otherwise, the patch
appears. Faces
and
are distinct, since they are adjacent to
by distinct edges. Then, one of them is not a 7-gon. If it is a 5-gon, we obtain the patch
(
Figure 24b). If it is a 6-gon, we obtain the patch
(
Figure 24c).
In the second case, each pair of faces
and
contains at least one 5-gon, for otherwise, the patch
appears. If
is a 5-gon, then
is also a 5-gon, for otherwise, the patch
appears. Therefore, we can assume that
is a 5-gon, and similarly,
is a 5-gon; see
Figure 25a. The 6-loop
is a 6-belt, since any two non-subsequent faces of this loop are non-subsequent faces of the 6-belt surrounding one of the 3 pairs of adjacent 5-gons
,
,
. If
is a 5-gon, then we obtain a patch
D drawn in
Figure 25b. If both faces
and
are 6-gons, we obtain the patch
. If
is a 5-gon, then
is a 5-gon, for otherwise, we obtain the patch
. Thus, we can assume that
is a 5-gon; see
Figure 25c. The faces
form a 5-loop in the complement of the patch
D in the boundary of
P. They are pairwise distinct, since any two non-subsequent faces of this loop are adjacent to some of its face by distinct edges. Now, we have the 4-loop
.
, since these two faces are non-subsequent in the belt surrounding
. Since
P has no 4-belts,
. Since
P has no 3-belts,
and
are vertices, and all the faces in the 4-loop are 5-gons. Then
P is the 6-barrel. If
is a 6-gon, then
is also a 6-gon (see
Figure 25d), for otherwise, the patch
appears. Then, we obtain the patch
. The lemma is proven. ☐
We are ready to prove the following result.
Lemma 5. Only the 5- and the 6-barrel are irreducible polytopes in .
Proof. The 5- and the 6-barrel are evidently irreducible. Any polytope in is reducible by Lemma 3. If P is a fullerene different from the 5- and the 6-barrel and has adjacent 5-gons, then it is reducible by Lemma 4. If a fullerene has no adjacent 5-gons, then any its 5-gons belongs to a patch . Hence, P is reducible. ☐
Now, we will show how to avoid polytopes in and then in .
Lemma 6. Let P be a polytope in . If it can be reduced to a polytope in , then it can also be reduced to a polytope .
Proof. For a polytope
,
, the operation of a connected sum with the 5-barrel can be applied only along the central 5-gon of a patch
, for otherwise, two 7-gons appear. This operation transforms
into
. The only other operations that can be applied to the polytope
are a
-truncation, if
,
or
, if
,
, if
, and a
-truncation, if
. In all cases, any of the operations makes the transformation of the patches drawn in
Figure 26a. Then, the polytope
P also contains the patch
and can be reduced to a polytope
containing the patch
(see
Figure 26b). We have
, and the lemma is proven. ☐
Lemma 7. Any reducible polytope P in can be reduced to a polytope .
Proof. Let
P be reduced to a polytope
.
cannot be the 5-barrel, since the only operation applicable to the 5-barrel is a connected sum with the 5-barrel, which produces a patch
. Proposition 2 implies that
contains a patch
surrounded by a 5-belt
of polygons with at least six edges. By Lemma 6, we can assume that
. By Corollary 2, outside
, the polytope
does not contain patches of the form
. Consider the patch
D replaced during the operation. It has common faces with
, since
. For each operation different from the connected sum,
D contains no adjacent 5-gons; whence,
D intersects
by a boundary 5-gon. This 5-gon is transformed to a 6-gon. We claim that no other 5-gons in
D belong to
. Indeed, for
-truncations, the
k-gon belongs to
, and the
-gon lies outside
. For the operations
,
and
, the 6-gon next to the 5-gon belongs to
, while the next 6-gon lies outside
(for
, this is due to the fact that otherwise, the second 5-gon lies in
). Hence, for
and
, the second 5-gon lies outside
. For
up to a symmetry, the first and the second 6-gons are
and
in
Figure 27a. The third 6-gon
of
D cannot be
, since
. Furthermore,
, since
and
are non-adjacent as non-subsequent faces of the belt surrounding
. Similarly,
, since
and
are non-subsequent faces of the belt surrounding
. Furthermore,
and
are non-adjacent as non-subsequent faces of the belt surrounding the faces
. Hence,
. Thus,
lies outside
, and the second 5-gon in
D does not belong to
.
Then, the common 5-gon of
D and
is subdivided into two faces, which are either two 5-gons or a 5-gon and a 6-gon. Up to a symmetry, we obtain
Figure 27b. If
is a 5-gon (see
Figure 27c), then the straightening along the edge
gives
Figure 27d and a polytope
. If
Q contains a patch
, then one of the 5-gons of this patch should arise during the straightening. However, any of the two possible 5-gons is adjacent to a non-pentagon and has neighbors either non-pentagons or adjacent to a non-pentagon; a contradiction. Hence,
, and
P is obtained from
Q by a
- or a
-truncation. If
is a 6-gon, then
is a 5-gon, and we obtain
Figure 28a. If
is a 7-gon, then straightening along the edge
, we obtain a polytope
, which belongs to
for the same reason as in the previous argument. Then,
P is obtained from
Q by a
-truncation. Similarly, if
is a 7-gon, then straightening the edge
, we obtain a polytope
. If both
and
are 6-gons, then we obtain the patch
(
Figure 28b). Reducing the patch (see
Figure 28c), we obtain a polytope
. It belongs to
by the same reasoning as in the arguments above. Then,
P is obtained from
Q by the operation
. This finishes the proof of the lemma. ☐
Lemma 7 implies that any polytope in different from the 5- and the 6-barrel can be reduced to the 6-barrel by a sequence of our operations in such a way that the intermediate polytopes also belong to . This finishes the proof of Theorem 7. ☐
Proof of the third main result (Theorem 8). Consider a polytope
. If
, then the theorem follows from Theorem 7. If
and
P has two adjacent 5-gons, then the theorem follows from Lemmas 4 and 7. Thus, it remains to consider the case of polytopes with the 7-gon and all the 5-gons isolated. By a thick path, we call a sequence of faces
such that any two subsequent faces are adjacent. It is easy to see that any two faces on a simple 3-polytope can be connected by a thick path. Let us call a length of the thick path consisting of
k faces the number
. We will use the idea presented in [
26,
49] for fullerenes. Consider the 7-gon and the shortest thick path among all thick paths connecting it to 5-gons. Then, all the faces except for the first and the last are 6-gons. Since the path is the shortest, each 6-gon cannot intersect the next and the previous faces by adjacent edges. We say that the path goes “forward” in the 6-gon, if these edges of intersection are opposite. If they are not opposite and not adjacent, then the path “turns left” or “turns right”, depending on the orientation of the boundary of the polytope. In the shortest path, all the 6-gons are distinct, and non-subsequent faces are not adjacent. Moreover, there cannot be two subsequent turns to the same side, and it is possible to modify the shortest path to have no more than one turn (see the details in [
26,
49]).
Lemma 8. Let Γ
be the shortest path among all thick paths connecting the 7-gon with 5-gons in a polytope with the 7-gon and all the 5-gons isolated. If Γ
has no turns, then it is contained in the patch drawn in Figure 29a. If it has one turn, then it is contained in the patch drawn in Figure 30a.
Proof. The path itself forms a patch on the polytope P. To prove that is contained in the desired patch, it is sufficient to show that all the faces in each figure are distinct on the polytope, and the faces are adjacent on the polytope if and only if they are adjacent in the figure. Let have length k. Let us call the distance between faces of a disk on a figure the length of the shortest thick path connecting them in the figure. If two faces are distinct or non-adjacent in the figure and the distance between them is at most three, then they are respectively distinct or non-adjacent on the polytope, since either they are adjacent, if the distance is 1, or are non-subsequent faces of the belt surrounding a face or a pair of adjacent faces, if the distance is two or three. Thus, if two faces in the figure are distinct or non-adjacent, but the corresponding condition is not valid on the polytope, then the distance between them is at least four. We claim that for any two faces in each figure, there is a thick path of length at most with the same ends as containing both faces. Indeed, each figure consists of faces lying in the union of the face and two thick paths of lengths k and : and for the first figure and and for the second. If both faces lie on the same path, we can take this path. If they lie on different paths, then take the path of length . Then, the face C lying on the other path is adjacent to two subsequent faces of the first path. Substitute the segment for to obtain the new path of length . If one of the faces is , then take the path containing the second face. If it has length k, then simply add the segment . If it has length , then substitute for to obtain the desired path.
Let two distinct or non-adjacent faces of one of the figures respectively coincide or be adjacent on the polytope. Take a thick path of length at most containing them. Since the faces coincide or are adjacent on the polytope, we can shorten the path deleting the segment between these faces. This segment consists of at least three intermediate faces, whence the new path has length at most and is shorter than ; a contradiction. Thus, the lemma is proven. ☐
Now, reduce the obtained patch to the corresponding patch drawn in
Figure 29d or
Figure 30e by straightenings along edges inverse to
-,
- and
-truncations (see
Figure 29b,c or
Figure 30b–d, respectively). Then,
P is obtained from the polytope
Q with the last patch substituted for the first patch in
P by the corresponding truncations. Furthermore,
Q can not contain a patch
, since all the 5-gons outside the replaced patch are disjoint, and inside the patch, there are at most two 5-gons; hence,
. All the intermediate polytopes are
-polytopes, since they are obtained from
Q by
-truncations,
.
This finishes the proof of the theorem. ☐
3. Discussion
Let us discuss the place of our results and methods in previous studies. They lie on the crossroads of the mathematical study of fullerenes and the study of -connected graphs.
Fullerenes obtained their name in chemistry after famous American architect and philosopher Richard Buckminster Fuller in 1980s, since the discovered molecules resembled his geodesic domes (see [
55]), architectural constructions for roofing large areas without points of support inside. However, even before they obtained their name, fullerenes were studied in mathematics. For example, the famous Buckminsterfullerene
, which has the form of a soccer ball, has been known since ancient times as an Archimedean solid truncated icosahedron. Fullerenes were studied by M. Goldberg [
56] under the name medial polyhedra as candidates for polytopes with maximal volume among all the 3-polytopes with the given area of the surface and number of faces. Later, in [
57], he proposed the construction of fullerenes with icosahedral symmetry, which was later rediscovered by D.L.D. Caspar and A. Klug [
58] in the biological context and studied by H.S.M. Coxeter in [
59]. These polytopes are now sometimes called Goldberg polytopes. In [
60], B. Grunbaum and T.S. Motzkin, answering the question by H.S.M. Coxeter, constructed a fullerene with any prescribed number of 6-gons different from one.
Since the discovery of fullerenes in chemistry in 1985, a question of enumeration of all the combinatorial types (isomers) of fullerenes with the given number of faces arose. First attempts were made by D.E. Manolopoulos, J.C. May and S.E. Down [
61], who introduced a spiral method. It gives a linear order of all the faces of a fullerene such that each face is adjacent to the previous and the next faces. Nevertheless, in [
62], P.W. Fowler and D.E. Manolopoulos found an example of a fullerene without a spiral. Later, different generalizations of this method were introduced by G. Brinkmann [
63] and P.W. Fowler, A. Graovac, J. Žerovnik and T. Pisanski [
22] with no strict proof that the method is applicable for all the fullerenes. In [
64], L.N. Wirz, P. Schwerdtfeger and J.E. Avery introduced a new generalized face-spiral algorithm and proved its completeness. They created a computer program fullerene [
65] for enumeration of fullerenes.
Another effective approach for the enumeration of fullerenes was introduced by G. Brinkmann and A. W. M. Dress in [
66]. It is based on cutting a fullerene surface into several patches by a zig-zag edge-path, which has at most two successive edges on each face, and the enumeration of possible patches. This method led to the program fullgen (see [
67]).
A nice parametrization of the set of all fullerenes was given by W.P. Thurston [
36] on the basis of combinatorial and metric geometry of spaces with non-negative curvature. His results imply that the number of fullerenes with given number
m of faces grows like
.
Later, a new method based on growing fullerenes from seed (see [
68]) appeared. The idea was to build any fullerene from a finite set of seeds by growth operations substituting a new patch for a patch on a fullerene with a lesser number of faces and the same boundary. In [
51], G. Brinkmann, J.E. Graver and C. Justus proved that there cannot be finite sets of growth operations transforming fullerenes into fullerenes sufficient to build any fullerene from a finite set of seeds. In [
49], M. Hasheminezhad, H. Fleischner and B.D. McKay found an explicit infinite set of such operations with the seeds being the 5-barrel and the fullerene
(see the Introduction and
Figure 9). On the base of these operations, a new algorithm of the generation of fullerenes was built. It starts from seeds, applies different possible operations according to some restrictions and stores the obtained fullerenes. The corresponding program was named buckygen (see [
69]). It helped to find mistakes in fullgen and enumerate all fullerenes with at most 400 vertices (see [
70]). On the basis of fullgen and buckygen, several computer programs to study and visualize fullerenes were created [
71,
72].
Let us mention that a new method of fullerene generation was introduced by V.M. Buchstaber and N.Yu. Erokhovets in [
4]. It is based on the recursive generation of simple partitions of a disk by three types of operations and a gluing of these disks into surfaces of polytopes with the possible addition of belts of 6-gons between them. This method is close to the method of F. Kardoš, M. Krnc, B. Lužar and R. Škrekovski [
52,
73] for the generation of cyclic
k-edge cuts in fullerene graphs.
Of course, there are many more methods, results and names in the mathematical theory of fullerenes, but it is difficult to name all of them here.
On the other hand, in the graph and the polytope theories, methods to construct
-connected and
-connected plane graphs for
described in the Introduction were developed by A. Kotzig [
45], G.B. Faulkner and D.H. Younger [
46], D. Barnette [
8,
9], J.W. Butler [
16], T. Inoue [
38], V. Volodin [
47] and V.M. Buchstaber and N.Yu. Erokhovets [
4]. These methods allow one to construct any simple 3-polytope different from the
k-barrels with
-connected graph from the 5- or the 6-barrel by
-truncations,
and connected sums with the 5-barrel along a face and any simple 3-polytope different from the
k-barrels with
-connected graph from the 6-barrel by only
-truncations,
. On the basis of these methods, G. Brinkmann and B.D. McKay [
74] created a computer program to construct such polytopes. These methods were generalized by E.R.L. Aldred, D.A. Holton and B. Jackson [
75], W. McCuaig [
76] and N. Robertson, P.D. Seymour and R. Thomas [
17] to the case of non-planar graphs. T. Dǒslić [
21,
24] proved that the graph of any fullerene is
-connected. K. Kutnar, D. Marušič [
53] and F. Kardoš, R. Škrekovski [
52] proved that it is not
-connected, if and only if a fullerene is a
-nanotube.
Our methods and results developed jointly with V.M. Buchstaber [
4,
13,
23,
26,
48] combine both methods and results on the construction of fullerenes by growth operations in [
49,
68,
69] and on the construction of
-connected graphs in [
4,
8,
9,
16]. Namely,
-nanotubes are connected sums of copies of the 5-barrel. Any other fullerene different from the 5-barrel can be constructed by the above method from the 6-barrel by
-truncations. However, it is impossible to stay always in the class of fullerenes, and a priori intermediate polytopes can have any numbers of
k-gons,
. In [
4], it was proven that it is possible to consider at intermediate steps only simple polytopes with 5-, 6- and one 7-gonal face adjacent to a 5-gon. It seems that the appearance of a 7-gon was not extensively studied by mathematicians (although it was considered in [
30], and other mathematical generalizations of fullerenes were introduced; see [
32,
77,
78,
79]), but there are many works in physics and chemistry of fullerenes, which state that this is natural in the formation of fullerenes (see, for example, [
80,
81,
82]).
An advantage of our method is that instead of an infinite set of operations, we have only four growth operations increasing the number of faces by one on account of allowing one 7-gon adjacent to a 5-gon. The first of these operations is the famous Endo–Kroto operation [
50] (a
-truncation), which is the only
-truncation transforming fullerenes into fullerenes. The second operation (a
-truncation) creates a 7-gon; the third operation (a
-truncation) moves this 7-gon; and the forth operation (a
-truncation) eliminates it. These operations may be used to create a fullerene-generating algorithm and a program similar to buckygen. A disadvantage of the method is that the number of polytopes with a 7-gon seems to be larger than the number of fullerenes, and the algorithm should store at the same time these polytopes. Let us mention that in [
4], it is proven that to construct fullerenes, it is sufficient to use only polytopes with 5-, 6- and one 7-gon adjacent to a 5-gon and all the 5-gons isolated from each other on account of considering three of the four our truncations, the operations
,
,
(
Figure 13) and four additional operations, which are compositions of the four our truncations.
Comparing our method with the method in [
49], it can be proven (see, for example, [
26]) that to reduce an
-fullerene, only the operations
,
and
,
, with all the faces
being 6-gons, and the operation
with
and
being 6-gons and
being a 5-gon, are necessary. Any of these operations can be represented as a composition of
-,
-,
- and
-truncations in a way similar to the schemes in
Figure 29 and
Figure 30 (see [
26]). Thus, our method to reduce an
-fullerene is almost equivalent to the method in [
49]. Nevertheless, for fullerenes with adjacent 5-gons, the methods differ. Namely, according to [
49], to reduce such a fullerene, only operations
,
,
are necessary. However, if
and
are 5-gons in
, we obtain exactly the operation of adding a pair of edges due to D. Barnette and J.W. Butler. This operation transforms the 5-barrel into the 6-barrel; hence, it cannot be represented as a composition of two
-truncations,
.
New results of this article concern mainly polytopes with 5-, 6- and one 7-gonal face. We prove that fullerenes together with these polytopes form a very natural subclass in the class of all -polytopes. We prove that if such a polytope has a 7-gon and contains a patch consisting of a 5-gon surrounded by 5-gons, then it can be obtained from a fullerene by connected sums with the 5-barrel. Any other polytope with a 7-gon is a -polytope. We construct such polytopes with the 7-gon adjacent to a 5-gon from the 6-barrel by the four previous operations and three new operations , and , which are compositions of them. All the intermediate polytopes either belong to the same class or are -fullerenes. Moreover, operation has type with and being 6-gons, and has type with , and being 6-gons, while does not have the type or for any . However, operation with and being 6-gons and being a 5-gon is a composition of and a -truncation. We generalize this result to the case when the 7-gon is not adjacent to 5-gons by adding a -truncation and allowing at intermediate steps -polytopes with 5-, 6- and, at most, two 7-gons.