Abstract
A description of the 11 well-known uninodal planar nets is given by Cayley color graphs or alternative Cayley color graphs of plane groups. By applying methods from topological graph theory, the nets are derived from the bouquet with rotations mostly as voltages. It thus appears that translation, as a symmetry operation in these nets, is no more fundamental than rotations.
1. Introduction
What is the origin of symmetry in crystal structures? The interplay between topology and symmetry in crystal structures has already been considered in [1] and [2]. However, what is at stake is the very origin of symmetry and, more particularly, translational symmetry in condensed matter. Clearly, if some local geometric configuration corresponds to a minimum potential energy for the compositional unit, then a stable extended structure will be generated when every structural subset of identical composition reproduces this same configuration. As a particularly important consequence, translational symmetry may follow as a combination of proper or improper rotational symmetry operations. However, conversely, rotational symmetry operations may result from translational symmetry combined with topological restrictions, as previously discussed in [2]; that is, a full space-group may arise out of a small set of local topology and symmetry conditions. Uninodal nets for which the asymmetric unit displays a single node provide a suitable material to illustrate these relations. It is known for instance that the full symmetry group of the square lattice net can be deduced from its labeled quotient graph [2], a topological description of the periodic structure with no reference to point-symmetry. In this essay, we analyze the complementary proposition and show that two-periodic (planar) uninodal nets can be sufficiently described by using only rotational symmetry operations in association with a topological description.
A well-suited theoretical framework for such a study, called topological graph theory, combines topology and group theory into a single mathematical object named a voltage graph [3]. Labeled quotient graphs, introduced by Chung et al. [4] in the “vector method”, were the first application of topological graph theory to crystallography. In this method, a finite graph with edges labeled by lattice vectors represents the topology of the structure. Further progress was made by Klein [5], who used symmetry-labeled graphs: the use of symmetry operations as labels of the graph led to a substantial reduction in the size of the graph. However, symmetry labels were taken from a given space-group, and vertices were assigned a specific Wyckoff position in this space-group. These graphs were thus called spatial graphs by Klein, emphasizing that they represent graphs embedded in Euclidian space and not abstract graphs. In general, spatial graphs are not quotient graphs. The concept of symmetry-labeled quotient graphs was introduced by Eon [6]. Such graphs were obtained as quotient graphs of the periodic net by a non-trivial subgroup H of their space-group G (i.e., , where T is the full translation subgroup of the net), with edges assigned symmetry operations that generate H. These objects are truly combinatorial in nature, in the sense that the derived periodic net is isomorphic with the initial net, independently of any geometric support. However, the respective symmetry operations used in that paper were most frequently glide reflections or screw rotations. In this work, we consider only proper rotations or reflections as symmetry labels.
The paper is organized as follows. Definitions and main properties of voltage graphs and their application to the description of the combinatorial topology of crystal structures are reviewed in Section 2. The main text deals with the application of the methodology to the description of uninodal two-periodic (planar) nets. These nets were chosen because of their importance in crystal chemistry [7] as well as for their scarce number: it is known that there are exactly 11 uninodal two-periodic planar nets [8]. Section 3 presents a description of the square lattice net sql according to the vector-method, including an analysis of the ideal two-dimensional space-group (plane group) of the net. Section 4 introduces a description of sql using a symmetry-labeled quotient graph, showing that the full plane group of the net, including its translational symmetry, is generated by two proper rotations. The analysis of the 10 remaining uninodal two-periodic planar nets is performed along the same lines in the next sections; the different nets are analyzed in order of growing complexity. The paper ends with some general observations concerning the description of uninodal planar nets.
2. Methodology
The method is adapted from the work developed by Gross and Tucker [3]. Voltage graphs applied to the analysis of crystal structures are graph-theoretical objects that can be informally interpreted as a combinatorial description of the asymmetric unit of a periodic structure. However, a voltage graph also carries information about the symmetry operations that are necessary to recreate the whole structure from the asymmetric unit, which makes them so powerful. Because here we restrict our analysis to uninodal nets, the asymmetric unit contains a single vertex; in this case, all edges of the voltage graph start and end at the same vertex. Such edges are called loops and the corresponding graph is called a bouquet; the bouquet admits n loops. These loops are oriented and assigned a symmetry operation, called the voltage on the loop. A unique structure can then be derived from this voltage graph as follows. First, we form the symmetry group generated by the whole set of voltages. We call V the single vertex of the bouquet ; the vertex set of the derived graph is defined as the set : . Voltages indicate which vertices of the derived graph have to be linked. We suppose some loop is assigned voltage . Then, for every , there is an edge starting at vertex and ending at vertex . This edge, usually denoted as , is an oriented edge. From [3], it is known that the group acts freely on the derived graph as follows: A symmetry operation maps (i) vertex to vertex , and (ii) edge to edge . Hence, is a subgroup of the full symmetry group of the derived graph. In fact, the graph obtained from the previous construction is known as the Cayley color graph of the group with voltages as generators (colors). It may happen that Cayley color graphs present double edges when the respective generator has order 2. Indeed, supposing , then both edges and , which are different by construction, link the two vertices and . In this case, we substitute the pair of oriented edges by a single non-oriented edge. This modified construction is known as the alternative Cayley color graph of the group. Of course, crystal structures bear no orientation, but it may be helpful to keep orientations in the derived graph in order to make clear the relationship with the voltage graph.
A correlated approach is used in [9], where the authors provide different descriptions of the 17 two-dimensional space-groups (plane groups) through a list of possible generators and associated relators. They have also drawn the respective Cayley diagrams (Cayley and alternative Cayley graphs), which are naturally isomorphic to uninodal two-periodic planar nets. However, several of the generated nets happen to be isomorphic, and, conversely, not all planar nets have been derived. The four nets cem, fsz, htb and tts are missing. This paper focuses on planar nets, asking whether they can all be derived from the bouquet exclusively using point-symmetry operations as voltages. The proposed description also follows a principle of economy, looking for the smallest possible number of loops in the bouquet. Clearly, a minimum of two loops is necessary to describe a two-periodic net, whatever the nature of the voltage. The results reported in Table 1 show that most planar nets can be obtained from or .

Table 1.
Generators used as voltages for bouquets in the description of uninodal two-periodic nets, respective relators, space-groups and unit cell size of an embedding of the alternative Cayley color graph in comparison with those of the net.
3. The Square Lattice Net
3.1. The Vector Method
As an illustration of the general method, we consider the description of the sql net from its labeled quotient graph, the bouquet , as given in Figure 1. In this case, according to the vector method [4], voltages are vectors in , and the generated group is a translation group of rank 2. The vertex set is defined as . If two orthogonal vectors a and b are used as a basis of the lattice in the plane, with correspondence and , one obtains the derived net with the orientation as given in Figure 1. We observe that, locally, the derived net has the same structure as the voltage graph: for each color, there is one outgoing and one incoming edge at every vertex. The green edge links vertex to vertex , and the red edge links vertex to vertex .
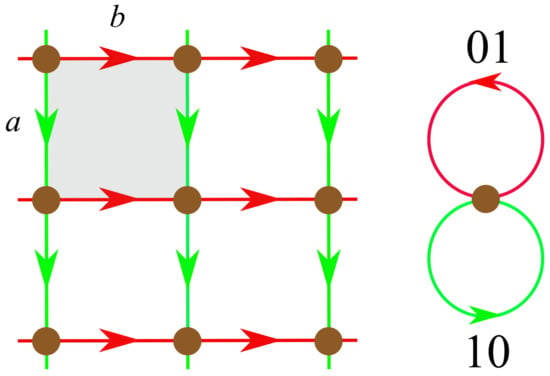
Figure 1.
(Left) A geometric realization (embedding) of the square lattice net (sql) in the Euclidian plane with oriented edges, and (Right) its labeled quotient graph with voltages in . The two classes of edges in the net are given the same color as the representative loop in .
We consider now the full symmetry group of the sql net. Because sql is a lattice net, it is a crystallographic net [10], which means, by definition, that its automorphism group is isomorphic to a space-group [11]. Because it is also a minimal net [12], the factor group of its space-group is isomorphic to the automorphism group of the voltage graph [2]. In order to determine the point group of sql, we thus look for generators of the automorphism group of the bouquet and then for an interpretation as symmetry operations in Euclidian space.
These mathematical properties arise from the relationship between loops in the bouquet and lines in the embedding of the net. As a result of the construction method described above, a loop unwraps along an infinite line oriented in the crystallographic direction given by the associated voltage; the relationship is evidenced in Figure 1 through both the color and the orientation of the respective elements. For instance, the red loop with voltage 01 unwraps along red lines with direction 01. Equivalently, any red (green) line projects onto the red (green) loop. The effect of a point symmetry operation on the net is to perform a permutation of the loops in the voltage graph. For instance, the reflection in the a-axis changes the orientation of every line along b; as a permutation, it can be written . The automorphism group of the bouquet is generated by the three permutations , and associated respectively to reflections in the axes , and and is thus of order 8. Because there is a single vertex per unit cell, the maximum space-group of sql is the symmorphic group .
3.2. An Example of a Symmetry-Labeled Quotient Graph
The above description of sql is based on translation operations in the Euclidian plane. In this section, we consider extensively a derivation of sql from the bouquet with two 4-fold rotations as voltages on the loops, as shown in Figure 2. The given representation of the net was obtained after placing the initial vertex close to the origin and considering two anticlockwise 4-fold rotations and with centers at and , respectively. These initial elements are shown in brown in the figure. Because voltages have order 4, each loop unwraps to a 4-cycle: starting from vertex at the origin, the green loop unwraps to the green 4-cycle around the center of rotation , and similarly the red loop unwraps to the red 4-cycle around the center of rotation . Because we know that acts freely on the derived net, we also obtain by this rotation the three other red 4-cycles at the corners of the unit cell. We note that this unit cell, as drawn in Figure 2, corresponds to the space-group generated by the two rotations and , which happens to be a supercell of sql.
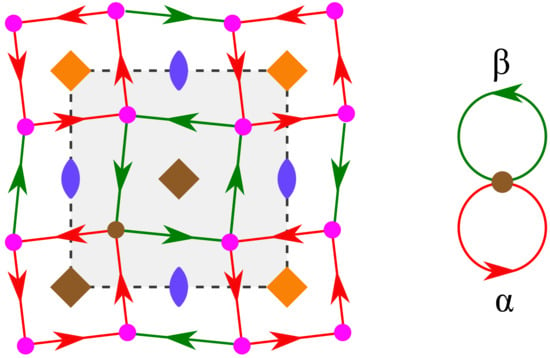
Figure 2.
(Left) The square lattice net and a symbolic representation of the space-group generated by a single vertex and two 4-fold rotation centers (in brown) using (Right) the bouquet with the respective rotations and as voltages. The two classes of edges in the net are given the same color as the representative loop in . Note that the initial vertex has been slightly shifted in relation to the origin, thus providing a truly embedding with a unit cell.
To obtain a better understanding of the derived net, or equivalently of the Cayley color graph of the generated group, we can use a representation of the two initial rotations by extended matrices such as follows:
We note first that the two combinations and represent 2-fold rotations with centers at and , respectively.
We also note that monomials of degree 4 correspond to translations, such as the two following combinations.
More generally, the two generators satisfy the three relations . From an abstract point of view, these relations are enough to define the group . It can be checked that the group , generated by the two given translations, is abelian and normal in and that the factor group admits four cosets represented by 1, , and , showing that G, as an abstract group, is isomorphic to the space-group , but with a unit cell in comparison with the primitive cell of the former embedding shown in Figure 1. The identification of the derived net N with sql can be achieved by analyzing the labeled quotient graph , as follows.
It is more appropriate in this case to construct directly from instead of using the derived net N. This can be done by denoting the four vertex cosets as with and working out the edges between them as well as the respective voltages in T. We consider first the loop with voltage in : this loop indicates that, for any , there are two edges linking vertex to vertices and . We thus have four edges forming a 4-cycle with zero voltage in . The case of the loop with voltage is more difficult. There are similarly two edges from to and ; these vertices should be first rewritten as with in order to assign voltage x to the edge from to in . For instance,
The value is chosen in order to obtain a monomial of degree 4 for the translation x. The final result comes from the relation in G (a consequence of the relations = = 1). We should thus add an edge from to with voltage . The complete labeled quotient graph is shown in Figure 3, where the two translations and have been written as 20 and 02, respectively, in accordance with the above matrices.
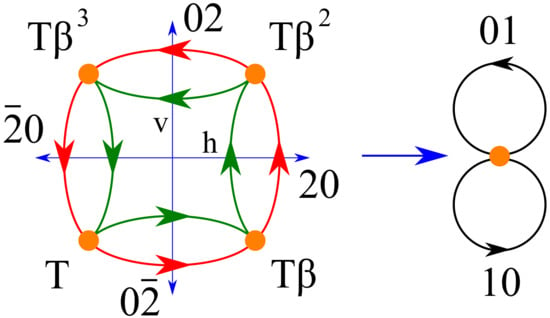
Figure 3.
(Left) The labeled quotient graph of the net N derived from the symmetry-labeled bouquet in Figure 2; vertices correspond to T-cosets in ; edge colors match the classes according to the two generators and , as given in Figure 2. The quotient by the reflections and through blue lines h and v is (Right) the bouquet with half voltages 10 and 01 (see text).
The isomorphism between the derived net N and sql can be worked out through labeled quotient graphs, as indicated in Figure 3. There are indeed two freely acting automorphisms of that leave the voltages over cycles unchanged and that should be interpreted as images of translations in N, thus extending the group T. We first define the automorphism exchanging (i) T with and with ; (ii) green and red horizontal edges between T and , as well as those between and ; and (iii) vertical edges between T and with those of the same color between and . A second automorphism is defined similarly, this time exchanging colors for vertical edges and keeping colors for horizontal edges; and act on as reflections in the blue v and h lines, respectively. The graph thus has a single vertex class and two edge classes for the automorphism group ; the four horizontal edges form a first class and the four vertical edges form a second class. Hence its quotient is the bouquet with all horizontal edges mapped on the upper loop and all vertical edges mapped on the lower loop. More precisely, both 2-cycles with voltage 02 (resp. 20) are wrapped on the upper (resp. lower) loop. This means that the voltages on the loops are respectively 01 and 10.
4. The Kagome Net
We consider more briefly a second example of a symmetry-labeled bouquet, this time in order to derive the kagome (kgm) net. As given in Table 1, we use as voltages on the loops of the bouquet the 3-fold rotations and with centers at and , respectively. These symmetry operations can be represented by the following matrices:
It is easily verified that these matrices satisfy the relation , and, conversely, that the group generated by these two matrices is isomorphic to the abstract group . Because monomials of degree 3 have the identity as the rotation part, they generate a translation group T; in this case, with and . This group is normal in G, with only three cosets given, for example, as T, and . The determination of the labeled quotient graph of the derived net N and its identification are performed as explained above for sql. For instance, according to the voltages assigned to loops in the bouquet , the green edge outgoing from in goes to . After this vertex has been rewritten in the form , one can see that the respective edge goes from to and must be assigned voltage x. In particular, we have
where the relation was used to develop the product in the basis . The resulting labeled quotient graph is shown in Figure 4. The identification of the net as kgm can be performed by using, for instance, the program SYSTRE [13].
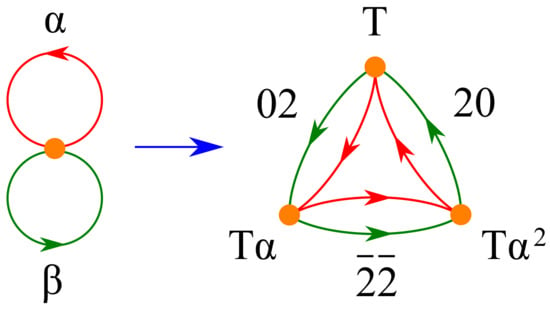
Figure 4.
(Left) The bouquet with loops assigned 3-fold rotations, and (Right) the labeled quotient graph of the derived net with translation group (see text).
The net is shown in Figure 5, where the symmetry group of the Cayley color graph has been put into evidence. The correspondence between the labeled quotient graph and the net can be seen by analyzing the local structure at any vertex. In kgm, any vertex admits one incoming and one outgoing red (resp. green) edge, in accordance with the bouquet . The nature of the respective symmetry operation can be read in the open space between the two edges of the same color, here as a 3-fold rotation. This observation applies to any net in further sections. We note also the two-color 6-cycle (strong ring) associated with the relator . It is a general fact that generators form one-color cycles while relators give rise to multicolor cycles.
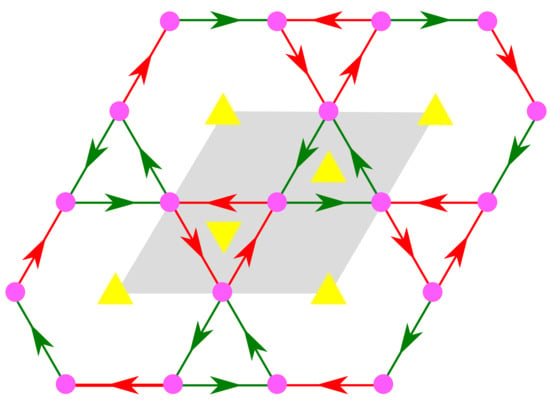
Figure 5.
The kgm net derived from the bouquet with loops assigned 3-fold rotations (in the center of the unit cell).
5. The Honeycomb Net
The square lattice and kagome nets do not represent the general situation, since vertices have an even degree in both nets. In this case, we have been able to identify the net derived from the symmetry-labeled bouquet with the Cayley color graph of the group generated by the voltages. We study here the example of the honeycomb (hcb) net with vertices of degree 3, which is identified with an alternative Cayley color graph. To this end, we consider the bouquet with loops assigned a 6-fold rotation and a 2-fold rotation with respective centers at and , represented by the following matrices:
It can be verified that these matrices satisfy the relations . The bouquet and the derived net are shown in Figure 6a and Figure 6c, respectively. Because is of order 2, the respective outgoing and incoming edges at any vertex are identified in the derived net, which thus has degree 3. Any vertex can be used as the initial vertex for generating the whole net if the 2-fold rotation is that associated to the incident red edge and the 6-fold rotation is that located in the angle between the two incident green edges. It is worth noting that the two relators and are associated with strong rings (6-cycles) of the net. The formal identification of the derived net N with hcb runs as in the previous cases. We first note that the two combinations and generate a translation (abelian) group T of rank 2, which is normal in the abstract group ; there are six T-cosets that may be written as with . Using these cosets, the bouquet can be unwrapped to the labeled quotient graph shown in Figure 6b. The analysis of the automorphism shows that it can be associated to the existence of a translation of the derived net with , indicating that the derived net is indeed isomorphic to hcb, with a triple unit cell.
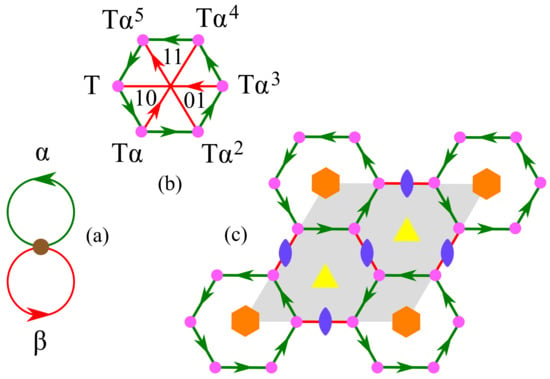
Figure 6.
(a) The bouquet with loops assigned 6-fold and 2-fold rotations, (b) the labeled quotient graph unwrapped from the bouquet , and (c) the derived hcb net showing all symmetry elements in the extended unit cell. We note the absence of orientation on red edges obtained after the identification of ingoing and outgoing edges associated to the 2-fold rotation (see text).
6. Decorated sql and hcb Nets
As for the honeycomb net, the nets fes (decorated sql) and hca (decorated hcb) are described by the bouquet with two rotations as voltages: (i) a 4-fold rotation and a 2-fold rotation with an extra relator for fes, and (ii) a 3-fold rotation and a 2-fold rotation with an extra relator for hca. These relators are interpreted as 8- and 12-cycles in the respective derived nets. A translation (normal, abelian) group T is generated by the two combinations and with four cosets in the case of fes. The translation group T of hca is generated by the two combinations and . There are six cosets: and . Because the derivation is rather straightforward, only the final nets are shown in Figure 7. We note that the edges associated to 2-fold rotations have no orientation.
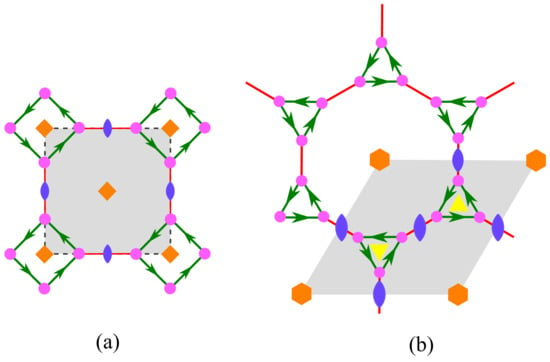
Figure 7.
(a) The fes net and (b) the hca net generated from the bouquet . We note the absence of orientation on red edges obtained after identification of ingoing and outgoing edges associated to the respective 2-fold rotations (see text).
7. The htb Net
The htb (hexagonal tungsten bronze) net, shown in Figure 8, is described by the bouquet with a 6-fold rotation and a 3-fold rotation as voltages, with relator . The translation group T is generated by the two combinations and and admits six cosets given as . We note again the presence in the net of a two-color 4-cycle (strong ring), associated to the relator.
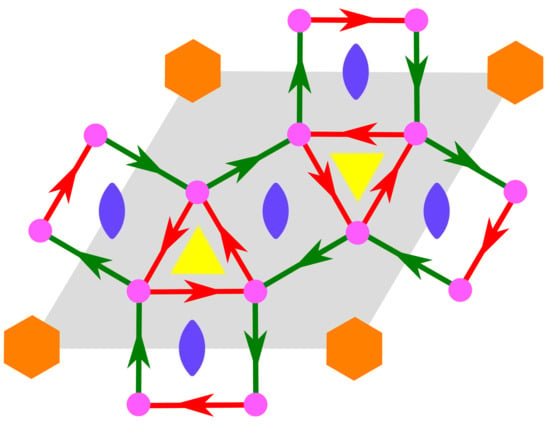
Figure 8.
The htb net generated from the bouquet with 6- and 3-fold rotations as voltages.
8. The Hexagonal Lattice Net
The hexagonal lattice net (hxl) is regular, of degree 6 and can be described using the bouquet with voltages , and , corresponding to 3-fold rotations, which can be represented by the following matrices:
These operations satisfy the relations . Clearly, every monomial of degree 3 in , and defines a translation in the plane. The two combinations and can be used as a basis for the translation group T. Using the three cosets T, and , one may construct the labeled quotient graph shown in Figure 9b, which can then be unwrapped to the representation of the hxl net given in Figure 9c. The net hxl is thus isomorphic to the Caley color graph of with the three generators , and . We note again the correlation between strong rings of the net and relators of the space-group, in particular, the relator associated to the green–blue–red 3-cycle.
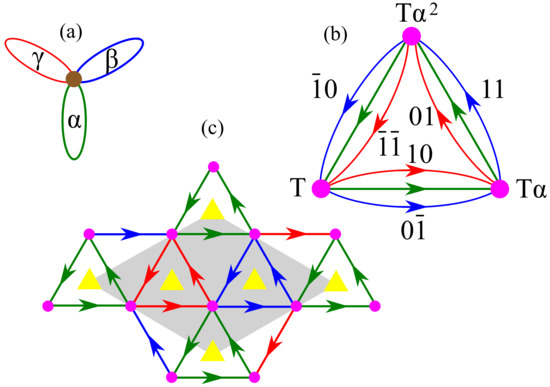
Figure 9.
(a) The bouquet with loops assigned 3-fold rotations. (b) The labeled quotient graph unwrapped from (a). (c) The derived hxl net showing all symmetry elements in the extended unit cell (see text).
9. fsz
Three voltages on the bouquet , given as a 6-fold rotation , a 3-fold rotation and a 2-fold rotation with relator , are necessary to describe the net fsz shown in Figure 10. As for the htb net, the translation group is generated by the two combinations and . We note the blue–red–green cycle associated with the relator .
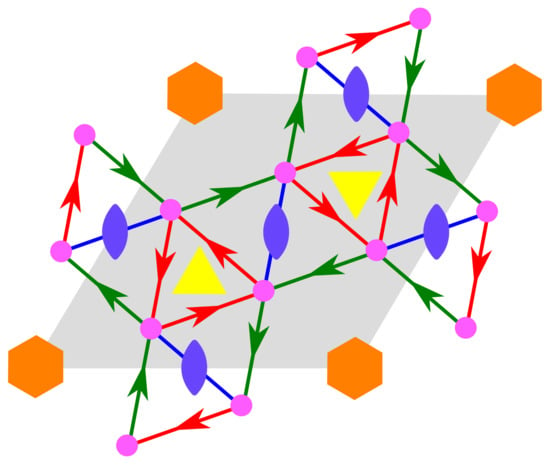
Figure 10.
The net fsz as derived from the bouquet with loops assigned 6-, 3- and 2-fold rotations. We ntoe the absence of orientation on the blue edge associated to the 2-fold rotation.
10. tts
Again, three voltages on the bouquet , given as two 4-fold rotations and and a 2-fold rotation with relator , are necessary to describe the net tts shown in Figure 11. We note the strong similarity of this representation of tts with that of sql given in Figure 2. This fact clearly reflects the similarity of their symmetry-labeled quotient graphs, as that of tts is obtained from that of sql by adding a third loop with voltage . The relationship is evident in Table 1.
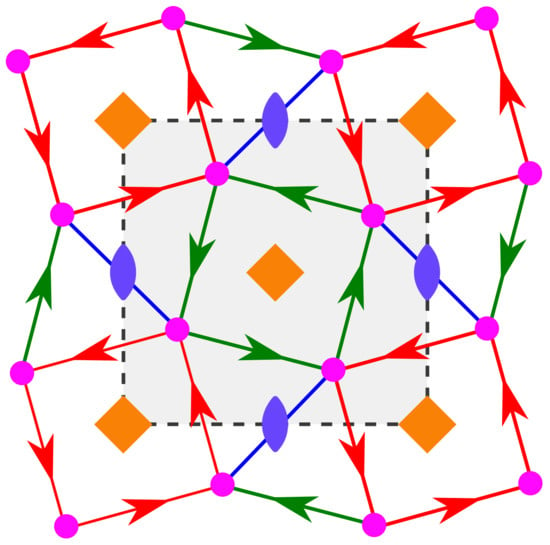
Figure 11.
The net tts as derived from the bouquet with loops assigned two 4-fold rotations and one 2-fold rotation. We note the absence of orientation on the blue edge associated to the 2-fold rotation and the three-color 3-cycle associated to the relator.
11. fxt
Differently from the other two-periodic uninodal nets, fxt only admits three reflections, , and , as voltages of the bouquet . These reflections are coupled as a 6-fold rotation , a 3-fold rotation and a 2-fold rotation . As a result, the alternative Cayley color graph has no orientation and its space-group is the full group . The determination of the translation group T can be performed by comparison with htb. Indeed, only even combinations of reflections can generate a translation, and the pairing of reflections yields then a combination of the three rotations , and , which is quite similar to the expression of translations for htb whose generators obey similar relations. Hence, we can take the two combinations and as generators of T, which admits 12 cosets, given as and . The derived net is shown in Figure 12.
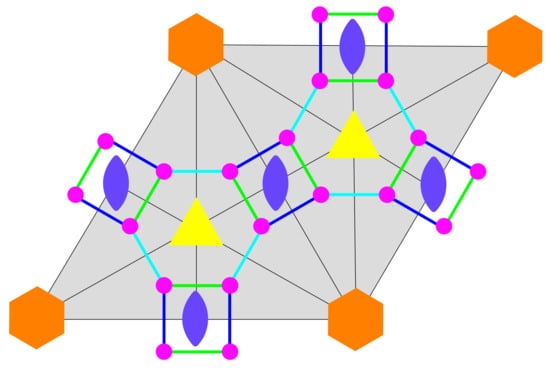
Figure 12.
The net fxt as derived from the bouquet , where each loop has been assigned a reflection; we note the absence of orientation.
12. cem
The last net of the list has degree 5 and admits the bouquet as its quotient graph. Three out of the four voltages correspond to 2-fold rotations , and . The fourth voltage is in fact the translation formed by the combination of the first two rotations: . The relator is called the commutator of and , a notation used for the combination . Because any monomial of degree 2 in , and defines a translation, the latter relator expresses the linear dependence of the three possible combinations as so that the derived net shown in Figure 13 is indeed two-periodic. We note that the relator is associated to a 3-cycle, while is associated to a 4-cycle, both strong rings of the net. Because there are only 2-fold rotations, the generated group is isomorphic to , with only two cosets, represented as T and , for instance.
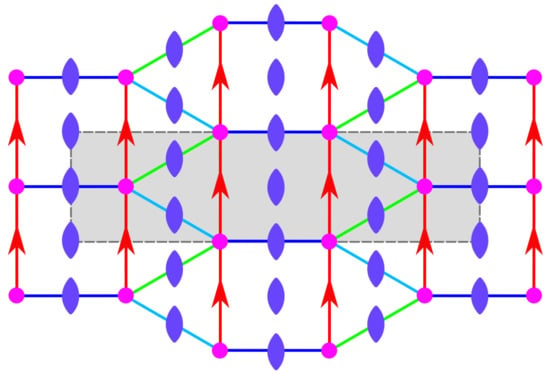
Figure 13.
Symmetric representation in of the alternative Cayley color graph isomorphic to the net cem, as derived from the bouquet , where three out of the four loops have been assigned a reflection; only symmetry elements from are shown. We note the absence of orientation along the respective edges.
13. Final Considerations
The results of the previous sections are summarized in Table 1, where a set of generators and respective relators is provided for the whole collection of uninodal planar nets, as given in the Reticular Chemistry Structure Resource [14]; also given are the symbols of the generated two-dimensional space-groups versus those of the full space-groups of the nets and the relative size of the unit cells. We note that relators and relations are in a one-to-one correspondence: r is a relator if and only if r = 1 is a relation. We observe also that more than one set of generators is usually possible to describe the same net.
All nets but cem are generated by using rotations or reflections as voltages of some bouquet with . Even in the case of cem, it must be said that a single voltage corresponds to a translation, and this translation is given as the combination of two 2-fold rotations, themselves given as voltages. Hence, in all cases, the whole space-group is generated by no more than three point-symmetry operations. Of course, these operations have distinct fixed points; otherwise they would generate a point-group. This is quite different from the conventional description of space-groups in International Tables, for instance, where given relations strictly concern the linear part of symmetry operations, because translations are always implicitly assumed and explicitly given as generators. In fact, even the geometrical interpretation as point-group operations, of generators given in Table 1, is needless. The space-group is abstractly generated from the relations listed in Table 1. Following general theorems from topological graph theory, the generated group acts freely (without fixed points) on the derived graph, that is, on the alternative Cayley color graph of the group, so that the generated space-group is a subgroup of the full space-group of the respective net.
The use of symmetry-labeled quotient graphs as representations of periodic nets presents some advantages compared with the more usual description by translation-labeled quotient graphs. Indeed, the description by the bouquet is more compact and brings immediate information concerning the transitivity class of the net. It clearly shows the existence of a single kind of vertex and provides an upper limit to the number of edges, equal to the number of loops. Moreover, strong rings of the net are immediately known from the given generators and their relators. A single glance at Table 1, for instance, informs that fes admits 4- and 8-rings. We emphasize again that translations appear in this analysis as a simple consequence of point-symmetry operations; of course, this does not generalize to an arbitrary net.
Acknowledgments
CNPq (Conselho Nacional de Pesquisa e Desenvolvimento) of Brazil is thanked for Grant 303367/2014-8; no specific funds were received for covering the costs to publish in open access.
Conflicts of Interest
The author declares no conflict of interest. The founding sponsor had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Thimm, G. Crystal topologies—The achievable and inevitable symmetries. Acta Cryst. 2009, A65, 213–226. [Google Scholar] [CrossRef] [PubMed]
- Eon, J.-G. Euclidian embeddings of periodic nets: Definition of a topologically induced complete set of geometric descriptors for crystal structures. Acta Cryst. 2011, A67, 68–86. [Google Scholar] [CrossRef] [PubMed]
- Gross, J.L.; Tucker, T.W. Topological Graph Theory; Dover Publications: Mineola, NY, USA, 2001. [Google Scholar]
- Chung, S.J.; Hahn, T.H.; Klee, W.E. Nomenclature and generation of 3-periodic nets—The vector method. Acta Cryst. 1984, A40, 42–50. [Google Scholar] [CrossRef]
- Klein, H.-J. The use of periodic graphs for representing and analysing crystal structures. Z. Kristallogr. 2012, 227, 612–618. [Google Scholar] [CrossRef]
- Eon, J.-G. From symmetry-labeled quotient graphs of crystal nets to coordination sequences. Struct. Chem. 2012, 23, 987–996. [Google Scholar] [CrossRef]
- O’Keeffe, M.; Hyde, B.G. Plane Nets in Crystal Chemistry. Philos. Trans. R. Soc. Lond. 1980, 295, 553–618. [Google Scholar] [CrossRef]
- Smirnova, N.L. On Kepler-Shubnikov Nets. Crystallogr. Rep. 2009, 54, 743–748. [Google Scholar] [CrossRef]
- Coxeter, H.S.M.; Moser, W.O.J. Generators and Relations for Discrete Groups; Springer-Verlag: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Moreira de Oliveira, M., Jr.; Eon, J.-G. Non-crystallographic nets: Characterization and first steps towards a classification. Acta Cryst. 2014, A70, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Klee, W.E. Crystallographic nets and their quotient graphs. Cryst. Res. Technol. 2004, 39, 959–968. [Google Scholar] [CrossRef]
- Beukemann, A.; Klee, W. E. Minimal nets. Z. Kristallogr. 1992, 201, 37–51. [Google Scholar] [CrossRef]
- Delgado-Friedrichs, O.; O’Keeffe, M. Identification and symmetry computation for crystal nets. Acta Cryst. 2003, A59, 351–360. [Google Scholar] [CrossRef]
- O’Keeffe, M.; Peskov, M.A.; Ramsden, S.J.; Yaghi, O.M. The Reticular Chemistry Structure Resource (RCSR) database of, and symbols for, crystal nets. Acc. Chem. Res. 2008, 41, 1782–1789. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).