1. Introduction
In a digital image, edges can be defined as abrupt changes of the image intensity. Edge is one of the most essential features contained in an image. The result of edge detection not only retains the main information of an image, but also reduces the amount of data to be processed drastically. Therefore, edge detection has been used as a front-end step in many image processing and computer vision applications [
1].
Since the abrupt changes in an image can be reflected by their derivatives, differentiation-based methods are widely used in edge detection. Generally, edges can be detected by finding the maximum of first-order derivatives or the zero-crossing of second-order derivatives of the image intensity. From the original contribution of Roberts in 1965, there have been a large number of works concerning this topic. Some researchers have paid attention to constructing optimal filters according to some reasonable hypotheses and criteria (see [
2,
3,
4,
5]), while some others are interested in designing discrete masks, such as the well-known Prewitt, Sobel and Laplacian of Gaussian (LoG) operators. Some recently developed methods can be found in [
6,
7,
8].
The differentiation-based edge detection methods need to calculate derivatives numerically. As we know, numerical differentiations are unstable since a small perturbation of the data may cause huge errors in its derivatives [
9]. In real applications, the image is often corrupted by noise during the processes of collection, acquisition and transmission. In order to calculate derivatives of the noisy data stably, some regularization methods should be introduced. There have been much work into this over the past years, such as the Tikhonov regularization [
10], the Lavrentiev regularization [
11], the Lanczos method [
12], the mollification method [
9] and the total variation method [
13]. Some of the regularization methods for computing the first-order numerical differentiation have been applied to detecting image edges (see [
10,
13]).
Compared with the first-order numerical differentiation, the computation of second-order derivatives is more unstable and more likely to be influenced by noises. However, the edge detection based on second-order derivatives has higher localization accuracy and a stronger response to final details [
14]. The most common second-order derivative used in edge detection is the Laplacian operation due to its variable separability and rotation invariance. In order to overcome the instability of Laplacian operation, one of the existing works is the LoG [
2]. Since the image data is discrete, the sampled representation of the LoG and some related issues have been discussed in [
15]. The performance of a LoG detector depends mainly on the choice of the scale parameter. For larger scales, the zero-crossings deviate from the true edges, which may cause poor localization. For small scales, there would be many false zero-crossings produced by noises. Besides the LoG detector, a model for designing a discrete mask of the Laplacian operator is introduced in [
7].
In view of the above-mentioned facts, a natural idea is to compute the Laplacian operation by the regularization method and construct a novel edge detection algorithm based on this. By rewriting the Laplacian operation as an integral equation of the first kind, a PDE-based regularization for computing the Laplacian operation has been proposed in [
16]. In this paper, the PDE-based regularization method will be generalized to edge detection. Based on the objective parameter selection for edge detection given in [
17], we will introduce a new choice strategy of the regularization parameter. Comparative experiments with the LoG detector and the Laplacian-based mask given in [
7] are considered.
The paper is organized as follows. In
Section 2, the PDE-based regularization method for computing the Laplacian operation of image data is given. The novel edge detection algorithm based on the regularized Laplacian operation is given in
Section 3. Comparative experiments are shown in
Section 4. Finally, the main conclusions are summarized in
Section 5.
2. Regularized Laplacian Operation
Considering the image intensity as a function
of two variables, the Laplacian operation can be defined as
Without loss of generality, we assume the value of
on the boundary of
is zero, i.e.,
. Otherwise, denote
as the solution of
and replace
by
. Since the latter satisfies
it has
Problem (1) is the Dirichlet problem of the Poisson equation. According to the classic theory of the Poisson equation, the relationship between
and
can be expressed as
where
is the Green function of the Dirichlet problem (see [
18]). Since
is a rectangular domain, the Green function has the explicit expression
where
The calculation of Laplacian operation
is equivalent to solving the integral Equation (2), which can be simplified in the following.
Denote
as the noise data of
; the calculation of the Laplacian operation
is unstable, which means the noise may be amplified. A stabilized strategy is to solve the equivalent Equation (2) by the regularization method. Solving the integral Equation (2) by the Lavrentiev regularization method, an efficient method is given in [
16]. The Laplacian operation can be computed approximately by solving the regularization equation
where
is the regularization parameter, and
is the regularized Laplacian operation. Assuming that
is a function satisfying
then it has
. Equation (3) can be rewritten as
This boundary value problem of PDE can be solved by classic numerical methods, and then the regularized Laplacian operation
can be expressed as
From the above rewriting, we can see that (4) and (5) are equivalent to the integral Equation (3). Compared with solving the regularization Equation (3) directly, the computational burden of solving (4) and (5) is reduced drastically.
The work of [
16] mainly focuses on the choice of the regularization parameter
and the error estimate of the regularized Laplacian operation
. Unfortunately, the choice strategy given in [
16] depends on the noise level of the noise data, which is unknown in practice. Since the choice strategy of the regularization parameter plays an important role in the regularization method, as the authors stated in [
16], the selection of parameter
in the edge detection algorithm should be considered carefully.
3. The Edge Detection Algorithm
In this section, we will construct the novel edge detection algorithm based on the regularized Laplacian operation given in
Section 2.
The first thing we are concerned with is the weakness of the Lavrentiev regularization. Notice that
, it has
. The parameter
is usually a small number, which means the error of the regularized Laplacian operation on the boundary can be amplified
times. Thus, the computation is meaningless on
. In fact, the validity of the regularized Laplacian operation
has been weakened when
is close to the boundary. Experiments in [
16] have shown that the weakness only affects the points very close to the boundary. Hence, except a few pixels which are as close as possible to the boundary of the image domain, the edge detection results will be acceptable.
The second thing we are concerned with is the choice strategy of the regularization parameter
. Since the noise level of an image data is unknown, the choice strategy given in [
16] cannot be carried out. Considering only the edge detection problem, the objective parameter selection given in [
17] can be adopted to choose the regularization parameter.
Once the regularization parameter is chosen, the regularized Laplacian operation can be obtained by solving Equations (4) and (5), where Equation (4) can be solved by the standard finite difference method or finite element method.
Combined with the objective parameter selection given in [
17], the main framework of the choice strategy is summarized as follows:
Step 1: Regularization parameters are used to generate N different edge maps by the proposed edge detection algorithm. Then, N potential ground truths (PGTs) are constructed, and each PGTi includes pixels which have been identified as edges by at least i different edge maps.
Step 2: Each PGTi is compared with each edge map Dj, and it generates four different probabilities: Among them, TPA,B (true positive) means the probability of pixels which have been determined as edges in both edge maps A and B; FPA,B (false positive) means the probability of pixels determined as edges in A, but non-edges in B; TNA,B (true negative) means the probability of pixels determined as non-edges in both A and B; and FNA,B (false negative) means the probability of pixels determined as edges in B, but non-edges in A.
Step 3: For each PGT
i, we average the four probabilities over all edge maps D
j, and get
, where
, and the expressions of other probabilities are similar. Then, a statistical measurement of each PGT
i is given by the Chi-square test:
where
The PGT
i with the highest
is considered as the estimated ground truth (EGT).
Step 4: Each edge map’s Dj is then matched to the EGT by four new probabilities: The Chi-square measurements are obtained by the same way as in Step 3. Then, the best edge map is the one which gives the highest , and the corresponding regularization parameter is the one we want.
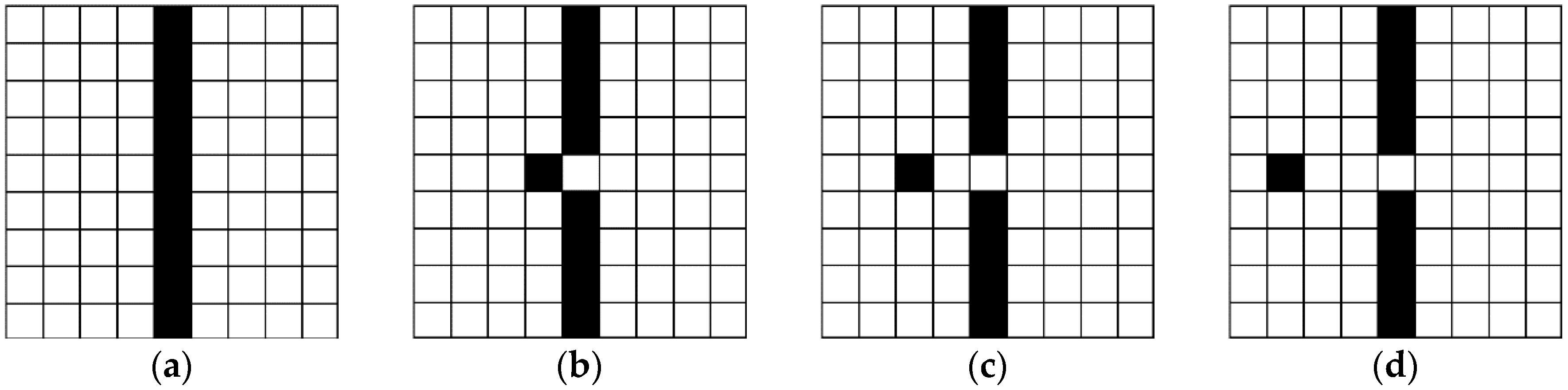
The Chi-square measure (6) can reflect the similarity of two edge maps, and the bigger the value of the Chi-square measurement, the better. As Lopez-Molina et al. stated in [
19], the Chi-square measurement can evaluate the errors caused by spurious responses (false positives, FPs) and missing edges (false negatives, FNs), but it cannot work on the localization error when the detected edges deviate from their true position. For example, a reference edge image and three polluted edge maps are given in
Figure 1. Compared with the reference edge (
Figure 1a), the Chi-square measurements of the three polluted edge maps are the same, yet their localization accuracies are different. In order to reflect the localization error in these edge maps, distance-based error measures should be introduced.
The Baddeley’s delta metric (BDM) is one of the most common distance-based measures [
20]. It has been proven to be an ideal measure for the comparison of edge detection algorithms [
19,
21]. Let
A and
B be two edge maps with the same resolution
, and
be the set of pixels in the image. The value of BDM between
A and
B is defined as
where
is the Euclidean distance from
to the closest edge points in
A, the parameter
is a given positive integer and
for a given constant
. Compared with the reference edge
in
Figure 1, the BDMs of the three polluted edge maps
are given in
Table 1 with different parameters
and
. The smaller the value of BDM, the better. As we can see from
Table 1, localization errors of the three edge maps are apparently distinguished. Therefore, the Chi-square measure (6) will be replaced by the BDM (7) in the choice strategies of the regularization parameter.
4. Experiments and Results
In order to show the validity of the proposed edge detection algorithm, some comparative experiments are given in this section. In the experiments, our regularized edge detector (RED) will be compared with the LoG detector and the Laplacian-based edge detector (LED) proposed in [
7].
As Yitzhaky and Peli said in [
17], the parameter selection for edge detection depends mainly on the set of parameters used to generate the initial detection results. In order to reduce this influence properly, the range of the parameter is set to be large enough that instead of forming a very sparse edge map it forms a very dense one. The scale parameter of the LoG detector is set from 1.5 to 4 in steps of 0.25. The regularization parameter of the regularized edge detector is set from 0.01 (≈0) to 0.1 in steps of 0.01. The images we used are taken from [
22], and some of them are shown in
Figure 2. The optimal edge maps given in [
22] will be seen as the ground truth in our quantitative comparisons.
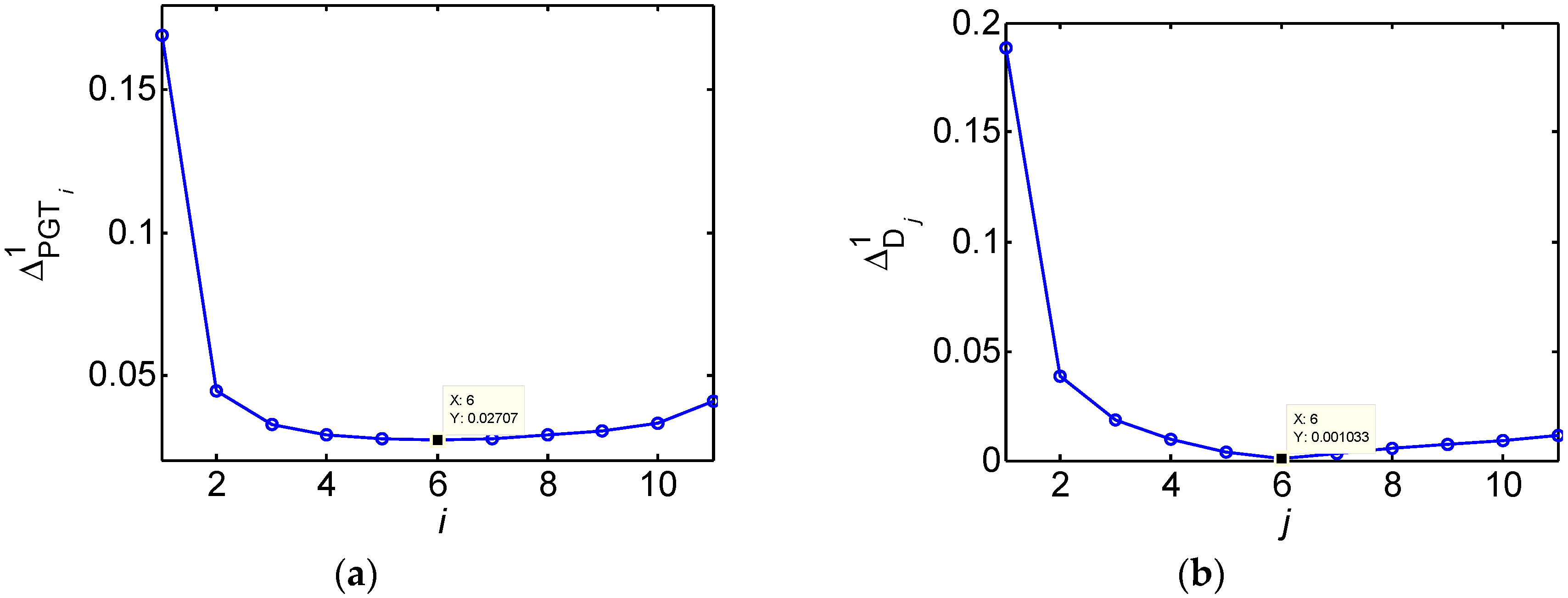
Let us first consider the choice strategy of the regularization parameter
, where the parameters in BDM are set as
. Taking the airplane image as an example, the BDM of each
is shown in
Figure 3a, from which we can see the EGT is PGT
6. Compared with the EGT, the BDM of each edge map D
j is shown in
Figure 3b, from which we can see the best edge map is D
6. Hence, the regularization parameter is chosen as
. The choice of the scale parameter in the LoG detector is carried out similarly. It does not need any parameters in the LED.
For the airplane image, the ground truth and edges detected by the three edge detectors are shown in
Figure 4. From
Figure 4b, we can see that the influence of the Lavrentiev regularization’s weakness on the RED is negligible. From
Figure 4b,c, we can see that the RED is better than the LoG detector for noise suppression and maintaining continuous edges. Comparing
Figure 4d with
Figure 4b,c, we can see the superiority of the parameter-dependent edge detector. Similar results for the elephant image are shown in
Figure 5. For some images taken from [
22], quantitative comparisons of the edges detected by the LoG detector, the RED and the LED against the ground truth are given in
Table 2. Since the smaller the value of BDM, the better, this shows that the RED has better performance than the LoG detector and the LED in most cases.