Lower Approximation Reduction Based on Discernibility Information Tree in Inconsistent Ordered Decision Information Systems

Abstract

Attribute reduction is an important topic in the research of rough set theory, and it has been widely used in many aspects. Reduction based on an identifiable matrix is a common method, but a lot of space is occupied by repetitive and redundant identifiable attribute sets. Therefore, a new method for attribute reduction is proposed, which compresses and stores the identifiable attribute set by a discernibility information tree. In this paper, the discernibility information tree based on a lower approximation identifiable matrix is constructed in an inconsistent decision information system under dominance relations. Then, combining the lower approximation function with the discernibility information tree, a complete algorithm of lower approximation reduction based on the discernibility information tree is established. Finally, the rationality and correctness of this method are verified by an example.

1. Introduction

Rough set theory [1], as a new mathematical tool, is mainly used to deal with imprecise, inconsistent, and incomplete information. Because the purpose and starting point of rough set theory is to analyze and deduce data directly, discover hidden knowledge and reveal potential laws, it is a method of data mining or knowledge discovery [2,3,4,5]. Compared with other methods dealing with uncertainties, such as data mining based on evidence theory, the most significant difference is that it does not require any prior knowledge beyond the data set that the problem needs to deal with. In recent years, great advances have been made in the popularization and application of rough set theory. Based on formal concept analysis, Xu et al. [6] proposed two operators between objects and attributes, established a new cognitive system model, and provided a method for arbitrary transformation of information granules in a cognitive system. Then, Xu and Li [7] established a model and mechanism of a two-way learning system in a fuzzy dataset based on information granules. Medina and Ojeda-Aciego [8] proposed that multi-adjoint frames can be applied to general T-concept lattices and then proved that the common information of two concept lattices can be regarded as a sublattice of the Cartesian product of two concept lattices. In the field of data mining, Kumar et al. [9] combined the fuzzy C-means algorithm, based on fuzzy membership, with the improved artificial bee colony algorithm and proposed a hybrid algorithm to overcome the shortcomings of local optimum in the original clustering problem.

Rough set and fuzzy set are closely related to each other and both can deal with imprecision, vagueness, and uncertainty in incomplete data analysis. The application of fuzzy sets is also very extensive. Pozna et al. [10] proposed a new data symbol representation framework, gave the related primitive operators, and discussed the applications related to the modeling of a fuzzy reasoning system. Jankowski et al. [11] analyzed the impact of online advertising on advertising effect and user experience and proposed a balanced method of advertising resource development based on fuzzy multi-objective modeling. Not only in these aspects, but also in other areas, rough set theory plays an important role, such as in pattern recognition, machine learning, intelligent control and other fields [12,13,14,15,16,17].

Attribute reduction [18,19,20,21,22] is one of the core contents of knowledge discovery. It describes how to delete unnecessary knowledge in an information system, to reduce the quantity of information to be processed in data mining and improve the efficiency of data mining. Since Skowron [23] proposed an attribute reduction algorithm based on an identifiable matrix, the intuitive simplicity of identifiable matrix has attracted the attention of many scholars. Liang et al. [24] extended information entropy, which can effectively measure the fuzziness of rough sets. Cao et al. [25] measured the importance of attributes in decision tables from the definition of information entropy. Based on this, an effective decision table reduction algorithm was proposed. Hu et al. [26] established a rough set complete reduction algorithm based on concept lattice model and investigated a decision table attribute reduction method based on concept lattice. Jiang and Wang [27] studied a rough set attribute reduction algorithm based on discernibility matrix. The influence of different discernibility matrices on the efficiency of attribute reduction is analyzed. Then a new discernibility matrix is defined to reduce the number of elements in the matrix to improve the efficiency. Yang [28] put forward a new discernibility matrix storage method (C-Tree) to realize the compression storage of a discernibility matrix. In recent references, there are many other attribute reduction methods [29,30,31,32,33,34,35,36,37]. Although the appearance of duplicate elements in a discernibility matrix is eliminated and the compression storage of a discernibility matrix is realized, the method is useless for redundant parent set elements. Hence, Jiang [38] investigated an attribute reduction algorithm based on a discernibility information tree. This algorithm cannot only delete duplicate elements in the discernibility matrix, but also eliminate the influence of parent set elements in most cases and realize compression and storage of the discernibility matrix. Because the above research is carried out under the equivalence relation, and the number of elements in the discernibility matrix under the dominance relation is two times that under the equivalence relation, the advantage of the discernibility information tree compression and storage in the ordered information system is more obvious. Based on this advantage, we generalize the discernibility information tree of equivalence relation to dominance relation. Each attribute set is regarded as a path mapped to the discernibility information tree in the identifiable matrix. The same identifiable attribute set is stored on the same path. Compared with the identifiable matrix, the discernibility information tree eliminates the occupancy of the space of the repeated attribute set. For the attribute sets with the same prefix, take $\{a,b,c,d\}$ and $\{a,b\}$ for example, when the two paths occur simultaneously, the path of the attribute set with fewer elements $\{a,b\}$ is selected to replace the path of $\{a,b,c,d\}$, and the path of $\{a,b\}$ is mapped onto the discernibility information tree, which reduces the space occupation of redundant elements. Finally, based on this tree, the algorithm of approximation reduction is established. This is the motivation of this article, behind the research presented here.

The paper is organized as follows. Related concepts and definitions are reviewed briefly in Section 2, the basic knowledge of lower approximation reduction and discernibility information trees are briefly reviewed. In Section 3, the discernibility information tree based on the lower approximation identifiable matrix is constructed by combining the lower approximation identifiable attribute set with the ordered tree, and the corresponding algorithm is also provided. Then, a complete lower approximation reduction algorithm is established based on a discernibility information tree. In Section 4, to illustrate the effectiveness of the proposed method in this paper, a detailed example is presented to verify and explain the lower approximation reduction based on discernibility information system in the inconsistent decision information system. Finally, Section 5 covers some conclusions.

2. Preliminary

In this section, we will review the basic knowledge of this article such as inconsistent ordered information system with decision, lower approximation identifiable matrix and lower approximation reduction based on dominance relation. At the same time, we will introduce the related concepts of the discernibility information tree needed in the continuation of this paper.

2.1. Inconsistent Ordered Decision Information System (IODIS)

A decision information system is a quintuple $DIS=(U,AT\cup DT,F,G)$, where U is a non-empty finite universe, $AT$ is a finite non-empty set of condition attributes, $DT$ is a finite non-empty set of decision attributes and $AT\cap DT=\varnothing$, $F=\{f:U\to V_a,a\in AT\}$ are mapping sets of object attribute value, in which $f:U\times AT\to V_a$ is a total function such that $f(x,a)\in V_a$ for each $a\in AT$, $x\in U$. In the meantime, $G=\{g:U\to V_d,d\in DT\}$ are mapping sets of object attribute value, in which $g:U\times DT\to V_d$ is a total function such that $g(x,d)\in V_d$ for each $d\in DT$, $x\in U$.

Definition 1.

Let $DIS=(U,AT\cup DT,F,G)$ be a decision information system. If $R_{AT}⊈R_{DT}$, then it is called an inconsistent decision information system $\left(IDIS\right)$, otherwise it is called a consistent decision information system.

In classical information systems of Pawlak approximation space, each condition attribute set and decision attribute set determines a binary indistinguishable relation, i.e., equivalence relation. However, in real life, many practical problems are based on dominance relations. We suppose that the domain of criterion $a\in AT$ is preordered by the relation ${⪰}_a$. The statement $x_i{⪰}_a{x}_j$ indicates that $x_i$ is at least as good as y with respect to criterion a. We say that $A\subseteq AT$ are criteria. Then $x_i{⪰}_A{x}_j\iff x_i{⪰}_a{x}_j(\forall a\in A)$. The dominance relation with respect to condition attribute set $AT$ can be defined as

$$\begin{array}{c}{R}_{AT}^{⪰}=\{(x_i,x_j)\in U\times U|x_j{⪰}_a{x}_i,\forall a\in AT\}.\hfill \end{array}$$

(1)

Based on dominance relation $R_{AT}^{⪰}$, dominance classes can be defined as

$$\begin{array}{c}{\left[x_i\right]}_{AT}^{⪰}=\{x_j\in U|(x_i,x_j)\in R_{AT}^{⪰}\}.\hfill \end{array}$$

(2)

Similarly, the dominance relation and dominance classes with respect to decision attribute set $DT$ can be defined as

$$\begin{array}{c}{R}_{DT}^{⪰}=\{(x_i,x_j)\in U\times U|x_j{⪰}_d{x}_i,\forall d\in DT\},\hfill \end{array}$$

(3)

$$\begin{array}{c}{\left[x_i\right]}_{DT}^{⪰}=\{x_j\in U|(x_i,x_j)\in R_{DT}^{⪰}\}.\hfill \end{array}$$

(4)

Definition 2.

Let $IDIS=(U,AT\cup DT,F,G)$ be an inconsistent decision information system. $\forall A\subseteq AT,D\subseteq DT$, if $R_A^{⪰}$ and $R_D^{⪰}$ are dominance relations corresponding to condition attribute set A and decision attributes set D in IDIS, then it is called an inconsistent ordered decision information system (IODIS).

In the following, the abbreviation of an inconsistent order decision information system (IODIS) will be represented by $S^{⪰}$ for brevity.

Proposition 1.

Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an inconsistent ordered decision information system, $A\subseteq AT$, $\forall x_i,x_j\in U$. Then the following results hold

(1) 

$R_A^{⪰}\supseteq R_{AT}^{⪰}$, ${\left[x_i\right]}_A^{⪰}\supseteq {\left[x_i\right]}_{AT}^{⪰}$;

(2) 

$x_j\in {\left[x_i\right]}_A^{⪰}$, $x_i\in {\left[x_j\right]}_A^{⪰}\iff {\left[x_j\right]}_A^{⪰}={\left[x_i\right]}_A^{⪰}$;

(3) 

${\left[x_i\right]}_A^{⪰}=\bigcup \{{\left[x_j\right]}_A^{⪰}|x_j\in {\left[x_i\right]}_A^{⪰}\}$;

(4) 

${\left[x_i\right]}_A^{⪰}={\left[x_j\right]}_A^{⪰}\iff f(x_i,a)=f(x_j,a)(\forall a\in A)$.

If a binary relation is no longer an equivalence relation but a dominance relation, the dominance class constitutes a cover of the universe and no longer forms a partition.

2.2. Lower Approximation Reduction in an IODIS

In an inconsistent information system, condition attributes are screened out by the method of lower approximation reduction. Meanwhile, it is better to mine the hidden information and discover the rules. Moreover, deletion of unnecessary condition attributes also can save space. Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an inconsistent ordered decision information system, $A\subseteq AT$, $D\subseteq DT$, and $R_A^{⪰},R_D^{⪰}$ are dominance relations with respect to A and D. We denote that in the following

$$\begin{array}{c}U/R_A^{⪰}=\{{\left[x_i\right]}_A^{⪰}|x_i\in U\},\hfill \end{array}$$

(5)

$$\begin{array}{c}U/R_D^{⪰}=\{D_1,D_2,\dots ,D_r\},\hfill \end{array}$$

(6)

$$\begin{array}{c}{\underline{\eta }}_A^{⪰}=(\underline{R_A^{⪰}}\left(D_1\right),\underline{R_A^{⪰}}\left(D_2\right),\dots ,\underline{R_A^{⪰}}\left(D_r\right)).\hfill \end{array}$$

(7)

where ${\underline{\eta }}_A^{⪰}$ is called a lower approximation function based on $R_A^{⪰}$.

Definition 3.

Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an IODIS and $\forall A\subseteq AT$. If ${\underline{\eta }}_A^{⪰}={\underline{\eta }}_{AT}^{⪰}$, then A is called a lower approximation coordination set based on dominance relation $R_{AT}^{⪰}$. Moreover, if $\forall B\subseteq A$, it does not satisfy that ${\underline{\eta }}_B^{⪰}={\underline{\eta }}_A^{⪰}$. Then A is called a lower approximation reduction in an IODIS.

According to the above Definition 3, it is easy to get the conclusions included in Theorem 1.

Theorem 1.

Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an IODIS and $\forall A\subseteq AT$. Then

A is a lower approximation coordination set $⟺\forall D_i\in U/R_D^{⪰}$, then

$$\begin{array}{c}\hfill \underline{R_A^{⪰}}\left(D_i\right)=\underline{R_{AT}^{⪰}}\left(D_i\right)(i=1,2,\dots ,r).\end{array}$$

(8)

Definition 4.

Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an IODIS and $D_i\in U/R_D^{⪰}(i=1,2,\dots ,r)$. Then denote

$$\begin{array}{c}{D}_{⪰AT}^{\underline{\eta }}=\{(x_i,x_j)|x_i\in \underline{R_{AT}^{⪰}}\left(D_i\right),x_j\notin \underline{R_D^{⪰}}\left(D_i\right),\hfill \end{array}$$

(9)

$$\begin{array}{c}{\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)=\left\{\begin{array}{cc}\{a_k\in AT|f(x_i,a_k)>f(x_j,a_k)\}\hfill & (x_i,x_j)\in D_{⪰AT}^{\underline{\eta }}\hfill \\ \varnothing \hfill & (x_i,x_j)\notin D_{⪰AT}^{\underline{\eta }}.\hfill \end{array}\right.\hfill \end{array}$$

(10)

Therefore, ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)$ is called a lower approximation identifiable attribute set under the dominance relation $R_{AT}^{⪰}$ with respect to objects $x_i,x_j$ in an IODIS. Moreover, combining the lower approximation identifiable attribute set of all objects, the lower approximation identifiable matrix is defined as

$$\begin{array}{c}Di{s}_{⪰AT}^{\underline{\eta }}={({\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)|x_i,x_j\in U)}_{\left|U\right|\times \left|U\right|}.\hfill \end{array}$$

(11)

Theorem 2.

Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an $IODIS$ and $\forall A\subseteq AT$. Then

$$\begin{array}{c}{\underline{\eta }}_A^{⪰}={\underline{\eta }}_{AT}^{⪰}⟺\forall (x_i,x_j)\in D_{⪰AT}^{\underline{\eta }},thenA\cap {\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)\ne \varnothing .\hfill \end{array}$$

(12)

Definition 5.

Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an IODIS and the lower approximation identifiable matrix is $Di{s}_{⪰AT}^{\underline{\eta }}$ based on dominance relation $R_{AT}^{⪰}$. Then the lower approximation identifiable formula can be defined as

$$\begin{array}{c}{M}_{⪰AT}^{\underline{\eta }}=\wedge \{\vee \{a_k|a_k\in {\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)\},(x_i,x_j)\in D_{⪰AT}^{\underline{\eta }}\}.\hfill \end{array}$$

(13)

Theorem 3.

Let $S^{⪰}=(U,AT\cup DT,F,G)$ be an IODIS. Then the minimal disjunctive normal form of identifiable formula $M_{⪰AT}^{\underline{\eta }}$ is

$$\begin{array}{c}Mi{n}_{⪰}^{\underline{\eta }}={\vee }_{k=1}^p({\wedge }_{s=1}^{q_k}{a}_s).\hfill \end{array}$$

(14)

Meanwhile, $B_k=\{a_s|s=1,2,\dots ,q_k\}$, then $\{B_k|k=1,2,\dots ,p\}$ are the sets of all lower approximation reductions based on dominance relation $R_{AT}^{⪰}$.

2.3. Discernibility Information Tree

Discernibility information tree is an ordered tree which is sorted from left to right according to the order of condition attributes and is a compressed storage method based on an identifiable attribute set of identifiable matrices. It eliminates the storage space of duplicated elements and reduces unnecessary space waste. The characteristics of the discernibility information tree are as follows [17]:

(1)

The subtree of the discernibility information tree is also an ordered tree, which is arranged from left to right in the order of the condition attribute set.

(2)

Each node of the discernibility information tree is composed of four parts: prefix pointer, successor pointer, node name, pointer with the same name. The prefix pointer points to previous level node (i.e., the parent node) of this node, and the subsequent pointer points to the successor node (i.e., the child node) of this node. The node name marks the condition attribute name corresponding to the node, and the same name pointer points to the node in the discernibility information tree that has the same node name in other paths.

(3)

Each node in the discernibility information tree has at most $\left|AT\right|$ child nodes, where $\left|AT\right|$ is the number of condition attributes in the ordered decision information system.

3. The Method of the Lower Approximation Reduction Based on Discernibility Information Tree in an IODIS

In this section, combined with the lower approximation identifiable matrix, a discernibility information tree algorithm based on the lower approximation identifiable matrix is given under a dominance relation.

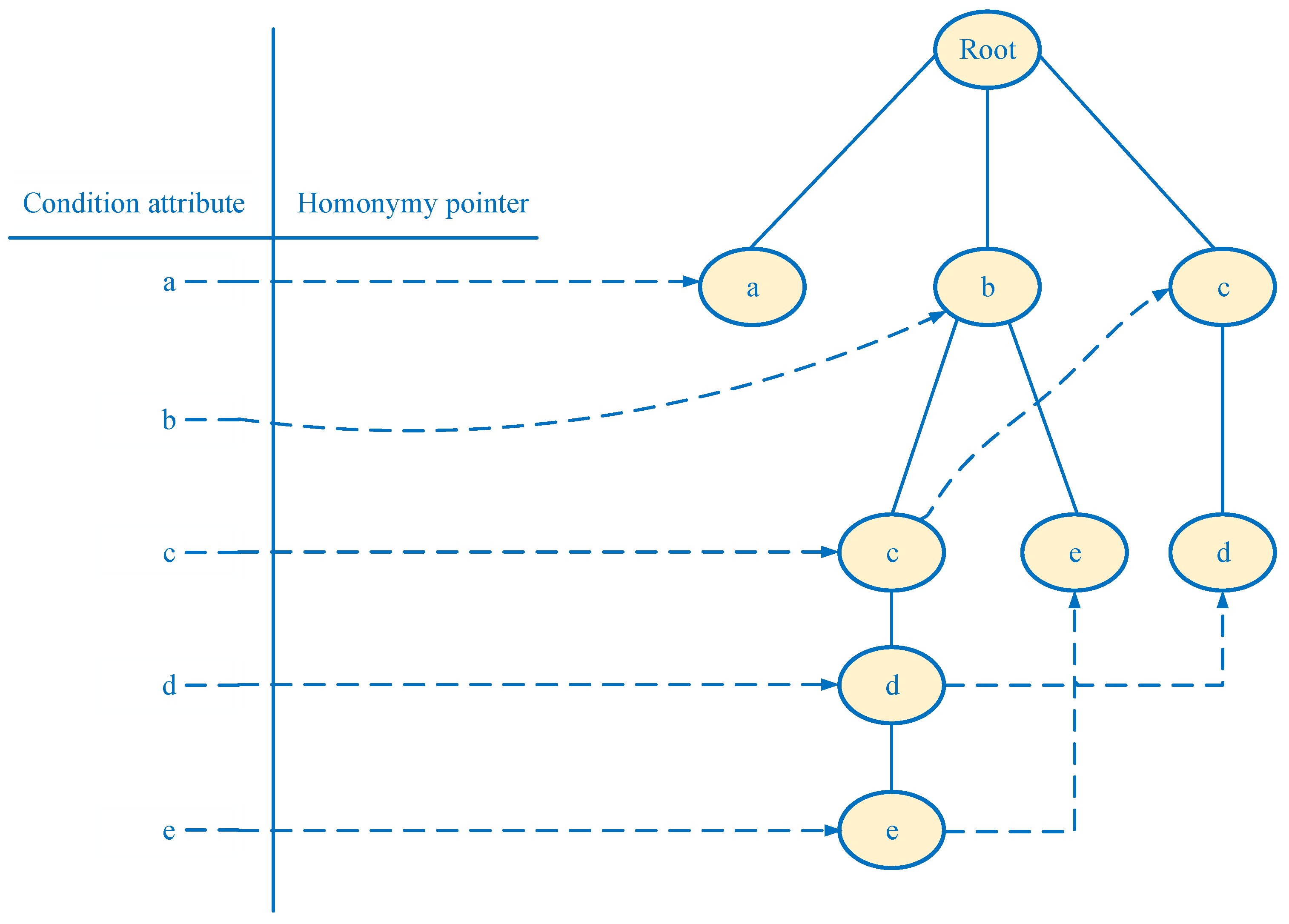
Discernibility information tree is a virtual tree structure. It does not need to process data one by one, but only the nodes in the tree through the tree structure. Each set of identifiable attributes is taken as a branch to form a path to achieve the goal. Then, the same set of identifiable attributes is stored in the same path, which reduces the waste of storage space. In addition, the set of identifiable attributes with the same prefix is mapped to the path corresponding to the smallest set of identifiable attributes. Without extending the path, the space occupied by redundant nodes is reduced.

It can be seen from Algorithm 1 that the strategies of non-extended path and of deleting subtrees are used in constructing the discernibility information tree based on the lower approximation identifiable matrix in the ordered decision information system. Through the construction of the discernibility information tree, the following characteristics are summed up. First, map the same lower approximation identifiable attribute set to the same path. Then, map an identifiable attribute set with the same prefix to the path corresponding to the smallest identifiable attribute set. For example, for identifiable attribute sets $\{a,b,c,d,e\}$ and $\left\{a\right\}$, which have the same prefix a, the smallest identifiable attribute set $\left\{a\right\}$ is chosen to map to the path $<a>$. Finally, identifiable attribute sets in lower approximation identifiable matrices have shared prefixes, such as $\{b,c,d,e\}$ and $\{b,d\}$, with shared prefixes b. It can compress and store the lower approximation identifiable matrix and reduce the space-time complexity of constructing the discernibility information tree based on the lower approximation identifiable matrix.

Algorithm 1: The algorithm of discernibility information tree in an inconsistent ordered decision information system.

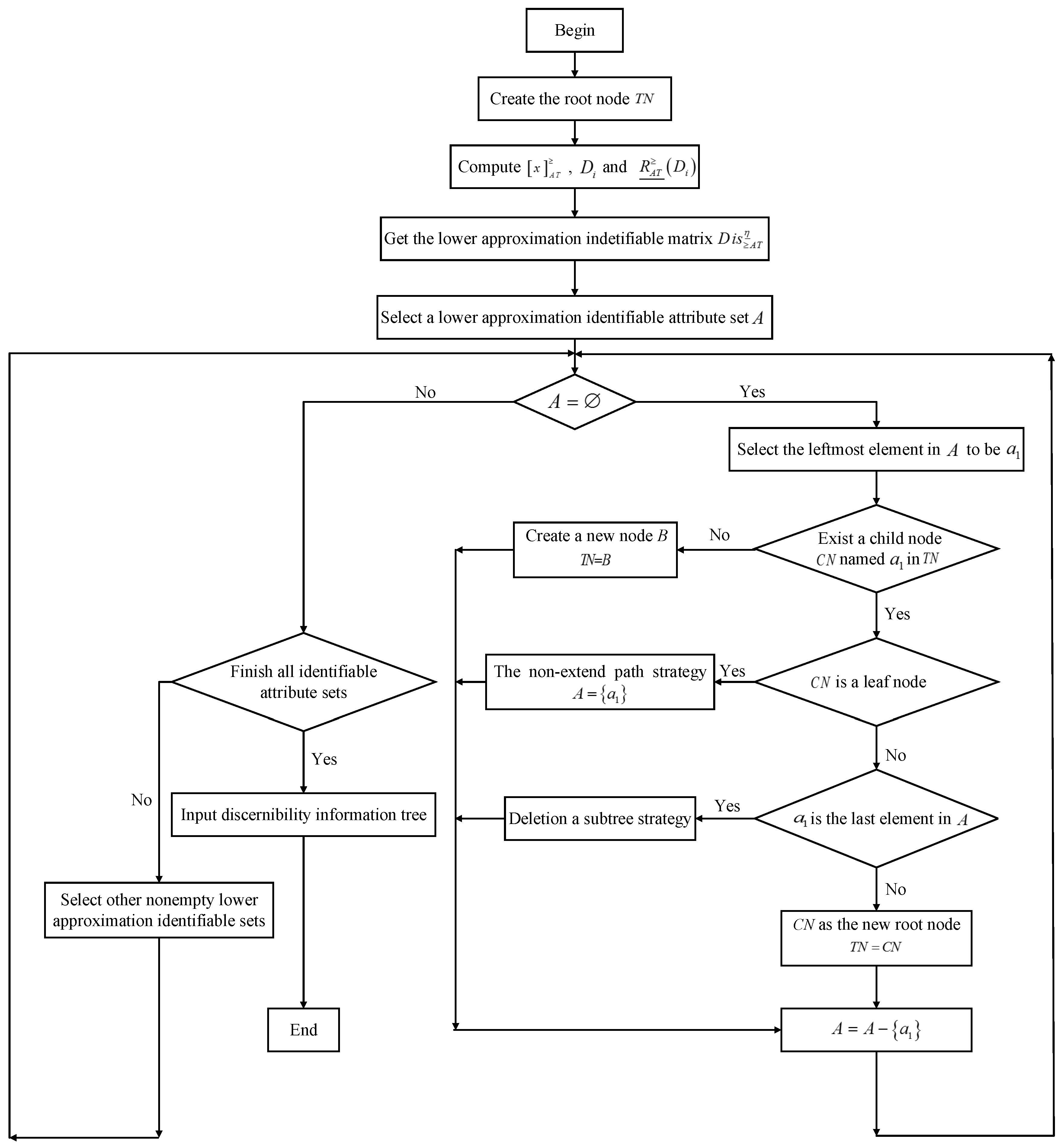
To introduce the algorithm step more clearly and intuitively, the flow chart is used to better explain how the Algorithm 1 is carried out (in Figure 1).

In the following, based on the lower approximation identifiable matrix, the properties and proofs of the discernibility information tree are given.

Theorem 4.

The discernibility information tree based on the lower approximation identifiable matrix includes all the condition attributes that are needed to obtain the lower approximation reduction of the inconsistent ordered decision information system.

Proof. 

Suppose $PS$ be the lower approximation identifiable attribute sets corresponding to all paths in the discernibility information tree. The lower approximation identifiable matrix is expressed by $Di{s}_{⪰AT}^{\underline{\eta }}$. It is easy to know $PS\subseteq Di{s}_{⪰AT}^{\underline{\eta }}$. For any $x,y\in U$, it satisfies that ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x,y)\in Di{s}_{⪰AT}^{\underline{\eta }}$. There are a $(x^{{}^{\prime }},y^{{}^{\prime }})\in U\times U$ and ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x^{{}^{\prime }},y^{{}^{\prime }})\in PS$ such that ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x^{{}^{\prime }},y^{{}^{\prime }})\subseteq {\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x,y)$. It is known from the lower approximation identifiable matrix that ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x^{{}^{\prime }},y^{{}^{\prime }})\wedge {\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x,y)={\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x,y)$. Therefore, a discernibility information tree based on the lower approximation identifiable matrix includes all the condition attributes that are needed to obtain the lower approximation reduction of the inconsistent ordered decision information system. □

Theorem 5.

In the discernibility information tree based on the lower approximation identifiable matrix, the union of identifiable attribute sets which are corresponding to paths with only one node constitutes the core $Cor{e}_{DT}^{⪰}\left(AT\right)$ of the condition attribute set in the decision information system.

Proof. 

According to the discernibility information tree based on lower approximation identifiable matrix, if the attribute name of a node in the information tree is a, there exists a path in the discernibility information tree that only includes the node a, and then there exists a path corresponding to the lower approximation identifiable attribute set $\left\{a\right\}$. In the lower approximation identifiable matrix, if $a\in AT$ and $\left\{a\right\}\in Di{s}_{⪰AT}^{\underline{\eta }}$, then it is said that a is a necessary relative to the condition attribute set $AT$. The collection of all necessary attributes of $AT$ constitutes the relative core of $AT$ relative to decision attribute set $DT$. Thus, the theorem has been proved. □

Theorem 6.

Let A be a condition attribute set represented by all the children of the root node in the discernibility information tree. Then ${\underline{\eta }}_A^{⪰}={\underline{\eta }}_{AT}^{⪰}$ in an IODIS.

Proof. 

Let $PS$ be an identifiable attribute set representing all paths based on the lower approximation identifiable matrix in discernibility information tree. Theorem 4 shows that the discernibility information tree based on the lower approximation identifiable matrix contains all the attributes that are needed to obtain the lower approximation reduction of the inconsistent ordered decision information system. For any ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x,y)\in PS$, there is ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x,y)\cap A\ne \varnothing$. Therefore, according to Theorem 2 of the lower approximation coordination set, we can see that ${\underline{\eta }}_A^{⪰}={\underline{\eta }}_{AT}^{⪰}$. □

For a given inconsistent decision information system $S^{⪰}=(U,AT\cup DT,F,G)$ based on dominance relation, we derive that the number of objects is $\left|U\right|$ and that the number of condition attributes is $\left|AT\right|$. Then the number of a subset of a non-empty condition attribute set can be obtained is ${\left|U\right|}^2$ at most in a lower approximation identifiable matrix. Assuming that the number of non-empty subsets of a condition attribute set in the identifiable matrix is P and $P\ll {\left|U\right|}^2$. As can be seen from the process of constructing discernibility information tree based on lower approximation identifiable matrix, a discernibility information tree can have at most P different paths and there are at most $AT$ nodes in each path. Therefore, there are at most $\left|AT\right|\times P$ nodes in a discernibility information tree. Because there are many paths sharing prefixes in the discernibility information tree based on the lower approximation identifiable matrix, the actual number of nodes in the discernibility information tree is much less than $\left|AT\right|\times P$. Thus, in the worst case, the spatial complexity of the discernibility information tree based on the lower approximation identifiable matrix is $O(|AT||U{|}^2)$.

In addition, the algorithm iterates at most ${\left|U\right|}^2$ times. Meanwhile, during each iteration, it inserts at most $AT$ nodes and deletes $N_i$ nodes $(i=1,2,\dots ,|U{|}^2)$. Thus, the time complexity of the algorithm is ${O\left|AT\right|\left|U\right|}^2+(N_1+N_2+\dots +N_{{\left|U\right|}^2})$. Since the discernibility information tree contains up to ${\left|AT\right|\left|U\right|}^2$ nodes, ${\left|AT\right|\left|U\right|}^2$ is a maximum value of $(N_1+N_2+\dots +N_{{\left|U\right|}^2})$. Therefore, the time complexity of the discernibility information tree based on the lower approximation identifiable matrix is $O(|AT||U{|}^2)$.

After constructing the discernibility information tree based on the lower approximation identifiable matrix, it avoids the classification and sorting of many identifiable attribute sets. Based on an ordered tree, a concise and intuitive path map is established, which not only realizes the compression and storage of data, but also makes the lower approximation reduction for the inconsistent ordered decision information system. In the following, a complete algorithm of lower approximation reduction is given based on the discernibility information tree.

Based on the analysis of the time complexity of Algorithm 1, we can know that there are at most ${\left|AT\right|\left|U\right|}^2$ nodes in the differential information tree. According to the construction process of Algorithm 2, we can know that the maximum number of iterations is $\left|AT\right|$ times. Assuming that $N_i(i=1,2,\dots ,|AT|)$ nodes are deleted during each iteration, the maximum number of nodes deleted after $\left|AT\right|$ times iteration is $(N_1+N_2+\dots +N_{\left|AT\right|})={\left|AT\right|\left|U\right|}^2$. Thus, the complexity of Algorithm 2 is $O(|AT||U{|}^2)$.

Algorithm 2: The algorithm of lower approximation reduction based on the discernibility information tree in an IODIS.

The flow chart in Figure 2 illustrates the implementation process of Algorithm 2 more directly, which is helpful to understand the operation of the program.

At present, there are many methods for attribute reduction of decision tables, such as the attribute importance measure reduction algorithm. Based on the discernibility matrix of the decision table, the most important attribute is selected to be added to the core attribute set according to the importance measure of the attribute, and then the relative attribute reduction of the decision table is obtained. However, in the case of large data sets, the importance measure of computing all attributes greatly increases the time complexity of the algorithm. Similarly, relative reduction algorithm based on conditional entropy also has some shortcomings. When computing conditional entropy or information gain, floating-point calculation is needed many times, which greatly increases the time complexity of the algorithm and reduces the efficiency of the algorithm. Currently, the most commonly used algorithm is the reduction algorithm based on discernibility matrix. The basic method of this algorithm is to obtain identifiable functions and simplify it to become a disjunctive normal form. The algorithm can guarantee the completeness of the algorithm. However, in the process of simplification, if there are many repeated objects and too many comparisons between objects, the complexity of time and space will be increased. Moreover, the heuristic algorithm based on the discernibility matrix is mainly based on the discernibility matrix to find the core, and then, according to the heuristic rule, add the attributes until the condition is satisfied. Although the time performance of this algorithm is improved greatly, the complete reduction cannot be guaranteed. In this paper, by establishing a virtual tree structure, duplicate identifiable attribute sets are mapped to the same path to reduce the space occupation of repetitive attributes. At the same time, the redundant parent set elements are deleted by sharing a prefix, and the discernibility matrix is compressed and stored. This method not only saves space and reduces the time complexity, but also realizes the completeness of the algorithm.

Moreover, we will prove the completeness of Algorithm 2. In an inconsistent ordered decision information system $S^{⪰}=(U,AT\cup DT,F,G)$, the following two conditions are required to prove the completeness of the Algorithm 2 ($A\subseteq AT$).

• ${\underline{\eta }}_A^{⪰}={\underline{\eta }}_{AT}^{⪰}$;
• $\forall a\in A$, then ${\underline{\eta }}_{A-\left\{a\right\}}^{⪰}\ne {\underline{\eta }}_{AT}^{⪰}$.

According to the equivalent condition of the lower approximation reduction, the above conditions can be transformed into the following forms by Theorem 2.

• $\forall (x_i,x_j)\in D_{⪰AT}^{\underline{\eta }}$, then $A\cap {\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)\ne \varnothing$;
• $\forall a\in A$, $\exists (x_i,x_j)\in D_{⪰AT}^{\underline{\eta }}$ such that $(A-\{a\})\cap {\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)=\varnothing$.

The above two expressions will prove the completeness of the reduction by the lower approximation identifiable set. Because the discernibility information tree based on the lower approximation identifiable matrix contains all the condition attributes needed for lower approximation reduction, the above two formulas are transformed into the following.

• $\forall M\in DS$, $M\cap A\ne \varnothing$;
• $\forall a\in A$, $\exists M\in DS$ such that $T\cap (A-\{a\})=\varnothing$.

where $DS$ represents a set of all paths in a discernibility information tree based on the lower approximation identifiable matrix.

Therefore, proving that the completeness of Algorithm 2 is equivalent to proving that the two formulas above are established. According to Algorithm 2, $M\cap A\ne \varnothing$ for any $M\in DS$. Based on Theorem 5, in the discernibility information tree, the union of identifiable attribute sets corresponding to paths with only one node constitutes the core $Cor{e}_{DT}^{⪰}\left(AT\right)$ of the condition attribute set of the decision information system. The core $Cor{e}_D^{⪰}\left(AT\right)$ of the decision table obtained in the third step of the Algorithm 2 is taken as part of the lower approximation reduction and all paths containing elements of core are deleted from the discernibility information tree. Suppose $S=A-Cor{e}_{DT}^{⪰}\left(AT\right)$. If b is the rightmost element of S, the child node on the rightmost side of the root node must be b in the current discernibility information tree, and the subtree that takes this node b as its root does not contain any node corresponding to any attribute in $S-\left\{b\right\}$. Therefore, for $b\in A$, $\exists M\in DS$ such that $M\cap (A-\{b\})=\varnothing$. Similarly, other elements in S also satisfy this condition. Thus, the lower approximation reduction combined the discernibility information tree is a complete reduction.

4. An Illustrative Example

In the following, we will construct the discernibility information tree under the dominance relation according to the steps of Algorithm 1 and implement the lower approximation reduction based on this tree in the inconsistent ordered decision information system. An inconsistent ordered decision table is given in

Table 1. An inconsistent ordered decision table.

U	a	b	c	d	e	$\mathit{Decision}$
$x_1$	2	1	3	2	3	2
$x_2$	4	0	2	1	2	3
$x_3$	2	0	2	1	2	4
$x_4$	4	0	1	0	2	1
$x_5$	3	3	5	4	5	4
$x_6$	3	3	5	4	5	4
$x_7$	2	2	3	2	4	2
$x_8$	4	3	4	3	5	3
$x_9$	4	4	4	3	6	4
$x_{10}$	1	4	5	4	6	1

, in which the object set is $U=\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}\}$, a condition attribute set $AT=\{a,b,c,d,e\}$ and a decision attribute set is $D=\{decision\}$.

First, after a simple calculation, we can get the dominance classes based on the dominance relation $AT$.

${\left[x_1\right]}_{AT}^{⪰}=\{x_1,x_5,x_6,x_7,x_8\}$,	${\left[x_2\right]}_{AT}^{⪰}=\{x_2,x_8,x_9\}$,
${\left[x_3\right]}_{AT}^{⪰}=\{x_1,x_2,x_3,x_5,x_6,x_7,x_8,x_9\}$,	${\left[x_4\right]}_{AT}^{⪰}=\{x_2,x_4,x_8,x_9\}$,
${\left[x_5\right]}_{AT}^{⪰}=\{x_5,x_6\}$,	${\left[x_6\right]}_{AT}^{⪰}=\{x_5,x_6\}$,
${\left[x_7\right]}_{AT}^{⪰}=\{x_5,x_6,x_7,x_8,x_9\}$,	${\left[x_8\right]}_{AT}^{⪰}=\{x_8,x_9\}$,
${\left[x_9\right]}_{AT}^{⪰}=\left\{x_9\right\}$,	${\left[x_{10}\right]}_{AT}^{⪰}=\left\{x_{10}\right\}$.

Based on decision attribute set D, decision classes are

• $D_1={\left[x_3\right]}_D^{⪰}={\left[x_5\right]}_D^{⪰}={\left[x_6\right]}_D^{⪰}={\left[x_9\right]}_D^{⪰}=\{x_3,x_5,x_6,x_9\}$,
• $D_2={\left[x_2\right]}_D^{⪰}={\left[x_8\right]}_D^{⪰}=\{x_2,x_3,x_5,x_6,x_8,x_9\}$,
• $D_3={\left[x_1\right]}_D^{⪰}={\left[x_7\right]}_D^{⪰}=\{x_1,x_2,x_3,x_5,x_6,x_7,x_8,x_9\}$,
• $D_4={\left[x_4\right]}_D^{⪰}={\left[x_7\right]}_D^{⪰}={\left[x_{10}\right]}_D^{⪰}=\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}\}$.

According to the above dominance classes, we can obtain $R_{AT}⊈R_D$. Thus, it is an inconsistent ordered decision information system. Next, we get lower approximations with respect to $D_i(i=1,2,\dots ,r)$

• $\underline{R_{AT}^{⪰}}\left(D_1\right)=\{x_5,x_6,x_9\}$
• $\underline{R_{AT}^{⪰}}\left(D_2\right)=\{x_2,x_5,x_6,x_8,x_9\}$
• $\underline{R_{AT}^{⪰}}\left(D_3\right)=\{x_1,x_2,x_3,x_5,x_6,x_7,x_8,x_9\}$
• $\underline{R_{AT}^{⪰}}\left(D_4\right)=\{x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9,x_{10}\}$

Then, based on the lower approximation identifiable attribute set ${\mathcal{D}}_{⪰AT}^{\underline{\eta }}(x_i,x_j)$, the lower approximation identifiable matrix is shown in

Table 2. A lower approximation identifiable matrix in an IODIS.

U	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$	${\mathit{x}}_7$	${\mathit{x}}_8$	${\mathit{x}}_9$	${\mathit{x}}_{10}$
$x_1$	⌀	⌀	⌀	$\{b,c,d,e\}$	⌀	⌀	⌀	⌀	⌀	$\left\{a\right\}$
$x_2$	$\left\{a\right\}$	⌀	$\left\{a\right\}$	$\{c,d\}$	⌀	⌀	$\left\{a\right\}$	⌀	⌀	$\left\{a\right\}$
$x_3$	⌀	⌀	⌀	$\{c,d\}$	⌀	⌀	⌀	⌀	⌀	$\left\{a\right\}$
$x_4$	⌀	⌀	⌀	⌀	⌀	⌀	⌀	⌀	⌀	⌀
$x_5$	$\{a,b,c,d,e\}$	$\{b,c,d,e\}$	$\{a,b,c,d,e\}$	$\{b,c,d,e\}$	⌀	⌀	$\{a,b,c,d,e\}$	$\{c,d\}$	⌀	$\left\{a\right\}$
$x_6$	$\{a,b,c,d,e\}$	$\{b,c,d,e\}$	$\{a,b,c,d,e\}$	$\{b,c,d,e\}$	⌀	⌀	$\{a,b,c,d,e\}$	$\{c,d\}$	⌀	$\left\{a\right\}$
$x_7$	⌀	⌀	⌀	$\{b,c,d,e\}$	⌀	⌀	⌀	⌀	⌀	$\left\{a\right\}$
$x_8$	$\{a,b,c,d,e\}$	⌀	$\{b,c,d,e\}$	$\{b,c,d,e\}$	⌀	⌀	$\{a,b,c,d,e\}$	⌀	⌀	$\left\{a\right\}$
$x_9$	$\{a,b,c,d,e\}$	$\{b,c,d,e\}$	$\{a,b,c,d,e\}$	$\{b,c,d,e\}$	⌀	⌀	$\{a,b,c,d,e\}$	$\{b,e\}$	⌀	$\left\{a\right\}$
$x_{10}$	⌀	⌀	⌀	⌀	⌀	⌀	⌀	⌀	⌀	⌀

.

Furthermore, the root node of the discernibility information tree based on the lower approximate identifiable matrix is created. According to each subset of condition attribute set in the lower approximation identifiable matrix, the attributes in the subset are ordered from left to right in the ordered decision information system.

Next, a lower approximation identifiable attribute set of the lower approximation identifiable matrix is selected, and the corresponding path is created. Here we select the first subset $\{a,b,c,d,e\}$ as the first path $<a,b,c,d,e>$ and insert the discernibility information tree. Since the second identifiable attribute set is also $\{a,b,c,d,e\}$, it is also mapped to the first path. In the same way, the same identifiable attribute set is mapped to the same path. For another identifiable attribute set $\left\{a\right\}$ in the lower approximation identifiable matrix, its corresponding path $<a>$ is established. Since it is included in the first path, the strategy of deleting subtree is adopted. Delete all nodes $b,c,d$ after a, but keep node a. That is, the original path $<a,b,c,d,e>$ is modified to the path $<a>$. Next, another condition attribute set $\{b,c,d,e\}$ maps the new path $<b,c,d,e>$ and creates a new node b. As for the lower approximation identifiable attribute set $\{b,e\}$, the corresponding path $<b,e>$ is constructed, which has a shared prefix b with the previous path $<b,c,d,e>$. Afterwards, we insert the path $<c,d>$ corresponding to the condition attribute set $\{c,d\}$ into the discernibility information tree. Similarly, we repeat the above procedure until inserting the last path into the discernibility information tree. Finally, Figure 3 shows a lower approximation discernibility information tree based on Algorithm 1 and Table 2.

In Algorithm 2, we will give a lower approximation reduction under the discernibility information tree. Before that, we first give all the results of reduction through the original method. According to Definition 5 and Theorem 2, the minimum disjunctive normal form is obtained by using conjunctive and disjunctive methods. Then, all the lower approximation reductions are obtained.

$$\begin{array}{l}\hspace{1em}(a\vee b\vee c\vee d\vee e)\wedge (b\vee c\vee d\vee e)\wedge (c\vee d)\wedge (b\vee e)\wedge a\\ =(c\vee d)\wedge (b\vee e)\wedge a\\ =(a\wedge b\vee c)\vee (a\wedge b\vee d)\vee (a\wedge c\vee e)\vee (a\wedge d\vee e)\end{array}$$

Therefore, lower approximation reductions are $\{a,b,c\},\{a,b,d\},\{a,c,e\},\{a,d,e\}$. Next, combined with Algorithm 2, a lower approximation reduction method based on the discernibility information tree is presented. The specific steps are as follows.

(1)

According to the first step of Algorithm 2, we first establish an empty set A.

(2)

Based on the lower approximation identifiable matrix, a path with only one node $\left\{a\right\}$ is selected in the discernibility information tree. Then, delete all the paths that contains only one node $\left\{a\right\}$. That means removing the path $<a>$.

(3)

$A=A\cup \left\{a\right\}$.

(4)

Choose the right child node c of the root node in the discernibility information tree and $A=A\cup \left\{c\right\}$.

(5)

Delete paths $<b,c,d,e>$ and $<c,d>$ that contain the node c.

(6)

At this point, there is only one path $<b,e>$ on the discernibility information tree. Afterwards, select the node b and delete the path $<b,e>$. Finally, $A=A\cup \left\{b\right\}$.

(7)

At this time, the root node of the discernibility information tree has no child nodes. Thus, the algorithm is finished. A lower approximation reduction based on discernibility information tree is $A=\{a,b,c\}$.

According to the above method, the lower approximation reduction is obtained. By comparing it to the original results, the correctness of the method is verified, and its effectiveness is demonstrated. The method of the discernibility information tree reduces the space occupation of redundant attributes and reduces the computational load.

5. Conclusions

In this paper, a data structure of ordered decision information system based on discernibility information tree is proposed, which can compress and store lower approximation identifiable attribute sets. Compared with the minimal disjunctive normal form of the lower approximation identifiable formulas, the spatial complexity of the lower approximation reduction of inconsistent ordered information systems is greatly reduced by using this discernibility information tree. However, based on the construction of the discernibility information tree, the order of attributes inserted in the discernibility information tree is the original order of attributes in the decision table, without considering the influence of attribute importance measure on the construction of the discernibility information tree. Therefore, our next step is to improve the construction of the discernibility information tree by combining the importance measure of attributes and the core.