Geometric Objects: A Quality Index to Electromagnetic Energy Transfer Performance in Sustainable Smart Buildings
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution
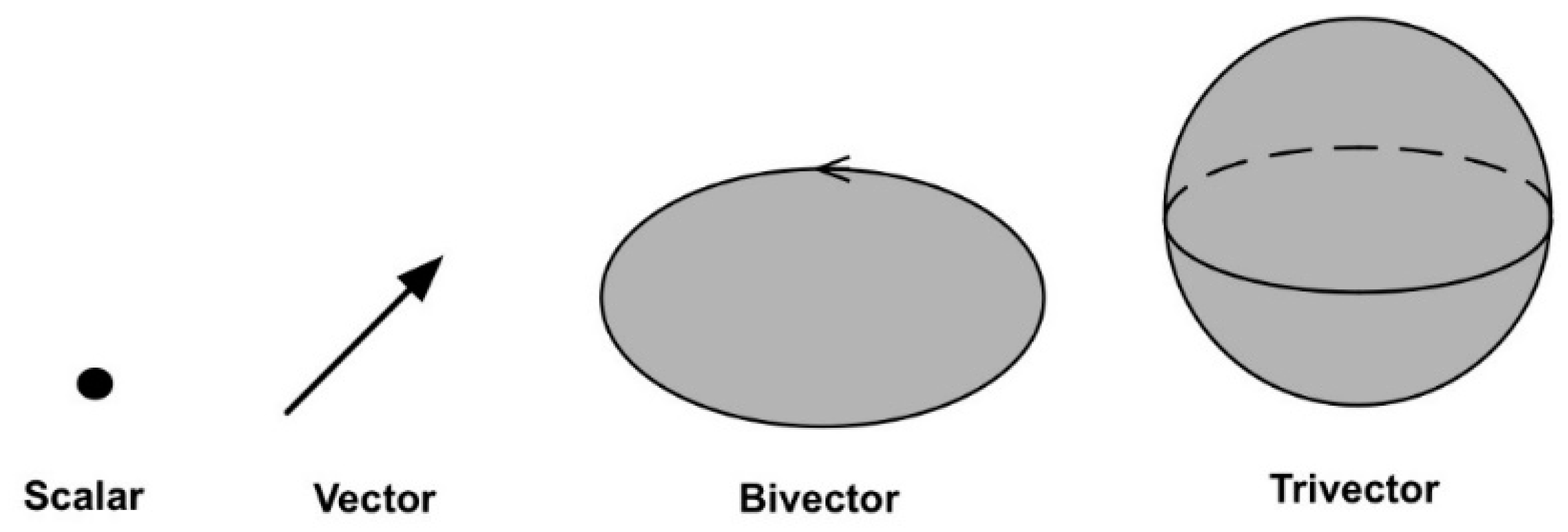
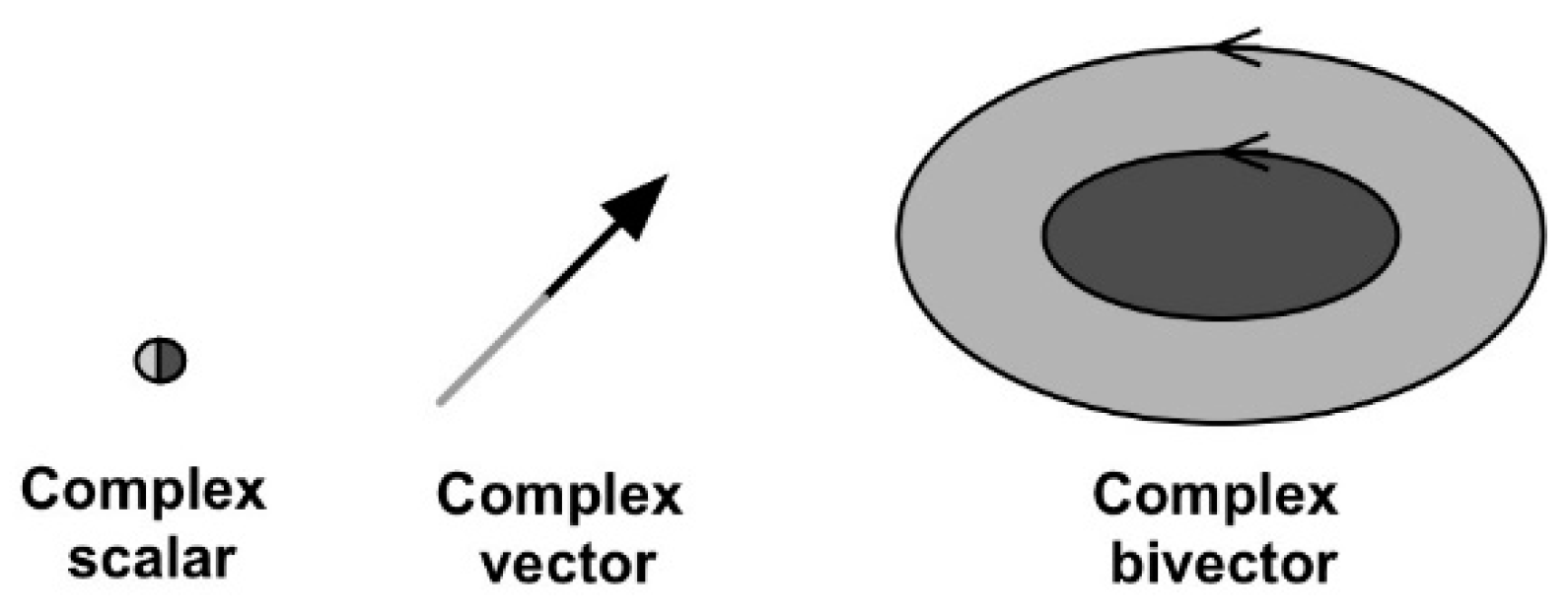
2. Geometric Objects
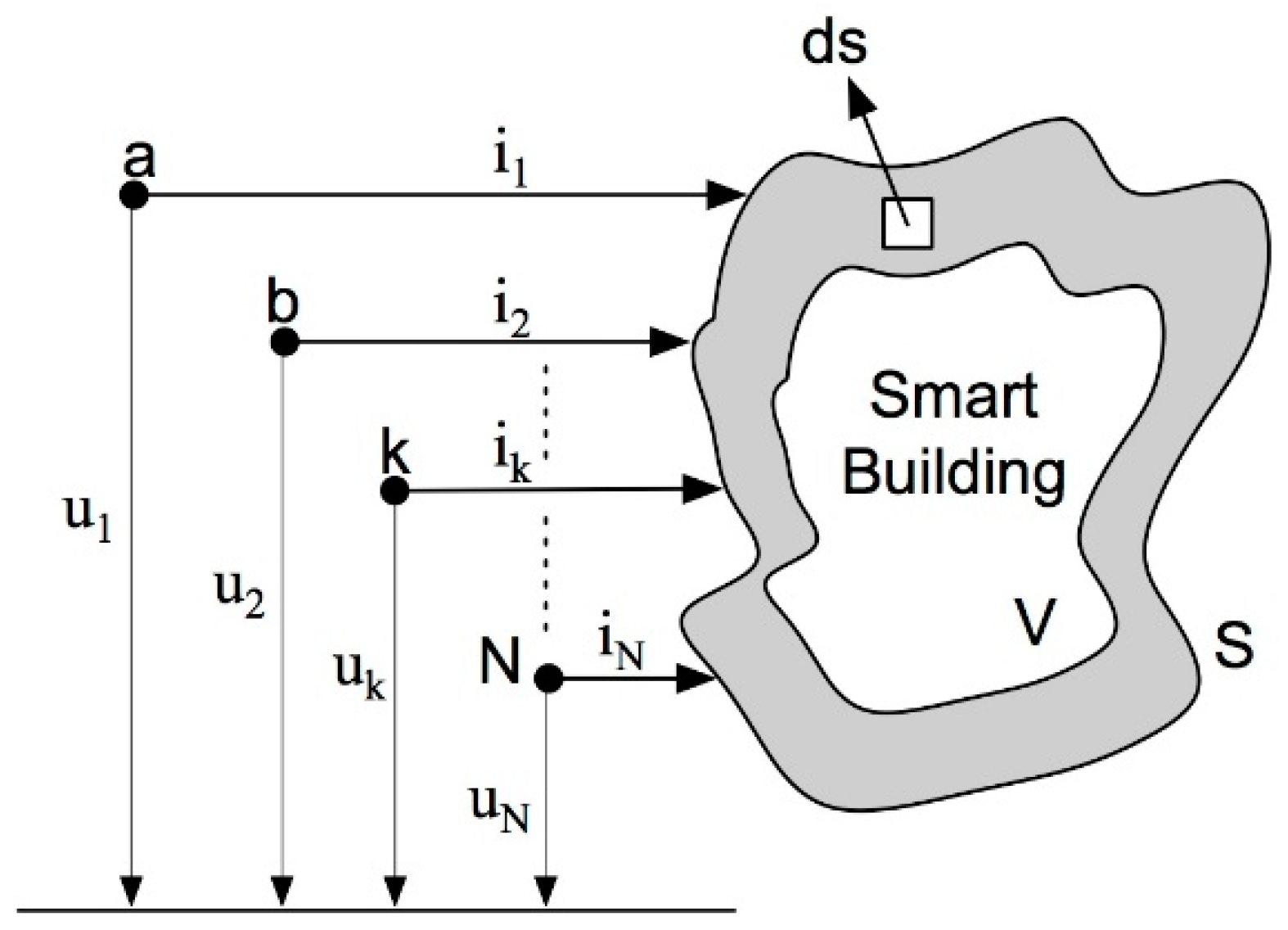
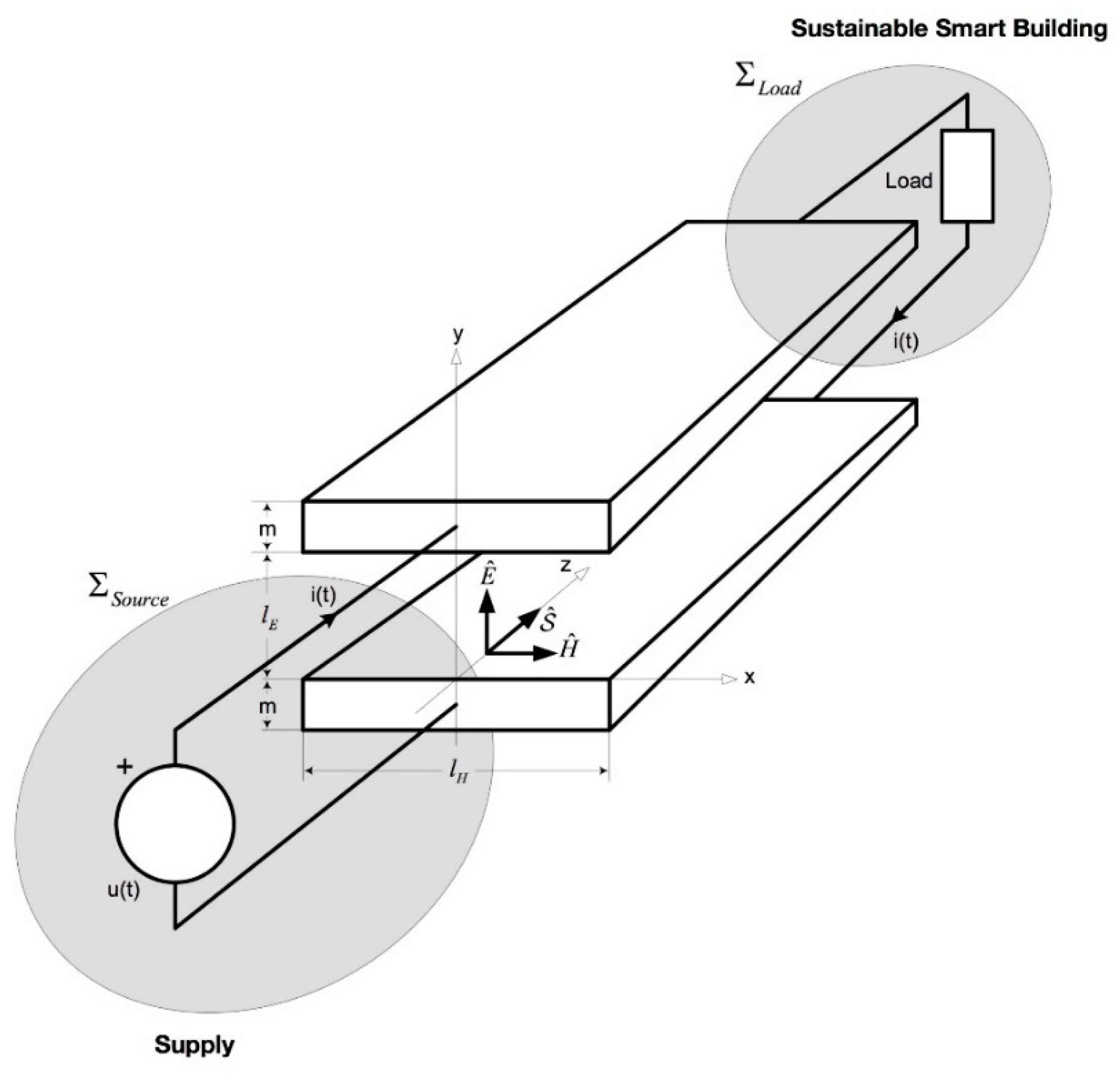
3. The System Model
- -
- Electric power (energy) is dissipated.
- -
- Electric power (energy) in the system derives from an electric field and magnetic field interactions.
4. Generalized Poynting Multivector
5. Formulation of Electromagnetic Energy Quality Index
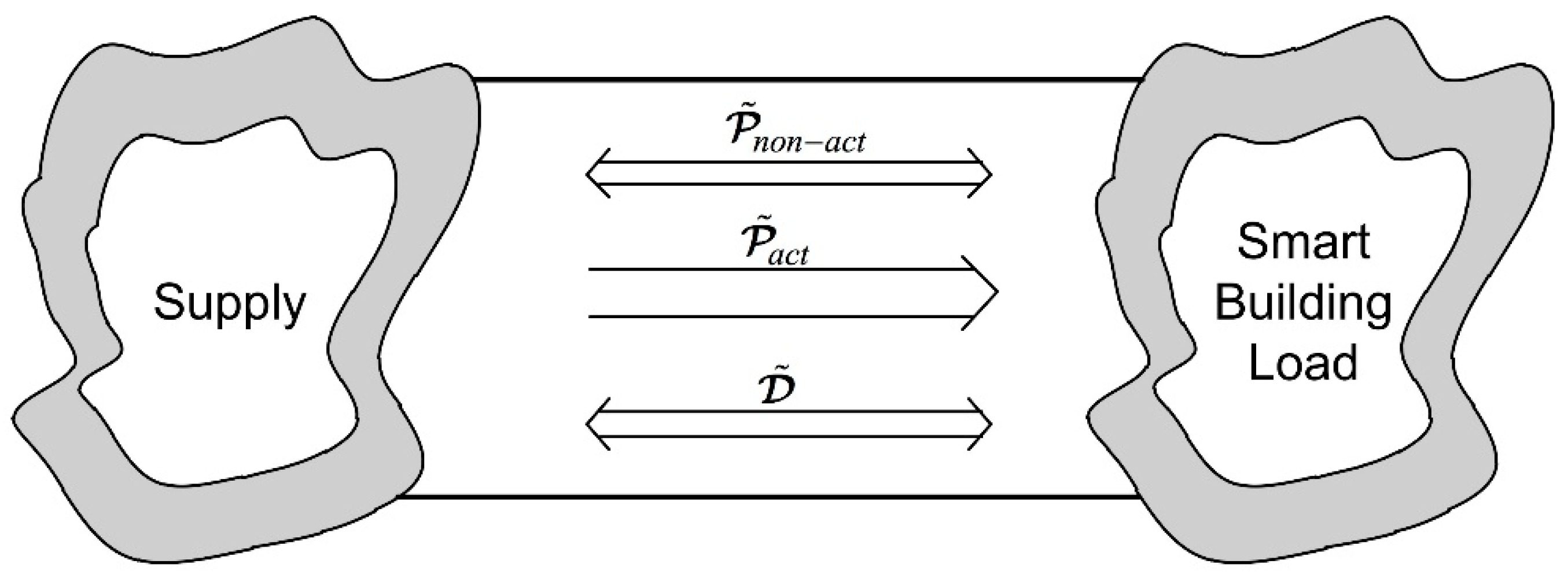
5.1. Energy Flow on Electrical Systems
5.2. Electromagnetic Quality Index (EQI)
5.3. Illustrative Comparison between Different Non-Active Electromagnetic Geometric Objects
- Sinusoidal case:and
- Multi-sinusoidal linear case:
- Multi-sinusoidal non-linear case:
6. Numerical Example
6.1. Linear Load Supplied by A Sinusoidal Voltage Source
6.2. Linear Load Supplied by A Non-Sinusoidal Sinusoidal Voltage Source
6.3. Non-Linear Load Supplied by A Non-Sinusoidal Sinusoidal Voltage Source
7. Conclusions
Author Contributions
Conflicts of Interest
Glossary of Symbols
| real numbers | |
| complex vector space | |
| Geometric Algebra in n-dimensional real space | |
| Complex Geometric Algebra | |
| time generalized geometric euclidean space | |
| frequency generalized geometric euclidean space | |
| Euclidean canonical basis | |
| canonical basis of | |
| basis vector of | |
| basis bivectors of | |
| trivector or pseudoscalar of | |
| λ, μ | scalars or 0-grade geometric object |
| a, b | vectors or 1-grade geometric object |
| B | bivector or 2-grade geometric object |
| J | pseudoscalar or n-grade geometric object |
| generic multivector | |
| generalized Poynting multivector (GPM) | |
| Poynting multivector (PM) | |
| Complementary Poynting multivector (CPM) | |
| electric field geometric phasor | |
| magnetic field geometric phasor | |
| generalized geometric product | |
| inner product | |
| outer product | |
| j | imaginary unit |
| * | conjugated operation |
| † | reverse operation |
| ~ | multivector characterization |
| p-th harmonic voltage rms value | |
| q-th harmonic current rms value | |
| P | active power or real part of 0-grade power multivector |
| Q | reactive power or imaginary part of 0-grade power multivector |
| D | distortion power or 2-grade power |
| power multivector | |
| apparent power multivector | |
| ωp | p-th harmonic frequency |
| αp | phase angle of p-th voltage geometric phasor |
| βq | phase angle of q-th current geometric phasor |
| φq | q-th impedance phase angle |
| electromagnetic quality index multivector (EQI) | |
| PF | power factor |
References
- Ibrahim, M.; El-Zaart, A.; Adams, C. Smart Sustainable Cities roadmap: Readiness for transformation towards urban sustainability. Sustain. Cities Soc. 2018, 37, 530–540. [Google Scholar] [CrossRef]
- Höjer, M.; Wangel, J. Smart sustainable cities: Definition and challenges. In ICT Innovations for Sustainability; Hilty, L., Aebischer, B., Eds.; Springer: Cham, Switzerland, 2015; pp. 333–349. [Google Scholar]
- Pervez, H.S.; Nursyarizal, B.M.N.; Perumal, N.; Irraivan, E.; Taib, I. A review on optimized control systems for building energy and comfort management of smart sustainable buildings. Renew. Sustain. Energy Rev. 2014, 34, 409–429. [Google Scholar] [CrossRef]
- Nardi, I.; Lucchi, E.; Rubeis, T.; Ambrosini, D. Quantification of heat energy losses through the building envelope: A state-of-the-art analysis with critical and comprehensive review on infrared thermography. Build. Environ. 2018, 146, 190–205. [Google Scholar] [CrossRef]
- Karmellos, M.; Kiprakis, A.; Mavrotas, G. A multi-objective approach for optimal prioritization of energy efficiency measures in buildings: Model, software and case studies. Appl. Energy. 2015, 139, 131–150. [Google Scholar] [CrossRef]
- Poynting, J.H. On the transfer of energy in the electromagnetic field. Philos. Trans. R. Soc. 1884, 175, 343–361. [Google Scholar] [CrossRef]
- Steinmetz, C.P. Theory and Calculation of Alternating Current Phenomena; McGraw Publishing Company: New York, NY, USA, 1900. [Google Scholar]
- Emanuel, A.E. Powers in nonsinusoidal situations a review of definitions and physical meaning. IEEE Trans. Power Deliv. 1990, 5, 1377–1389. [Google Scholar] [CrossRef]
- Emanuel, A.E. Poynting vector and the physical meaning of nonactive powers. IEEE Trans. Instrum. Meas. 2005, 54, 1457–1462. [Google Scholar] [CrossRef]
- Lundin, U.; Bolund, B.; Leijon, M. Poynting vector analysis of synchronous generators using field simulations. IEEE Trans. Magn. 2007, 43, 3601–3606. [Google Scholar] [CrossRef]
- Faria, J.A.B. The role of Poynting’s vector in polyphase power calculations. Eur. Trans. Electr. Power 2009, 19, 683–688. [Google Scholar] [CrossRef]
- De León, F.; Cohen, J. AC power theory from Poynting Theorem: Accurate identification of instantaneous power components in nonlinear-switched circuits. IEEE Trans. Power Deliv. 2010, 25, 2104–2112. [Google Scholar] [CrossRef]
- Cheng, P.; Yang, F.; Luo, H.; Guo, H.; Ran, W.; Yang, Y.; Ullah, I. A method to calculate the reactive power of iced transmission line based on Poynting vector and FDFD. Int. J. Appl. Electromagn. Mech. 2016, 50, 417–433. [Google Scholar] [CrossRef]
- Emanuel, A.E. About the Rejection of Poynting Vector in Power Systems Analysis. Electr. Power Qual. Util. J. 2007, 13, 43–49. [Google Scholar]
- Emanuel, A.E. Power Definitions and the Physical Mechanism of Power Flow; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Todeschini, G.; Emanuel, A.E.; Ferrero, A.; Morando, A.P. A Poynting vector approach to the study of the Steinmetz compensator. IEEE Trans. Power Deliv. 2007, 22, 1830–1833. [Google Scholar] [CrossRef]
- Ferrero, A.; Leva, S.; Morando, A.P. An approach to the non-active power concept in terms of the poynting-park vector. Eur. Trans. Electr. Power 2001, 11, 291–299. [Google Scholar] [CrossRef]
- Czarnecki, L.S. Considerations on the Concept of Poynting Vector Contribution to Power Theory Development. In Proceedings of the 6th International Workshop on Power Definitions and Measurements Under Nonsinusoidal Conditions, Milano, Italy, 13–15 October 2003. [Google Scholar]
- Czarnecki, L.S. Could Power Properties of Three-Phase Systems Be Described in Terms of the Poynting Vector? IEEE Trans. Power Deliv. 2006, 21, 339–344. [Google Scholar] [CrossRef]
- Balci, M.; Hocaoglu, M.; Power, S.A. Transition from Poynting vector to instantaneous power. In Proceedings of the 12th International Conference on Harmonics and Quality of Power, Cascais, Portugal, 1–5 October 2006. [Google Scholar]
- Stahlhut, J.W.; Browne, T.J.; Heydt, G.T. The Assessment of the Measurement of the Poynting Vector for Power System Instrumentation. In Proceedings of the 39th North American Power Symposium, Las Cruces, NM, USA, 30 September–2 October 2007; pp. 237–241. [Google Scholar]
- Castilla, M.; Bravo, J.C.; Ordonez, M.; Montano, J.C. An approach to the multivectorial apparent power in terms of a generalized poynting multivector. Prog. Electromagn. Res. B 2009, 15, 401–422. [Google Scholar] [CrossRef]
- Clifford, W.K. Applications of Grassmann’s Extensive Algebra. Am. J. Math. 1878, 1, 350. [Google Scholar] [CrossRef]
- Hestenes, D. A unified language for mathematics and physics. their Appl. Math. Phys. 1986. [Google Scholar] [CrossRef]
- Chappell, J.M.; Drake, S.P.; Seidel, C.L.; Gunn, L.J.; Iqbal, A.; Allison, A.; Abbott, D. Geometric algebra for electrical and electronic engineers. Proc. IEEE 2014. [Google Scholar] [CrossRef]
- Doran, C.; Lasenby, A. Geometric Algebra for Physicists; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Castilla, M.; Bravo, J.C.; Ordóñez, M.; Montaño, J.C. Clifford theory: A geometrical interpretation of multivectorial apparent power. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 3358–3367. [Google Scholar] [CrossRef]
- Castilla, M.; Bravo, J.C.; Ordonez, M.; Montaño, J.C.; Lopez, A.; Borras, D.; Gutierrez, J. The geometric algebra as a power theory analysis tool. In Proceedings of the 2008 International School on Nonsinusoidal Currents and Compensation, Lagow, Poland, 10–13 June 2008. [Google Scholar]
- Castilla, M.; Bravo, J.C.; Ordóñez, M. Geometric algebra: A multivectorial proof of Tellegen’s theorem in multiterminal networks. IET Circuits, Devices Syst. 2008, 2, 383–390. [Google Scholar] [CrossRef]
- Bravo, J.C.; Castilla, M.V. Energy Conservation Law in Industrial Architecture: An Approach through Geometric Algebra. Symmetry 2016, 8, 92. [Google Scholar] [CrossRef]
- Castro-Núñez, M.; Londoño-Monsalve, D.; Castro-Puche, R.M. the conservative power quantity based on the flow of energy. J. Eng. 2016, 2016, 269–276. [Google Scholar] [CrossRef]
- Petroianu, A.I. A geometric algebra reformulation and interpretation of Steinmetz’s symbolic method and his power expression in alternating current electrical circuits. Electr. Eng. 2015, 97, 175–180. [Google Scholar] [CrossRef]
- Menti, A.; Zacharias, T.; Milias-Argitis, J. Geometric Algebra: A Powerful Tool for Representing Power Under Nonsinusoidal Conditions. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 601–609. [Google Scholar] [CrossRef]
- Castro-Nunez, M.; Castro-Puche, R. Advantages of Geometric Algebra Over Complex Numbers in the Analysis of Networks With Nonsinusoidal Sources and Linear Loads. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 2056–2064. [Google Scholar] [CrossRef]
- Herrera, R.S.S.; Salmeron, P.; Vazquez, J.R.R.; Litran, S.P.P.; Perez, A. Generalized instantaneous reactive power theory in poly-phase power systems. In Proceedings of the 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bravo, J.C.; Castilla, M.V. Geometric Objects: A Quality Index to Electromagnetic Energy Transfer Performance in Sustainable Smart Buildings. Symmetry 2018, 10, 676. https://doi.org/10.3390/sym10120676
Bravo JC, Castilla MV. Geometric Objects: A Quality Index to Electromagnetic Energy Transfer Performance in Sustainable Smart Buildings. Symmetry. 2018; 10(12):676. https://doi.org/10.3390/sym10120676
Chicago/Turabian StyleBravo, Juan C., and Manuel V. Castilla. 2018. "Geometric Objects: A Quality Index to Electromagnetic Energy Transfer Performance in Sustainable Smart Buildings" Symmetry 10, no. 12: 676. https://doi.org/10.3390/sym10120676
APA StyleBravo, J. C., & Castilla, M. V. (2018). Geometric Objects: A Quality Index to Electromagnetic Energy Transfer Performance in Sustainable Smart Buildings. Symmetry, 10(12), 676. https://doi.org/10.3390/sym10120676




